2006年江西高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_江西

2006 年江西高考文科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分）  1  1．（5分）已知集合P{x|x(x1)…0}，Qx 0，则P  Q等于( )  x1  A． B．{x|x…1} C．{x|x1} D．{x|x…1或x0}  2．（5分）函数y4sin(2x )1的最小正周期为( ) 3  A． B． C．2 D．4 2 3．（5分）在各项均不为零的等差数列{a }中，若a a2 a 0(n…2)，则S 4n( n n1 n n1 2n1 ) A．2 B．0 C．1 D．2 4．（5分）下列四个条件中， p是q的必要不充分条件的是( ) A． p:ab，q:a2 b2 B． p:ab，q:2a 2b C． p:ax2 by2 c为双曲线，q:ab0 c b D． p:ax2 bxc0，q:  a0 x2 x 5．（5分）若 f(x)是定义在R上的可导函数，且满足(x1)f(x)…0，则必有( ) A． f(0) f （2）2f （1） B． f(0) f （2）2f （1） C． f(0) f （2）„ 2f （1） D． f(0) f （2）…2f （1） 1 6．（5分）若不等式x2 ax1…0对一切x(0, )成立，则a的最小值为( ) 2 5 A．0 B．2 C． D．3 2 2 7．（5分）在( x  )n的二项展开式中，若常数项为60，则n等于( ) x A．3 B．6 C．9 D．12 8．（5分）袋中有40个小球，其中红色球16个、蓝色球12个，白色球8个，黄色球4个， 第1页 | 共20页从中随机抽取10个球作成一个样本，则这个样本恰好是按分层抽样方法得到的概率为( ) C1C2C3C4 A． 4 8 12 16 C10 40 C2C1C3C4 B． 4 8 12 16 C10 40 C2C3C1C4 C． 4 8 12 16 C10 40 C1C3C4C2 D． 4 8 12 16 C10 40 9．（5分）如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰， 以下4个命题中，假命题是( ) A．等腰四棱锥的腰与底面所成的角都相等 B．等腰四棱锥的侧面与底面所成的二面角都相等或互补 C．等腰四棱锥的底面四边形必存在外接圆 D．等腰四棱锥的各顶点必在同一球面上    10．（5分）已知等差数列{a }的前n项和为S ，若OBaOAa OC，且A、B、C三 n n 1 200 点共线（该直线不过原点O)，则S ( ) 200 A．100 B．101 C．200 D．201 x2 y2 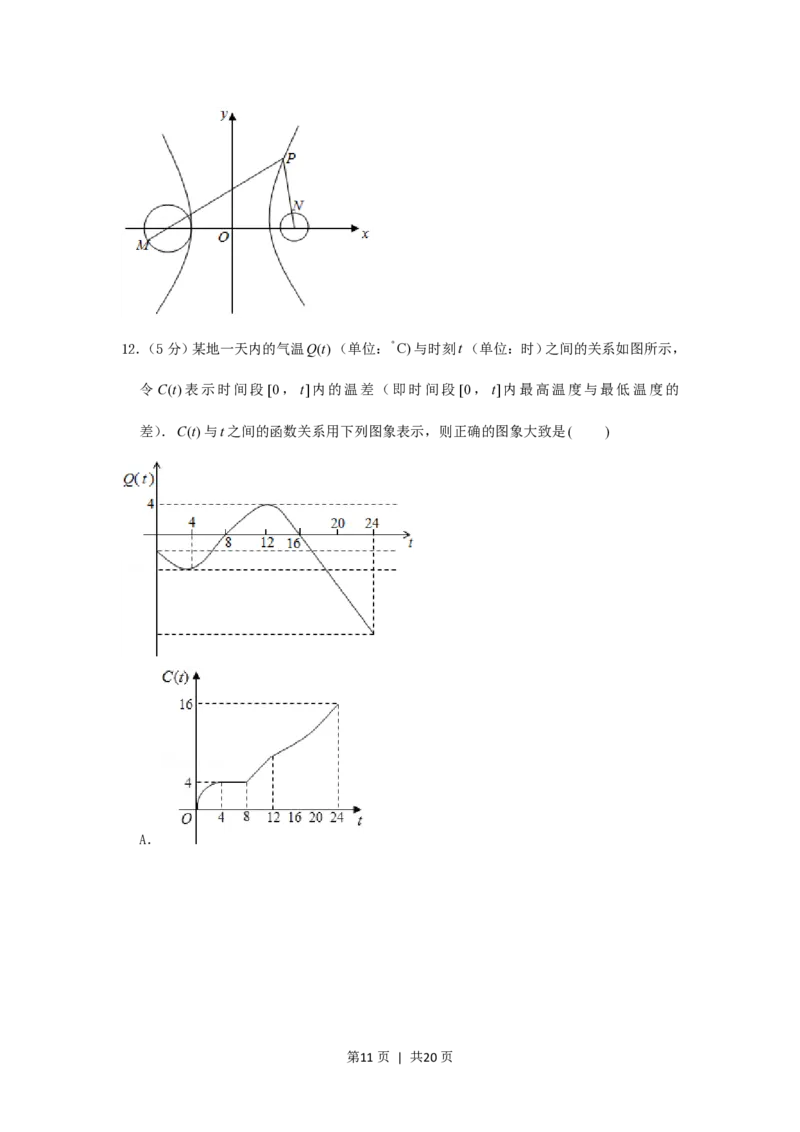11．（5 分） P是双曲线  1的右支上一点， M 、 N分别是圆(x5)2  y2 4和 9 16 (x5)2  y2 1上的点，则|PM ||PN|的最大值为( ) A．6 B．7 C．8 D．9 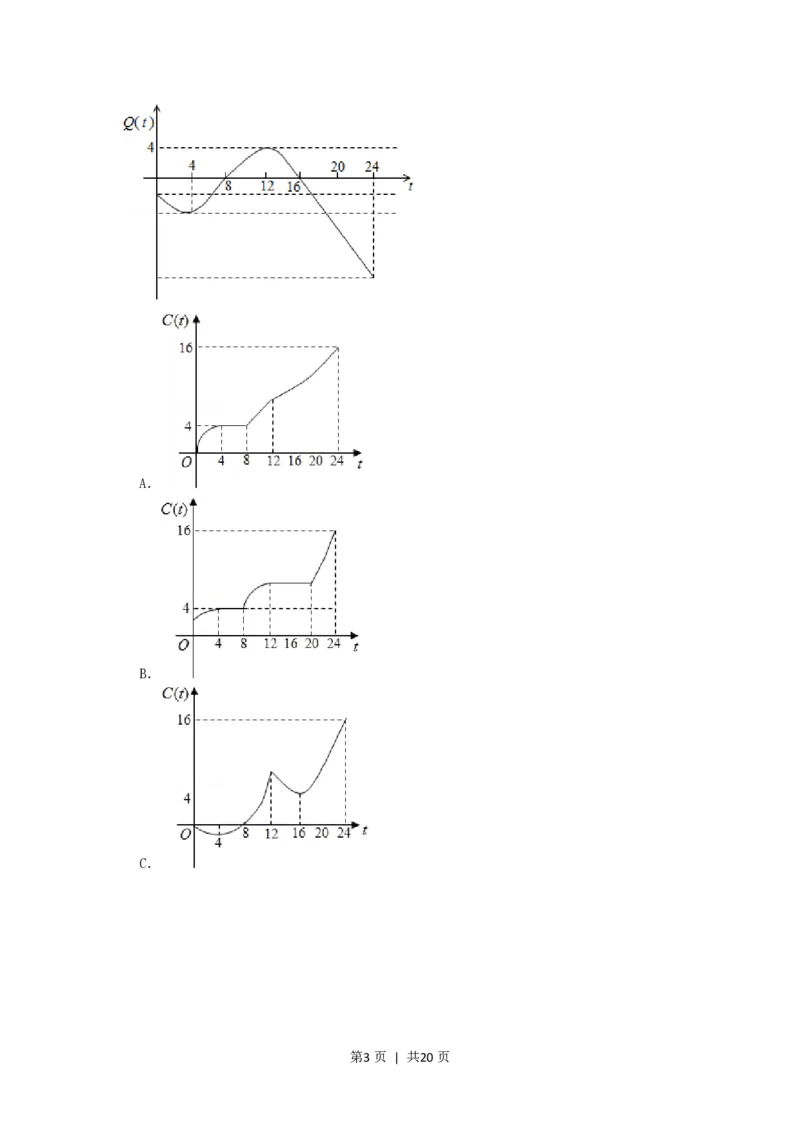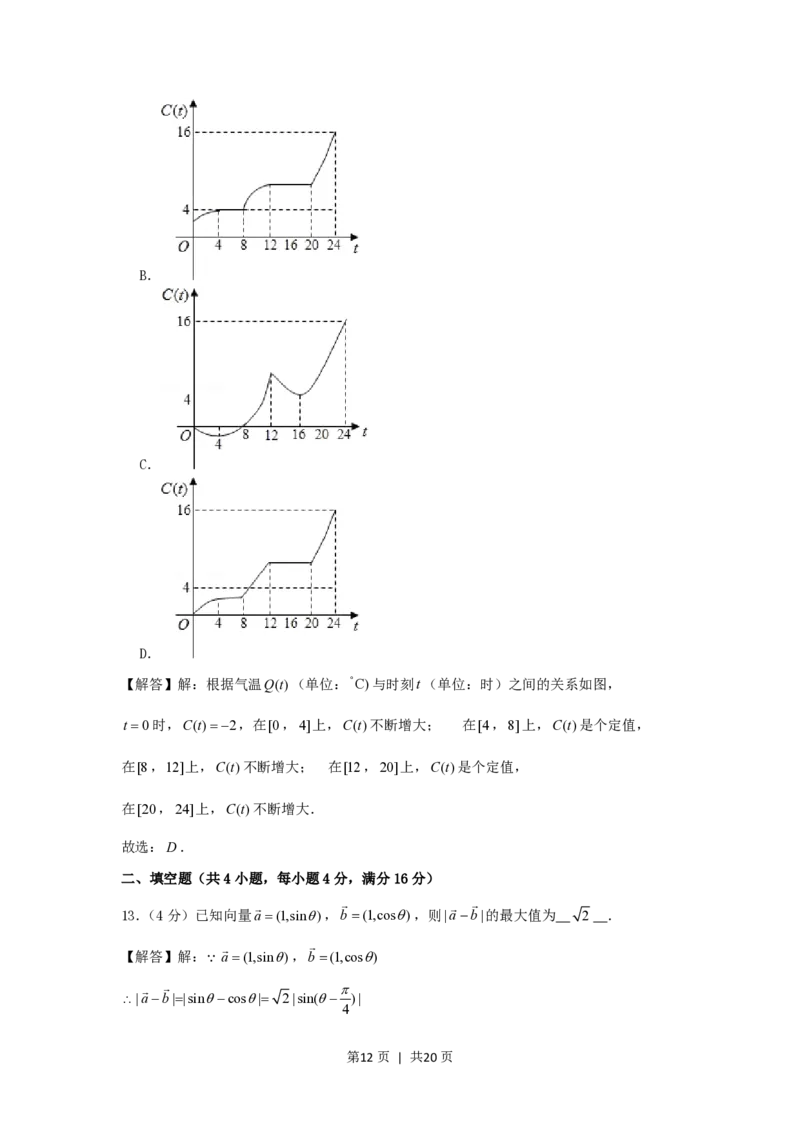12．（5分）某地一天内的气温Q(t)（单位：C)与时刻t（单位：时）之间的关系如图所示， 令 C(t)表示时间段[0， t]内的温差（即时间段[0， t]内最高温度与最低温度的 差）．C(t)与t之间的函数关系用下列图象表示，则正确的图象大致是( ) 第2页 | 共20页A． B． C． 第3页 | 共20页D． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）已知向量a(1,sin)，b  (1,cos)，则|ab  |的最大值为 ． 14．（4 分）设 f(x)log (x6)的反函数为 f1(x)，若[f1(m)6][f1(n)6]27，则 3 f(mn) ． 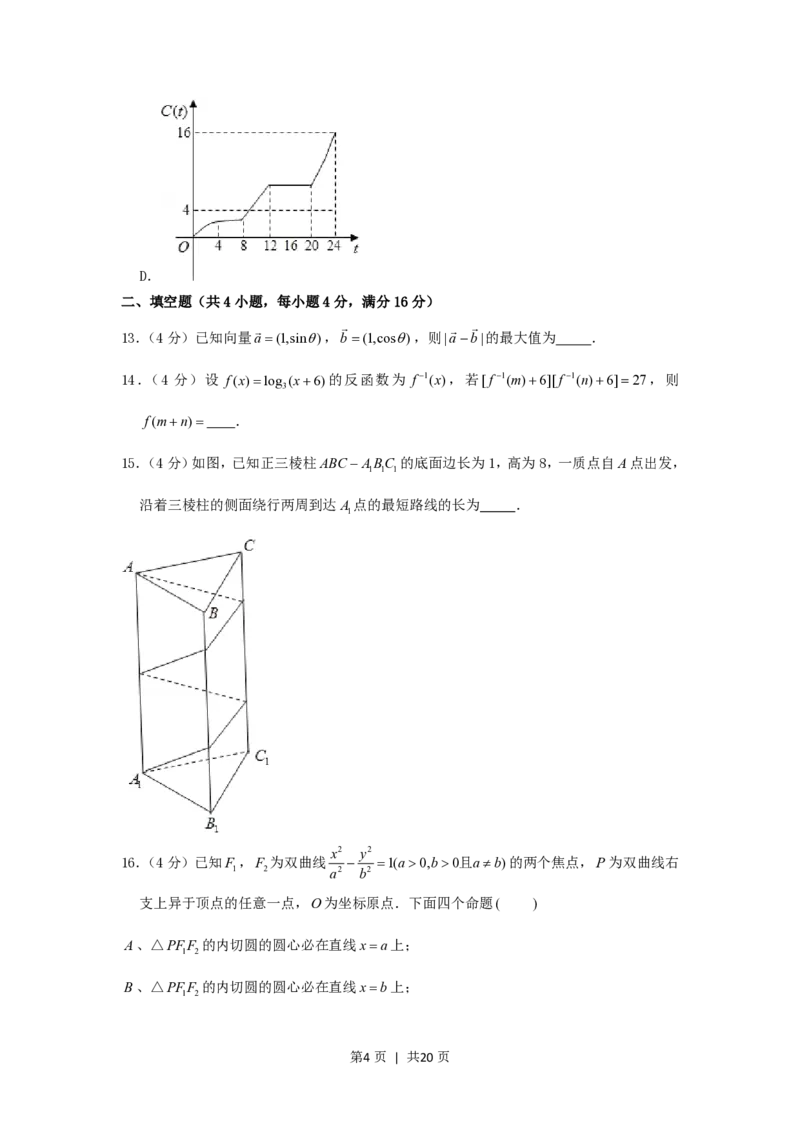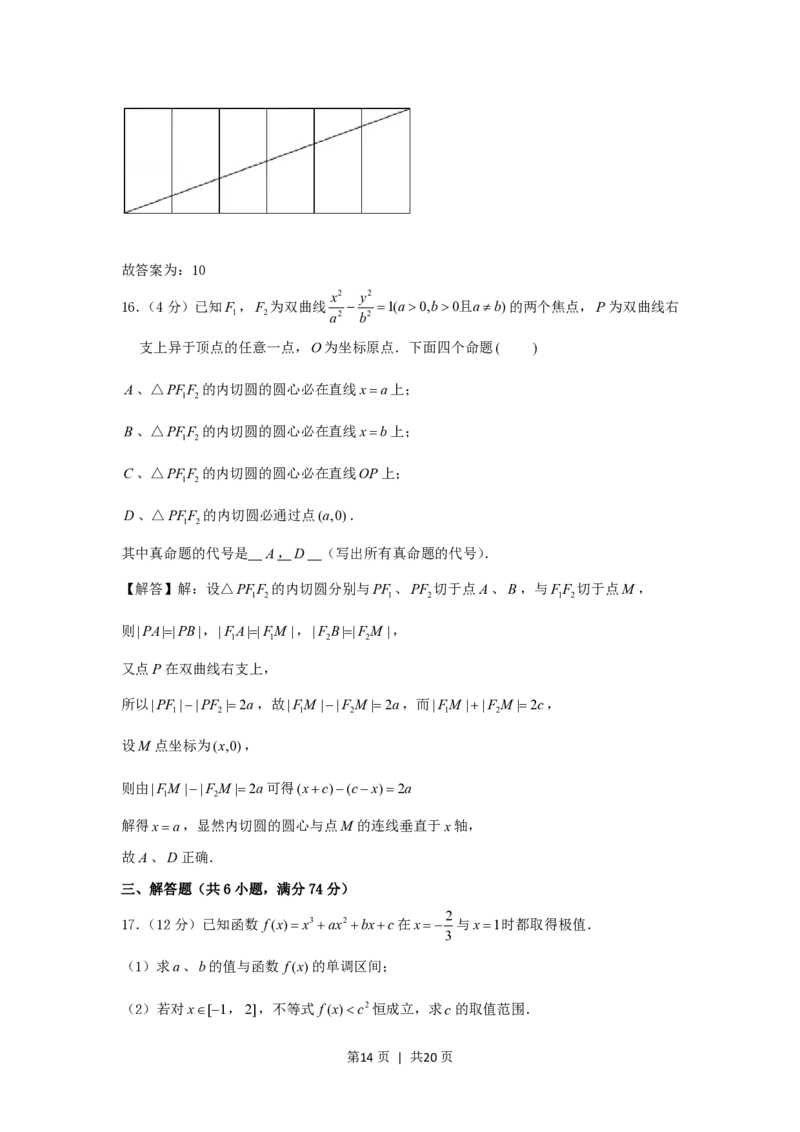15．（4分）如图，已知正三棱柱ABCABC 的底面边长为1，高为8，一质点自A点出发， 1 1 1 沿着三棱柱的侧面绕行两周到达A点的最短路线的长为 ． 1 x2 y2 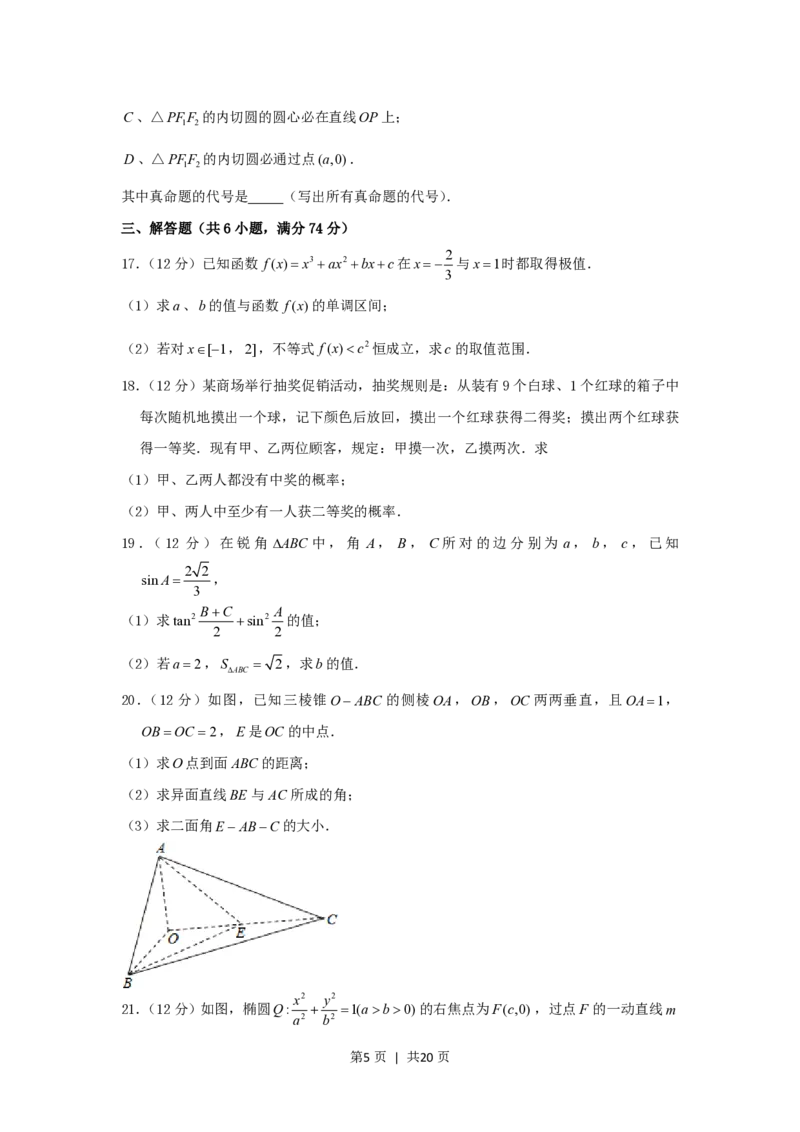16．（4分）已知F ，F 为双曲线  1(a0,b0且ab)的两个焦点，P为双曲线右 1 2 a2 b2 支上异于顶点的任意一点，O为坐标原点．下面四个命题( ) A、△PFF 的内切圆的圆心必在直线xa上； 1 2 B、△PFF 的内切圆的圆心必在直线xb上； 1 2 第4页 | 共20页C、△PFF 的内切圆的圆心必在直线OP上； 1 2 D、△PFF 的内切圆必通过点(a,0)． 1 2 其中真命题的代号是 （写出所有真命题的代号）． 三、解答题（共6小题，满分74分） 2 17．（12分）已知函数 f(x)x3 ax2 bxc在x 与x1时都取得极值． 3 （1）求a、b的值与函数 f(x)的单调区间； （2）若对x[1，2]，不等式 f(x)c2恒成立，求c的取值范围． 18．（12分）某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中 每次随机地摸出一个球，记下颜色后放回，摸出一个红球获得二得奖；摸出两个红球获 得一等奖．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．求 （1）甲、乙两人都没有中奖的概率； （2）甲、两人中至少有一人获二等奖的概率． 19．（12 分）在锐角 ABC 中，角 A， B， C所对的边分别为 a， b， c，已知 2 2 sinA ， 3 BC A （1）求tan2 sin2 的值； 2 2 （2）若a2，S  2，求b的值． ABC 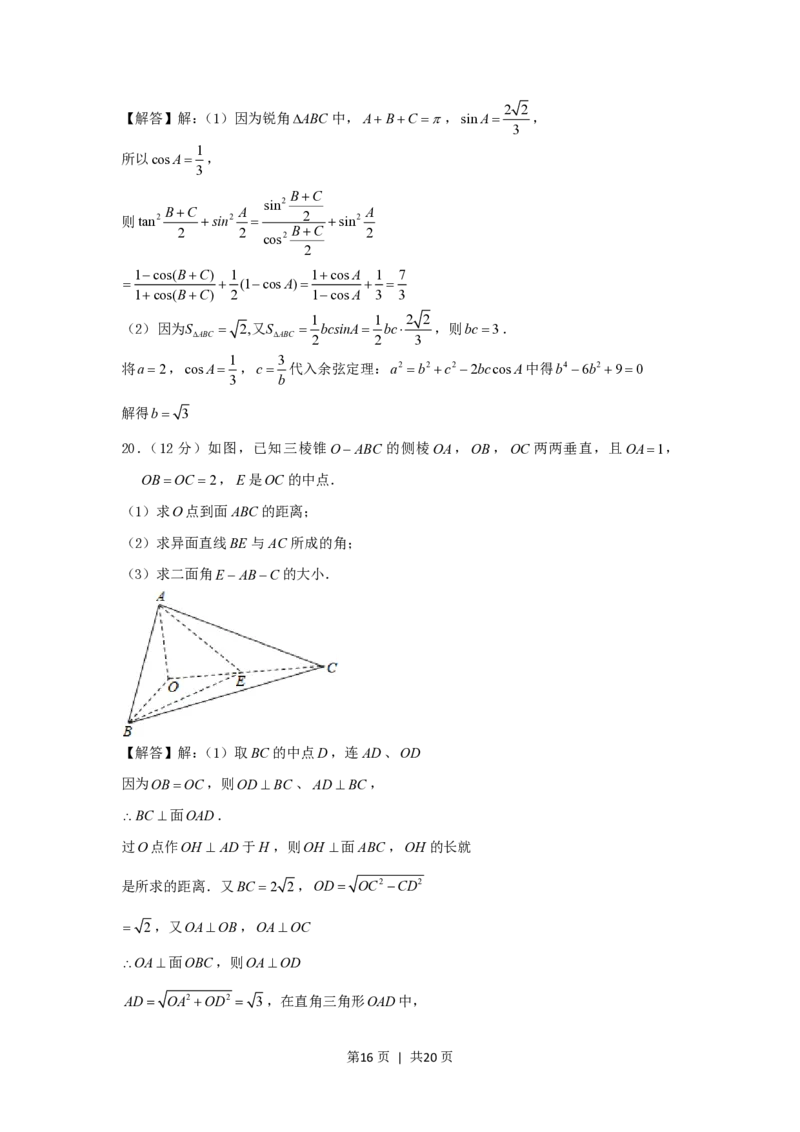20．（12 分）如图，已知三棱锥OABC 的侧棱OA，OB，OC两两垂直，且OA1， OBOC 2，E是OC的中点． （1）求O点到面ABC的距离； （2）求异面直线BE 与AC所成的角； （3）求二面角EABC的大小． x2 y2 21．（12分）如图，椭圆Q:  1(ab0)的右焦点为F(c,0)，过点F 的一动直线m a2 b2 第5页 | 共20页绕点F 转动， 并且交椭圆于A，B两点，P为线段AB的中点． （1）求点P的轨迹H 的方程；  （2）若在Q的方程中，令a2 1cossin，b2 sin(0„ )． 2 设轨迹H 的最高点和最低点分别为M 和N．当为何值时，MNF为一个正三角形？ 2a a 22．（14 分）已知各项均为正数的数列{a }，满足： a 3，且 n1 n a a ， n 1 2a a n n1 n n1 nN*． （1）求数列{a }的通项公式； n 1 1 1 （2）设S a2 a2 a2，T   a ，求S T ，并确定最小正整数n， n 1 2 n n a2 a2 a2 n n 1 2 n 使S T 为整数． n n 2006年江西高考文科数学真题参考答案 一、选择题（共12小题，每小题5分，满分60分）  1  1．（5分）已知集合P{x|x(x1)…0}，Qx 0，则P  Q等于( )  x1  A． B．{x|x…1} C．{x|x1} D．{x|x…1或x0} 【解答】解：P{x|x…1或x„ 0}，Q{x|x1}，所以P Q{x|x1}  故选：C．  2．（5分）函数y4sin(2x )1的最小正周期为( ) 3  A． B． C．2 D．4 2 第6页 | 共20页 【解答】解： y4sin(2x )1  3 2 T  ， 2 故选：B． 3．（5分）在各项均不为零的等差数列{a }中，若a a2 a 0(n…2)，则S 4n( n n1 n n1 2n1 ) A．2 B．0 C．1 D．2 【解答】解：设公差为d，则a a d，a a d ， n1 n n1 n 由a a2 a 0(n…2)可得2a a2 0， n1 n n1 n n 解得a 2（零解舍去）， n 故S 4n2(2n1)4n2， 2n1 故选：A． 4．（5分）下列四个条件中， p是q的必要不充分条件的是( ) A． p:ab，q:a2 b2 B． p:ab，q:2a 2b C． p:ax2 by2 c为双曲线，q:ab0 c b D． p:ax2 bxc0，q:  a0 x2 x 【解答】解： A． p不是q的充分条件，也不是必要条件； B． p是q的充要条件； C． p是q的充分条件，不是必要条件； D．正确 故选：D． 5．（5分）若 f(x)是定义在R上的可导函数，且满足(x1)f(x)…0，则必有( ) A． f(0) f （2）2f （1） B． f(0) f （2）2f （1） 第7页 | 共20页C． f(0) f （2）„ 2f （1） D． f(0) f （2）…2f （1） 【解答】解： (x1)f(x)…0  x1时， f(x)…0；x1时， f(x)„ 0 f(x)在(1,)为增函数；在(,1)上为减函数 f （2）…f （1） f(0)…f （1） f(0) f （2）…2f （1） 故选：D． 1 6．（5分）若不等式x2 ax1…0对一切x(0, )成立，则a的最小值为( ) 2 5 A．0 B．2 C． D．3 2 a 【解答】解：设 f(x)x2 ax1，则对称轴为x 2 a 1 1 若 … ，即a„ 1时，则 f(x)在[0， ]上是减函数， 2 2 2 1 5 应有 f( )…0 „ a„ 1 2 2 a 1 若 „ 0，即a…0时，则 f(x)在[0， ]上是增函数， 2 2 应有 f(0)10恒成立， 故a…0 a 1 若0„  „ ，即1„ a„ 0， 2 2 a a2 a2 a2 则应有 f( )  11 …0恒成立， 2 4 2 4 故1„ a„ 0 5 综上，有 „ a． 2 故选：C． 2 7．（5分）在( x  )n的二项展开式中，若常数项为60，则n等于( ) x A．3 B．6 C．9 D．12 第8页 | 共20页2 n3r 【解答】解：T Cr( x)nr ( )r 2rCrx 2 ，nN*，rN* r1 n x n n3r0 由 ，解得n6， 2rCr 60 n 故选：B． 8．（5分）袋中有40个小球，其中红色球16个、蓝色球12个，白色球8个，黄色球4个， 从中随机抽取10个球作成一个样本，则这个样本恰好是按分层抽样方法得到的概率为( ) C1C2C3C4 A． 4 8 12 16 C10 40 C2C1C3C4 B． 4 8 12 16 C10 40 C2C3C1C4 C． 4 8 12 16 C10 40 C1C3C4C2 D． 4 8 12 16 C10 40 【解答】解： 这个样本要恰好是按分层抽样方法得到的概率  依题意各层次数量之比为4:3:2:1， 即红球抽4个，蓝球抽3个，白球抽2个，黄球抽一个， C1C2C3C4 根据古典概型公式得到结果为 4 8 12 16 ； C10 40 故选：A． 9．（5分）如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰， 以下4个命题中，假命题是( ) A．等腰四棱锥的腰与底面所成的角都相等 B．等腰四棱锥的侧面与底面所成的二面角都相等或互补 C．等腰四棱锥的底面四边形必存在外接圆 D．等腰四棱锥的各顶点必在同一球面上 【解答】解：因为“等腰四棱锥”的四条侧棱都相等， 所以它的顶点在底面的射影到底面的四个顶点的距离相等， 第9页 | 共20页故A，C正确， 且在它的高上必能找到一点到各个顶点的距离相等， 故D正确，B不正确，如底面是一个等腰梯形时结论就不成立． 故选：B．    10．（5分）已知等差数列{a }的前n项和为S ，若OBaOAa OC，且A、B、C三 n n 1 200 点共线（该直线不过原点O)，则S ( ) 200 A．100 B．101 C．200 D．201 【解答】解： A，B，C三点共线  a a 1 1 200 200(a a ) 又 s  1 200  200 2 s 100 200 故选：A． x2 y2 11．（5 分） P是双曲线  1的右支上一点， M 、 N分别是圆(x5)2  y2 4和 9 16 (x5)2  y2 1上的点，则|PM ||PN|的最大值为( ) A．6 B．7 C．8 D．9 x2 y2 【解答】解：双曲线  1中，如图： 9 16 a3，b4，c5，  F(5,0)，F (5,0)， 1 2 |PF ||PF |2a6，  1 2 |MP|„ |PF ||MF |，|PN|… |PF ||NF |， 1 1 2 2 |PN|„ |PF ||NF |， 2 2 所以，|PM ||PN|„ |PF ||MF ||PF ||NF | 1 1 2 2 612 9． 故选：D． 第10页 | 共20页12．（5分）某地一天内的气温Q(t)（单位：C)与时刻t（单位：时）之间的关系如图所示， 令 C(t)表示时间段[0， t]内的温差（即时间段[0， t]内最高温度与最低温度的 差）．C(t)与t之间的函数关系用下列图象表示，则正确的图象大致是( ) 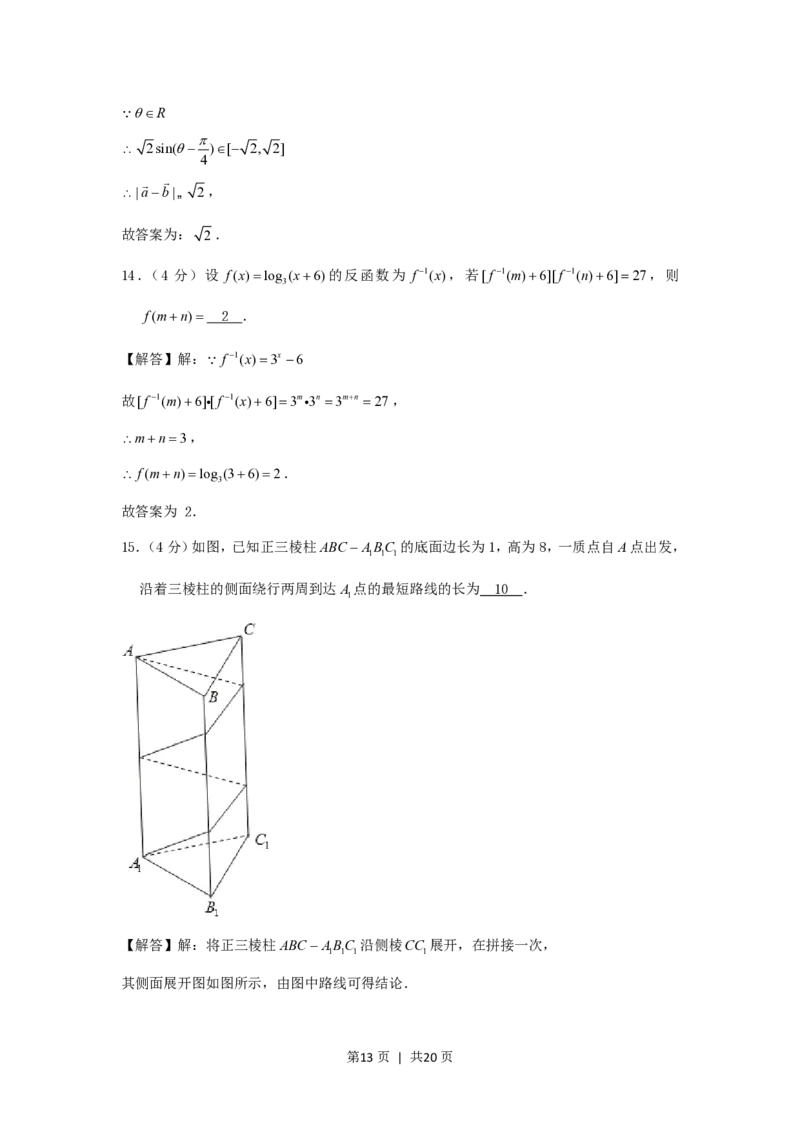A． 第11页 | 共20页B． C． D． 【解答】解：根据气温Q(t)（单位：C)与时刻t（单位：时）之间的关系如图， t 0时，C(t)2，在[0，4]上，C(t)不断增大； 在[4，8]上，C(t)是个定值， 在[8，12]上，C(t)不断增大； 在[12，20]上，C(t)是个定值， 在[20，24]上，C(t)不断增大． 故选：D． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）已知向量a(1,sin)，b  (1,cos)，则|ab  |的最大值为 2 ． 【解答】解： a(1,sin)，b  (1,cos)  |ab  ||sincos| 2|sin(  )| 4 第12页 | 共20页R    2sin( )[ 2, 2] 4 |ab  |„ 2， 故答案为： 2． 14．（4 分）设 f(x)log (x6)的反函数为 f1(x)，若[f1(m)6][f1(n)6]27，则 3 f(mn) 2 ． 【解答】解： f1(x)3x 6  故[f1(m)6][f1(x)6]3m 3n 3mn 27，   mn3， f(mn)log (36)2． 3 故答案为 2． 15．（4分）如图，已知正三棱柱ABCABC 的底面边长为1，高为8，一质点自A点出发， 1 1 1 沿着三棱柱的侧面绕行两周到达A点的最短路线的长为 10 ． 1 【解答】解：将正三棱柱ABCABC 沿侧棱CC 展开，在拼接一次， 1 1 1 1 其侧面展开图如图所示，由图中路线可得结论． 第13页 | 共20页故答案为：10 x2 y2 16．（4分）已知F ，F 为双曲线  1(a0,b0且ab)的两个焦点，P为双曲线右 1 2 a2 b2 支上异于顶点的任意一点，O为坐标原点．下面四个命题( ) A、△PFF 的内切圆的圆心必在直线xa上； 1 2 B、△PFF 的内切圆的圆心必在直线xb上； 1 2 C、△PFF 的内切圆的圆心必在直线OP上； 1 2 D、△PFF 的内切圆必通过点(a,0)． 1 2 其中真命题的代号是 A，D （写出所有真命题的代号）． 【解答】解：设△PFF 的内切圆分别与PF 、PF 切于点A、B，与FF 切于点M ， 1 2 1 2 1 2 则|PA||PB|，|FA||FM |，|F B||FM |， 1 1 2 2 又点P在双曲线右支上， 所以|PF ||PF |2a，故|FM ||FM |2a，而|FM ||FM |2c， 1 2 1 2 1 2 设M 点坐标为(x,0)， 则由|FM ||FM |2a可得(xc)(cx)2a 1 2 解得xa，显然内切圆的圆心与点M 的连线垂直于x轴， 故A、D正确． 三、解答题（共6小题，满分74分） 2 17．（12分）已知函数 f(x)x3 ax2 bxc在x 与x1时都取得极值． 3 （1）求a、b的值与函数 f(x)的单调区间； （2）若对x[1，2]，不等式 f(x)c2恒成立，求c的取值范围． 第14页 | 共20页【解答】解；（1） f(x)x3 ax2 bxc， f(x)3x2 2axb  2 12 4  1 f( )  ab0 a 由 3 9 3 解得， 2  f(1)32ab0  b2 f(x)3x2 x2(3x2)(x1)，函数 f(x)的单调区间如下表： x (, 2 )  2 ( 2 ，1) 1 (1,) 3 3 3 f(x)  0  0  f(x)  极大值  极小值  2 2 所以函数 f(x)的递增区间是(, )和(1,)，递减区间是( ，1)． 3 3 1 （2） f(x)x3  x2 2xc,x[1,2]， 2 2 22 当x 时， f(x) c为极大值，而 f （2）2c，所以 f （2）2c为最大值． 3 27 要使 f(x)c2对x[1，2]恒成立，须且只需c2  f （2）2c． 解得c1或c2． 18．（12分）某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中 每次随机地摸出一个球，记下颜色后放回，摸出一个红球获得二得奖；摸出两个红球获 得一等奖．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．求 （1）甲、乙两人都没有中奖的概率； （2）甲、两人中至少有一人获二等奖的概率． 9 9 729 【解答】解：（1）P  ( )2  1 10 10 1000 1 9 1 1 9 18 1 18 131 （2）法一：P  ( )2  ( )2      2 10 10 10 10 10 102 10 102 500 1 1 9 1 1 9 131 法二：P  2   2   2 10 10 10 10 10 10 500 9 1 1 9 9 131 法三：P 1 (    ) 2 10 10 10 10 10 500 19．（12 分）在锐角 ABC 中，角 A， B， C所对的边分别为 a， b， c，已知 2 2 sinA ， 3 BC A （1）求tan2 sin2 的值； 2 2 （2）若a2，S  2，求b的值． ABC 第15页 | 共20页2 2 【解答】解：（1）因为锐角ABC 中，ABC ，sinA ， 3 1 所以cosA ， 3 BC sin2 则tan2 BC sin2 A  2 sin2 A 2 2 BC 2 cos2 2 1cos(BC) 1 1cosA 1 7   (1cosA)   1cos(BC) 2 1cosA 3 3 1 1 2 2 （2）因为S  2,又S  bcsinA bc ，则bc3． ABC ABC 2 2 3 1 3 将a2，cosA ，c 代入余弦定理：a2 b2 c2 2bccosA中得b4 6b2 90 3 b 解得b 3 20．（12 分）如图，已知三棱锥OABC 的侧棱OA，OB，OC两两垂直，且OA1， OBOC 2，E是OC的中点． （1）求O点到面ABC的距离； （2）求异面直线BE 与AC所成的角； （3）求二面角EABC的大小． 【解答】解：（1）取BC的中点D，连AD、OD 因为OBOC，则ODBC、ADBC， BC 面OAD． 过O点作OH  AD于H ，则OH 面ABC，OH 的长就 是所求的距离．又BC 2 2，OD OC2 CD2  2，又OAOB，OAOC OA面OBC，则OAOD AD OA2 OD2  3，在直角三角形OAD中， 第16页 | 共20页OAOD 2 6 有OH     AD 3 3 （2）取OA的中点M ，连EM 、BM ， 则EM //AC，DBEM 是异面直线BE 与AC 5 所成的角，易求得EM  ，BE  5， 2 17 2 BM  ．由余弦定理可求得cosDBEM  ， 2 5 2 BEM arccos 5 （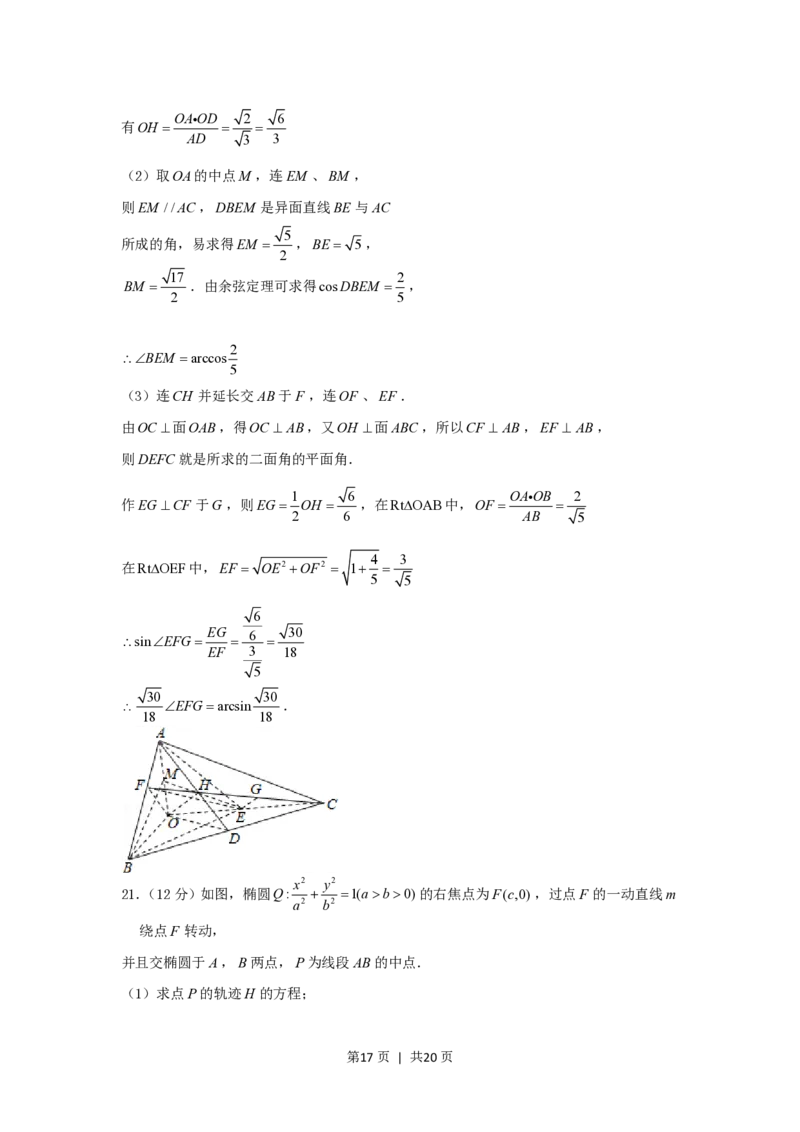3）连CH 并延长交AB于F ，连OF 、EF ． 由OC 面OAB，得OC  AB，又OH 面ABC，所以CF  AB，EF  AB， 则DEFC就是所求的二面角的平面角． 1 6 OAOB 2 作EGCF 于G，则EG OH  ，在RtOAB中，OF    2 6 AB 5 4 3 在RtOEF中，EF  OE2 OF2  1  5 5 6 EG 6 30 sinEFG   EF 3 18 5 30 30  EFGarcsin ． 18 18 x2 y2 21．（12分）如图，椭圆Q:  1(ab0)的右焦点为F(c,0)，过点F 的一动直线m a2 b2 绕点F 转动， 并且交椭圆于A，B两点，P为线段AB的中点． （1）求点P的轨迹H 的方程； 第17页 | 共20页 （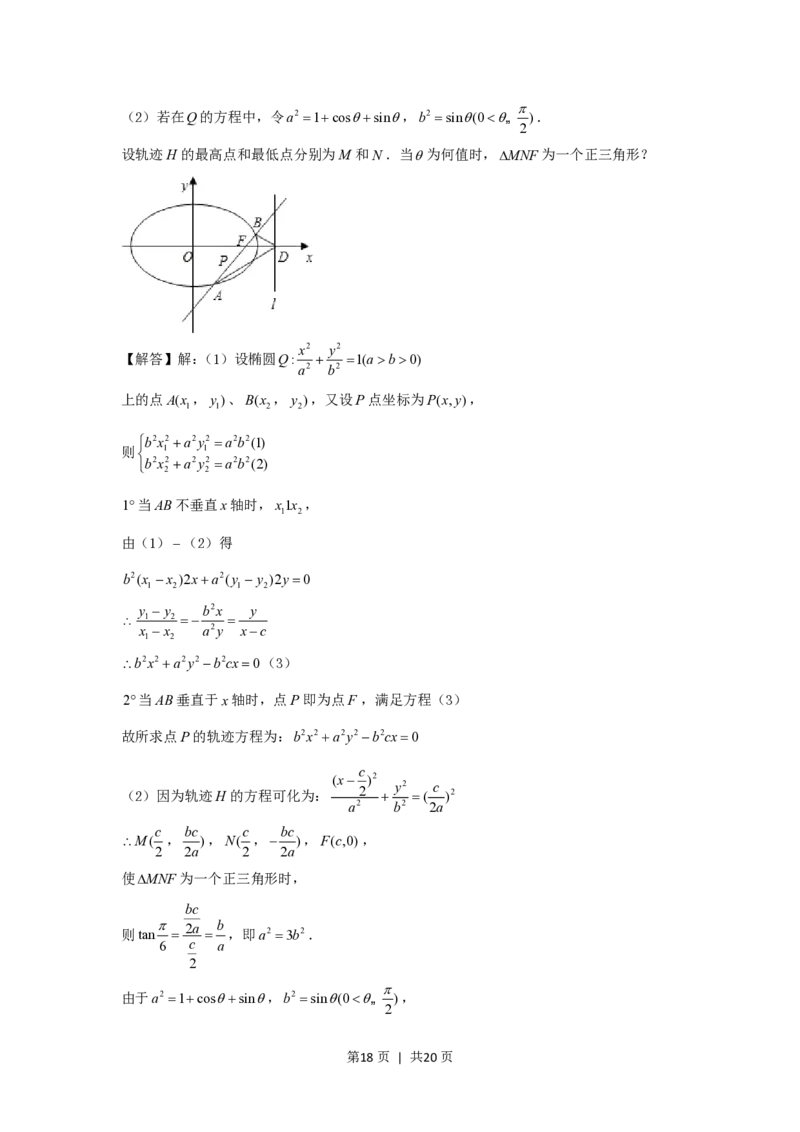2）若在Q的方程中，令a2 1cossin，b2 sin(0„ )． 2 设轨迹H 的最高点和最低点分别为M 和N．当为何值时，MNF为一个正三角形？ x2 y2 【解答】解：（1）设椭圆Q:  1(ab0) a2 b2 上的点A(x ，y )、B(x ，y )，又设P点坐标为P(x,y)， 1 1 2 2 b2x2 a2y2 a2b2(1) 则 1 1 b2x2 a2y2 a2b2(2) 2 2 1当AB不垂直x轴时，x1x ， 1 2 由（1）（2）得 b2(x x )2xa2(y  y )2y0 1 2 1 2 y  y b2x y  1 2   x x a2y xc 1 2 b2x2 a2y2 b2cx0（3） 2当AB垂直于x轴时，点P即为点F ，满足方程（3） 故所求点P的轨迹方程为：b2x2 a2y2 b2cx0 c (x )2 （2）因为轨迹H 的方程可化为： 2  y2 ( c )2 a2 b2 2a c bc c bc M( ， )，N( ， )，F(c,0)， 2 2a 2 2a 使MNF为一个正三角形时， bc  2a b 则tan   ，即a2 3b2． 6 c a 2  由于a2 1cossin，b2 sin(0„ )， 2 第18页 | 共20页则1cosqsinq3sin， 4 得arctan 3 2a a 22．（14 分）已知各项均为正数的数列{a }，满足： a 3，且 n1 n a a ， n 1 2a a n n1 n n1 nN*． （1）求数列{a }的通项公式； n 1 1 1 （2）设S a2 a2 a2，T   a ，求S T ，并确定最小正整数n， n 1 2 n n a2 a2 a2 n n 1 2 n 使S T 为整数． n n 1 1 【解答】解：（1）条件可化为a  2(a  )， n1 a n a n1 n 1 1 8 因此{a  }为一个等比数列，其公比为2，首项为a   ， n a 1 a 3 n 1 1 8 2n2 所以a   2n1  (nN*)① n a 3 3 n 1 因a 0，由①式解出a  (2n1 22n2 9)② n n 3 1 1 1 （2）由①式有S T (a  )2 (a  )2 (a  )2 2n n n 1 a 2 a n a 1 2 n 23 24 25 2n2 ( )2 ( )2 ( )2 ( )2 2n 3 3 3 3 64  (4n 1)2n(nN*) 27 64 为使S T  (4n 1)2n(nN*)为整数， n n 27 4n 1 当且仅当 为整数． 27 当n1，2时，显然S T 不为整数， n n 当n33时，4n 1(13)n 1ð13ð232 33(ð3 3n3ðn) n n n n 3C1 32C2 n 3n1 只需 n n  为整数，  27 9 2 因为3n1与3互质， 所以为9的整数倍． n 3n1 当n9时， 13为整数，  9 2 故n的最小值为9． 第19页 | 共20页第20页 | 共20页