数学试卷_2024-2025高三（6-6月题库）_2024年10月试卷_1027山东省中昇大联考2024-2025学年高三上学期10月联考_山东省中昇大联考2024-2025学年高三上学期10月联考数学试题

学年高三 月检测
2024-2025 10 5.对于函数 y  f(x)，xR，“y  f(x) 的图象关于 y轴对称”是“ y  f(x)是奇函数”的
数学
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
本试卷满分150分，考试用时 120分钟。
注意事项： 6.设函数 f  x sin  2x  ，则下列结论正确的是
1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。  6
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如

需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题 A. f  x 的图像关于直线x 对称
3
卡上。写在本试卷上无效。
3.考试结束后，将本试卷和答题卡一并交回。 B. f  x 的图像关于点    ,0  对称
 6 
一、单项选择题：本题共 8 小题，每小题 5分，共 40 分.在每小题给出的四个选项中，只有
一项是符合题目要求的. C. f  x 的最小正周期为 ,且在 

0, 

上为增函数
 12
1.命题“xR，x2  x”的否定是

D.把 f  x 的图像向右平移 个单位，得到一个偶函数的图像
A.xR，x2  x B.xR，x2  x 12
1 
C.xR，x2  x D.xR，x2  x 7.函数 f  x log 2  3x 在点P 3 ,0  处的切线方程为
2.设集合M {x x2 x60}，N {x1≤x≤3}，则M N  A.3x y10 B.3x3y10
A.[1,2) B.[1,2] C.(2,3] D.[2,3] C.3x yln210 D.3x 3ln2  y10
1
3.若a 30.7,b(
3
)0.8,clog
3
2，则a,b,c的大小关系是
8. y f  x  是 定 义 在 R 上 的 函 数 ， 对 于 任 意 的 xR ， 都 有 f  x  f  2x  ，
A.abc B.bac C.cba D.cab

f  1x f  x3 ，且x 0,1  时，有 f  x sin x，则函数 y11f  x x2的所有零
 1 2
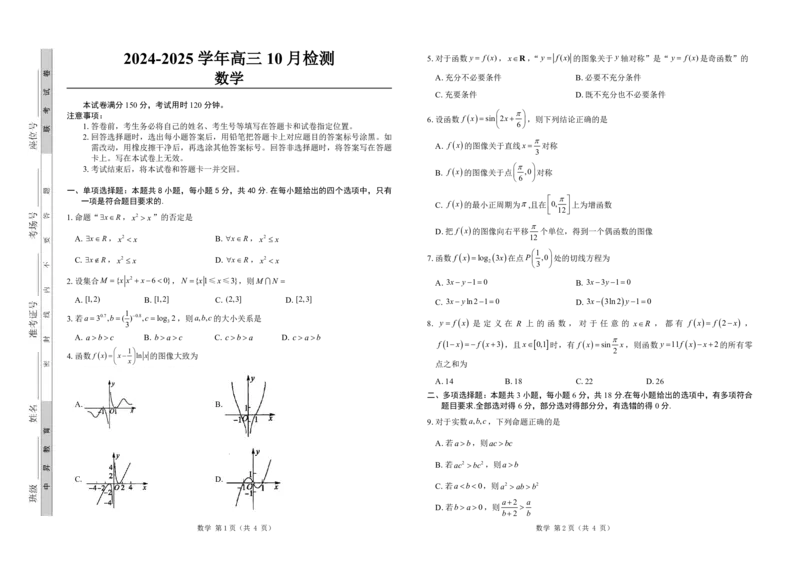
4.函数 f xx ln x 的图像大致为
 x 点之和为
A.14 B.18 C.22 D.26
二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合
A. B. 题目要求.全部选对得6分，部分选对得部分分，有选错的得0分.
9.对于实数a,b,c，下列命题正确的是
A.若ab，则acbc
B.若ac2 bc2，则ab
C. D.
C.若ab0，则a2 abb2
a2 a
D.若ba0，则 
b2 b
数学 第1页（共 4 页） 数学 第2页（共 4 页）
{#{QQABDQAUoggIABJAAAgCAQFiCgEQkgACAYgOBAAIoAAAyQNABAA=}#}10.在平面直角坐标系xOy中，若角的顶点为坐标原点，始边与x 轴的非负半轴重合，终边 17.（15分）在△ABC中，D为BC的中点，AB 4， AC 2 2 .
经过点P(3a,4a)  a 0 ，则2cos sin  （1）若AD 2，求BAC的余弦值；

2 2 （2）延长AD到点E,使AD 2DE，连接BE，EC，若ABC  ，求BE的长.
A. B.2 C. D.2 4
5 5
x2,x1,
11.已知函数 f  x  则下列关于函数 f  x 的结论正确的是
x2,1 x2,
A. f  f 1  1 B.若 f  x 3，则x 的值是 3
C. f  x 1的解集为,1  D. f  x 的值域为,4  2a
18.（17分）已知函数 f(x)lnx 1a (aR).
x
三、填空题：本题共3小题，每小题5分，共15分.
（1）讨论函数 f(x)的单调性；
1
12.若函数 f  x  x2 xa的定义域和值域均为  1,b  ，则b的值为__________.
2 （2）若 f(x)0在(0,)恒成立，求整数a的最大值.
4 1
13.已知0 x2，则  的最小值是______________.
2x x
1 11
14.已知，都是锐角，cos ，cos  ，则tan____________.
7 14
四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.
 
15.（13 分）函数 f  x  Asin x A0,0,  的图像上相邻两个最高点的距离
 2  19.（17分）对于四个正数m、n 、p、q ，若满足mq  np ，则称有序数对 m,n 是 p,q 的
 
为，其中一个最高点坐标为M  ,3. “下位序列”.
 8 
（1）对于2、3、7、11，有序数对
3,11
是
2,7
的“下位序列”吗？请简单说明理由；
（1）求函数 f  x 的解析式；
a c ac
（2）设a 、b、c、d 均为正数，且 a,b 是 c,d 的“下位序列”，试判断 、 、
（2）求函数 f  x 在区间 0,上的单调递增区间. b d bd
之间的大小关系；
 
（3）设正整数n 满足条件：对集合 m 0m2024,mN 内的每个m，总存在正整数k，
使得 m,2024 是 k,n 的“下位序列”，且 k,n 是 m1,2025 的“下位序列”，求正整
a2x
16.（15分）已知函数 f(x) (aR)是奇函数.
2x 1 数n 的最小值.
（1）求实数a的值；
（2）用定义法证明函数 f(x)在R上是减函数；
 
（3）若对于任意实数t，不等式 f t2 kt  f(1t)0恒成立，求实数k的取值范围.
数学 第3页（共 4 页） 数学 第4页（共 4 页）
{#{QQABDQAUoggIABJAAAgCAQFiCgEQkgACAYgOBAAIoAAAyQNABAA=}#}