文档内容
陕西省西安中学高 2025 届高三第一次质量检测考试
数学试题
(时间:120分钟 满分:150分 命题人:赵昕媛)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1. 已知集合 ,则 ( )
A. B. C. D.
2. “ ”是“函数 在 上单调递增”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
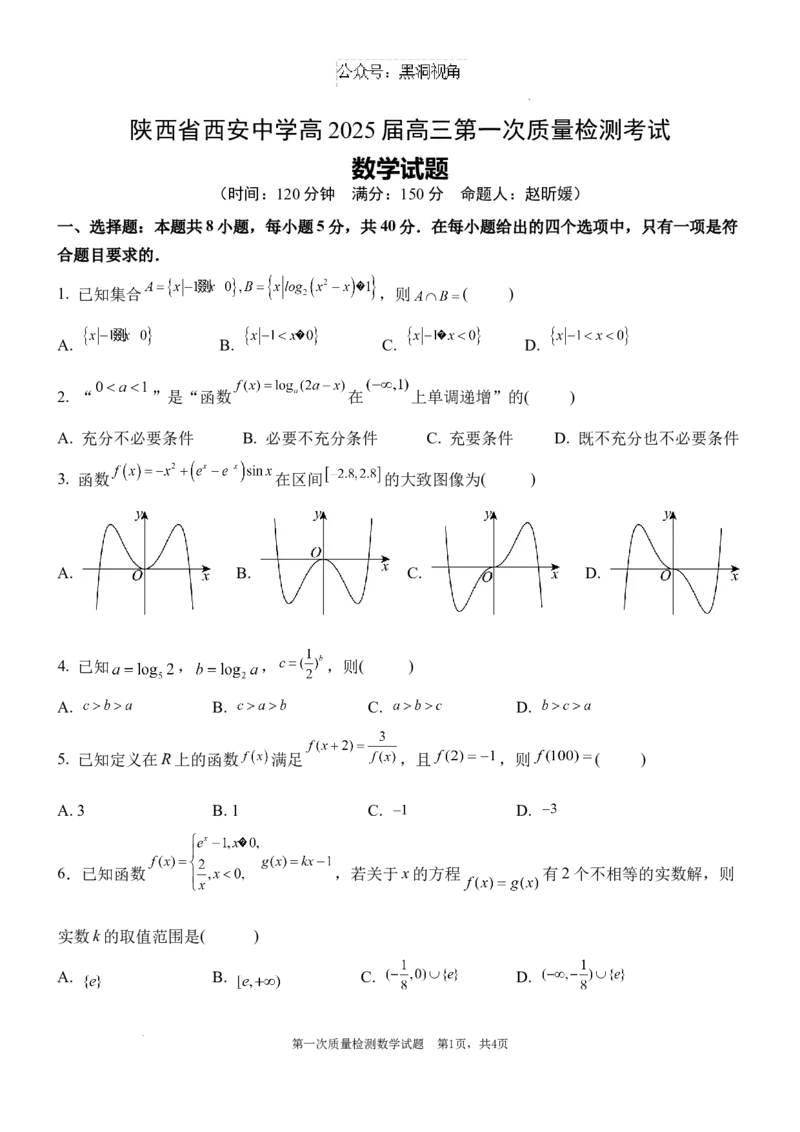
3. 函数 在区间 的大致图像为( )
A. B. C. D.
4. 已知 , , ,则( )
A. B. C. D.
5. 已知定义在R上的函数 满足 ,且 ,则 ( )
A. 3 B. 1 C. D.
6.已知函数 ,若关于x的方程 有2个不相等的实数解,则
实数k的取值范围是( )
A. B. C. D.
第一次质量检测数学试题 第1页,共4页
学科网(北京)股份有限公司7. 已知函数 ,则( )
A. 有三个极值点 B. 有三个零点
C. 直线 是曲线 的切线 D.点 是曲线 的对称中心
8. 已知函数 , ,若方程 有且仅有5个不相等的整数解,
则其中最大整数解和最小整数解的和等于( )
A. B. 28 C. D. 14
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列导数运算正确的是( )
A. B. C. D.
10.甲乙丙等5人的身高互不相同,站成一排进行列队训练,则( )
A. 甲乙不相邻的不同排法有48种
B. 甲乙中间恰排一个人的不同排法有36种
C. 甲乙不排在两端的不同排法有36种
D. 甲乙丙三人从左到右由高到矮的不同排法有20种
11. 已知 ,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分.
第一次质量检测数学试题 第2页,共4页
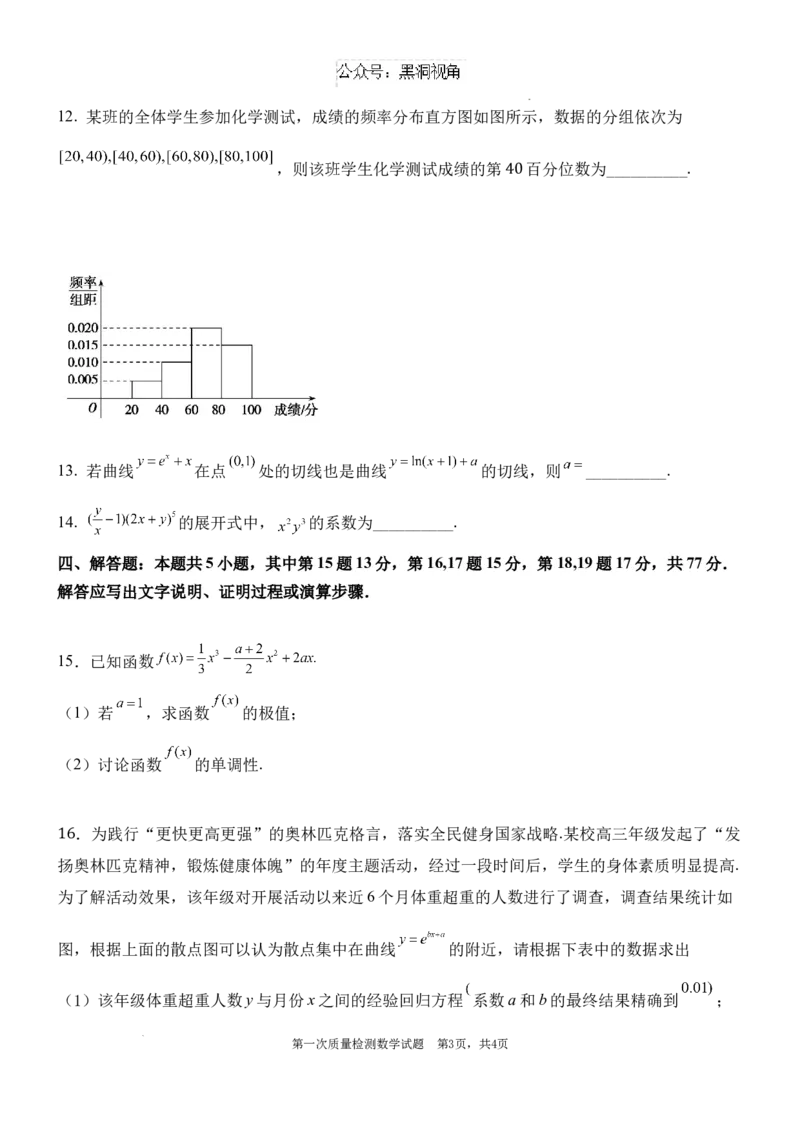
学科网(北京)股份有限公司12. 某班的全体学生参加化学测试,成绩的频率分布直方图如图所示,数据的分组依次为
,则该班学生化学测试成绩的第 百分位数为__________
40 .
13. 若曲线 在点 处的切线也是曲线 的切线,则 __________.
14. 的展开式中, 的系数为__________
.
四、解答题:本题共5小题,其中第15题13分,第16,17题15分,第18,19题17分,共77分.
解答应写出文字说明、证明过程或演算步骤.
15.已知函数
(1)若 ,求函数 的极值;
(2)讨论函数 的单调性.
.为践行“更快更高更强”的奥林匹克格言,落实全民健身国家战略.某校高三年级发起了“发
扬奥林匹克精神,锻炼健康体魄”的年度主题活动,经过一段时间后,学生的身体素质明显提高.
16
为了解活动效果,该年级对开展活动以来近6个月体重超重的人数进行了调查,调查结果统计如
图,根据上面的散点图可以认为散点集中在曲线 的附近,请根据下表中的数据求出
(1)该年级体重超重人数y与月份x之间的经验回归方程 系数a和b的最终结果精确到 ;
第一次质量检测数学试题 第3页,共4页
学科网(北京)股份有限公司(2)预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下.
月份x 1 2 3 4 5 6
体重超标人数y 98 77 54 48 32 27
附:经验回归方程: 中, , ;参考数据: ,
, ,
17. 已知函数 , R , ,且
(1)当 且 时,求不等式 的解集;
(2)若函数 在区间 上有零点,求t的取值范围.
18. 某企业对某品牌芯片开发了一条生产线进行试产.其芯片质量按等级划分为五个层级,分别对
应如下五组质量指标值: 根据长期检测结果,得到芯片的质量指
标值X服从正态分布 ,并把质量指标值不小于80的产品称为A等品,其它产品称为B等
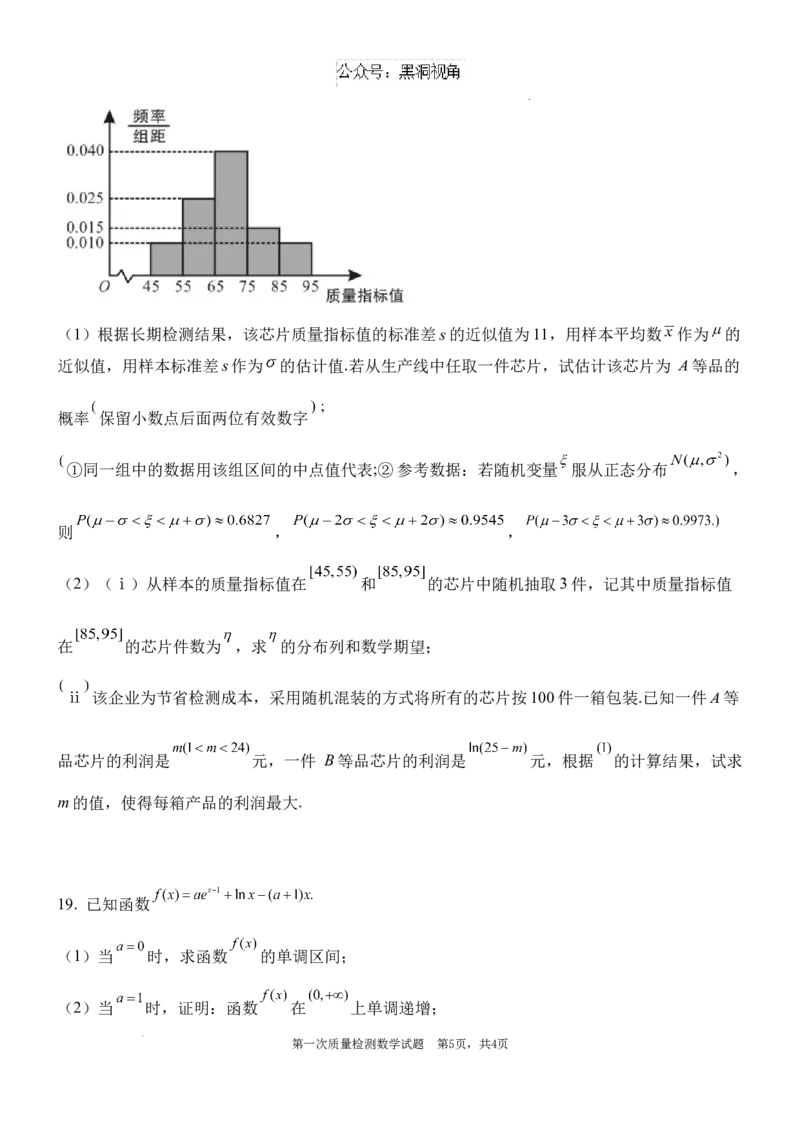
品.现从该品牌芯片的生产线中随机抽取100件作为样本,统计得到如图所示的频率分布直方图.
第一次质量检测数学试题 第4页,共4页
学科网(北京)股份有限公司(1)根据长期检测结果,该芯片质量指标值的标准差s的近似值为11,用样本平均数 作为 的
近似值,用样本标准差s作为 的估计值.若从生产线中任取一件芯片,试估计该芯片为 A等品的
概率 保留小数点后面两位有效数字
①同一组中的数据用该组区间的中点值代表;②参考数据:若随机变量 服从正态分布 ,
则 , ,
(2)(ⅰ)从样本的质量指标值在 和 的芯片中随机抽取3件,记其中质量指标值
在 的芯片件数为 ,求 的分布列和数学期望;
ⅱ 该企业为节省检测成本,采用随机混装的方式将所有的芯片按100件一箱包装.已知一件A等
品芯片的利润是 元,一件 B等品芯片的利润是 元,根据 的计算结果,试求
m的值,使得每箱产品的利润最大.
19. 已知函数
(1)当 时,求函数 的单调区间;
(2)当 时,证明:函数 在 上单调递增;
第一次质量检测数学试题 第5页,共4页
学科网(北京)股份有限公司(3)若 是函数 的极大值点,求实数a的取值范围.
第一次质量检测数学试题 第6页,共4页
学科网(北京)股份有限公司