数学试卷+详细解析答案（一题多解）_2024-2025高三（6-6月题库）_2024年08月试卷_0831福建省泉州市2025届高中毕业班质量监测（一）

保密★使用前 泉州市 2025 届高中毕业班质量监测（一） 2024.08 高 三 数 学 本试卷共19题，满分150分，共8页。考试用时120分钟。 注意事项： 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上。 2．考生作答时，将答案答在答题卡上。请按照题号在各题的答题区域（黑色线框）内 作答，超出答题区域书写的答案无效。在草稿纸、试题卷上答题无效。 3．选择题答案使用 2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号； 非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。 4．保持答题卡卡面清洁，不折叠、不破损。考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项 是符合题目要求的。 1．设集合A{xR x 4}，B{0,1,4,9,16}，则A B A．{0,1} B．{0,1,4} C．{0,1,4,9} D．{1,4,9,16} 【命题意图】本小题主要考查集合的运算、不等式等知识；考查运算求解能力等；考查函数 与方程思想、化归与转化思想等；体现基础性，导向对发展数学运算等核心素 养的关注． 【试题解析】解法一：（排除法）因x0符合题意，排除D；因为x9符合题意，排除A，B； 故选C． 解法二：因为A{xR x 4}{xR0≤x＜16}，所以A B {0,1,4,9}， 故选C． 2．若复数z满足z(1i)1i，则z4= A．1 B．1 C．i D．16 【命题意图】本小题主要考查复数的概念、四则运算等基础知识；考查运算求解能力、推理 论证能力；考查化归与转化思想、函数与方程思想；体现基础性，导向对数学 运算等核心素养的关注． 高三数学试题 第1页（共8页）【试题解析】解法一：设zabi(a,bR )，则(abi)(1i)ab(ba)i1i， 解得a0，b1，所以zi，所以z4 1，故选A． 1+i (1i)2 2i 解法二：因为z(1i)1i，所以z   i，z4 1，故选A． 1i (1i)(1i) 2 解法三：方程两边同时平方，有z2(2i)2i，所以z2 1，z4 1，故选A． π 3．已知向量a,b,c满足|a||b|，a与b的夹角为 ，abc0，则a与c的夹角为 3 π π 2π 5π A． B． C． D． 6 3 3 6 【命题意图】本小题主要考查向量的数量积等基础知识，考查运算求解等能力，考查化归与 转化，数形结合等思想，体现基础性，导向对发展数学运算等核心素养的关注. 【试题解析】解法一：设|a||b|1，由题得cab，所以 π 1 3 aca(ab)a2 ab|a|2 |a||b|cos 1  ， 3 2 2 c2 (ab)2 a2 2abb2 3，所以|c| 3， ac 3 5π 所以cosa,c  ，又a,c[0,π]，所以a,c ， |a||c| 2 6 故选D． 1 3 解法二：建立直角坐标系，设|a||b|1，则a(1,0)，b( , )， 2 2 3 3 3 3 3 所以cab( , )，所以ac ，|c| ( )2 ( )2  3， 2 2 2 2 2 ac 3 5π 所以cosa,c  ，又a,c[0,π]，所以a,c ， |a||c| 2 6 故选D． 解法三：运用向量运算的几何表示，构造平面图形，观察图形可快速得解. 4．若sin 3cos2，则tan 3 3 A． 3 B． C． D． 3 3 3 【命题意图】本小题主要考查三角函数的定义、三角恒等变换等知识，考查运算求解能力等， 考查函数与方程思想、特殊与一般思想等，体现基础性，导向对发展直观想象、 高三数学试题 第2页（共8页）数学运算、逻辑推理等核心素养的关注. 1 3 3 【试题解析】解法一：（特殊法）由题知sin ，cos 满足条件，所以tan ． 2 2 3 故选C． 1 3 π 解法二：由题得 sin cos1，所以sin( )1， 2 2 3 π π π 所以 2kπ ，kZ，所以2kπ ，kZ 3 2 6 π π 3 tantan(2kπ )tan  ．故选C． 6 6 3 解法三：由题得sin22 3sincos3cos24， 所以3sin22 3sincoscos20，即( 3sincos)2 0， 3 所以 3sincos0，即tan ．故选C． 3 解法四：由题得sin2 3cos，所以(2 3cos)2 cos21， 所以4cos24 3cos30，即(2cos 3)2 0， 3 1 3 所以cos ，sin2 3cos ，所以tan ．故选C． 2 2 3 解法五：观察sin 3cos2，知sin,cos同正，为第一象限角，其正  切值为正，排除A，B． 若tan 3，可取 ，则sin 3cos 3， 3 不符合已知条件，排除D，故应选C．  a x 1,x 4, 5．若函数 f(x) x 在R上单调递增，则实数a的取值范围是  ax3,x4 A. (0,1) B．(1,4] C．(1,8] D．(1,16] 【命题意图】本小题主要考查分段函数、基本初等函数、函数的单调性等知识，考查运算求 解能力、抽象概括能力等，考查函数与方程思想、转化和化归的思想等，体现 基础性和综合性，导向对发展数学运算、逻辑推理、数学抽象等核心素养的关 注． 【试题解析】由指数函数的底数要求只讨论a0且a1， 高三数学试题 第3页（共8页）a 由题意得x 4, f(x)x 3为单调递增，故0a≤16， x 又x4时， f(x)ax3为单调递增，故a1， a 再由a1≤4 1，即得a≤4，综上，1a≤4， 4 故选B． 6．已知正四棱台的顶点都在同一球面上，其上、下底面边长分别为 2,2 2，高为3，则该 球的表面积为 20 5π A．40π B．20π C．16π D． 3 【命题意图】本小题主要考查多面体、球的表面积等基础知识，考查空间想象能力、运算求 解能力等，考查数形结合、转化和化归的思想等，体现基础性和综合性，导向 对发展直观想象、数学运算、逻辑推理等核心素养的关注． 【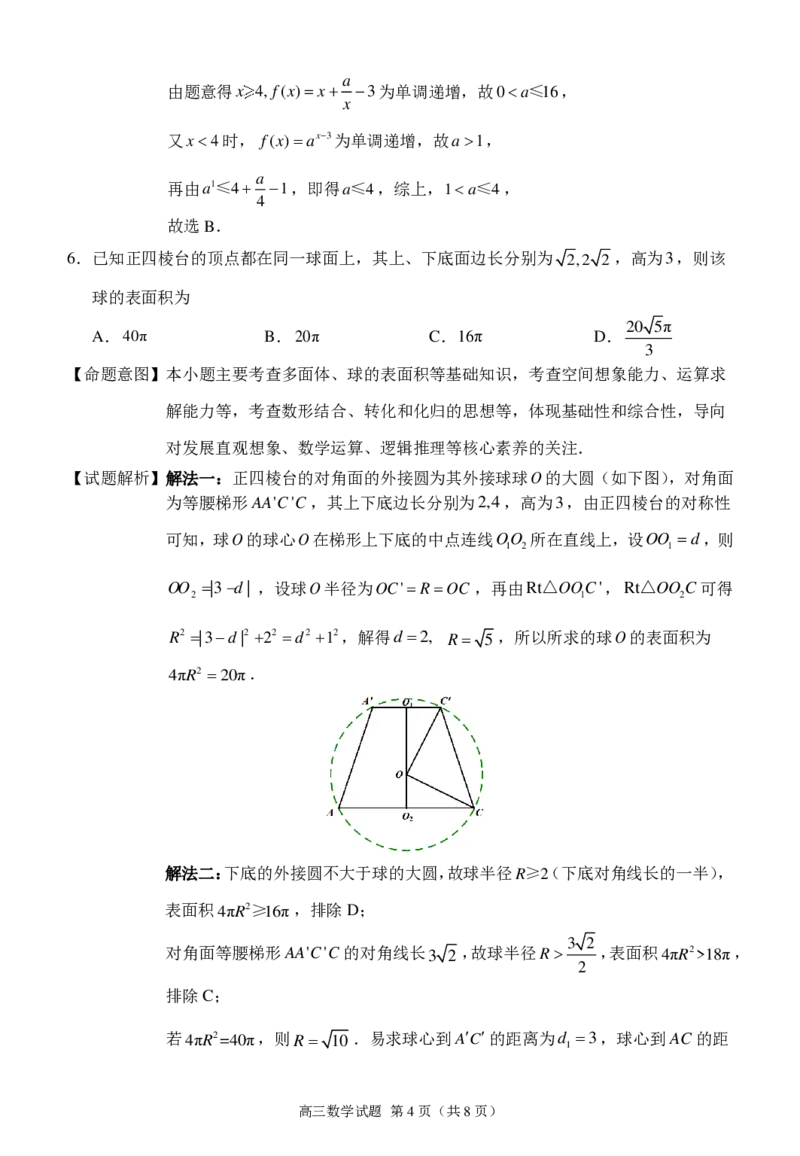试题解析】解法一：正四棱台的对角面的外接圆为其外接球球O的大圆（如下图），对角面 为等腰梯形AA'C'C，其上下底边长分别为2,4，高为3，由正四棱台的对称性 可知，球O的球心O在梯形上下底的中点连线OO 所在直线上，设OO d，则 1 2 1 OO |3d| ，设球O半径为OC'ROC ，再由Rt△OOC'，Rt△OOC可得 2 1 2 R2 |3d|2 22 d2 12，解得d 2, R 5，所以所求的球O的表面积为 4πR2 20π． 解法二：下底的外接圆不大于球的大圆，故球半径R≥2（下底对角线长的一半）， 表面积4πR2≥16π，排除D； 3 2 对角面等腰梯形AA'C'C的对角线长3 2 ，故球半径R ，表面积4πR2>18π， 2 排除C； 若4πR2=40π，则R 10 ．易求球心到AC的距离为d 3，球心到AC 的距 1 高三数学试题 第4页（共8页）离为d  6，无法满足|d d |h3，或|d d |h3，故A不正确． 2 1 2 1 2 故选B． 7．已知函数 f(x)满足 f(x y) f(x) f(y)2xy，若 f(1)1，则 f(25) A．25 B．125 C．625 D．15625 【命题意图】本小题主要考查函数的基本性质、递推数列等基础知识；考查推理论证、运算 求解等能力；考查化归与转化、特殊与一般的函数思想；体现基础性，综合性， 导向对逻辑推理、数学运算等核心素养的关注． 【试题解析】解法一：由题意取xn(nN),y1，可得 f(n1) f(n) f(1)2n  f(n1)2f(1)2(n1)2n  f(n2)3f(1)2(n2)2(n1)2n  (n1)f(1)2(12n) (n1)f(1)n(n1) 即知 f(n)nf(1)n(n1)nn(n1)n2，则 f(25)625． 故选C． 解法二：令g(x)=f(x)x2,则g(x y) f(x y)(x y)2  f(x) f(y)2xy(x y)2  f(x) f(y)x2 y2 g(x)g(y)， 所以g(n)g(n1)g(1)ng(1)n(f(1)12)0， 即g(n) f(n)n2 0，所以 f(n)n2，则 f(25)625．故选C． 解法三：由 f(xy) f(x) f(y)2xy可构造满足条件的函数 f(x)x2， 可以快速得到 f(25)625． 故选C． 1 1 8．已知函数 f(x)cosx cos2x cos3x，则 2 3 A．π是 f(x)的一个周期 B．xπ是 f(x)图象的一条对称轴 π C．( ,0)是 f(x)图象的一个对称中心 D． f(x)在区间(0,π)内单调递减 2 【命题意图】本小题主要考查三角函数的图象与性质、三角恒等变换等知识；考查推理论 高三数学试题 第5页（共8页）证能力、运算求解能力等，考查特殊与一般思想、函数与方程思想、化归与转化 思想等；体现基础性、综合性，导向对发展直观想象、逻辑推理、数学运算、数 学抽象等核心素养的关注． 1 1 1 1 5 【试题解析】解法一：（排除法）因为 f(π)cosπ cos2π cos3π1   ， 2 3 2 3 6 1 1 1 1 11 f(0)cos0 cos0 cos01   ，所以 f(π) f(0)，故A错误； 2 3 2 3 6 同理 f(π)f(0)，故C错误； π π 1 1 3π 1 因为 f( )cos  cosπ cos  ， 2 2 2 3 2 2 2π 2π 1 4π 1 6π 5 f( )cos  cos  cos  3 3 2 3 3 3 12 π 2π 所以 f( ) f( )，故D错误． 2 3 故选B． 1 1 解法二：因为 f(xπ)cos(xπ) cos2(xπ) cos3(xπ)， 2 3 1 1 cosx cos2x cos3x 2 3 所以 f(xπ) f(x)，故A错误； 1 1 因为 f(πx)cos(πx) cos2(πx) cos3(πx) 2 3 1 1 cosx cos2x cos3x，所以 f(πx) f(πx)，故B正确； 2 3 1 1 1 1 因为 f(x)cos(x) cos2(x) cos3(x) cosx cos2x cos3x， 2 3 2 3 所以f(x) f(xπ)，故C错误； 因为 f(x)sinxsin2xsin3x[sin(2xx)sin(2xx)]sin2x 2sin2xcosxsin2xsin2x(2cosx1) π 所以当x(0, )时，sin2x0，2cosx10，此时 f(x)0； 2 π 2π 2π 同理当x( ， )时， f(x)0；当x( ,π)时， f(x)0； 2 3 3 π π 2π 所以 f(x)在(0, )上单调递减，在( , )上单调递增， 2 2 3 高三数学试题 第6页（共8页）2π 在( ,π)上单调递减，故D错误； 3 故选B． 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题 目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。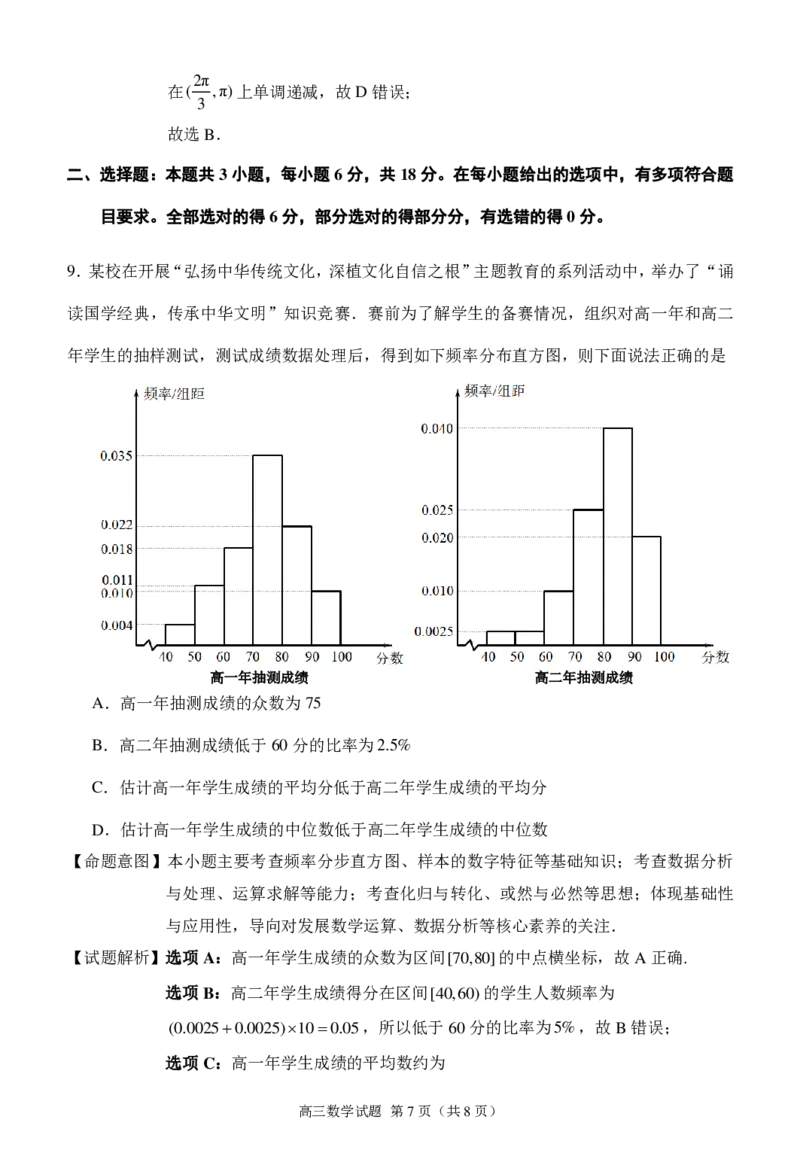 9．某校在开展“弘扬中华传统文化，深植文化自信之根”主题教育的系列活动中，举办了“诵 读国学经典，传承中华文明”知识竞赛．赛前为了解学生的备赛情况，组织对高一年和高二 年学生的抽样测试，测试成绩数据处理后，得到如下频率分布直方图，则下面说法正确的是 高一年抽测成绩 高二年抽测成绩 A．高一年抽测成绩的众数为75 B．高二年抽测成绩低于60分的比率为2.5% C．估计高一年学生成绩的平均分低于高二年学生成绩的平均分 D．估计高一年学生成绩的中位数低于高二年学生成绩的中位数 【命题意图】本小题主要考查频率分步直方图、样本的数字特征等基础知识；考查数据分析 与处理、运算求解等能力；考查化归与转化、或然与必然等思想；体现基础性 与应用性，导向对发展数学运算、数据分析等核心素养的关注． 【试题解析】选项A：高一年学生成绩的众数为区间[70,80]的中点横坐标，故A正确. 选项B：高二年学生成绩得分在区间[40,60)的学生人数频率为 (0.00250.0025)100.05，所以低于60分的比率为5%，故B错误； 选项C：高一年学生成绩的平均数约为 高三数学试题 第7页（共8页）450.04550.11650.18750.35850.22950.174分； 高二年学生成绩的平均数约为 450.025550.025650.1750.25850.4950.280.75分. 因为7480.75，故C正确. 选项D：高一年学生成绩的中位数位于[70,80)，高二年学生成绩的中位数位于 [80,90)，故D正确． 故选ACD． 10．已知函数 f xax3 bx1，则 A． f x的值域为R B． f x图象的对称中心为(0,1) C．当ab0时， f x无极值 D．当b3a0时， f x在区间(1,1)内单调递减 【命题意图】本小题主要考查导数的应用、函数的基本性质等基础知识；考查推理论证、运 算求解等能力；考查数形结合、化归与转化等思想；体现基础性与综合性，导 向对发展直观想象、逻辑推理、数学运算等核心素养的关注． 【试题解析】A选项：当a,b至少一个不为0，则函数 f x为三次函数或者一次函数， 值域均为R；当a,b均为0时，值域为{1}，故A错误． B选项：函数g(x) f x1ax3bx满足g(x)ax3 bxg(x)， 可知g(x)为奇函数，其图象关于(0,0)中心对称， 所以 f x的图象为g(x)的图象向上移动一个单位后得到的， 即关于(0,1)中心对称，【或者用 f x2 f x验证】，故B正确． C 选项： fx3ax2 b，当ab0时，3ax2 b恒大于0或者恒小于0，所以 函数 f x在R上单调，无极值．故C正确． D选项： fx3ax2 b，当b3a0时，取a1,b1，当x(1,1)时， fx3x2 1， f x在区间(1,1)上不单调．D选项错误； b b 另一方面，当b0时， f 'x3ax2 b≥01 ≤x≤ 1， f x在 3a 3a 高三数学试题 第8页（共8页）b b [ , ]((1,1))单调递增. 故D错误． 3a 3a 故选BC． 11．在平面直角坐标系xOy中，已知F(1,0),F (1,0)，M(x,y)是动点．下列命题正确的是 1 2 A．若|MF ||MF |2，则M 的轨迹的长度等于2 1 2 4y2 B．若 MF  MF 1，则M 的轨迹方程为4x2  1 1 2 3 C．若|MF ||MF |4，则M 的轨迹与圆x2  y2 6没有交点 1 2 |MF | D．若 1 2，则OM OF 的最大值为3 |MF | 2 2 【命题意图】本小题主要考查曲线与方程、向量数量积等基础知识；考查运算求解、推理论 证等能力；考查化归与转化、数形结合、函数与方程等思想；体现基础性、综 合性与创新性，导向对发展数学运算、直观想象、逻辑推理、数学抽象等核心 素养的关注． 【试题解析】选项A：因为|MF ||MF |2|FF |，所以M 的轨迹为线段FF ， 1 2 1 2 1 2 从而M 的轨迹的长度等于2，故A正确． 选项B：因为 MF  MF 1，由双曲线的定义知， 1 2 M 的轨迹是以F,F 为焦点的双曲线的右支，而结论的方程中未限制范围，故B 1 2 4y2 错误.（由c1,2a1，得M 的轨迹方程为4x2  1(x0)）． 3 选项C：解法一：由|MF ||MF |4，得 (x1)2 y2 (x1)2 y24 ，化简 1 2 (x2y21)24x2 16, 33 得，(x2  y2 1)2 4x2 16，联立 得x2  6， x2y2 6 4 这与x2≤6矛盾，所以方程组无解，故M 的轨迹与圆x2y2 6没有交点， 故C正确． 解法二：若有交点M(x,y)，则MF MF (1x,y)(1x,y)x2  y2 15， 1 2 又MF MF |MF ||MF |cosMF,MF 4|cosMF,MF ≤4，矛盾，所 1 2 1 2 1 2 1 2 以M 的轨迹与圆x2y2 6没有交点，故C正确． 选项D： |MF | 解法一：由 1 2得， (x1)2  y2 2 (x1)2  y2 ， |MF | 2 高三数学试题 第9页（共8页）5 16 化简得(x )2  y2  ， 3 9 5 4 所以M 的轨迹是以( ,0)为圆心，半径为 的圆. 3 3 OM OF 等于OM 在x轴上的投影的长度， 2 由图知其最大值为3，故D正确． 5 4 解法二：同法一得M 的轨迹是以( ,0)为圆心，半径为 的圆. 3 3 OM OF (x,y)(1,0)x，由圆的方程知x可取到最大值3， 2 故D正确． |MF | 解法三：由 1 2得， |MF | 2 |MF ||MF ||MF |≤|FF |2,|MO|≤|OF ||MF |≤3，当M 在F F的反向 1 2 2 1 2 2 2 2 1 延长线上时取等号． ① OM OF |MO|cosMOF≤|MO|≤3； 2 2 ②当M 在F F的反向延长线上，且|MF |2时， 2 1 2 |MF | 满足条件 1 2，此时OM OF 3． |MF | 2 2 所以OM OF 的最大值为3，故D正确． 2 故选ACD． 三、填空题：本题共3小题，每小题5分，共15分。 12．若曲线ylnx在x2处的切线与直线axy10垂直，则a ． 【命题意图】本小题主要考查导数的几何意义、直线的位置关系等基础知识；考查运算求解、 推理论证等能力；考查化归与转化、数形结合、函数与方程等思想；体现基础 性与应用性，导向对数学运算、逻辑推理等核心素养的关注． 1 1 【试题解析】由题意得函数ylnx的导函数为y ，故在x2处切线的斜率为 ， x 2 1 直线axy10的斜率存在为a，根据题意得， a1，解得a2. 2 故答案为2. 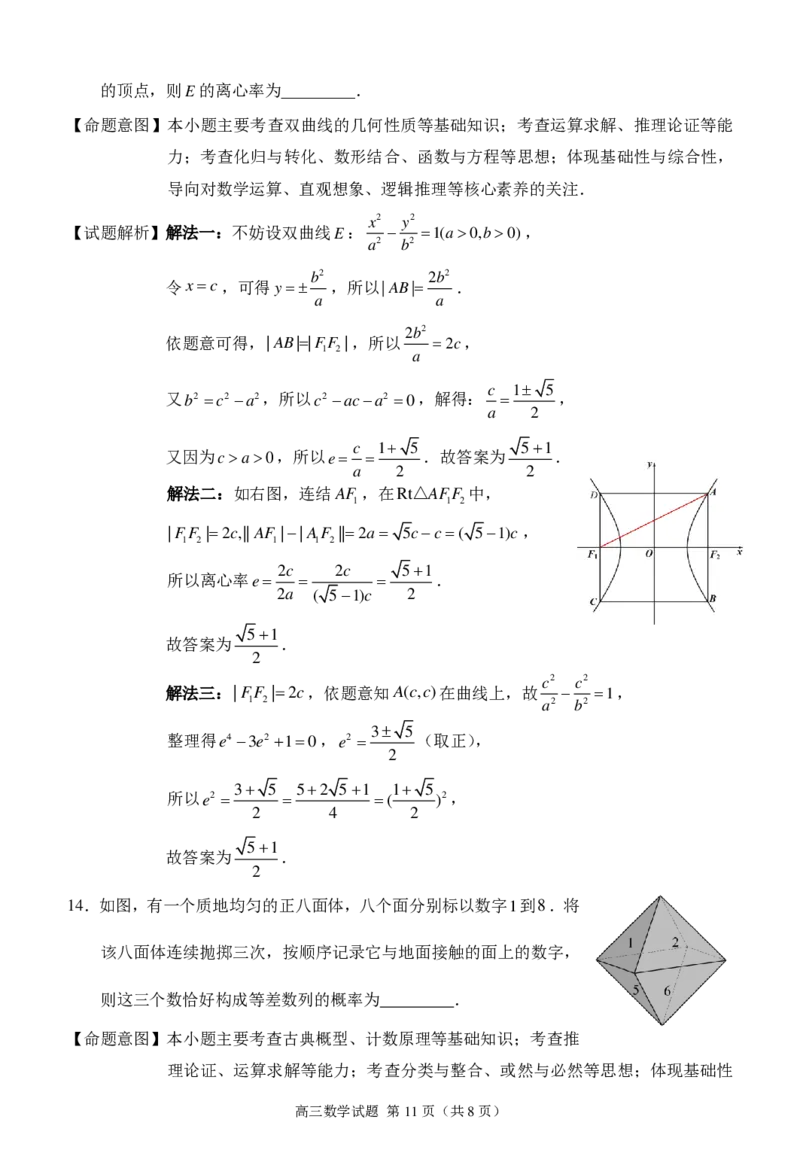13．过双曲线E的两个焦点分别作实轴的垂线，交E于四个点，若这四个点恰为一个正方形 高三数学试题 第10页（共8页）的顶点，则E的离心率为 ． 【命题意图】本小题主要考查双曲线的几何性质等基础知识；考查运算求解、推理论证等能 力；考查化归与转化、数形结合、函数与方程等思想；体现基础性与综合性， 导向对数学运算、直观想象、逻辑推理等核心素养的关注． x2 y2 【试题解析】解法一：不妨设双曲线E：  1(a0,b0)， a2 b2 b2 2b2 令xc，可得y ，所以|AB| ． a a 2b2 依题意可得，|AB||FF |，所以 2c， 1 2 a c 1 5 又b2 c2 a2，所以c2 aca2 0，解得：  ， a 2 c 1 5 51 又因为ca0，所以e  ．故答案为 ． a 2 2 解法二：如右图，连结AF ，在Rt△AFF 中， 1 1 2 |FF |2c,||AF ||AF ||2a 5cc( 51)c， 1 2 1 1 2 2c 2c 51 所以离心率e   ． 2a ( 51)c 2 51 故答案为 ． 2 c2 c2 解法三：|FF |2c，依题意知A(c,c)在曲线上，故  1， 1 2 a2 b2 3 5 整理得e4 3e2 10，e2  （取正）， 2 3 5 52 51 1 5 所以e2   ( )2， 2 4 2 51 故答案为 ． 2 14．如图，有一个质地均匀的正八面体，八个面分别标以数字1到8．将 该八面体连续抛掷三次，按顺序记录它与地面接触的面上的数字， 则这三个数恰好构成等差数列的概率为 ． 【命题意图】本小题主要考查古典概型、计数原理等基础知识；考查推 理论证、运算求解等能力；考查分类与整合、或然与必然等思想；体现基础性 高三数学试题 第11页（共8页）与应用性，导向对发展数据分析、逻辑推理、数学运算、数学建模等核心素养 的关注． 【试题解析】由题意可知所有可能情况共有83种，按顺序记录的三个数恰好构成等差数列， 可以按照公差为3,2,1,0,1,2,3分类，其中公差为3,2,1和3,2,1的做法数对 应相等. 公差为0的有(1,1,1),(2,2,2),,(8,8,8)共8种做法； 公差为1的有(1,2,3),(2,3,4), (6,7,8)共6种做法，同公差为1的； 公差为2的有(1,3,5),(2,4,6),(3,5,7),(4,6,8)共4种做法，同公差为2的； 公差为3的有(1,4,7),(2,5,8)共2种做法，同公差为3的； 8624222 32 1 所以三个数恰好构成等差数列的概率P   . 888 512 16 1 故答案为 . 16 高三数学试题 第12页（共8页）四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。 15．（13分） cb sin(AB) △ABC的内角A,B,C所对的边分别为a,b,c，已知  ． c sinC （1）求A； （2）若BAC的角平分线与BC交于点D，AD2，AC2 3，求ac． 【命题意图】本小题主要考查正弦定理、余弦定理等基础知识，考查逻辑推理能力、运算求 解能力等，考查函数与方程思想、数形结合思想等，体现基础性和综合性，导 向对发展直观想象、逻辑推理、数学运算等核心素养的关注。 sinC sinB sin(A B) 【试题解析】（1）依题意，由正弦定理可得 ， ···· 1分 sinC sinC 所以sinC sinB sin(A B)， ······················································· 2分 又sinC sin[π (A B)] sin(A B)， ··············································· 3分 所以sinB sin(A B) sin(A B) 2cosAsinB， ································ 4分 1 因为B (0,π)，所以sinB 0，所以cosA ， ······························· 5分 2 π 又A (0,π)，所以A ． ····························································· 6分 3 （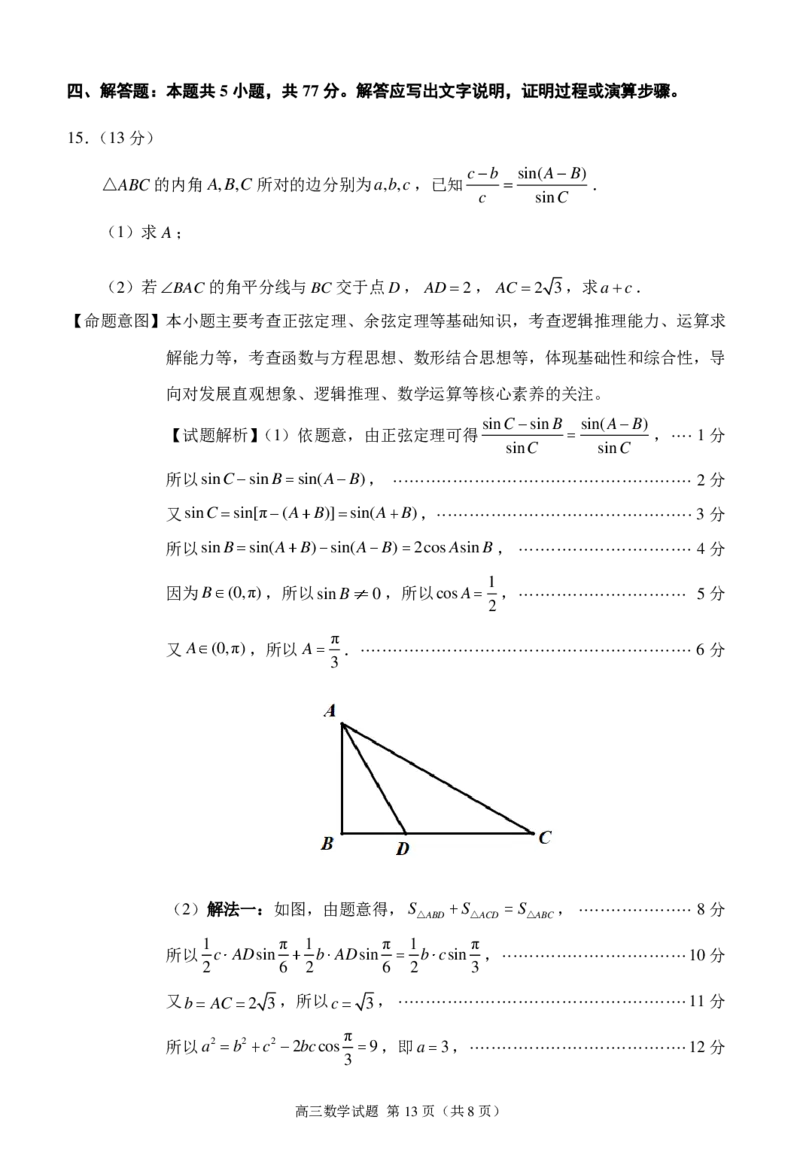2）解法一：如图，由题意得，S S S ， ····················· 8分 △ABD △ACD △ABC 1 π 1 π 1 π 所以 c ADsin b ADsin b csin ， ·································· 10分 2 6 2 6 2 3 又b AC 2 3，所以c 3， ····················································· 11分 π 所以a2 b2 c2 2bccos 9，即a 3， ········································ 12分 3 高三数学试题 第13页（共8页）所以a c 3 3． ····································································· 13分 π 解法二：如图，△ACD中，因为AD 2，AC 2 3， CAD ， 6 π 由余弦定理得，CD2 22 (2 3)2 2 2 2 3cos 4， ····················· 8分 6 所以CD AD 2， ······································································ 9分 π 所以C CAD ， ··································································· 10分 6 π 所以B π A C ， ······························································· 11分 2 π π 所以a bcos 3，c bsin 3， ·············································· 12分 6 6 所以a c 3 3． ····································································· 13分 16．（15分） 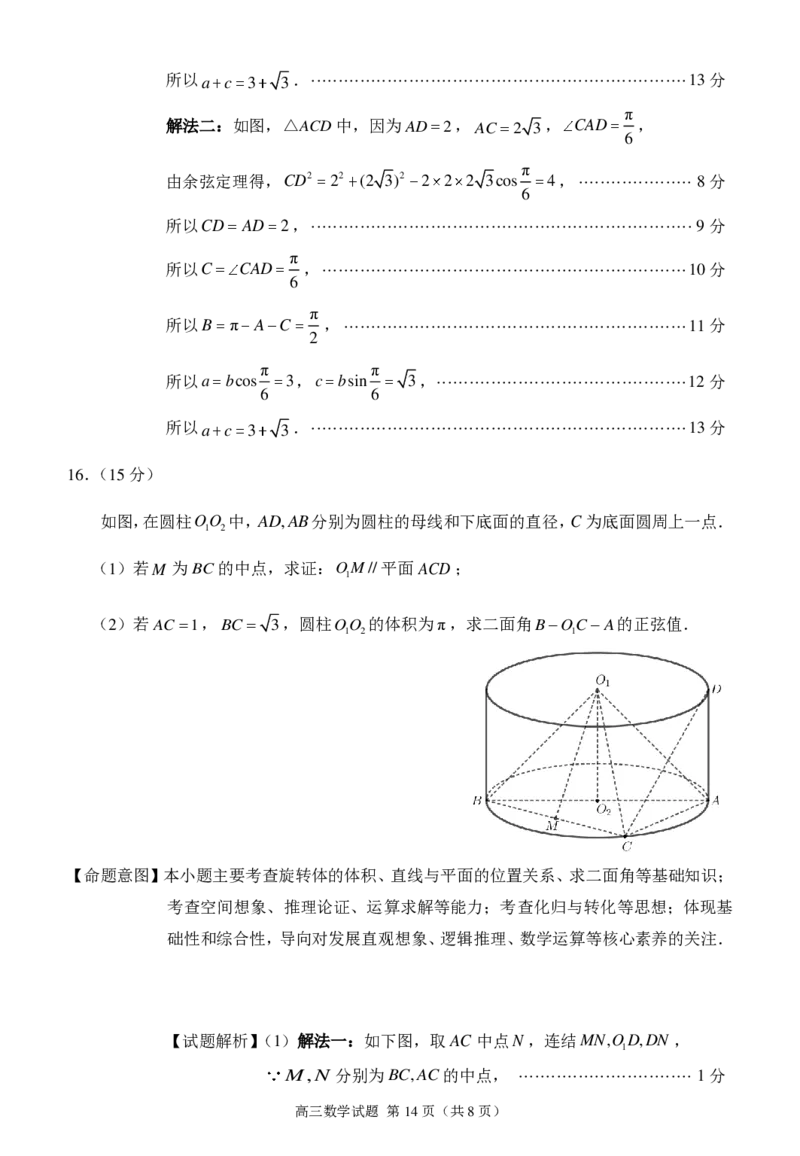如图，在圆柱OO 中，AD,AB分别为圆柱的母线和下底面的直径，C为底面圆周上一点． 1 2 （1）若M 为BC的中点，求证：OM//平面ACD； 1 （2）若AC 1，BC 3，圆柱OO 的体积为π，求二面角BOCA的正弦值． 1 2 1 【命题意图】本小题主要考查旋转体的体积、直线与平面的位置关系、求二面角等基础知识； 考查空间想象、推理论证、运算求解等能力；考查化归与转化等思想；体现基 础性和综合性，导向对发展直观想象、逻辑推理、数学运算等核心素养的关注． 【试题解析】（1）解法一：如下图，取AC 中点N，连结MN,OD,DN ， 1 M,N 分别为BC,AC的中点， ································ 1分 高三数学试题 第14页（共8页）1 MN∥AB ，MN  AB AO ， ······························ 2分 2 2 又 圆柱上下底面平行， 且与平面AOOD交于AO 和OD， 2 1 2 1  AO∥OD，且AO =OD， ······································ 3分 2 1 2 1 又MN∥OD且MN=OD， 1 1 四边形MNDO 为平行四边形， ·································· 4分 1 OM∥ND， ·························································· 5分 1 又OM 平面ACD，ND平面ACD 1 OM//平面ACD． ················································· 6分 1 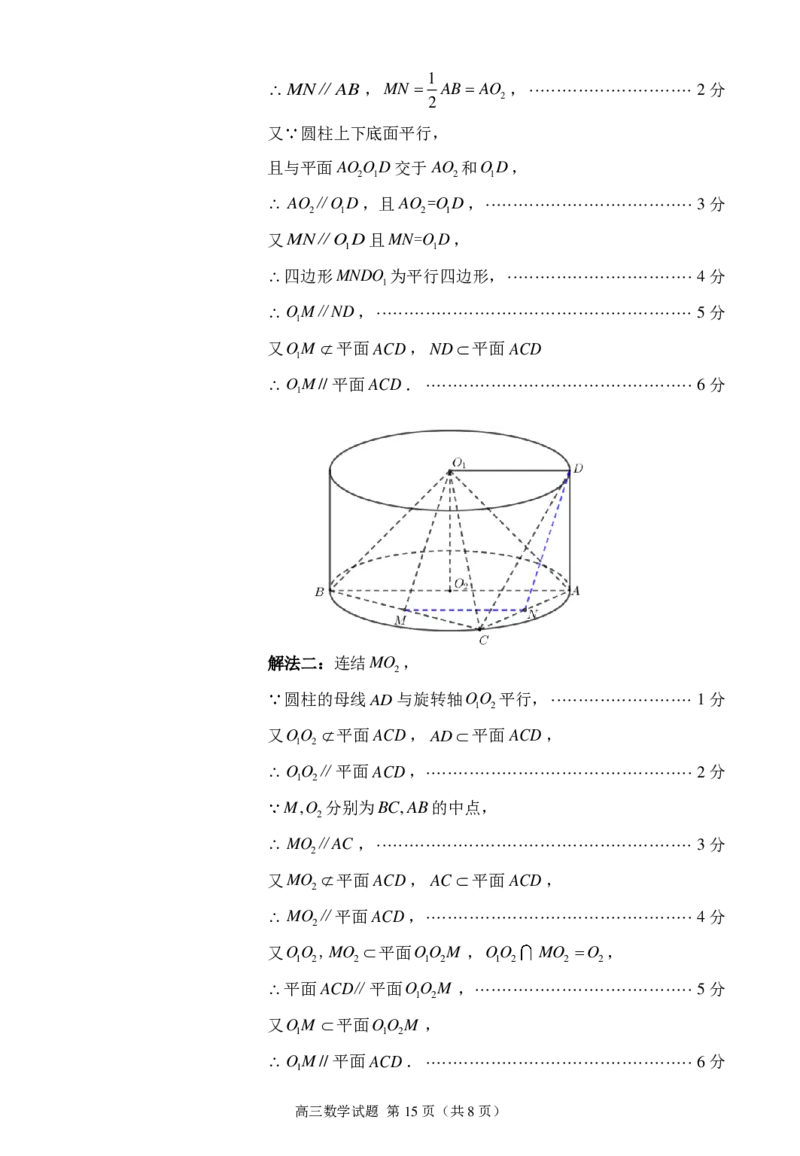解法二：连结MO ， 2 圆柱的母线AD与旋转轴OO 平行， ·························· 1分 1 2 又OO 平面ACD，AD平面ACD， 1 2 OO∥平面ACD， ················································· 2分 1 2 M,O 分别为BC,AB的中点， 2 MO∥AC， ·························································· 3分 2 又MO 平面ACD，AC平面ACD， 2 MO∥平面ACD， ················································· 4分 2 又OO ,MO 平面OO M ，OO MO O ， 1 2 2 1 2 1 2 2 2 平面ACD∥平面OO M ， ········································ 5分 1 2 又OM 平面OO M ， 1 1 2 OM//平面ACD． ················································· 6分 1 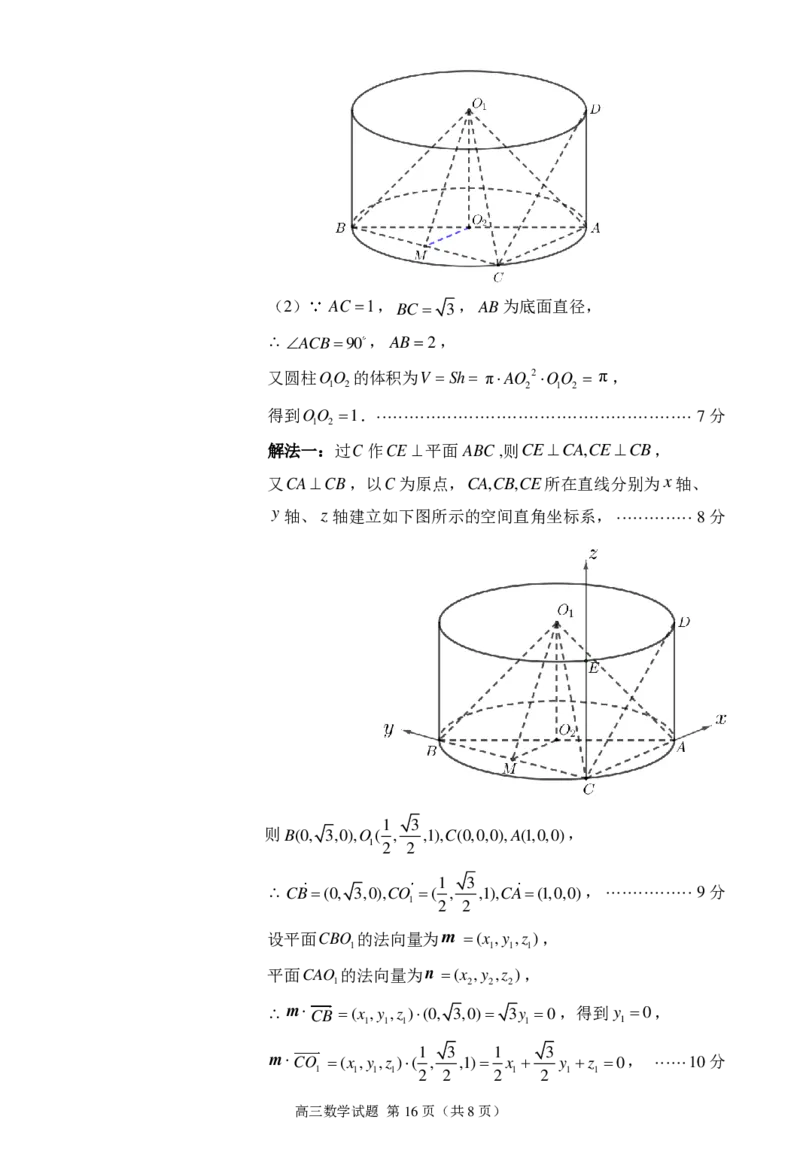高三数学试题 第15页（共8页）（2） AC 1，BC 3，AB为底面直径， ACB90 ，AB2， 又圆柱OO 的体积为V Sh πAO2OO  π， 1 2 2 1 2 得到OO 1． ·························································· 7分 1 2 解法一：过C作CE 平面ABC,则CECA,CECB， 又CACB，以C为原点，CA,CB,CE所在直线分别为x轴、 y轴、z轴建立如下图所示的空间直角坐标系， ·············· 8分 1 3 则B(0, 3,0),O( , ,1),C(0,0,0),A(1,0,0)， 1 2 2 1 3 CB(0, 3,0),CO ( , ,1),CA(1,0,0)， ················ 9分 1 2 2 设平面CBO 的法向量为m (x,y ,z )， 1 1 1 1 平面CAO 的法向量为n (x ,y ,z )， 1 2 2 2 m CB (x,y ,z )(0, 3,0) 3y 0，得到y 0， 1 1 1 1 1 1 3 1 3 mCO (x,y ,z )( , ,1) x  y z 0， ······ 10分 1 1 1 1 2 2 2 1 2 1 1 高三数学试题 第16页（共8页）取x 2,z 1，可得m=(2,0,1)， ··························· 11分 1 1 又n CA (x ,y ,z )(1,0,0)0，得到x 0， 2 2 2 2 1 3 1 3 nCO (x ,y ,z )( , ,1) x  y z 0， ··· 12分 1 2 2 2 2 2 2 2 2 2 2 取y 2,z  3 ，可得n(0,2, 3)， ······················· 13分 2 2 设二面角BOCA的大小为， 1 |mn| 3 3 则|cos|  = ， ······························ 14分 |m||n| 5 7 35 32 4 70 则sin 1cos2  35 35 4 70 即二面角BOCA的正弦值为 ． ······················· 15分 1 35 解法二：如下图，连结MO ，过O 作O I OM ，垂足I ， 2 2 2 1 取AC 中点N，连结ON ，过O 作O J ON ，垂足J ， 1 2 2 1 平面O IJ 交直线OC于点K，连结O K,IJ ， 2 1 2 M,O 分别为BC，AB的中点， 2 MO∥AC，又AC BC， 2 MO BC ， ························································· 8分 2 OO 平面ABC， 1 2 OO  BC，又MO OO O ， 1 2 2 1 2 2 BC 平面OO M ， ··············································· 9分 1 2 O I 平面OO M ，BC  O I ， 2 1 2 2 又O I OM ，BC OM M ， 2 1 1 O I 平面BCO ， 2 1 同理可证O J 平面ACO ， 2 1 O I  OC, O J  OC,，又O I O J O ， 2 1 2 1 2 2 2 OC 平面O IJ ，即OC 平面O IKJ， ··················· 10分 1 2 1 2 OCIK,OCJK， ············································· 11分 1 1 IKJ 为二面角BOCA的平面角， ······················· 12分 1 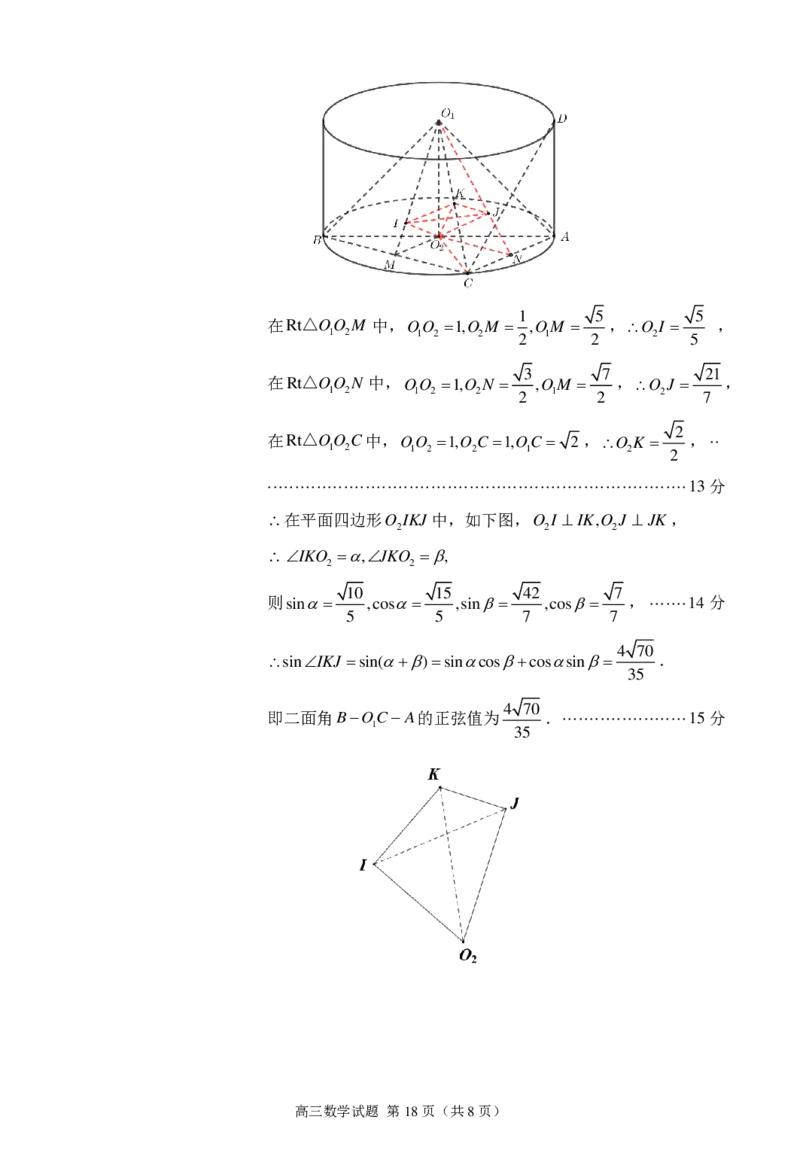高三数学试题 第17页（共8页）1 5 5 在Rt△OO M 中，OO 1,O M  ,OM  ，O I  ， 1 2 1 2 2 2 1 2 2 5 3 7 21 在Rt△OO N 中，OO 1,O N  ,OM  ，O J  ， 1 2 1 2 2 2 1 2 2 7 2 在Rt△OO C中，OO 1,O C 1,OC  2 ，O K  ， ·· 1 2 1 2 2 1 2 2 ············································································· 13分 在平面四边形O IKJ中，如下图，O I IK,O J JK， 2 2 2 IKO ,JKO , 2 2 10 15 42 7 则sin ,cos ,sin ,cos ， ······· 14分 5 5 7 7 4 70 sinIKJ sin()sincoscossin ． 35 4 70 即二面角BOCA的正弦值为 ． ······················· 15分 1 35 高三数学试题 第18页（共8页）17.（15分） x2 y2 2 5 已知椭圆E：  1ab0的左、右焦点分别为F,F ，离心率为 ，且经过点(2, )． a2 b2 1 2 3 3 （1）求E的方程； （2）过F 且不垂直于坐标轴的直线l交E于A,B两点，点M 为AB的中点，记△MFF 的 1 1 2 S 面积为S ，△BFF 的面积为S ，求 1 的取值范围． 1 1 2 2 S 2 【命题意图】本题主要考查椭圆的标准方程、直线与椭圆的位置关系等基础知识；考查运算 求解、推理论证等能力；考查化归与转化、数形结合、函数与方程等思想；体 现基础性与综合性，导向对数学运算、直观想象、逻辑推理等核心素养的关注． c2 a2 b2 4 【试题解析】（1）因为e2    ， ······················································ 1分 a2 a2 9 所以5a2 9b2， ··········································································· 2分 5 4 25 因为点(2, )在椭圆上，所以  1， ······································· 3分 3 a2 9b2 4 25 即  1，解得a2 9， ························································· 4分 a2 5a2 所以b2 5， ··············································································· 5分 x2 y2 所以椭圆E的方程为  1． ····················································· 6分 9 5 c 2 4 25 【若方程求错，能体现  ,  1,c2 a2 b2各得1分】 a 3 a2 9b2 （1）解法一： 由（1）得F(2,0)，依题意设l:xmy（2 m≠0）， ····························· 7分 1 x2 y2   1, 由9 5 消去x，得(5m2 9)y2 20my250， ························· 8分  xmy2  20m y  y  ,   1 2 5m2 9 设A(x ,y ),B(x ,y )，则 ······································ 9分 1 1 2 2 25 y y   1 2 5m2 9 y  y 设M(x ,y )，则y  1 2 ， o o o 2 高三数学试题 第19页（共8页）1 y  y  FF  y 1 2 S 2 1 2 o 2 1 y 1    1 1， ········································· 10分 S 1 y 2 y 2  FF  y 2 2 2 1 2 2  20m y  y  ,   1 2 5m2 9 (y  y )2 16m2 由 得， 1 2  ， y y  25 y 1 y 2 5m2 9  1 2 5m2 9 y y 16m2 即 1  2 2 ································································ 11分 y y 5m2 9 2 1 m2 1 16 16m2 因为m2 0，所以0  ，所以  0 ·················· 12分 5m2 9 5 5 5m2 9 16 y y 所以  1  2 20， 5 y y 2 1 y 令 1 t(t0且t1)， ······························································· 13分 y 2 16 1 1 则 t 20，解得5t ，且t 1， ···························· 14分 5 t 5 1 S 所以0 t1 2，所以 1 的取值范围为(0,2)． ····························· 15分 2 S 2 解法二： 由（1）得F(2,0)，依题意设l:yk(x2)(k 0)， ···························· 7分 1 x2 y2   1, 由9 5 消去y，得(9k2 5)x2 36k2x36k2 450， ················ 8分  yk(x2)  36k2 x x  ,  1 2 9k2 5 设A(x ,y ),B(x ,y )，则 ， 1 1 2 2  36k2 45 x x    1 2 9k2 5  20k y  y k(x x )4k  ,   1 2 1 2 9k2 5 所以 ············································· 9分  y y k2(x 2)(x 2) 25k2   1 2 1 2 9k2 5 y  y 设M(x ,y )，则y  1 2 ， o o o 2 高三数学试题 第20页（共8页）1 y  y  FF  y 1 2 S 2 1 2 o 2 1 y 1 y 1    1 1  1 1 ， ···························· 10分 S 1 y 2 y 2 y 2  FF  y 2 2 2 2 1 2 2 y 令 1 t(t0且t1)， ······························································· 11分 y 2  20k  20k y  y  , (t1)y  ,   1 2 9k2 5   2 9k2 5 则y ty 代入 可得， 1 2  y y  25k2  ty 2  25k2 ,   1 2 9k2 5   2 9k2 5 (t1)2 16 消去y 得：  ， ······················································ 12分 2 t 9k2 5 16 16 因为k2 0，所以  0， ·············································· 13分 5 9k2 5 16 (t1)2 1 所以  0，解得5t ，且t 1， ························· 14分 5 t 5 1 S 所以0 t1 2，所以 1 的取值范围为(0,2)． ····························· 15分 2 S 2 18．（17分） 已知曲线C : ylnx，C : yex． 1 2 （1）证明：ex lnx； （2）若曲线E 关于直线l对称的曲线为E ，则称l为E 与E 的一条对称轴.请写出C 与C 1 2 1 2 1 2 的一条对称轴，并探究是否存在其它的对称轴； （3）已知A,B 是C 上的两点，A ,B 是C 上的两点，若四边形ABB A 为正方形，其周 1 1 1 2 2 2 1 1 2 2 长为L，证明：L4 e2．（参考数据：ln20.693, e 1.649） 【命题意图】本题主要考查基本初等函数、函数的单调性与对称性、导数的几何意义、导数 的应用等基础知识；考查运算求解、推理论证等能力；考查化归与转化、数形 结合、函数与方程等思想；体现基础性、综合性与应用性，导向对数学运算、 直观想象、逻辑推理等核心素养的关注． 【试题解析】解法一：（1）要证原命题，只需证ex lnx0， 1 设函数F(x)ex lnx，其导函数为F(x)ex  ,x0， ··························· 1分 x 高三数学试题 第21页（共8页）显然F(x)在(0,)单调递增， 1 且F( ) e20，F(1)e10， ·············································· 2分 2 1 1 故存在唯一的x ( ,1)满足F(x )0，即ex0  ， ·························· 3分 0 2 0 x 0 从而可得在(0,x ) F(x)0 F(x)单调递减； 0 在(x ,) F(x)0 F(x)单调递增； 0 所以F(x)在x x 处取到最小值F(x )ex0 lnx ， ····························· 4分 0 0 0 1 其中ex0  ，即x lnx ， x 0 0 0 1 所以F(x ) x≥20. ······························································· 5分 0 x 0 0 故本题得证. （2）C 与C 的一条对称轴为直线l:yx， ······································· 6分 1 2 且l是C 与C 的唯一对称轴， ·························································· 7分 1 2 证明如下：由（1）分析得ex≥1x，当且仅当x0时取等号， 即曲线C 与直线l :yx1相切于点Q(0,1)， 2 2 且曲线C 在直线l 的上方（除点Q）； ··············································· 8分 2 2 同理曲线C 与直线l :yx1相切于点P(1,0)， 1 1 且曲线C 在直线l 的下方（除点P）； 1 1 而平行线l,l 的距离为 2， ···························································· 9分 1 2 故曲线C 上的任意点与C 上任意点的距离不小于 2， 1 2 注意到P,Q两点距离恰为 2， 故可得结论①：曲线C 上的任意点与C 上任意点的距离最小值为 2， 1 2 当且仅当这两点分别为P,Q时取到. ················································· 10分 反证法：假设C 与C 存在除l以外的其它对称轴l， 1 2 那么P关于l的对称点P， 注意到P,Q两点关于直线l:yx对称，故P在C 上且异于点Q， 2 同理Q关于l的对称点Q，其中Q在C 上且异于点P， 1 根据对称性可得 2 |PQ||PQ|， 高三数学试题 第22页（共8页）这与①矛盾，故假设不成立. 故l是C 与C 的唯一对称轴. ··················· 11分 1 2 （3）由题意，不妨设A(x,lnx)，B(x ,lnx )，B (x ,ex3)，A (x ,ex4)， 1 1 1 1 2 2 2 3 2 4 其中x x x ,x x x ， 4 1 2 4 3 2 并由（2）分析得A,B 分别与A ,B 关于直线y x对称， 1 1 2 2 可得AA l，BB l ，且x ex3,lnx x ,x ex4,lnx x ， ··········· 12分 1 2 1 2 2 2 3 1 1 4 由正方形可得|BA||BB |，即 2(x x ) 2(x x ) 1 1 1 2 2 1 2 3 所以x x ，即正方形对角线AB x轴， 1 3 1 2 因为|BB ||AB|，即 2(ex3 lnx ) 2(lnx lnx) 1 2 1 1 2 2 1 即ex3 lnx 2lnx …②，······························································· 13分 1 2 又因为x x ，lnx x ，所以②式可化为ex1 lnx 2x 1 3 2 3 1 1 故x 为方程ex lnx2x0的根， ··················································· 14分 1 即H(x)ex lnx2x(x0)的零点为x ， 1 1 1 1 1 因为H(x)ex  2 x1 2x 1 2 x 110， x x x x 所以H(x)在(0,)单调递增， 1 且H( ) eln210，h(1)e20， 2 1 所以 x 1， ············································································ 15分 2 1 1 所以正方形的边长|BB | 2|ex3 lnx |ex1 x ， x 1，················· 16分 1 2 2 1 2 1 令(x)ex x(x0)，且|BB |(x )， 1 2 1 (x)ex 10，所以(x)在(0,)单调递增， 1 1 1 则(x )( ) e ，即正方形的边长大于 e ， 1 2 2 2 所以正方形的周长L4 e2.························································· 17分 解法二：（1）对任意x0,lnxex，即证ex lnx0， 先证明：ex 1≥x，即证ex x1≥0， ··············································· 1分 设h(x)ex x1，其导函数h'(x)ex 1， ········································· 2分 在区间(,0),h'(x)0，h(x)单调递减； 高三数学试题 第23页（共8页）在区间(0,),h'(x)0，h(x)单调递增； 故当且仅当x0时 h(x)取到最小值h(0)0， ···································· 3分 所以h(x)≥0，即ex 1≥x； 同样也可得elnx 1lnx，即x1lnx，即xlnx1， ························· 4分 所以ex 1lnx1，即ex lnx≥20， ············································· 5分 本题得证. （2）同解法一； （3）同解法一． 19．（17分） n 已知正整数 p,q满足 p≤q，正整数a(i 1,2,,n)满足a≤p，a2  pq．对于确定的 i i i i1 n 正整数 p,q ，记a 的最小值为 f p,q．例如：当 p2,q3时，2322 12 12或 i i1 n 2312 12 12 12 12 12，a 4或6， f 2,34． i i1 n （1）当 pq3时，写出a 的所有值及 f(3,3)的值； i i1 （2）探究 f 3,3k1 (kN*)的值； n 1 2 （3）证明：  ． f2(3,3k1) 27 k1 【命题意图】本题主要考查整数的离散性、数列的求和、不等式等知识，考查阅读理解能力、 逻辑思维能力与创新能力等关键能力；考查数形结合思想、转化与化归思想； 体现综合性、应用性与创新性，彰显高考的选拔特点，导向对发展数学抽象、 逻辑推理、数学运算等核心素养的关注． 【试题解析】 n （1）a 的所有值为：3,5,7,9， ··································· 4分【写对1个得1分】 i i1 所以 f(3,3)3． ············································································· 5分 （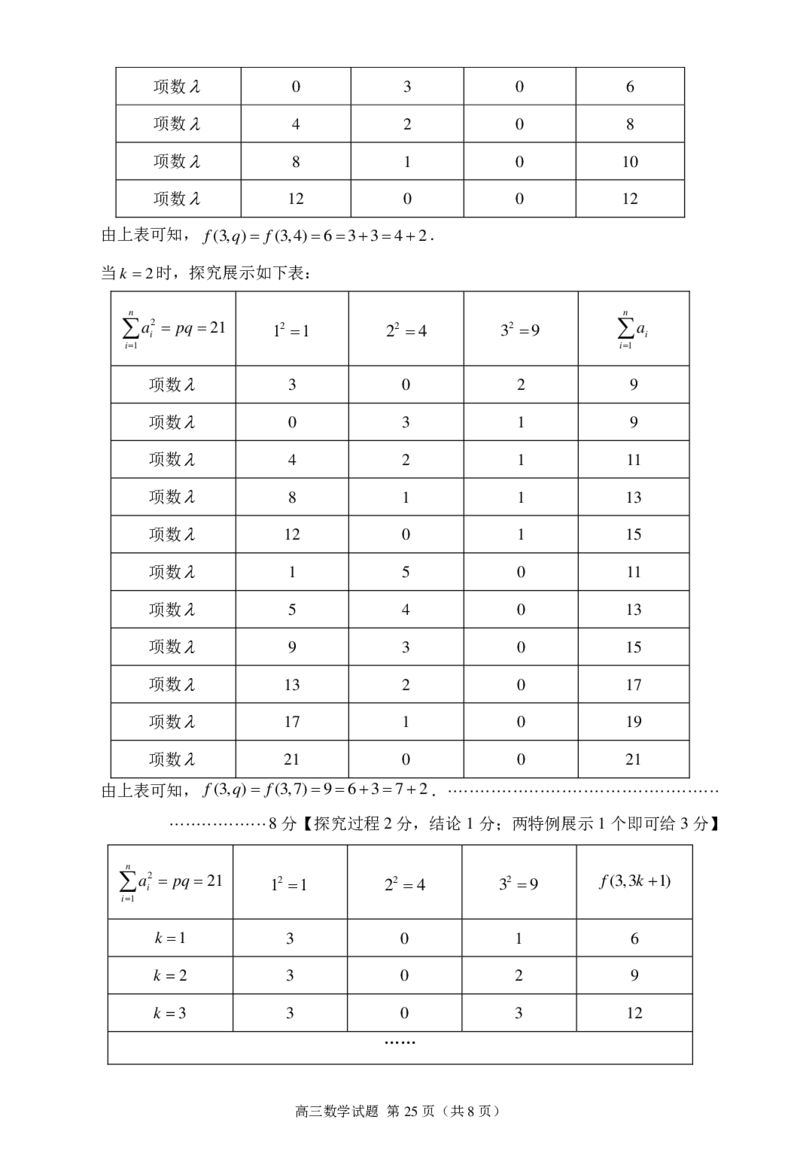2）当k 1时，探究展示如下表： n n a2  pq12 12 1 22 4 32 9 a i i i1 i1 项数 3 0 1 6 高三数学试题 第24页（共8页）项数 0 3 0 6 项数 4 2 0 8 项数 8 1 0 10 项数 12 0 0 12 由上表可知， f(3,q) f(3,4)63342. 当k 2时，探究展示如下表： n n a2  pq21 12 1 22 4 32 9 a i i i1 i1 项数 3 0 2 9 项数 0 3 1 9 项数 4 2 1 11 项数 8 1 1 13 项数 12 0 1 15 项数 1 5 0 11 项数 5 4 0 13 项数 9 3 0 15 项数 13 2 0 17 项数 17 1 0 19 项数 21 0 0 21 由上表可知， f(3,q) f(3,7)96372． ·················································· ·················· 8分【探究过程2分，结论1分；两特例展示1个即可给3分】 n a2  pq21 12 1 22 4 32 9 f(3,3k1) i i1 k 1 3 0 1 6 k 2 3 0 2 9 k 3 3 0 3 12 „„ 高三数学试题 第25页（共8页）k n 3 0 n 3n3 猜想q3k1 (kN*)时， f(3,q) f(3,3k1)3k3q2． ······························ ······································································· 9分【结论正确1分】 证明如下： a,a , ,a 的各项的取值只有1,2,3三种可能， 1 2 n 记其中取值为1,2,3的项数分别为,,． 1 2 3 n 取3, 0, k，有a2 312 k32 9k3， 1 2 3 i i1 n 此时a 31k33k3． i i1 n 假设3k3不是a 的最小值，则存在',','N， i 1 2 3 i1 使得' 4' 9' 9k3，且' 2' 3' 3k2． 1 2 3 1 2 3 3 消去k，得2' 2' 3，' '  ， 1 2 1 2 2 '=0， '=1， '=0， 因为',','N，所以 1 或 1 或 1 1 2 3 '=0， '=0， '=1. 2 2 2 '=0， 1 则若 1 则' k N； '=0， 3 3 2 '=1， 2 若 1 则' k N； '=0， 3 9 2 '=0， 1 若 1 则' k N． '=1. 3 9 2 故矛盾． n 所以，3k3是a 的最小值， f(3,q)(3k1)2q2． i i1 ···························· 12分【证明方法不唯一；能讲出一定的理由可给1分】 （3）解法一： 1 1 1 1 11 1 由（2），    (  )． ···· 13分【裂项放缩】 f2(3,3k1) 9k12 9k(k1) 9 k k1 n 1 2 n 1 2 要证  ，即证  ， f2(3,3k1) 27 (k1)2 3 k1 k1 高三数学试题 第26页（共8页）1 1 1 1 n 1 1 因为左边    (  ) ····························· 14分【局部放缩】 4 9 16 25 k k1 k5 1 1 1 1 1 1       4 9 16 25 5 n1 2389 1   ···················································· 16分【求和】 91625 n1 2400 2   ． ·················································· 17分【比大小】 91625 3 故原不等式得证． 解法二： 1 1 由（2），  f2(3,3k1) 9k12 1 1 1 1 1 1 1    (  )． ················ 13分【裂项放缩】 9(k1)2 1 9k(k2) 18 k k2 n 1 2 n 1 2 要证  ，即证  ， f2(3,3k1) 27 (k1)2 3 k1 k1 1 1 n 1 1 因为左边  (  ) ········································· 14分【局部放缩】 36 18 k k2 k2 1 1 1 1 1 1   (    ) 36 18 2 3 n1 n2 2 1 1 1   (  ) ·············································· 16分【求和】 27 18 n1 n2 2  ． ································································ 17分【比大小】 27 故原不等式得证． 解法三： 1 1 1 4 由（2），   f2(3,3k1) 9k12 94(k1)2 1 4 2 1 1   (  )． ························ 14分【裂项放缩】 94(k1)2 1 9 2k1 2k3 2 n 1 1 因为左边 (  ) ······································ 15分【写出求和式】 9 2k1 2k3 k1 2 1 1  (  ) 9 3 2n3 高三数学试题 第27页（共8页）2 2 1   ························································· 16分【求和】 27 92n3 2  ． ································································ 17分【比大小】 27 故原不等式得证． 高三数学试题 第28页（共8页）