文档内容
绝密 启用前
★
金科·新未来 2023~2024 学年度下学期期末质量检测
高二数学
全卷满分 150分,考试时间 120分钟。
注意事项:
1、答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上
的指定位置。
2、请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷、草稿纸和答题卡上的非答
题区域均无效。
3、选择题用 2B 铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答题卡上
作答;字体工整,笔迹清楚。
4.考试结束后,请将试卷和答题卡一并上交。
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知等差数列{ a }满足a +a =16,且a −a =4,则首项a =( )
n 3 6 5 3 1
A.−1 B.0 C.1 D.3
2.已知曲线 f ( x )=ax+lnx−2在点 ( 1, f ( 1 )) 处的切线方程是y =2x+b,则b=( )
A.−3 B.−2 C.1 D.-1
3.在各项为正的等比数列{ a }中,a 与a 的等比中项为2,则log a +log a =( )
n 8 10 2 6 2 12
A.4 B.3 C.1 D.2
1
4.函数 f ( x )= x3−x2 −3x ( x ≤0 )的最大值是( )
3
5
A. B.0 C.2 D.3
3
x2 y2
5.已知双曲线C: − =1的一条渐近线与圆E:(x− 10)2 + y2 =25相交于A,B两点,且 AB =8,
a2 b2
则双曲线C的离心率为( )
A. 2 B. 3 C. 5 D. 10
6.若函数 f ( x )=ax2 −e2x在区间(−2,−1 )上单调递减,则a的取值范围是( )
1 1 1
A.[ 2e,+∞) B. − ,+∞ C. −∞,− D. − ,0
2e4 e2 e2
1 1
7.已知n∈N*,a = ,b = ,数列{ a }与数列{ b }的公共项按从大到小的顺序排列组成一个
n 2n−1 n n2 +2n n n
学科网(北京)股份有限公司新数列{ c },则数列{ c }的前99项和为( )
n n
1 99 99 198
A. B. C. D.
2 199 197 199
8.在平面坐标系xOy中,一个质点从原点出发,每次移动一个单位长度,且上下左右四个方向移动的概率
相等,若该质点移动6次后所在坐标为( 2,0 ),则该质点移动的方法总数为( )
A.120 B.135 C.210 D.225
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.已知等差数列{ a }的前n项和为S ,等比数列{ b }的前n项积为T ,则( )
n n n n
A.{ a +b }不可能为等比数列 B.{ a b }可能为等差数列
n n n n
S T
C. n 是等差数列 D. n 是等比数列
n 2n
10.已知抛物线C: y2 =4x的焦点为F ,准线为l ,点P是C上位于第一象限的动点,点M 为l 与x轴的
交点,则下列说法正确的是( )
A.F 到直线l 的距离为2
B.以P为圆心 PF 为半径的圆与l 相切
C.直线MP斜率的最大值为2
D.若 FM = FP ,则△FMP的面积为2
11.已知函数 f ( x )=ex −x,g ( x )= x−lnx,则下列说法正确的是( )
A.g ( ex ) 在( 0,+∞)上是增函数
B.∀x >1,不等式 f ( ax )≥ f ( lnx2 ) 恒成立,则正实数a的最小值为 2
e
C.若 f ( x )=t有两个零点x ,x ,则x + x >0
1 2 1 2
lnt 1
D.若 f ( x )= g ( x )=t(t >2),且x > x >0,则 的最大值为
1 2 2 1 x −x e
2 1
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.已知变量x和 y的统计数据如下表:
x 1 2 3 4 5
y 1.5 2 m 4 4.5
若由表中数据得到经验回归直线方程为 y =0.8x+0.6,则m =_________.
学科网(北京)股份有限公司13.已知函数 f ( x )=2ax−ex,若 f ( x )的图象经过第一象限,则实数a的取值范围是_________.
14.不透明的袋子中装有2个白球,3个黑球(除颜色外,质地大小均相同),学生甲先取出2个球(不放
回),学生乙在剩下的3个球中随机取一个,已知甲至少取走了1个黑球,则乙取出白球的概率为_________.
四、解答题:本题共 5 小题,共 77 分.解答应写出必要的文字说明、证明过程及演算步骤.
15.(本小题满分13分)
已知数列{ a }是公差不为零的等差数列,a = −11,且a ,a ,a 成等比数列.
n 1 2 5 6
(1)求{
a
}的通项公式;
n
(2)设S 为{ a }的前n项和,求S 的最小值.
n n n
16.(本小题满分15分)
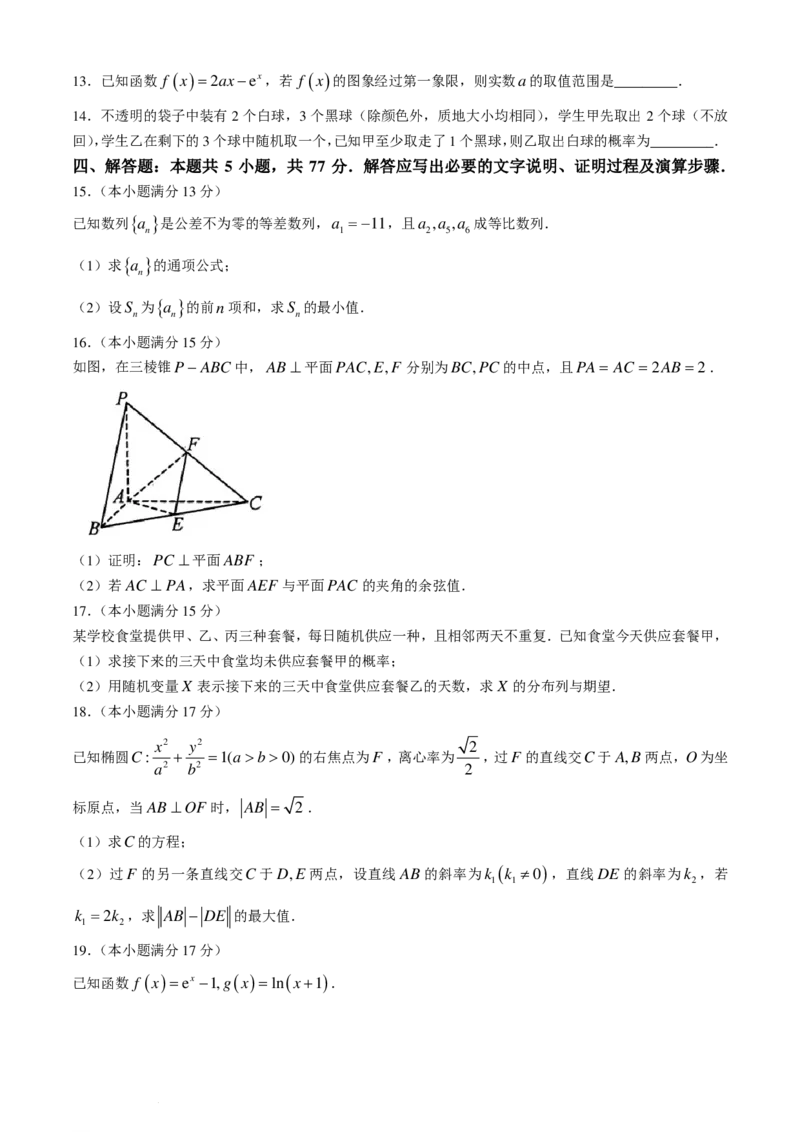
如图,在三棱锥P− ABC中,AB ⊥平面PAC,E,F 分别为BC,PC的中点,且PA= AC =2AB =2.
(1)证明:PC ⊥平面ABF ;
(2)若AC ⊥ PA,求平面AEF 与平面PAC 的夹角的余弦值.
17.(本小题满分15分)
某学校食堂提供甲、乙、丙三种套餐,每日随机供应一种,且相邻两天不重复.已知食堂今天供应套餐甲,
(1)求接下来的三天中食堂均未供应套餐甲的概率;
(2)用随机变量X 表示接下来的三天中食堂供应套餐乙的天数,求X 的分布列与期望.
18.(本小题满分17分)
x2 y2 2
已知椭圆C: + =1(a >b>0)的右焦点为F ,离心率为 ,过F 的直线交C于A,B两点,O为坐
a2 b2 2
标原点,当AB ⊥OF 时, AB = 2 .
(1)求C的方程;
(2)过F 的另一条直线交C于D,E 两点,设直线 AB的斜率为k ( k ≠0 ),直线DE 的斜率为k ,若
1 1 2
k =2k ,求 AB − DE 的最大值.
1 2
19.(本小题满分17分)
已知函数 f ( x )=ex −1,g ( x )=ln ( x+1 ).
学科网(北京)股份有限公司(1)若 f ( x )≥kg ( x )在( 0,+∞)上恒成立,求k的取值范围;
(2)设A ( x ,y )( x >0 )为 y = f ( x )图象上一点,B ( x ,y )( x >0 )为 y = −g ( x )图象上一点,O为坐
1 1 1 2 2 2
标原点,若∠AOB为锐角,证明:x > x2.
2 1
学科网(北京)股份有限公司金科·新未来 2023~2024 学年度下学期期末质量检·高二数学
参考答案、提示及评分细则
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C A D A D B B D BC ABD ABD
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.【答案】C
a +a =2a +7d =16
【解析】设等差数列{ a }的公差为d ,因为a +a =16,且a −a =4,所以 3 6 1 ,
n 3 6 5 3 a −a =2d =4
5 3
a =1
所以 1 .故选C.
d =2
2.【答案】A
1
【 解 析 】 函 数 f ( x )=ax+lnx−2 , 求 导 得 f′( x )=a+ , 依 题 意 , f′( 1 )=a+1=2 , 得
x
a =1, f ( x )= x+lnx−2,显然 f ( 1 )= −1,因此−1=2+b,所以b=−3.故选A.
3.【答案】D
【 解 析 】 因 为 a 与 a 的 等 比 中 项 为 2 , 所 以 a a =22 =4 , 所 以
8 10 8 10
log a +log a =log ( a ⋅a )=log ( a ⋅a )=log 4=2.故选D.
2 6 2 12 2 6 12 2 8 10 2
4.【答案】A
1
【解析】因为 f ( x )= x3−x2 −3x ( x ≤0 ),所以 f′( x )= x2 −2x−3,令 f′( x )>0,得x<−1,令
3
f′( x )<0,得−1< x<0,所以函数 f ( x )在(−∞,−1 )上单调递增,在(−1,0 )上单调递减,所以 f ( x )的
5
最大值是 f (−1 )= .故选A.
3
5.【答案】D
b
【解析】根据题意得,圆心 E 到C 的渐近线的距离为 52 −42 =3,∴设渐近线方程为 y = x ,则
a
10b b2 b2
=3,∴ =9,e= 1+ = 10,故选D.
a2 +b2 a2 a2
6.【答案】B
e2x e2x
【解析】依题意, f′( x )=2ax−2e2x ≤0 在(−2,−1 )恒成立,即a ≥ 恒成立,设g ( x )= ,则
x x
学科网(北京)股份有限公司e2x( 2x−1 ) 1
g′( x )= ,所以g′( x )≤0,所以g ( x )在(−2,−1 )单调递减,所以a ≥ g (−2 )= − ,故选
x2 2e4
B.
7.【答案】B
【解析】因为数列{ 2n−1 }是正奇数数列,对于数列 { n2 +2n } 等价于 { (n+1)2 −1 } ,当n为奇数时,设
n =2k −1 ( k∈N* ) ,则 (n+1)2 −1=4k2 −1 为奇数;当 n 为偶数时,设 n =2k ( k∈N* ) ,则
(n+1)2 −1=(2k +1)2 −1=4k ( k +1 ) 为 偶 数 , 所 以
1 1 1 1 1 1
c = ,c = = = − , 所 以
n 4n2 −1 n 4n2 −1 ( 2n−1 )( 2n+1 ) 22n−1 2n+1
1 1 1 1 1 1 1 1 99
c +c ++c = × 1− + − ++ − = × 1− = ,故选B.
1 2 99 2 3 3 5 197 199 2 199 199
8.【答案】D
【解析】情形一,质点往右移动4次,往左移动2次,C2 =15,
6
情形二,质点往右移动3次,往左移动1次,往上移动一次,往下移动一次,C3A3 =120,
6 3
情形三,质点往右移动2次,往上移动2次,往下移动2次,C2C2 =90,
6 4
所以质点移动的方法总数为225,故选D.
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.【答案】BC(全部选对得6分,选对1个得3分,有选错的得0分)
【解析】对于A,当{ a }为常数列,且a =0时,因为{ b }是等比数列,所以{ a +b }为等比数列,所以
n n n n n
A错误.
对于B,当{
b
}为常数列时,因为{
a
}为等差数列,所以{
a b
}为等差数列,所以B正确.
n n n n
n ( n+1 ) S ( n+1 ) S S 1
对于 C,设{ a }的公差为d ,则S =na + d ,得 n =a + d ,因为 n+1 − n = d ,
n n 1 2 n 1 2 n+1 n 2
S
所以数列 n 是等差数列,所以C正确.
n
T +1
n
对于D,设{ b }的公比为q,则
2n+1
=
T
n+1 ⋅
2n
=
b
n+1 =
1
bqn,当q≠1时,
1
bqn不是常数,所以
T
n
n T 2n+1 T 2 2 1 2 1 2n
n n
2n
不是等比数列,所以D错误.故选BC.
学科网(北京)股份有限公司10.【答案】ABD(全部选对得6分,选对1个得2分,选对2个得4分,有选错的得0分)
【解析】易知F ( 1,0 ),准线l:x = −1,所以F 到直线l 的距离为2,A选项正确;
由抛物线的定义,点P到准线的距离等于 PF ,所以以P为圆心 PF 为半径的圆与l 相切,B 选项正确;
当直线MP与抛物线相切时,MP的斜率取得最大值.设直线MP:x =my−1,与抛物线 y2 =4x联立可
得:y2 −4my+4=0,令Δ=16m2 −16=0得:m = ±1,所以直线MP斜率的最大值为1,C选项错误;
y2 y2
若 FM = FP =2,设P 0 ,y ,则 0 +1=2,解得y =2,
4 0 4 0
1
所以△FMP的面积为 ×2× y =2,D选项正确,故选ABD.
2 0
11.【答案】ABD(全部选对得6分,选对1个得2分,选对2个得4分,有选错的得0分)
1
【解析】A项中,令t =ex,则x =lnt ,由x∈( 0,+∞)知t >1,此时函数为 y =t−lnt,y′=1− >0,所
t
以函数 y =t−lnt在( 1,+∞)上是单调增函数,即g ( ex ) 在( 0,+∞)上是增函数,所以 A 项正确;B 项中,
x >1时,lnx2 >0,又a为正实数,所以ax >0,又 f′( x )=ex −1>0,所以 f ( x )单调递增,所以不等
2lnx 2lnx 2−2lnx
式等价于ax ≥lnx2对∀x >1恒成立,即a ≥ ,令ϕ( x )= ,知ϕ′( x )= ,所以ϕ( x )
x x x2
max
2
在( 1,e )上递增,在( e,+∞)上递减,所以(ϕ( x ) ) =ϕ( e )= ,所以B项正确;C项中,易知 f ( x )=ex −x
max e
在(−∞,0 )上递减,在( 0,+∞)上递增,f(x) = f ( 0 )=1,所以t >1,不妨设x < x ,则必有x <0< x ,
min 1 2 1 2
若 x + x > 0,则等价于 x >−x >0 ,等价于 f ( x )> f (−x ) ,等价于 f ( x )> f (−x ) ,令
1 2 2 1 2 1 1 1
F ( x )= f ( x )− f (−x ),x∈(−∞,0 ) ,F′( x )= f′( x )+ f′(−x )=ex +e−x −2>0,即F ( x )在(−∞,0 )上
递增,所以F ( x )< F ( 0 )=0,则x ∈(−∞,0 )时,f ( x )< f (−x ),所以x + x >0不成立,即C错误;
1 1 1 1 2
D项中,由 f ( x )=ex −x在(−∞,0 )上递减,在( 0,+∞)上递增,g ( x )在( 0,1 )上递减,在( 1,+∞)上递增,
易知 f ( x )= g ( x )有唯一的解x ∈( 0,1 ),又 f ( 1 )=e−1<2,所以x > x >1,由 f ( x )= g ( x ),即
0 2 1 1 2
ex 1 −x = x −lnx =elnx 2 −lnx , 即 有 f ( x )= f ( lnx ) , 所 以 x =lnx , 即 ex 1 = x , 所 以
1 2 2 2 1 2 1 2 2
lnt lnt lnt lnt 1
= = ,又t >2,所以 = ,所以D正确.
x −x ex 1 −x t x −x e
2 1 1 2 1 min
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.【答案】3
学科网(北京)股份有限公司 ( )
【解析】易知x=3,经验回归直线 y =0.8x+0.6过样本点的中心 x,y ,所以y =0.8×3+0.6=3,所以
1.5+2+m+4+4.5=5×3,解得m =3.
e
13.【答案】
,+∞
2
ex ex
【解析】由 f ( x )的图象经过第一象限,得∃x >0,使得 f ( x )>0,即2a > ,设g ( x )= (x >0),
x x
ex( x−1 )
求导得g′( x )= ,当0< x<1时,g′( x )<0,当x >1时,g′( x )>0,函数g ( x )在( 0,1 )上单
x2
e
调递减,在( 1,+∞)上单调递增,则g(x) = g ( 1 )=e,有2a >e,所以实数a的取值范围是 ,+∞ .
min 2
4
14.【答案】
9
【解析】甲取走1个黑球1个白球的方法数为C1C1 =6,取走2个黑球的方法数为C2 =3,所以乙取出白
2 3 3
6 1 3 2 4
球的概率为P = × + × = .
6+3 3 6+3 3 9
四、解答题:本题共 5 小题,共 77 分.解答应写出必要的文字说明、证明过程及演算步骤.
15.【答案】(1)a =2n−13(2)−36
n
【解析】(1)设{ a }的公差为d ,
n
则a = −11+d,a = −11+4d,a = −11+5d ,
2 5 6
依题意,a2 =a a ,
5 2 6
即(−11+4d)2 =(−11+d )(−11+5d ),
整理得,11d ( d −2 )=0,
解得,d =2或d =0(舍),
所以a =−11+2 ( n−1 )=2n−13;
n
a +a −11+2n−13
(2)S = 1 n ×n = ×n =n2 −12n,
n 2 2
因为S =n2 −12n =(n−6)2 −36≥ −36,
n
当且仅当n =6时,等号成立,
所以S 的最小值为−36.
n
学科网(北京)股份有限公司6
16.【答案】(1)略(2)
3
【解析】(1)因为F 为PC的中点,PA= AC,所以PC ⊥ AF ,
因为AB ⊥平面PAC,PC ⊂平面PAC ,所以AB ⊥ PC,
又AF AB= A,AF,AB⊂平面ABF ;
所以PC ⊥平面ABF ;
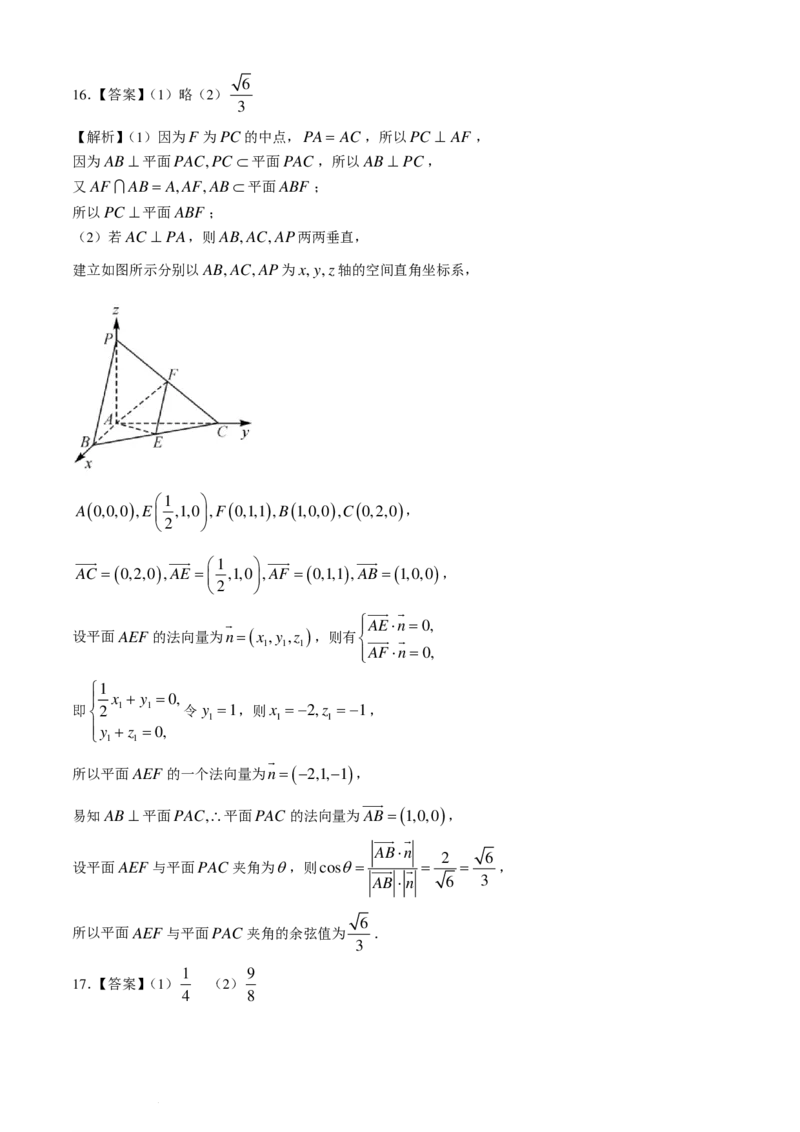
(2)若AC ⊥ PA,则AB,AC,AP两两垂直,
建立如图所示分别以AB,AC,AP为x,y,z轴的空间直角坐标系,
1
A
(
0,0,0
)
,E ,1,0,F
(
0,1,1
)
,B
(
1,0,0
)
,C
(
0,2,0
),
2
1
AC =( 0,2,0 ) ,AE = ,1,0,AF =( 0,1,1 ) ,AB =( 1,0,0 ),
2
AE⋅n=0,
设平面AEF 的法向量为n=( x ,y ,z ),则有
1 1 1
AF⋅n=0,
1
x + y =0,
即2 1 1 令 y =1,则x = −2,z = −1,
1 1 1
y +z =0,
1 1
所以平面AEF 的一个法向量为n=(−2,1,−1 ),
易知AB ⊥平面PAC,∴平面PAC 的法向量为AB =( 1,0,0 ),
AB⋅n
2 6
设平面AEF 与平面PAC 夹角为θ,则cosθ= = = ,
AB ⋅ n 6 3
6
所以平面AEF 与平面PAC 夹角的余弦值为 .
3
1 9
17.【答案】(1) (2)
4 8
学科网(北京)股份有限公司1 1 1
【解析】(1)记事件A=“接下来的三天中食堂都未供应套餐甲”,则P ( A )=1× × = ,所
2 2 4
1
以接下来的三天中食堂均未供应套餐甲的概率为 ;
4
(2)X 的所有可能取值分别为0,1,2,
1 1 1 1
则P ( X =0 )= × × = ,
2 2 2 8
1 1 1
P ( X =2 )= ×1× =
2 2 4
1 1 5
P ( X =1 )=1− − =
4 8 8
X 的分布列为
X 0 1 2
1 5 1
P
8 8 4
1 5 1 9
所以X 的期望为E ( X )=0× +1× +2× = .
8 8 4 8
x2 2
18.【答案】(1) + y2 =1 (2)
2 3
【解析】(1)设焦距为2c,当AB ⊥OF 时,将x =c代入椭圆方程可得,
c2 y2 b2
+ =1,解得 y = ± ,
a2 b2 a
b2 c 2
所以 AB =2 = 2,又 = ,解得a = 2,b=1,
a a 2
x2
所以C的方程为 + y2 =1;
2
1
(2)设直线AB:x =m y+1m = ,A ( x ,y ) ,B ( x ,y ),
1 1 k 1 1 2 2
1
x =m y+1
与椭圆线方程联立 1 可得, ( m2 +2 ) y2 +2m y−1=0,
x2 +2y2 −2=0 1 1
−2m −1
由韦达定理, y + y = 1 ,y y = ,
1 2 m2 +2 1 2 m2 +2
1 1
所以 AB = 1+m2 y − y = 1+m2 ( y + y )2 −4y y
1 1 2 1 1 2 1 2
4m2 −1 1
= 1+m2 1 −4 =2 21− ,
1 ( m2 +2 )2 m2 +2 m2 +2
1 1 1
学科网(北京)股份有限公司 1
同理可得, CD =2 21− ,
m2 +2
2
1 1
AB − DE =2 2 − ,因为k =2k ,所以m =2m ,
m2 +2 m2 +2 1 2 2 1
1 2
1 1 3 2m2
故 AB − DE =2 2 − = 1
m2 +2 4m2 +2 2m4 +5m2 +2
1 1 1 1
3 2 3 2 2
= ≤ = ,
2 4+5 3
2m2 +5+
1 m2
1
当且仅当k = ±1时,等号成立,
1
2
所以||AB − DE 的最大值为 .
3
19.【答案】(1)k ≤1(2)略
【解析】(1)先证明 f ( x )> x,构造函数F ( x )= f ( x )−x =ex −x−1,
则F′( x )=ex −1>0,故F ( x )单调递增,从而F ( x )> F ( 0 )=0,
即ex > x+1,因此x >ln ( x+1 ),
当k ≤1时,kln ( x+1 )≤ln ( x+1 )< x1时,构造函数G ( x )= f ( x )−kg ( x )=ex −1−kln ( x+1 ),
k k
则G′( x )=ex − ,G′( x )单调递增,且G′( 0 )=1−k <0,G′( lnk )= k− >0,
x+1 1+lnk
故存在x ∈( 0,lnk ),使得G′( x )=0,且x∈( 0,x )时,G′( x )<0,即G ( x )单调递减,
0 0 0
则当x∈(
0,x
)时,G (
x
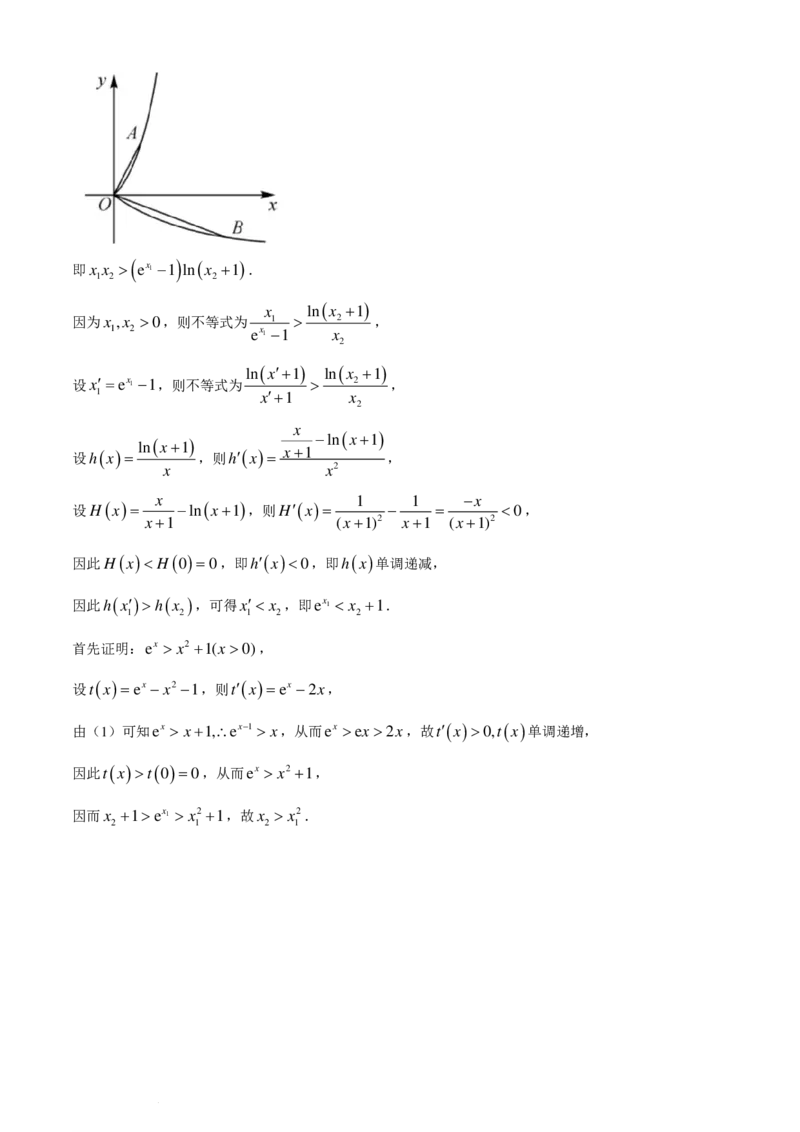
)0,则OA⋅OB>0,即x x + y y >0,
1 2 1 2
学科网(北京)股份有限公司即x x > ( ex 1 −1 ) ln ( x +1 ).
1 2 2
x ln ( x +1 )
因为x ,x >0,则不等式为 1 > 2 ,
1 2 ex 1 −1 x
2
ln ( x′+1 ) ln ( x +1 )
设x′ =ex 1 −1,则不等式为 > 2 ,
1 x′+1 x
2
x
设h ( x )= ln ( x+1 ) ,则h′( x )= x+1
−ln ( x+1 )
,
x x2
x 1 1 −x
设H ( x )= −ln ( x+1 ),则H′( x )= − = <0,
x+1 (x+1)2 x+1 (x+1)2
因此H ( x )< H ( 0 )=0,即h′( x )<0,即h ( x )单调递减,
因此h ( x′)>h ( x ),可得x′< x ,即ex 1 < x +1.
1 2 1 2 2
首先证明:ex > x2 +1(x >0),
设t ( x )=ex −x2 −1,则t′( x )=ex −2x,
由(1)可知ex > x+1,∴ex−1 > x,从而ex >ex >2x,故t′( x )>0,t ( x )单调递增,
因此t ( x )>t ( 0 )=0,从而ex > x2 +1,
因而x +1>ex 1 > x2 +1,故x > x2.
2 1 2 1
学科网(北京)股份有限公司