文档内容
2023-2024 学年高二数学期末模拟卷
全解全析
一、单项选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个选项是
符合题目要求的.
1.设集合 , ,则 ( )
A. B.
C. D.
【答案】C
【详解】因为 , ,所以 ,故选:C.
2. 的展开式中 的系数为( )
A. B. C. D.
【答案】D
【详解】对于 ,由二项展开式的通项得 ,
令 解得 ,则所求系数为 ,故选:D
3.已知 ,“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【详解】取 , ,则可知由“ ”无法推出“ ”.
, ,两边平方化简得 ;
则 ,“ ”是“ ”的必要不充分条件;故选:B
原创精品资源学科网独家享有版权,侵权必究!
1
学学科科网网((北北京京))股股份份有有限限公公司司4.已知函数 ,则 ( )
A. B. C. D.
【答案】D
【详解】令 ,则 .故选:D.
5.现有8个市三好学生名额分给六个班,其中一班和二班每班至少2个名额,三班和四班每班至少1个名
额,五班和六班可以不分配名额,则名额分配方式共有( )种.
A.21 B.56 C.70 D.126
【答案】A
【详解】依题意,首先给一班和二班每班 个名额,三班和四班每班 个名额,则还剩下 个名额,
将剩下的 个名额给一个班级,有 种方法;将剩下的 个名额给两个班级,有 种方法;
综上可得:一共有 种分配方法.
故选:A
6.已知随机变量 服从正态分布 , ,则 ( )
A.0.2 B.0.3 C.0.6 D.0.7
【答案】A
【详解】因为随机变量 服从正态分布 , ,
所以 .故选:A.
7.某同学参加社团面试,已知其第一次通过面试的概率为0.7,第二次面试通过的概率为0.5.若第一次未
通过,仍可进行第二次面试,若两次均未通过,则面试失败,否则视为面试通过,则该同学通过面试的概
率为( )
A.0.85 B.0.7 C.0.5 D.0.4
【答案】A
【详解】依题意,第一次面试不通过的概率为0.3,第二面试不通过的概率为0.5,
因此面试失败的概率为 ,
所以该同学通过面试的概率为 .故选:A
原创精品资源学科网独家享有版权,侵权必究!
2
学学科科网网((北北京京))股股份份有有限限公公司司8.已知 为正实数,且满足 ,则 的最小值为( )
A. B. C.8 D.6
【答案】C
【详解】根据题意,
当且仅当 ,即 时,等号成立.故选:C
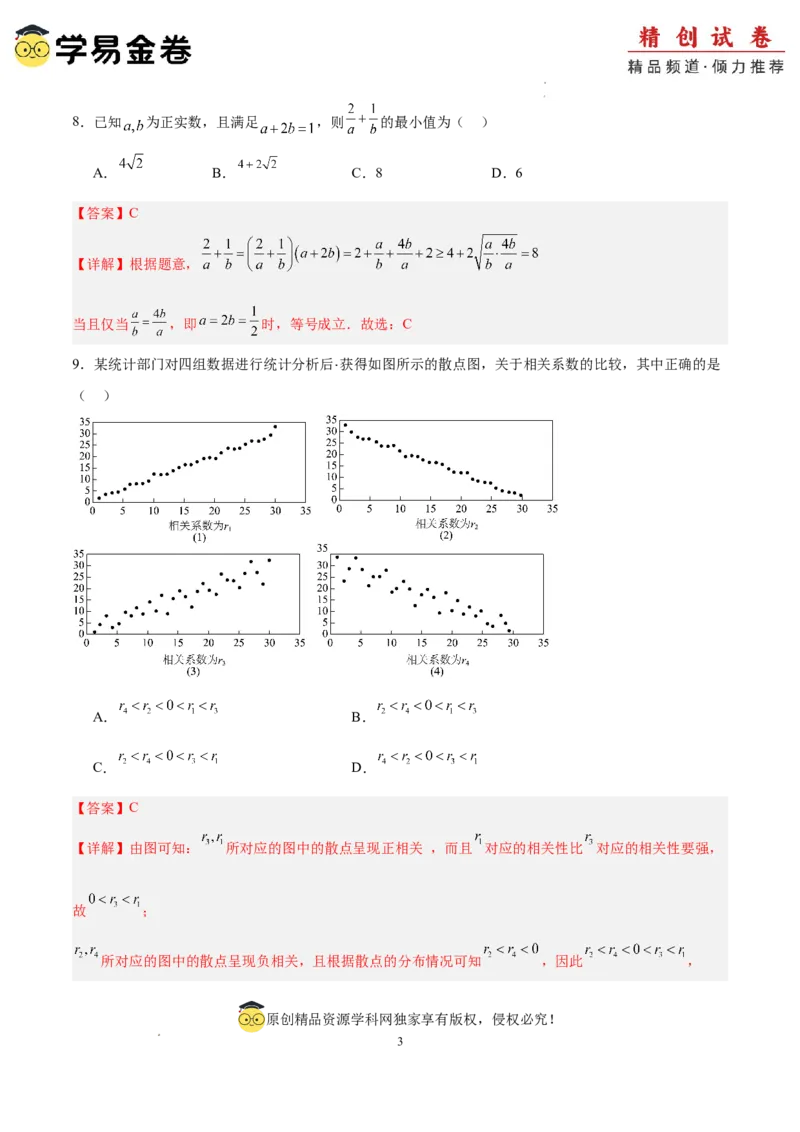
9.某统计部门对四组数据进行统计分析后 获得如图所示的散点图,关于相关系数的比较,其中正确的是
( )
A. B.
C. D.
【答案】C
【详解】由图可知: 所对应的图中的散点呈现正相关 ,而且 对应的相关性比 对应的相关性要强,
故 ;
所对应的图中的散点呈现负相关,且根据散点的分布情况可知 ,因此 ,
原创精品资源学科网独家享有版权,侵权必究!
3
学学科科网网((北北京京))股股份份有有限限公公司司故选:C.
10.已知函数 ,若函数 有两个零点,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【详解】函数 有两个零点,即函数 的图象与 的图象有两个交点,
函数 的定义域为 , ,
令 ,解得 ,
, 的变化情况如下表:
- 0 +
单调递减 单调递增
所以,函数 在区间 上单调递减,在区间 上单调递增,
故当 时,有极小值 ,
令 ,解得 ,当 时, ;当 时, ,
当 无限趋向于负无穷大时, 无限趋向于0;当 无限趋向于正无穷大时时,
无限趋向于正无穷大,
由此作出函数 的大致图象:
原创精品资源学科网独家享有版权,侵权必究!
4
学学科科网网((北北京京))股股份份有有限限公公司司由图象得:当 时,交点为0个;当 或 时,交点为1个;当 时,交点为2个.
若函数 的图象与 的图象有两个交点,则由图可知,实数 的取值范围为 .
故选:A.
二、填空题:本题共5小题,每小题5分,共25分.
11.设 ,则 .
【答案】 /
【详解】因为 ,所以 ,
所以 .故答案为:
12.在等比数列 中, , ,则 ;公比 .
【答案】 或 或
【详解】由 ,得 ,解得 ,或 .
故答案为: 或 ; 或
13.某公司人力资源部为了解员工的工作积极性和对待公司改革态度的关系,调查了75名员工,得到以下
列联表:
工作态度
支持改革情
合计
况 欠积
积极
极
原创精品资源学科网独家享有版权,侵权必究!
5
学学科科网网((北北京京))股股份份有有限限公公司司支持 40 20 60
不支持 5 10 15
合计 45 30 75
根据统计结果,认为“平时工作态度积极和支持公司改革有关”犯错误的概率不超过 .
附: ,其中 .
0.10 0.05 0.005 0.001
2.706 3.841 7.879 10.828
【答案】
【详解】设零假设 :平时工作态度积极和支持公司改革无关,
,
故认为“平时工作态度积极和支持公司改革有关”犯错误的概率不超过 .
故答案为: .
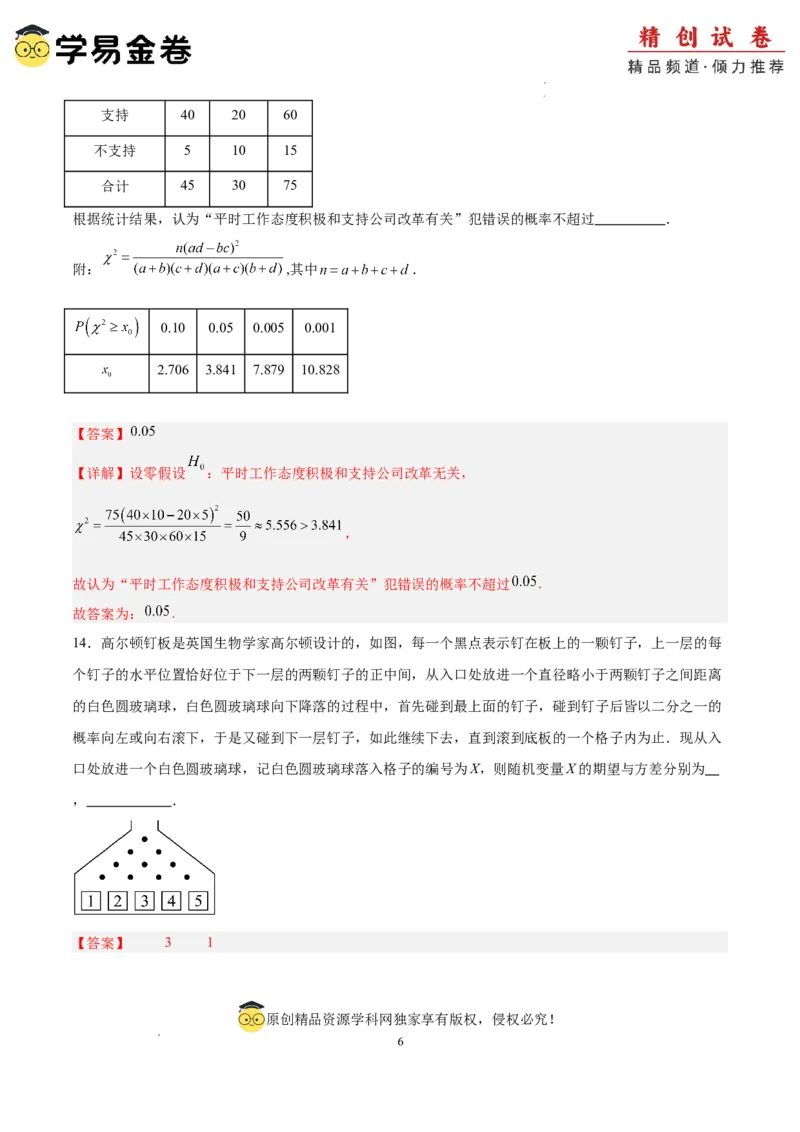
14.高尔顿钉板是英国生物学家高尔顿设计的,如图,每一个黑点表示钉在板上的一颗钉子,上一层的每
个钉子的水平位置恰好位于下一层的两颗钉子的正中间,从入口处放进一个直径略小于两颗钉子之间距离
的白色圆玻璃球,白色圆玻璃球向下降落的过程中,首先碰到最上面的钉子,碰到钉子后皆以二分之一的
概率向左或向右滚下,于是又碰到下一层钉子,如此继续下去,直到滚到底板的一个格子内为止.现从入
口处放进一个白色圆玻璃球,记白色圆玻璃球落入格子的编号为X,则随机变量X的期望与方差分别为
, .
【答案】 3 1
原创精品资源学科网独家享有版权,侵权必究!
6
学学科科网网((北北京京))股股份份有有限限公公司司【详解】由题意可知:白色圆玻璃球从起点到进入格子一共跳了4次,向左或向右的概率均为 ,
则向左的次数 ,可知 , ,
又因为 ,所以 , .
故答案为:3;1.
15.若集合A具有以下性质:
(1)0∈A,1∈A;
(2)若x∈A,y∈A;则x﹣y∈A,且x≠0时, ∈A.
则称集合A是“好集”.下列命题中正确的有
①.集合B={﹣1,0,1}是“好集” ②.有理数集Q是“好集”
③.整数集Z不是“好集” ④.设集合A是“好集”,若x∈A,y∈A,则x+y∈A
【答案】②③④
【详解】解:对于①,假设集合 是“好集”,因为 , ,所以 ,这与 矛盾,
所以集合 不是“好集”.故①错误;
对于②,因为 , ,且对任意的 , 有 ,且 时, ,所以有理数集 是
“好集”,故②正确;
对于③,因为 ,但 ,所以整数集 不是“好集”.故③正确;
因为集合 是“好集”,所以 ,又 ,所以 ,即 ,又 ,所以 ,即
,故④正确.故选:②③④.
三、解答题:本题共6小题,共85分.解答应写出文字说明、证明过程或演算步骤.
16.袋中装有大小相同的4个红球和6个白球,从中取出4个球.
(1)若取出的球必须是两种颜色,则有多少种不同的取法?
(2)若取出的红球个数不少于白球个数,则有多少种不同的取法?
(3)取出一个红球记2分,取出一个白球记1分,若取4球的总分不低于5分,则有多少种不同的取法?
【答案】(1) 种 (2) 种 (3) 种
【详解】(1)分三类:3红1白,2红2白,1红3白这三类,
原创精品资源学科网独家享有版权,侵权必究!
7
学学科科网网((北北京京))股股份份有有限限公公司司由分类加法计数原理有 (种).
(2)分三类:4红,3红1白,2红2白,由分类加法计数原理共有:
(种).
(3)由题意知,取4球的总分不低于5,只要取出的4个球中至少一个红球即可.
因此共有取法: (种).
17.已知函数 .
(1)求 在 处的切线方程;
(2)求 在区间 上的最小值.
【答案】(1) (2)
【详解】(1) , , ,
所以 在 处的切线方程为 ,即 ;
(2) ,令 ,得 ,
1 3
0
减函数 增函数
所以 在区间 上的最小值为 .
18.某高新技术企业新研发出了一种产品, 该产品由三个电子元件构成, 这三个电子元件在 生产过程
中的次品率分别为 ,组装过程中不会造成电子元件的损坏,若有 一个电子元件是次品, 则该
产品为次品. 现安排质检员对这批产品一一检查, 确保无任 何一件次品流入市场.
(1)若质检员检测出一件次品, 求该产品仅有一个电子元件是次品的概率;
原创精品资源学科网独家享有版权,侵权必究!
8
学学科科网网((北北京京))股股份份有有限限公公司司(2)现有两种方案, 方案一: 安排三个质检员先行检测这三个元件, 次品不进入组装生 产线; 方案二: 安
排一个质检员检测成品, 一旦发现次品, 则取出重新更换次品的 电子元件, 更换电子元件的费用为
20 元/个. 已知每个质检员每月的工资约为 3000 元,该企业每月生产该产品 件 ,请从企业
获益的角度选择最优方案.
【答案】(1)
(2)当 且 时,选方案一; 当 且 时,选方案二
【详解】(1)记“质检员检测出一件次品”为事件 ,
“该产品仅有一个电子元件是次品”为 .
,
,
所以 .
(2)设一件产品中所含电子元件为次品的个数为 ,则 可取 , , , ,
所以 ,
,
,
,
则 的分布列为
0 1 2 3
原创精品资源学科网独家享有版权,侵权必究!
9
学学科科网网((北北京京))股股份份有有限限公公司司所以 .
若选方案一, 则企业每月支出质检员工资共 元.
若选方案二, 则企业每月支出质检员工资和更换电子元件费用共计
.
若 ,则 .
所以当 且 时,选方案一;
当 且 时,选方案二.
19.设 是公比不为1的等比数列, ,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)求 的公比;
(2)求数列 的前 项和.
条件①: 为 , 的等差中项;条件②:设数列 的前 项和为 , .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】条件性选择见解析,(1)-2;(2)
【详解】解:选① (1)因为 为 的等差中项,所以 所以 ,
因为 所以 所以 , (舍)
选② (1)因为 ,所以 ,
因为 ,所以 ,所以
原创精品资源学科网独家享有版权,侵权必究!
10
学学科科网网((北北京京))股股份份有有限限公公司司(2)由题得等比数列 的首项 ,所以 ,
设数列 的前 项和为 ,
因为数列 是以 为首项, 为公差的等差数列,
所以 .
20.已知函数 .
(1)求函数 的极值;
(2)若对任意 ,求 的取值范围.
【答案】(1) 的极小值为 ,无极大值. (2)
【详解】(1) ,得 ,
当 时, ,函数 在 单调递减,
当 时, ,函数 在 单调递增,
所以 的极小值为 ,无极大值.
(2)对任意 ,即 ,
设 ,
①当 时, 在 单调递增, 单调递增, ,成立;
②当 时,令 在 单调递增,
在 单调递增, ,成立;
原创精品资源学科网独家享有版权,侵权必究!
11
学学科科网网((北北京京))股股份份有有限限公公司司③当 时,当 时, 单调递减, 单调递减,
,不成立.
综上可知 .
21.设数列 满足:① ;②所有项 ;③ .设集合
,将集合 中的元素的最小值记为 .换句话说, 是数列 中满足不等式
的所有项的项数的最小值.我们称数列 为数列 的伴随数列.例如,数列1,3,5的伴随数
列为1,2,2,3,3.
(1)请写出数列1,5,7的伴随数列;
(2)设 ,求数列 的伴随数列 的前30项之和;
(3)若数列 的前 项和 (其中 常数),求数列 的伴随数列 的前 项和 .
【答案】(1)1,2,2,2,2,3,3. (2)110
(3)
【详解】(1)由伴随数列的定义可知,数列1,5,7的伴随数列为1,2,2,2,2,3,3.
(2)由 ,得 ∴
当 时, ; 当 时, ;
当 时, ;
当 时, ;
当 时, ,
原创精品资源学科网独家享有版权,侵权必究!
12
学学科科网网((北北京京))股股份份有有限限公公司司∴ .
(3) ,得 ,
当 时, , 也符合,所以 ,
由 ,得 ,
使得 成立的 的最小值为 ,则 , , , ,
,
当 时, ,
当 时, ,
当 时, ,
所以
原创精品资源学科网独家享有版权,侵权必究!
13
学学科科网网((北北京京))股股份份有有限限公公司司