2006年辽宁高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_辽宁

2006 年辽宁高考理科数学真题及答案 第I卷（选择题 共60分） 参考公式： 如果事件A、B互斥，那么 球的表面积公式 P（A+B）=P（A）+P（B） S 4R2 如果事件A、B相互独立，那么 球的体积公式 P（A·B）=P（A）·P（B） 4 V  R3 如果事件A在一次试验中发生的概率P，那 球 3 么n次独立重复试验中恰好发生k次的概率 其 中 R 表 示球的半径 P (k)CkPk(1P)nk n n 一．选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，选择 一个符合题目要求的选项. （1）设集合A={1,2}，则满足A∪B={1,2,3}的集合B的个数是 （A）1 （B）3 （C）4 （D）8 （2）设 f(x)是R上的任意函数，则下列叙述正确的是 （A） f(x) f(x)是奇函数 （B） f(x)| f(x)| 是奇函数 （C） f(x)－ f(x)是偶函数 （D） f(x)+ f(x)是偶函数 （3）给出下列四个命题： ①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行. ③若直线l ,l 与同一平面所成的角相等，则l ,l 互相平行. 1 2 1 2 ④若直线l ,l 是异面直线，则与l ,l 都相交的两条直线是异面直线. 1 2 1 2 其中假命题的个数是 （A）1 （B）2 （C）3 （D）4 （4）双曲线x2  y2  4的两条渐近线与直线x 3围成一个三角形区域，表示该区域的不 等式组是 x y 0 x y 0 x y 0 x y 0     （A）x y 0 （B）x y 0 （C）x y 0 （D）x y 3     0 x 3 0 x 3 0 x 3 0 x 3     （5）设○+ 是R上的一个运算，A是R的非空子集. 若对任意a,bA,有abA，则称 A对运算○+ 封闭. 下列数集对加法、减法、乘法和法（除数不等于零）四则运算都封闭的是 第1页 | 共15页（A）自然数集 （B）整数集 （C）有理数集 （D）无理数集 （6）△ABC的三内角A，B，C，所对边的长分别为a,b,c，设向量p(ac,b)、q=(ba,ca). 若p∥q，，则角C的大小为    2 （A） （B） （C） （D） 6 3 2 3 （7）与方程y e2x 2ex 1 (x 0)的曲线关于直线y  x对称的曲线的方程为 （A）y ln(1 x) （B）y ln(1 x) （C）y  ln(1 x) （D）y  ln(1 x) x2 y2 x2 y2 （8）曲线  1(m6)与曲线  1(5 n9)的 10m 6m 5n 9n （A）焦距相等 （B）离心率相等 （C）焦点相同 （D）准线相同 （9）在等比数列{a }中，a  2,前n项和为S ，若数列{a 1}也是等比数列，则S 等 n 1 n n n 于 （A）2n1 2 （B）3n （C）2n （D）3n 1 （10）直线y  2k与曲线9k2x2  y2 18k2 | x|(kR,且k  0)的公共点的个数为 （A）1 （B）2 （C）3 （D）4 1 1 （11）已知函数 f(x)  (sinxcosx) |sinxcosx|,则 f(x)的值域是 2 2 2 2 2 （A）[－1，1] （B）[ ,1] （C）[1, ] （D）[1, ] 2 2 2 （12）设O（0，0），A（1，0），B（0，1），点P是线段AB上的一个动点，AP AB. 若OPAB  PAPB，则实数的取值范围是 1 2 （A） 1 （B）1 1 2 2 1 2 2 2 （C） 1 （D）1 1 2 2 2 2 第II卷（非选择题 共90分） 二．填空题：本大题共4小题，每小题4分，共16分. ex,x 0, 1 （13）设g(x)   则g(g( ))  . lnx,x 0, 2 第2页 | 共15页4 6 4 6 4 6 (  )(  ) (  )  5 7 52 72 5n 7n （14）lim = . n 5 4 5 4 5 4 (  )(  ) (  )  6 5 62 52 6n 5n （15）5名乒乓球队员中，有2名老队员和3名新队员，现从中选出3名队员排成1,2,3号 参加团体比赛，则入选的3名队员中至少有1名老队员，且1、2号中至少有1名新 队员的排法有 种.（以数作答） （16）若一条直线与一个正四棱柱各个面所成的角都为，则cos= . 三．解答题：本大题共小题，共74分，解答应写出文字说明、证明过程或演算步骤。 （17）（本小题满分12分） 已知函数 f(x) sin2 x2sinxcosx3cos2 x,xR.求： （Ⅰ）求函数 f(x)的最大值及取得最大值的自变量x的集合； （Ⅱ）函数 f(x)的单调增区间. 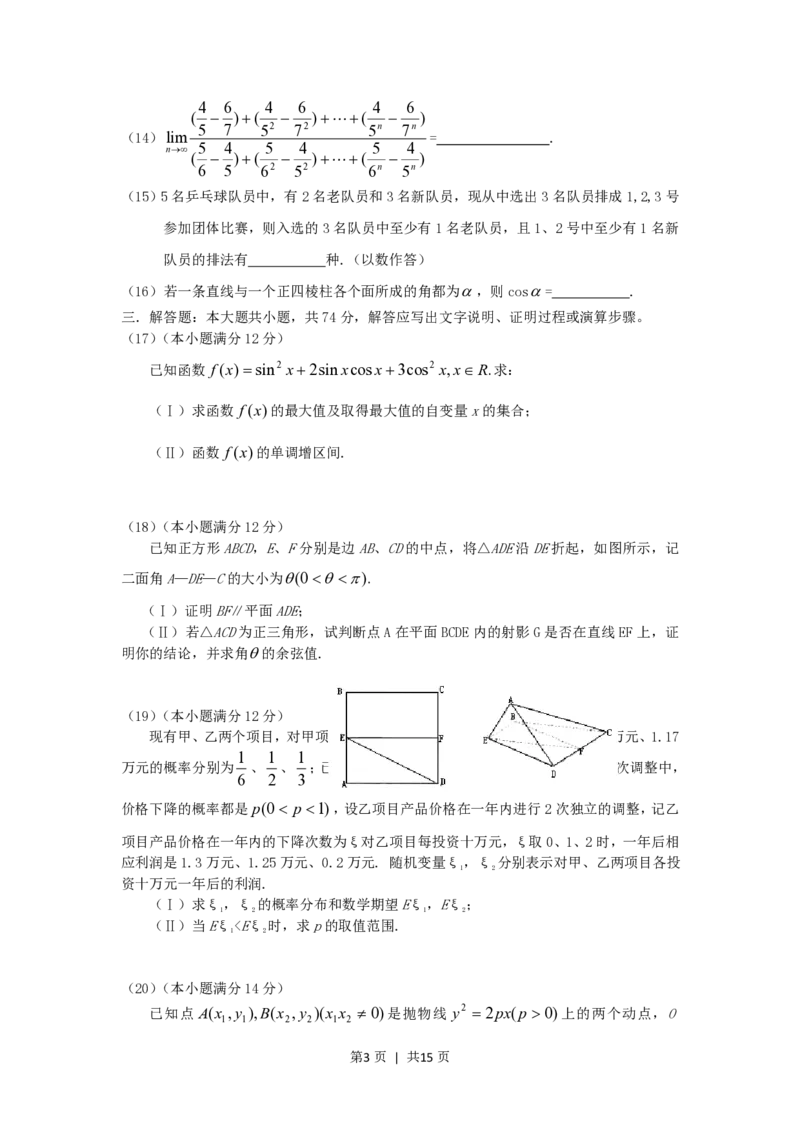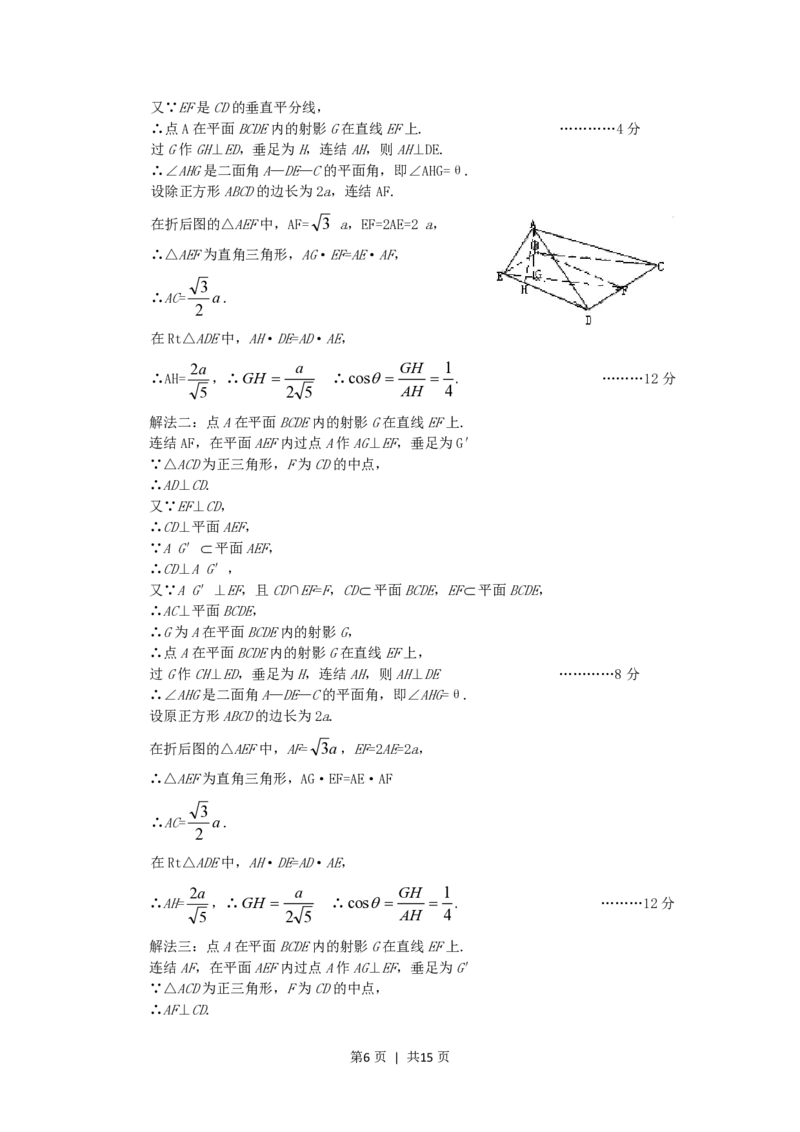（18）（本小题满分12分） 已知正方形ABCD，E、F分别是边AB、CD的中点，将△ADE沿DE折起，如图所示，记 二面角A—DE—C的大小为(0). （Ⅰ）证明BF∥平面ADE； （Ⅱ）若△ACD为正三角形，试判断点A在平面BCDE内的射影G是否在直线EF上，证 明你的结论，并求角的余弦值. （19）（本小题满分12分） 现有甲、乙两个项目，对甲项目每投资十万元，一年后剩是1.2万元、1.18万元、1.17 1 1 1 万元的概率分别为 、 、 ；已知乙项目的利润与产品价格的调整有关，在每次调整中， 6 2 3 价格下降的概率都是 p(0 p 1)，设乙项目产品价格在一年内进行2次独立的调整，记乙 项目产品价格在一年内的下降次数为ξ对乙项目每投资十万元，ξ取0、1、2时，一年后相 应利润是1.3万元、1.25万元、0.2万元. 随机变量ξ，ξ 分别表示对甲、乙两项目各投 1 2 资十万元一年后的利润. （Ⅰ）求ξ，ξ 的概率分布和数学期望Eξ，Eξ； 1 2 1 2 （Ⅱ）当Eξ