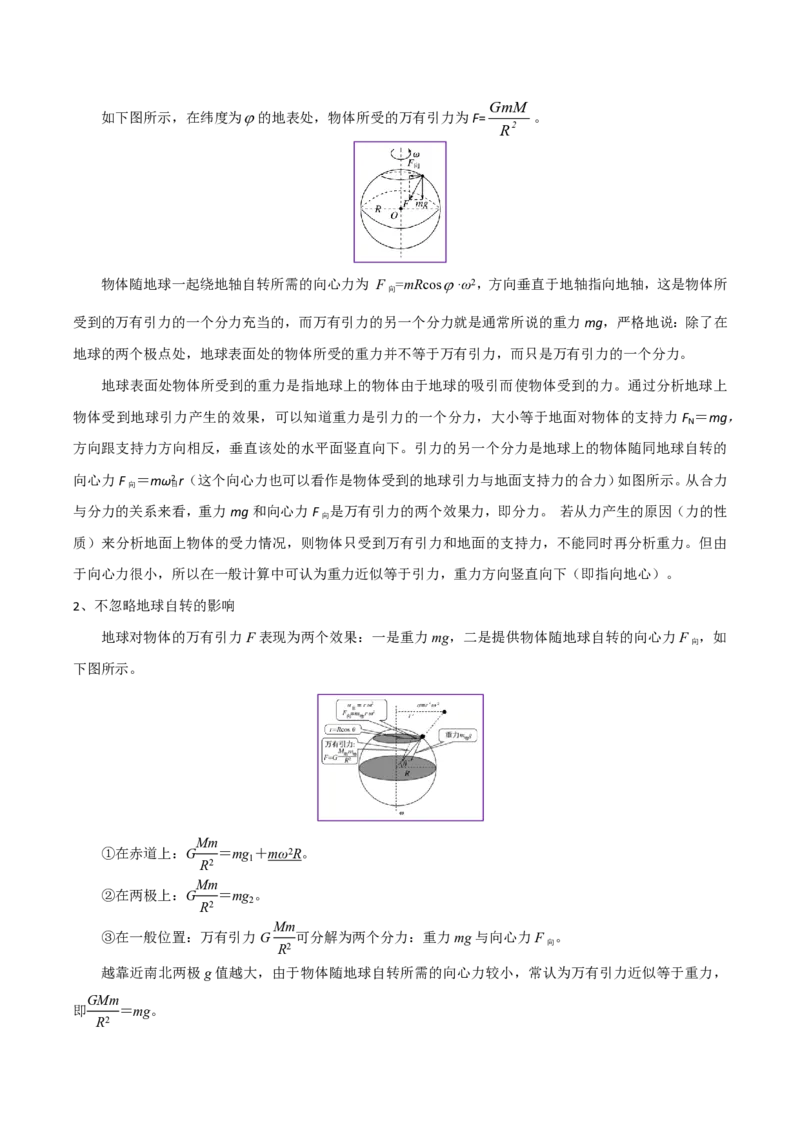
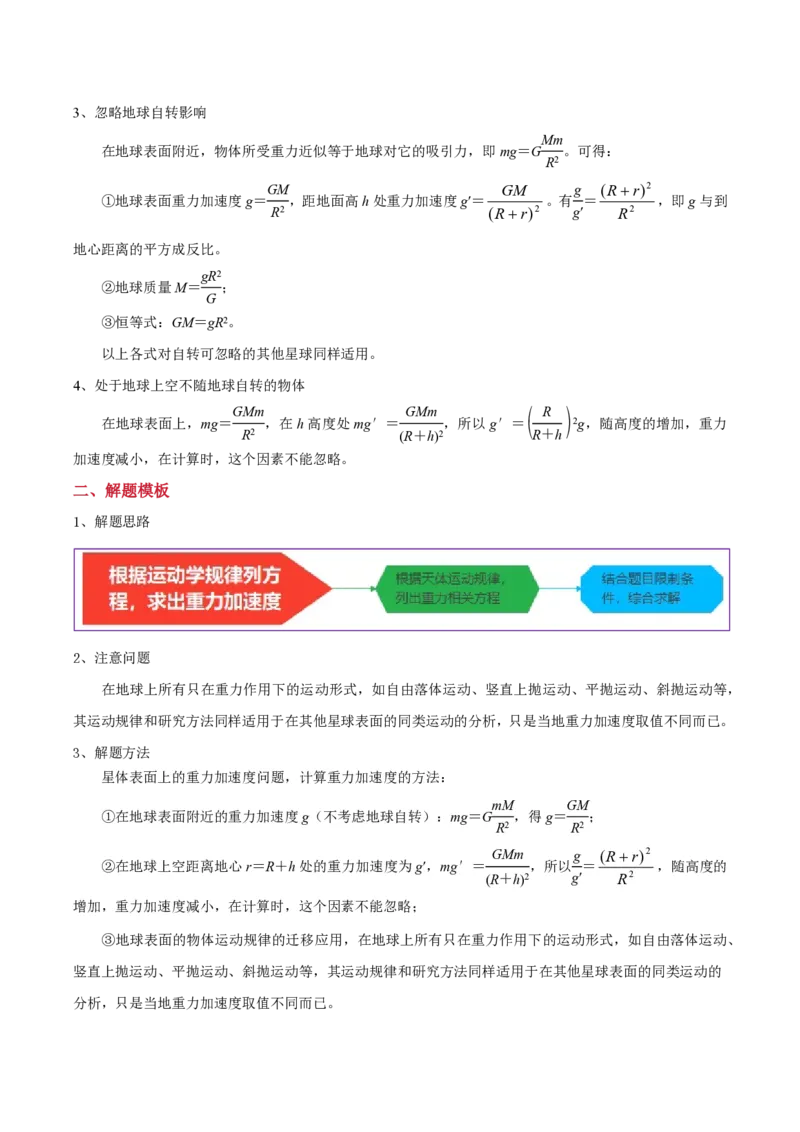
文档内容
模板 06 万有引力与航天(四大题型)
本节导航:
题型01 天体质量和密度的估算 题型02 卫星及其变轨问题
题型03 天体表面重力加速度的相关问题 题型04 双星和多星问题
题型 01 天体质量和密度的估算
1、问题涉及情景新颖,常与最新的航天科技结合出题,出题角度不难但易错。
2、公式的选用灵活多变,学生要谨记其本质为万有引力提供向心力,掌握各个公式是解题的关键。
一、必备基础知识
1、开普勒三大定律
定律 内容 图示
开普勒第一定律 所有行星绕太阳运动的轨道都是椭圆,太
(轨道定律) 阳处在椭圆的一个焦点上。
开普勒第二定律 对任意一个行星来说,它与太阳的连线在
(面积定律) 相等的时间内扫过相等的面积。
所有行星的轨道的半长轴的三次方跟它
开普勒第三定律 的公转周期的二次方的比值都相等。即
(周期定律) a3
k ,k是一个与行星无关的常量。
T2
2、万有引力定律
内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m
1
和m 的乘积成正比,与它们之间距离r的二次方成反比。
2
m m
表达式:F=G 1 2 ,其中G叫做引力常量,G 6.671011Nm2 /kg2 牛顿得出了万有引力与物
。
r2体质量及它们之间距离的关系,但没有测出引力常量G。英国物理学家卡文迪什通过实验推算出引力常量G
的值。
适用条件:①适用于质点间的相互作用;②两个质量分布均匀的球体可视为质点或者一个均匀球体与
球外一个质点,r是两球心间的距离或者球心到质点间的距离;③两个物体间的距离远远大于物体本身的大
小,r为两物体质心间的距离。
3、天体(卫星)运动问题的两点思路
Mm v2 4π2r
①天体运动的向心力来源于天体之间的万有引力,即G =ma =m =mω2r=m 。
n
r2 r T2
Mm
②在中心天体表面或附近运动时,万有引力近似等于重力,即G =mg(g表示天体表面的重力加速
R2
度)。
二、解题模板
1、解题思路
2、注意问题
区分中心天体的半径和环绕天体的轨道半径,只有近地环绕天体的轨道半径才等于中心天体的半径。
该类型的题目是求解中心天体的质量和密度,是不能求解环绕天体的质量和密度。
3、解题方法
①利用天体表面的重力加速度g和天体半径R。
Mm gR2 M M 3g
由于G =mg,故天体质量M= ,天体密度ρ= = = 。
R2 G V 4 4πGR
πR3
3
②通过观察卫星绕天体做匀速圆周运动的周期T和轨道半径r。
Mm 4π2 4π2r3
由万有引力等于向心力,即G =m r,得出中心天体质量M= ;若已知天体半径R,则天体
r2 T2 GT2
M M 3πr3
的平均密度ρ= = = ;若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r等于
V 4 GT2R3
πR3
3
3π
天体半径R,则天体密度ρ= 。可见,只要测出卫星环绕天体表面运动的周期T,就可估算出中心天体
GT2
的密度。(2024·北京·高考真题)科学家根据天文观测提出宇宙膨胀模型:在宇宙大尺度上,所有的宇宙
物质(星体等)在做彼此远离运动,且质量始终均匀分布,在宇宙中所有位置观测的结果都一样。以某一
点O为观测点,以质量为m的小星体(记为P)为观测对象。当前P到O点的距离为r ,宇宙的密度为
0
。
0
(1)求小星体P远离到2r 处时宇宙的密度ρ;
0
(2)以O点为球心,以小星体P到O点的距离为半径建立球面。P受到的万有引力相当于球内质量集中于
mm
O点对P的引力。已知质量为m 和m 、距离为R的两个质点间的引力势能E G 1 2 ,G为引力常量。
1 2 p R
仅考虑万有引力和P远离O点的径向运动。
a.求小星体P从r 处远离到2r 。处的过程中动能的变化量E ;
0 0 k
b.宇宙中各星体远离观测点的速率v满足哈勃定律vHr,其中r为星体到观测点的距离,H为哈勃系数。
H与时间t有关但与r无关,分析说明H随t增大还是减小。
思路分析
第一问的思路:
在宇宙中所有位置观测的结果都一样, 根据质量相同即
则小星体P运动前后球内质量相同 可求出密度
第二问的思路:
根据密度和半径 由能量守恒定律 根据a问得到速度与半径的
可求得质量 求得动能变化量 关系,联立哈勃定律可求解
详细解析
1 2
【答案】(1) ;(2)a.ΔE Gπmr2;b.H随t增大而减小
8 0 k 3 0 0
【详解】(1)在宇宙中所有位置观测的结果都一样,则小星体P运动前后距离O点半径为r 和2r 的球内
0 0
质量相同,即
4 4
πr3 π2r 3
0 3 0 3 0
解得小星体P远离到2r 处时宇宙的密度
0
1
8 0
(2)a.此球内的质量
4
M πr3
0 3 0P从r 处远离到2r 处,由能量守恒定律得,动能的变化量
0 0
Mm GMm 2
ΔE G Gπmr2
k r 2r 3 0 0
0 0
b.由a知星体的速度随r 增大而减小,星体到观测点距离越大,运动时间t越长,由vHr知,H减小,
0
故H随t增大而减小。
(2024·广东·模拟预测)2021年2月10日19时52分,我国首次火星探测任务“天问一号”探测
器实施近火捕获制动,成功实现环绕火星运动,成为我国第一颗人造火星卫星。设想某一天一位宇航员到
达火星后进行如下实验:如图所示,将支架水平固定在火星表面上,摆轴末端用细绳连接一质量为m的小
球。拉直细绳并给小球一个垂直细绳的初速度,让它在竖直平面内做完整的圆周运动。在最低点a和最高
点b,细绳拉力大小分别为T 、T ,阻力不计。已知火星的半径为R,万有引力常量为G。求:
a b
(1)火星表面重力加速度的大小g;
(2)火星的质量M。
T T
【答案】(1)g a b
6m
T T R2
(2)M a b
6Gm
【详解】(1)设绳长为l,在a点时
mv2
T mg a
a l
在b点时
mv2
T mg b
b l
由机械能守恒定律可得
1 1
mv2 mv22mgl
2 a 2 b
联立解得T T
g a b
6m
(2)由题可知
Mm
G mg
R2
解得
T T R2
M a b
6Gm
题型 02 卫星及其变轨问题
1、该题型常与较新的卫星结合出题,题目一般较长,一般介绍的内容可以忽略,本质就是圆周运动规
律的应用。
2、题型难度不大,考查公式较多,需要学生具备一定的综合分析能力。
一、必备基础知识
1、卫星轨道
卫星运动的轨道平面一定通过地心,一般分为赤道轨道、极地轨道和倾斜轨道。
2、运行规律
𝑀𝑚 𝑣2 4𝜋2
卫星做匀速圆周运动。万有引力提供向心力:即由G =m =mrω2=m r=ma 可推导出:①线
n
𝑟2 𝑟 𝑇2
Mm v2 GM Mm GM
速度:G m v ;②角速度:G mω2r ω ;③周期:
r2 r r r2 r3
Mm 4π2 r3 Mm GM
G m r T 2π ;④向心加速度:G ma a 。
r2 T2 GM r2 r2
3、三种卫星
①近地卫星:在地球表面附近环绕地球做匀速圆周运动其运行的轨道半径可近似认为等于
地球的半径,其运行线速度约为7.9 km/s。②地球同步卫星:地球同步卫星,是相对于地面静止的,这种卫星位于赤道上方某一高度的稳定轨道
上,且绕地球运动的周期等于地球的自转周期。
③极地卫星:运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
4、三大宇宙速度
数值
宇宙速度 意义
(km/s)
第一宇宙速度 是人造地球卫星的最小发射速度,也是人造地球卫星
7.9
(环绕速度) 绕地球做圆周运动的最大运行速度。
第二宇宙速度 使物体挣脱地球引力束缚的最小发射速度。
11.2
(脱离速度)
第三宇宙速度
16.7 使物体挣脱太阳引力束缚的最小发射速度。
(逃逸速度)
发射速度为v,第一宇宙速度为v,第二宇宙速度为v,第三宇宙速度为v,发射物体的运动情况跟宇
1 2 3
宙速度息息相关,它们的关系如下表所示:
v<v 发射物体无法进入外太空,最终仍将落回地面;
1
v≤v<v 发射物体进入外太空,环绕地球运动;
1 2
v≤v<v 发射物体脱离地球引力束缚,环绕太阳运动;
2 3
v≥v 发射物体脱离太阳系的引力束缚,逃离太阳系中。
3
5、两类变轨的比较
两类变轨 离心运动 近心运动
变轨起因 卫星速度突然增大 卫星速度突然减小
Mm v2 Mm v2
受力分析 G <m G >m
r2 r r2 r[来源:学科网ZXXK]
变为椭圆轨道运动或在较大半径圆轨 变为椭圆轨道运动或在较小半径圆轨
变轨结果
道上运动 道上运动
应用 卫星的发射和回收
二、解题模板
1、解题思路2、注意问题
地球同步卫星的轨道平面、周期、角速度、高度、速率、绕行方向、向心加速度都是一定的。
轨道平面一定(只能位于赤道上空,轨道平面和赤道平面重合);
周期一定(与地球自转周期相同,大小为T=24h=8.64×104s。);
角速度一定(与地球自转的角速度相同);
Mm 2 2 GT2M
高度一定(根据G m Rh得h 3 R)=3.6×107m);
Rh2 T 42
2Rh
线速度一定(根据线速度的定义,可得v =3.08km/s,小于第一宇宙速度);
T
GMm GM
向心加速度一定(根据 =ma,可得a= =g=0.23 m/s2);
R+h2 n n R+h2 h
绕行方向一定(与地球自转的方向一致)。
卫星变轨时半径的变化,根据万有引力和所需向心力的大小关系判断;稳定在新轨道上的运行速度变
GM
化由v= 判断;卫星在不同轨道上运行时机械能不同,轨道半径越大,机械能越大;卫星经过不同轨
r
道相交的同一点时加速度相等,外轨道的速度大于内轨道的速度。
3、解题方法
卫星变轨的判断及处理思路方法:①要增大卫星的轨道半径,必须加速;②当轨道半径增大时,卫星
的机械能随之增大。
Mm v2 4π2
卫星向心加速度的不同表述形式:G =ma ;a = =rω2= r。
n n
r2 r T2
解决力与运动关系的思想还是动力学思想,解决力与运动的关系的桥梁还是牛顿第二定律:卫星的a 、
n
v、ω、T是相互联系的,其中一个量发生变化,其他各量也随之发生变化;a 、v、ω、T均与卫星的质量无
n
关,只由轨道半径r和中心天体质量共同决定。
卫星变轨解题方法:
轨道渐变问题:当卫星由于某种原因速度逐渐改变时,万有引力不再等于向心力,卫星将做变轨运行。
Mm v2
当卫星的速度逐渐增加时,G <m ,即万有引力不足以提供向心力,卫星将做离心运动,轨道半径
r2 r
GM
变大,当卫星进入新的轨道稳定运行时由v= 可知其运行速度比原轨道时减小。
r
Mm v2
当卫星的速度逐渐减小时,G >m ,即万有引力大于所需要的向心力,卫星将做近心运动,轨道半
r2 rGM
径变小,当卫星进入新的轨道稳定运行时由v= 可知其运行速度比原轨道时增大。
r
离心运动:
mv2 GM
当v增大时,所需向心力 增大,卫星将做离心运动,轨道半径变大,由v= 知其运行速度要减
r r
小,此时重力势能、机械能均增加。同一卫星在不同轨道上运行时机械能不同,轨道半径(半长轴)越大,
机械能越大。
mv2 GM
卫星向心运动:当v减小时,所需向心力 减小,因此卫星将做向心运动,轨道半径变小,由v=
r r
知其运行速度将增大,此时重力势能、机械能均减少。情景分析,如下图所示:
先将卫星发送到近地轨道Ⅰ;使其绕地球做匀速圆周运动,速率为v,变轨时在P点处点火加速,短
1
时间内将速率由v增加到v,使卫星进入椭圆形的转移轨道Ⅱ;卫星运行到远地点Q时的速率为v,此时
1 2 3
进行第二次点火加速,在短时间内将速率由v增加到v,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。
3 4
注意:卫星在不同轨道相交的同一点处加速度相等,但是外轨道的速度大于内轨道的速度。中心天体
相同,但是轨道不同(不同圆轨道或椭圆轨道),其周期均满足开普勒第三定律。
变轨过程物体的分析如下:
速度 根据以上分析可得:v > v >v >v
4 3 2 1
加速度 在P点,卫星只受到万有引力作用,所以卫星当从轨道Ⅰ或者轨道Ⅱ上经
过P点时,卫星的加速度是一样的;同理在Q点也一样。
周期 r3
根据开普勒第三定律 =k可得T