模板04曲线运动（六大题型）（解析版）_20241224_230817_2024-2025高三（6-6月题库）_2025年01月试卷_01012025年高考物理答题技巧与模板构建

模板 04 曲线运动（六大题型） 本节导航： 题型01 平抛运动规律的求解 题型02 平抛运动在斜面上的三种模型 题型03 平抛运动与圆周运动的组合问题 题型04 平抛运动的临界问题 题型05 斜抛运动规律的应用 题型06 类平抛运动规律的应用 题型 01 平抛运动规律的求解 1、平抛运动内容是高考的必考知识点，是最典型的曲线运动之一，注意考查运动的合成与分解。 2、试题的呈现形式丰富，提问角度设置新颖，学生需要掌握平抛运动的规律和重要推论。 一、必备基础知识 1、运动规律 水平方向：做匀速直线运动，速度：v ＝v ，位移：x＝v t； x 0 0 1 竖直方向：做自由落体运动，速度：v ＝gt，位移：y＝ gt2； y 2 gt 合速度为v  v2 v2 即v  v2 (gt)2 ，方向：v与水平方向夹角为tana  ，即 x y 0 v 0 gt a  tan1( )。 v 0 合位移为 即 ，S 与水平方向夹角为 ，即 S  x2  y2 1 gt S  (v t)2 ( gt2)2 tan 0 2 2v 0 。 gt tan1( ) 2v 0 2、运动图示3、重要推论 ①做平抛运动的物体任一时刻的瞬时速度的反向延长线一定通过此时水平位移的中点。 ②速度方向与水平方向的夹角为α，位移与水平方向的夹角为θ，则tan2tan。 二、解题模板 1、解题思路 2、注意问题 解答平抛运动问题时，一般的方法是将平抛运动沿水平和竖直两个方向分解，这样分解的优点是不 用分解初速度也不用分解加速度。 画出速度(或位移)分解图，通过几何知识建立合速度(或合位移)、分速度(或分位移)及其方向间的关 系，通过速度(或位移)的矢量三角形求解未知量。 如果知道速度的大小或方向，应首先考虑分解速度。 如果知道位移的大小或方向，应首先考虑分解位移。 3、解题方法 ①分解速度：对于一个做平抛运动的物体来说，如果知道了某一时刻的速度方向，则我们常常是从 “分解速度”的角度来研究问题。 方法突破：初速度v 做平抛运动的物体，经历时间t速度和水平方向的夹角为α，由平抛运动的规 0 v gt y 律得：tan α＝ ＝ ，从而得到初速度v 、时间t、偏转角α之间的关系，进而求解。 0 v v x 0 ②分解位移：对于做平抛运动的物体，如果知道某一时刻的位移方向（如物体从已知倾角的斜面上 水平抛出后再落回斜面，斜面倾角就是它的位移与水平方向之间的夹角），则我们可以把位移沿水平方 向和竖直方向进行分解，然后运用平抛运动的规律来研究问题。 方法突破：以初速度v 做平抛运动的物体，经历时间t位移和水平方向的夹角为θ，由平抛运动的 0 1 y 规律得：水平方向做匀速直线运动x＝v t，竖直方向做自由落体运动y＝ gt2，tan θ＝ ，结合上面三个 0 2 x关系式求解。 ③假设法：假设法是在不违背原题所给条件的前提下，人为地加上或减去某些条件，以使问题方便 求解。利用假设法处理某些物理问题，往往能突破思维障碍，找出新的解题途径，化难为易，化繁为简。 方法突破：对于平抛运动，飞行时间由高度决定，水平位移由高度和初速度决定，所以当高度相同 时，水平位移与初速度成正比。但有时高度不同，水平位移就很难比较，这时我们可以采用假设法，例 如移动水平地面使其下落高度相同，从而做出判断。 ④重要推论法：有些平抛运动问题按照常规的方法进行合成、分解、计算，虽然也能够解决问题， 但是过程复杂，计算繁琐，如果选择平抛运动的一些重要推论则问题会相对简便很多。 方法突破：做平抛运动的物体，任意时刻速度方向的反向延长线一定通过此时水平位移的中点。 做平抛运动的物体在任一时刻或任一位置时，设其速度方向与水平方向的夹角为α，位移与水平方 向的夹角为θ，则tan α＝2tan θ。 （2024·新疆河南·高考真题）如图，一长度l 1.0m的均匀薄板初始时静止在一光滑平台上， 薄板的右端与平台的边缘O对齐。薄板上的一小物块从薄板的左端以某一初速度向右滑动，当薄板运动 l 的距离l  时，物块从薄板右端水平飞出；当物块落到地面时，薄板中心恰好运动到O点。已知物块 6 与薄板的质量相等。它们之间的动摩擦因数0.3，重力加速度大小g 10m/s2。求 （1）物块初速度大小及其在薄板上运动的时间； （2）平台距地面的高度。 思路分析 第一问的思路： 第二问的思路：详细解析 1 5 【答案】（1）4m/s； s；（2） m 3 9 【详解】（1）物块在薄板上做匀减速运动的加速度大小为 a g 3m/s2 1 薄板做加速运动的加速度 mg a  3m/s2 2 m 对物块 1 ll v t at2 0 2 1 对薄板 1 l  a t2 2 2 解得 v 4m/s 0 1 t  s 3 （2）物块飞离薄板后薄板得速度 v a t 1m/s 2 2 物块飞离薄板后薄板做匀速运动，物块做平抛运动，则当物块落到地面时运动的时间为 l l  t'  2 6  1 s v 3 2 则平台距地面的高度 1 5 h gt'2  m 2 9 （2024·辽宁鞍山·二模）如图所示，半径R1.0m的半球紧贴着竖直墙固定在水平地面上。 体积可忽略的小球在竖直墙最高点最右侧以v 水平向右抛出。已知墙高H 1.8m，忽略空气阻力，小球 0 落地后不反弹。试求： （1）若小球刚好击中半球的最高点，则小球水平抛出的初速度v 大小。 0 （2）若小球不与半球相碰，则小球水平抛出的初速度v 大小的取值范围。 0【答案】（1）2.5m/s；（2）v 1.5 6m/s 0 【详解】（1）小球做平抛运动，竖直方向上有 1 H R gt2 2 1 水平方向上有 Rv t 01 解得 v 2.5m/s 0 （2）小球恰不与半球相碰，即轨迹恰好与圆轨道相切，设此时速度方向与竖直方向所成夹角为θ，由几 何关系有 v tan 0 gt 水平方向有 RRcosv t 0 竖直方向上有 1 H Rsin gt2 2 且 sin2cos21 解得 v 1.5 6m/s 0 小球水平抛出初速度范围为v 1.5 6m/s 0 题型 02 平抛运动在斜面上的三种模型这类题型是平抛运动的推广，求解过程既需要运用平抛运动的知识，还要充分考虑斜面的约束，掌 握三角函数等的知识，综合求解。 一、必备基础知识 1、模型特点 平抛运动与斜面结合的问题，一般是研究物体从斜面顶端平抛到落回斜面的运动过程，解决这类问 题一般仍是在水平和竖直方向上分解。求解的关键在于深刻理解通过与斜面的关联而给出的隐含条件。 2、三种模型 ①垂直打斜面，其特点为在撞击斜面的时刻，速度方向与水 平方向的夹角与斜面的倾角互余。 ②顺着斜面抛，其特点为全过程位移的方向沿斜面方向，即竖直位移与水平位移之比等于斜面倾角 的正切。 ③抛体切入斜面，其特点为速度方向与斜面平行。 二、解题模板 1、解题思路 2、注意问题 在解答该类问题时，除要运用平抛运动的位移和速度规律外，还要充分利用斜面倾角，找出斜面倾 角同位移和速度与水平方向夹角的关系，从而使问题得到顺利解决。 物体从斜面上某一点水平抛出又落在斜面上，即满足平抛运动规律。在解答这类问题时，除要运用 平抛运动的位移和速度规律，还要充分运用斜面倾角，找出斜面倾角同位移和速度与水平方向夹角的关 系，从而顺利解决问题。 3、解题方法 方法 内容 斜面 运动时间水平：v ＝v 𝑣0 𝑣0 x 0 由tan θ＝ ＝ 得t＝ 竖直：v ＝gt 𝑣𝑦 𝑔𝑡 分解速度 y 𝑣0 合速度：v＝ v2 x ＋v2 y 𝑔 𝑡𝑎𝑛 𝜃 水平：x＝v t 𝑦 𝑔𝑡 0 由tan θ＝ ＝ 得t＝ 1 𝑥 2𝑣0 分解位移 竖直：y＝ gt2 2 2𝑣0𝑡𝑎𝑛 𝜃 合位移：s＝ x2＋y2 𝑔 水平：v ＝v x 0 𝑣𝑦 𝑔𝑡 竖直：v ＝gt y 由tan θ＝ ＝ 得t＝ 𝑣0 𝑣0 分解速度 合速度： 𝑣0𝑡𝑎𝑛 𝜃 2 2 v＝ 𝑣 ＋𝑣 𝑔 𝑥 𝑦 （2024·山东泰安·三模）如图所示，倾角θ=37°的光滑斜面AB固定在水平面上，现将一弹力 球从斜面的顶端A点以初速度v =10m/s水平向右抛出，弹力球恰好落在斜面的底端B点。已知重力加 0 速度g取10m/s2，sin37°=0.6，cos37°=0.8，不计空气阻力。 （1）求斜面的长度； （2）若弹力球与斜面碰撞时，沿斜面方向的速度不变，垂直斜面方向的速度大小不变，方向反向，现 仅调整弹力球从A点水平抛出时的速度大小，使弹力球与斜面碰撞1次后仍能落到B点，求调整后弹力 球水平抛出的速度大小。 思路分析 第一问的思路： 第二问的思路：详细解析 25 17 【答案】（1）18.75m；（2） m/s 17 【详解】（1）弹力球做平抛运动，竖直方向有 1 gt2 Lsin37 2 水平方向有 v t Lcos37 0 联立解得斜面的长度为 L18.75m （2）将平抛运动分解为沿斜面方向的匀加速运动和垂直斜面方向的类竖直上抛运动，设调整后弹力球水平 抛出时的速度大小沿垂直斜面方向的分速度大小为 v v sin37  1 沿斜面方向的分速度大小为 v v cos37 ∥ 1 垂直斜面方向的加速度大小为 g  gcos37  沿斜面方向的加速度大小为 g  gsin37 ∥ 弹力球每次从斜面离开到再次落回斜面过程中用时为 2v t   g  沿斜面方向有 1 v 2t g (2t)2 L  2  25 17 联立解得v  m/s 1 17 （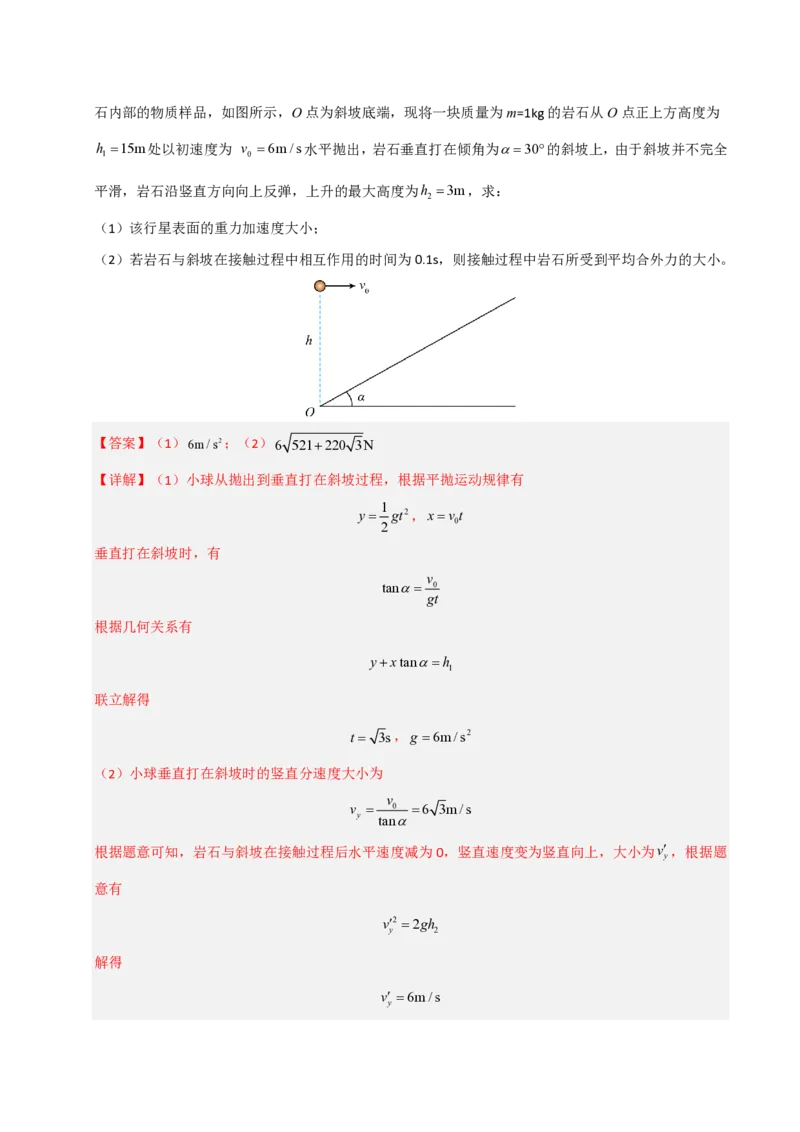2024·四川德阳·模拟预测）为了采集某行星岩石内部的物质样品，先将岩石用行星探测车 运往高处，然后水平抛出，让岩石重重地砸在行星表面，这样就可以将坚硬的岩石撞碎，进而采集到岩石内部的物质样品，如图所示，O点为斜坡底端，现将一块质量为m=1kg的岩石从O点正上方高度为 h 15m处以初速度为 v 6m/s水平抛出，岩石垂直打在倾角为30的斜坡上，由于斜坡并不完全 1 0 平滑，岩石沿竖直方向向上反弹，上升的最大高度为h 3m，求： 2 （1）该行星表面的重力加速度大小； （2）若岩石与斜坡在接触过程中相互作用的时间为0.1s，则接触过程中岩石所受到平均合外力的大小。 【答案】（1）6m/s2；（2）6 521220 3N 【详解】（1）小球从抛出到垂直打在斜坡过程，根据平抛运动规律有 1 y gt2，xv t 2 0 垂直打在斜坡时，有 v tan 0 gt 根据几何关系有 yxtanh 1 联立解得 t  3s，g 6m/s2 （2）小球垂直打在斜坡时的竖直分速度大小为 v v  0 6 3m/s y tan 根据题意可知，岩石与斜坡在接触过程后水平速度减为0，竖直速度变为竖直向上，大小为v，根据题 y 意有 v2 2gh y 2 解得 v 6m/s y则岩石与斜坡在接触过程中，水平方向根据动量定理可得 Ft 0mv x 0 解得 F 60N x 竖直方向根据动量定理可得 F tmgt mv (mv ) y y y 解得 F (6660 3)N y 则接触过程中岩石对小球的平均作用力大小为 F  F2F2 6 521220 3N x y 则接触过程中岩石所受到平均合外力的大小为6 521220 3N。 题型 03 平抛运动与圆周运动的组合问题 1、这类题型有两种命题角度：①前一部分为平抛运动，后一部分为圆周运动；②前一部分为圆周 运动，后一部分为平抛运动。这两部分区分明显，在不同部分运用各自的规律。 2、注意两部分运动的衔接点以及题中的其它约束，如角度或高度等。 一、必备基础知识 1、水平面的组合问题 物体先做水平面内的匀速圆周运动，后做平抛运动。 2、竖直面的组合问题 此类问题有时物体先做竖直面内的变速圆周运动，后做平抛运动，有时物体先做平抛运动，后做竖 直面内的变速圆周运动，有时要结合能量关系求解。 二、解题模板 1、解题思路2、注意问题 这类问题往往是平抛运动与圆周运动的组合，各部分问题独立存在，分段明显，但是互相联系，两 个过程的衔接点是速度。 要注意题目中的约束条件，比如角度等。 3、解题方法 水平面的解题方法：①明确水平面内匀速圆周运动的向心力来源，根据牛顿第二定律和向心力公式 列方程；②平抛运动一般是沿水平方向和竖直方向分解速度或位移；③速度是联系前后两个过程的关键 物理量，前一个过程的末速度是后一个过程的初速度。 竖直面的解题方法：①首先要明确是“轻杆模型”还是“轻绳模型”，然后分析物体能够达到圆周最高 点的临界条件；②注意前后两过程中速度的连续性。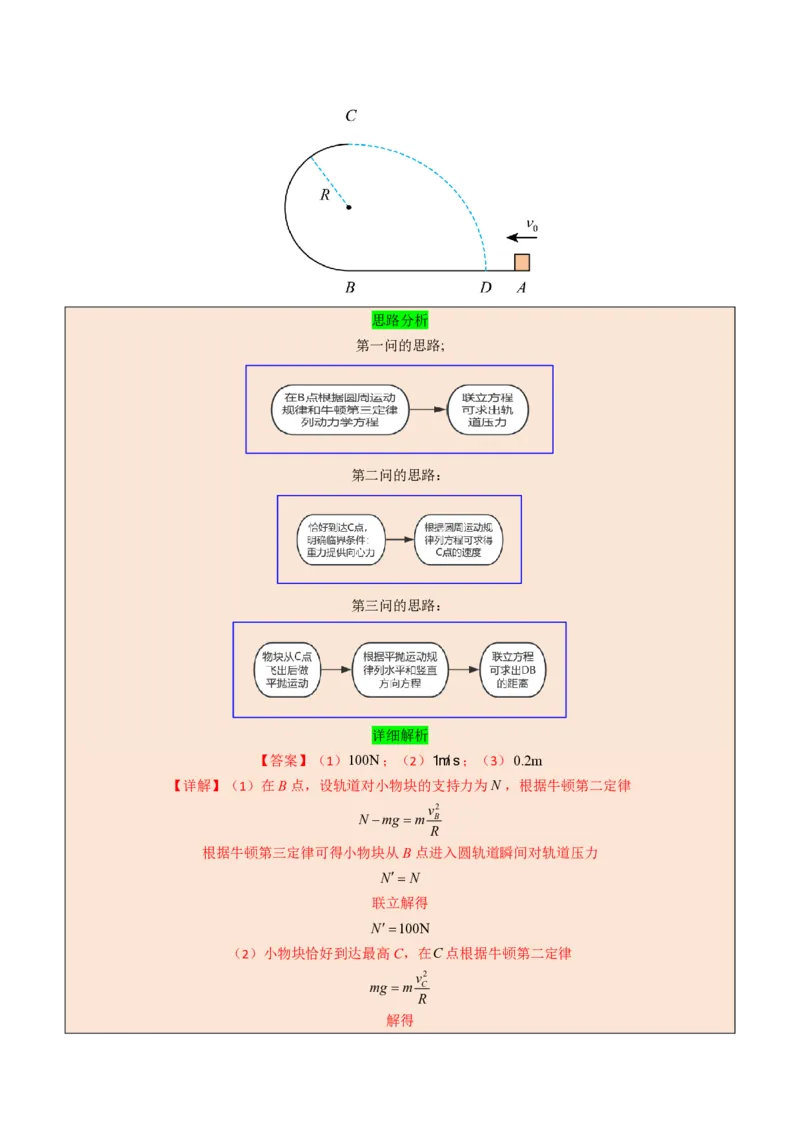 （2024·广东·模拟预测）如图所示，水平轨道AB与竖直半圆形轨道BC在B点相切。质量 m1kg的小物块（可视为质点）以一定的初速度从水平轨道的A点向左运动，进入圆轨道后，沿圆轨 道内侧做圆周运动，恰好到达最高C，之后离开圆轨道，做平抛运动，落在圆轨道上的D点。已知小物 块在B点进入圆轨道瞬间，速度v 3m/s，圆轨道半径R0.1m，重力加速度g 10m/s2，忽略空气阻 B 力。求： （1）小物块从B点进入圆轨道瞬间对轨道压力的大小； （2）小物块到达C点的瞬时速度v 的大小； C （3）小物块的落点D与B点的距离。思路分析 第一问的思路; 第二问的思路： 第三问的思路： 详细解析 【答案】（1）100N；（2）1m/s；（3）0.2m 【详解】（1）在B点，设轨道对小物块的支持力为N ，根据牛顿第二定律 v2 Nmg m B R 根据牛顿第三定律可得小物块从B点进入圆轨道瞬间对轨道压力 NN 联立解得 N100N （2）小物块恰好到达最高C，在C点根据牛顿第二定律 v2 mg m C R 解得v 1m/s C （3）小物块从C点飞出后做平抛运动，竖直方向 1 2R gt2 2 水平方向 x v t DB C 联立解得 x 0.2m DB （2024·广东·模拟预测）游客在动物园里常看到猴子在荡秋千和滑滑板，其运动可以简化为 如图所示的模型，猴子需要借助悬挂在高处的秋千绳飞跃到对面的滑板上，质量为m18kg的猴子在竖 直平面内绕圆心O做圆周运动。若猴子某次运动到O点的正下方时松手，猴子飞行水平距离H 4m后 跃到对面的滑板上，O点离平台高度也为H，猴子与O点之间的绳长h3m，重力加速度大小 g 10m/s2，不考虑空气阻力，秋千绳视为轻绳，猴子可视为质点，求： （1）猴子落到滑板时的速度大小； （2）猴子运动到O点的正下方时绳对猴子拉力的大小。 【答案】（1）10m/s；（2）660N 【详解】（1）设猴子松手后飞行的时间为t，由平抛运动规律在竖直方向上有 1 H h gt2 2 在水平方向上有 H v t x 解得 v 4 5m/s x 在竖直方向上有v2 2g(H h) y 解得 v 2 5m/s y 得猴子落到平台时的速度大小 v v2v2 10m/s x y （2）设猴子运动到O点的正下方时绳对选手拉力的大小为F ，猴子做圆周运动的半径为 Rh 猴子经过圆周运动轨迹最低点时，由牛顿第二定律得 v2 F mg m x R 11 解得绳对猴子拉力的大小F  mg 660N 3 题型 04 平抛运动的临界问题 1、这类题目中有“刚好”“恰好”“正好”“取值范围”“多长时间”“多大距离”等词语，表 明题述的过程中存在临界点。 2、这类题目中有“最大”“最小”“至多”“至少”等字眼，表明题述的过程中存在着极值。 一、必备基础知识 1、问题特点 在体育运动中，像乒乓球、排球、网球等都有中间网及边界问题，要求球既能过网，又不能出边界， 某物理量(尤其是球速)往往要有一定的范围限制，在这类问题中，确定临界状态，画好临界轨迹，是解 决问题的关键点。 二、解题模板 1、解题思路2、注意问题 此类问题的临界条件：通常为位置关系的限制或速度关系的限制，列出竖直方向与水平方向上的方 程，将临界条件代入即可求解。 在分析此类问题时一定要注意从实际出发寻找临界点，画出物体运动过程的草图，明确临界条件。 3、解题方法 ①找出情景中临界条件，如“恰好”、“最大”、“最小”等关键词，明确其含义。。 ②画出运动过程的草图，确定物体的临界位置，标注位移、速度等临界值。 明确临界过程的轨迹，运用曲线运动的规律进行求解。 分析平抛运动中的临界问题时一般运用极限分析的方法，即把要求的物理量设定为极大或极小，让临界 问题突现出来，找到产生临界的条件。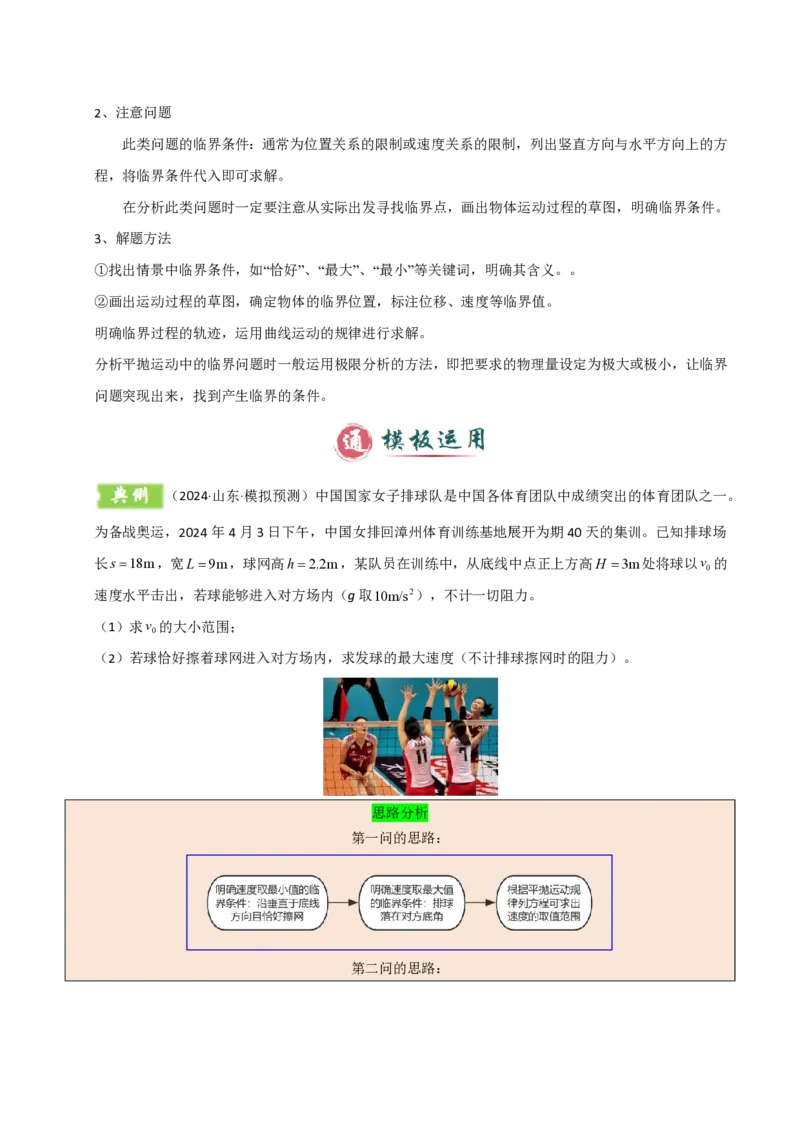 （2024·山东·模拟预测）中国国家女子排球队是中国各体育团队中成绩突出的体育团队之一。 为备战奥运，2024年4月3日下午，中国女排回漳州体育训练基地展开为期40天的集训。已知排球场 长s18m，宽L9m，球网高h2.2m，某队员在训练中，从底线中点正上方高H 3m处将球以v 的 0 速度水平击出，若球能够进入对方场内（g取10m/s2），不计一切阻力。 （1）求v 的大小范围； 0 （2）若球恰好擦着球网进入对方场内，求发球的最大速度（不计排球擦网时的阻力）。 思路分析 第一问的思路： 第二问的思路：详细解析 3 255 【答案】（1）22.5m/sv  m/s；（2）v 6 15m/s 0 2 m 【详解】（1）当排球的初速度v 沿垂直于底线方向且恰好擦网时有最小值，竖直方向有 0 1 H h gt2 2 1 水平方向有 s vt 2 11 解得 v 22.5m/s 1 当排球落在对方底角时，初速度v 有最大值，竖直方向有 0 1 H  gt2 2 2 水平方向有 L 2 s2  v t 2 2 2 解得 3 255 v  m/s 2 2 3 255 所以能进入对方场内的速度范围22.5m/sv  m/s。 0 2 （2）当排球落在侧边线上时，满足条件初速度沿着垂直于底线方向的分量 v 22.5m/s 垂 初速度沿着平行于底线方向的分量 L 2 3 15 v   m/s 平 t 2 2 则有 v  v2 v2 6 15m/s m 垂 平 （2024·浙江金华·模拟预测）如图所示，AOB是游乐场中的滑道模型，位于竖直平面内，由1 两个半径为R的 圆周连接而成，它们的圆心O、O 与两圆弧的连接点O在同一竖直线上。O B沿水 4 1 2 2 池的水面方向，B点右侧为无穷大水平面，水平面上有一系列沿O B方向的漂浮的木板，木板的质量为 2 M，长度为2l。一质量为m的小孩（可视为质点）可由弧AO的任意点静止开始下滑。不考虑水与木板 接触面的阻力，设木板质量足够大且始终处于水平面上。 （1）若小孩恰能在O点脱离滑道，求小孩静止下滑处距O点的高度？ （2）凡能在O点脱离滑道的小孩，其落水点到O 的距离范围？ 2 （3）若小孩从O点静止下滑，求脱离轨道时的位置与O 的连线与竖直方向夹角的余弦值？ 2 （4）某小孩从O点脱离滑道后，恰好落在某木板的中央，经过一段时间振荡和调节后，该木板和小孩 处于静止状态，小孩接下来开始在木板上表演水上漂。如果小孩能一次跳离木板，求小孩做功的最小值？ R 2 1 【答案】（1）h ；（2） 2Rs2R；（3）cos ；（4）W  mgl 2 3 min 2 【详解】（1）若小孩恰能在O点脱离滑道，此时向心力由重力提供 mv2 mg  R 根据机械能守恒可得 1 mgh mv2 2 解得小孩静止下滑处距O点的高度为 R h 2 （2）凡能在O点脱离滑道的小孩，其距离O点的高度范围是 R hR 2 由机械能守恒可得 1 mgh mv2 2 平抛运动的初速度为 v 2gh平抛运动的时间为 2R t g 其落水点到O 的距离为 2 2R svt  2gh 2 hR g 其落水点到O 的距离范围为 2 2Rs2R （3）若小孩从O点静止下滑，脱离轨道时的位置与O 的连线与竖直方向夹角设为，则 2 mv2 mgcos 1 R 由机械能守恒可得 1 mgR(1cos) mv2 2 1 解得 2 cos 3 （4）根据题意，木板质量足够大，分析第一次跳离木板，可看作斜向右上方的斜抛运动，水平位移最 小为l，水平初速度为v ，竖直初速度为v ，则有 x y l 2v  y v g x 小孩做功为 1 1 1 1 g2l2 W  mv2  mv2 mv2  m(v2 ) 2 2 x 2 y 2 x 4v2 x g2l2 1 根据数学知识可知，当v2  时，存在最小的功，为W  mgl x 4v2 min 2 x 题型 05 斜抛运动规律的应用 斜抛运动是平抛运动的推广，生活中符合斜抛运动的例子较多，这部分知识常与生活场景结合在一 起进行考查，在解决此类问题时要将所学物理知识与实际情境联系起来，抓住问题实质，将问题转化为熟知的物理模型和物理过程求解。 一、必备基础知识 1、运动规律 水平方向：不受外力，以v v cos为初速度做匀速直线运动；水平位移x v t v cost； x 0 x 0 竖直方向：竖直方向只受重力，初速度为v v sin，做竖直上抛运动；任意时刻的速度公式是 0y 0 1 v v gt，位移公式为y v t  gt2。 y 0y 0y 2 2、运动图示 g 轨迹方程为：y tanx x2，为抛物线。 2v2 cos2 0 二、解题模板 1、解题思路 2、注意问题 斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上(下)抛运动的合运动。 竖直方向的运动不是自由落体运动，而是竖直上（下）抛运动。 三维空间的斜抛运动要注意水平方向的选取。 3、解题方法 研究方法：运动的合成与分解 水平方向：匀速直线运动； 竖直方向：竖直上（下）抛运动。 斜上抛运动可用逆向思维法求解，从抛出点到最高点的运动可逆过程分析，看成平抛运动，分析完整的斜上抛运动，还可根据对称性求解某些问题。 一些运动量的求解如下表所示。 当物体落地时v  v  v sin，由 v v gt 知，飞 y 0y 0 y 0y 飞行时间 2v sin 行时间t  0 。 g g 由轨迹方程y tanx x2，令y=0得落回抛出高度 2v2 cos2 0 v2sin2 时的水平射程是x  0 。由轨迹方程可得：①当抛射角 g 射程  450时射程最远，①当抛射角 450时射程最远， v2 x  0 ；②初速度相同时，两个互余的抛射角具有相同的射程， max g 例如300和600的两个抛射角在相同初速度的情况下射程是相等的。 斜上抛的物体达到最大高度时v v gt v singt=0，此 y 0y 0 v sin 1 时t  0 ，代入y v t  gt2即得到抛体所能达到的最大 射高 g 0y 2 v2sin2 v2 高度y  0 ，即当900时，射高最大H  0 。 max 2g 2g （2024·山东济宁·三模）某旋转喷灌机进行农田喷灌的示意图如图所示，喷口出水速度的方 向可调节。该喷灌机的最大功率为P2000W，喷灌机所做功的75%转化为水的动能，喷口的横截面积 S 30cm2，水的密度1103kg/m3，重力加速度g 10m/s2，3.14，喷口距离地面的高度 h0.55m，忽略空气阻力，不考虑供水水压对水速的影响。求： （1）喷灌机的最大喷水速度v； （2）喷口出水速度方向与水平面夹角30时，该喷灌机的最大喷灌面积S 。（保留三位有效数字） m 思路分析第一问的思路： 第二问的思路： 详细解析 【答案】（1）10m/s；（2）285m2 【详解】（1）设在∆t时间内从喷口处喷出水的质量为∆m，则 mvtS 由能量关系 1 75%Pt  mv2 2 解得 v=10m/s （2）喷口出水速度方向与水平面夹角30时，则 1 hvtsin30 gt2 2 xvtcos30 该喷灌机的最大喷灌面积 S x2 m 解得S =285m2 m （2024·山东菏泽·二模）如图，电力工人在倾角37的山坡上架设电线，竖直电线杆高 h40m，工人将拖线器（拖线器为一连接细线的重物）抛出，拖线器恰好能够越过电线杆顶端，忽略 空气阻力、人的身高和细线质量，g 10m/s2。求： （1）拖线器抛出时的最小速度大小及方向； （2）拖线器抛出点到电线杆底部的距离； （3）拖线器在山坡上的落点到电线杆底部的距离。【答案】（1）16 2m/s，方向垂直斜面向上；（2）48m；（3）48m 【详解】（1）电线杆顶端到山坡的垂直距离 y hcos37 1 设初速度沿垂直斜面方向的分速度为v ，平行斜面方向的分速度为v y0 x0 v y  y0 t 1 2 1 v g t y0 y1 g gcos37 y g gsin37 x 联立解得 t 2 2s 1 v 16 2m/s y0 v  v2 v2 0 x0 y0 当v 0时，抛出时的速度最小 x0 v v 0 y0 即 v 16 2m/s 0 方向垂直斜面向上 （2）平行斜面方向 1 x  g t2 1 2 x1抛出点到线杆底部的距离 d x hsin37 1 1 代入数据解得 d 48m 1 （3）由对称性可知，垂直斜面方向下落时间t 与上升时间t 相等，抛出点到落点距离 2 1 1 x g (t t )2 2 x 1 2 落点到电线杆底部的距离 d xd 2 1 代入数据解得d 48m 2 题型 06 类平抛运动规律的应用 1、类平抛运动的处理方法与平抛运动相似，类平抛的受到的恒力不是重力，可以其它性质的力。 2、高考这部分知识常与电学结合一起考查。 3、传送带上的物体受力较少，难点在于物体和传送带间的相对运动情况的变化会导致摩擦力的变 化，从而使得物体的运动情况变得复杂。 一、必备基础知识 1、模型特点 有些物体的运动与平抛运动很相似，也是在与初速度方向垂直的恒定外力作用下运动，其轨迹与平 抛运动相似，我们把这种运动称为类平抛运动，这样的运动系统称作“类平抛”模型。 2、特点 受力特点：物体所受合力为恒力，且与初速度的方向垂直。 运动特点：在初速度v 方向做匀速直线运动，在合力方向做初速度为零的匀加速直线运动，加速度 0 F合 a＝ 。 m 3、模型中的木板长度 当滑块从木板的一端运动到另一端的过程中，并且滑块和木板同向运动，则滑块的位移和木板的位移之差等于木板的长度。 当滑块从木板的一端运动到另一端的过程中，并且滑块和木板反向运动，则滑块的位移和木板的位移之 和等于木板的长度。 二、解题模板 1、解题思路 2、注意问题 类平抛运动与平抛运动的区别在于是否合外力为重力，求解类平抛运动时要准确分析物体所受的合 外力。 求解时要根据物体受力特点和运动特点判断该问题是否属于类平抛运动问题。 3、解题方法 ①常规分解法：将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力方向) 的匀加速直线运动，两分运动彼此独立，互不影响，且与合运动具有等时性。 ②特殊分解法：对于有些问题，可以过抛出点建立适当的直角坐标系，将加速度分解为ax、ay，初速度 v 分解为v 、v ，然后分别在x、y方向列方程求解。 0 x y 在具体的物理情景中，常把复杂的曲线运动，分解成几个简单的直线运动来处理。用类似平抛运动 的解决方法解决问题，例如带电粒子在电场中的偏转运动等。 （2024·广东高三·阶段练习）正在公路上行驶的汽车，只需按下一个键，就能轻松切换到飞 行模式，变身飞机跃入天空，这就是飞行汽车!一辆飞行汽车在平直的公路上以30m/s的速度行驶，某 时刻司机启动飞行模式，汽车保持水平速度不变，沿竖直方向开始匀加速爬升，经过一段时间爬升到 200m高处。用x表示水平位移，y表示竖直位移，这一过程的yx图像如图所示。取g 10m/s2，求汽 车飞行时： （1）从启动飞行模式，到离地200m高处需要多长时间； （2）到达200m高处时竖直速度和瞬时速度的大小（可用根式表示）。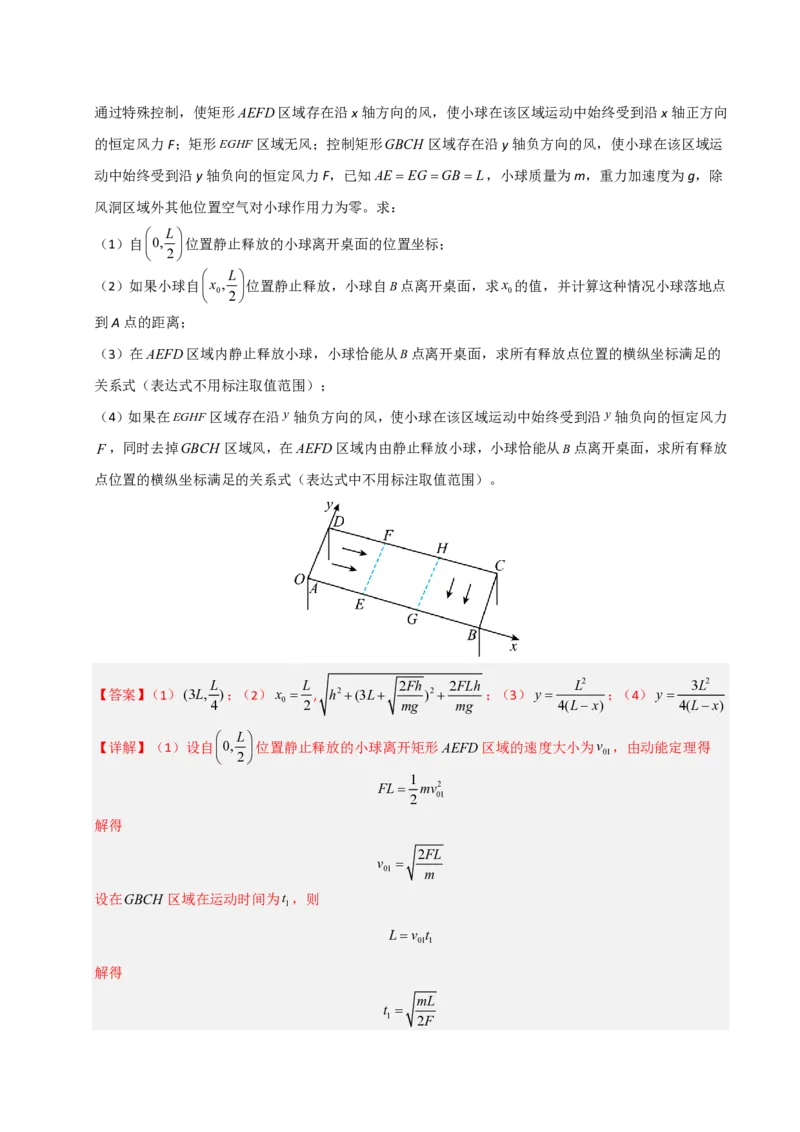思路分析 第一问的思路： 第二问的思路： 详细解析 【答案】（1）20s；（2）20m/s，10 13m/s 【详解】（1）由题可知，汽车在水平方向做匀速直线运动，根据yx图像可知，到离地200m高处时的水 平位移x为600m，则从启动飞行模式，到离地200m高处的时间为 x 600m t   20s v 30m/s 0 （2）由题可知，汽车在竖直方向上做初速度为零的匀加速直线运动，根据匀变速运动规律有 v y y t 2 可得，到达200m高处时竖直速度的大小为 2y 2200m v   20m/s y t 20s 则到达200m高处时的瞬时速度的大小为 v v2v2 10 13m/s 0 y （2024·河南·模拟预测）风洞是以人工的方式控制气流，是进行空气动力实验最常用、最有 效的工具之一、某同学在实验室模拟风洞控制小球在光滑水平桌面运动。如图所示，光滑水平桌面高为 h，长方形ABCD为桌面，AB3L，ADL，以A点为坐标原点，沿AB边为x轴，沿AD边为y轴。通过特殊控制，使矩形AEFD区域存在沿x轴方向的风，使小球在该区域运动中始终受到沿x轴正方向 的恒定风力F；矩形EGHF区域无风；控制矩形GBCH 区域存在沿y轴负方向的风，使小球在该区域运 动中始终受到沿y轴负向的恒定风力F，已知AE EGGBL，小球质量为m，重力加速度为g，除 风洞区域外其他位置空气对小球作用力为零。求：  L （1）自0, 位置静止释放的小球离开桌面的位置坐标；  2  L （2）如果小球自x , 位置静止释放，小球自B点离开桌面，求x 的值，并计算这种情况小球落地点  0 2 0 到A点的距离； （3）在AEFD区域内静止释放小球，小球恰能从B点离开桌面，求所有释放点位置的横纵坐标满足的 关系式（表达式不用标注取值范围）； （4）如果在EGHF区域存在沿y轴负方向的风，使小球在该区域运动中始终受到沿y轴负向的恒定风力 F ，同时去掉GBCH 区域风，在AEFD区域内由静止释放小球，小球恰能从B点离开桌面，求所有释放 点位置的横纵坐标满足的关系式（表达式中不用标注取值范围）。 L L 2Fh 2FLh L2 3L2 【答案】（1）(3L, )；（2）x  , h2(3L )2 ；（3）y ；（4）y 4 0 2 mg mg 4(Lx) 4(Lx)  L 【详解】（1）设自0, 位置静止释放的小球离开矩形AEFD区域的速度大小为v ，由动能定理得  2 01 1 FL mv2 2 01 解得 2FL v  01 m 设在GBCH 区域在运动时间为t ，则 1 Lv t 011 解得 mL t  1 2F加速度 F a m 沿y轴负方向的位移大小 1 1 F mL 1 y  at2   ( )2  L 1 2 1 2 m 2F 4 小球离开桌面的位置纵坐标 L L y y  2 1 4 小球离开桌面的位置横坐标 x3L  L L 自0, 位置静止释放的小球离开桌面的位置坐标(3L, )。  2 4  L （2）如果小球自x , 位置静止释放，小球离开矩形AEFD区域的速度大小为v ，由动能定理得  0 2 02 1 F(Lx ) mv2 0 2 02 解得 2F(Lx ) v  0 02 m 设在GBCH 区域在运动时间为t ，则 2 Lv t 02 2 解得 m t L 2 2F(Lx ) 0 小球自B点离开桌面，沿y轴负方向的位移大小 1 1 F m 1 y  at2   (L )2  L 2 2 1 2 m 2F(Lx ) 2 0 解得 L x  0 2 设小球自B点离开桌面到落到地面的时间为t ，则 3 1 h gt 2 2 3 解得2h t  3 g 沿y轴负方向的速度大小 F m FL v at  L  y 2 m L m 2F(L ) 2 小球自B点离开桌面后，沿x轴正方向的位移大小 2FLh xv t  02 3 mg 沿y轴负方向的位移大小 2FLh yv t  y 3 mg 小球落地点到A点的距离 2FLh 2FLh s h2(3Lx)2y2  h2(3L )2 mg mg （3）在AEFD区域内静止释放小球，小球恰能从B点离开桌面时，释放点的坐标为(x,y)。小球离开矩 形AEFD区域的速度大小为v ，由动能定理得 03 1 F(Lx) mv2 2 03 解得 2F(Lx) v  03 m 设在GBCH 区域在运动时间为t ，则 4 Lv t 03 4 解得 m t L 4 2F(Lx) 沿y轴负方向的位移大小 1 1 F m L2 y at2   L2  2 4 2 m 2F(Lx) 4(Lx) （4）如果在EGHF区域存在沿y轴负方向的风，使小球在该区域运动中始终受到沿y轴负向的恒定风力 F ，同时去掉GBCH 区域风，在AEFD区域内由静止释放小球，小球恰能从B点离开桌面，设释放点的位置坐标(x,y)，小球离开矩形AEFD区域的速度大小为v ，由动能定理得 04 1 F(Lx) mv2 2 04 解得 2F(Lx) v  04 m 设在EGHF区域在运动时间为t ，则 5 Lv t 04 5 解得 m t L 5 2F(Lx) 沿y轴负方向的速度大小 F m F v at  L L y 5 m 2F(Lx) 2m(Lx) 小球恰能从B点离开桌面时速度与x轴正方向的夹角为，则 v y tan y  v L 04 L 2 3L2 解得y 4(Lx)2 1．（2024·广东广州·模拟预测）如图所示，水平放置的圆盘半径为R1m，在其边缘C点固定一个高度不 计的小桶，在圆盘直径CD的正上方放置一条水平滑道AB，滑道与CD平行。滑道右端B与圆盘圆心O 在同一竖直线上，其高度差为h1.25m。在滑道左端静止放置质量为m0.4kg的物块（可视为质点）， 物块与滑道间的动摩擦因数为0.2。当用一大小为F 4N的水平拉力向右拉动物块的同时，圆盘从 图示位置以角速度2rad/s绕穿过圆心O的竖直轴匀速转动，拉力作用一段时间后撤掉，物块在滑 道上继续滑行，过B点水平抛出恰好落入小桶内，重力加速度g取10m/s2。求：(1)物块到达B点时的速度大小； (2)水平滑道AB的最小长度。 【答案】(1)2m/s (2)0.8m 【详解】（1）物块做平抛运动，设物块离开滑道时的速度为v，落入小桶所用时间为t，则水平方向上 有 Rvt 竖直方向上有 1 h gt2 2 解得 t 0.5s，v2m/s （2）设拉动物块时的加速度为a ，所用时间为t ，由牛顿第二定律得 1 1 Fmg ma 1 解得 a 8m/s2 1 撤去拉力后，设物块的加速度为a ，所用时间为t ，由牛顿第二定律得 2 2 mg ma 2 解得 a 2m/s2 2 圆盘转过一圈时物块落入小桶内，拉力作用时间最短，水平滑道AB长度最小，圆盘转过一圈的时间 2 T  1s  物块在滑道上先加速后减速，则有 vat a t 11 2 2物块滑行时间、抛出后在空中运动时间与圆盘转动周期关系为 t t t T 1 2 解得 t 0.3s，t 0.2s 1 2 加速位移 1 s  at2 0.36m 1 2 11 加速的末速度为 v at 2.4m/s 1 11 减速位移 1 s vt  a t 2 0.44mAB的最小长度 2 12 2 2 2 ss s 0.8m 1 2 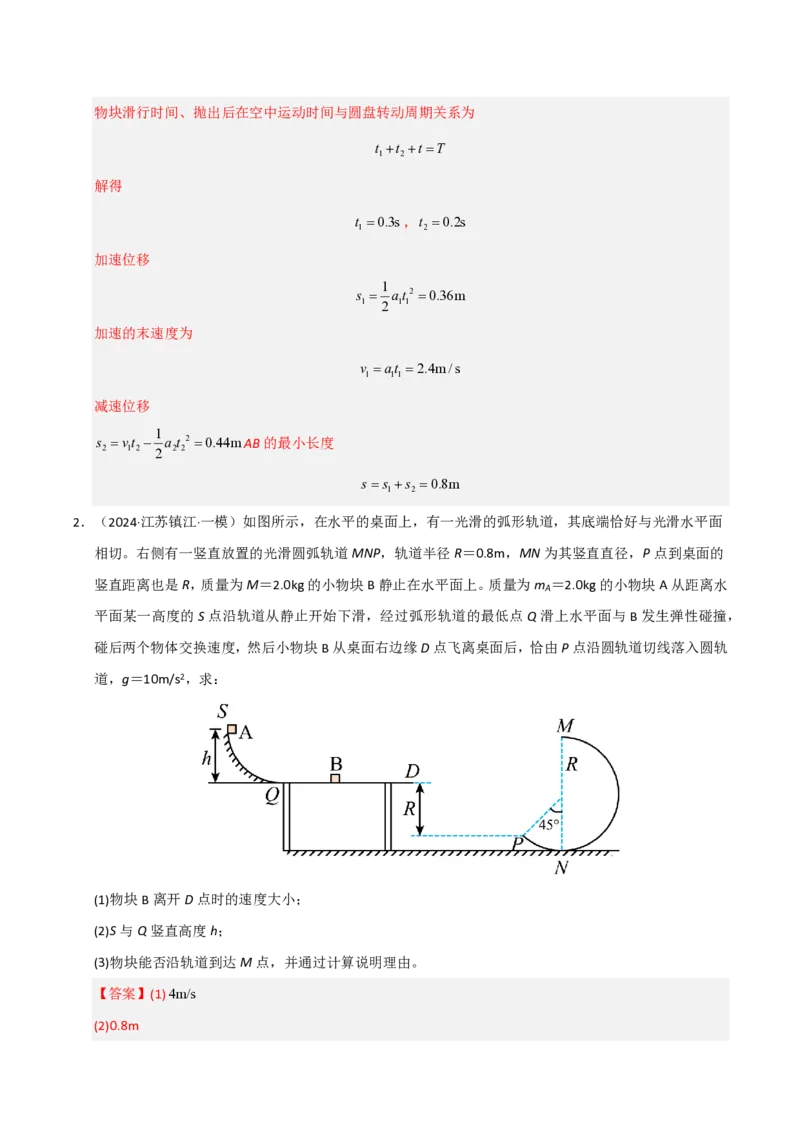2．（2024·江苏镇江·一模）如图所示，在水平的桌面上，有一光滑的弧形轨道，其底端恰好与光滑水平面 相切。右侧有一竖直放置的光滑圆弧轨道MNP，轨道半径R＝0.8m，MN为其竖直直径，P点到桌面的 竖直距离也是R，质量为M＝2.0kg的小物块B静止在水平面上。质量为m ＝2.0kg的小物块A从距离水 A 平面某一高度的S点沿轨道从静止开始下滑，经过弧形轨道的最低点Q滑上水平面与B发生弹性碰撞， 碰后两个物体交换速度，然后小物块B从桌面右边缘D点飞离桌面后，恰由P点沿圆轨道切线落入圆轨 道，g＝10m/s2，求： (1)物块B离开D点时的速度大小； (2)S与Q竖直高度h； (3)物块能否沿轨道到达M点，并通过计算说明理由。 【答案】(1)4m/s (2)0.8m(3)见解析 【详解】（1）A、B碰撞后，因二者交换速度，所以A静止，物块B由D点做平抛运动，落到P点时其 竖直速度为vy，有 v2 2gR y 又 v y tan45 v D 解得 v 4m/s D （2）设A与B碰撞前的速度为v ，A与B相碰交换速度，所以 0 v v 4m/s 0 D A从S滑到Q的过程中，根据机械能守恒定律得 1 m gh m v2 A 2 A 0 解得 h0.8m （3）设物块能沿轨道到达M点，且到达时其速度为v ，从D到M由动能定理得 M 1 1 m gRcos45 m v2  m v2 B 2 B M 2 B D 解得 v 2.2m/s gR 2.8m/s M 即物块不能到达M点。 1 3．（2024·山西运城·二模）如图甲所示， 半径R0.45m的光滑 圆弧轨道固定在竖直平面内，B为轨道的 4 最低点，B点右侧的光滑水平面上紧挨B点有一静止的小平板车，平板车质量M=1kg，长度l=1m小车 的上表面与B点等高，距地面高度h0.2m、质量m1kg的物块（可视为质点）从圆弧最高点A由静 止释放。取g 10m/s2。试求：(1)物块滑到轨道上的B点时对轨道的压力大小； (2)若锁定平板车并在上表面铺上一种特殊材料，其动摩擦因数从左向右随距离均匀变化，如图乙所示， 求物块滑离平板车时的速率； (3)若解除平板车的锁定并撤去上表面铺的材料后，物块与平板车上表面间的动摩擦因数0.2，物块仍 从圆弧最高点A由静止释放，求物块落地时距平板车右端的水平距离。 【答案】(1)30N (2)1m/s (3)0.2m 【详解】（1）物体从圆弧轨道顶端滑到B点的过程中根据动能定理有 1 mgR mv2 2 B 解得 v 3m/s B 在B点由牛顿第二定律得 v2 Nmg m B R 解得 N=30N 根据牛顿第三定律可知，在B点时物块对轨道的压力大小为30N，方向竖直向下。 （2）根据图乙可知，物块在小车上滑行时的摩擦力做功 mgmg 0.20.6101 W  1 1 l  J4J f 2 2 从物体开始滑到滑离平板车过程中由动能定理得 1 mgRW  mv2 f 2 解得 v=1m/s （3）当平板车不固定时，对物块有mg a  2m/s2 1 m 对平板车有 mg a  2m/s2 2 M 经过时间t 物块滑离平板车，则 有 1 1 1 v t  at2 a t2 l B1 2 11 2 21 解得 t =0.5s，（舍去另一解1s） 1 物体滑离平板车的速度 v =v -a t =2m/s 物 B 1 1 此时平板车的速度 v a t 1m/s 车 21 物块滑离平板车做平抛运动，则有 1 h gt2 2 2 解得 t 0.2s 2 物块落地时距平板车右端的水平距离 x=（v -v ）t 物 车 2 解得 x=0．2m 4．（22-23高一下·云南昆明·期中）如图，一个质量为0．6kg的小球以某一初速度从P点水平抛出，恰好 从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧瞬间速度大小不变）。已知圆弧 的半径R=0.1m，B点和C点分别为圆弧的最低点和最高点，θ=60°，小球到达A点时的位置与P点间的 3 水平距离为 m，取重力加速度g=10m/s2，求： 8 （1）若小球恰好能过C点，求小球在C点的速度大小； （2）若小球恰好能过C点，且轨道的B点和C点受到小球的压力之差为6mg，求小球运动到B点时的 速度大小； （3）小球做平抛运动的初速度大小v 。 05 【答案】（1）1m/s；（2） 5m/s；（3） m/s 2 【详解】（1）小球恰好过C点，则 v2 mg m C R 解得 v 1m/s C （2）小球恰好过C点，则在C点小球对轨道的压力为0，根据牛顿第三定律，小球受到的支持力等于小 球对轨道的压力大小，根据题意有 F F  6mg B C 在B点有 v2 F mg m B B R 代入数据解得 v  5m/s B （3）小球到A点的速度如图所示 根据几何关系有 gt tan60 v 0 水平方向 3 xv t  m 0 8联立解得 5 v  m/s 0 2 5．（2024·江苏扬州·模拟预测）如图，餐桌上表面离地面的高度h1.25m，餐桌中心是一个半径为r2m 的圆盘，圆盘可绕中心轴转动，近似认为圆盘与餐桌在同一水平面内且两者之间的间隙可忽略不计。已 知放置在圆盘边缘的m1kg的小物体与圆盘间的动摩擦因数为0.45，小物体与餐桌间的动摩擦因数 1 为 0.3，最大静摩擦力等于滑动摩擦力，缓慢增大圆盘的转动速度，物体从圆盘上甩出后，在餐桌 2 上做匀减速直线运动，恰好不会滑出餐桌落到地上，g取10m/s2，不计空气阻力。 （1）为使物体不从圆盘滑到餐桌上，求圆盘的边缘线速v 的最大值； 0 （2）物体在餐桌上滑行的时间； （3）若餐桌上洒上了油，导致物体与餐桌间的动摩擦因数减小，物体沿桌面匀减速直线运动后落地， 落地点距离圆桌中心的水平距离2 2m，求此过程桌面对物体做的功。 【答案】（1）3m/s；（2）1s；（3）4J 【详解】（1）对物体，有 mv2 mg 0 1 r 解得 v 3m/s 0 （2）在餐桌上有 mgma 2 可得 a3m/s2 恰好不会滑出桌面落到地上 v2 2ax 0 可得x1.5m 恰好不会滑出桌面落到地上 v at 0 可得 t1s （3）在餐桌上有 mgma 3 1 物体滑出桌面的过程中 v2v2 2ax 0 1 飞出桌面后竖直方向 1 h gt2 2 水平方向 x vt 1 故物体落地时距离圆桌中心的水平距离 s r2（xx）2 1 解得 4   3 15 则此过程桌面对物体做的功为 W mgx4J 3 6．（2024·宁夏石嘴山·模拟预测）如图所示，光滑轨道的左端为半径为R1m的圆弧形、右端为水平面， 二者相切，水平面比水平地面高H 0.8m，一质量为m1kg的小球A从距离水平面高h0.2m处由静 止开始滑下，与静止于水平面上的质量为m 的小球B发生弹性正碰，碰后小球B做平抛运动，落地时 B 发生的水平位移为x0.4m，重力加速度g 10m/s2。求： （1）A球刚滑到圆弧最低点时受到轨道支持力的大小； （2）碰后瞬间B球的速度大小； （3）B球的质量。【答案】（1）14N；（2）1m/s；（3）3kg 【详解】（1）A球滑到圆弧最低点有 1 mgh mv2 2 1 在最低点有 v2 F mg m 1 N R 解得 F  N （2）B球碰后做平抛运动，竖直方向有 1 H  gt2 2 水平方向有 xv t B 解得 v 1m/s B （3）A球与B球发生碰撞，动量守恒，有 mv mv m v 1 A B B 弹性碰撞有 1 1 1 mv2  mv2  m v2 2 1 2 A 2 B B 解得 m 3kg B 7．（2024·山东青岛·三模）网球运动正在逐步走进中学校园，受到众多同学的喜爱。如图，某同学正在网 球场练习发球，他将质量m0．05kg的网球从离水平地面高度h1．8m处，以某一初速度v 水平击出， 0 网球第一次落在距击球点水平距离L 24m处的地面上，然后经地面多次反弹，最终停下来。已知网球 11 3 与地面第一次碰后，竖直分速度反向，大小变为碰前的 ，水平分速度方向不变，大小变为碰前的 。 2 4 不计网球所受空气阻力，网球与地面碰撞时间极短，重力加速度g 10m/s2，计算结果可保留根号，求 （1）该同学击球过程对网球所做的功W； （2）网球第一次与地面碰撞过程中地面对网球的冲量I ； （3）网球第二次接触地面处与击球点间的水平距离L 。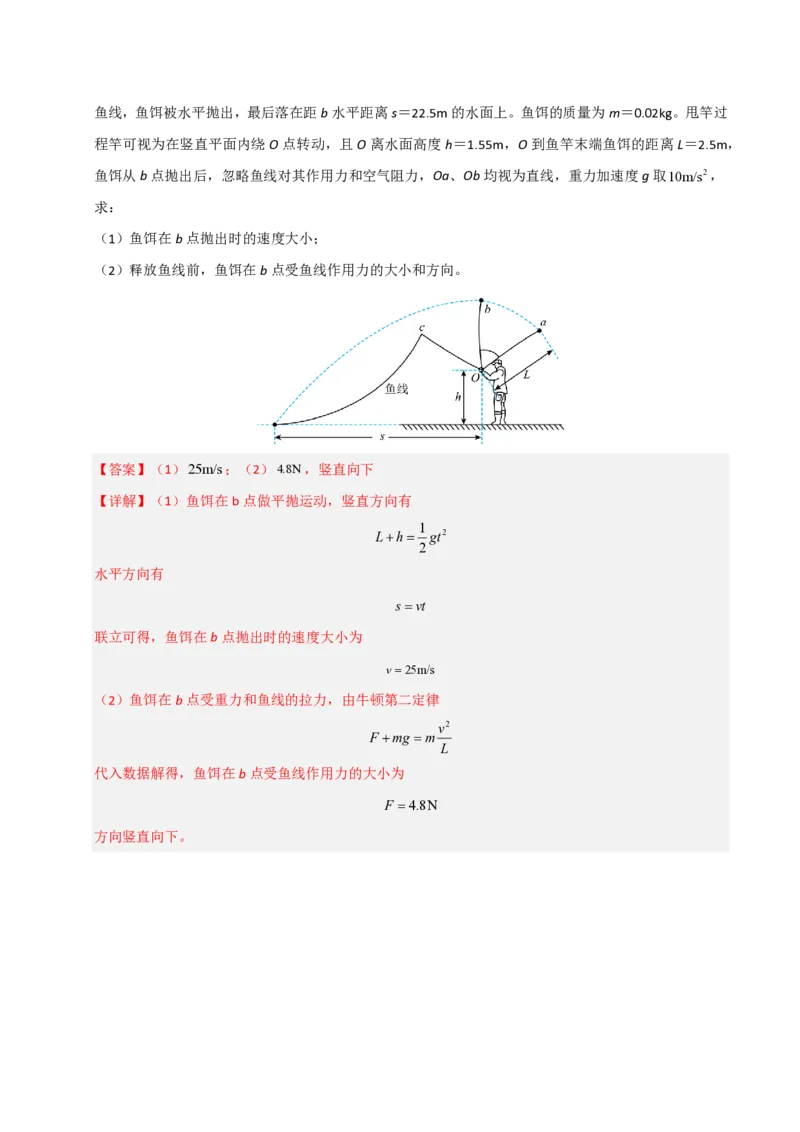 2 I 【答案】（1）40J；（2）I  181 N； tan x 1.1；（3）42m I 20 y 【详解】（1）设网球第一次落地前运动时间为t ，根据运动的合成和分解 1 1 L v t ，h gt2 1 01 2 1 解得 1 W  mv2 40J 2 0 （2）网球第一次落地时根据动量定理得 3  gt  I m v mv ，I m 1 mgt x 4 0 0 y  2  1 解得 181 I  I2 I2  N x y 20 地面对网球的冲量I 与水平方向的夹角 I tan y 1.1 I x （3）设网球第一次弹起后经时间t 再次落地，根据运动学公式 2 gt gt  1  1 gt 2 2 2 解得 3 L  L  v t 42m 2 1 4 0 2 8．（2024·辽宁葫芦岛·二模）“路亚”是一种钓鱼方法，用这种方法钓鱼时先把鱼饵通过鱼线收到鱼竿末端， 然后用力将鱼饵甩向远处。如图所示，钓鱼爱好者在a位置开始甩竿，鱼饵被甩至最高点b时迅速释放鱼线，鱼饵被水平抛出，最后落在距b水平距离s＝22.5m的水面上。鱼饵的质量为m＝0.02kg。甩竿过 程竿可视为在竖直平面内绕O点转动，且O离水面高度h＝1.55m，O到鱼竿末端鱼饵的距离L＝2.5m， 鱼饵从b点抛出后，忽略鱼线对其作用力和空气阻力，Oa、Ob均视为直线，重力加速度g取10m/s2， 求： （1）鱼饵在b点抛出时的速度大小； （2）释放鱼线前，鱼饵在b点受鱼线作用力的大小和方向。 【答案】（1）25m/s；（2）4.8N，竖直向下 【详解】（1）鱼饵在b点做平抛运动，竖直方向有 1 Lh gt2 2 水平方向有 svt 联立可得，鱼饵在b点抛出时的速度大小为 v25m/s （2）鱼饵在b点受重力和鱼线的拉力，由牛顿第二定律 v2 Fmg m L 代入数据解得，鱼饵在b点受鱼线作用力的大小为 F 4.8N 方向竖直向下。