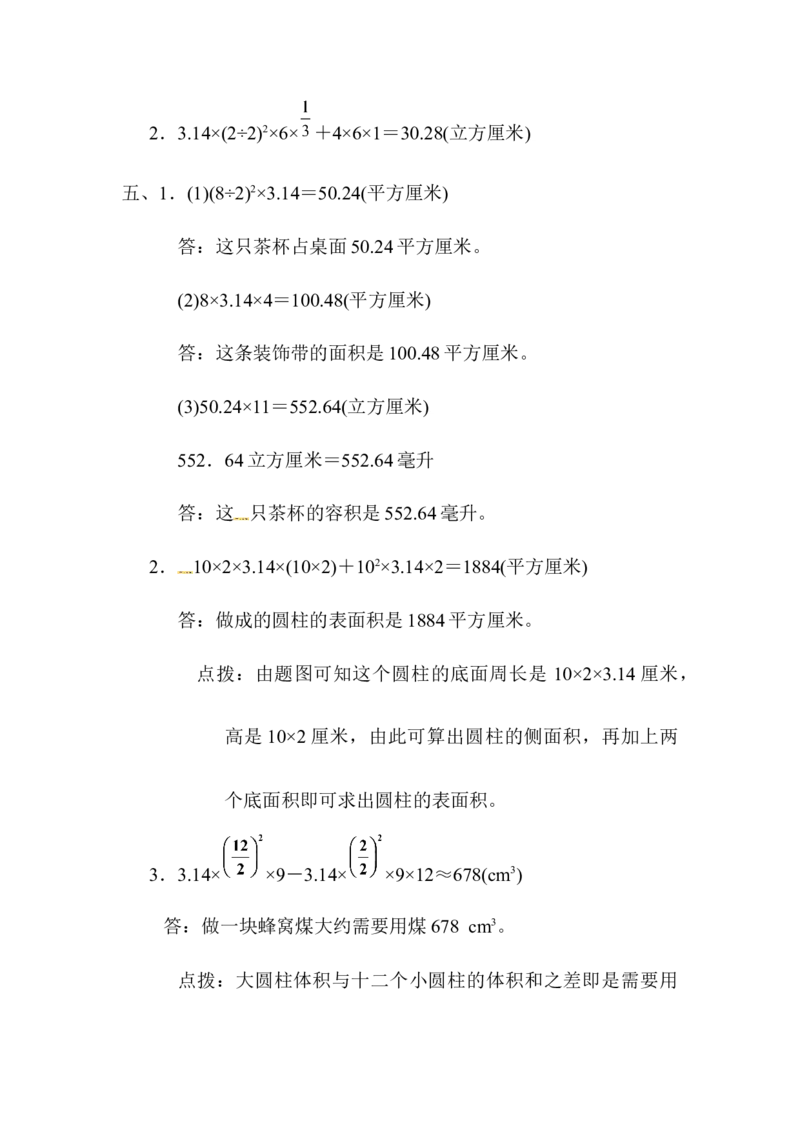文档内容
第二单元过关检测卷
一、填一填。(每空2分,共20分)
1.一个圆柱底面半径是 6 厘米,高是 5 厘米,它的侧面积是(
)平方厘米,表面积是( )平方厘米,体积是( )立方
厘米。
2.圆锥的体积是27立方厘米,高是15厘米,它的底面积是(
) 平方厘米。
3.一个圆柱形的橡皮泥,底面直径和高都是 3厘米,把它捏成与它
等底的圆锥形,圆锥形橡皮泥的高是( )厘米。
4.将一根长 1米的圆柱形木料截成相同的三段,表面积增加了 6平
方米,原木料的体积是( )立方米。
5.一种压路 机滚筒是一个圆柱体,它的底面直径是 1.2 米,长是
2米,如果旋转10圈,一共压路( )平方米。
6.一个圆柱和一个圆锥等底等高,它们的体积差是 48 立方厘米,
圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
7.一个直角三角形的两直角边长分别是 5 厘米、9 厘米,以其中一条直角边所在直线为轴旋转一周后形成的几何体的体积较大的是(
)立方厘米。
二、判断对错。(每题2分,共10分)
1.一个圆柱只有一条高,一个圆锥有无数条高。 ( )
2.圆柱底面半径扩大为原来的 3倍,高也扩大为原来的 3倍,体积
就扩大为原来的9倍。 ( )
3.把一个圆柱形 的木块削成一个最大的圆锥,削去部分的体积是
圆锥体积的 3倍。 (
)
4.圆柱的底面直径是 3 厘米,高 9.42 厘米,侧面沿高剪开后是一
个正方形。 (
)
5.一个圆柱和一个圆锥等底等高,圆柱的体积是 12 立方分米,则
圆柱的体积比圆锥的体积多 8立方分米。 (
)
三、选一选。(每题3分,共12分)1.一个圆柱的底面直径是 10 厘米,若高增加 2 厘米,则侧面积增
加( )平方厘米。
A.31.4 B.20
C.62.8 D.40
2.一个圆柱的底面半径是 4 cm,侧面沿高展开后是一个正方形,
那么这个圆柱的高是( )cm。
A.25.12 B.50.24
C.12.56 D.100.48
3.一个圆柱和一个圆锥的底面积相等,体积的比是 3 ∶1,那么高
的比是( )。
A.3 ∶1 B.1 ∶1
C.1 ∶3 D.1 ∶2
4.把一根长 1.2 米的圆柱形钢材按 1 ∶2 ∶3 截成 3 根小圆柱形钢
材,表面积比原来增加 56平方厘米,这 3根小圆柱形钢材中最长
的一根比最短的一根体积大( )立方厘米。
A.560 B.1500C.840 D.980
四、看图计算。(单位:厘米)(1题10分,2题7分,共17分)
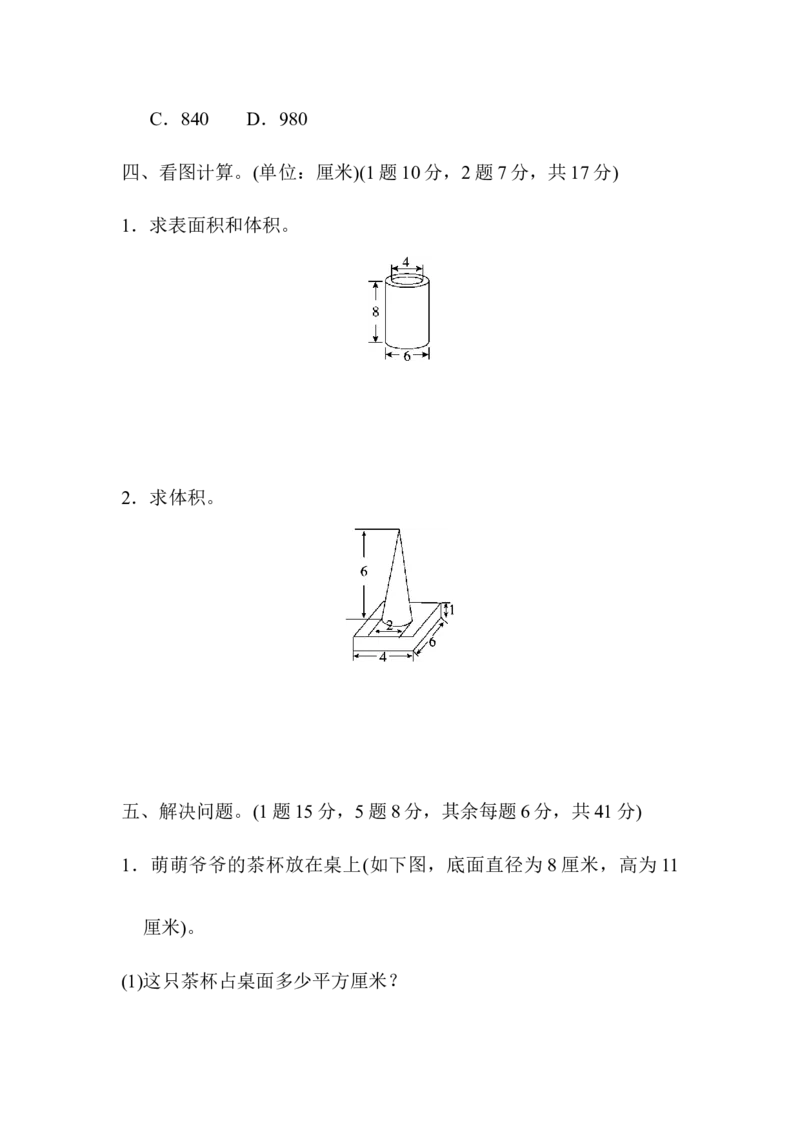
1.求表面积和体积。
2.求体积。
五、解决问题。(1题15分,5题8分,其余每题6分,共41分)
1.萌萌爷爷的茶杯放在桌上(如下图,底面直径为 8 厘米,高为 11
厘米)。
(1)这只茶杯占桌面多少平方厘米?(2)怕爷爷烫伤手,萌萌特意贴上一条装饰带,宽 4 厘米。这条装饰
带的面积是多少平方厘米?(接头处忽略不计)
(3)这只茶杯的容积是多少毫升?(杯壁厚度忽略不计)
[来源:学+科+网Z+X+X+K]
2.有一张长方形铁皮,剪出两个圆及一个长方形(如图 所示),正
好可以做成一个底面半径为 10厘米的圆柱(接头处忽略不计),做
成的圆柱的表面积是多少平方厘米?[来源:学*科*网Z*X*X*K]
3.如下图所示,做一块蜂窝煤大约需要用煤多少立方厘米?(得数
保留整数)
4.把一个底面直径是 10 厘米的圆锥形木块,从顶点处沿高切成完
全相同的两块,这时表面积增加了 120 平方厘米。原来的圆锥形
木块的体积是多少?
5.一个圆柱形水桶,内部的底面半径是 20 cm,高是 45 cm,里面
盛有30 cm深的水。将一个底面半径是 15 cm的圆锥形铁块完全
浸入水里,水不溢出,水面上升了3 cm,圆锥形铁块的高是多少?答案
一、1.188.4;414.48;565.2 2.5.4 3. 9
4.1.5 5.75.36 6.72;24 7.423.9
二、1.× 2.× 3.× 4.√ 5.√
三、1.C 2.A 3.B
4.A 点拨:把一根圆柱形钢材截成 3 根小圆柱形钢材,增加
了4个底面,而已知表面积比原来增加了 56平方厘米,所以底
面积为56÷4=14(平方厘米)。 由题意可知 3根小圆柱形钢材的
长分别为 20 厘米、40 厘米、60 厘米。所以最长的一根比最短
的一根体积大14×(60-20)=560(立方厘米) 。
四、1.表面积:6×3.14×8+4×3.14×8+[(6÷2)2×3.14-(4÷2)2×3.14]×2
=282.6(平方厘米)
体积:3.14×(6÷2)2×8-3.14×(4÷2)2×8=125.6(立方厘米)
点拨:图形的表面积是外壁的侧面积+内壁的侧面积+上、
下两个圆环的面积。2.3.14×(2÷2)2×6× +4×6×1=30.28(立方厘米)
[来源:学,科,网]
五、1.(1)(8÷2)2×3.14=50.24(平方厘米)
[来源:Z。xx。k.Com]
答:这只茶杯占桌面50.24平方厘米。
(2)8×3.14×4=100.48(平方厘米)
答:这条装饰带的面积是100.48平方厘米。
(3)50.24×11=552.64(立方厘米)
[来源:Z。xx。k.Com]
552.64立方厘米=552.64毫升
答:这 只茶杯的容积是552.64毫升。
2. 10×2×3.14×(10×2)+102×3.14×2=1884(平方厘米)
答:做成的圆柱的表面积是1884平方厘米。
点拨:由题图可知这个圆柱的底面周长是 10×2×3.14 厘米,
高是 10×2 厘米,由此可算出圆柱的侧面积,再加上两
个底面积即可求出圆柱的表面积。
3.3.14× ×9-3.14× ×9×12≈678(cm3)
答:做一块蜂窝煤大约需要用煤678 cm3。
点拨:大圆柱体积与十二个小圆柱的体积和之差即是需要用煤的体积。
4.120÷2÷ ÷10=12(厘米)
3.14× ×12× =314(立方厘米)
答:原来 的圆锥形木块的体积是314立方厘米。
点拨:增加的表面积是以圆锥的高为高,底面直径为底的两
个三角形的面积,因此圆锥的高为 120÷2÷ ÷10=
12(厘米)。
5.3.14×202×3=3768(cm3) 3.14×152=706.5(cm2)
3768×3÷706.5=16(cm)
答:圆锥形铁块的高是16 cm。
点拨:上升的水的体积即是放入的圆锥形铁块的体积。上升
的水的体积为 3.14×202×3=3768(cm3),圆锥形铁块的
底面积为 3.14×152=706.5(cm2),所以圆锥形铁块的高
可由公式 V= Sh 的变形公式 h=3V÷S 求得,即3768×3÷706.5=16(cm)。