文档内容
第一单元 等式、方程的含义
1. 判断。
(1)等式可能是方程,方程一定是等式。( )
(2)含有未知数的式子叫方程。( )
(3)a 比 b 少 c,列成式子是 a-c=b 或 b-a=c。( )
2. 看图列方程。
( 1 ) 正 方 形 周 长 6 米 ( 2 )
(3)
梨树棵
吃了个 还剩9个
米
桃树100棵
一箱苹果有24个
3. 根据“妈妈比钱惠大 26 岁”,填写下面的数量关系。
( )的年龄+26=( )的年龄
( )的年龄-26=( )的年龄
1参考答案
1. (1)√(2)×(3)√
2. (1)4x=6 (2)5x=100 (3)x+9=24
3. 钱惠 妈妈
妈妈 钱惠
2用等式性质解方程(1)
1. 在○里填上“>”、“<”或“=”。
当 =12 时, +19○30 60- ○32
2. 解方程。
-162=189 0.58+ =0.95
3. 列方程解决实际问题。
(1)一件上衣 68 元,比裤子贵 29 元,一条裤子多少元?
(2)一件羽绒服优惠 120 元后卖 284 元,这件羽绒服原价多少元?
1参考答案
1. > >
2. -162=189 0.58+ =0.95
解: -162+162=189+162 解: 0.58+ -0.58=0.95-0.58
=351 =0.37
3. (1)解:设一条裤子 x 元。
X+29=68
x+29-29=68-29
X=38
答:一条裤子 38 元。
(2)解:设这件羽绒服原价 x 元。
X-120=284
x-120+120=284+120
X=404
答:这件羽绒服原价 404 元。
2用等式性质解方程(2)
1. 在○里填上“>”、“<”或“=”。
当 =0.2 时,0.6 ○0.12 ÷2○0.2
2. 解方程。
6 =2.94 ÷0.9=1.84
3. 列方程解决实际问题。
一个宇航员在地球上的体重是 84 千克,是他在月球上体重的 6 倍。
他在月球上的体重是多少千克?
1参考答案
1. = <
2. 6 =2.94 ÷0.9=1.84
解:6 ÷6=2.94÷6 解: ÷0.9×0.9=1.84×0.9
=0.49 =1.656
3. 解:设他在月球上的体重是 x 千克。
6X=84
6X÷6=84÷6
X=14
答:他在月球上的体重是 14 千克。
2练习一
1. 用含有字母的式子填空。
(1)一块地有 a 公顷,共收 7200 千克小麦,平均每公顷收小麦
( )千克。
(2)红花有 朵,黄花的朵数是红花的 4.5 倍,黄花有( )朵,
红花比黄花少( )朵。
(3)吴婷去年重 千克,今年比去年重 2.5 千克,今年重
( )千克。
2. 选择正确答案的序号填在括号里。
(1)
+3=+5,那么
( )。
A.大于 B.小于 C.等于 D.无法确定
(2)下面的式子中,( )是方程。
A.45÷9=5 B.4=2 C.
+8<15 D.
+8
(3)如果 +1.5=7.5,那么 1.5 =( )。
A.6 B.9 C.13.5 D.12
(4)3 个连续自然数的和是 102,则最小的数是( )。
A.32 B.33 C.34 D.35
3. 列方程解决实际问题。
一种饮料有两种包装规格,大瓶容量 1.5 升,是小瓶容量的 3 倍。小
瓶饮料容量是多少升?
1参考答案
1. (1)7200÷x
(2)4.5x 3.5x
(3)x+2.5
2. (1)A (2)B (3) B (4) A
3. 解:设小瓶饮料容量是 x 升。
3X=1.5
3X÷3=1.5÷3
X=0.5
答:小瓶饮料容量是 0.5 升。
2列一步计算方程解决实际问题
1. 解方程。
X÷8=160 5X=10.5 X + 0.7=2.3
2. 判断。
(1)如果 ÷0.5=0.5,那么 =1。( )
(2)等式两边同时乘或除以同一个数,所得的结果仍然是等式。
( )
3. 列方程解决实际问题。
张月今年 12 岁,比她妈妈小 27 岁。她妈妈今年多少岁?
1参考答案
1. X÷8=160 5X=10.5 X + 0.7=2.3
解 : X ÷ 8 × 8=160 × 8 解 : 5X ÷ 5=10.5 ÷ 5 解 : X +
0.7-0.7=2.3-0.7
X=1280 X=2.1 X=1.6
2. (1)× (2) ×
3. 解:设她妈妈今年 x 岁。
X-12=27
X-12+12=27+12
X=39
答:她妈妈今年 39 岁。
2列两步计算方程解决实际问题
1. 解方程。
3X+8=26 5X-12=88 6X + 0.7=12.7
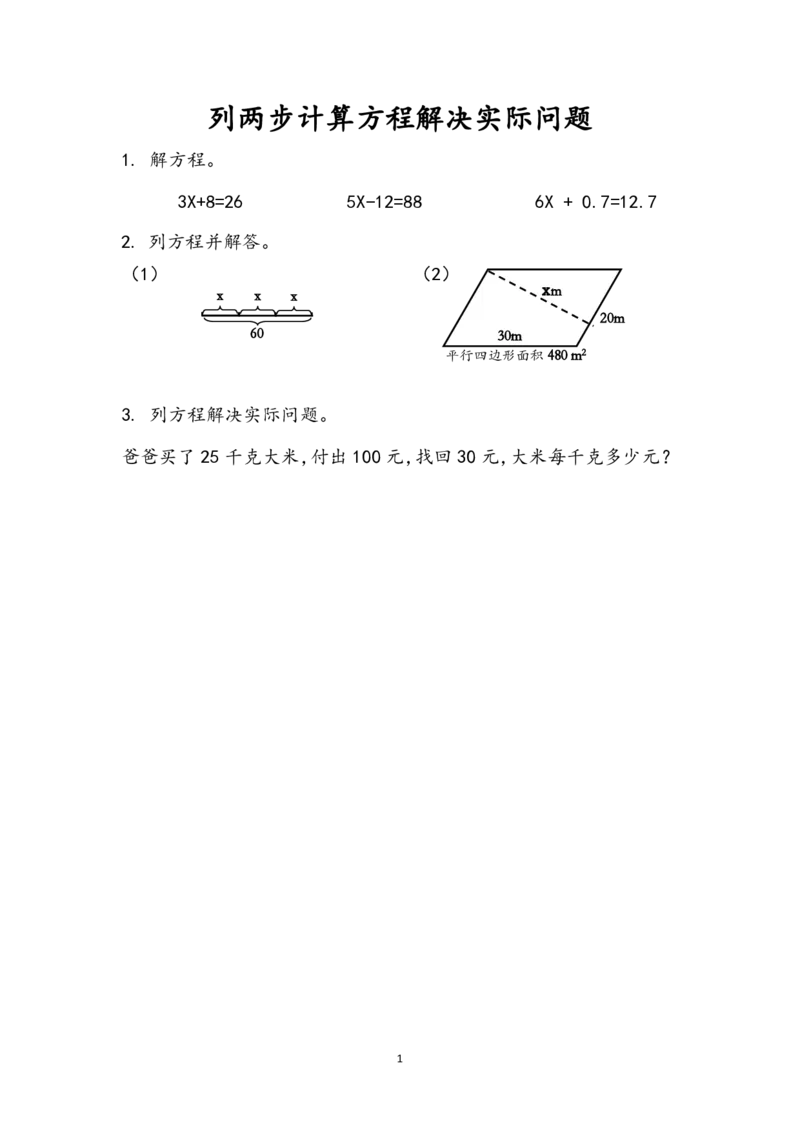
2. 列方程并解答。
(1) (2)
xm
x x x
20m
60 30m
平行四边形面积480 m2
3. 列方程解决实际问题。
爸爸买了 25 千克大米,付出 100 元,找回 30 元,大米每千克多少元?
1参考答案
1. 3X+8=26 5X-12=88 6X + 0.7=12.7
解: 3X=26-8 解:5X=88+12 解:6X =12.7-0.7
3X=18 5X=100 6X=12
X=6 X=20 X=2
2. (1) 3x=60 (2) 20 x=480
解:x=60÷3 解:x=480÷20
x=20 x=24
3. 解:设大米每千克 x 元。
25X+30=100
25X=70
X=2.8
答:大米每千克 58 元。
2练习二
1.明明用 40 元去买书,买了 x 本,每本 6.2 元,买书用了(
)元。当 x=3 时,应找回( )元。
2. 选择。
(1)下面的式子中,( )是方程。
A.15÷3=5 B.6y=25 C.x+7<33 D. x+8
(2)甲乙两筐苹果,甲筐 32 千克,乙筐 x 千克。从甲筐拿 4 千克放
入乙筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x+4=32 C.x-8=32 D.x+4=32-4
3. 列方程解决实际问题。
某个项目今年约完成投资 16.9 亿元,比去年的 3 倍少 5.9 亿元,去
年投资多少亿元?
1参考答案
1. 6.2x 21.4
2. (1) B (2) D
3. 解:设去年投资 x 亿元。
3X-5.9=16.9
3X=16.9+5.9
3X=22.8
X=7.6
答:去年投资 7.6 亿元。
2列形如 ax±bx=c 的方程解决实际问题
1. 如果 15+x=28,那么 15+x-15=28○□;
如果 3x=42,那么 3x÷3=42○□。
2.解方程。
4X+2.4=27 13.5X-X=100
3. 列方程解决实际问题。
进入冬季后,学校用电量大幅上升,12 月份比 11 月份多用电 2000
度,12 月份用电量是 11 月份的 2.6 倍。11 月份用电多少度?
1参考答案
1. -15 ÷3
2. 4X+2.4=27 13.5X-X=100
解:4 X=27-2.4 解:12.5 X=100
4 X=24.6 X=100÷12.
X=24.6÷4 X=8
X=6.15
3. 解:设 11 月份用电 x 度。
2.6X-x=2000
1.6X=2000
X=1250
答:11 月份用电 1250 度。
2列形如 ax±b×c=d 的方程解决实际问题
1.根据数量关系列出方程。(不用求解)
(1)上衣单价x元,买 8 件这样的上衣一共用去 420 元。
(2)一班和二班共有 100 名学生,一班有x名,二班有 48 名。
(3)树上原来有x个桃,摘下 26 个,还剩 34 个。
2.解方程。
22.5×2+5x=135 6x-1.5x=3.6+2.7
3. 列方程解决实际问题。
一根绳子长 294 厘米,绕树 10 圈后还多出 44 厘米。这棵树一圈长多
少厘米?
1参考答案
1. (1)8x=420
(2)48+x=100
(3)x-26=34
2. 22.5×2+5x=135 6x-1.5x=3.6+2.7
解: 45+5x=135 解:4.5x=6.3
5x=135-45 x=6.3÷4.5
5x=90 x=1.4
x=18
3. 解:设这棵树一圈长 x 厘米。
10X+44=294
10X=294-44
10X=250
X=25
答:这棵树一圈长 25 厘米。
2练习三
1. 根据“张明比李红重 16 千克”,知道:( )体重+16=
( )体重。
2.如果 x÷3=0.18,那么 x+1.56=( )。
3. 列方程解决实际问题。
师徒两人同时给商品打包装,师傅每小时打 45 个,徒弟每小时打 15
个。经过几小时师傅比徒弟正好多打 120 个包装?
1参考答案
1. 李红 张明
2. 2
3. 解:设经过 x 小时师傅比徒弟正好多打 120 个包装。
45X-15x=120
30X=120
X=4
答:经过 4 小时师傅比徒弟正好多打 120 个包装。
2整理和复习(1)
1.解方程。
10x = 5.5 2X-2×0.3=8 1.3 x÷2=0.39
2. 只列方程不解答。
⑴ 一件衣服降价 25 元以后售价是 150 元。这件衣服原价多少元?
⑵一个面积是 4.8 平方米的长方形,长是 9.6 米,宽是多少米?
3. 列方程解决实际问题。
一列客车和一列货车从相距568千米的甲乙两地同时出发,相向而行,
2 小时后,两车之间还相距 108 千米。已知客车每小时行驶 120 千米,
求货车行驶的速度。
1参考答案
1. 10x = 5.5 2X-2×0.3=8 1.3 x÷2=0.39
解:x =5.5÷10 解:2x-0.6 =8 解:1.3 x =0.39×2
x =0.55 2 x =8+0.6 1.3 x =0.78
2 x =8.6 x =0.78÷
1.3
x =8.6÷2 x =0.6
x =4.3
2.(1)解:设这件衣服原价 x 元。
x-25=150
⑵解:设宽是 x 米。
9.6x=4.8
3. 解:设货车行驶的速度是每小时 x 千米。
120×2+2x+108=568
240+2X=460
2X=220
X=110
答:货车行驶的速度是每小时 110 千米。
2整理和练习(2)
1.解方程。
5χ- 2χ= 60 4χ+20=120
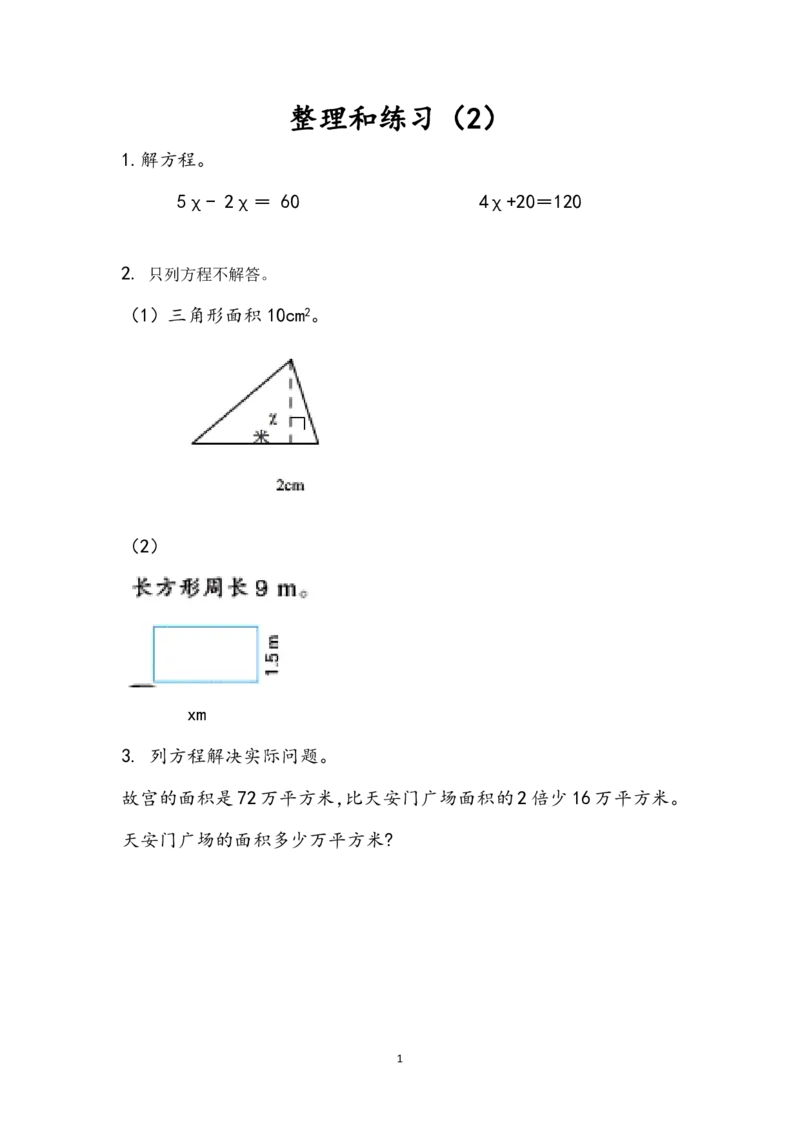
2. 只列方程不解答。
(1)三角形面积 10cm2。
(2)
xm
3. 列方程解决实际问题。
故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。
天安门广场的面积多少万平方米?
1参考答案
1. 5χ- 2χ= 60 4χ+20=120
解: 3χ= 60 解:4χ=120-20
χ= 60÷3 4χ=100
χ= 20 χ=100÷4
χ=25
2.(1)2x÷2=10
⑵2x+1.5×2=9
3. 解:设天安门广场的面积 x 万平方米。
2x-16=72
2x=72+16
2x=88
x=88÷2
x=44
答:天安门广场的面积是 44 万平方米。
2第二单元 单式折线统计图
某电器城 2007 年下半年空调和冰箱销售台数如下:
台 月
份
数
7 月 8 月 9 月 10 月 11 月 12 月
/
种 台
类
空调 450 750 550 370 250 600
冰箱 300 500 350 300 250 200
1.根据上表中的数据制成折线统计图。
2007 年下半年空调和冰箱销售情况统计图
空调
台数/台
冰箱
800
700
600
500
400
300
200
100
0 月份
7月 8月 9月 10月 11月 12月
2.平均每月销售空调多少台?
3.如每台冰箱获利 100 元,那么这个电器城 2007 年下半年冰箱销售
中共获利多少万元。
1参考答案
1.图略
2.(450+750+550+370+250+600)÷6=495(台)
答:平均每月销售空调 495 台。
3.(300+500+350+300+250+200)×10=19000(元)=1.9(万元)
答:那么这个电器城 2007 年下半年冰箱销售中共获利 1.9 万元。
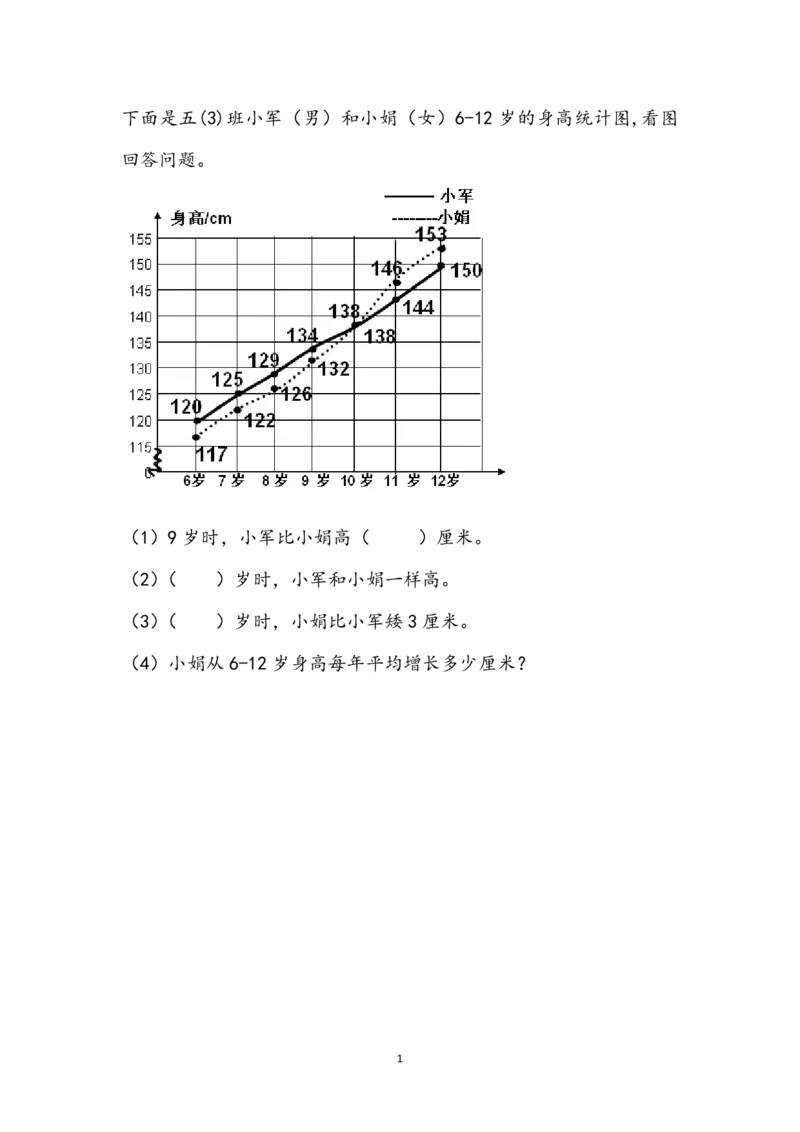
2下面是五(3)班小军(男)和小娟(女)6-12 岁的身高统计图,看图
回答问题。
(1)9 岁时,小军比小娟高( )厘米。
(2)( )岁时,小军和小娟一样高。
(3)( )岁时,小娟比小军矮 3 厘米。
(4)小娟从 6-12 岁身高每年平均增长多少厘米?
1答案:
(1)2
(2)10
(3)7
(4)(153-117)÷(12-6)=6(厘米)
答:小娟从 6-12 岁身高每年平均增长 6 厘米。
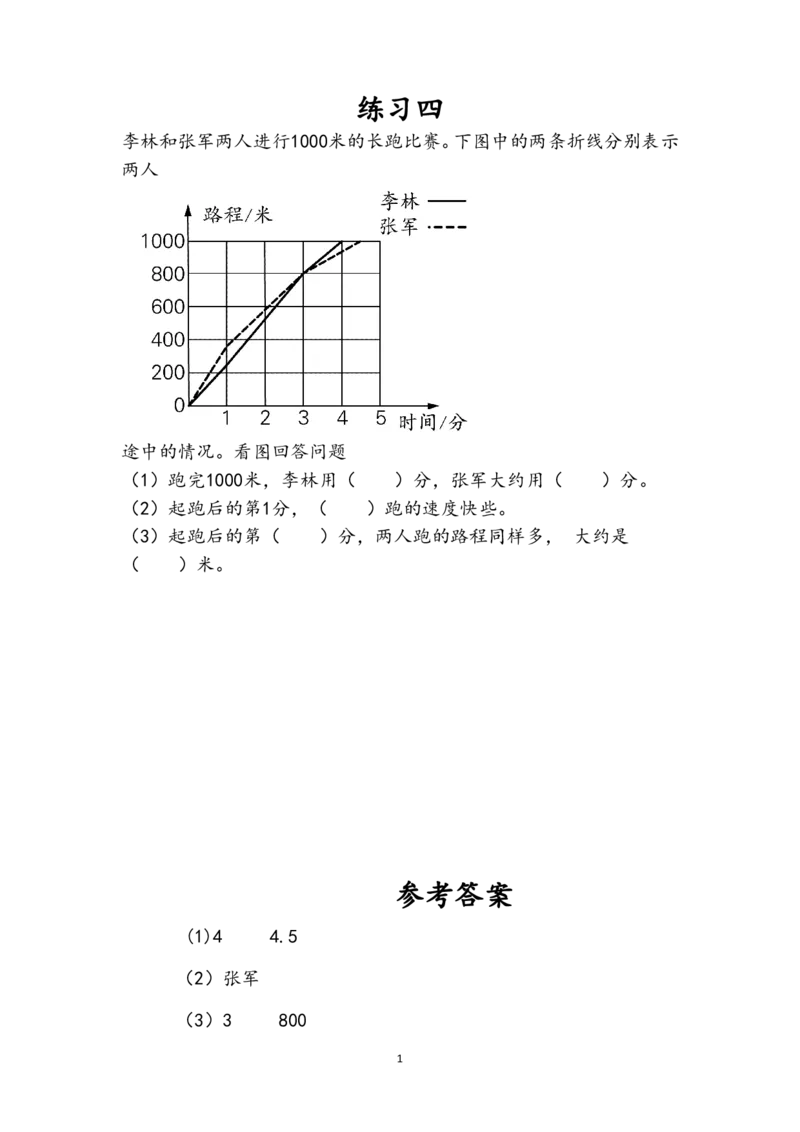
2练习四
李林和张军两人进行1000米的长跑比赛。下图中的两条折线分别表示
两人
途中的情况。看图回答问题
(1)跑完1000米,李林用( )分,张军大约用( )分。
(2)起跑后的第1分,( )跑的速度快些。
(3)起跑后的第( )分,两人跑的路程同样多, 大约是
( )米。
参考答案
(1)4 4.5
(2)张军
(3)3 800
1蒜叶的生长
1.可以用( )统计图,记录蒜叶的生长。
2.测量蒜叶和根须的长度时,都应以( )作单位。
3.阳光下和房间里,( )蒜叶生长的比较好 。
参考答案
1.复式折线
2.毫米
3.阳光下
1第三单元 因数和倍数的认识
1. 根据算式填空:3×6=18,18是( )的倍数, 18也是( )
的倍数;( )和( )都是18的因数。
2.按顺序写出所有积是 24 的整数乘法算式。
1×24=24
( )×( )=24
( )×( )=24
( )×( )=24
3.写出 50 以内 4 的倍数。
50 以内 4 的倍数有:( )
1参考答案
1.3 6 3 6
2. (2 )×( 12 )=24
( 3 )×( 8 )=24
( 4 )×( 6 )=24
3. 50 以内 4 的倍数有:( 4、8、12、16、20、24、28、32、36、
40、44、48 )
22和5的倍数特征
1. 2的倍数个位是( )。
2. 5的倍数个位是( )。
3.在□里填合适的数字。
(1)使 15□是 2 的倍数,□里可以填( )。
(2)使 15□是 5 的倍数,□里可以填( )。
参考答案
1.0、2、4、6、8
2. 0、5
3. (1)0、2、4、6、8
(2)0、5
13的倍数的特征
1. 3的倍数的特征是( )。
2. 42、55、45、51、126、357中3的倍数有( )。
3.在□里填合适的数字。
(1)使 31□是 3 的倍数,□里可以填( )。
( 2 ) 使 31 □ 是 3 的 倍 数 , 又 是 2 的 倍 数 , □ 里 可 以 填
( )。
参考答案
1.各位上数字之和是 3 的倍数
2. 42、45、51、126、357
3. (1)2、5、8
(2)2、8
1练习五
1. 2和5的倍数的特征是( )。
2. 50以内2、3、5的倍数有( )。
3.在□里填合适的数字。
( 1 ) 使 75 □ 是 3 的 倍 数 , 又 是 5 的 倍 数 , □ 里 可 以 填
( )。
( 2 ) 使 31 □ 是 2 的 倍 数 , 又 是 5 的 倍 数 , □ 里 可 以 填
( )。
参考答案
1.个位上的数字是 0
2. 30
3. (1)0
(2)0
1质数和合数
1. 判断。
(1)最小的质数是1。( )
(2)最小的合数是4。( )
2. ( )既不是质数也不是合数。
3.50 以内最小的质数是( ),最大的质数是( ),最小的合
数是( ),最大的合数是( )。
参考答案
1. (1)×
(2)√
2. 1
3. 2 47 4 49
1质因数和分解质因数
1. 根据算式填空:28=4×7,( )和( )都是28的因数,
( )是28的质因数。
2.在括号里填合适的质数。
8=( )+( )
13=( )+( )
3.把下面的数分解质因数。
56 39 36
参考答案
1.4 7 7
2. 8=( 3 )+( 5 )
13=( 2 )+( 11 )
3.56=2×2×2×7
39=3×13
36=2×2×3×3
1练习六
1. 根据算式填空:15=3×5,( )和( )都是15的因数,
( )和( )是15的质因数。
2.48 的因数有( ),48 的质因数有( )。
3.把下面的数分解质因数。
98 72 250
参考答案
1.3 5 3 5
2. 1、2、3、4、6、8、12、16、24、48 2、3
3. 98 72 250
98=2×7×7
72=2×2×2×3×3
250=2×5×5×5
1公因数和最大公因数
1. 12的因数有( ),16的因数有( ),12和16的公因
数有( )。
2.20 和 35 的公因数有( ),最大公因数是( )。
3.找出下面每组数的最大公因数。
15 和 7 12 和 36
参考答案
1.1、2、3、4、6、12 1、2、4、8、16 1、2、4
2. 1、5 5
3. 1 12
1公倍数和最小公倍数
1. 8的倍数有( ),12的倍数有( ),8和12的公倍数
有( )。
2.20 和 35 的公倍数有( ),最小公倍数是( )。
3.找出下面每组数的最小公倍数。
15 和 7 12 和 36
参考答案
1.8、16、24、32、40、48…… 12、24、36、48、60、72……
24、48、72……
2. 140、280、420…… 140
3. 105 36
1练习七
在18、25、36、60、78、105、275、300中。
1.( )既是2的倍数,又是3的倍数。
2.( )既是2的倍数,又是5的倍数。
3.( )既是3的倍数,又是5的倍数。
4. ( )是36的54最大公因数。
5. ( )是15的12最小公倍数。
参考答案
1.18、36、60、78、300
2.60、300
3.60、105、300
4.18
5.60
1整理与练习(1)
1. 24 和 30 的公因数有( ), 24 和 30 的最大公因数是
( )。
2.在 15、18、20、25、40 中,( )既有因数 2,又有因数 3;
( )是 3 和 5 的公倍数;( )和( )有公因数 2 和 5。
3.李菲家客厅长 4.8 米,宽 4.2 米,选用边长( )分米的方砖铺
地不需要切割。
参考答案
1.1、2、3、6、 6
2. 18 15 20 40
3.1、2、3、6、
1整理与练习(2)
1.写出下面每组数的最大公因数和最小公倍数。
4 和 6 3 和 8 5 和 20
最大公因数:____ 最大公因数:_____ 最大公因数:_____
最小公倍数:____ 最小公倍数:_____ 最小公倍数:_____
2. a=3b,那么它们的最小公倍数是( ),最大公因数是( )。
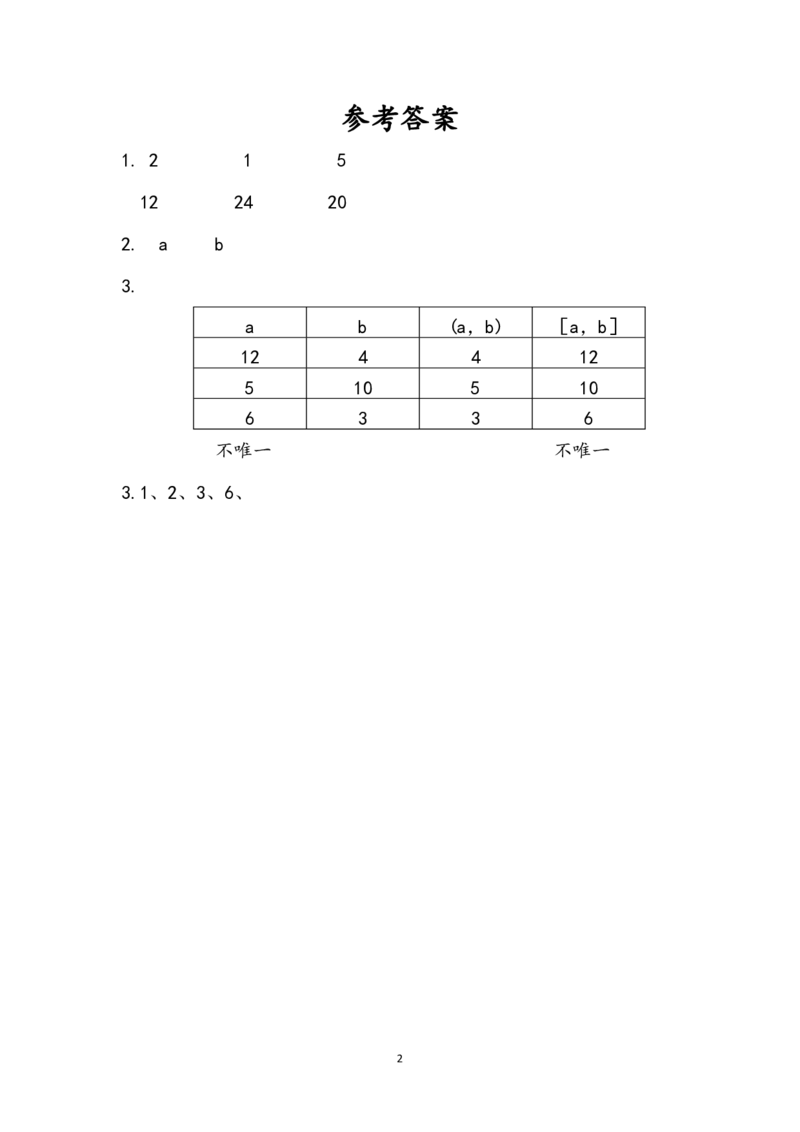
3. 下表中 a、b 是自然数。(a,b)是最大公因数,[a,b]是最小公
倍数。
a b (a,b) [a,b]
12 4
5 10
3 3
1参考答案
1. 2 1 5
12 24 20
2. a b
3.
a b (a,b) [a,b]
12 4 4 12
5 10 5 10
6 3 3 6
不唯一 不唯一
3.1、2、3、6、
2和与积的奇偶性
1.奇数+奇数=( ) 偶数+偶数=( )
奇数×奇数=( ) 偶数×偶数=( )
2.第一次按开关灯亮,第二次按开关灯灭,依次这样按下去,第 12
次按开关灯( ),第 23 次按开关灯( )。
3. 4 个连续自然数的和是奇数还是偶数?举例说明。
参考答案
1.偶数 偶数
奇数 偶数
2.灭 亮
3. 偶数。如 4+5+6+7=22。
1第四单元 分数的意义和分数单位
5
1. 表示把( )平均分成( )份,表示这样的( )份。
7
2.一堆煤可以烧 12 天,,平均每天烧这堆煤的 ,5 天烧这堆
煤的 。
3
3. 的分数单位是( ),再添( )个这样的分数单位就
20
是最小的质数。
参考答案
1. 单位“1” 7 5
1 5
2.
12 12
1
3. 37
20
1分数与除法的关系
1.把 4 米长的绳子平均剪成 5 段,每段是这根绳子的 ,每段长
米。
2. 12 分= 小时 15 厘米= 米 5 时= 天
3.有 12 枝铅笔,平均分给 2 个同学。每枝铅笔是铅笔总数的 ,
每人分得的铅笔是铅笔总数的 。
参考答案
1 4
1.
5 5
12 15
2. 5
60 100
24
1 1
3.
12 2
1求一个数是另一个数的几分之几
1. 的个数是 的 ,
的个数是 的 。
2.判断。
2
(1)一堆煤,已经烧了 ,是把已经烧的煤看作单位“1”。
7
( )
(2)把 12 个足球平均分给 4 个班,每班分得的足球数占总个数的
1
。( )
12
1
(3)把一根铁丝锯了 4 次,平均每段的长是总长的 。 ( )
4
3. 合唱队有女生 15 人,男生 20 人,
(1)女生人数是男生的 。
(2)男生人数是总人数的 。
参考答案
7 4
1.
4 7
2.(1)×(2)×(3)×
15 20
3.
20 35
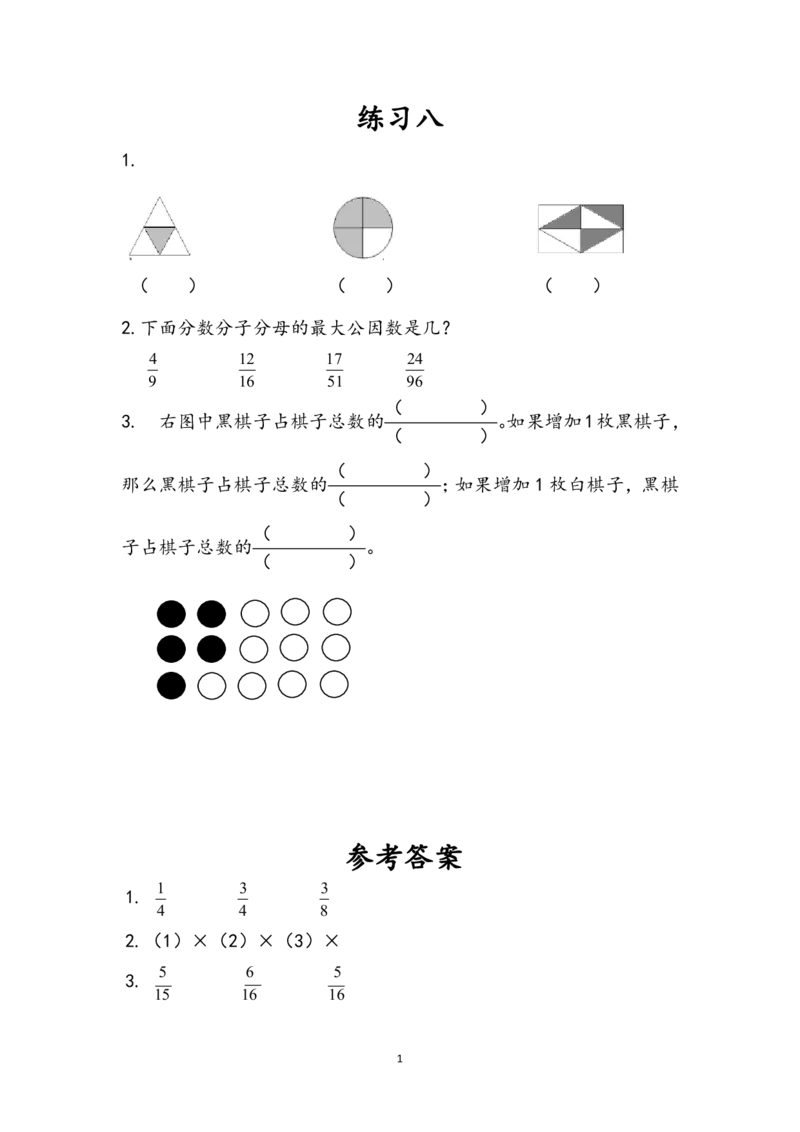
1练习八
1.
( ) ( ) ( )
2.下面分数分子分母的最大公因数是几?
4 12 17 24
9 16 51 96
( )
3. 右图中黑棋子占棋子总数的 。如果增加1枚黑棋子,
( )
( )
那么黑棋子占棋子总数的 ;如果增加 1 枚白棋子,黑棋
( )
( )
子占棋子总数的 。
( )
参考答案
1 3 3
1.
4 4 8
2.(1)×(2)×(3)×
5 6 5
3.
15 16 16
1真分数和假分数
1
1.分数单位是 的最大真分数是( ),最小假分数是( ),
9
最小带分数是( )。
2.判断。
(1)分子比分母小的分数是真分数,分子比分母大的分数是假分数。
( )
( 2 ) 真 分 数 都 小 于 1 , 假 分 数 都 大 于 1 。
( )
3. 分子是 5 的假分数有( ),分母是 6 的真分数有
( )。
1参考答案
8 10 1
1. 1
9 9 9
2.(1)√(2)×
5 5 5 5 1 2 3 4 5
3. 、 、 、 、 、 、 、
1 2 3 4 6 6 6 6 6
21. 把下面的假分数化成整数。
10 9 51
2 9 3
2. 在直线上面的 里填上假分数,下面的 里填上带分数。
6 9 12
4 4 4
0 1 2 3 4
3.用分数表示下面各题的商,是假分数的化成整数或带分数。
12÷7 50÷3 11÷12 25÷5
1答案:
1. 5 1 17
4 8 14 15
2.
4 4 4 4
2 1
1 3
4 4
5 2 11
3. 1 16 5
7 3 12
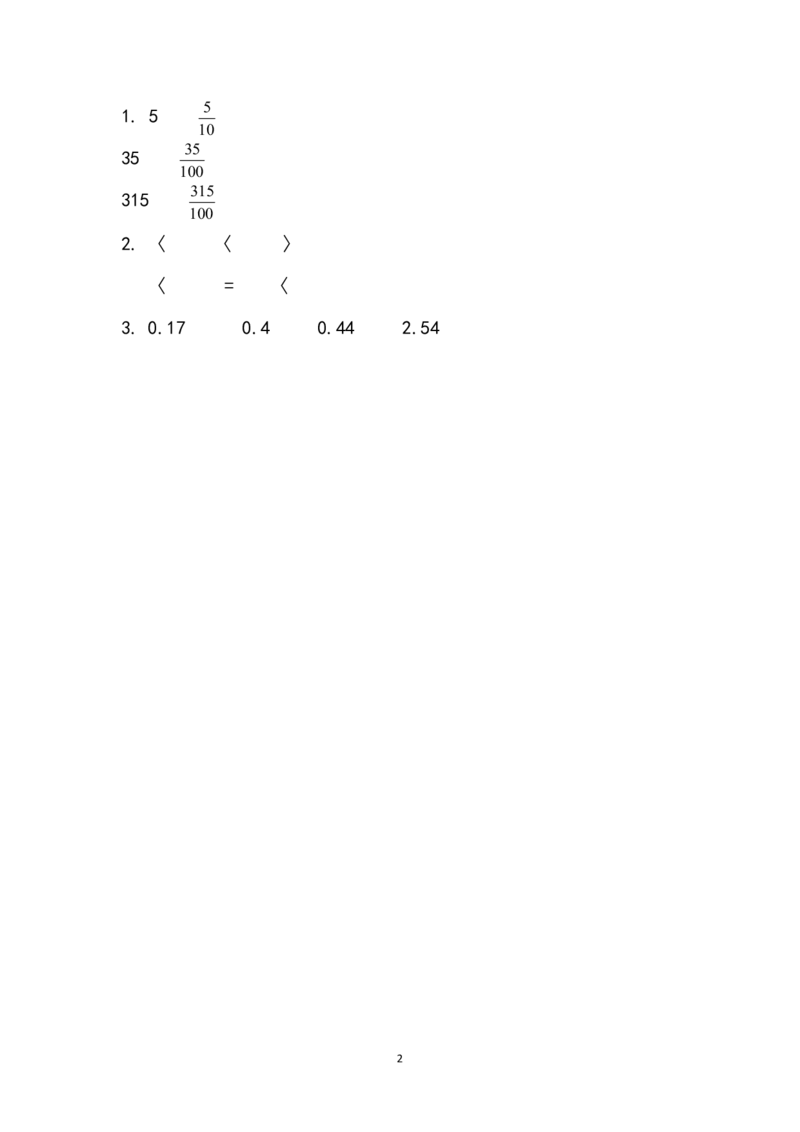
2分数与小数的互化
( )
1.0.5 里面有( )个十分之一,是 。
( )
( )
0.35 里面有( )个百分之一,是 。
( )
( )
0.315 里面有( )个千分之一,是 。
( )
2. 在( )里填上〉、 〈或=。
5 9 7 13
( ) ( )1 ( )1
7 7 8 12
2 3 2 7
( ) ( )0.4 ( )0.8
3 2 5 8
3. 直接把下列分数化成小数(除不尽的保留两位小数)。
1 2 4 13
2
6 5 9 24
参考答案
15
1. 5
10
35
35
100
315
315
100
2. 〈 〈 〉
〈 = 〈
3. 0.17 0.4 0.44 2.54
2( )
1.10 枝铅笔平均分给 5 个同学。每枝铅笔是铅笔总数的 ,每人
( )
( )
分得的铅笔是铅笔总数的 。
( )
2. 把 3 米长的铁丝剪成同样长的 4 段,每段长是 1 米的( )。
1 6 15 1
1
3. ( )个 是 ; 里有( )个 ;( )个 是 3。
7 7 20 20 8
1答案:
1 1
1.
10 5
3
2.
4
3.6 15 24
21.判断。
2
(1)“一节课的时间是 小时”是把一节课的时间看作单位“1”。
3
( )
1
(2)把一根绳子分成 6 份,每份是这根绳子的 。( )
6
x x
2. 如果 是假分数, 是真分数,那么x是( )。
8 9
3. 如左图,阴影部分表示的面积是( )平
3平方米 ( )
方米,相当于 3 平方米的 。
( )
1答案:
1. (1)× (2)×
2.8
3 1
3.
4 4
2( )
12
1. 0.75= = = =( )÷16
( ) 12
9
2. 的分子减少 6,要使分数的大小不变,分母应该( )。
12
3. 下面的每组数是否相等,在相等的下面画“√”。
20 5 7 28 4 9
和 ( ) 和 ( ) 和
24 6 12 36 3 12
( )
1答案:
3
1. 9 16 12
4
2.减少 8
20 5 7 28 4 9
3. 和 ( √ ) 和 ( ) 和
24 6 12 36 3 12
( )
2
12
1. 34 48
36 4
2. 在下面最简分数的后面画“√”,不是最简分数的将约分的结果写
在括号内。
3 6 17 19
( ) ( ) ( )
5 8 68 29
( )
3. 把下面的分数约分。
20 28 9
24 36 12
1答案:
1. 27 16 3 36
3 6 3 17 1 19
2. (√) ( ) ( )
5 8 4 68 4 29
(√)
20 5 28 7 9 3
3. = = =
24 6 36 9 12 4
21. 把下面的分数约分,约分结果是假分数的化成整数或带分数。(10
分)
4 12 38 39
6 27 95 91
4
2. 一个分数的分子比分母少 24,约分之后是 ,这个分数是
7
( )。
5
3.把一个分数约分,用 2 约了两次,用 3 约了一次,得 ,原来这个
6
分数是 。
1答案:
4 2 12 4 38 2 39 3
1. = = = =
6 3 27 9 95 5 91 7
32
2.
56
60
3.
72
21. 1.涂一涂,填一填。
2 4
=
4
2. 选择。
15
(1)把 化成最简分数后,它的分数单位是( )。
24
1 1 1
A B C
24 12 8
6 3
(2)因为 = ,所以这两个分数的( )。
8 4
A 大小相等 B 分数单位相同 C 分数单位和大小都相同
3.把下面各组分数通分。
1 3 5 5
和 和
5 4 8 7
1答案:
1.
2 4
=
4 8
2. (1)C (2)A
1 4 3 15 5 35 5 40
3. = = = =
5 20 4 20 8 56 7 56
21. 在( )里填上〉、 〈或=。
5 9 7 13
( ) ( )1 ( )1
7 7 8 12
2 3 2 7
( ) ( )0.4 ( )0.8
3 2 5 8
2 1 5 1 3 9
2. 在 、 、 、 、 、 中最接近 0 的有( ),最接近 1
3 4 9 8 5 10
1
的有( ),最接近 的有( )。
2
3. 在括号内填上合适的最简分数。
5 7 1
<( ) ( )> >( )
6 8 6
1 1 7 4
< < < <
5 4 10 5
1答案:
1. 〈 〈 〉
〈 = 〉
1 9 5
2.
8 10 9
7 9 1
3.
6 8 7
9 3
20 4
21. 约分。
80 125 39 140
32 120 52 28
2. 通分并比较大小。
3 7 5 7 7 5 9
和 和 、 和
11 12 18 27 12 32 48
3
3. 一稿文章,小明 1.3 小时打完,小冬 1 小时打完。谁的打字速度
4
快些?
1答案:
80 5 125 25 39 3 140
1. = = = =5
32 2 120 24 52 4 28
3 36 7 77 5 15 7 14
2. = 、 = = 、 =
11 132 12 132 18 54 27 54
7 56 5 15 9 18
= 、 = 、 =
12 96 32 96 48 96
3
3.1.3<1
4
答:小明的打字速度快些。
23
1. 1 的分数单位是( ),它里面有( )个这样的单位,再增加
5
( )个这样的分数单位就是最小的合数。
1 1
2. 两根绳子测同一口井深,第一根露在井外 ,第二根露在井外 ,
3 2
第( )根绳子长。
a a
3. (a 是大于 0 的自然数),当 a 时, 是真分数,当 a
5 5
a a
时, 是假分数,当 a 时, 等于 3。
5 5
1答案:
1
1. 8 12
5
2.2
3.小于 5 大于等于 5 等于 15
2整理与练习(2)
1. 用分数表示下面各题的商,是假分数的化成整数或带分数。
12÷7 50÷3 11÷12 25÷5
2. 直接把下列分数化成小数(除不尽的保留两位小数)
3 5 6 4 3
8 8 9 9 10
3. 一块菜地 3 公顷,平均分成 5 份,每份是多少公顷?其中 4 份种
土豆,种土豆的面积占这块菜地的几分之几?
1参考答案
5 2 11
1. 1 16 5
7 3 12
2.0.375 0.625 0.67 0.44 0.3
3 4
3.3÷5= (公顷) 4÷5=
5 5
3 4
答:每份是 公顷,其中 4 份种土豆,种土豆的面积占这块菜地的 。
5 5
2球的反弹高度
1.同一个球从不同高度落下,其反弹高度( )。
2.同一个球从不同高度落下,其表示反弹高度与下落高度关系的分数
( )。
3. 比赛用的篮球,从 1.8 米的高度自由落下后,第一次反弹的高度
应大于( )米,小于( )米。
参考答案
1.不一样
2.大体不变
3. 1.2 1.4
1第五单元 异分母分数加减法
5 1 2 1 1 1 2 4
1. - = + = - = + =
8 4 3 6 5 8 3 9
1
2. 张大伯收了一批西瓜,第一天卖出了总数的 ,第二天卖出了总
5
1
数的 ,两天共卖出总数的几分之几?
6
5 1 1
3. 一根彩带长 米,第一次用去 米,第二次用去 米,这时比原来
6 2 6
短了多少米?
1参考答案
3 5 3 10
1.
8 6 40 9
1 1 11
2. + =
5 6 30
11
答:两天共卖出总数的 。
30
1 1 2
3. + = (米)
2 6 3
2
答:这时比原来短了 米。
3
。
2连加、连减、加减混合
2 4 1
1 1 1
1. - - = + + =
2 3 6 3 5 3
4 5
7 3 3
1 - + = -( - )=
9 9 10 7 10
3 1
2.一根电线用去 米,用去的比剩下的短 米,这根电线原来长多少
5 6
米?
2
3.王彬看一本书,第一天看了全书的 ,第二天比第一天多看了全书
9
4
的 。两天一共看了全书的几分之几?
27
1参考答案
4
10 3
1.0 1 1
5 9 7
3 3 1 41
2. + + = (米)
5 5 6 30
41
答:这根电线原来长 米。
30
2 2 4 16
3. +( + )=
9 9 27 27
16
答:两天共卖出总数的 。
27
2练习十二(1)
3 1 1 1 1 1 1 1
1. =
4 2 3 2 7 9 2 5
11
2. 空调厂去年上半年完成全年计划任务的 ,下半年和上半年完成
16
的同样多,空调厂去年实际超额完成全年计划任务的几分之几?
3. 有一筐 72 千克的苹果,第一天吃了它的 ,第二天吃了它的 。
还剩下几分之几?
1参考答案
1 5 2 7
1.
4 6 63 10
11 11 6
2. + -1=
16 16 16
6
答:空调厂去年实际超额完成全年计划任务的 。
16
1 5 5
3.1- - =
6 9 18
5
答:还剩下 。
18
2练习十二(2)
1 1 5 7
6 8 1 7 1 2 2
1. ― = ― = = =
5 7 6 12 7 13 7 9 3 9 3
11
2. 两个分母不同的分数相加,和是 ,这两个分数可能是
12
( ) ( )
和 。
( ) ( )
4 1 2
3. 商店里有食品 吨,支援灾区运走 吨,又卖出 吨,还剩下
5 3 5
多少吨?
1参考答案
2 1 8 5
1. 1 1
35 4 13 9
1 5
2. 答案不唯一
12 6
4 1 2 1
3. - - = (吨)
5 3 5 15
1
答:还剩下 吨。
15
2第六单元 圆的认识
1. 按照要求画圆。
(1) 半径2厘米。
(2) 直径6厘米。
2. 填写下表。
半径 2 分米 4.2 米
直径 8 厘米
3. 比较两个圆的大小。
(1)甲圆直径 6 厘米,乙圆直径 7 厘米。( )圆大
(2)甲圆半径 6 厘米,乙圆直径 7 厘米。( )圆大
1参考答案
1. 图略。
2.
半径 2 分米 4 厘米 4.2 米
直径 4 分米 8 厘米 2.1 米
3. (1)乙 (2)甲
2扇形的认识
1. 填写下表。
半径 4 分米 3 米
直径 17 厘米
2.3 时钟面的时针和分针的圆心角是( )度,6 时钟面的时针
和分针的圆心角是( )度。
3.先画一个圆,再在圆中画一个扇形,大小是圆的四分之三。
1参考答案
1.
半径 4 分米 8.5 厘米 3 米
直径 8 分米 17 厘米 6 米
2.90 180
3. 图略。
2练习十三
1.圆规两脚间的距离是 2 厘米,画出的圆半径( )厘米,直径
( )厘米。
2.边长 4 厘米的正方形里画一个最大的圆,圆的半径是( )厘米。
3. 长 8 厘米、宽 6 厘米的长方形里画一个最大的圆,圆的半径是
( )厘米。
参考答案
1. 2 4
2.2
3.3
1圆的周长(1)
1. 求出下面各圆的周长。
r=3 厘米 d=1.8 分米
2.判断。
(1)两个圆的半径相等,这两个圆的周长也一定相等。( )
(2)直径是半径的 2 倍。( )
(3)半个圆的周长就是圆周长的一半。( )
3.在右面长方形内画一个最大的圆,并求 出这个圆的周长。
8米
6米
1参考答案
1.2×3.14×3=18.84(厘米)
1.8×3.14=5.652(分米)
2.(1)√(2)×(3)×
3.图略
3.14×6=18.84(米)
26.5 圆的周长(2)
1.填空题。
(1)时钟的分针转动一周形成的图形是( )。
(2)一个圆的周长是同圆直径的( )倍。
(3)有一个圆形鱼池的半径是 10 米,如果绕其周围走一圈,
要走( )米。
(4)一个挂钟的时针长 5 厘米,一昼夜这根时针的尖端走了
( )厘米。
2.砂子堆在地面上占地正好是圆形,量出它一周的长度是
15.7 米,那么砂子堆的直径是多少米?
参考答案
1.(1)周长;(2)π(3)31.4;(4)62.8
2. 5 米练习十四
1. 求出下面各圆的半径。
C=6.28 分米 d=10 米
2. 把一张边长为 8 厘米的正方形纸片剪成 4 个同样大小的圆,每个
圆的周长是( )厘米。
3. 小明骑自行车过马路。自行车车轮的半径是 15 厘米,从马路的一
边到另一边,车轮正好滚动 15 圈。这条马路长多少米?
1参考答案
1.6.28÷3.14÷2=1(分米)
10÷2=5(米)
2.12.56
3.15×2×3.14×15=1413(厘米)=14.13(米)
答:这条马路长 14.13 米。
2圆的面积(1)
1. 求出下面各圆的面积。
r=3 厘米 d=8 分米
2. 在右面长方形内画一个最大的圆,并 求
出这个圆的面积。
6米
8米
3. 把一个圆剪拼成一个近似的长方形(如右图),这个圆的周长是
( )厘米,面积是( )平方厘米。
6.28厘米
1参考答案
1.3.14×3×3=28.26(平方厘米)
3.14×(8÷2)2=50.24(平方分米)
2.图略
3.14×(6÷2)2=28.26(平方米)
3.12.56 12.56
2圆的面积(2)
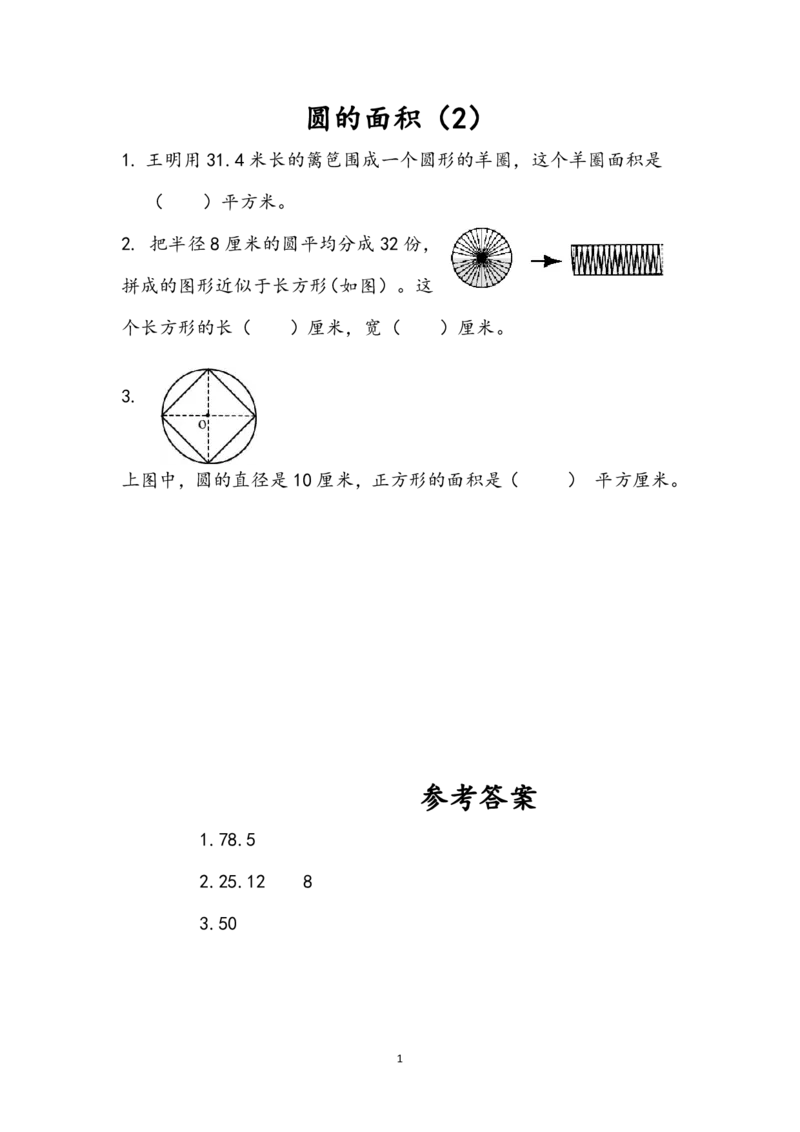
1. 王明用 31.4 米长的篱笆围成一个圆形的羊圈,这个羊圈面积是
( )平方米。
2. 把半径 8 厘米的圆平均分成 32 份,
拼成的图形近似于长方形(如图)。这
个长方形的长( )厘米,宽( )厘米。
3.
上图中,圆的直径是 10 厘米,正方形的面积是( ) 平方厘米。
参考答案
1.78.5
2.25.12 8
3.50
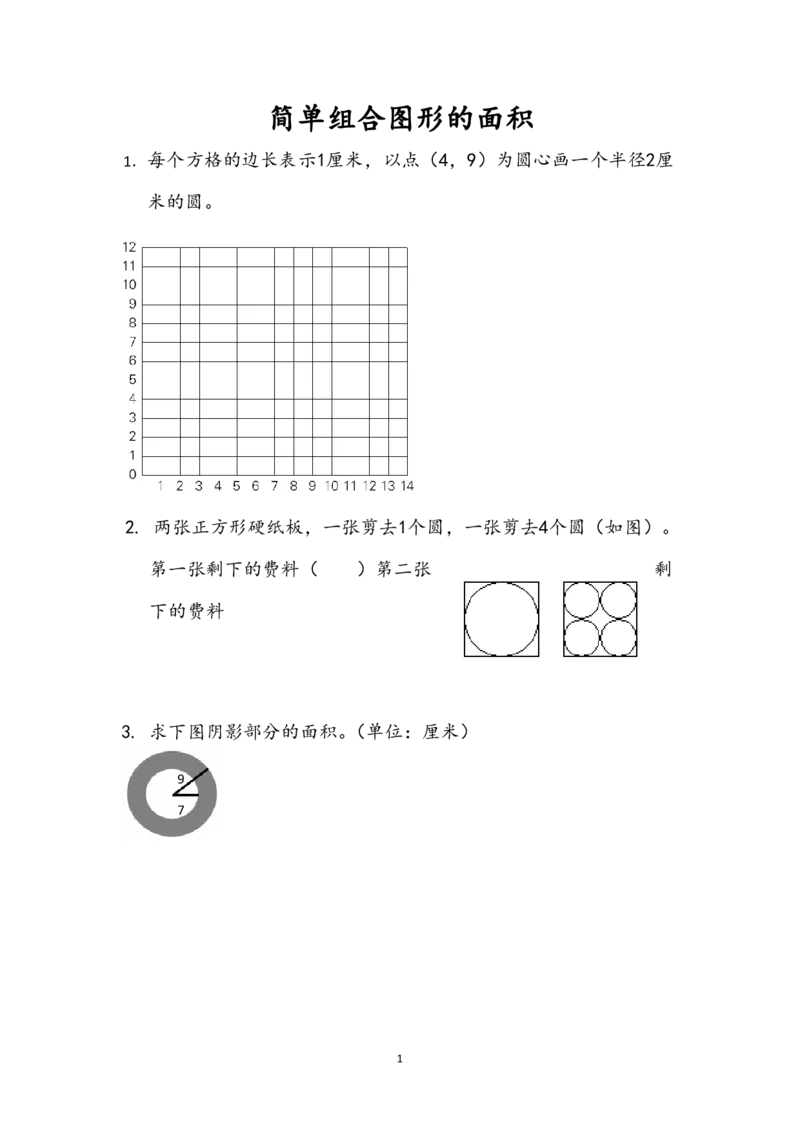
1简单组合图形的面积
1.每个方格的边长表示1厘米,以点(4,9)为圆心画一个半径2厘
米的圆。
2. 两张正方形硬纸板,一张剪去1个圆,一张剪去4个圆(如图)。
第一张剩下的费料( )第二张 剩
下的费料
3. 求下图阴影部分的面积。(单位:厘米)
9
7
1参考答案
1.
·
2.等于
3. 3.14×(92-72)=100.48(平方厘米)
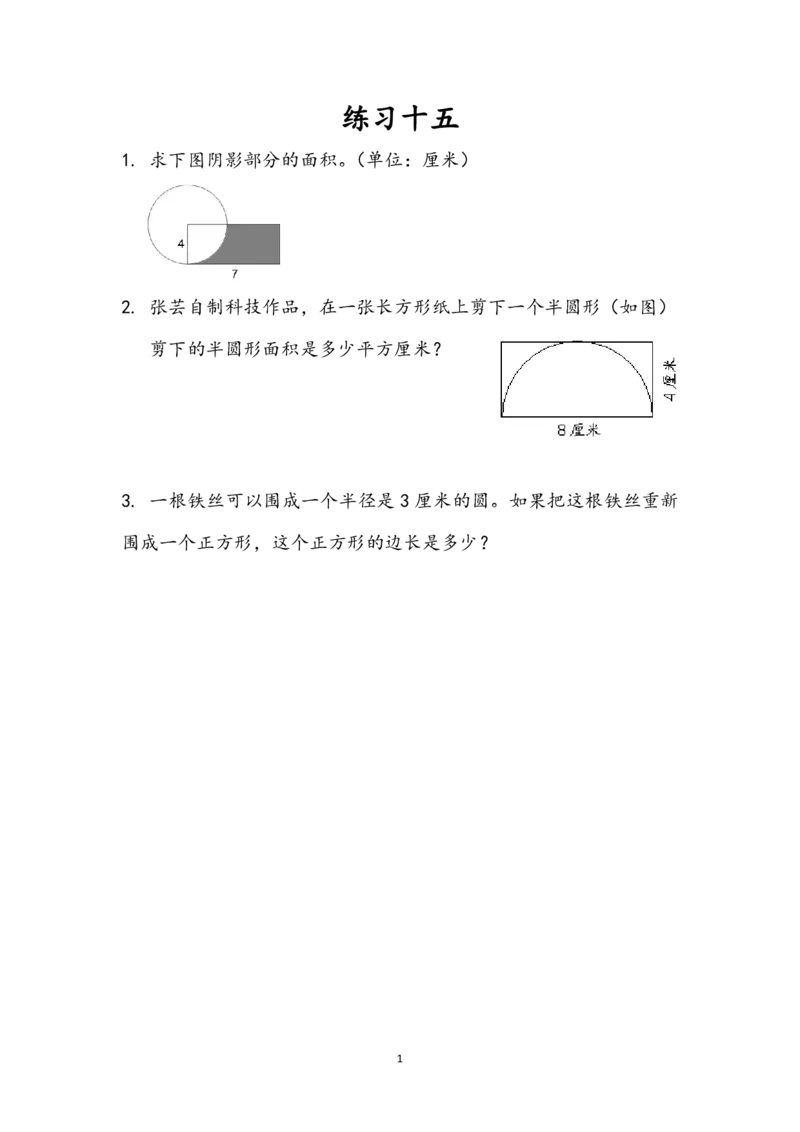
2练习十五
1. 求下图阴影部分的面积。(单位:厘米)
2. 张芸自制科技作品,在一张长方形纸上剪下一个半圆形(如图)
剪下的半圆形面积是多少平方厘米?
3. 一根铁丝可以围成一个半径是 3 厘米的圆。如果把这根铁丝重新
围成一个正方形,这个正方形的边长是多少?
1参考答案
1.4×7-3.14×4×4÷4=15.44 (平方厘米)
2. 3.14×42÷2=25.12(平方厘米)
答:剪下的半圆形面积是25.12平方厘米。
3.3.14×3×2÷4=4.71(厘米)
答:这个正方形的边长是 4.71 厘米。
2整理与练习(1)
1. 在面积是 16 平方厘米的正方形内画一个最大的圆,圆面积是
( )平方厘米。
2. 如图,从 A 点到 B 点有三条路,每条路都是由一
个或两个半圆组成的。比较这三条路的长度,你
认为:( )。
A、最上面的路最长 B、 最上面的路最短 C、三条路长度相等
3. 如图,在一块长方形空地上设计
三个圆形花圃,使花圃的面积尽
可能大。花圃的占地面积可以达
到多少平方米? (先在图中画一画,再列式计算)
1
米6
18米参考答案
1.12.56
2.c
3.
6÷2=3(米) 3×3×3.14=28.26(平方米) 28.26×3=84.78(平方
米)
答:花圃的占地面积可以达到84.78平方米。
2
米6
18米整理与练习(1)
( )
1. 把一张长方形纸对折,再对折,得到的图形面积是原来的 ,
( )
( )
如果原来长方形的面积是3平方分米,那么得到图形的形面积是
( )
平方分米。
2. 右图中,正方形的面积是100平方厘米,圆的面积
是( )平方厘米。
A、157 B、78.5 C、100
A、最上面的路最长 B、 最上面的路最短 C、三条路长度相等
3. 奶奶用 20.56 米长的篱笆在空地上围一个半圆形的养鸡场。这个
养鸡场的面积是多少平方米?
1参考答案
1 3
1.
4 4
2.A
3. 20.56÷(1+3.14÷2)=8(米) 8÷2=4(米)
4×4×3.14=50.24(平方米) 0.24÷2=25.12(平方米)
答:这个养鸡场的面积是 25.12 平方米。
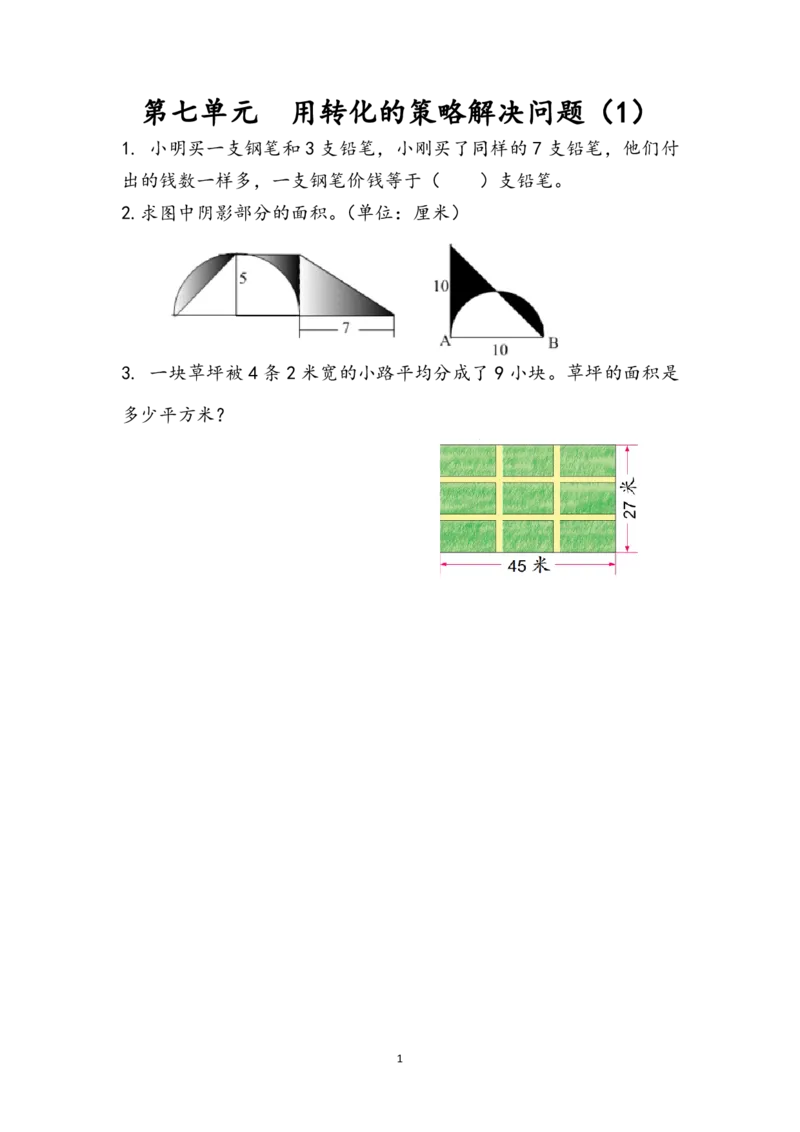
2第七单元 用转化的策略解决问题(1)
1. 小明买一支钢笔和 3 支铅笔,小刚买了同样的 7 支铅笔,他们付
出的钱数一样多,一支钢笔价钱等于( )支铅笔。
2.求图中阴影部分的面积。(单位:厘米)
3. 一块草坪被 4 条 2 米宽的小路平均分成了 9 小块。草坪的面积是
多少平方米?
1参考答案
1. 4
2. 5×7=35(平方厘米) 10×(10÷2)÷2=25(平方厘米)
3. 2×2=4(米)
(45-4)×(27-4)
=41×23
=943(平方米)
答:草坪的面积是 943 平方米。
2用转化的策略解决问题(2)
1 1 1 1 1 1 1
1.
2 4 8 16 32 64 128
2.求图中阴影部分的面积。(单位:厘米)
3. 4 个圆的直径都是 2 厘米,阴影部分的面积是多少平方厘米?
1参考答案
1 1 1 1 1 1 1
1.
2 4 8 16 32 64 128
1
1
128
127
128
2.5×(5×2)=50(平方厘米)3.14×62 ÷2=56.52 (平方厘米)
3. 4×4+3.14×(4÷2)2×3=53.68(平方厘米)
答:阴影部分的面积是 53.68 平方厘米。
2练习十六
1. 9998+998+98+8=
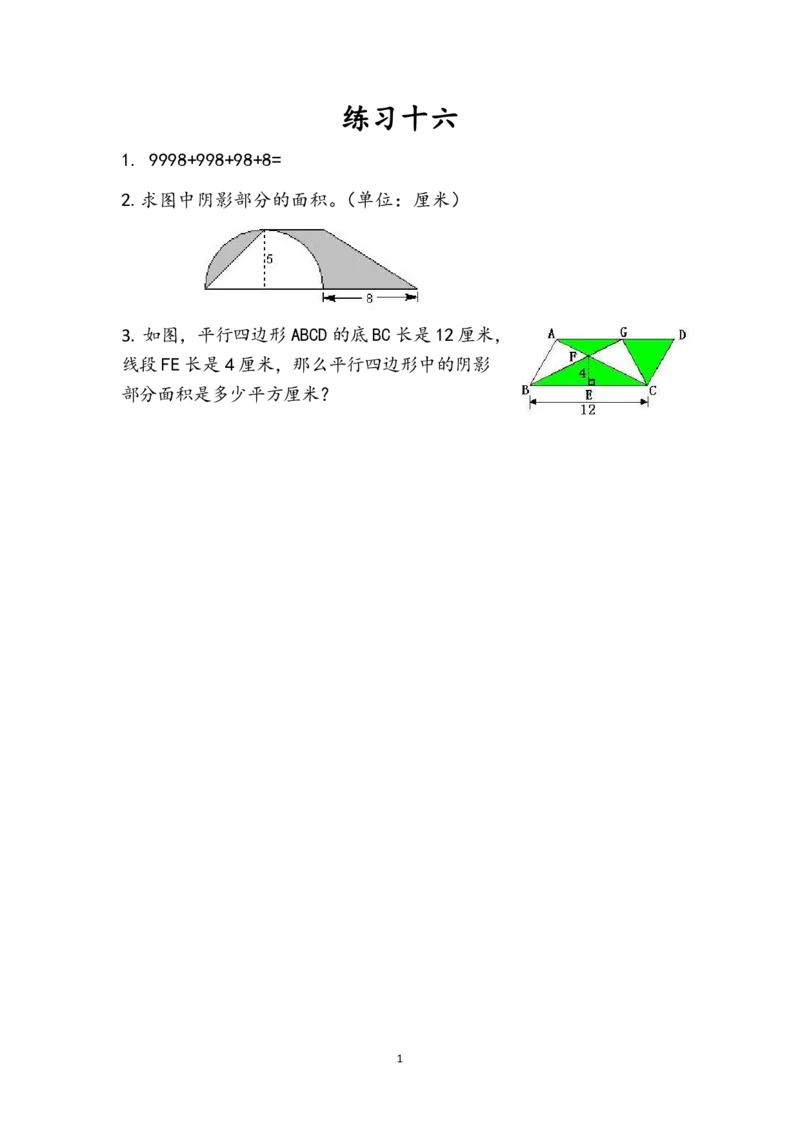
2.求图中阴影部分的面积。(单位:厘米)
3. 如图,平行四边形ABCD 的底BC 长是12 厘米,
线段FE 长是4 厘米,那么平行四边形中的阴影
部分面积是多少平方厘米?
1参考答案
1. 9998+998+98+8=10000+1000+100+10-2×4=11102
2.5×8=40(平方厘米)
3. 12×4÷2×2=48(平方厘米)
答:平行四边形中的阴影部分面积是48 平方厘米。
2第八单元 数的世界(1)
1.运用等式的性质在横线上填上合适的数,在方框里填上合适的运算
符号。
(1)12X=14.4 (2)Y-4.5=4.5
12X÷12=14.4 ___。 Y-4.5 ___=4.5+4.5
(3)7.5+X=75 (4)a÷2.5=10
7.5+X ___=75-7.5 a÷2.5×2.5=10 ___
2. 把每题的正确答案圈出来。
(1)X+6=28 (X=34,X=22)
(2)如果 X+30=50,那么 X/2=(20,10)
3. 3 个连续的奇数的和是 57,中间的数是 M,你能列方程求 M 的值
吗?
1参考答案
1. (1) ÷12 (2) +4.5 (3) -7.5 (4) ×2.5
2. (1)X=22
(2)X/2=10
3. M+2+M+M-2=57
3M=57
M=19
答:M 的值是 19。
2数的世界(2)
1. 写出分子与分母的最大公因数。
6 15 10 6
( ) ( ) ( ) ( )
18 45 40 9
2.判断 。
(1)一个数是 12 的倍数,也是 12 的因数,这个数是 12。( )
( 2 ) 两 个 数 的 公 因 数 一 定 是 这 两 个 数 的 因 数 。
( )
(3)两个数的公因数和公倍数的个数都是无限的。 ( )
(4)相邻的两个自然数的最小公倍数是其中的较大数。 ( )
3. 把 45 厘米、60 厘米的两根彩带剪成长度一样的短彩带且没有剩
余,每根短彩带最长是多少厘米?一共可以剪成多少段?
1参考答案
1.6 15 10 3
2.(1)√(2)√(3)×(4)×
3.(45,60)=15
45÷15=3(段)
60÷15=4(段)
3+4=7(段)
答:每根短彩带最长是 15 厘米,一共可以剪成 7 段。
2图形王国
1. 1.涂一涂,填一填。
3
< <
4
( )
2. 一个钟面被分成两部分(如右图),较小部分占整个钟面的 ,
( )
( )
较大部分占整个钟面的 。
( )
3. 奶奶用 15.7 米长的篱笆靠墙围一个半圆形的养鸡场。
这个养鸡场的面积是多少平方米?
1参考答案
1.
3 7 15
< <
4 8 16
1 2
2.
3 3
3. 15.7×2=31.4(米) 31.4÷3.14=10(米)
10÷2=5(米)5×5×3.14=78.5(平方米)78.5÷2=39.25(平方米)
答:这个养鸡场的面积是 39.25 平方米。
2统计天地
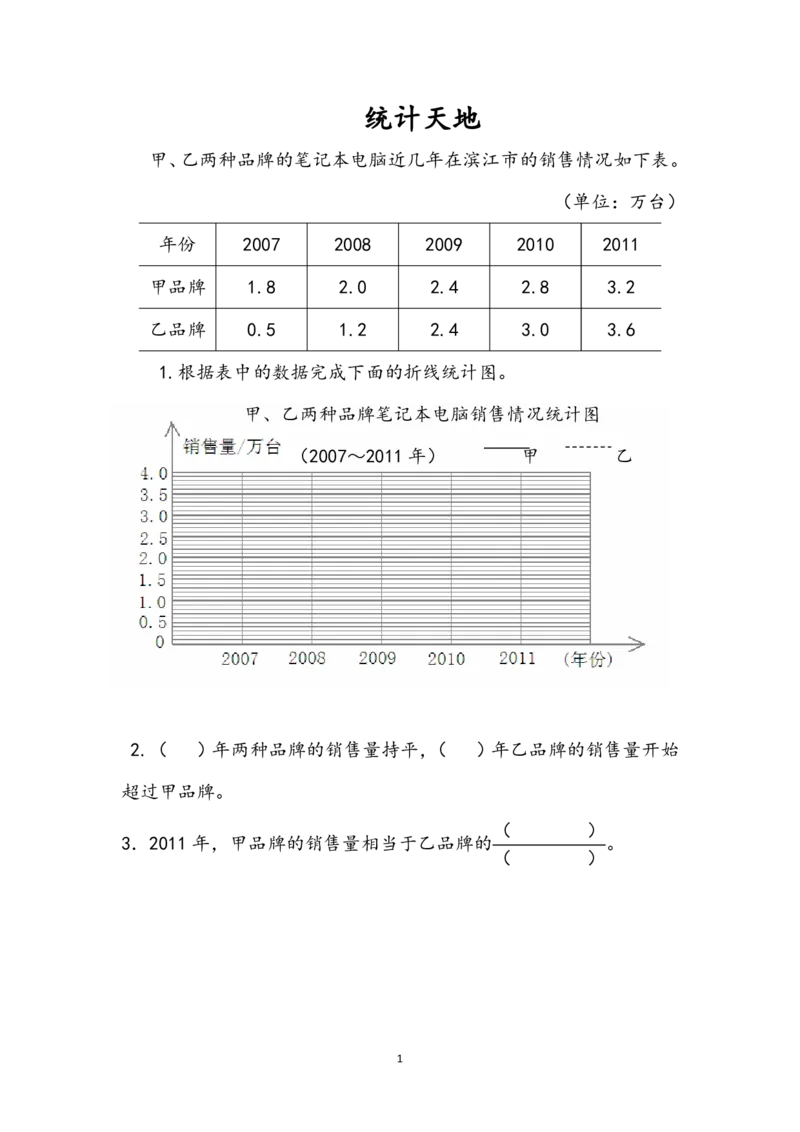
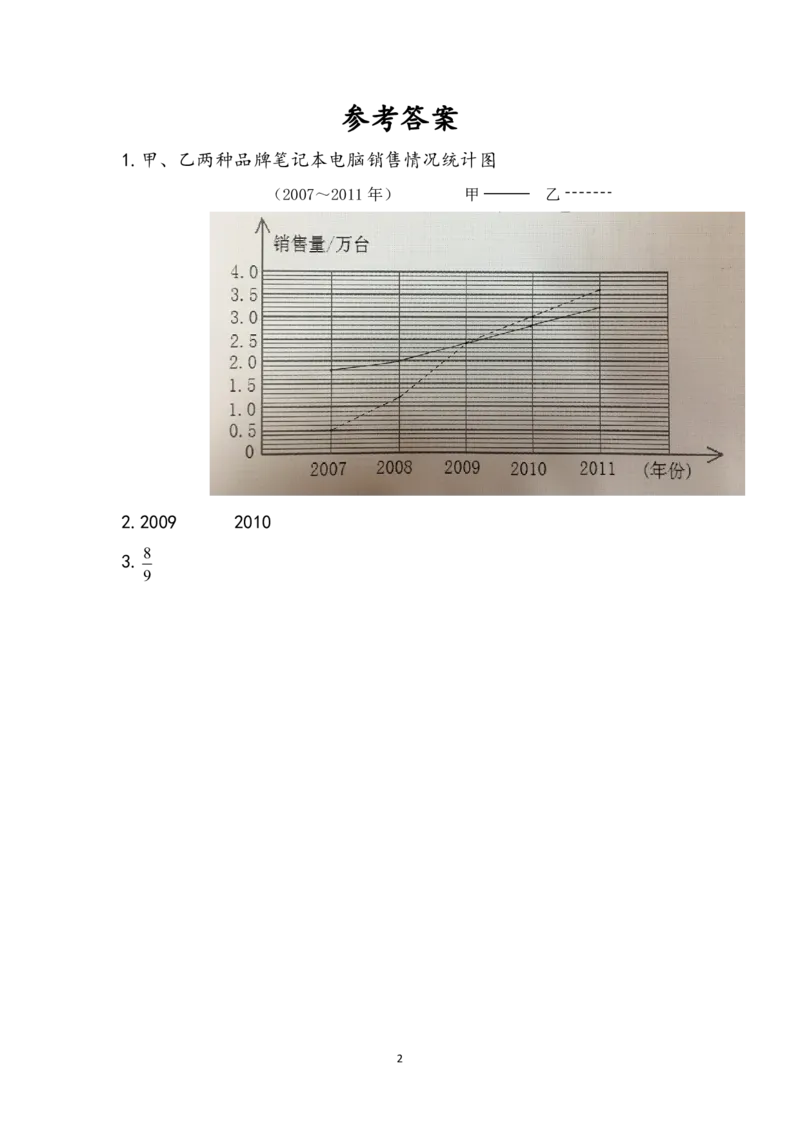
甲、乙两种品牌的笔记本电脑近几年在滨江市的销售情况如下表。
(单位:万台)
年份 2007 2008 2009 2010 2011
甲品牌 1.8 2.0 2.4 2.8 3.2
乙品牌 0.5 1.2 2.4 3.0 3.6
1.根据表中的数据完成下面的折线统计图。
甲、乙两种品牌笔记本电脑销售情况统计图
(2007~2011 年) 甲 乙
2.( )年两种品牌的销售量持平,( )年乙品牌的销售量开始
超过甲品牌。
( )
3.2011 年,甲品牌的销售量相当于乙品牌的 。
( )
1参考答案
1.甲、乙两种品牌笔记本电脑销售情况统计图
(2007~2011年) 甲 乙
2.2009 2010
8
3.
9
2应用广角
1.11 只李子的重量等于 2 只苹果和 1 只桃子的重量,2 只李子和 1 只
苹果的重量等于 1 只桃子的重量,那么,一只桃子的重量等于
( )只李子的重量。
2. 王师傅 8 天上一次夜班,李师傅 6 天上一次夜班。3 月 2 日他们
二人同时上夜班,至少经过( )天,他们两人同时上夜班。
3. 一辆公共汽车从起点站开出时车上有一些乘客。到了第二站,先
下车 5 人,又上车 8 人;到了第三站,先下车 4 人,上车 10 人,这
时车上共有乘客 26 人。这辆车从起点站开出时车上有多少人?
参考答案
1.5
2.24
3. 36-10+4=30(人) 30-8+5=27(人)
答:这辆车从起点站开出时车上有 27 人。
1