文档内容
2020年云南省昆明市中考数学试卷
一、填空题(本大题共6小题,每小题3分,共18分)
1.(3分)|﹣10|= .
2.(3分)分解因式:m2n﹣4n= .
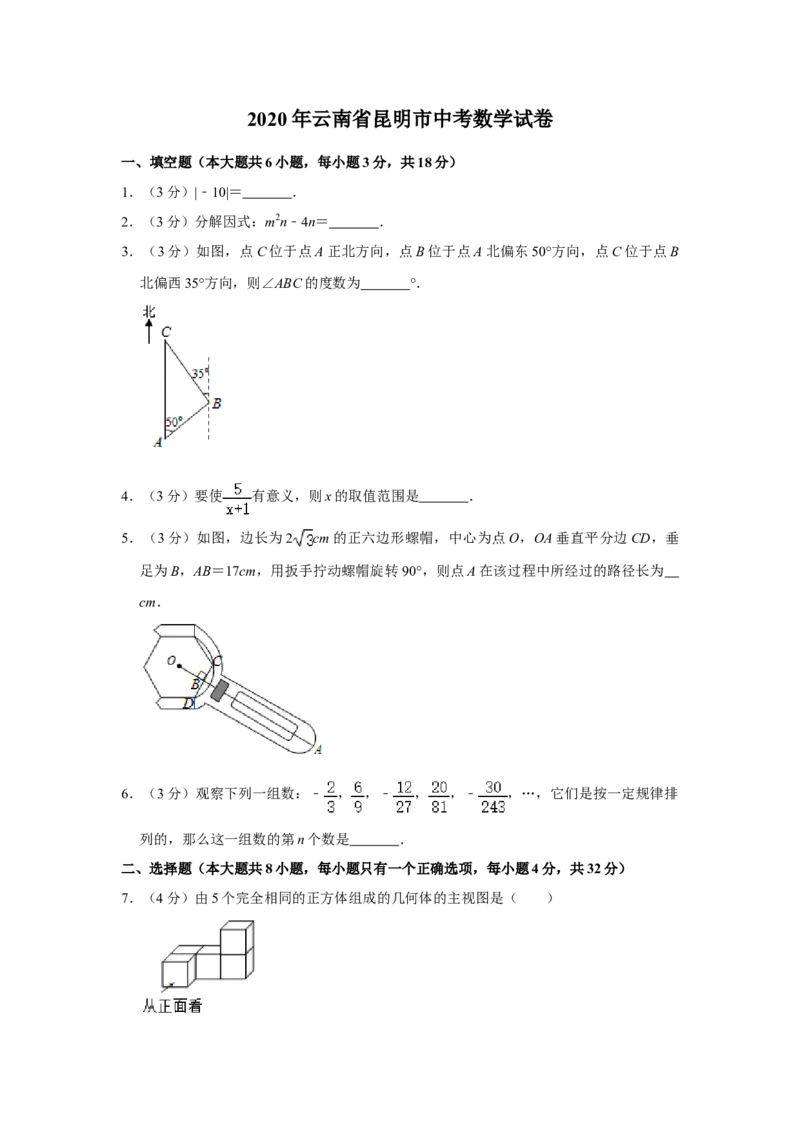
3.(3分)如图,点C位于点A正北方向,点B位于点A北偏东50°方向,点C位于点B
北偏西35°方向,则∠ABC的度数为 °.
4.(3分)要使 有意义,则x的取值范围是 .
5.(3分)如图,边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂
足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为
cm.
6.(3分)观察下列一组数:﹣ , ,﹣ , ,﹣ ,…,它们是按一定规律排
列的,那么这一组数的第n个数是 .
二、选择题(本大题共8小题,每小题只有一个正确选项,每小题4分,共32分)
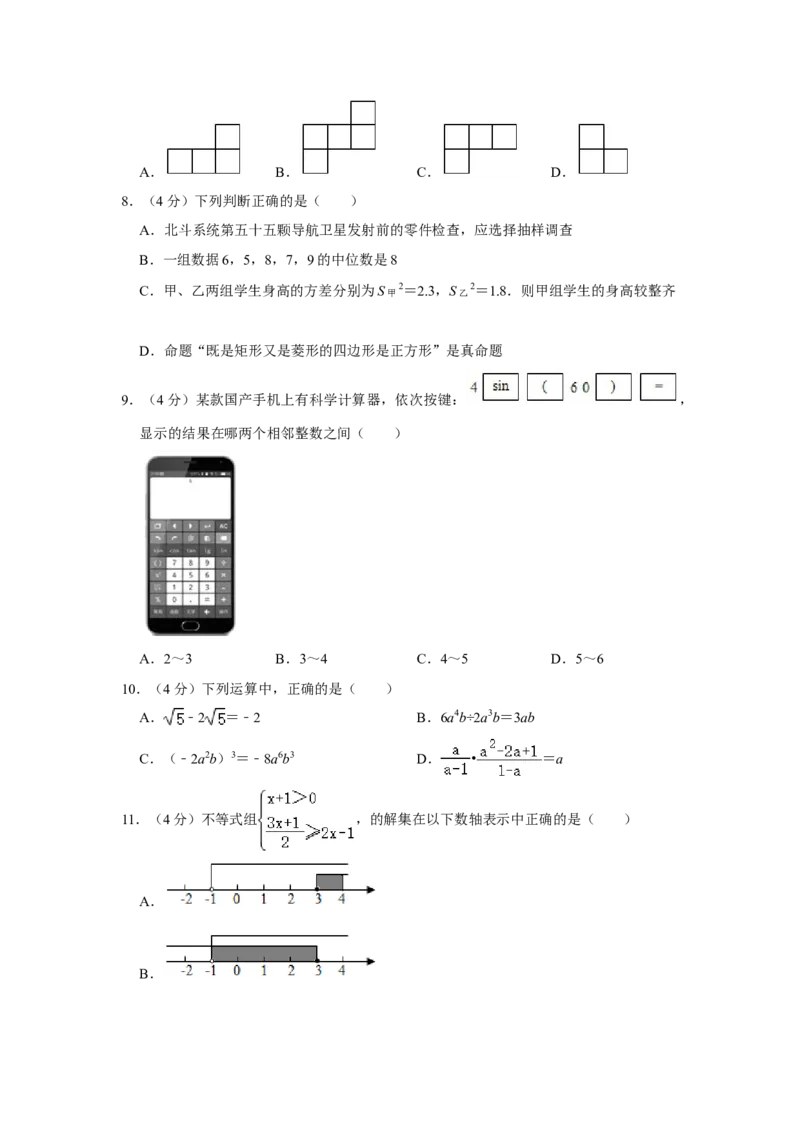
7.(4分)由5个完全相同的正方体组成的几何体的主视图是( )A. B. C. D.
8.(4分)下列判断正确的是( )
A.北斗系统第五十五颗导航卫星发射前的零件检查,应选择抽样调查
B.一组数据6,5,8,7,9的中位数是8
C.甲、乙两组学生身高的方差分别为S甲 2=2.3,S乙 2=1.8.则甲组学生的身高较整齐
D.命题“既是矩形又是菱形的四边形是正方形”是真命题
9.(4分)某款国产手机上有科学计算器,依次按键: ,
显示的结果在哪两个相邻整数之间( )
A.2~3 B.3~4 C.4~5 D.5~6
10.(4分)下列运算中,正确的是( )
A. ﹣2 =﹣2 B.6a4b÷2a3b=3ab
C.(﹣2a2b)3=﹣8a6b3 D. • =a
11.(4分)不等式组 ,的解集在以下数轴表示中正确的是( )
A.
B.C.
D.
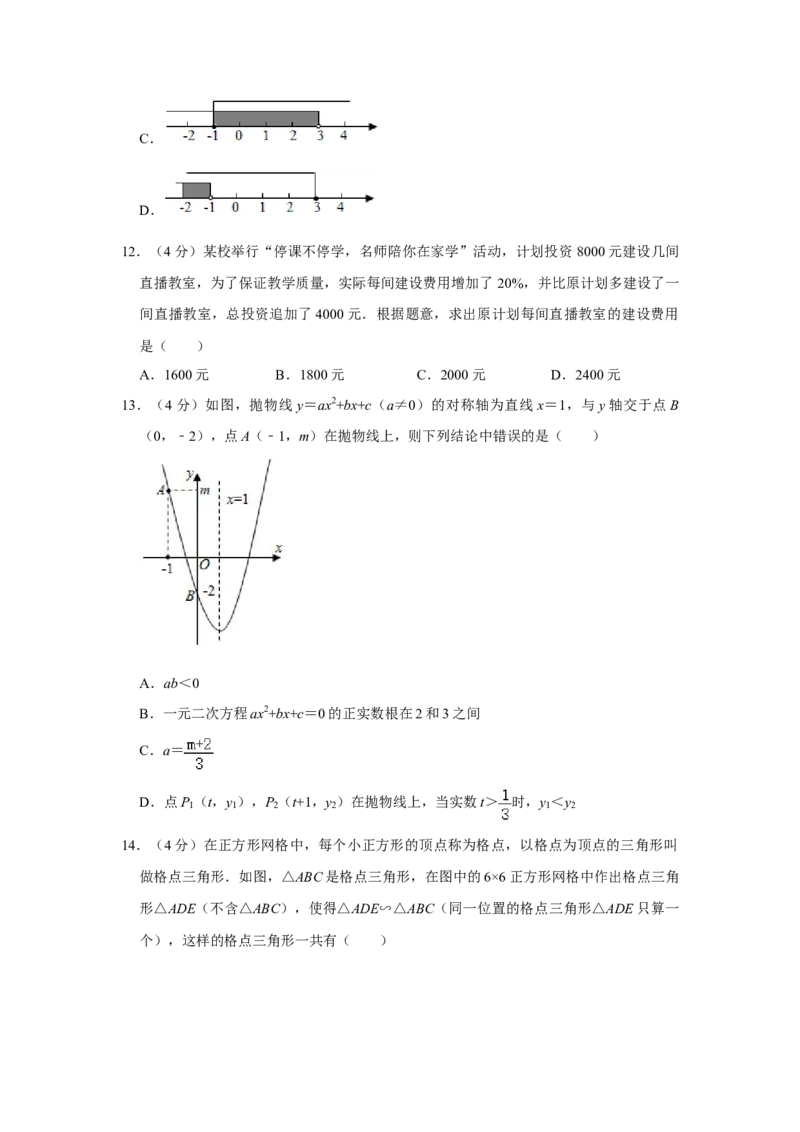
12.(4分)某校举行“停课不停学,名师陪你在家学”活动,计划投资 8000元建设几间
直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了一
间直播教室,总投资追加了4000元.根据题意,求出原计划每间直播教室的建设费用
是( )
A.1600元 B.1800元 C.2000元 D.2400元
13.(4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B
(0,﹣2),点A(﹣1,m)在抛物线上,则下列结论中错误的是( )
A.ab<0
B.一元二次方程ax2+bx+c=0的正实数根在2和3之间
C.a=
D.点P (t,y ),P (t+1,y )在抛物线上,当实数t> 时,y <y
1 1 2 2 1 2
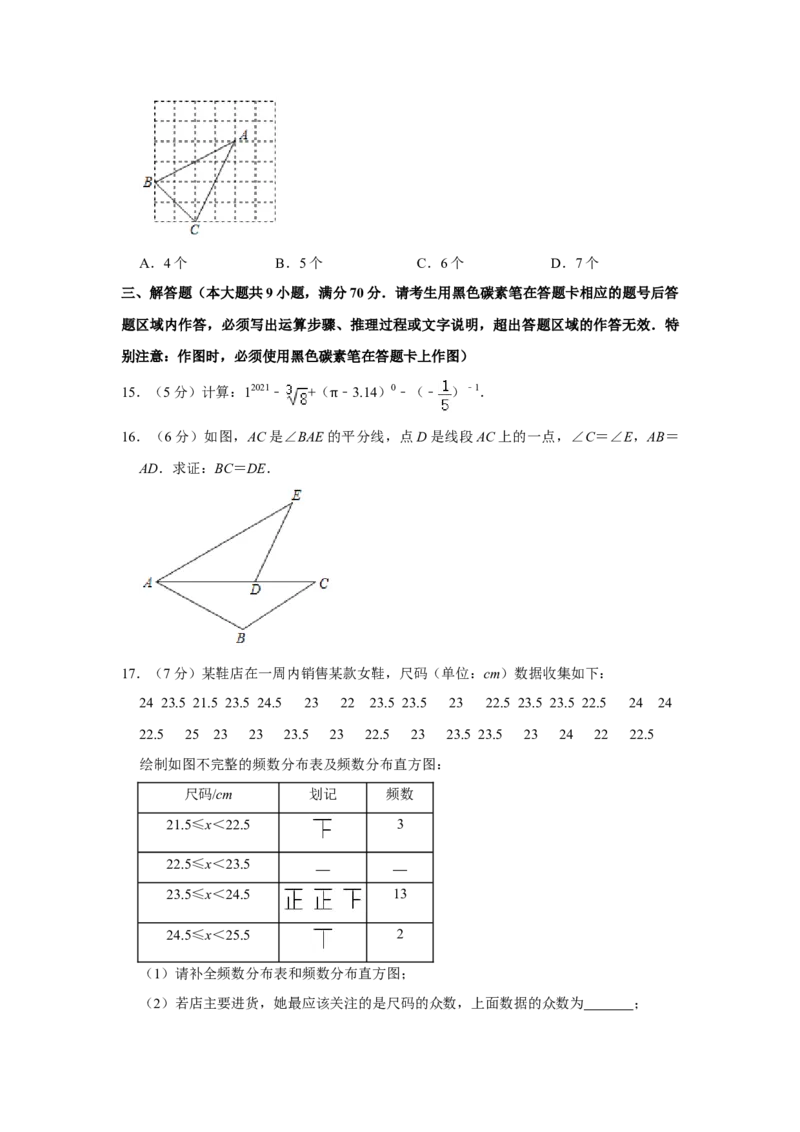
14.(4分)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫
做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角
形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一
个),这样的格点三角形一共有( )A.4个 B.5个 C.6个 D.7个
三、解答题(本大题共9小题,满分70分.请考生用黑色碳素笔在答题卡相应的题号后答
题区域内作答,必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效.特
别注意:作图时,必须使用黑色碳素笔在答题卡上作图)
15.(5分)计算:12021﹣ +( ﹣3.14)0﹣(﹣ )﹣1.
π
16.(6分)如图,AC是∠BAE的平分线,点D是线段AC上的一点,∠C=∠E,AB=
AD.求证:BC=DE.
17.(7分)某鞋店在一周内销售某款女鞋,尺码(单位:cm)数据收集如下:
24 23.5 21.5 23.5 24.5 23 22 23.5 23.5 23 22.5 23.5 23.5 22.5 24 24
22.5 25 23 23 23.5 23 22.5 23 23.5 23.5 23 24 22 22.5
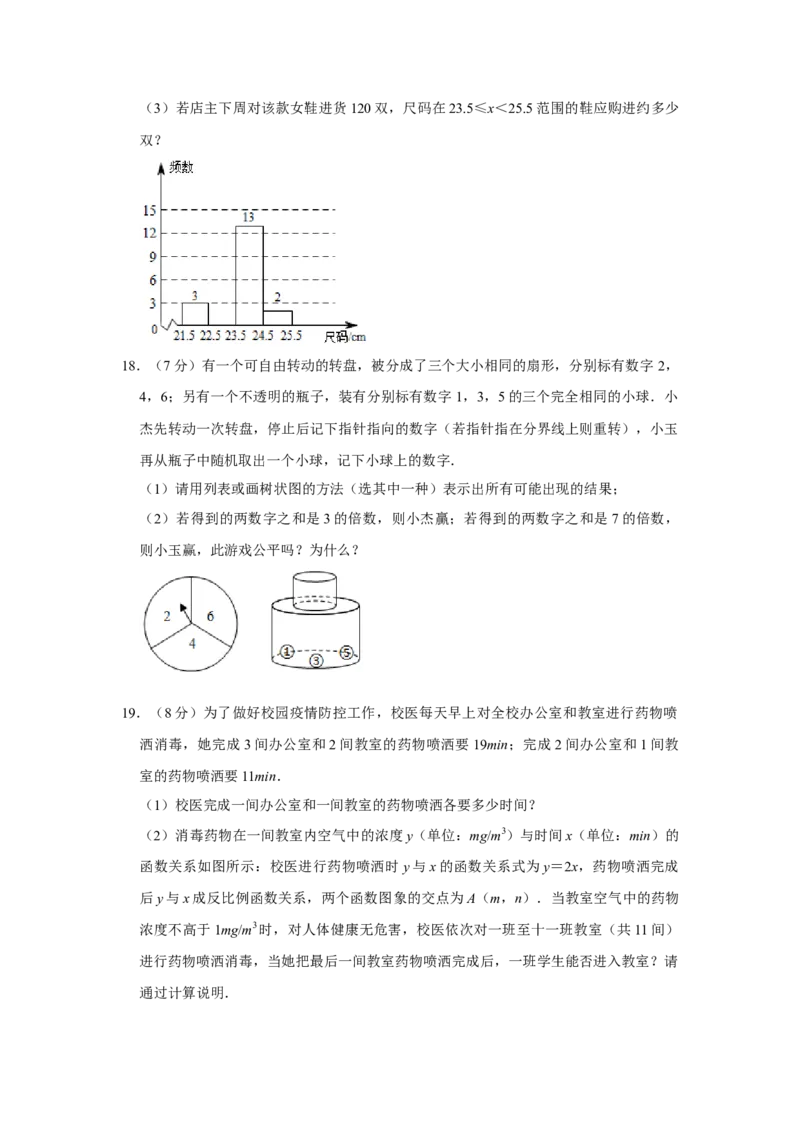
绘制如图不完整的频数分布表及频数分布直方图:
尺码/cm 划记 频数
21.5≤x<22.5 3
22.5≤x<23.5
23.5≤x<24.5 13
24.5≤x<25.5 2
(1)请补全频数分布表和频数分布直方图;
(2)若店主要进货,她最应该关注的是尺码的众数,上面数据的众数为 ;(3)若店主下周对该款女鞋进货120双,尺码在23.5≤x<25.5范围的鞋应购进约多少
双?
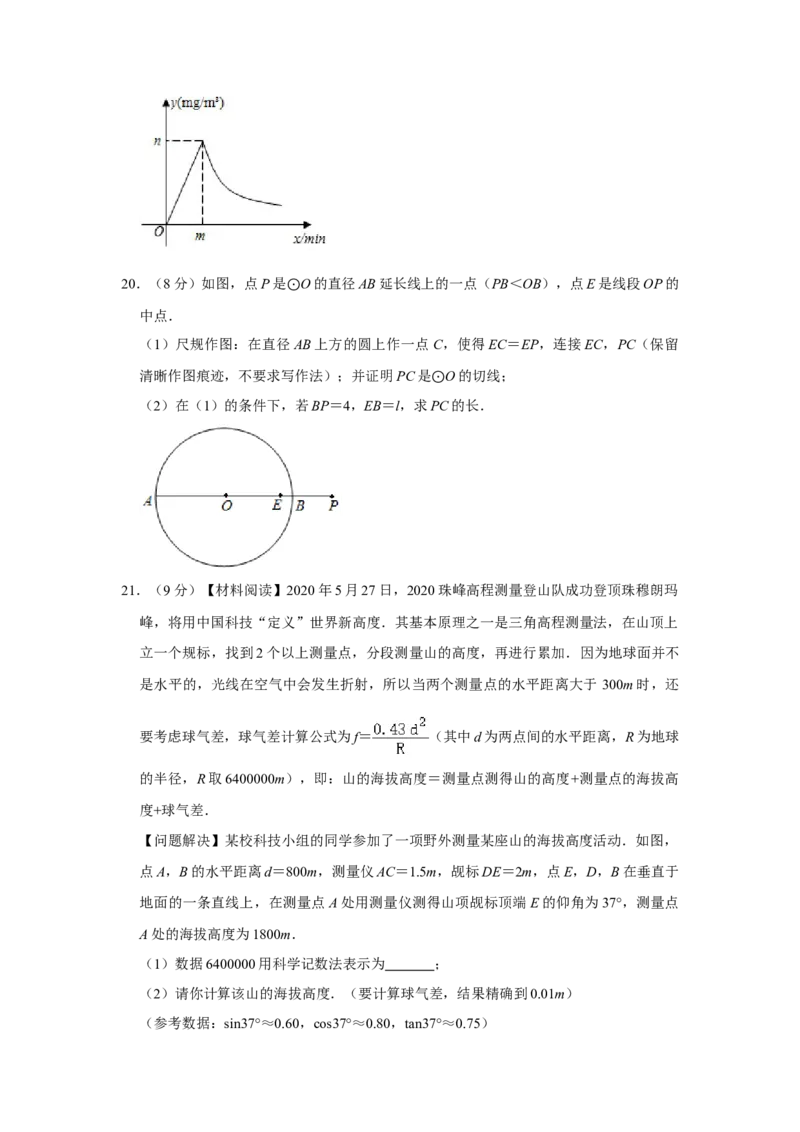
18.(7分)有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字 2,
4,6;另有一个不透明的瓶子,装有分别标有数字 1,3,5的三个完全相同的小球.小
杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉
再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
(2)若得到的两数字之和是3的倍数,则小杰贏;若得到的两数字之和是7的倍数,
则小玉赢,此游戏公平吗?为什么?
19.(8分)为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷
洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教
室的药物喷洒要11min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
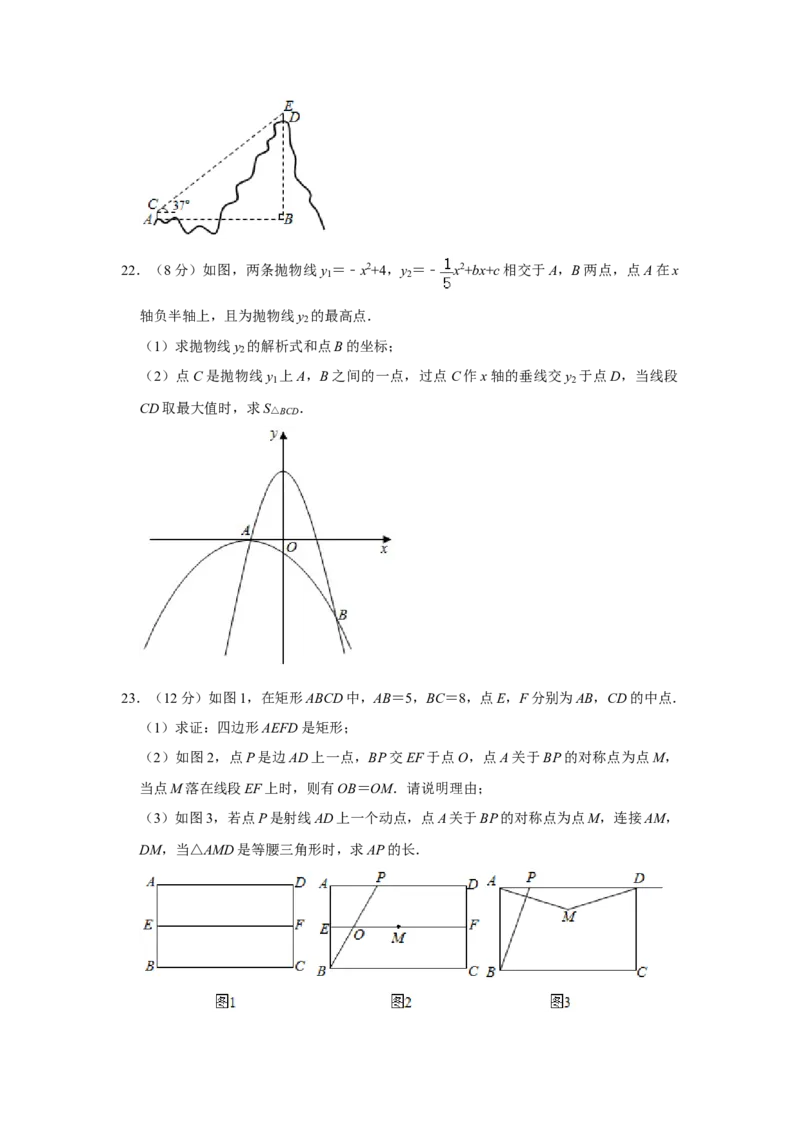
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的
函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成
后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物
浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)
进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请
通过计算说明.20.(8分)如图,点P是 O的直径AB延长线上的一点(PB<OB),点E是线段OP的
中点. ⊙
(1)尺规作图:在直径AB上方的圆上作一点C,使得EC=EP,连接EC,PC(保留
清晰作图痕迹,不要求写作法);并证明PC是 O的切线;
(2)在(1)的条件下,若BP=4,EB=l,求P⊙C的长.
21.(9分)【材料阅读】2020年5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛
峰,将用中国科技“定义”世界新高度.其基本原理之一是三角高程测量法,在山顶上
立一个规标,找到2个以上测量点,分段测量山的高度,再进行累加.因为地球面并不
是水平的,光线在空气中会发生折射,所以当两个测量点的水平距离大于 300m时,还
要考虑球气差,球气差计算公式为f= (其中d为两点间的水平距离,R为地球
的半径,R取6400000m),即:山的海拔高度=测量点测得山的高度+测量点的海拔高
度+球气差.
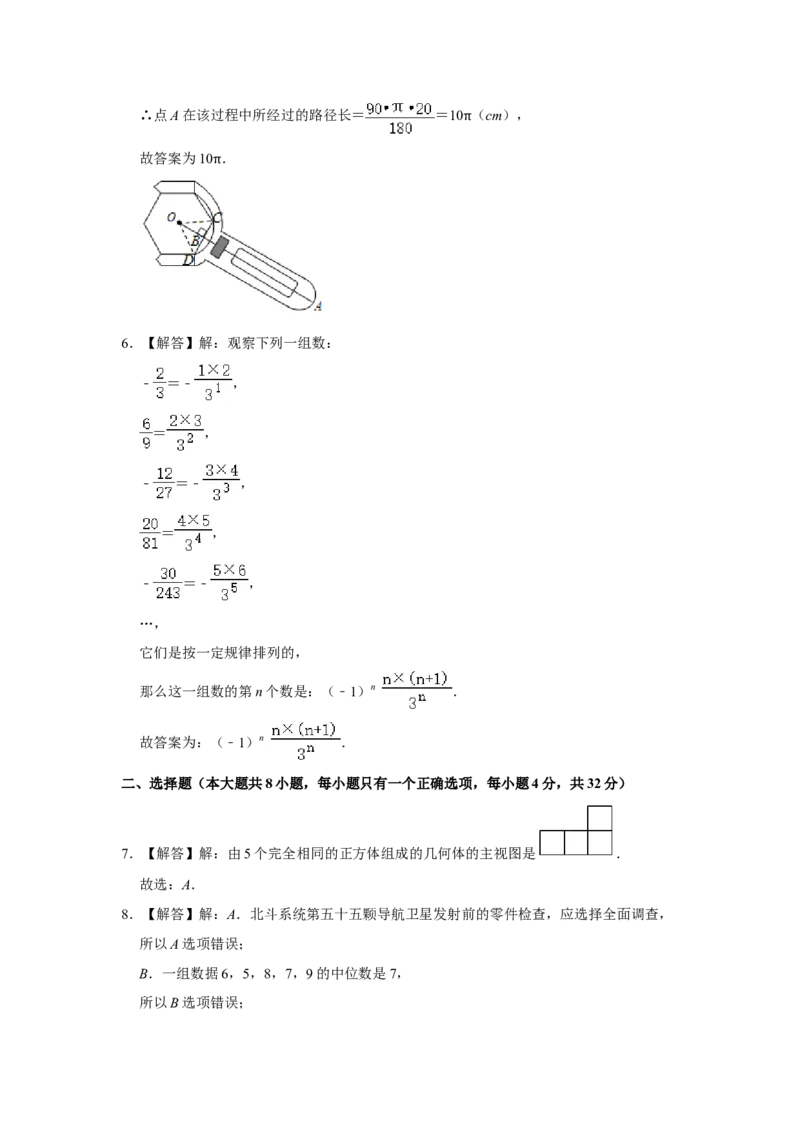
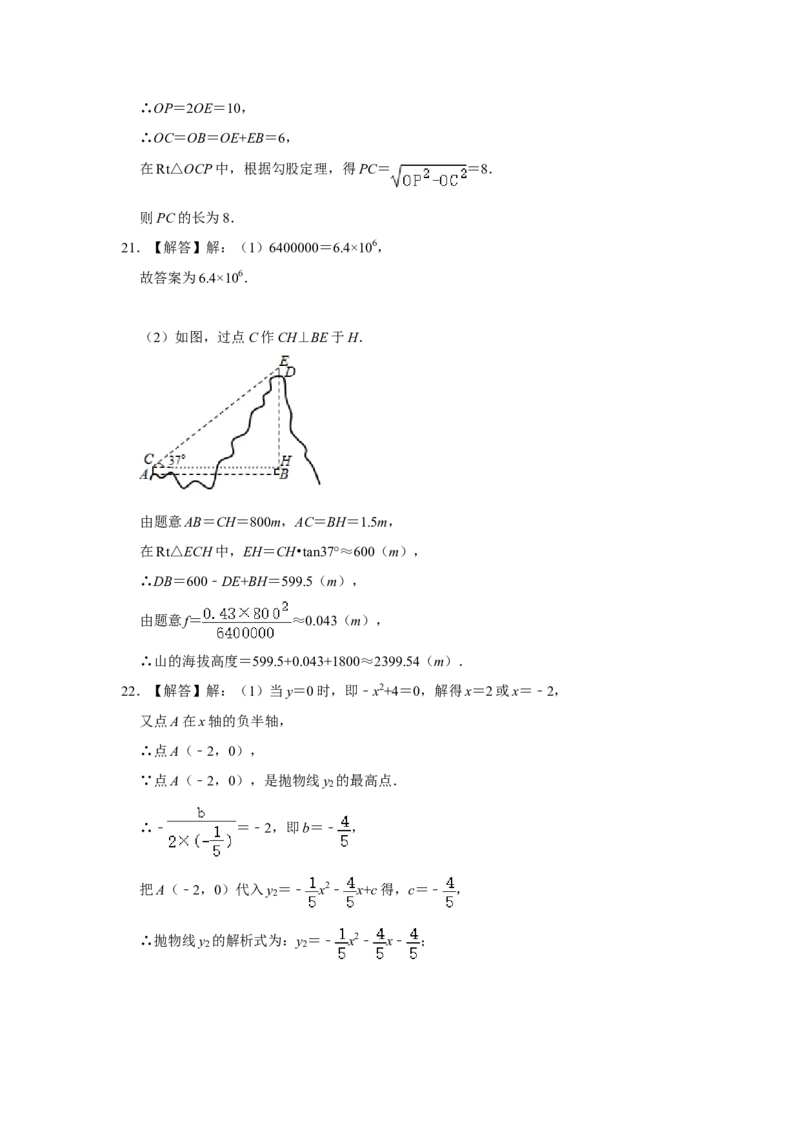
【问题解决】某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图,
点A,B的水平距离d=800m,测量仪AC=1.5m,觇标DE=2m,点E,D,B在垂直于
地面的一条直线上,在测量点A处用测量仪测得山项觇标顶端E的仰角为37°,测量点
A处的海拔高度为1800m.
(1)数据6400000用科学记数法表示为 ;
(2)请你计算该山的海拔高度.(要计算球气差,结果精确到0.01m)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)22.(8分)如图,两条抛物线y =﹣x2+4,y =﹣ x2+bx+c相交于A,B两点,点A在x
1 2
轴负半轴上,且为抛物线y 的最高点.
2
(1)求抛物线y 的解析式和点B的坐标;
2
(2)点C是抛物线y 上A,B之间的一点,过点C作x轴的垂线交y 于点D,当线段
1 2
CD取最大值时,求S△BCD .
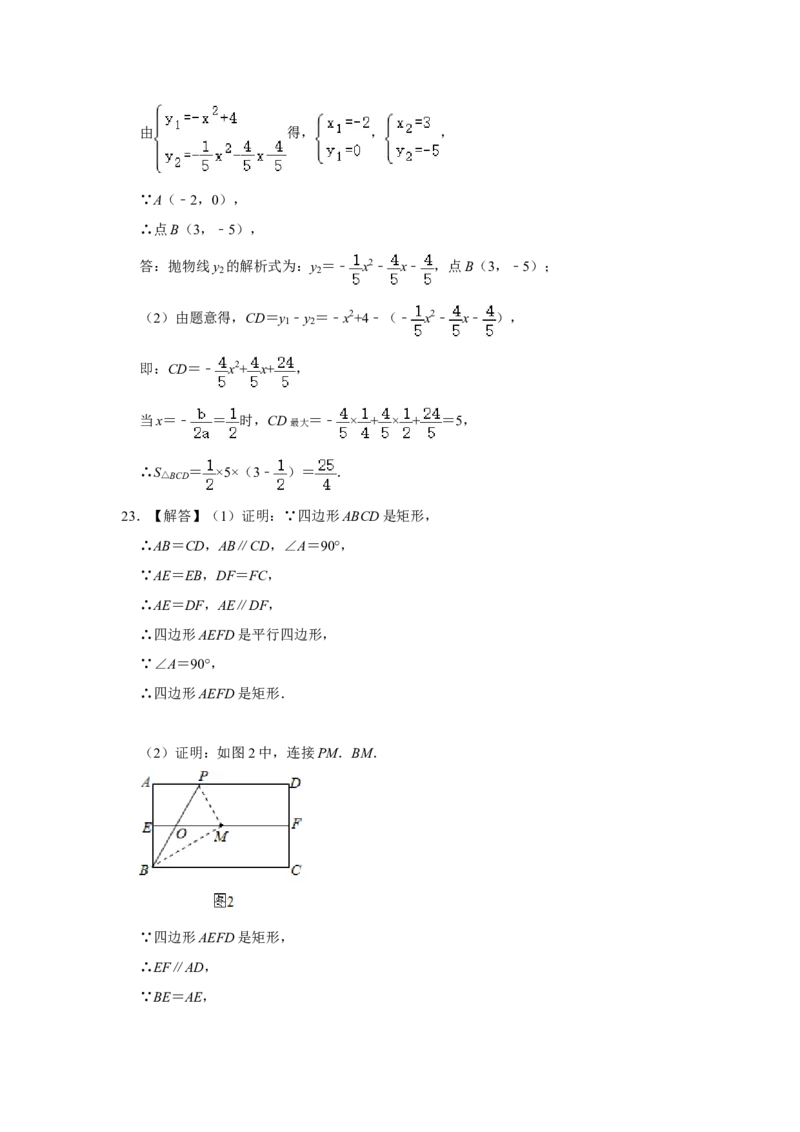
23.(12分)如图1,在矩形ABCD中,AB=5,BC=8,点E,F分别为AB,CD的中点.
(1)求证:四边形AEFD是矩形;
(2)如图2,点P是边AD上一点,BP交EF于点O,点A关于BP的对称点为点M,
当点M落在线段EF上时,则有OB=OM.请说明理由;
(3)如图3,若点P是射线AD上一个动点,点A关于BP的对称点为点M,连接AM,
DM,当△AMD是等腰三角形时,求AP的长.2020年云南省昆明市中考数学试卷
参考答案与试题解析
一、填空题(本大题共6小题,每小题3分,共18分)
1.【解答】解:根据负数的绝对值等于它的相反数,得|﹣10|=10.
故答案为:10.
2.【解答】解:原式=n(m2﹣4)=n(m+2)(m﹣2),
故答案为:n(m+2)(m﹣2)
3.【解答】解:如图所示:由题意可得,∠1=∠A=50°,
则∠ABC=180°﹣35°﹣50°=95°.
故答案为:95.
4.【解答】解:要使分式 有意义,
需满足x+1≠0.
即x≠﹣1.
故答案为:x≠﹣1.
5.【解答】解:连接OD,OC.
∵∠DOC=60°,OD=OC,
∴△ODC是等边三角形,
∴OD=OC=DC=2 (cm),
∵OB⊥CD,
∴BC=BD= (cm),
∴OB= BC=3(cm),
∵AB=17cm,
∴OA=OB+AB=20(cm),∴点A在该过程中所经过的路径长= =10 (cm),
π
故答案为10 .
π
6.【解答】解:观察下列一组数:
﹣ =﹣ ,
= ,
﹣ =﹣ ,
= ,
﹣ =﹣ ,
…,
它们是按一定规律排列的,
那么这一组数的第n个数是:(﹣1)n .
故答案为:(﹣1)n .
二、选择题(本大题共8小题,每小题只有一个正确选项,每小题4分,共32分)
7.【解答】解:由5个完全相同的正方体组成的几何体的主视图是 .
故选:A.
8.【解答】解:A.北斗系统第五十五颗导航卫星发射前的零件检查,应选择全面调查,
所以A选项错误;
B.一组数据6,5,8,7,9的中位数是7,
所以B选项错误;C.甲、乙两组学生身高的方差分别为S甲 2=2.3,S乙 2=1.8.则乙组学生的身高较整齐,
所以C选项错误;
D.命题“既是矩形又是菱形的四边形是正方形”是真命题,
所以D选项正确.
故选:D.
9.【解答】解:使用计算器计算得,
4sin60°≈3.464101615,
故选:B.
10.【解答】解:A、 ﹣2 =﹣ ,此选项错误,不合题意;
B、6a4b÷2a3b=3a,此选项错误,不合题意;
C、(﹣2a2b)3=﹣8a6b3,正确;
D、 • = • =﹣a,故此选项错误,不合题意;
故选:C.
11.【解答】解: ,
∵解不等式 得:x>﹣1,
解不等式 ①得:x≤3,
∴不等式②组的解集是﹣1<x≤3,
在数轴上表示为: ,
故选:B.
12.【解答】解:设原计划每间直播教室的建设费用是 x元,则实际每间建设费用为
1.2x,根据题意得:
,
解得:x=2000,
经检验:x=2000是原方程的解,
答:每间直播教室的建设费用是2000元,
故选:C.
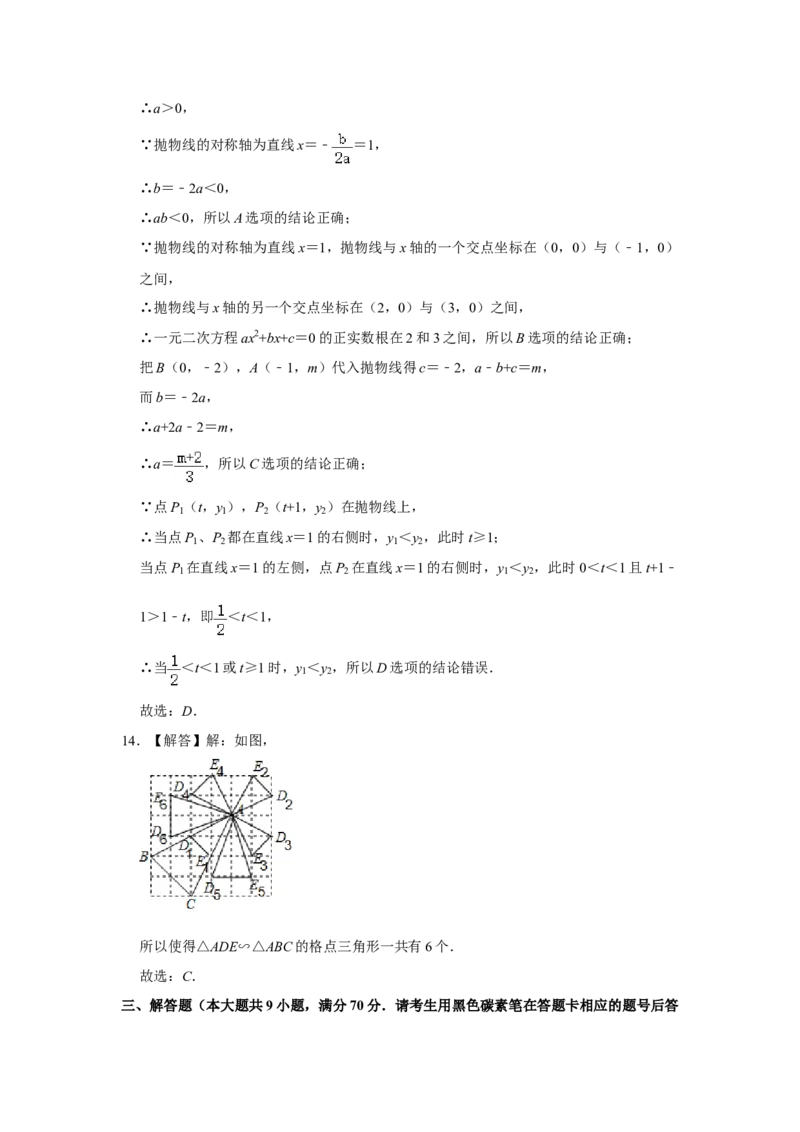
13.【解答】解:∵抛物线开口向上,∴a>0,
∵抛物线的对称轴为直线x=﹣ =1,
∴b=﹣2a<0,
∴ab<0,所以A选项的结论正确;
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标在(0,0)与(﹣1,0)
之间,
∴抛物线与x轴的另一个交点坐标在(2,0)与(3,0)之间,
∴一元二次方程ax2+bx+c=0的正实数根在2和3之间,所以B选项的结论正确;
把B(0,﹣2),A(﹣1,m)代入抛物线得c=﹣2,a﹣b+c=m,
而b=﹣2a,
∴a+2a﹣2=m,
∴a= ,所以C选项的结论正确;
∵点P (t,y ),P (t+1,y )在抛物线上,
1 1 2 2
∴当点P 、P 都在直线x=1的右侧时,y <y ,此时t≥1;
1 2 1 2
当点P 在直线x=1的左侧,点P 在直线x=1的右侧时,y <y ,此时0<t<1且t+1﹣
1 2 1 2
1>1﹣t,即 <t<1,
∴当 <t<1或t≥1时,y <y ,所以D选项的结论错误.
1 2
故选:D.
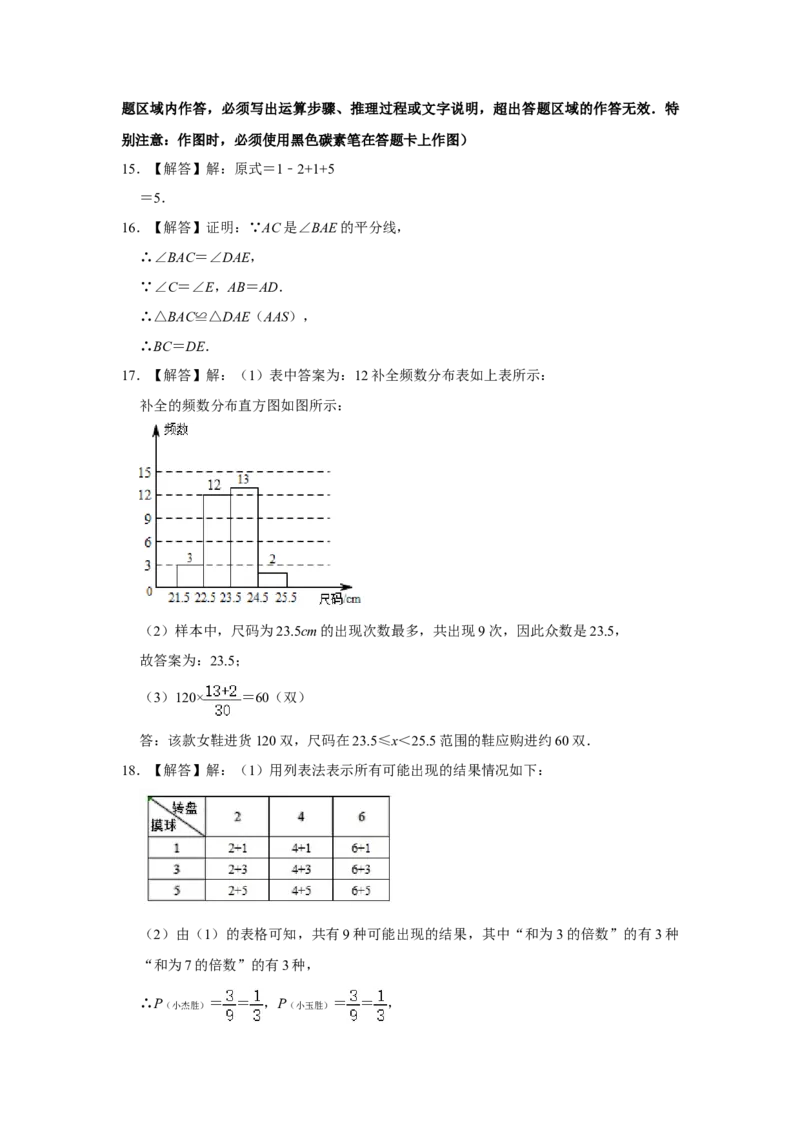
14.【解答】解:如图,
所以使得△ADE∽△ABC的格点三角形一共有6个.
故选:C.
三、解答题(本大题共9小题,满分70分.请考生用黑色碳素笔在答题卡相应的题号后答题区域内作答,必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效.特
别注意:作图时,必须使用黑色碳素笔在答题卡上作图)
15.【解答】解:原式=1﹣2+1+5
=5.
16.【解答】证明:∵AC是∠BAE的平分线,
∴∠BAC=∠DAE,
∵∠C=∠E,AB=AD.
∴△BAC≌△DAE(AAS),
∴BC=DE.
17.【解答】解:(1)表中答案为:12补全频数分布表如上表所示:
补全的频数分布直方图如图所示:
(2)样本中,尺码为23.5cm的出现次数最多,共出现9次,因此众数是23.5,
故答案为:23.5;
(3)120× =60(双)
答:该款女鞋进货120双,尺码在23.5≤x<25.5范围的鞋应购进约60双.
18.【解答】解:(1)用列表法表示所有可能出现的结果情况如下:
(2)由(1)的表格可知,共有9种可能出现的结果,其中“和为3的倍数”的有3种
“和为7的倍数”的有3种,
∴P(小杰胜) = = ,P(小玉胜) = = ,因此游戏是公平的.
19.【解答】解:(1)设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,
则 ,解得 ,
故校医完成一间办公室和一间教室的药物喷洒各要3min和5min;
(2)一间教室的药物喷洒时间为5min,则11个房间需要55min,
当x=5时,y=2x=10,故点A(5,10),
设反比例函数表达式为:y= ,将点A的坐标代入上式并解得:k=50,
故反比例函数表达式为y= ,
当x=55时,y= <1,
故一班学生能安全进入教室.
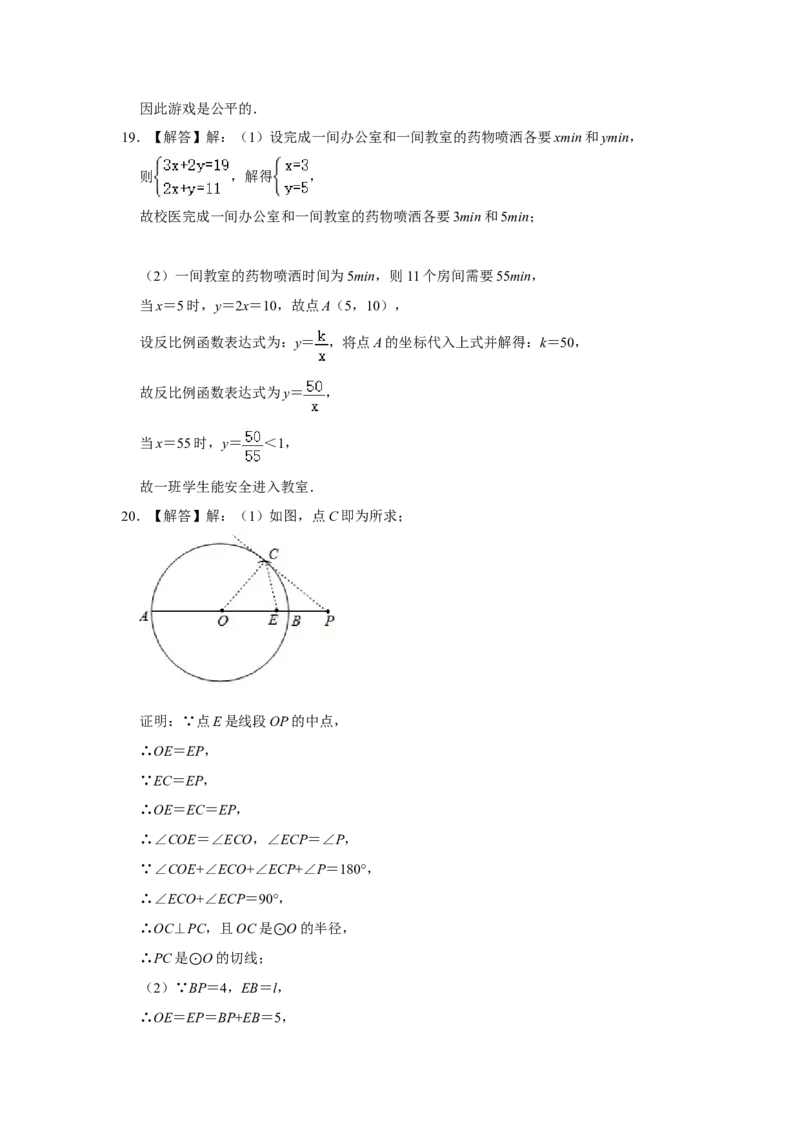
20.【解答】解:(1)如图,点C即为所求;
证明:∵点E是线段OP的中点,
∴OE=EP,
∵EC=EP,
∴OE=EC=EP,
∴∠COE=∠ECO,∠ECP=∠P,
∵∠COE+∠ECO+∠ECP+∠P=180°,
∴∠ECO+∠ECP=90°,
∴OC⊥PC,且OC是 O的半径,
∴PC是 O的切线;⊙
(2)∵⊙BP=4,EB=l,
∴OE=EP=BP+EB=5,∴OP=2OE=10,
∴OC=OB=OE+EB=6,
在Rt△OCP中,根据勾股定理,得PC= =8.
则PC的长为8.
21.【解答】解:(1)6400000=6.4×106,
故答案为6.4×106.
(2)如图,过点C作CH⊥BE于H.
由题意AB=CH=800m,AC=BH=1.5m,
在Rt△ECH中,EH=CH•tan37°≈600(m),
∴DB=600﹣DE+BH=599.5(m),
由题意f= ≈0.043(m),
∴山的海拔高度=599.5+0.043+1800≈2399.54(m).
22.【解答】解:(1)当y=0时,即﹣x2+4=0,解得x=2或x=﹣2,
又点A在x轴的负半轴,
∴点A(﹣2,0),
∵点A(﹣2,0),是抛物线y 的最高点.
2
∴﹣ =﹣2,即b=﹣ ,
把A(﹣2,0)代入y =﹣ x2﹣ x+c得,c=﹣ ,
2
∴抛物线y 的解析式为:y =﹣ x2﹣ x﹣ ;
2 2由 得, , ,
∵A(﹣2,0),
∴点B(3,﹣5),
答:抛物线y 的解析式为:y =﹣ x2﹣ x﹣ ,点B(3,﹣5);
2 2
(2)由题意得,CD=y ﹣y =﹣x2+4﹣(﹣ x2﹣ x﹣ ),
1 2
即:CD=﹣ x2+ x+ ,
当x=﹣ = 时,CD最大 =﹣ × + × + =5,
∴S△BCD = ×5×(3﹣ )= .
23.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠A=90°,
∵AE=EB,DF=FC,
∴AE=DF,AE∥DF,
∴四边形AEFD是平行四边形,
∵∠A=90°,
∴四边形AEFD是矩形.
(2)证明:如图2中,连接PM.BM.
∵四边形AEFD是矩形,
∴EF∥AD,
∵BE=AE,∴BO=OP,
由翻折可知,∠PMB=∠A=90°,
∴OM=OB=OP.
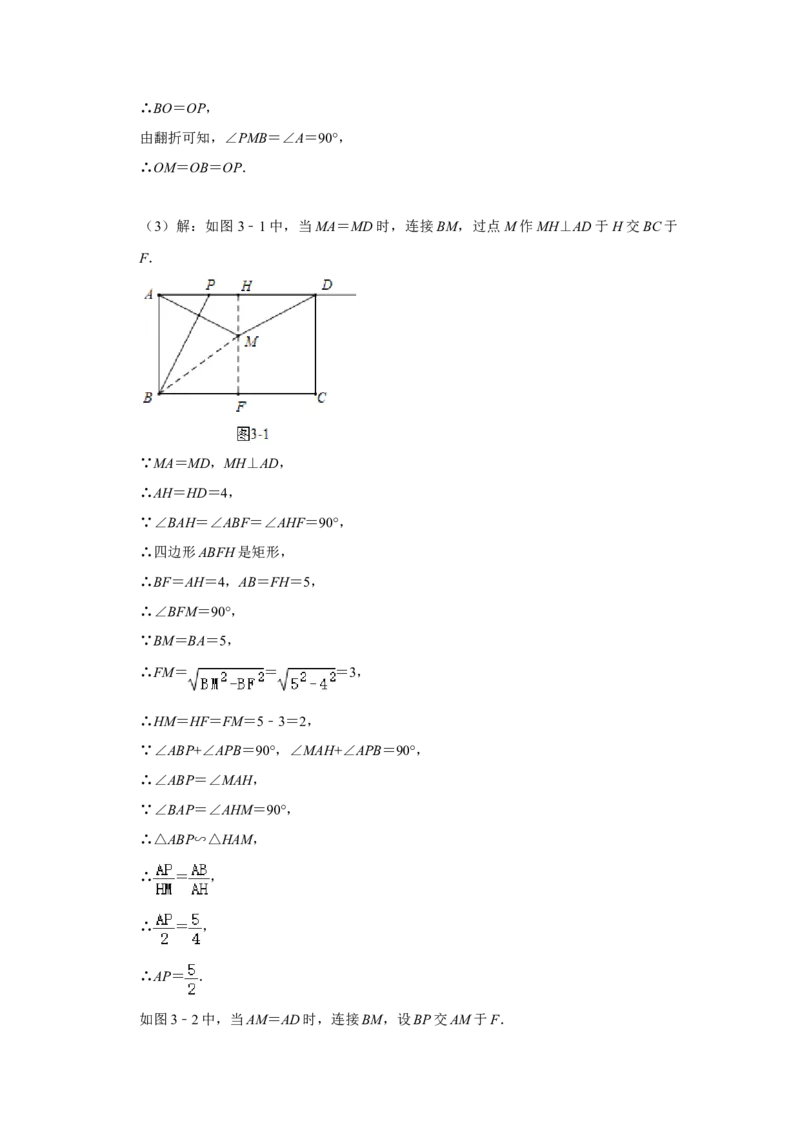
(3)解:如图3﹣1中,当MA=MD时,连接BM,过点M作MH⊥AD于H交BC于
F.
∵MA=MD,MH⊥AD,
∴AH=HD=4,
∵∠BAH=∠ABF=∠AHF=90°,
∴四边形ABFH是矩形,
∴BF=AH=4,AB=FH=5,
∴∠BFM=90°,
∵BM=BA=5,
∴FM= = =3,
∴HM=HF=FM=5﹣3=2,
∵∠ABP+∠APB=90°,∠MAH+∠APB=90°,
∴∠ABP=∠MAH,
∵∠BAP=∠AHM=90°,
∴△ABP∽△HAM,
∴ = ,
∴ = ,
∴AP= .
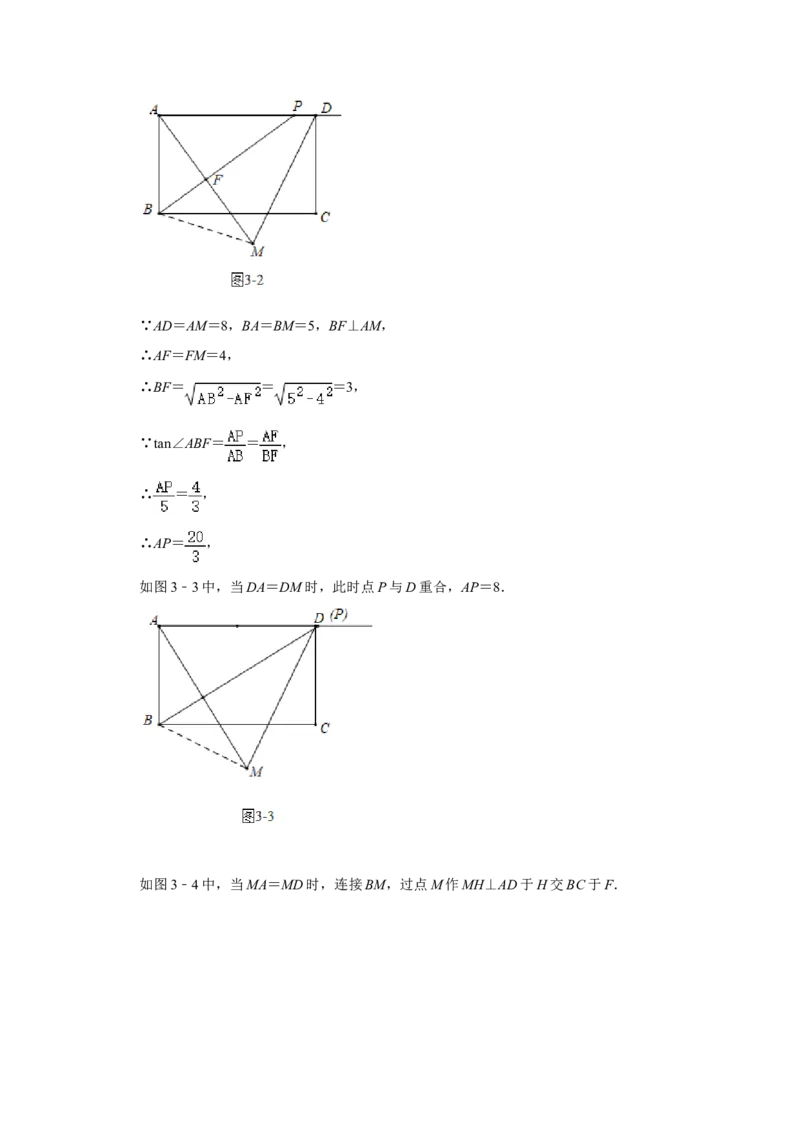
如图3﹣2中,当AM=AD时,连接BM,设BP交AM于F.∵AD=AM=8,BA=BM=5,BF⊥AM,
∴AF=FM=4,
∴BF= = =3,
∵tan∠ABF= = ,
∴ = ,
∴AP= ,
如图3﹣3中,当DA=DM时,此时点P与D重合,AP=8.
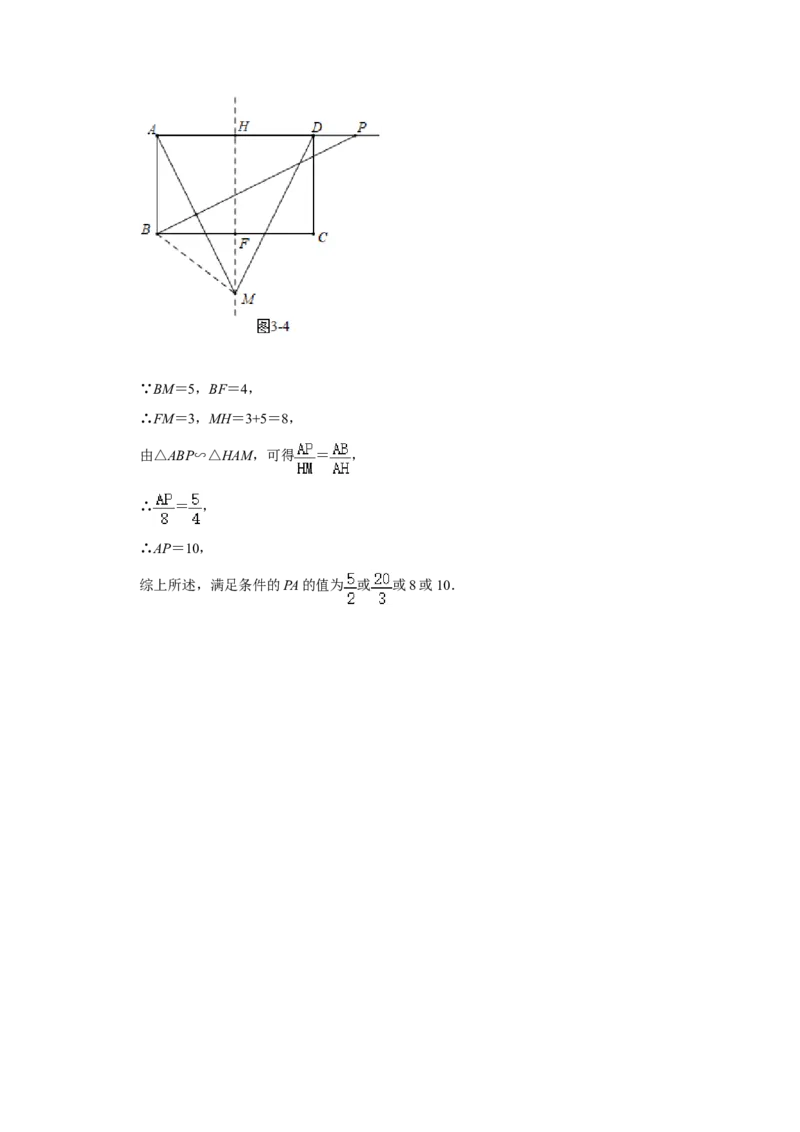
如图3﹣4中,当MA=MD时,连接BM,过点M作MH⊥AD于H交BC于F.∵BM=5,BF=4,
∴FM=3,MH=3+5=8,
由△ABP∽△HAM,可得 = ,
∴ = ,
∴AP=10,
综上所述,满足条件的PA的值为 或 或8或10.