文档内容
2020年吉林省中考数学试卷
一、选择题(共6小题).
1.﹣6的相反数是( )
A.6 B.﹣6 C. D.
2.国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少
11090000,脱贫攻坚取得决定性成就.数据11090000用科学记数法表示为( )
A.11.09×106 B.1.109×107 C.1.109×108 D.0.1109×108
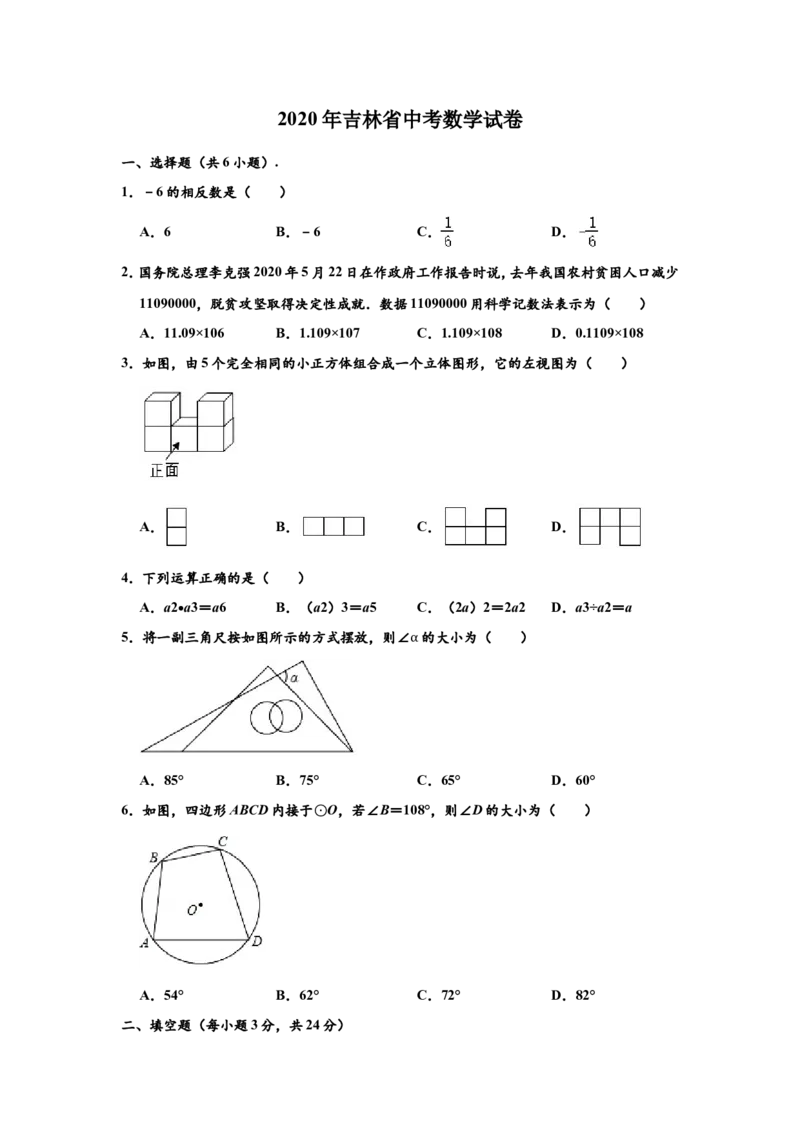
3.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为( )
A. B. C. D.
4.下列运算正确的是( )
A.a2•a3=a6 B.(a2)3=a5 C.(2a)2=2a2 D.a3÷a2=a
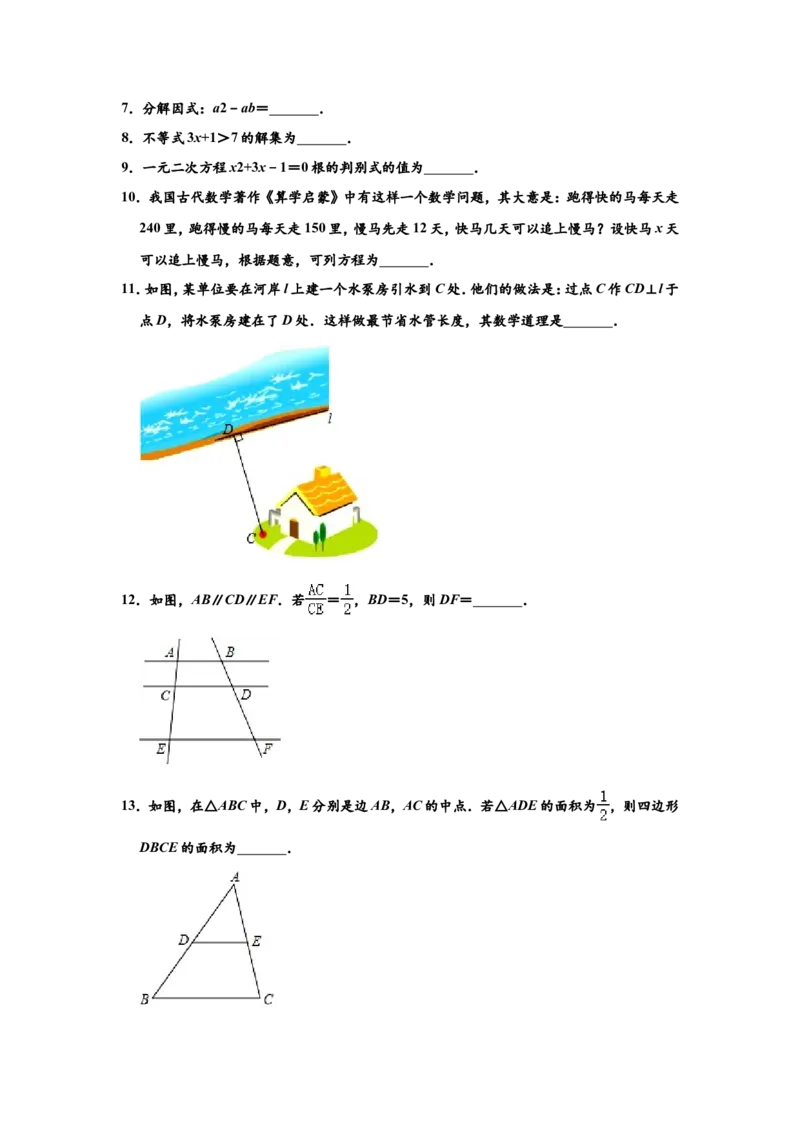
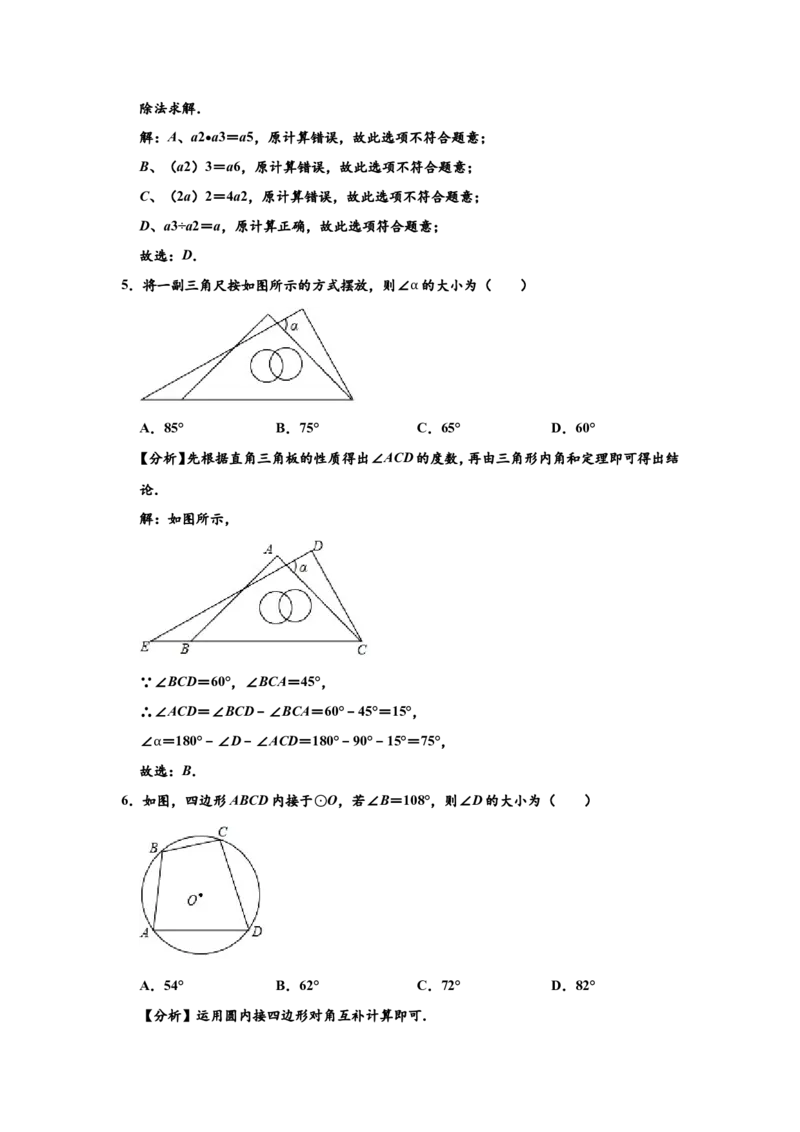
5.将一副三角尺按如图所示的方式摆放,则∠ 的大小为( )
α
A.85° B.75° C.65° D.60°
6.如图,四边形ABCD内接于 O,若∠B=108°,则∠D的大小为( )
⊙
A.54° B.62° C.72° D.82°
二、填空题(每小题3分,共24分)7.分解因式:a2﹣ab= .
8.不等式3x+1>7的解集为 .
9.一元二次方程x2+3x﹣1=0根的判别式的值为 .
10.我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走
240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?设快马x天
可以追上慢马,根据题意,可列方程为 .
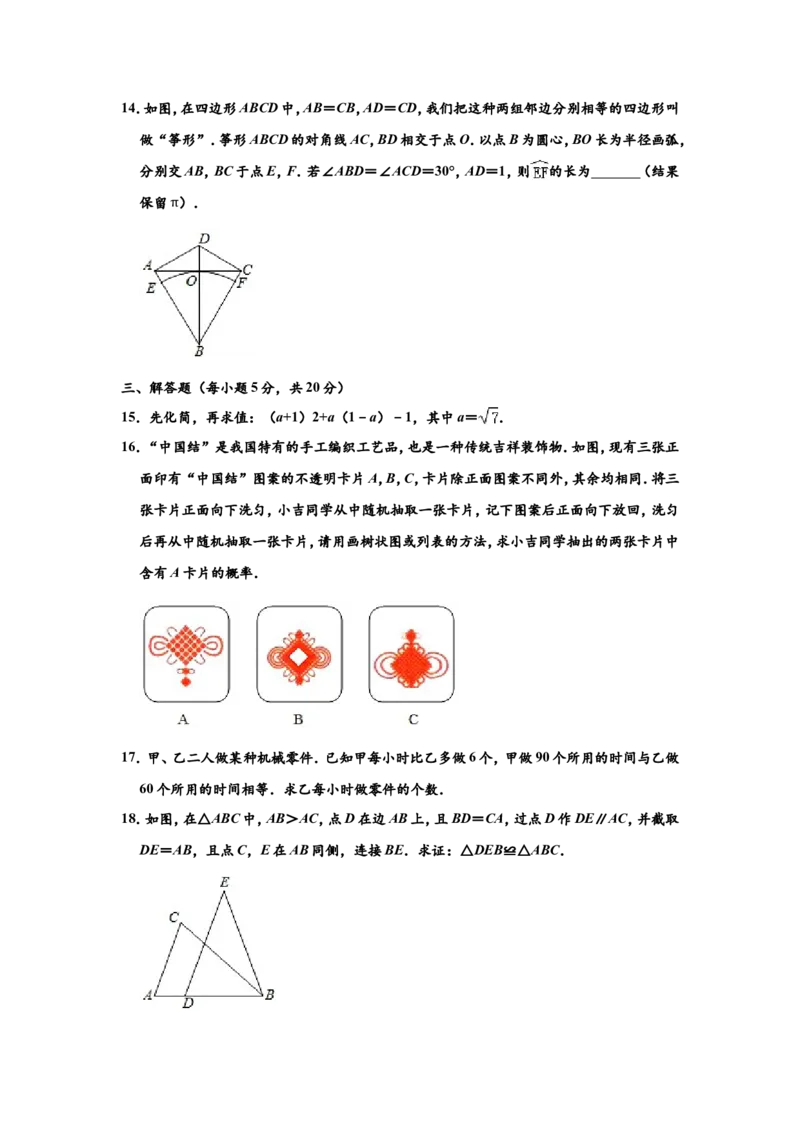
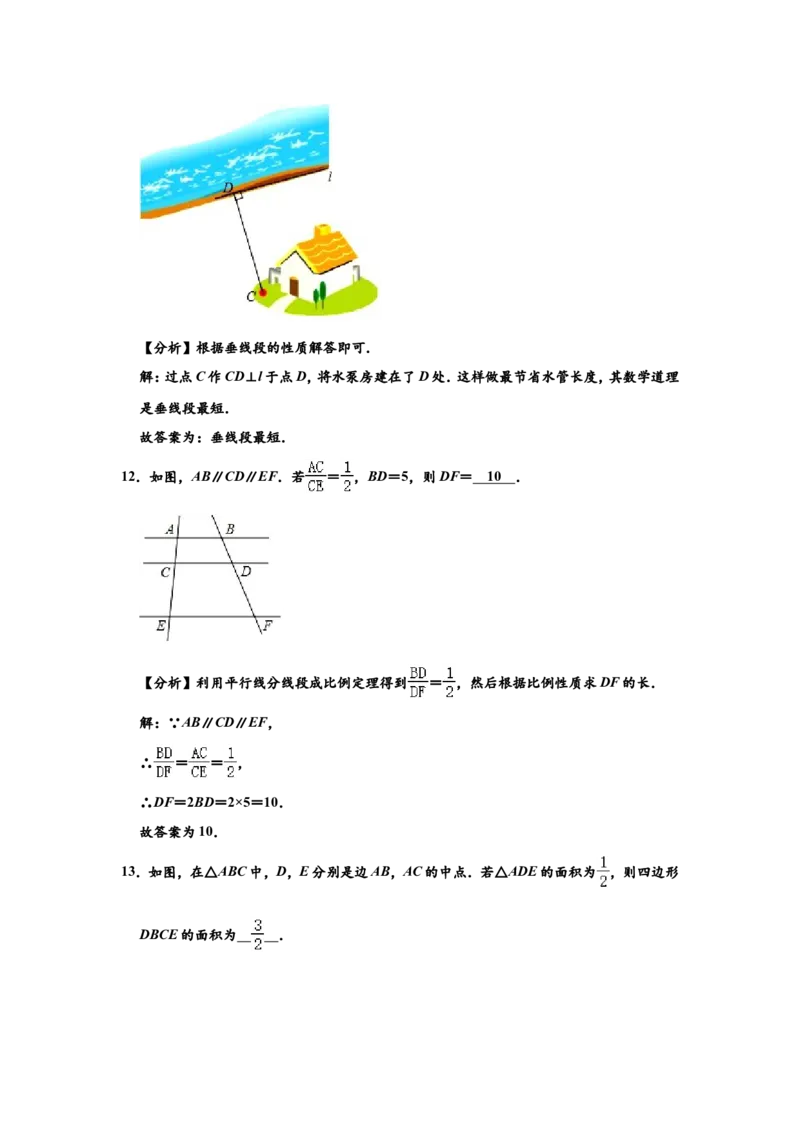
11.如图,某单位要在河岸l上建一个水泵房引水到C处.他们的做法是:过点C作CD⊥l于
点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
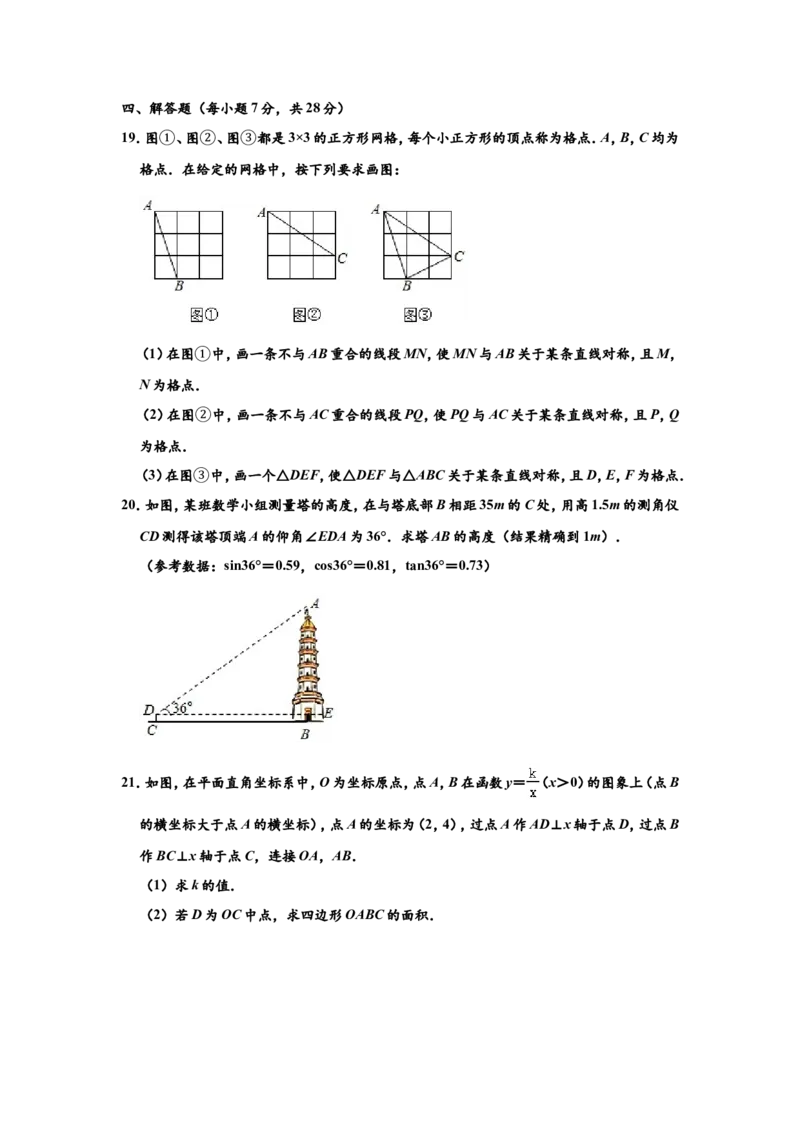
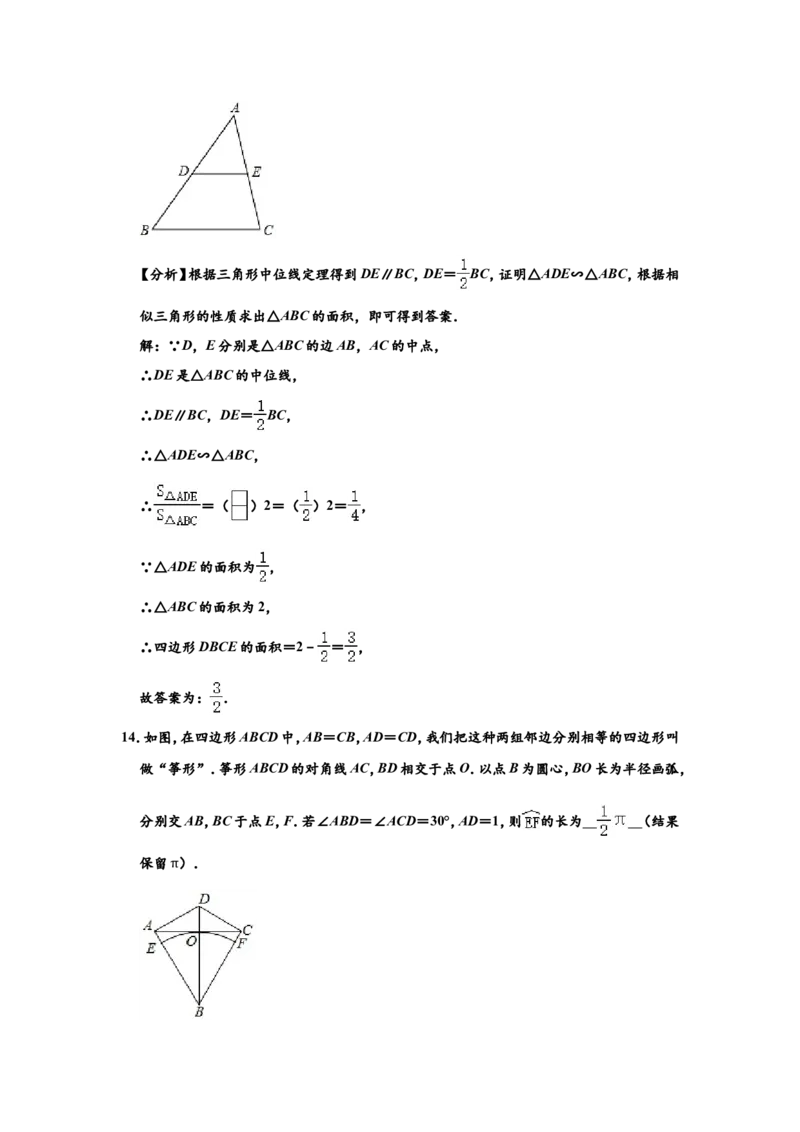
12.如图,AB∥CD∥EF.若 = ,BD=5,则DF= .
13.如图,在△ABC中,D,E分别是边AB,AC的中点.若△ADE的面积为 ,则四边形
DBCE的面积为 .14.如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫
做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长为半径画弧,
分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则 的长为 (结果
保留 ).
π
三、解答题(每小题5分,共20分)
15.先化简,再求值:(a+1)2+a(1﹣a)﹣1,其中a= .
16.“中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正
面印有“中国结”图案的不透明卡片A,B,C,卡片除正面图案不同外,其余均相同.将三
张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀
后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中
含有A卡片的概率.
17.甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做
60个所用的时间相等.求乙每小时做零件的个数.
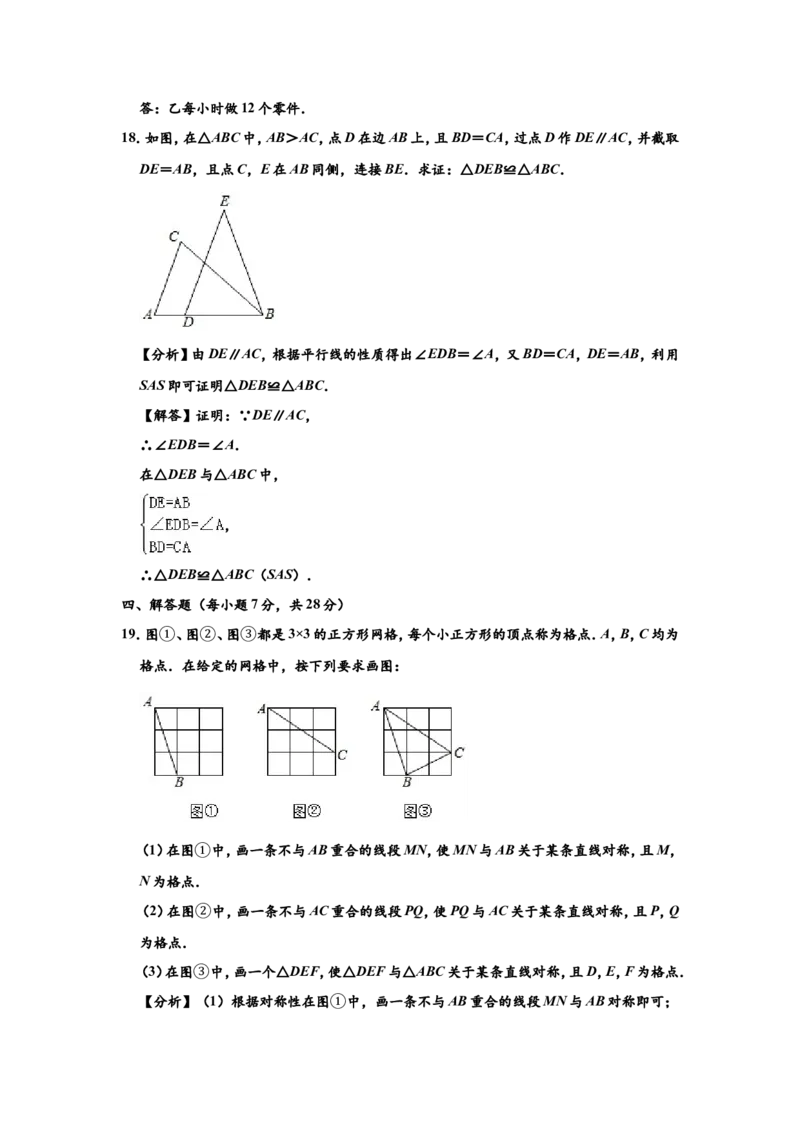
18.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取
DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.四、解答题(每小题7分,共28分)
19.图 、图 、图 都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为
格点①.在给②定的网③格中,按下列要求画图:
(1)在图 中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,
N为格点①.
(2)在图 中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q
为格点.②
(3)在图 中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.
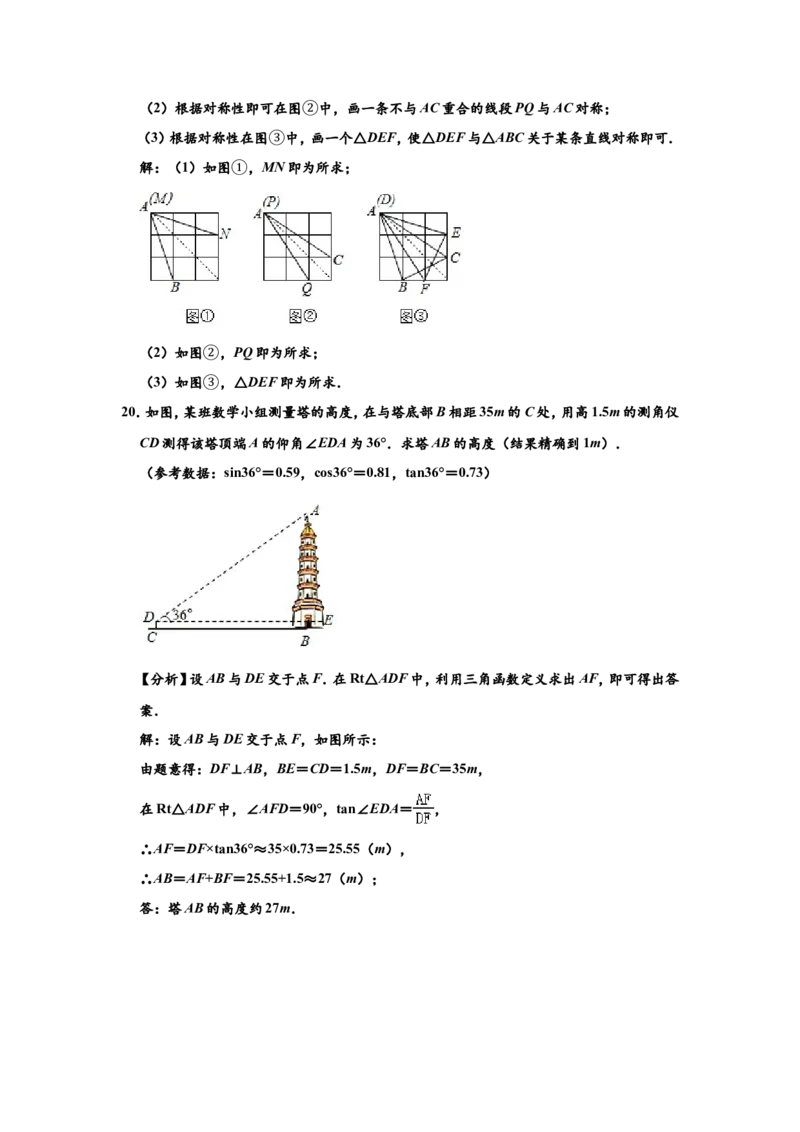
20.如图,某③班数学小组测量塔的高度,在与塔底部B相距35m的C处,用高1.5m的测角仪
CD测得该塔顶端A的仰角∠EDA为36°.求塔AB的高度(结果精确到1m).
(参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73)
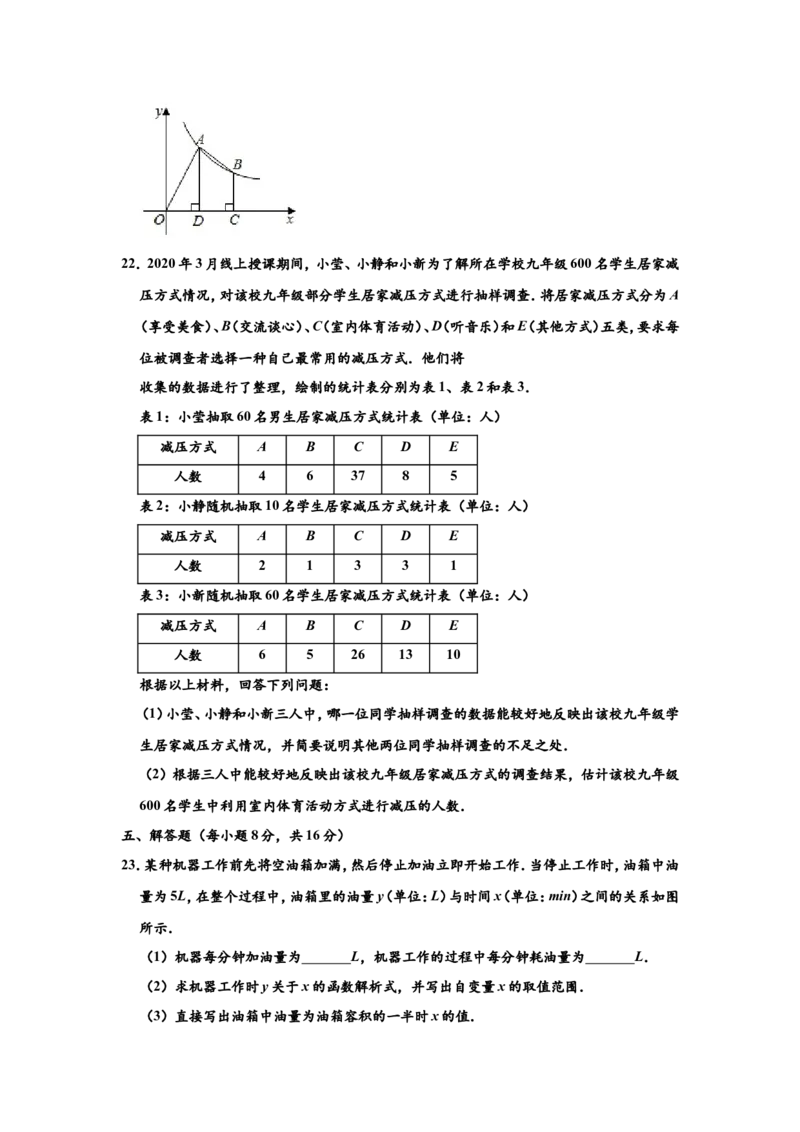
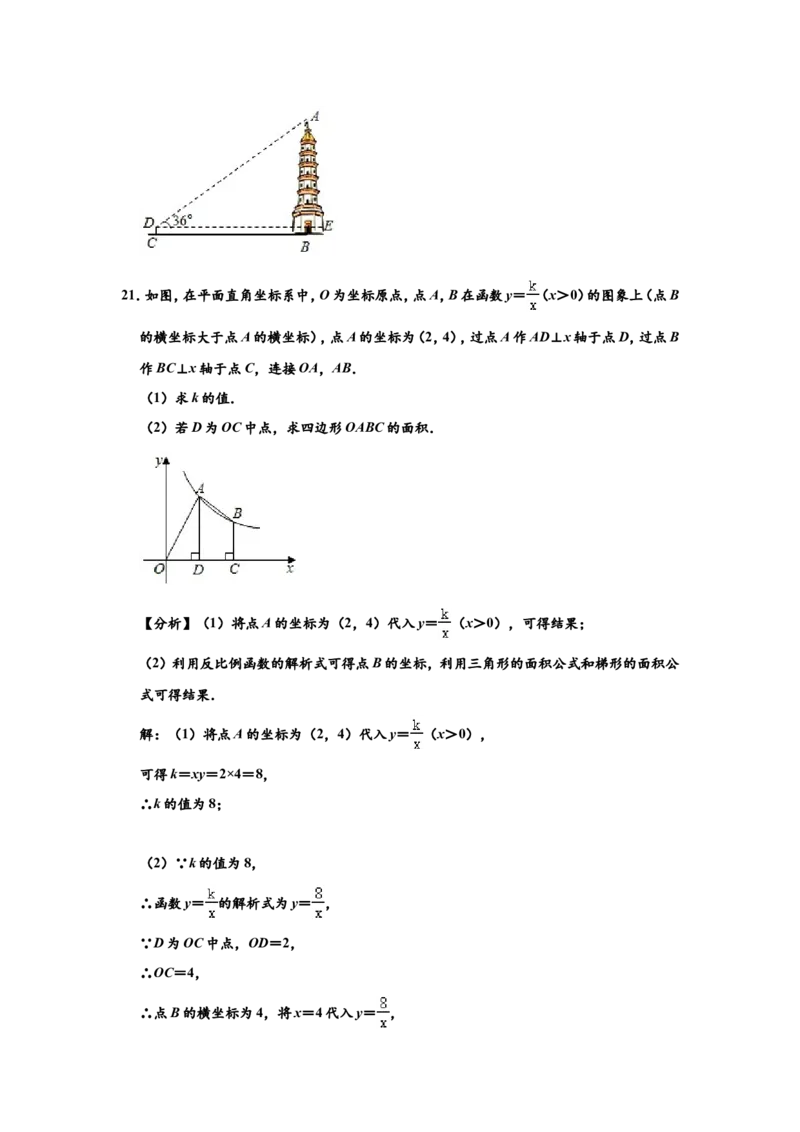
21.如图,在平面直角坐标系中,O为坐标原点,点A,B在函数y= (x>0)的图象上(点B
的横坐标大于点A的横坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B
作BC⊥x轴于点C,连接OA,AB.
(1)求k的值.
(2)若D为OC中点,求四边形OABC的面积.22.2020年3月线上授课期间,小莹、小静和小新为了解所在学校九年级600名学生居家减
压方式情况,对该校九年级部分学生居家减压方式进行抽样调查.将居家减压方式分为A
(享受美食)、B(交流谈心)、C(室内体育活动)、D(听音乐)和E(其他方式)五类,要求每
位被调查者选择一种自己最常用的减压方式.他们将
收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
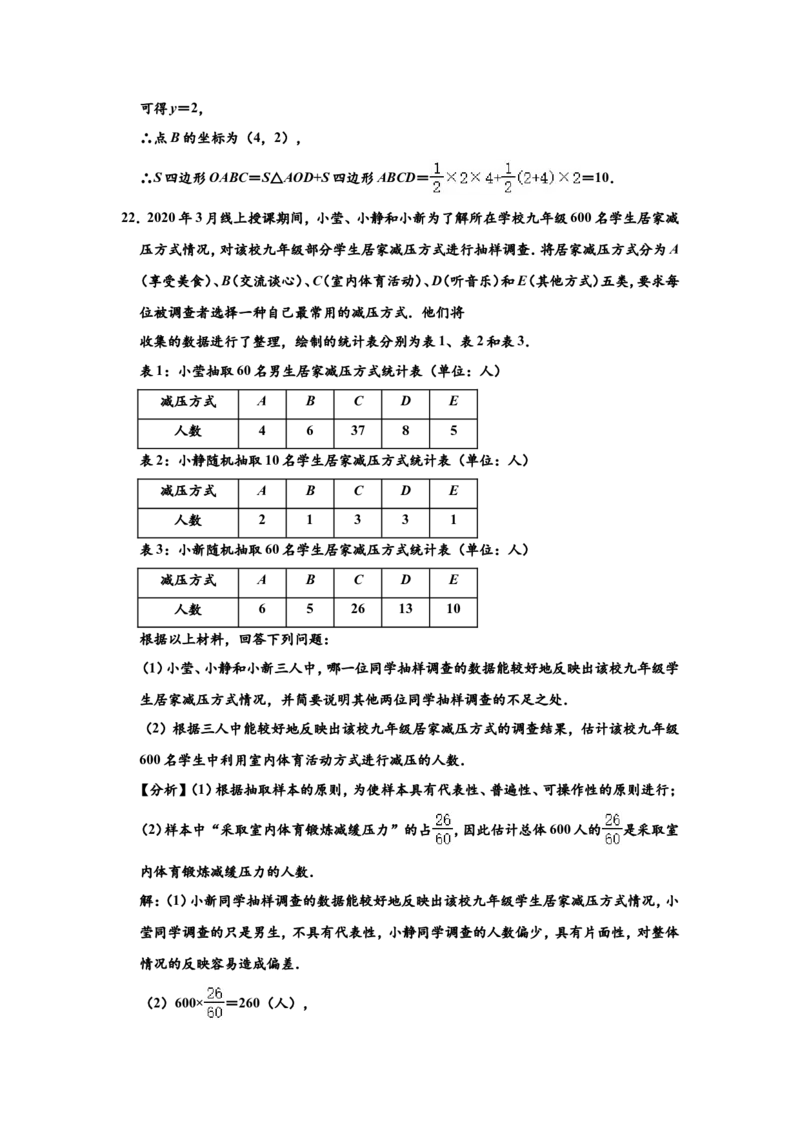
表1:小莹抽取60名男生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 4 6 37 8 5
表2:小静随机抽取10名学生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 2 1 3 3 1
表3:小新随机抽取60名学生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 6 5 26 13 10
根据以上材料,回答下列问题:
(1)小莹、小静和小新三人中,哪一位同学抽样调查的数据能较好地反映出该校九年级学
生居家减压方式情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据三人中能较好地反映出该校九年级居家减压方式的调查结果,估计该校九年级
600名学生中利用室内体育活动方式进行减压的人数.
五、解答题(每小题8分,共16分)
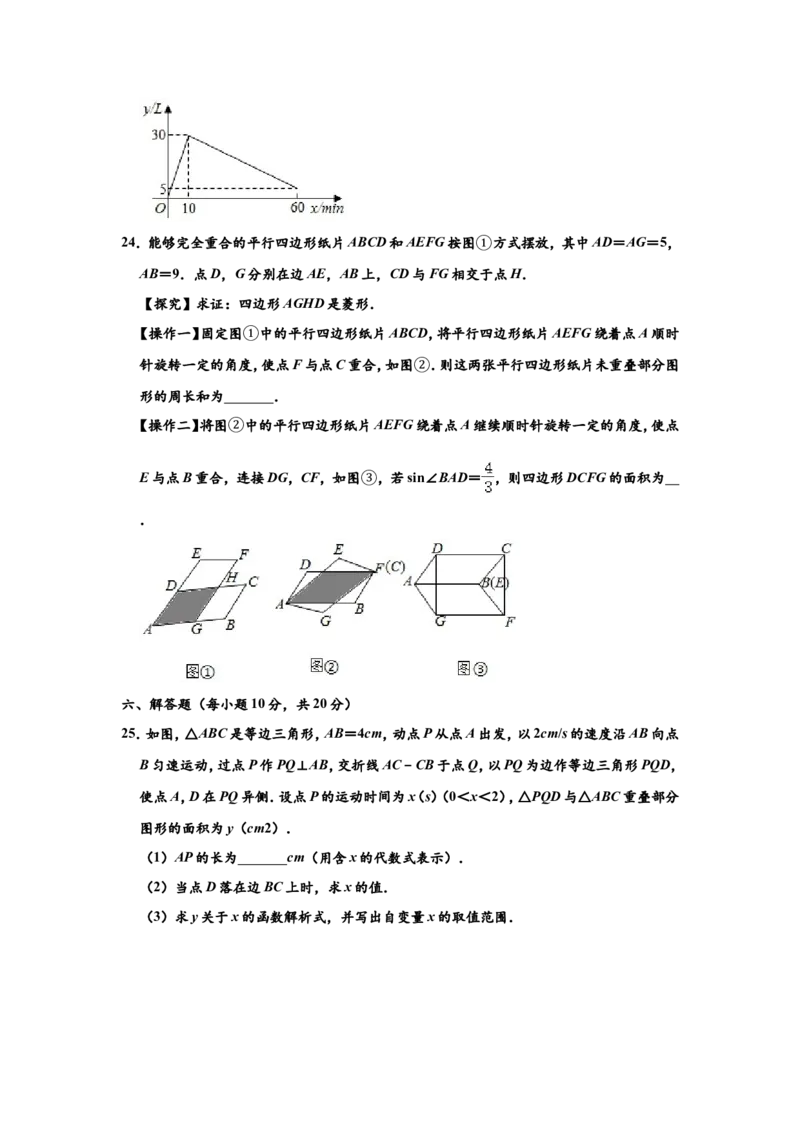
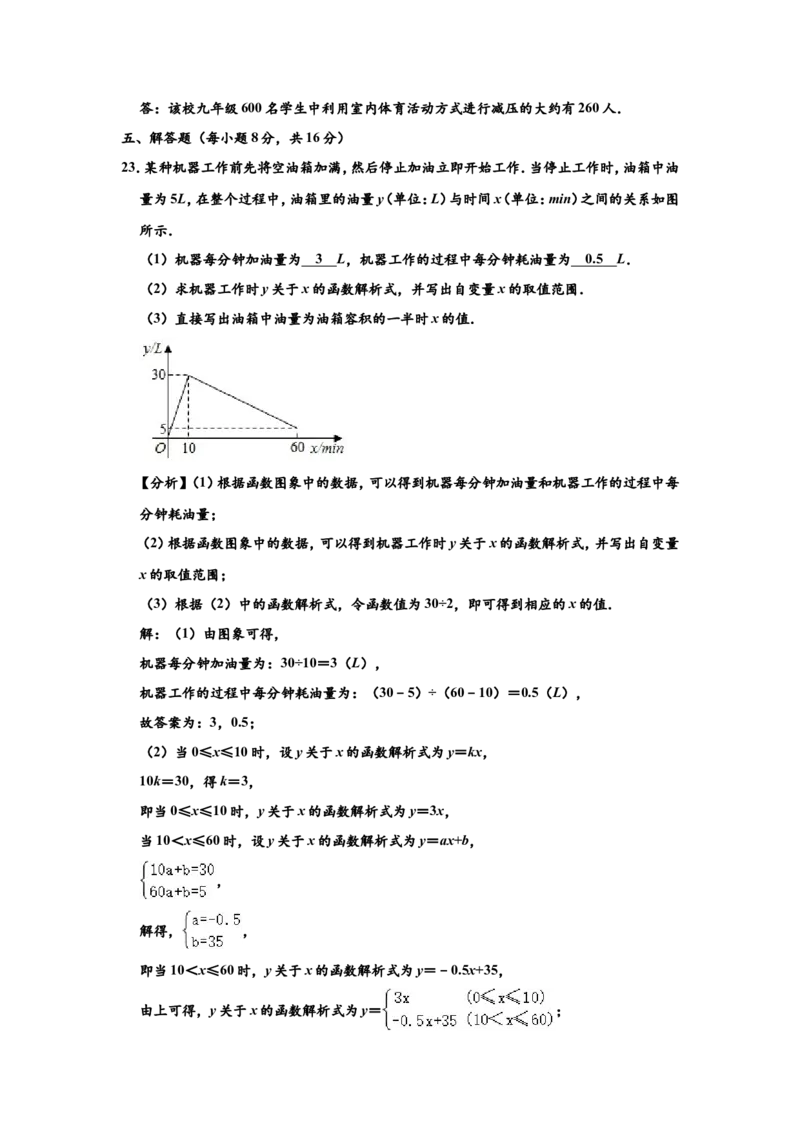
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油
量为5L,在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图
所示.
(1)机器每分钟加油量为 L,机器工作的过程中每分钟耗油量为 L.
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
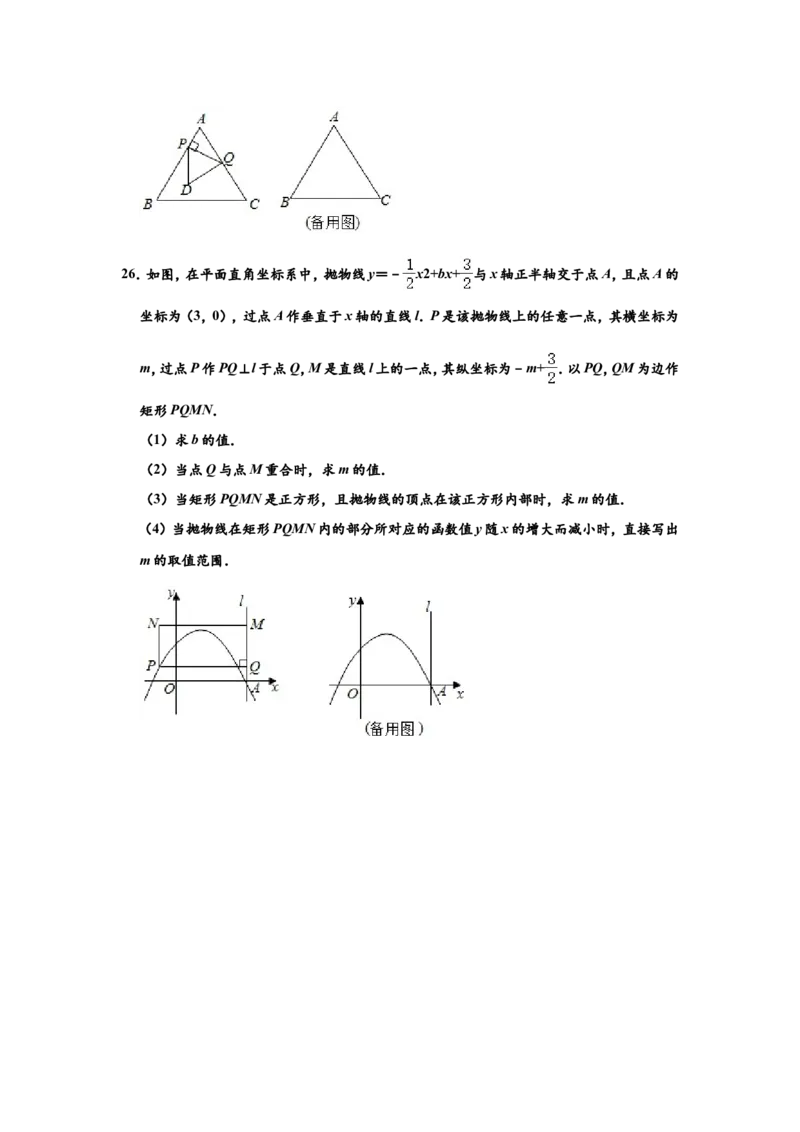
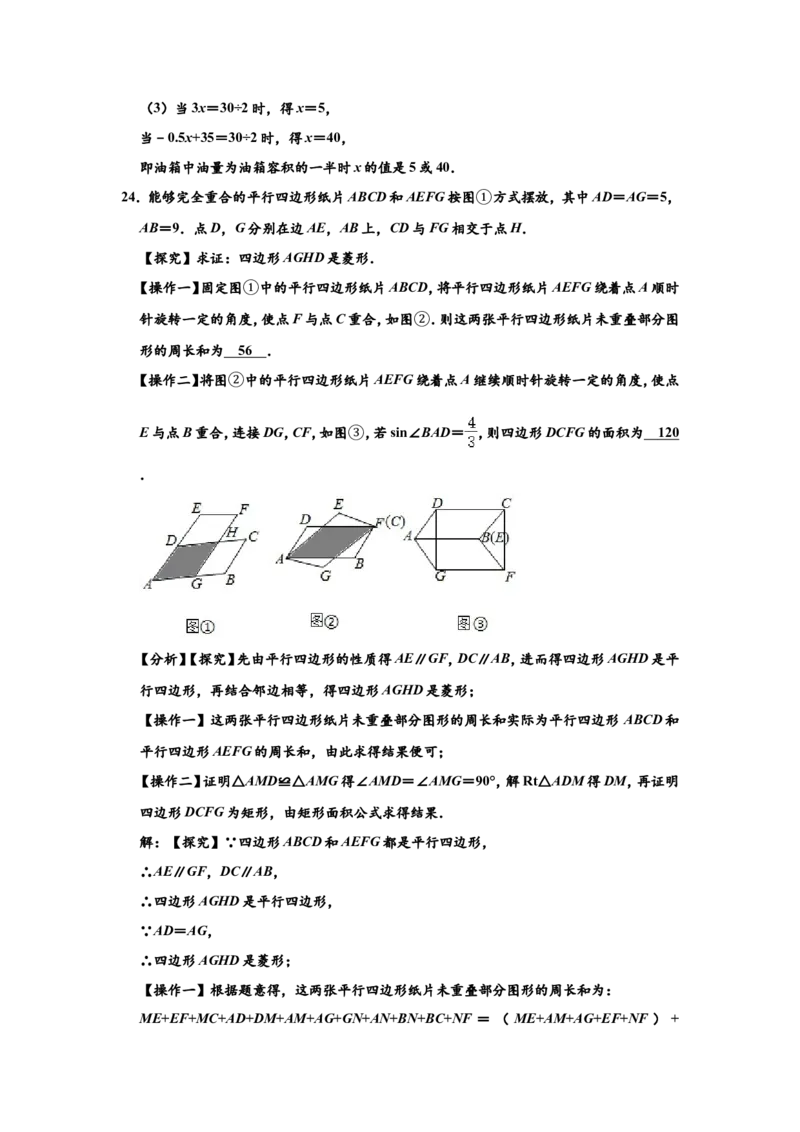
(3)直接写出油箱中油量为油箱容积的一半时x的值.24.能够完全重合的平行四边形纸片ABCD和AEFG按图 方式摆放,其中AD=AG=5,
AB=9.点D,G分别在边AE,AB上,CD与FG相交①于点H.
【探究】求证:四边形AGHD是菱形.
【操作一】固定图 中的平行四边形纸片ABCD,将平行四边形纸片AEFG绕着点A顺时
针旋转一定的角度①,使点F与点C重合,如图 .则这两张平行四边形纸片未重叠部分图
形的周长和为 . ②
【操作二】将图 中的平行四边形纸片AEFG绕着点A继续顺时针旋转一定的角度,使点
②
E与点B重合,连接DG,CF,如图 ,若sin∠BAD= ,则四边形DCFG的面积为
③
.
六、解答题(每小题10分,共20分)
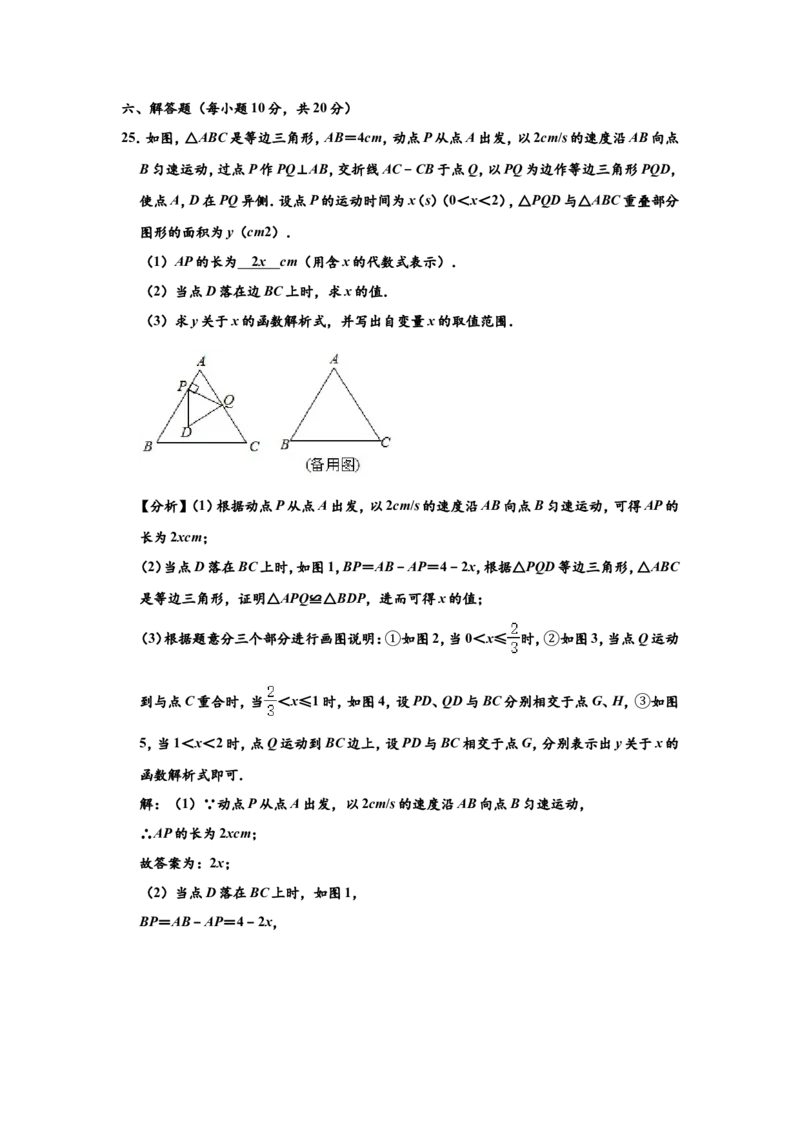
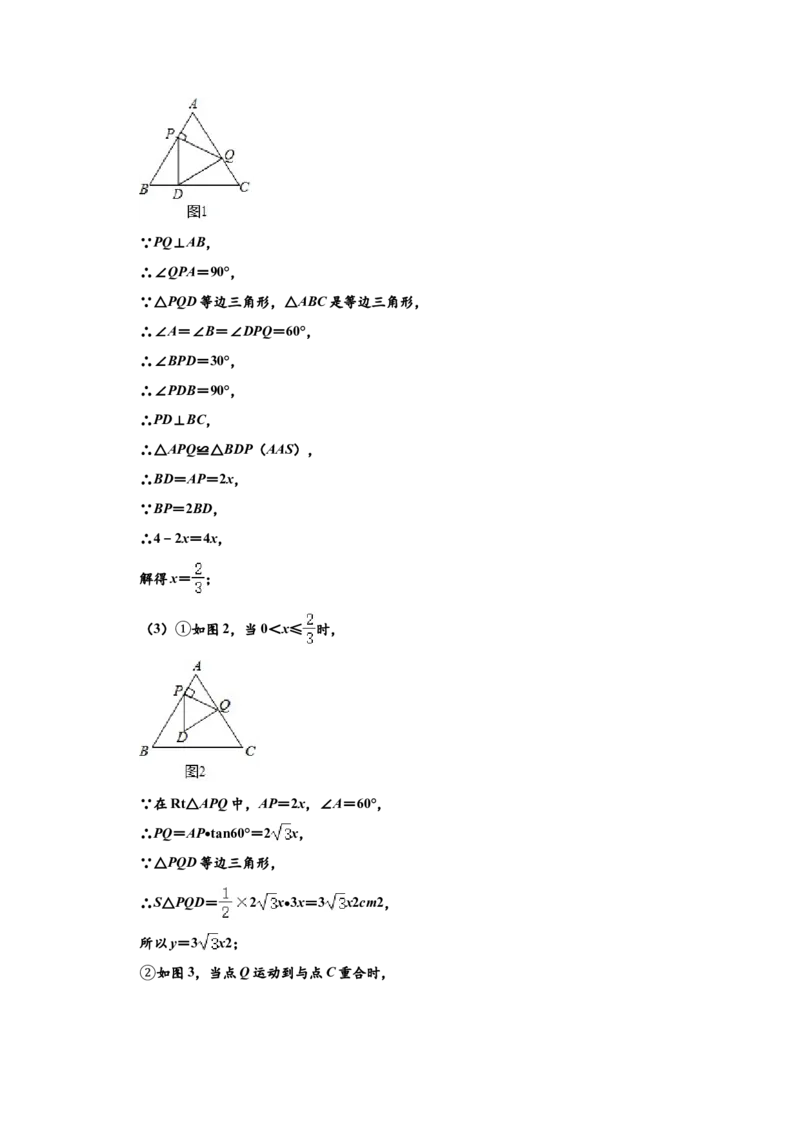
25.如图,△ABC是等边三角形,AB=4cm,动点P从点A出发,以2cm/s的速度沿AB向点
B匀速运动,过点P作PQ⊥AB,交折线AC﹣CB于点Q,以PQ为边作等边三角形PQD,
使点A,D在PQ异侧.设点P的运动时间为x(s)(0<x<2),△PQD与△ABC重叠部分
图形的面积为y(cm2).
(1)AP的长为 cm(用含x的代数式表示).
(2)当点D落在边BC上时,求x的值.
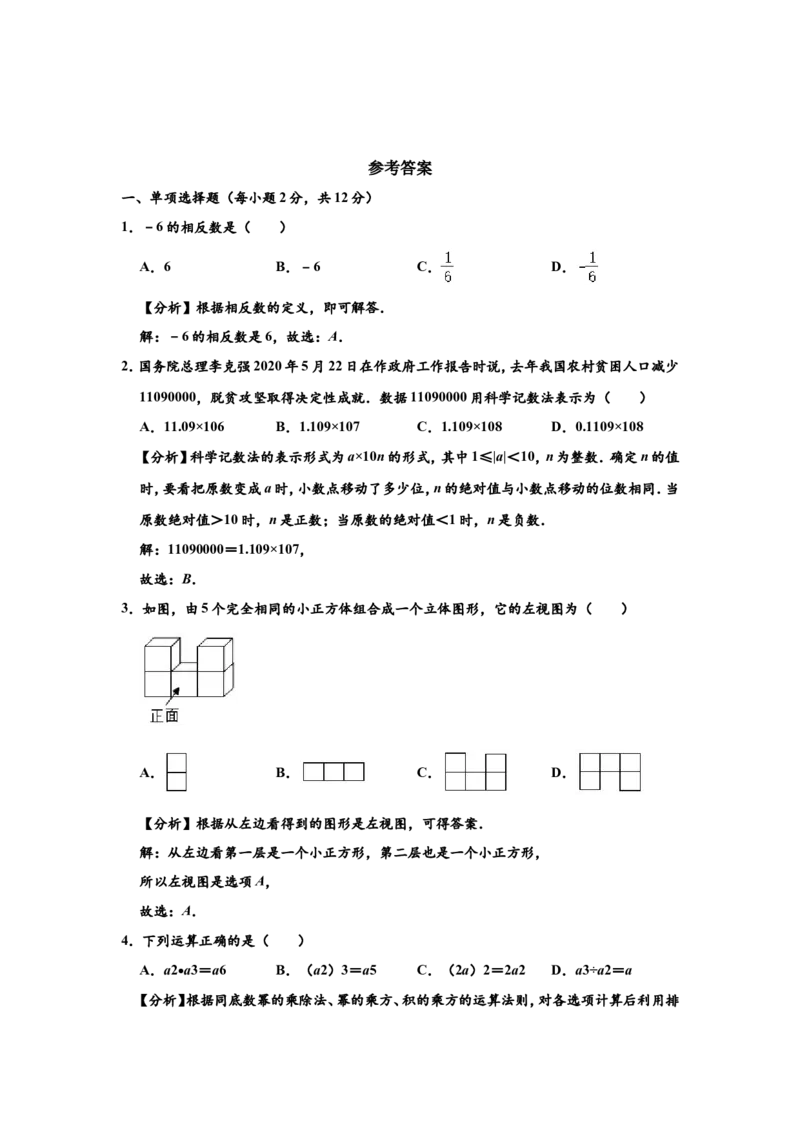
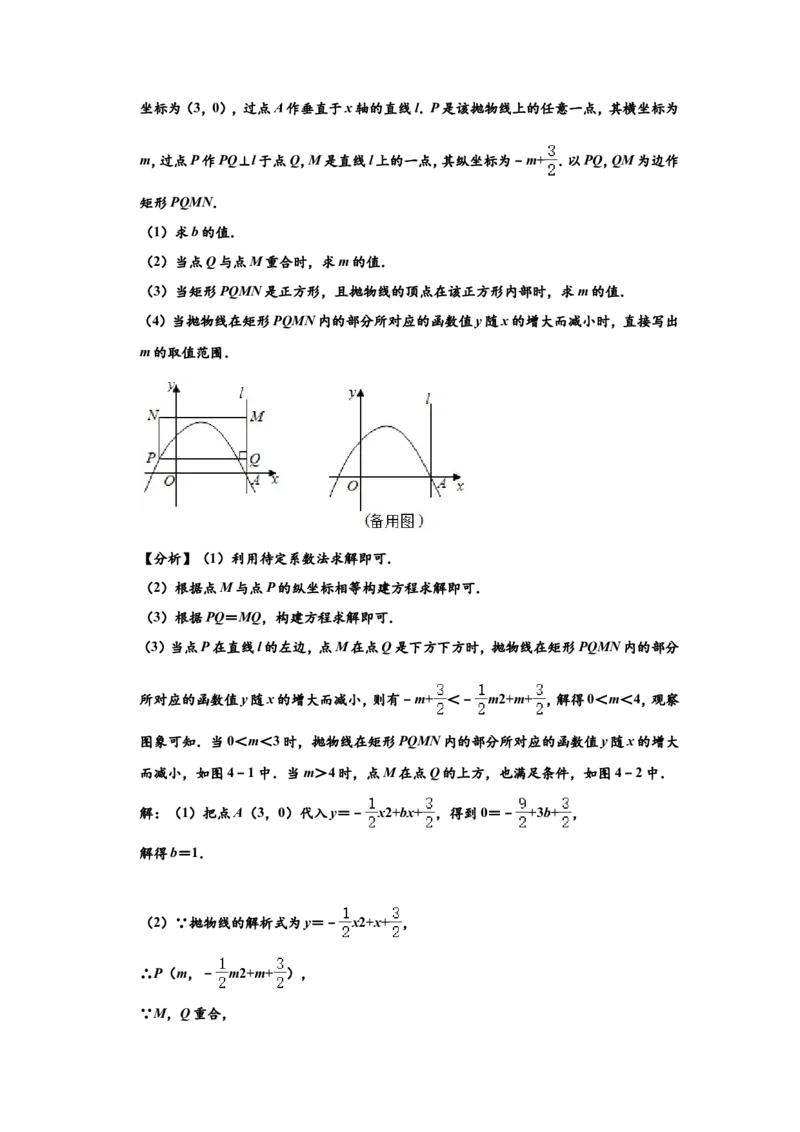
(3)求y关于x的函数解析式,并写出自变量x的取值范围.26.如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+ 与x轴正半轴交于点A,且点A的
坐标为(3,0),过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为
m,过点P作PQ⊥l于点Q,M是直线l上的一点,其纵坐标为﹣m+ .以PQ,QM为边作
矩形PQMN.
(1)求b的值.
(2)当点Q与点M重合时,求m的值.
(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值.
(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时,直接写出
m的取值范围.参考答案
一、单项选择题(每小题2分,共12分)
1.﹣6的相反数是( )
A.6 B.﹣6 C. D.
【分析】根据相反数的定义,即可解答.
解:﹣6的相反数是6,故选:A.
2.国务院总理李克强2020年5月22日在作政府工作报告时说,去年我国农村贫困人口减少
11090000,脱贫攻坚取得决定性成就.数据11090000用科学记数法表示为( )
A.11.09×106 B.1.109×107 C.1.109×108 D.0.1109×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值
时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当
原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
解:11090000=1.109×107,
故选:B.
3.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为( )
A. B. C. D.
【分析】根据从左边看得到的图形是左视图,可得答案.
解:从左边看第一层是一个小正方形,第二层也是一个小正方形,
所以左视图是选项A,
故选:A.
4.下列运算正确的是( )
A.a2•a3=a6 B.(a2)3=a5 C.(2a)2=2a2 D.a3÷a2=a
【分析】根据同底数幂的乘除法、幂的乘方、积的乘方的运算法则,对各选项计算后利用排除法求解.
解:A、a2•a3=a5,原计算错误,故此选项不符合题意;
B、(a2)3=a6,原计算错误,故此选项不符合题意;
C、(2a)2=4a2,原计算错误,故此选项不符合题意;
D、a3÷a2=a,原计算正确,故此选项符合题意;
故选:D.
5.将一副三角尺按如图所示的方式摆放,则∠ 的大小为( )
α
A.85° B.75° C.65° D.60°
【分析】先根据直角三角板的性质得出∠ACD的度数,再由三角形内角和定理即可得出结
论.
解:如图所示,
∵∠BCD=60°,∠BCA=45°,
∴∠ACD=∠BCD﹣∠BCA=60°﹣45°=15°,
∠ =180°﹣∠D﹣∠ACD=180°﹣90°﹣15°=75°,
故α选:B.
6.如图,四边形ABCD内接于 O,若∠B=108°,则∠D的大小为( )
⊙
A.54° B.62° C.72° D.82°
【分析】运用圆内接四边形对角互补计算即可.解:∵四边形ABCD内接于 O,∠B=108°,
∴∠D=180°﹣∠B=180°﹣⊙108°=72°,
故选:C.
二、填空题(每小题3分,共24分)
7.分解因式:a2﹣ab= a ( a ﹣ b ) .
【分析】直接把公因式a提出来即可.
解:a2﹣ab=a(a﹣b).
8.不等式3x+1>7的解集为 x > 2 .
【分析】移项、合并同类项、系数化为1即可得答案.
解:3x+1>7,
移项得:3x>7﹣1,
合并同类项得:3x>6,
系数化为1得:x>2,
故答案为:x>2.
9.一元二次方程x2+3x﹣1=0根的判别式的值为 1 3 .
【分析】根据一元二次方程根的判别式△=b2﹣4ac即可求出值.
解:∵a=1,b=3,c=﹣1,
∴△=b2﹣4ac=9+4=13.
所以一元二次方程x2+3x﹣1=0根的判别式的值为13.
故答案为:13.
10.我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走
240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?设快马x天
可以追上慢马,根据题意,可列方程为 ( 24 0 ﹣ 15 0 ) x = 150×1 2 .
【分析】设快马x天可以追上慢马,根据两马的速度之差×快马出发的时间=慢马的速度×
慢马提前出发的时间,即可得出关于x的一元一次方程,此题得解.
解:设快马x天可以追上慢马,
依题意,得:(240﹣150)x=150×12.
故答案为:(240﹣150)x=150×12.
11.如图,某单位要在河岸l上建一个水泵房引水到C处.他们的做法是:过点C作CD⊥l于
点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 垂线段最短 .【分析】根据垂线段的性质解答即可.
解:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理
是垂线段最短.
故答案为:垂线段最短.
12.如图,AB∥CD∥EF.若 = ,BD=5,则DF= 1 0 .
【分析】利用平行线分线段成比例定理得到 = ,然后根据比例性质求DF的长.
解:∵AB∥CD∥EF,
∴ = = ,
∴DF=2BD=2×5=10.
故答案为10.
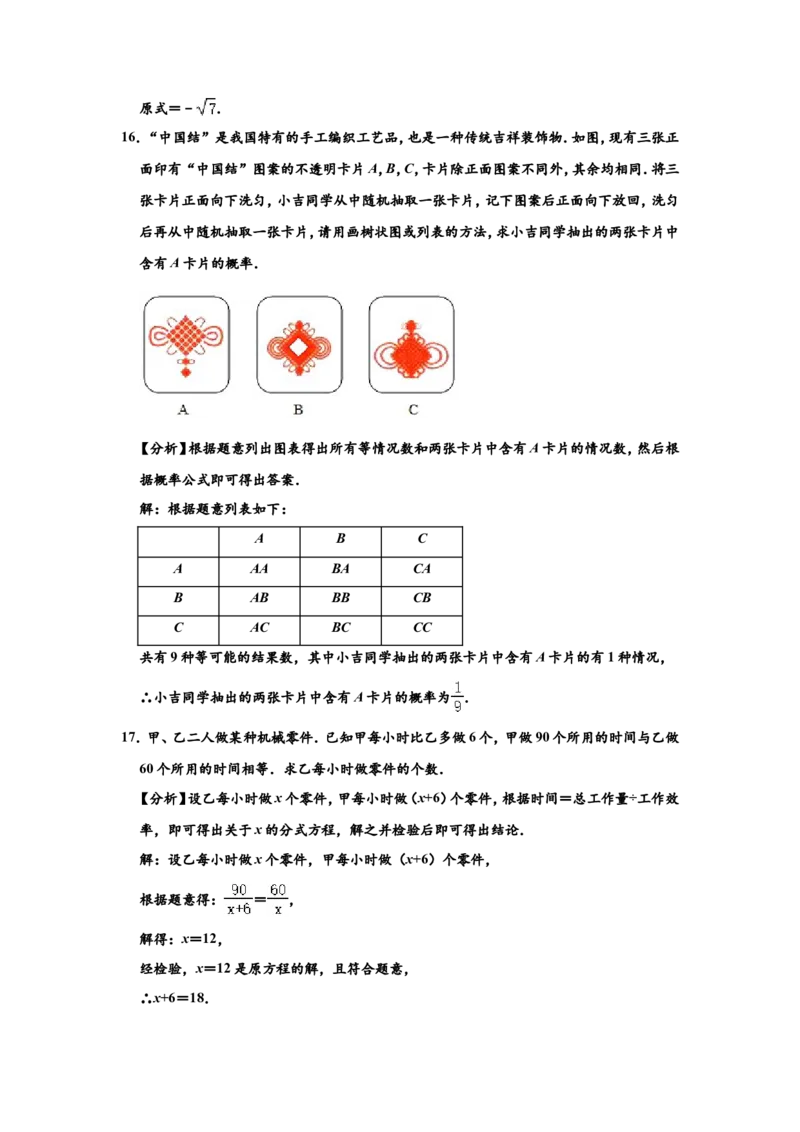
13.如图,在△ABC中,D,E分别是边AB,AC的中点.若△ADE的面积为 ,则四边形
DBCE的面积为 .【分析】根据三角形中位线定理得到DE∥BC,DE= BC,证明△ADE∽△ABC,根据相
似三角形的性质求出△ABC的面积,即可得到答案.
解:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE= BC,
∴△ADE∽△ABC,
∴ =( )2=( )2= ,
∵△ADE的面积为 ,
∴△ABC的面积为2,
∴四边形DBCE的面积=2﹣ = ,
故答案为: .
14.如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫
做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长为半径画弧,
分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则 的长为 (结果
保留 ).
π【分析】利用SSS证明△ABD≌△CBD,根据全等三角形的对应角相等即可得出∠ABD=
∠CBD=30°,∠ADB=∠CDB,CD=AD=1,即可求得∠ABC=60°,根据等腰三角形三
线合一的性质得出BD⊥AC,且AO=CO,进一步求得∠ACB=60°,即可求得∠BCD=
90°,根据含30°角的直角三角形的性质即可求得OB,然后根据弧长公式求得即可.
解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=30°,∠ADB=∠CDB,CD=AD=1,
∴∠ABC=60°,
∵AD=CD,∠ADB=∠CDB,
∴BD⊥AC,且AO=CO,
∴∠ACB=90°﹣30°=60°,
∴∠BCD=∠ACB+∠ACD=90°,
在Rt△BCD中,∵∠CBD=30°,
∴BD=2CD=2,
在Rt△COD中,∵∠ACD=30°,
∴OD= CD= ,
∴OB=BD﹣OD=2﹣ = ,
∴ 的长为: = ,
故答案为 .
三、解答题(每小题5分,共20分)
15.先化简,再求值:(a+1)2+a(1﹣a)﹣1,其中a= .
【分析】根据整式的混合运算顺序进行化简,再代入值即可.
解:原式=a2+2a+1+a﹣a2﹣1
=﹣a.
当a= 时,原式=﹣ .
16.“中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正
面印有“中国结”图案的不透明卡片A,B,C,卡片除正面图案不同外,其余均相同.将三
张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀
后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中
含有A卡片的概率.
【分析】根据题意列出图表得出所有等情况数和两张卡片中含有A卡片的情况数,然后根
据概率公式即可得出答案.
解:根据题意列表如下:
A B C
A AA BA CA
B AB BB CB
C AC BC CC
共有9种等可能的结果数,其中小吉同学抽出的两张卡片中含有A卡片的有1种情况,
∴小吉同学抽出的两张卡片中含有A卡片的概率为 .
17.甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做
60个所用的时间相等.求乙每小时做零件的个数.
【分析】设乙每小时做x个零件,甲每小时做(x+6)个零件,根据时间=总工作量÷工作效
率,即可得出关于x的分式方程,解之并检验后即可得出结论.
解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得: = ,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.答:乙每小时做12个零件.
18.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取
DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
【分析】由DE∥AC,根据平行线的性质得出∠EDB=∠A,又BD=CA,DE=AB,利用
SAS即可证明△DEB≌△ABC.
【解答】证明:∵DE∥AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
,
∴△DEB≌△ABC(SAS).
四、解答题(每小题7分,共28分)
19.图 、图 、图 都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为
格点①.在给②定的网③格中,按下列要求画图:
(1)在图 中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,
N为格点①.
(2)在图 中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q
为格点.②
(3)在图 中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.
【分析】③(1)根据对称性在图 中,画一条不与AB重合的线段MN与AB对称即可;
①(2)根据对称性即可在图 中,画一条不与AC重合的线段PQ与AC对称;
(3)根据对称性在图 中,②画一个△DEF,使△DEF与△ABC关于某条直线对称即可.
解:(1)如图 ,M③N即为所求;
①
(2)如图 ,PQ即为所求;
(3)如图②,△DEF即为所求.
20.如图,某班③数学小组测量塔的高度,在与塔底部B相距35m的C处,用高1.5m的测角仪
CD测得该塔顶端A的仰角∠EDA为36°.求塔AB的高度(结果精确到1m).
(参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73)
【分析】设AB与DE交于点F.在Rt△ADF中,利用三角函数定义求出AF,即可得出答
案.
解:设AB与DE交于点F,如图所示:
由题意得:DF⊥AB,BE=CD=1.5m,DF=BC=35m,
在Rt△ADF中,∠AFD=90°,tan∠EDA= ,
∴AF=DF×tan36°≈35×0.73=25.55(m),
∴AB=AF+BF=25.55+1.5≈27(m);
答:塔AB的高度约27m.21.如图,在平面直角坐标系中,O为坐标原点,点A,B在函数y= (x>0)的图象上(点B
的横坐标大于点A的横坐标),点A的坐标为(2,4),过点A作AD⊥x轴于点D,过点B
作BC⊥x轴于点C,连接OA,AB.
(1)求k的值.
(2)若D为OC中点,求四边形OABC的面积.
【分析】(1)将点A的坐标为(2,4)代入y= (x>0),可得结果;
(2)利用反比例函数的解析式可得点B的坐标,利用三角形的面积公式和梯形的面积公
式可得结果.
解:(1)将点A的坐标为(2,4)代入y= (x>0),
可得k=xy=2×4=8,
∴k的值为8;
(2)∵k的值为8,
∴函数y= 的解析式为y= ,
∵D为OC中点,OD=2,
∴OC=4,
∴点B的横坐标为4,将x=4代入y= ,可得y=2,
∴点B的坐标为(4,2),
∴S四边形OABC=S△AOD+S四边形ABCD= =10.
22.2020年3月线上授课期间,小莹、小静和小新为了解所在学校九年级600名学生居家减
压方式情况,对该校九年级部分学生居家减压方式进行抽样调查.将居家减压方式分为A
(享受美食)、B(交流谈心)、C(室内体育活动)、D(听音乐)和E(其他方式)五类,要求每
位被调查者选择一种自己最常用的减压方式.他们将
收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小莹抽取60名男生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 4 6 37 8 5
表2:小静随机抽取10名学生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 2 1 3 3 1
表3:小新随机抽取60名学生居家减压方式统计表(单位:人)
减压方式 A B C D E
人数 6 5 26 13 10
根据以上材料,回答下列问题:
(1)小莹、小静和小新三人中,哪一位同学抽样调查的数据能较好地反映出该校九年级学
生居家减压方式情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据三人中能较好地反映出该校九年级居家减压方式的调查结果,估计该校九年级
600名学生中利用室内体育活动方式进行减压的人数.
【分析】(1)根据抽取样本的原则,为使样本具有代表性、普遍性、可操作性的原则进行;
(2)样本中“采取室内体育锻炼减缓压力”的占 ,因此估计总体600人的 是采取室
内体育锻炼减缓压力的人数.
解:(1)小新同学抽样调查的数据能较好地反映出该校九年级学生居家减压方式情况,小
莹同学调查的只是男生,不具有代表性,小静同学调查的人数偏少,具有片面性,对整体
情况的反映容易造成偏差.
(2)600× =260(人),答:该校九年级600名学生中利用室内体育活动方式进行减压的大约有260人.
五、解答题(每小题8分,共16分)
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油
量为5L,在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图
所示.
(1)机器每分钟加油量为 3 L,机器工作的过程中每分钟耗油量为 0. 5 L.
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
(3)直接写出油箱中油量为油箱容积的一半时x的值.
【分析】(1)根据函数图象中的数据,可以得到机器每分钟加油量和机器工作的过程中每
分钟耗油量;
(2)根据函数图象中的数据,可以得到机器工作时y关于x的函数解析式,并写出自变量
x的取值范围;
(3)根据(2)中的函数解析式,令函数值为30÷2,即可得到相应的x的值.
解:(1)由图象可得,
机器每分钟加油量为:30÷10=3(L),
机器工作的过程中每分钟耗油量为:(30﹣5)÷(60﹣10)=0.5(L),
故答案为:3,0.5;
(2)当0≤x≤10时,设y关于x的函数解析式为y=kx,
10k=30,得k=3,
即当0≤x≤10时,y关于x的函数解析式为y=3x,
当10<x≤60时,设y关于x的函数解析式为y=ax+b,
,
解得, ,
即当10<x≤60时,y关于x的函数解析式为y=﹣0.5x+35,
由上可得,y关于x的函数解析式为y= ;(3)当3x=30÷2时,得x=5,
当﹣0.5x+35=30÷2时,得x=40,
即油箱中油量为油箱容积的一半时x的值是5或40.
24.能够完全重合的平行四边形纸片ABCD和AEFG按图 方式摆放,其中AD=AG=5,
AB=9.点D,G分别在边AE,AB上,CD与FG相交①于点H.
【探究】求证:四边形AGHD是菱形.
【操作一】固定图 中的平行四边形纸片ABCD,将平行四边形纸片AEFG绕着点A顺时
针旋转一定的角度①,使点F与点C重合,如图 .则这两张平行四边形纸片未重叠部分图
形的周长和为 5 6 . ②
【操作二】将图 中的平行四边形纸片AEFG绕着点A继续顺时针旋转一定的角度,使点
②
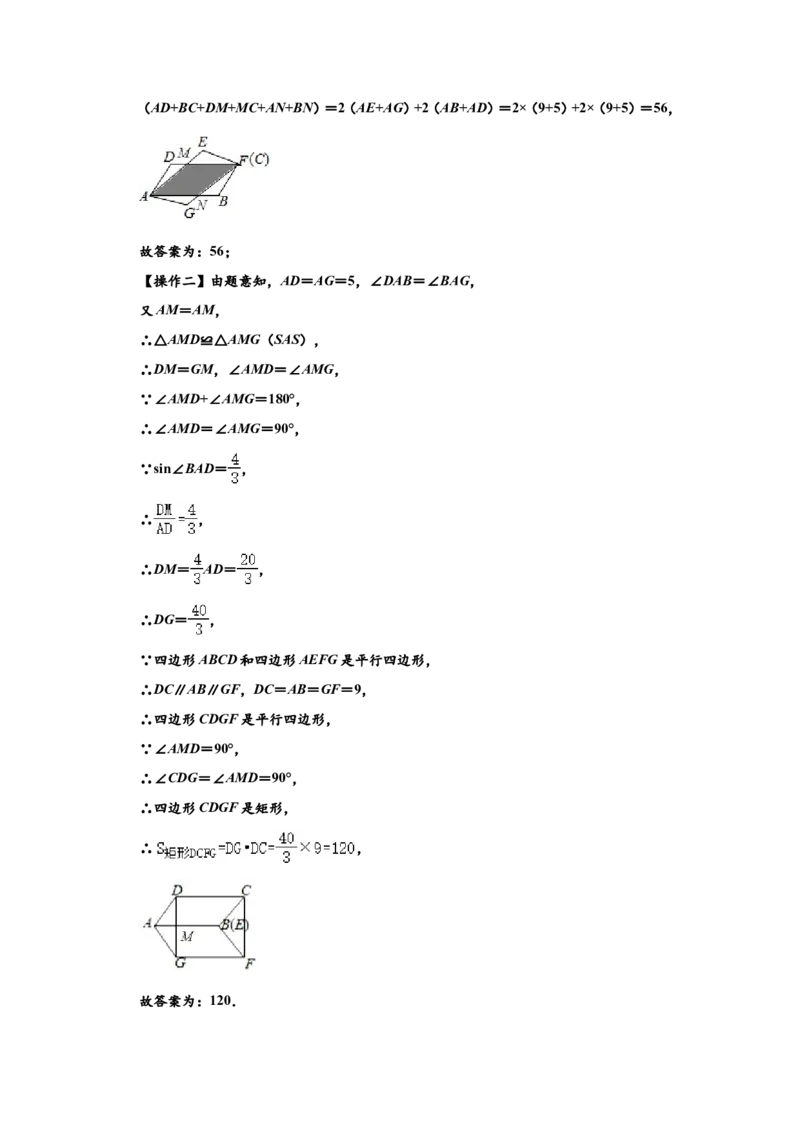
E与点B重合,连接DG,CF,如图 ,若sin∠BAD= ,则四边形DCFG的面积为 12 0
③
.
【分析】【探究】先由平行四边形的性质得AE∥GF,DC∥AB,进而得四边形AGHD是平
行四边形,再结合邻边相等,得四边形AGHD是菱形;
【操作一】这两张平行四边形纸片未重叠部分图形的周长和实际为平行四边形 ABCD和
平行四边形AEFG的周长和,由此求得结果便可;
【操作二】证明△AMD≌△AMG得∠AMD=∠AMG=90°,解Rt△ADM得DM,再证明
四边形DCFG为矩形,由矩形面积公式求得结果.
解:【探究】∵四边形ABCD和AEFG都是平行四边形,
∴AE∥GF,DC∥AB,
∴四边形AGHD是平行四边形,
∵AD=AG,
∴四边形AGHD是菱形;
【操作一】根据题意得,这两张平行四边形纸片未重叠部分图形的周长和为:
ME+EF+MC+AD+DM+AM+AG+GN+AN+BN+BC+NF = ( ME+AM+AG+EF+NF ) +(AD+BC+DM+MC+AN+BN)=2(AE+AG)+2(AB+AD)=2×(9+5)+2×(9+5)=56,
故答案为:56;
【操作二】由题意知,AD=AG=5,∠DAB=∠BAG,
又AM=AM,
∴△AMD≌△AMG(SAS),
∴DM=GM,∠AMD=∠AMG,
∵∠AMD+∠AMG=180°,
∴∠AMD=∠AMG=90°,
∵sin∠BAD= ,
∴ ,
∴DM= AD= ,
∴DG= ,
∵四边形ABCD和四边形AEFG是平行四边形,
∴DC∥AB∥GF,DC=AB=GF=9,
∴四边形CDGF是平行四边形,
∵∠AMD=90°,
∴∠CDG=∠AMD=90°,
∴四边形CDGF是矩形,
∴ ,
故答案为:120.六、解答题(每小题10分,共20分)
25.如图,△ABC是等边三角形,AB=4cm,动点P从点A出发,以2cm/s的速度沿AB向点
B匀速运动,过点P作PQ⊥AB,交折线AC﹣CB于点Q,以PQ为边作等边三角形PQD,
使点A,D在PQ异侧.设点P的运动时间为x(s)(0<x<2),△PQD与△ABC重叠部分
图形的面积为y(cm2).
(1)AP的长为 2 x cm(用含x的代数式表示).
(2)当点D落在边BC上时,求x的值.
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
【分析】(1)根据动点P从点A出发,以2cm/s的速度沿AB向点B匀速运动,可得AP的
长为2xcm;
(2)当点D落在BC上时,如图1,BP=AB﹣AP=4﹣2x,根据△PQD等边三角形,△ABC
是等边三角形,证明△APQ≌△BDP,进而可得x的值;
(3)根据题意分三个部分进行画图说明: 如图2,当0<x≤ 时, 如图3,当点Q运动
① ②
到与点C重合时,当 <x≤1时,如图4,设PD、QD与BC分别相交于点G、H, 如图
③
5,当1<x<2时,点Q运动到BC边上,设PD与BC相交于点G,分别表示出y关于x的
函数解析式即可.
解:(1)∵动点P从点A出发,以2cm/s的速度沿AB向点B匀速运动,
∴AP的长为2xcm;
故答案为:2x;
(2)当点D落在BC上时,如图1,
BP=AB﹣AP=4﹣2x,∵PQ⊥AB,
∴∠QPA=90°,
∵△PQD等边三角形,△ABC是等边三角形,
∴∠A=∠B=∠DPQ=60°,
∴∠BPD=30°,
∴∠PDB=90°,
∴PD⊥BC,
∴△APQ≌△BDP(AAS),
∴BD=AP=2x,
∵BP=2BD,
∴4﹣2x=4x,
解得x= ;
(3) 如图2,当0<x≤ 时,
①
∵在Rt△APQ中,AP=2x,∠A=60°,
∴PQ=AP•tan60°=2 x,
∵△PQD等边三角形,
∴S△PQD= 2 x•3x=3 x2cm2,
所以y=3 x2;
如图3,当点Q运动到与点C重合时,
②此时CP⊥AB,
所以AP= AB,即2x═2,
解得x=1,
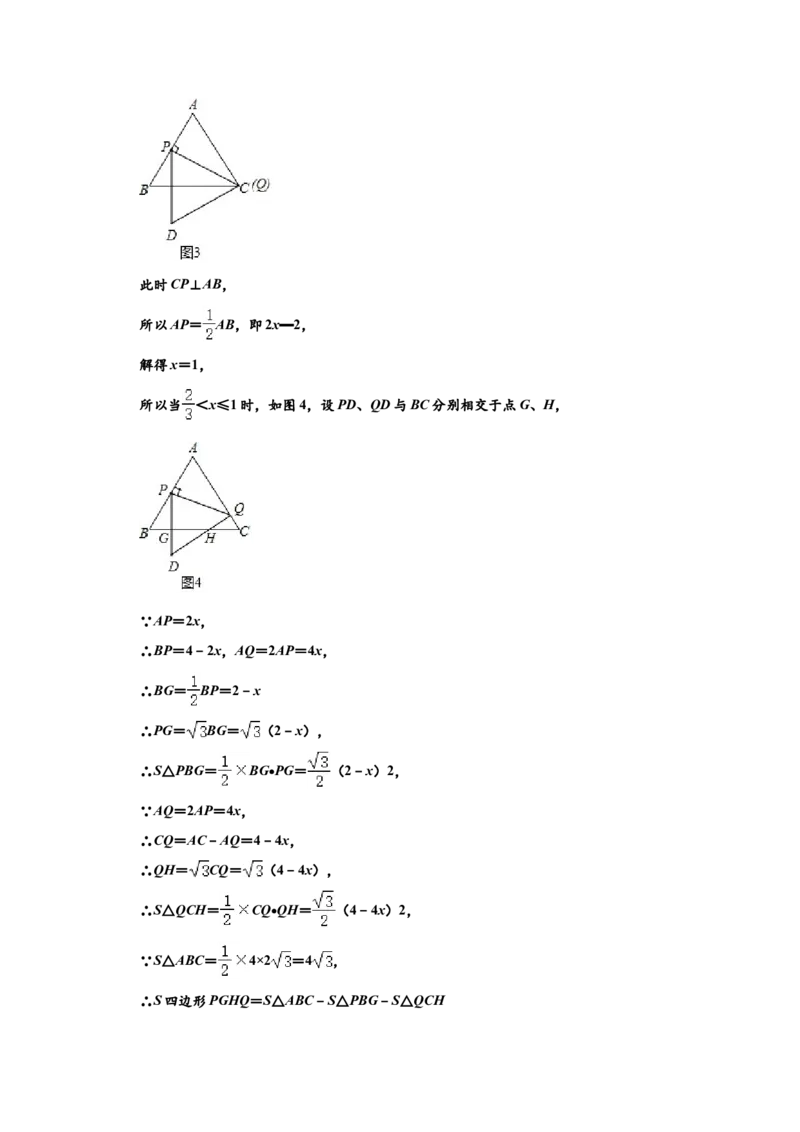
所以当 <x≤1时,如图4,设PD、QD与BC分别相交于点G、H,
∵AP=2x,
∴BP=4﹣2x,AQ=2AP=4x,
∴BG= BP=2﹣x
∴PG= BG= (2﹣x),
∴S△PBG= BG•PG= (2﹣x)2,
∵AQ=2AP=4x,
∴CQ=AC﹣AQ=4﹣4x,
∴QH= CQ= (4﹣4x),
∴S△QCH= CQ•QH= (4﹣4x)2,
∵S△ABC= 4×2 =4 ,
∴S四边形PGHQ=S△ABC﹣S△PBG﹣S△QCH=4 ﹣ (2﹣x)2﹣ (4﹣4x)2
=﹣ x2+18 x﹣6 ,
所以y=﹣ x2+18 x﹣6 ;
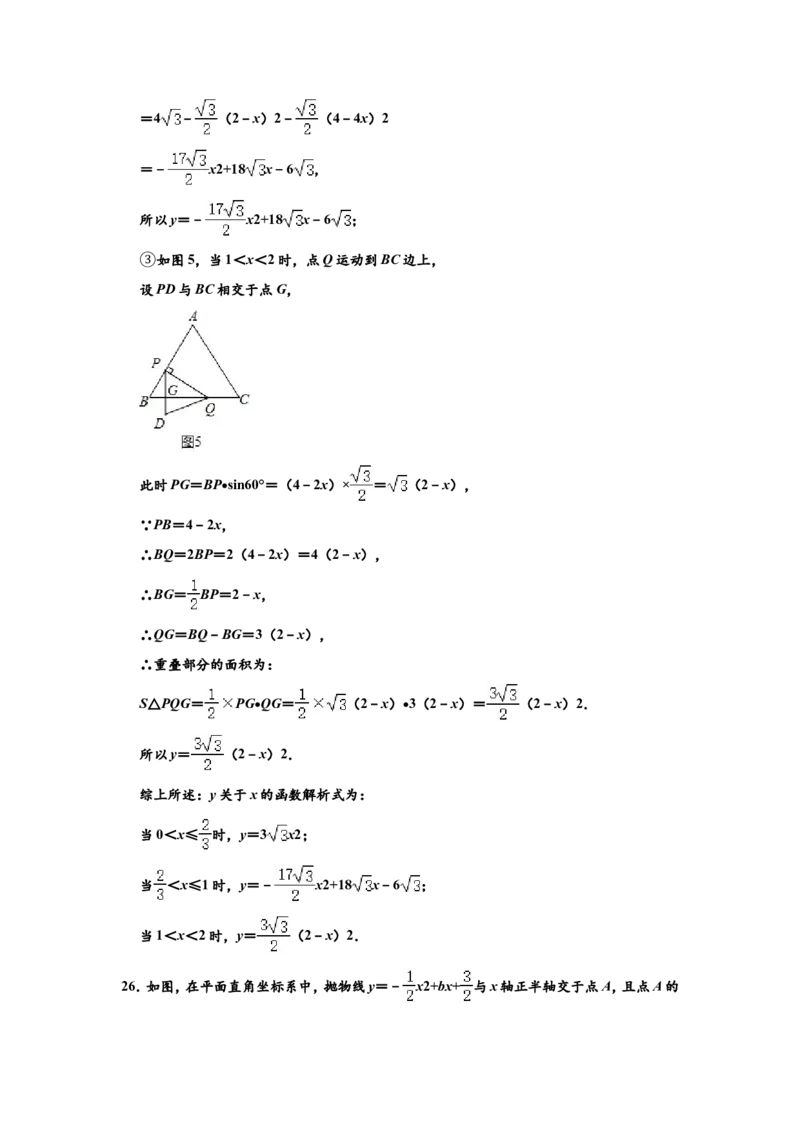
如图5,当1<x<2时,点Q运动到BC边上,
③设PD与BC相交于点G,
此时PG=BP•sin60°=(4﹣2x)× = (2﹣x),
∵PB=4﹣2x,
∴BQ=2BP=2(4﹣2x)=4(2﹣x),
∴BG= BP=2﹣x,
∴QG=BQ﹣BG=3(2﹣x),
∴重叠部分的面积为:
S△PQG= PG•QG= (2﹣x)•3(2﹣x)= (2﹣x)2.
所以y= (2﹣x)2.
综上所述:y关于x的函数解析式为:
当0<x≤ 时,y=3 x2;
当 <x≤1时,y=﹣ x2+18 x﹣6 ;
当1<x<2时,y= (2﹣x)2.
26.如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+ 与x轴正半轴交于点A,且点A的坐标为(3,0),过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为
m,过点P作PQ⊥l于点Q,M是直线l上的一点,其纵坐标为﹣m+ .以PQ,QM为边作
矩形PQMN.
(1)求b的值.
(2)当点Q与点M重合时,求m的值.
(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值.
(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时,直接写出
m的取值范围.
【分析】(1)利用待定系数法求解即可.
(2)根据点M与点P的纵坐标相等构建方程求解即可.
(3)根据PQ=MQ,构建方程求解即可.
(3)当点P在直线l的左边,点M在点Q是下方下方时,抛物线在矩形PQMN内的部分
所对应的函数值y随x的增大而减小,则有﹣m+ <﹣ m2+m+ ,解得0<m<4,观察
图象可知.当0<m<3时,抛物线在矩形PQMN内的部分所对应的函数值y随x的增大
而减小,如图4﹣1中.当m>4时,点M在点Q的上方,也满足条件,如图4﹣2中.
解:(1)把点A(3,0)代入y=﹣ x2+bx+ ,得到0=﹣ +3b+ ,
解得b=1.
(2)∵抛物线的解析式为y=﹣ x2+x+ ,
∴P(m,﹣ m2+m+ ),
∵M,Q重合,∴﹣m+ =﹣ m2+m+ ,
解得m=0或4.
(3)由题意PQ=MQ,且抛物线的顶点在该正方形内部
∴3﹣m=﹣m+ ﹣(﹣ m2+m+ ),
解得m=1﹣ 或1+ (不合题意舍弃),
∴m=1﹣ .
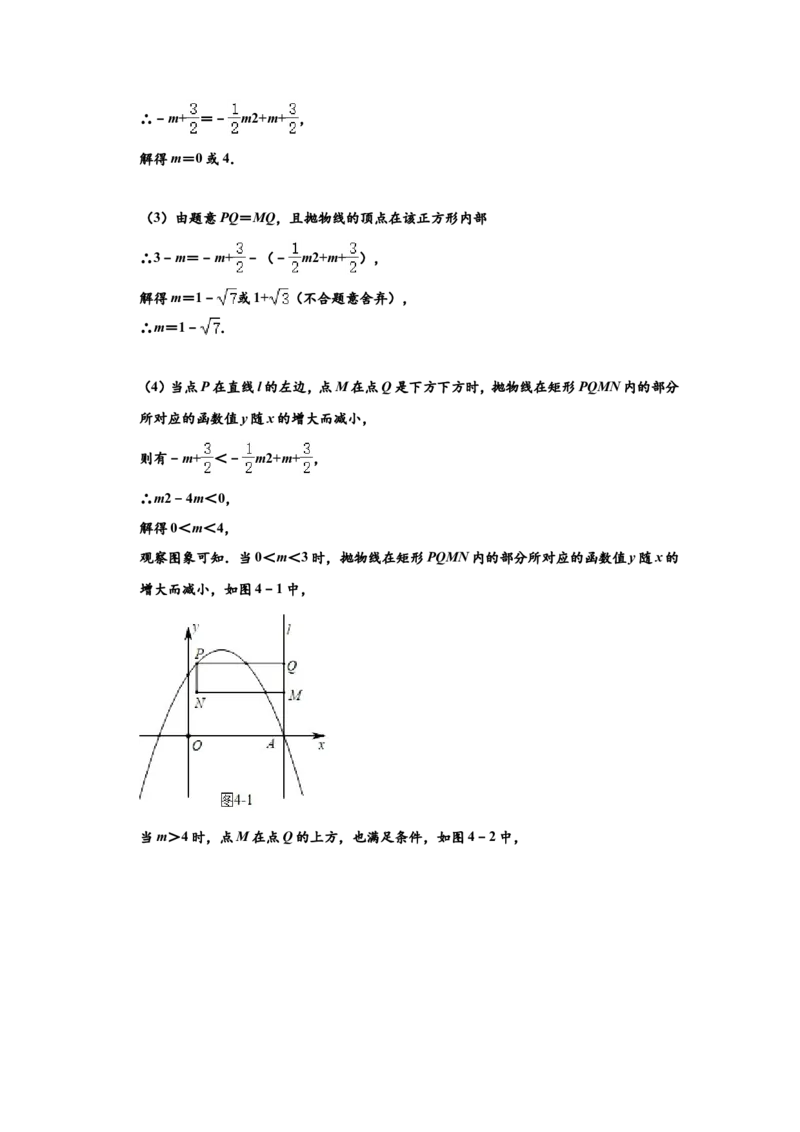
(4)当点P在直线l的左边,点M在点Q是下方下方时,抛物线在矩形PQMN内的部分
所对应的函数值y随x的增大而减小,
则有﹣m+ <﹣ m2+m+ ,
∴m2﹣4m<0,
解得0<m<4,
观察图象可知.当0<m<3时,抛物线在矩形PQMN内的部分所对应的函数值y随x的
增大而减小,如图4﹣1中,
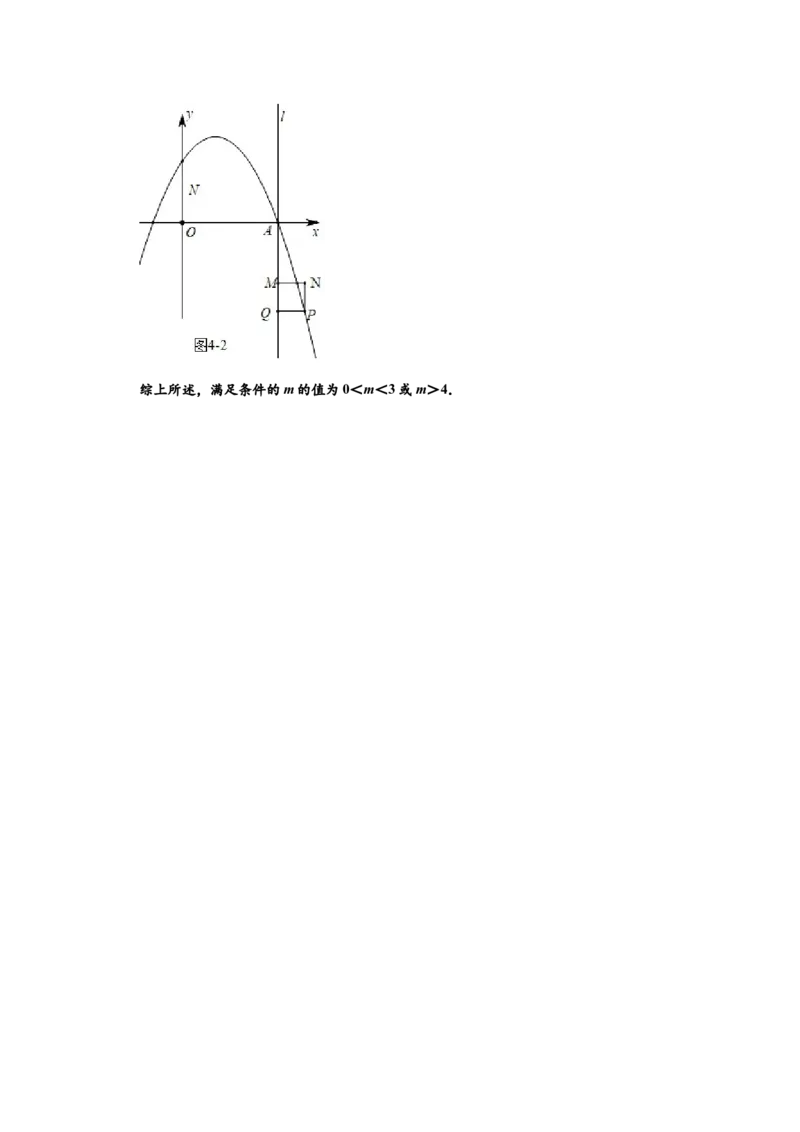
当m>4时,点M在点Q的上方,也满足条件,如图4﹣2中,综上所述,满足条件的m的值为0<m<3或m>4.