文档内容
2021年广东省广州市中考数学试卷
一、选择题(本大题共10题,每小题3分,满分30分)
1.下列四个选项中,为负整数的是( )
A.0 B.﹣0.5 C.﹣ D.﹣2
2.如图,在数轴上,点A、B分别表示a、b,且a+b=0,若AB=6,则点A表示的数为(
)
A.﹣3 B.0 C.3 D.﹣6
3.方程 = 的解为( )
A.x=﹣6 B.x=﹣2 C.x=2 D.x=6
4.下列运算正确的是( )
A.|﹣(﹣2)|=﹣2 B.3+ =3
C.(a2b3)2=a4b6 D.(a﹣2)2=a2﹣4
5.下列命题中,为真命题的是( )
(1)对角线互相平分的四边形是平行四边形
(2)对角线互相垂直的四边形是菱形
(3)对角线相等的平行四边形是菱形
(4)有一个角是直角的平行四边形是矩形
A.(1)(2) B.(1)(4) C.(2)(4) D.(3)(4)
6.为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学
生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2
名女学生的概率为( )
A. B. C. D.
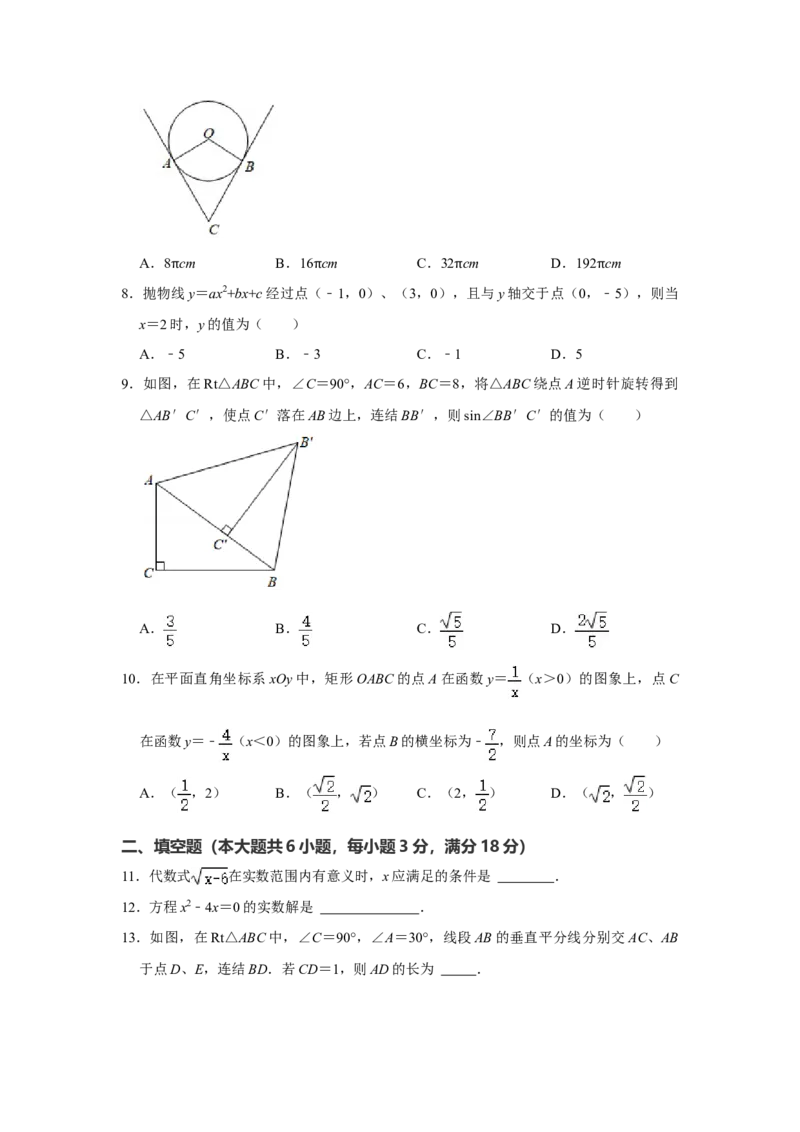
7.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若∠ACB=60°,则
劣弧AB的长是( )A.8 cm B.16 cm C.32 cm D.192 cm
8.抛物π线y=ax2+bx+c经过点(π﹣1,0)、(3,0),π且与y轴交于点(0,π﹣5),则当
x=2时,y的值为( )
A.﹣5 B.﹣3 C.﹣1 D.5
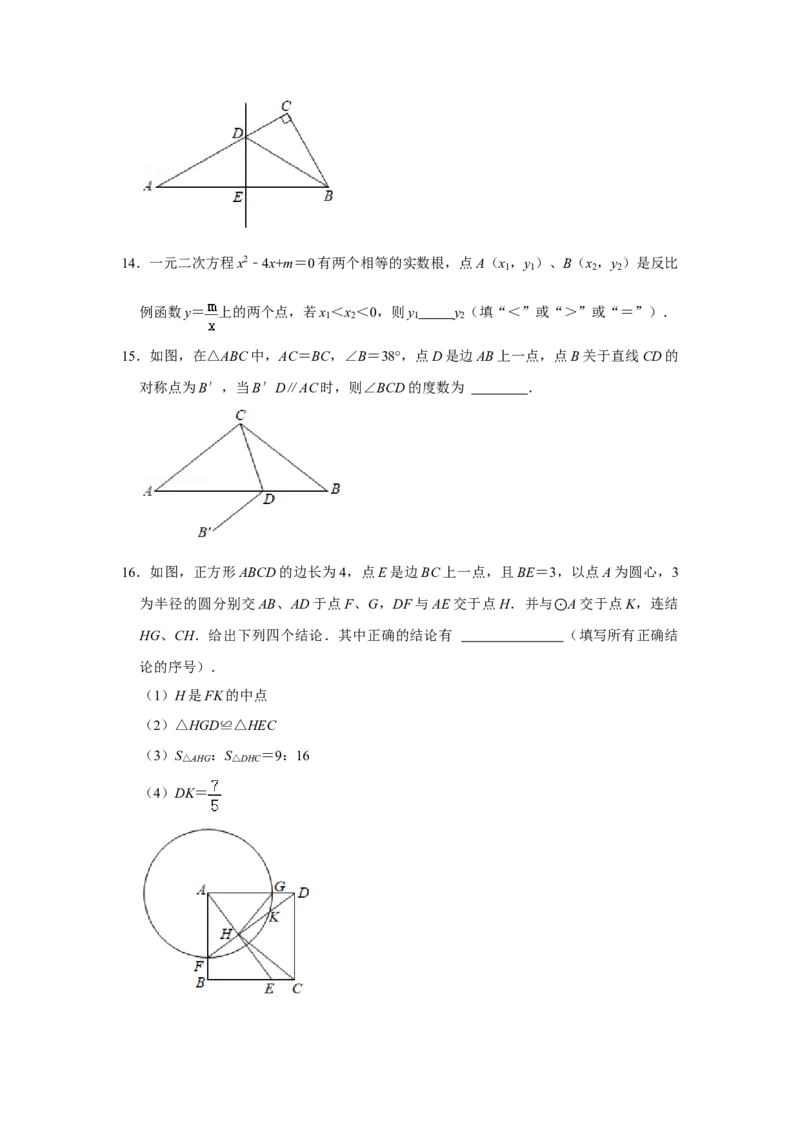
9.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到
△AB′C′,使点C′落在AB边上,连结BB′,则sin∠BB′C′的值为( )
A. B. C. D.
10.在平面直角坐标系xOy中,矩形OABC的点A在函数y= (x>0)的图象上,点C
在函数y=﹣ (x<0)的图象上,若点B的横坐标为﹣ ,则点A的坐标为( )
A.( ,2) B.( , ) C.(2, ) D.( , )
二、填空题(本大题共6小题,每小题3分,满分18分)
11.代数式 在实数范围内有意义时,x应满足的条件是 .
12.方程x2﹣4x=0的实数解是 .
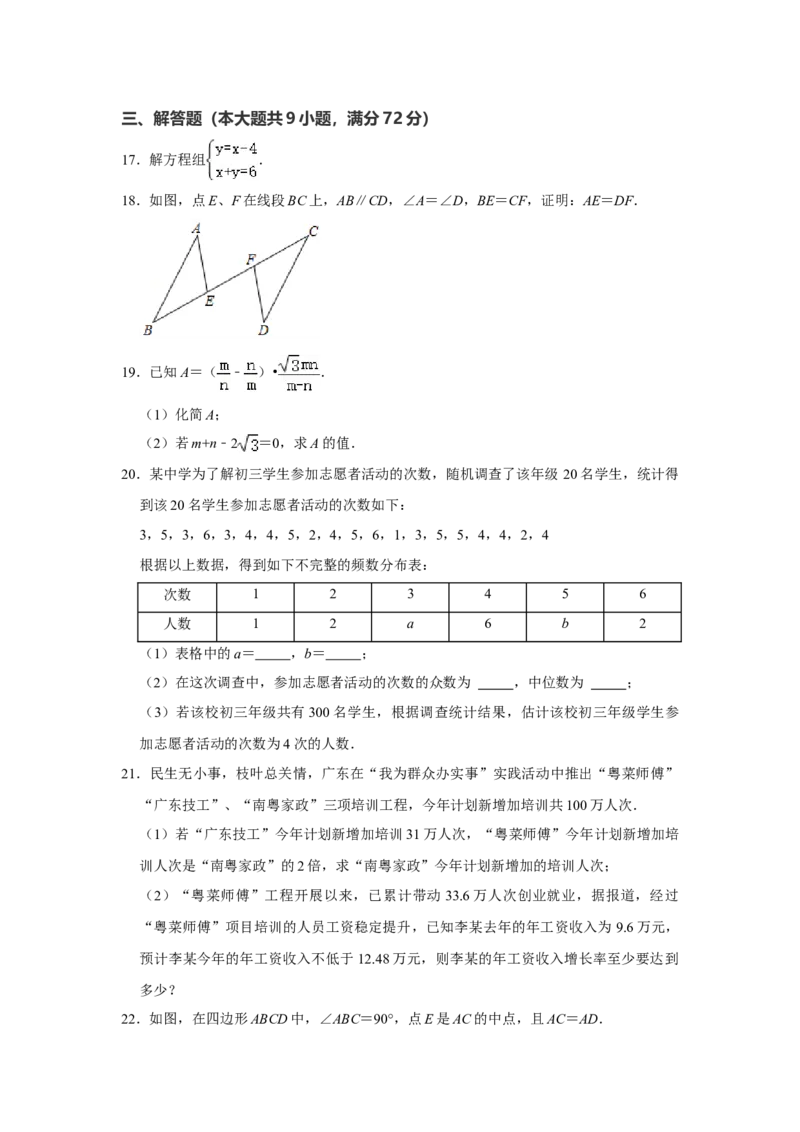
13.如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC、AB
于点D、E,连结BD.若CD=1,则AD的长为 .14.一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x ,y )、B(x ,y )是反比
1 1 2 2
例函数y= 上的两个点,若x <x <0,则y y (填“<”或“>”或“=”).
1 2 1 2
15.如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的
对称点为B′,当B′D∥AC时,则∠BCD的度数为 .
16.如图,正方形ABCD的边长为4,点E是边BC上一点,且BE=3,以点A为圆心,3
为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与 A交于点K,连结
HG、CH.给出下列四个结论.其中正确的结论有 ⊙(填写所有正确结
论的序号).
(1)H是FK的中点
(2)△HGD≌△HEC
(3)S△AHG :S△DHC =9:16
(4)DK=三、解答题(本大题共9小题,满分72分)
17.解方程组 .
18.如图,点E、F在线段BC上,AB∥CD,∠A=∠D,BE=CF,证明:AE=DF.
19.已知A=( ﹣ )• .
(1)化简A;
(2)若m+n﹣2 =0,求A的值.
20.某中学为了解初三学生参加志愿者活动的次数,随机调查了该年级 20名学生,统计得
到该20名学生参加志愿者活动的次数如下:
3,5,3,6,3,4,4,5,2,4,5,6,1,3,5,5,4,4,2,4
根据以上数据,得到如下不完整的频数分布表:
次数 1 2 3 4 5 6
人数 1 2 a 6 b 2
(1)表格中的a= ,b= ;
(2)在这次调查中,参加志愿者活动的次数的众数为 ,中位数为 ;
(3)若该校初三年级共有300名学生,根据调查统计结果,估计该校初三年级学生参
加志愿者活动的次数为4次的人数.
21.民生无小事,枝叶总关情,广东在“我为群众办实事”实践活动中推出“粤菜师傅”
“广东技工”、“南粤家政”三项培训工程,今年计划新增加培训共100万人次.
(1)若“广东技工”今年计划新增加培训31万人次,“粤菜师傅”今年计划新增加培
训人次是“南粤家政”的2倍,求“南粤家政”今年计划新增加的培训人次;
(2)“粤菜师傅”工程开展以来,已累计带动 33.6万人次创业就业,据报道,经过
“粤菜师傅”项目培训的人员工资稳定提升,已知李某去年的年工资收入为 9.6万元,
预计李某今年的年工资收入不低于12.48万元,则李某的年工资收入增长率至少要达到
多少?
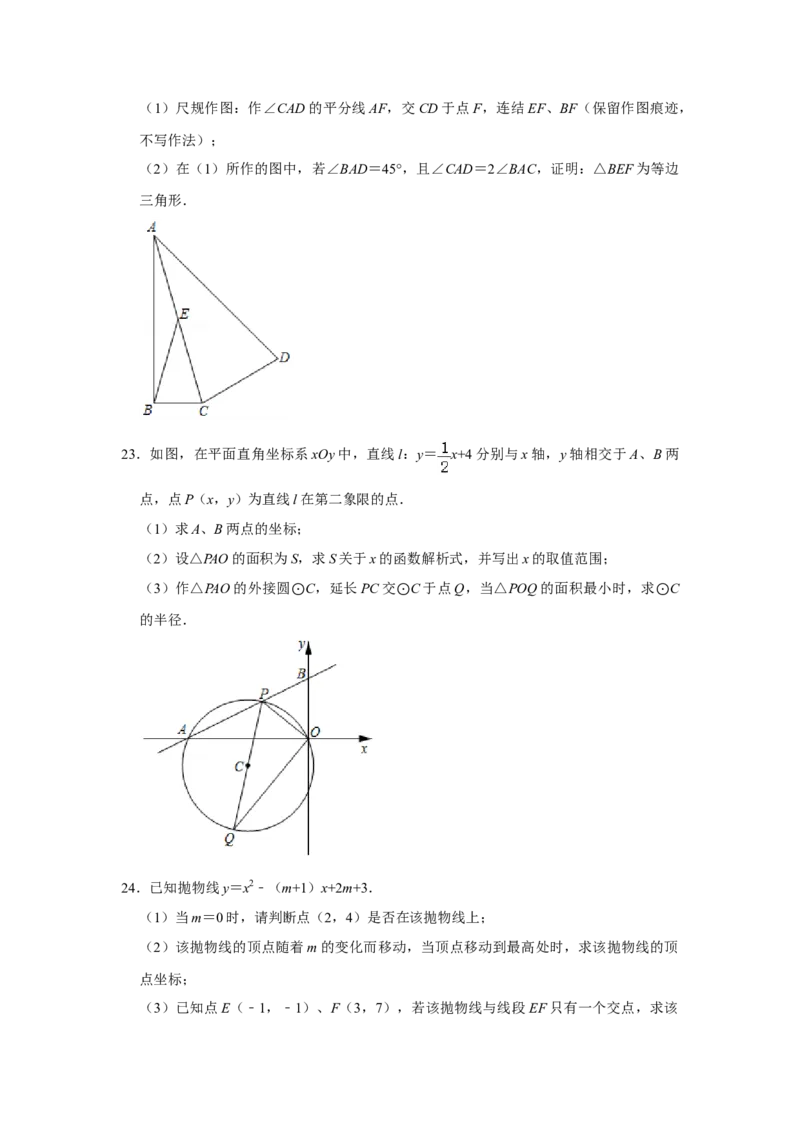
22.如图,在四边形ABCD中,∠ABC=90°,点E是AC的中点,且AC=AD.(1)尺规作图:作∠CAD的平分线AF,交CD于点F,连结EF、BF(保留作图痕迹,
不写作法);
(2)在(1)所作的图中,若∠BAD=45°,且∠CAD=2∠BAC,证明:△BEF为等边
三角形.
23.如图,在平面直角坐标系xOy中,直线l:y= x+4分别与x轴,y轴相交于A、B两
点,点P(x,y)为直线l在第二象限的点.
(1)求A、B两点的坐标;
(2)设△PAO的面积为S,求S关于x的函数解析式,并写出x的取值范围;
(3)作△PAO的外接圆 C,延长PC交 C于点Q,当△POQ的面积最小时,求 C
的半径. ⊙ ⊙ ⊙
24.已知抛物线y=x2﹣(m+1)x+2m+3.
(1)当m=0时,请判断点(2,4)是否在该抛物线上;
(2)该抛物线的顶点随着m的变化而移动,当顶点移动到最高处时,求该抛物线的顶
点坐标;
(3)已知点E(﹣1,﹣1)、F(3,7),若该抛物线与线段EF只有一个交点,求该抛物线顶点横坐标的取值范围.
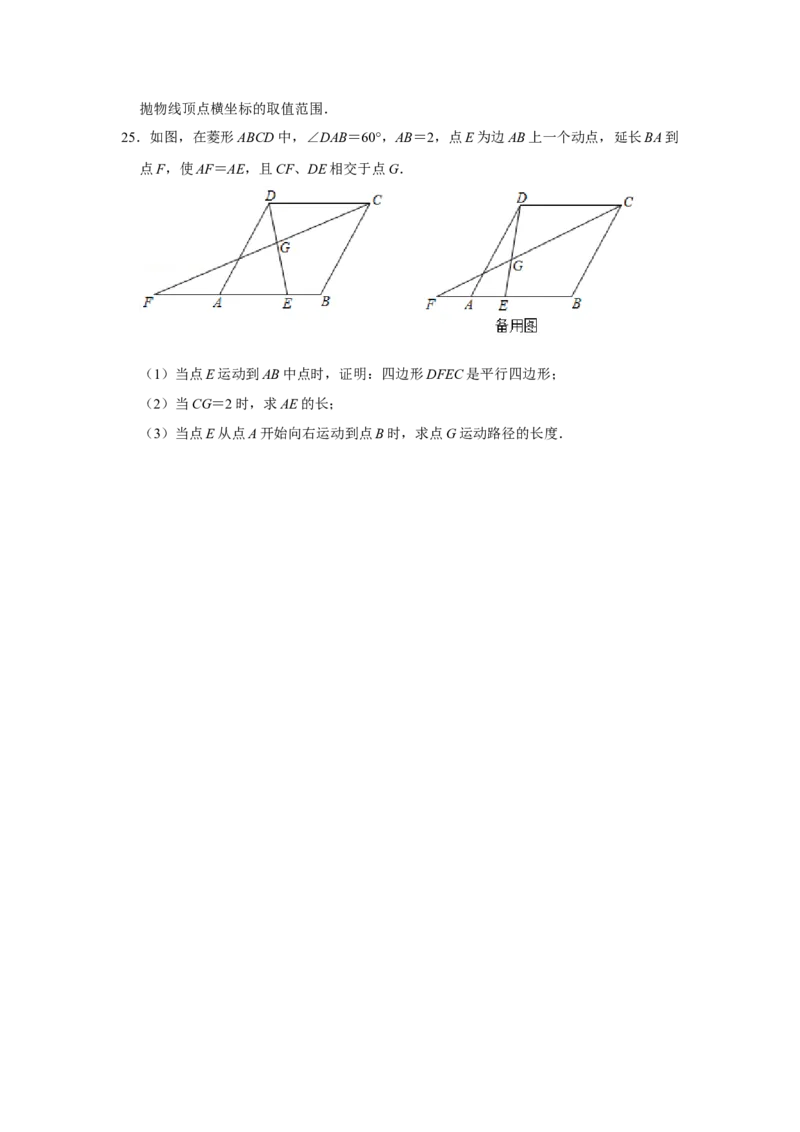
25.如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到
点F,使AF=AE,且CF、DE相交于点G.
(1)当点E运动到AB中点时,证明:四边形DFEC是平行四边形;
(2)当CG=2时,求AE的长;
(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.