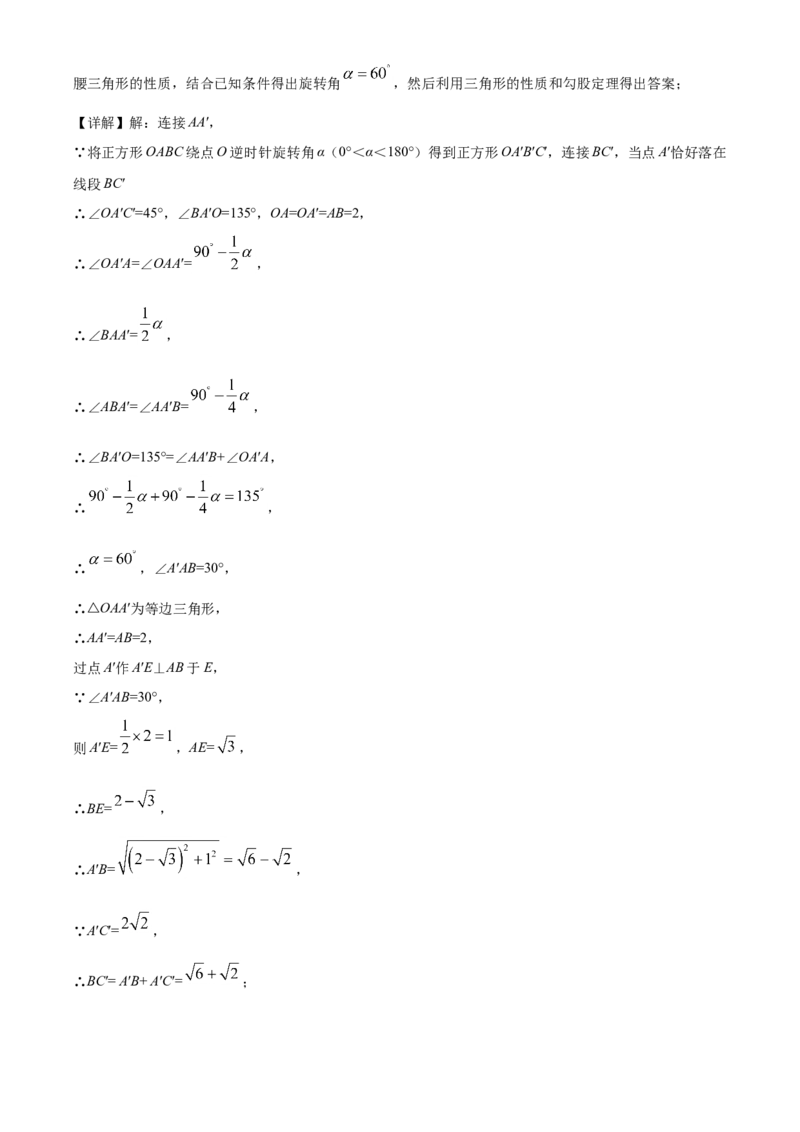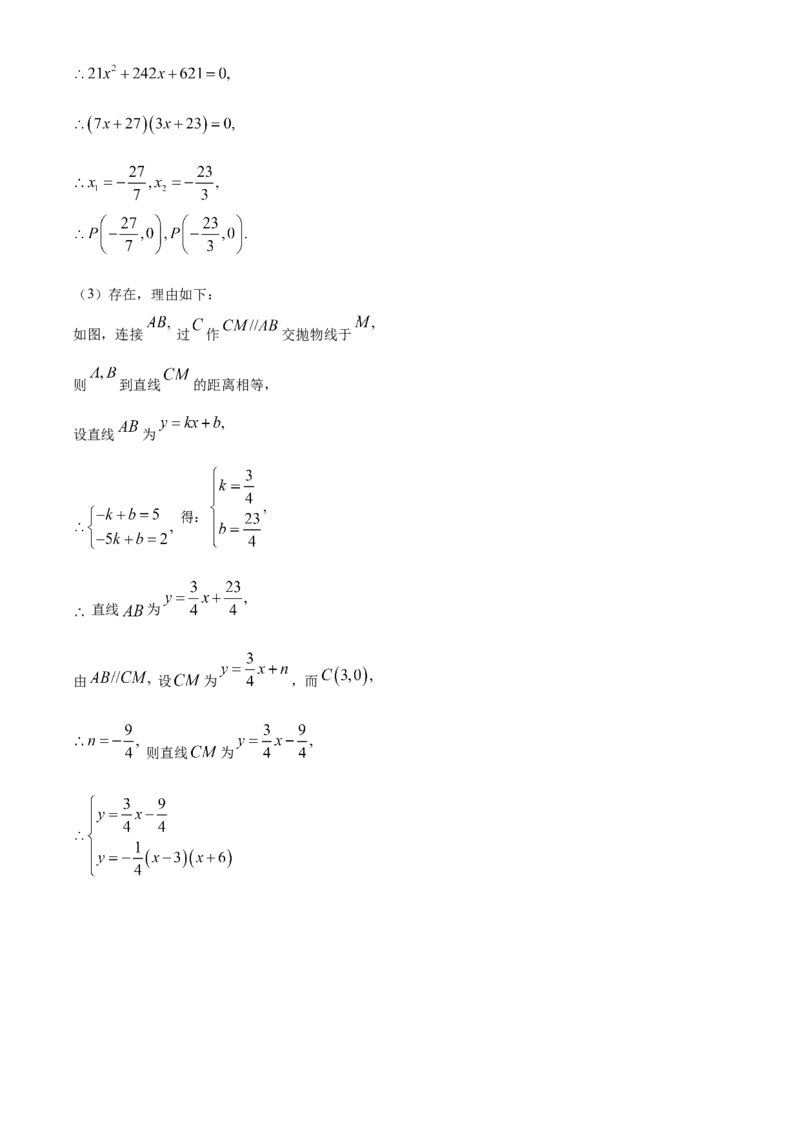文档内容
2021 年广西桂林市中考数学真题(解析版)
一、选择题(共12小题,每小题3分,共36分)
1. 有理数3,1,﹣2,4中,小于0的数是( )
A. 3 B. 1 C. ﹣2 D. 4
【答案】C
【解析】
【分析】根据有理数的大小比较即可得出结论.
【详解】解:∵ ,-2 ,
∴小于0的数是-2.
故选择C.
【点睛】本题考查有理数的大小比较,掌握有理数的大小比较方法是解题关键.
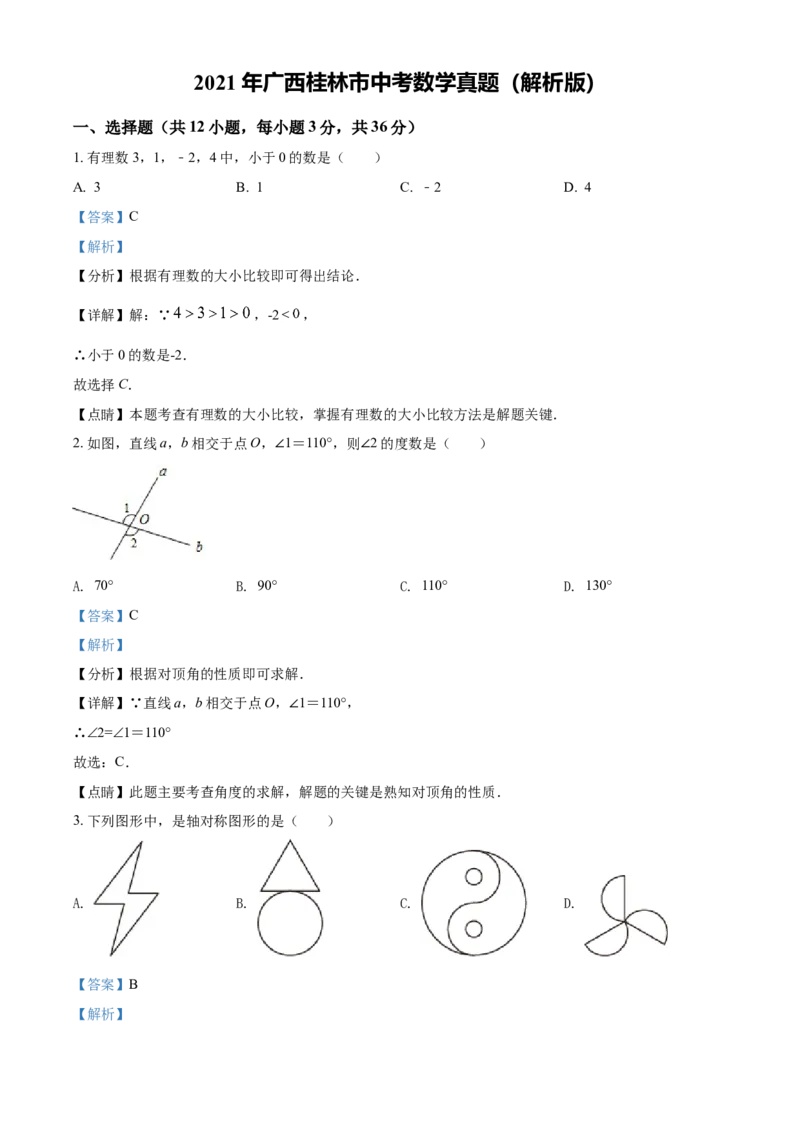
2. 如图,直线a,b相交于点O,∠1=110°,则∠2的度数是( )
A. 70° B. 90° C. 110° D. 130°
【答案】C
【解析】
【分析】根据对顶角的性质即可求解.
【详解】∵直线a,b相交于点O,∠1=110°,
∴∠2=∠1=110°
故选:C.
【点睛】此题主要考查角度的求解,解题的关键是熟知对顶角的性质.
3. 下列图形中,是轴对称图形的是( )
A. B. C. D.
【答案】B
【解析】【分析】直接利用轴对称图形的定义得出答案.如果一个图形沿一条直线折叠,直线两旁的部分能够互相
重合,这个图形叫做轴对称图形,这条直线叫做对称轴.
【详解】解:A.不是轴对称图形,不符合题意;
B.是轴对称图形,符合题意;
C.不是轴对称图形,不符合题意;
D.不是轴对称图形,不符合题意.
故选:B.
【点睛】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
此题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,
这个图形叫做轴对称图形,这条直线叫做对称轴.
的
4. 某班5名同学参加学校“感党恩,跟党走”主题演讲比赛,他们 成绩(单位:分)分别是8,6,8,7,
9,这组数据的中位数是( )
A. 6 B. 7 C. 8 D. 9
【答案】C
【解析】
【分析】根据中位数的定义即可求解.
【详解】把数据排列为6,7,8,8,9
故中位数是8
故选C.
【点睛】此题主要考查中位数的求解,解题的关键是熟知中位数的定义.
5. 若分式 的值等于0,则x的值是( )
A. 2 B. ﹣2 C. 3 D. ﹣3
【答案】A
【解析】
【分析】根据分式的值为0的条件:分子为0,分母不为0性质即可求解.
【详解】由题意可得: 且 ,解得 .
故选A.
【点睛】此题主要考查分式为零的条件,解题的关键是熟知分式的性质.
6. 细菌的个体十分微小,大约10亿个细菌堆积起来才有一颗小米粒那么大.某种细菌的直径是0.0000025
米,用科学记数法表示这种细菌的直径是( )A. 25×10﹣5米 B. 25×10﹣6米 C. 2.5×10﹣5米 D. 2.5×10﹣6米
【答案】D
【解析】
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为 a×10-n,与较大数的科学记数法不
同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:0.0000025=2.5×10-6.
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第
一个不为零的数字前面的0的个数所决定.
7. 将不等式组 的解集在数轴上表示出来,正确的是( )
A.
B.
C.
D.
【答案】B
【解析】
【分析】根据不等式组的解集表示方法即可求解.
【详解】不等式组 的解集在数轴上表示出来为
故选B.
【点睛】此题主要考查不等式的表示,解题的关键是熟知不等式的表示方法.8. 若点A(1,3)在反比例函数y 的图象上,则k的值是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】利用待定系数法把(1,3)代入反比例函数 得到关于k的一元一次方程,解之即可.
【详解】解:把(1,3)代入反比例函数 得:
=3,
解得:k=3,
故选择C.
【点睛】本题考查了待定系数法求反比例函数解析式,正确掌握待定系数法求反比例函数解析式方法,把
图象上点的坐标代入是解题的关键.
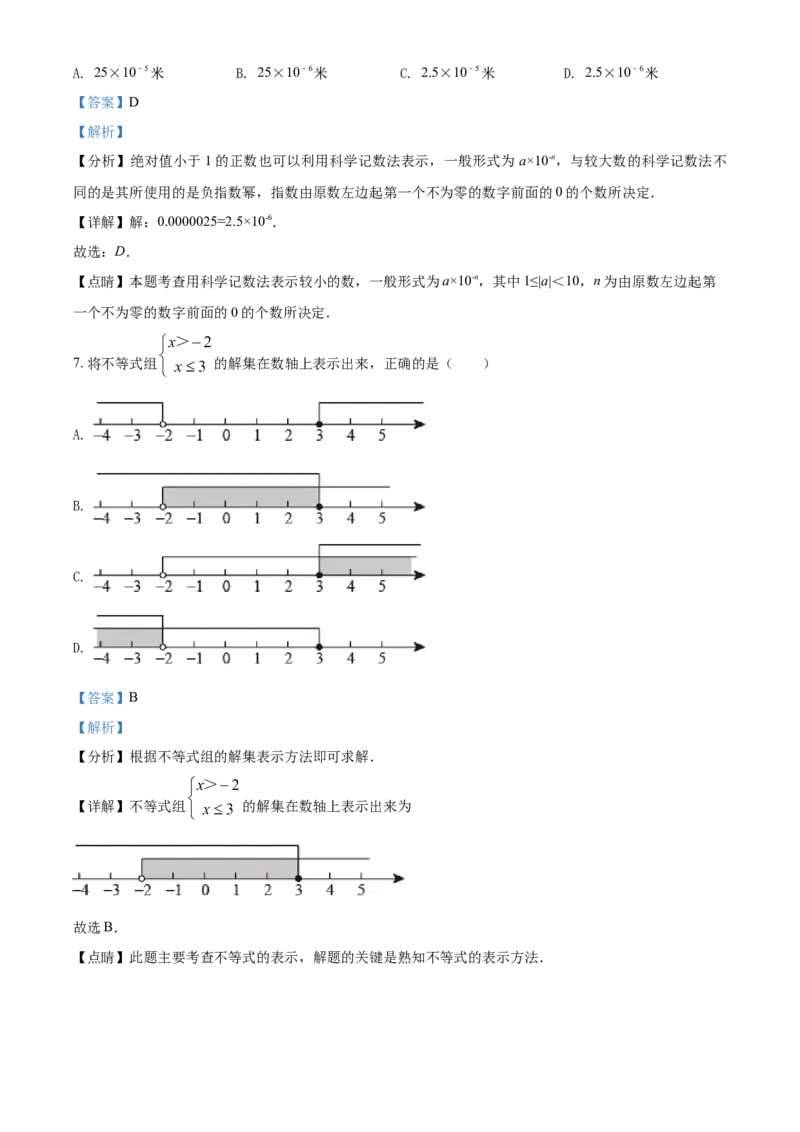
9. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )
A. 60° B. 90° C. 120° D. 150°
【答案】B
【解析】
【分析】直接根据直径所对的圆周角是直角进行判断即可.
【详解】解:∵AB是⊙O的直径,点C是⊙O上一点,
∴∠C=90°
故选:B
【点睛】此题主要考查了:半圆(或直径)所对的圆周角是直角,灵活掌握半圆(或直径)所对的圆周角
是直角是解答此题的关键.
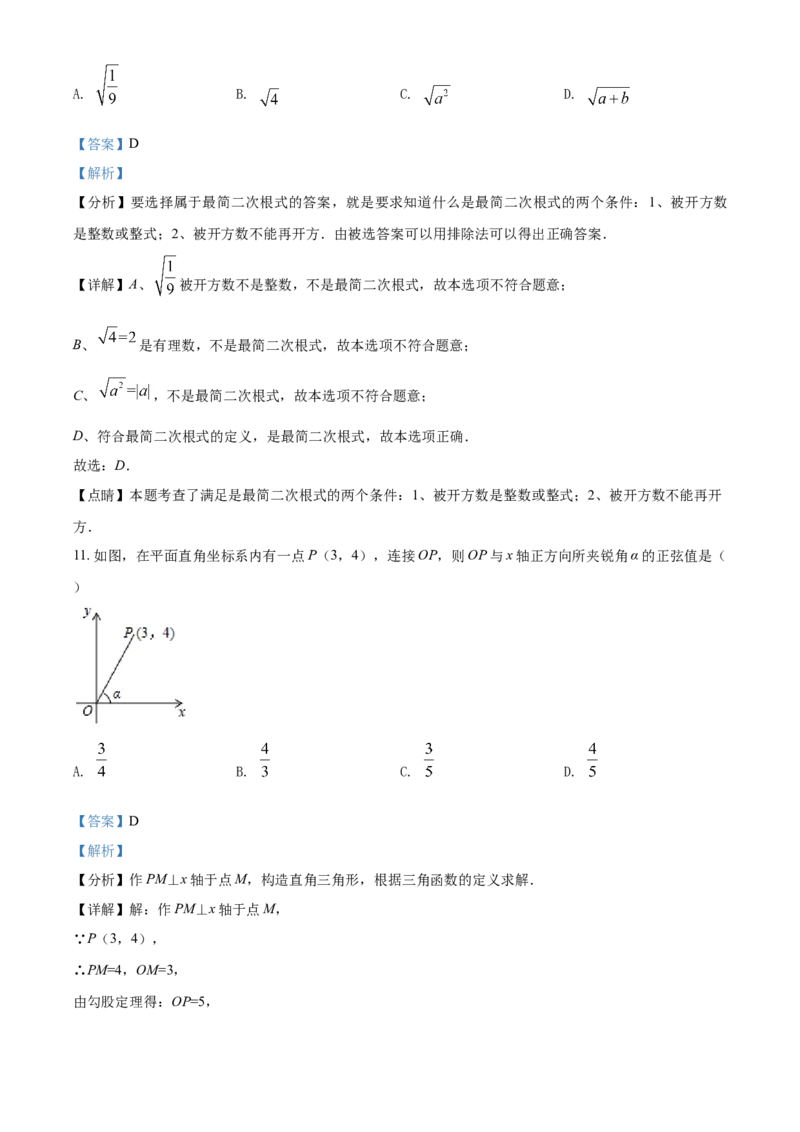
10. 下列根式中,是最简二次根式的是( )A. B. C. D.
【答案】D
【解析】
【分析】要选择属于最简二次根式的答案,就是要求知道什么是最简二次根式的两个条件:1、被开方数
是整数或整式;2、被开方数不能再开方.由被选答案可以用排除法可以得出正确答案.
【详解】A、 被开方数不是整数,不是最简二次根式,故本选项不符合题意;
B、 是有理数,不是最简二次根式,故本选项不符合题意;
C、 ,不是最简二次根式,故本选项不符合题意;
D、符合最简二次根式的定义,是最简二次根式,故本选项正确.
故选:D.
【点睛】本题考查了满足是最简二次根式的两个条件:1、被开方数是整数或整式;2、被开方数不能再开
方.
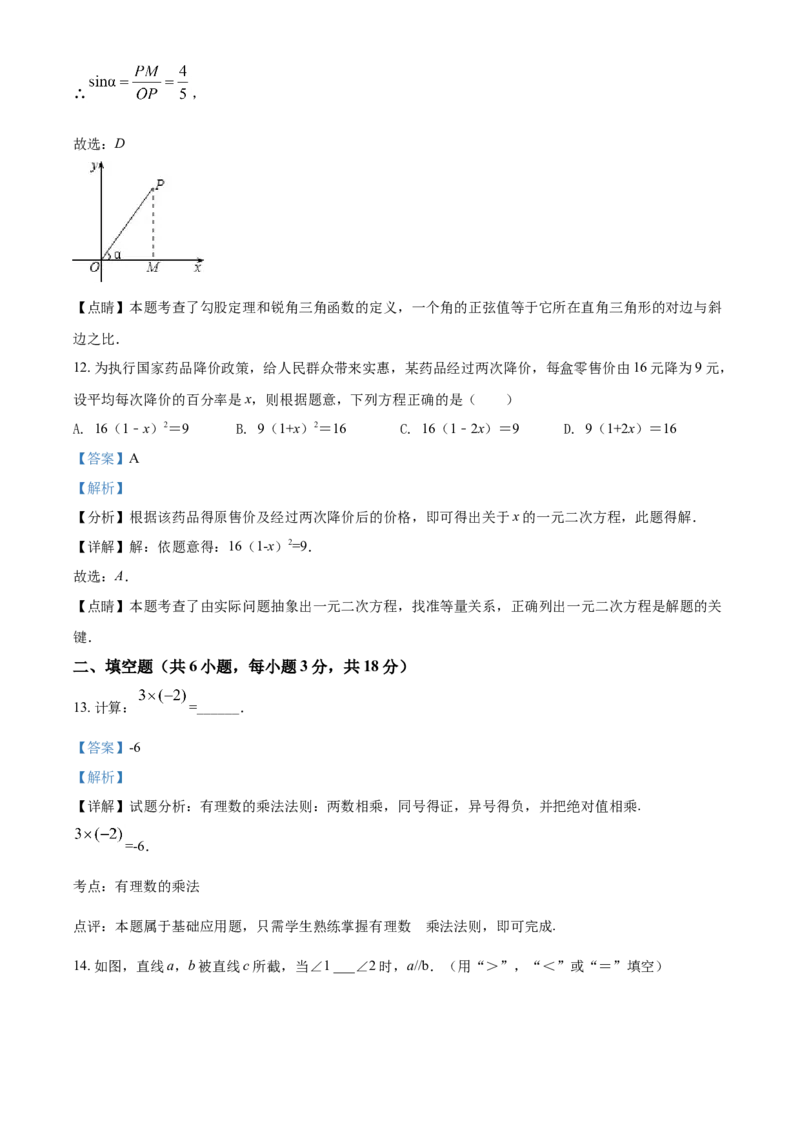
11. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是(
)
A. B. C. D.
【答案】D
【解析】
【分析】作PM⊥x轴于点M,构造直角三角形,根据三角函数的定义求解.
【详解】解:作PM⊥x轴于点M,
∵P(3,4),
∴PM=4,OM=3,
由勾股定理得:OP=5,∴ ,
故选:D
【点睛】本题考查了勾股定理和锐角三角函数的定义,一个角的正弦值等于它所在直角三角形的对边与斜
边之比.
12. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由16元降为9元,
设平均每次降价的百分率是x,则根据题意,下列方程正确的是( )
A. 16(1﹣x)2=9 B. 9(1+x)2=16 C. 16(1﹣2x)=9 D. 9(1+2x)=16
【答案】A
【解析】
【分析】根据该药品得原售价及经过两次降价后的价格,即可得出关于x的一元二次方程,此题得解.
【详解】解:依题意得:16(1-x)2=9.
故选:A.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关
键.
二、填空题(共6小题,每小题3分,共18分)
13. 计算: =______.
【答案】-6
【解析】
【详解】试题分析:有理数的乘法法则:两数相乘,同号得证,异号得负,并把绝对值相乘.
=-6.
考点:有理数的乘法
的
点评:本题属于基础应用题,只需学生熟练掌握有理数 乘法法则,即可完成.
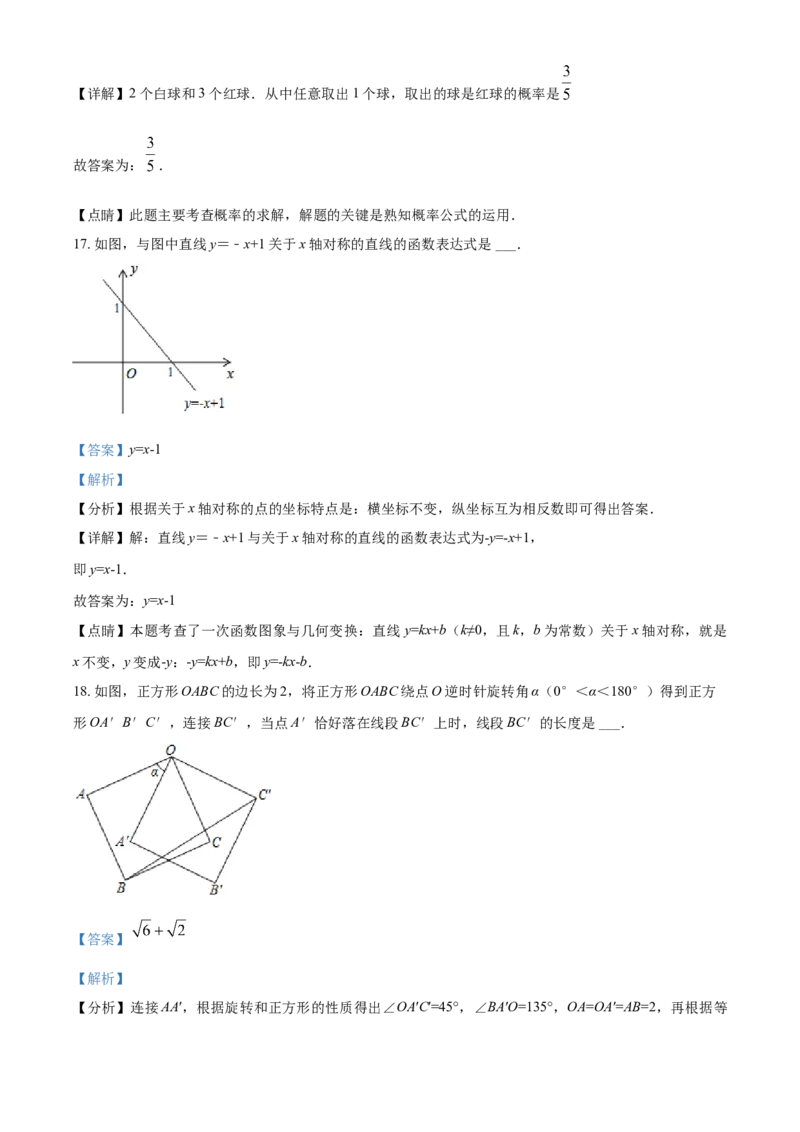
14. 如图,直线a,b被直线c所截,当∠1 ___∠2时,a//b.(用“>”,“<”或“=”填空)【答案】=.
【解析】
【分析】由图形可知∠1 与∠2 是同位角,利用直线平行判定定理可以确定∠1 =∠2,可判断a//b.
【详解】解:∵直线a,b被直线c所截,∠1与∠2是同位角,
∴当∠1 =∠2,a//b.
故答案为=.
【点睛】本题考查平行线判定,掌握平行线判定判定定理是解题关键.
15. 如图,在 ABC中,D、E分别是AB、AC的中点,若DE=4,则BC是________.
【答案】8
【解析】
【分析】根据三角形中位线定理解答即可.
【详解】∵D、E分别是AB和AC上的中点,
∴BC=2DE=8,
故答案为8.
16. 在一个不透明的袋中装有大小和质地都相同的5个球:2个白球和3个红球.从中任意取出1个球,取
出的球是红球的概率是 ___.
【答案】
【解析】
【分析】根据概率公式即可求解.【详解】2个白球和3个红球.从中任意取出1个球,取出的球是红球的概率是
故答案为: .
【点睛】此题主要考查概率的求解,解题的关键是熟知概率公式的运用.
17. 如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 ___.
【答案】y=x-1
【解析】
【分析】根据关于x轴对称的点的坐标特点是:横坐标不变,纵坐标互为相反数即可得出答案.
【详解】解:直线y=﹣x+1与关于x轴对称的直线的函数表达式为-y=-x+1,
即y=x-1.
故答案为:y=x-1
【点睛】本题考查了一次函数图象与几何变换:直线 y=kx+b(k≠0,且k,b为常数)关于x轴对称,就是
x不变,y变成-y:-y=kx+b,即y=-kx-b.
18. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方
形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 ___.
【答案】
【解析】
【分析】连接AA′,根据旋转和正方形的性质得出∠OA′C′=45°,∠BA′O=135°,OA=OA′=AB=2,再根据等腰三角形的性质,结合已知条件得出旋转角 ,然后利用三角形的性质和勾股定理得出答案;
【详解】解:连接AA′,
∵将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在
线段BC′
∴∠OA′C′=45°,∠BA′O=135°,OA=OA′=AB=2,
∴∠OA′A=∠OAA′= ,
∴∠BAA′= ,
∴∠ABA′=∠AA′B= ,
∴∠BA′O=135°=∠AA′B+∠OA′A,
∴ ,
∴ ,∠A′AB=30°,
∴△OAA′为等边三角形,
∴AA′=AB=2,
过点A′作A′E⊥AB于E,
∵∠A′AB=30°,
则A′E= ,AE= ,
∴BE= ,
∴A′B= ,
∵A′C′= ,
∴BC′= A′B+ A′C′= ;故答案为:
【点睛】本题考查了旋转的性质、正方形的性质、等腰直角三角形以及勾股定理,解题的关键是得出旋转
角 得出△OAA′为等边三角形.
三、解答题(本大题共8题,共66分)
19. 计算:|﹣3|+(﹣2)2.
【答案】7
【解析】
【分析】根据有理数的绝对值以及乘方的意义化简各数后即可得到答案.
【详解】解:|﹣3|+(﹣2)2
=3+4
=7
【点睛】此题主要考查了有理数的运算,正确化简各数是解答此题的关键.
20. 解一元一次方程:4x﹣1=2x+5.
【答案】x =3.
【解析】
【分析】先把方程化移项,合并同类项,系数化1法即可.
【详解】解:4 x﹣1=2x+5,
移项得:4 x﹣2x=5+1
合并同类项得:2 x=6,
∴系数化1得:x =3.
【点睛】本题考查了一元一次方程的解法移项、合并同类项、系数化1.掌握解一元一次方程常用的方法
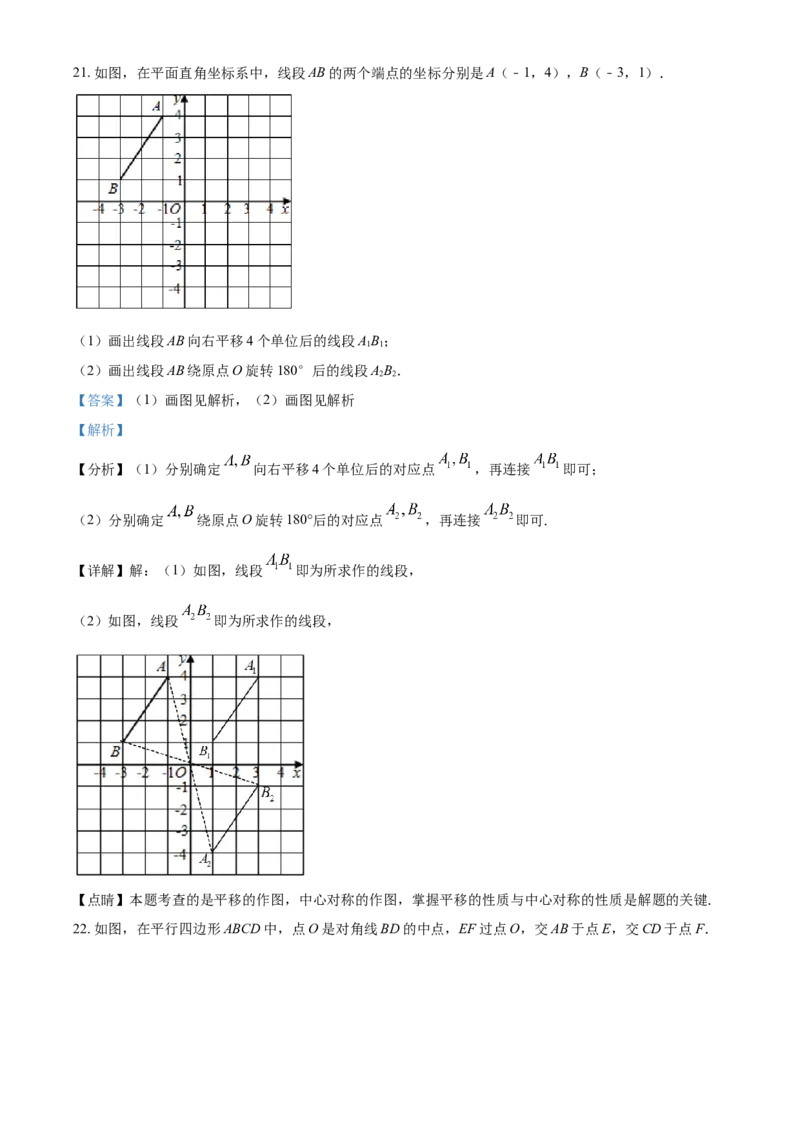
要根据方程的特点灵活选用合适的方法21. 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(﹣1,4),B(﹣3,1).
(1)画出线段AB向右平移4个单位后的线段AB;
1 1
(2)画出线段AB绕原点O旋转180°后的线段AB.
2 2
【答案】(1)画图见解析,(2)画图见解析
【解析】
【分析】(1)分别确定 向右平移4个单位后的对应点 ,再连接 即可;
(2)分别确定 绕原点O旋转180°后的对应点 ,再连接 即可.
【详解】解:(1)如图,线段 即为所求作的线段,
(2)如图,线段 即为所求作的线段,
【点睛】本题考查的是平移的作图,中心对称的作图,掌握平移的性质与中心对称的性质是解题的关键.
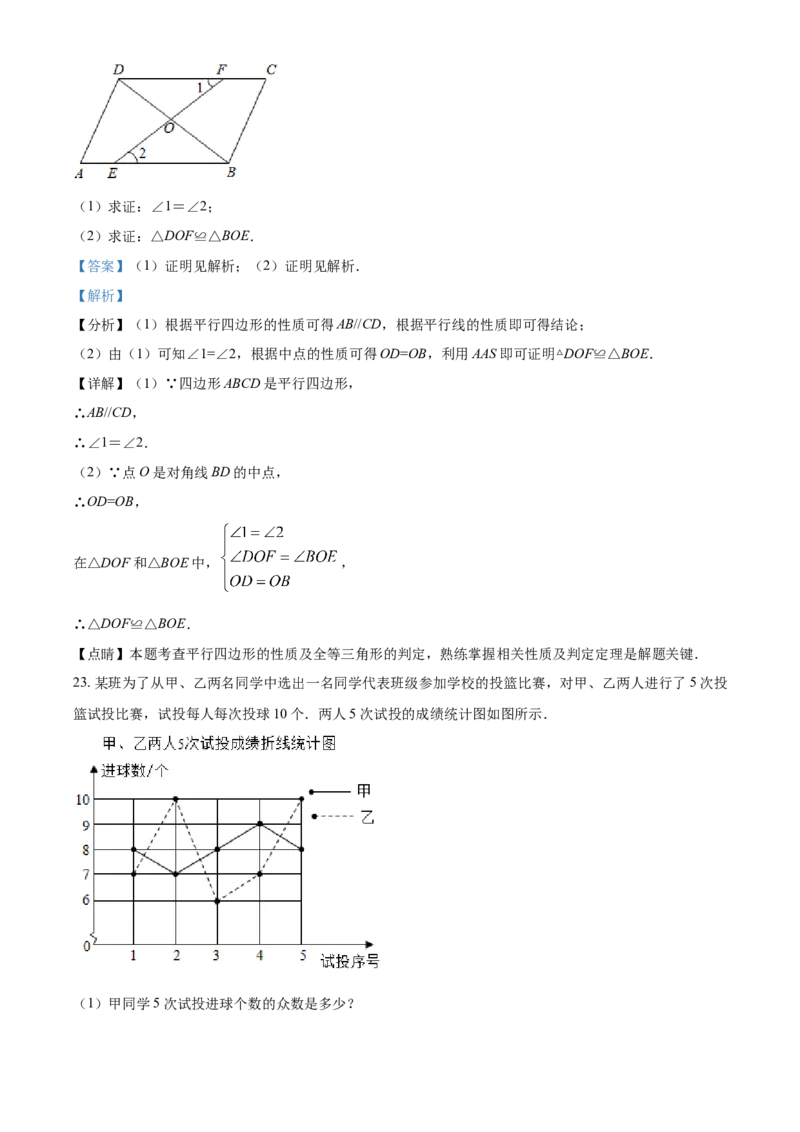
22. 如图,在平行四边形ABCD中,点O是对角线BD的中点,EF过点O,交AB于点E,交CD于点F.(1)求证:∠1=∠2;
(2)求证:△DOF≌△BOE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
【分析】(1)根据平行四边形的性质可得AB//CD,根据平行线的性质即可得结论;
(2)由(1)可知∠1=∠2,根据中点的性质可得OD=OB,利用AAS即可证明△DOF≌△BOE.
【详解】(1)∵四边形ABCD是平行四边形,
∴AB//CD,
∴∠1=∠2.
(2)∵点O是对角线BD的中点,
∴OD=OB,
在△DOF和△BOE中, ,
∴△DOF≌△BOE.
【点睛】本题考查平行四边形的性质及全等三角形的判定,熟练掌握相关性质及判定定理是解题关键.
23. 某班为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛,对甲、乙两人进行了5次投
篮试投比赛,试投每人每次投球10个.两人5次试投的成绩统计图如图所示.
(1)甲同学5次试投进球个数的众数是多少?(2)求乙同学5次试投进球个数的平均数;
(3)不需计算,请根据折线统计图判断甲、乙两名同学谁的投篮成绩更加稳定?
(4)学校投篮比赛的规则是每人投球10个,记录投进球的个数.由往届投篮比赛的结果推测,投进8个
球即可获奖,但要取得冠军需要投进10个球.请你根据以上信息,从甲、乙两名同学中推荐一名同学参加
学校的投篮比赛,并说明推荐的理由.
是
【答案】(1)众数 8个,(2) 个;(3)甲投篮成绩更加稳定;(4)推荐乙参加投篮比赛,理
由见解析.
【解析】
【分析】(1)根据众数定义求即可;
(2)根据平均数公式求即可;
(3)根据折线统计图甲投篮成绩波动较小,折线统计图乙投篮成绩波动较大,可得甲投篮成绩更加稳定;
(4)由乙的众数是10,取得冠军需要投进10个球,推荐乙参加投篮比赛即可.
【详解】解:(1)∵甲同学5次试投进球个数分别为8,7,8,9,8,
∴甲同学5次试投进球个数的众数是8个,
(2)乙同学5次试投进球个数分别为8,10,6,7,10,
∴ 个;
(3)根据折线统计图甲投篮成绩波动较小,折线统计图乙投篮成绩波动较大,
∴甲投篮成绩更加稳定;
(4)∵乙的众数是10,取得冠军需要投进10个球,而甲没有进10球的可能,为了能获得冠军,推荐乙
参加投篮比赛.
【点睛】本题考查众数,平均数,图形的波动大小,以及利用众数进行决策,掌握众数,平均数,图形的
波动大小,以及利用众数进行决策是解题关键.
24. 为了美化环境,建设生态桂林,某社区需要进行绿化改造,现有甲、乙两个绿化工程队可供选择,已
知甲队每天能完成的绿化改造面积比乙队多200平方米,甲队与乙队合作一天能完成800平方米的绿化改
造面积.
(1)甲、乙两工程队每天各能完成多少平方米的绿化改造面积?
(2)该社区需要进行绿化改造的区域共有12000平方米,甲队每天的施工费用为600元,乙队每天的施工
费用为400元,比较以下三种方案:①甲队单独完成;②乙队单独完成;③甲、乙两队全程合作完成.哪
一种方案的施工费用最少?
【答案】(1)甲队每天能完成绿化的面积是500平方米,乙队每天能完成绿化的面积是 300平方米;(2)选择方案①完成施工费用最少
【解析】
【分析】(1)设乙工程队每天能完成绿化的面积是x平方米,根据甲队与乙队合作一天能完成800平方米
的绿化改造面积,列出方程,求解即可;
(2)设应安排甲队工作a天,根据这次的绿化总费用不超过8万元,列出不等式,求解即可.
【详解】解:(1)设乙队每天能完成绿化的面积是x平方米,则甲队每天能完成绿化的面积是(x+200)
米,
依题意得:x+x+200=800
解得:x=300,
x+200=500
∴甲队每天能完成绿化的面积是500平方米,乙队每天能完成绿化的面积是300平方米.
(2)选择方案①甲队单独完成所需费用= (元);
选择方案②乙队单独完成所需费用= (元);
选择方案③甲、乙两队全程合作完成所需费用= (元);
∴选择方案①完成施工费用最少.
【点睛】本题考查了一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出方程;(2)利
用总费用=每天支出的费用×工作时间,分别求出选择各方案所需费用.
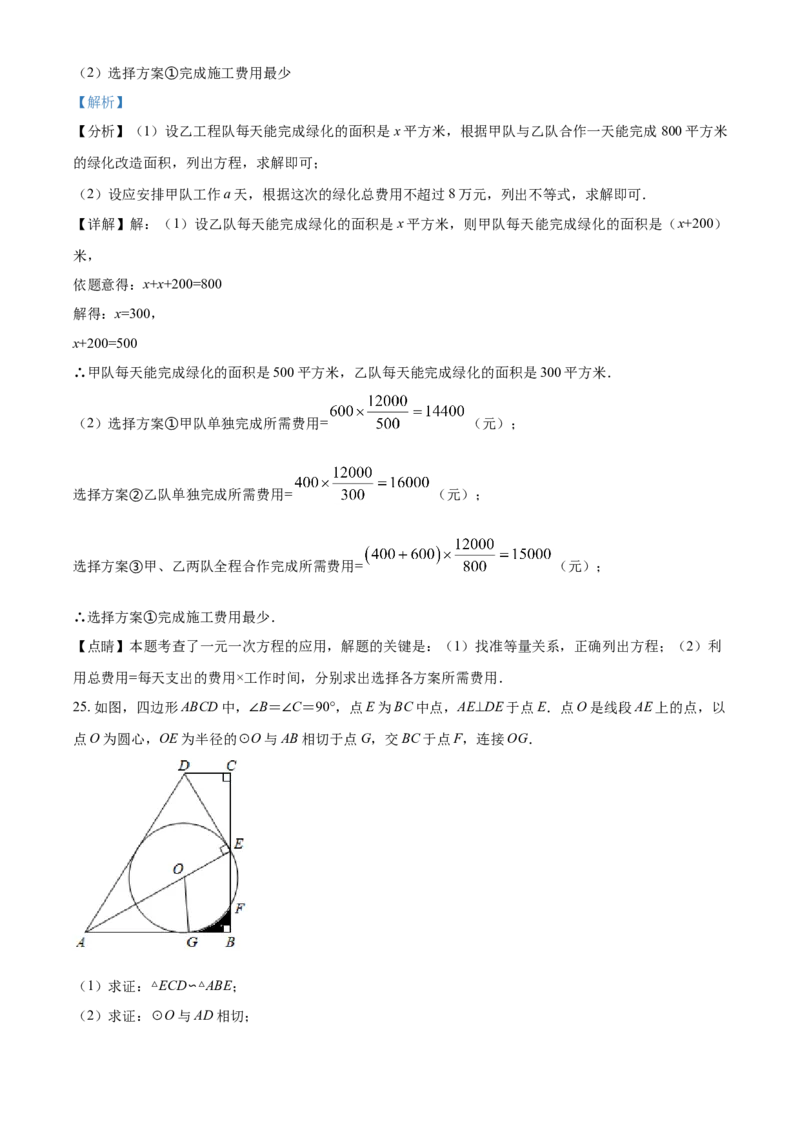
25. 如图,四边形ABCD中,∠B=∠C=90°,点E为BC中点,AE⊥DE于点E.点O是线段AE上的点,以
点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F,连接OG.
(1)求证:△ECD∽△ABE;
(2)求证:⊙O与AD相切;(3)若BC=6,AB=3 ,求⊙O的半径和阴影部分的面积.
【答案】(1)见解析(2)见解析(3)半径为2,面积为
【解析】
【分析】(1)根据垂直的性质及相似三角形的判定定理即可求解;
(2)延长DE、AB交于N点,先证明△DCE≌△NBE,再得到△AND是等腰三角形,得到
∠DAE=∠NAE,再通过角平分线的性质即可得到OG=OM=r,故可证明;
(3)求出∠FOG=60°,再根据梯形与扇形的面积公式即可求解.
【详解】(1)∵∠B=∠C=90°,AE⊥DE于点E.
∴∠EAB+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠EAB=∠DEC
由∠B=∠C=90°
∴△ECD∽△ABE;
(2)过点O作OM⊥AD,延长DE、AB交于N点
∴CD BN
∴∠CDE=∠N
∵点E为BC中点
∴CE=BE,
又∠EBN=∠C=90°
∴△DCE≌△NBE
∴DE=NE
∵AE⊥DN
∴AD=AN,∠ADE=∠ANE
∵∠DAE=90°-∠ADE,∠NAE=90°-∠ANE
∴∠DAE=∠NAE
∵AG是⊙O的切线
∴OG⊥AB
∵∠AMO=∠AGO=90°
∴OG=OM=r
∴OM是⊙O的切线;(3)∵BC=6,
∴BE=3
∵AB=3 ,
∴AE= =2BE
∴∠EAB=30°
∴AO=2OG,即AO=2r,
∵AE=AO+OE=3r=6
∴r=2
连接OF
∵∠OEF=60°,OE=OF
∴△OEF是等边三角形
∴∠EOF=60°,EF=OF=2,BF=3-2=1
∴∠FOG=180°-∠AOG-∠EOF=60°
在Rt AOG中,AG=
∴BG=AB-AG=
∴S =S -S = = .
阴 梯形OFBG 扇形FOG
【点睛】此题主要考查切线的判定与性质综合,解题的关键是熟知切线的判定定理、全等三角形与相似三
角形的判定与性质及扇形面积公式.
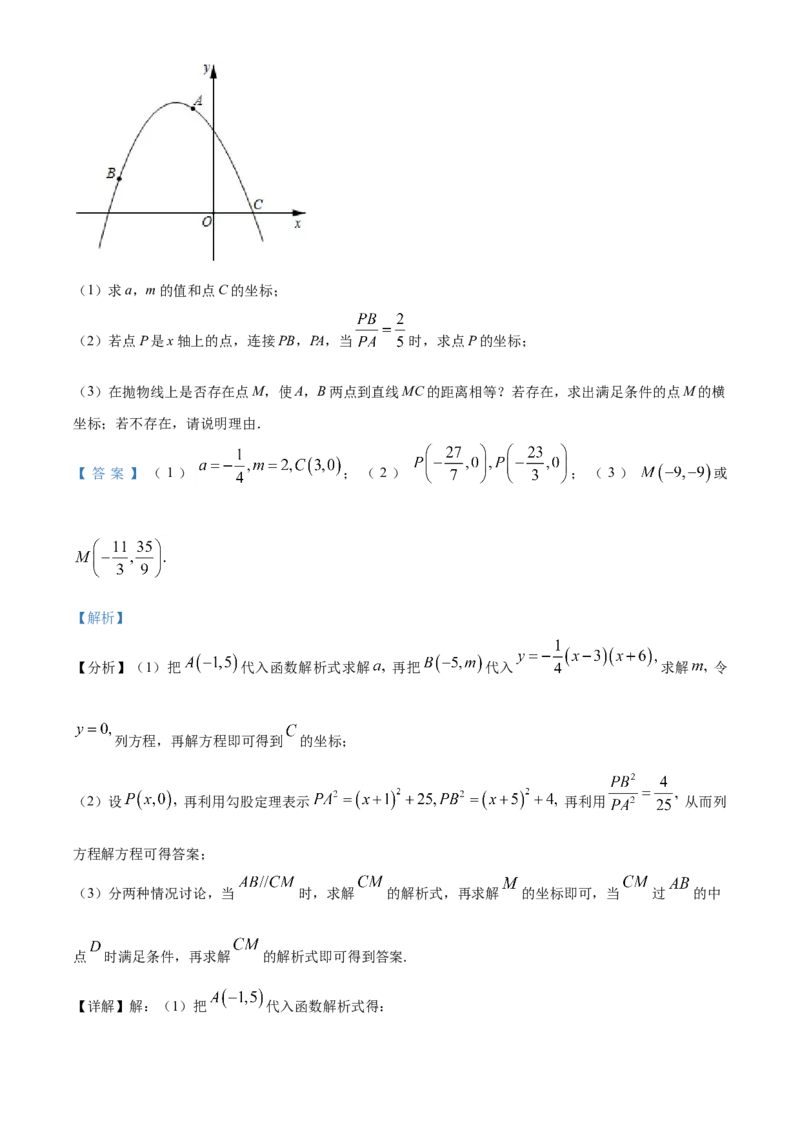
26. 如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m)与x轴的正半轴交于点
C.(1)求a,m的值和点C的坐标;
(2)若点P是x轴上的点,连接PB,PA,当 时,求点P的坐标;
(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横
坐标;若不存在,请说明理由.
【 答 案 】 ( 1 ) ; ( 2 ) ; ( 3 ) 或
【解析】
【分析】(1)把 代入函数解析式求解 再把 代入 求解 令
列方程,再解方程即可得到 的坐标;
(2)设 再利用勾股定理表示 再利用 从而列
方程解方程可得答案;
(3)分两种情况讨论,当 时,求解 的解析式,再求解 的坐标即可,当 过 的中
点 时满足条件,再求解 的解析式即可得到答案.
【详解】解:(1)把 代入函数解析式得:把 代入
令
结合题意可得:
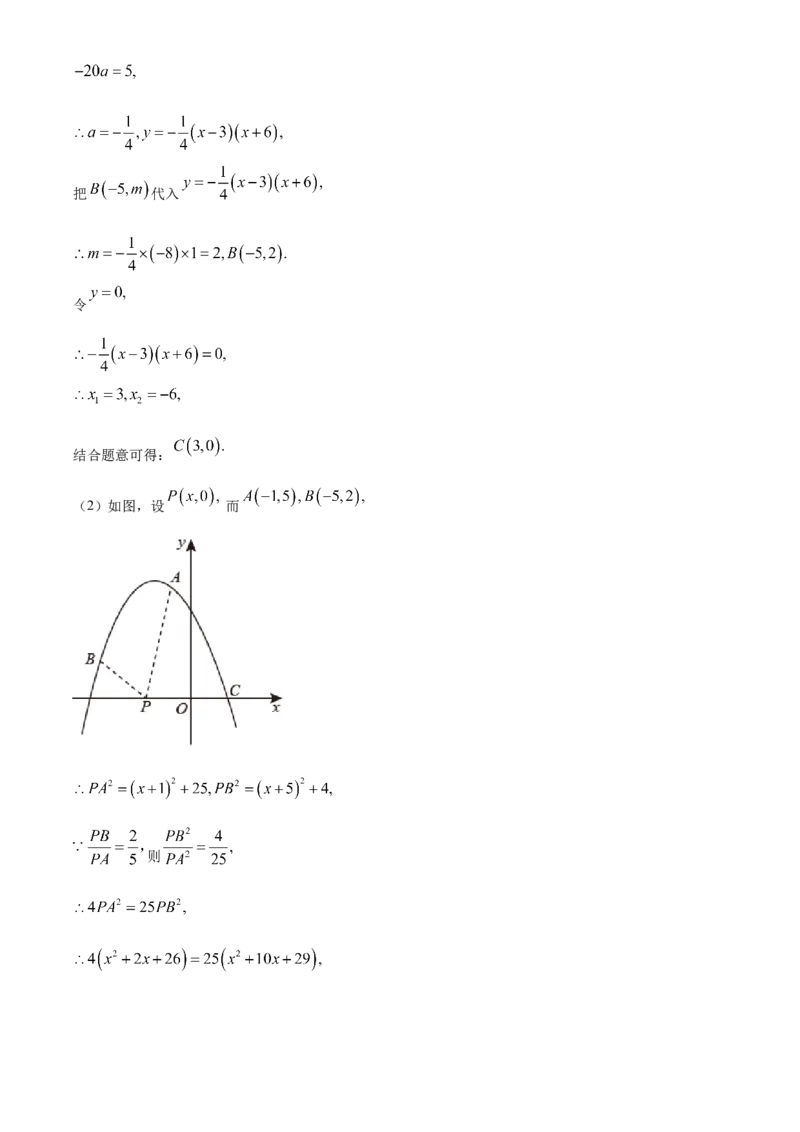
(2)如图,设 而
则(3)存在,理由如下:
如图,连接 过 作 交抛物线于
则 到直线 的距离相等,
设直线 为
得:
直线 为
由 设 为 ,而
则直线 为解得: 或
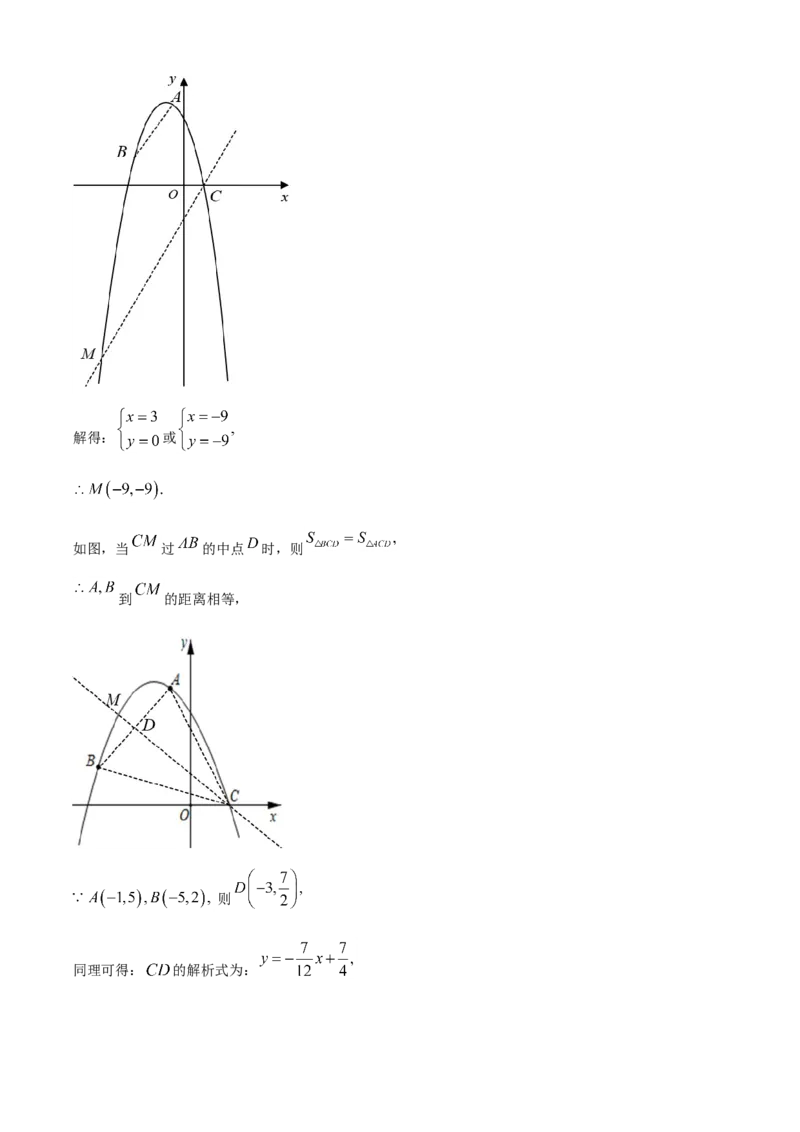
如图,当 过 的中点 时,则
到 的距离相等,
则
同理可得: 的解析式为:解得: 或
综上: 或
【点睛】本题考查的是利用待定系数法求解二次函数的解析式,勾股定理的应用,一元二次方程的解法,
两平行线之间的距离,三角形的中线的性质,灵活应用以上知识解题是解题的关键.