文档内容
2023—2024 学年安康市高三年级第三次质量联考
文科数学
考试满分:150分 考试时间:120分钟
注意事项:
1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码区域内。
2.全部答案在答题卡上完成,答在本试卷上无效。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需
改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案用0.5mm黑色笔迹签
字笔写在答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.设 ,则 ( )
A. B. C. D.
2.集合 ,则下列选项正确的是( )
A. B. C. D.
3.已知函数 ,公差不为0的等差数列 的前 项和为 .若 ,则
( )
A.1012 B.2024 C.3036 D.4048
4.若实数 满足约束条件 ,则 的最大值为( )
A.0 B.2 C.9 D.11
5.甲、乙、丙三人被随机的安排在周六、周日值班,每天至少要有一人值班,每人只在其中一天值班.则甲、
乙被安排在同一天值班的概率为( )
A. B. C. D.
6.在 中, 是 的中点, 与 相交于点 ,则 ( )
学科网(北京)股份有限公司A. B. C. D.
7.已知正数 满足 ,则( )
A. B. C. D.
8.已知 ,则 ( )
A. B. C. D.
9.侧棱长与底面边长均为 的正三棱柱的外接球的表面积为 ,则 ( )
A.12 B.8 C.6 D.4
10.已知直线 与椭圆 在第四象限交于 两点, 与 轴, 轴分别交于 两点,若
,则 的倾斜角是( )
A. B. C. D.
11.折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善
良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图
1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧 所在圆的半径分别是6和12,且
,则该圆台的体积为( )
图1 图2
A. B. C. D.
学科网(北京)股份有限公司12.在平面直角坐标系中,曲线 与坐标轴的交点都在圆 上, 为圆 的直径,点 是直
线 上任意一点,则 的最小值为( )
A.4 B.12 C.16 D.18
二、填空题:本题共4小题,每小题5分,共20分。
13.写出一个对称中心为 的奇函数 ___________.
14.已知数列 的前 项和为 ,且 ,则 ___________.
15.直线 与抛物线 交于 两点,若 ,则 ___________.
16.已知函数 ,都有 ,则 的取值范
围为___________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每
个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)作为一个基于大型语言处理模型的文字聊天工具,ChatGPT走红后,大模型的热度持续不减,
并日渐形成了“千模大战”的局面。百度的文心一言、阿里的通义千问、华为的盘古、腾讯的混元以及科大
讯飞的星火等多种大模型正如火如茶的发布上线。现有某大模型给出了会员有效期30天的两种不同费用,
100次的使用费为6元,500次的使用费为24元。后台调取了购买会员的200名用户基本信息,包括个人和
公司两种用户,统计发现购买24元的用户数是140,其中个人用户数比公司用户数少20,购买6元的公司用
户数是个人用户数的一半.
(1)完成如下用户类别与购买意向的 列联表;
购买6元 购买24元
个人用户
公司用户
总计
(2)能否有 的把握认为购买意向与用户类别有关?(运算结果保留三位小数)
附: ,临界值表如下:
0.10 0.05 0.025 0.01 0.005 0.001
学科网(北京)股份有限公司2.706 3.841 5.024 6.635 7.879 10.828
19.(12分)在三边均不相等的 中,角 对应的边分别为 ,若
.点 在线段 上,且 平分角 .
(1)求 ;
(2)若 ,求 的长度.
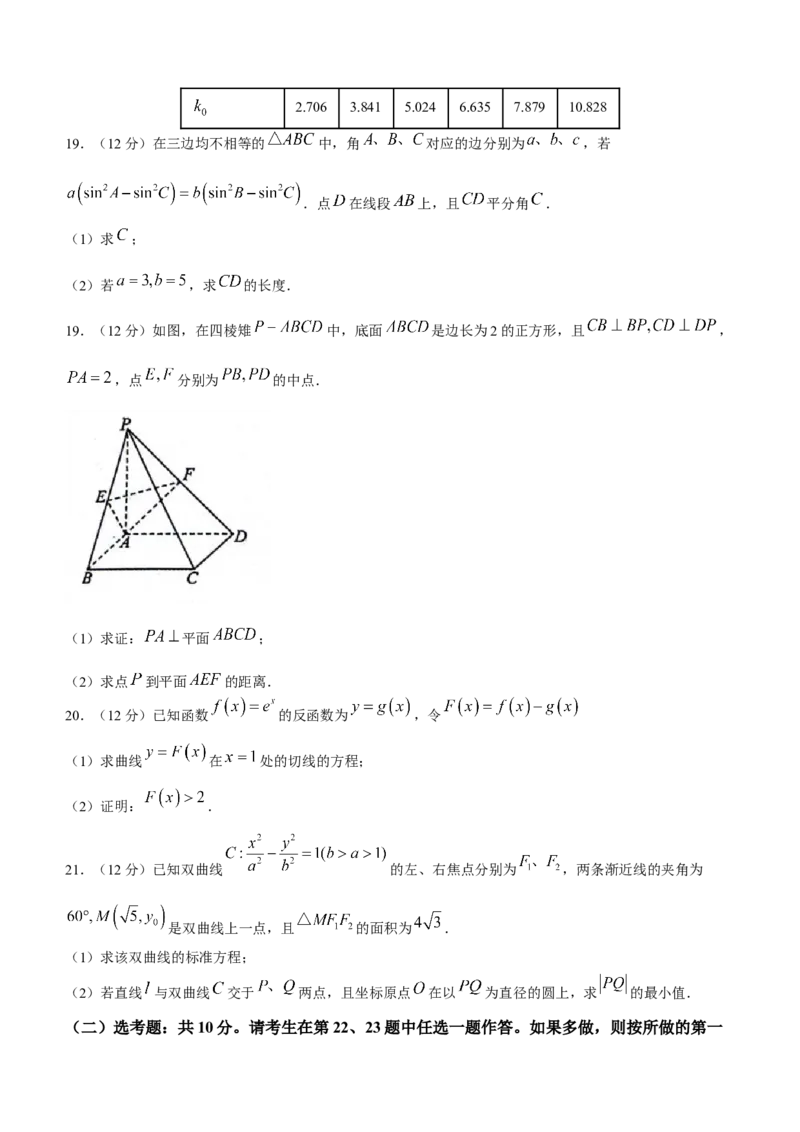
19.(12分)如图,在四棱雉 中,底面 是边长为2的正方形,且 ,
,点 分别为 的中点.
(1)求证: 平面 ;
(2)求点 到平面 的距离.
20.(12分)已知函数 的反函数为 ,令
(1)求曲线 在 处的切线的方程;
(2)证明: .
21.(12分)已知双曲线 的左、右焦点分别为 ,两条渐近线的夹角为
是双曲线上一点,且 的面积为 .
(1)求该双曲线的标准方程;
(2)若直线 与双曲线 交于 两点,且坐标原点 在以 为直径的圆上,求 的最小值.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一
学科网(北京)股份有限公司题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系 中,以坐标原点 为极点, 轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为
,曲线的参数方程为 ( 为参数),
(1)分别求曲线 和直线 的直角坐标方程;
(2)若直线 交曲线 于 两点,过线段 的中点 作 轴的平行线交 于一点 ,求点 的横坐标.
23.[选修4-5:不等式选讲](10分)
已知函数 .
(1)求函数 的最小值;
(2)若 为正实数,且 ,求 的最小值.
学科网(北京)股份有限公司2023-2024 学年安康市高三年级第三次质量联考
文科数学参考答案
1.【答案】D
【解析】由条件可得 ,所以 ,即
.故选D.
2.【答案】A
【解析】由条件可得 ,所以 ,故选A.
3.【答案】B
【解析】由题可知函数 的图象关于直线 对称,所以 ,所以 ,又
,故选B.
4.【答案】D
【解析】由约束条件 ,画出可行域,
,化为斜截式方程得 ,
联立 得 ,即 .
由题意可知,当直线 过点 时,直线在 轴上的截距最小,此时 最大.
把点 代入目标函数可得最大值,即最大值 .故选D.
5.【答案】C
【解析】由题意可知将3人分成两组,其中一组只有1人,另一组有2人.分别安排在周六、周日值班共有6
种情况:(甲乙,丙)、(甲丙,乙)、(乙丙,甲)、(甲,乙丙)、(乙,甲丙)、(丙,甲乙).显
然甲、乙被安排在同一天有2种情况,所以甲、乙被安排在同一天的概率为 .故选C.
学科网(北京)股份有限公司6.【答案】B
【解析】设 ,由 是 的中点,得 ,由 ,得 .
所以 ,且
由 与 相交于点 可知,点 在线段 上,也在线段 上,由三点共线的条件可得
,解得 ,所以 ,故选B.
7.【答案】A
【解析】由 ,得 且 ,所以方程 的实根为 ,方程 的实根为 ,
在同一坐标系下画出 的图象,显然 ,故选A.
8.【答案】A
【解析】由 ,解得 ,所以
,所以
.故选A.
9.【答案】C
【解析】由球的表面积公式 ,解得外接球半径 .因为底面三角形是边长为 的等
学科网(北京)股份有限公司边三角形,所以此三角形的外接圆半径为 ,由正三棱柱的外接球的特点可得,
,解得 .故选C.
10.【答案】C
【解析】由 可得线段 的中点,也是线段 的中点,设 ,线段 的中
点坐标为 ,则 .又点 在椭圆上,所以 ,
两式相减可得 , ,所以 ,所以
,即 .
又因为 四点共线,所以 ,综上可得 ,由 在第四
象限得 即 ,所以直线的倾斜角为 .故选C.
11.【答案】D
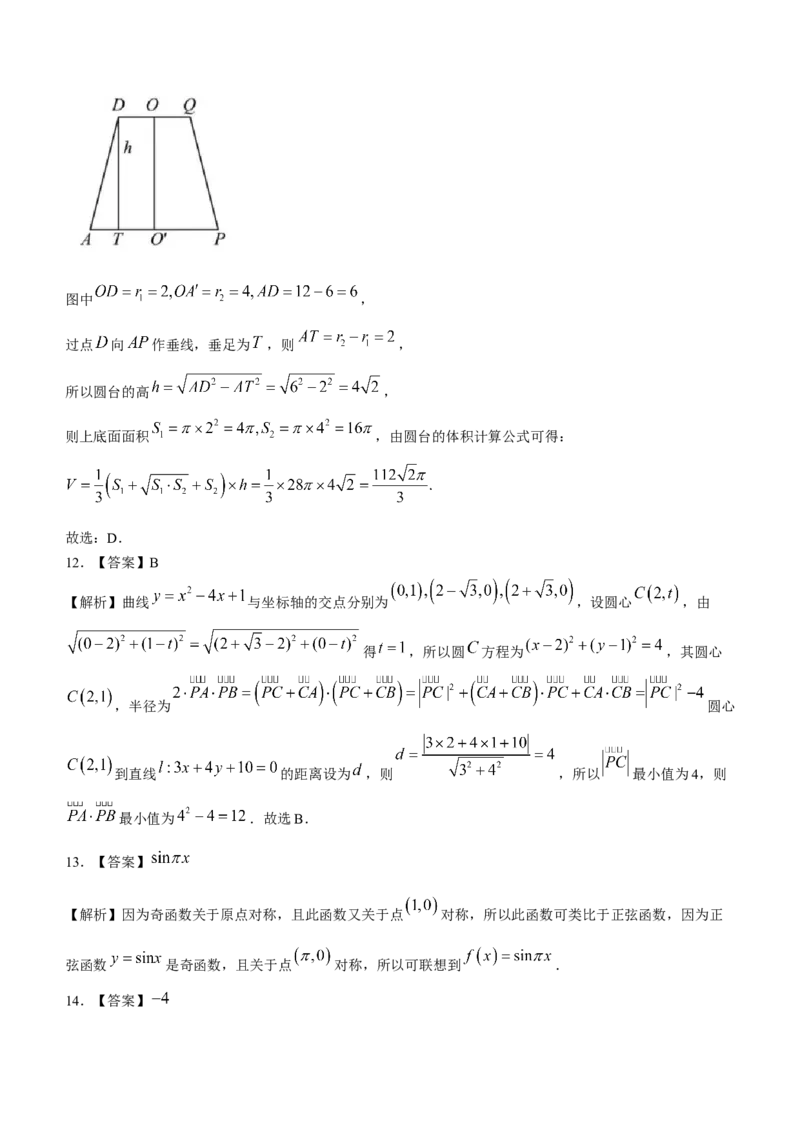
【解析】设圆台上下底面的半径分别为 ,由题意可知 ,解得 ,
,解得 ,作出圆台的轴截面,如图所示:
学科网(北京)股份有限公司图中 ,
过点 向 作垂线,垂足为 ,则 ,
所以圆台的高 ,
则上底面面积 ,由圆台的体积计算公式可得:
故选:D.
12.【答案】B
【解析】曲线 与坐标轴的交点分别为 ,设圆心 ,由
得 ,所以圆 方程为 ,其圆心
,半径为 圆心
到直线 的距离设为 ,则 ,所以 最小值为4,则
最小值为 .故选B.
13.【答案】
【解析】因为奇函数关于原点对称,且此函数又关于点 对称,所以此函数可类比于正弦函数,因为正
弦函数 是奇函数,且关于点 对称,所以可联想到 .
14.【答案】
学科网(北京)股份有限公司【解析】当 时, ,解得 .
当 时, ,两式相减得 ,
因为 ,所以 ,所以 ,所以数列 是首项为 ,公比为 的等比数列,所
以 ,即数列 是 ,故 ,所以 .
15.【答案】
【解析】由 ,联立得 ,
所以 ,且
显然直线 过抛物线 的焦点 .
所以 ,解得 .
16.【答案】
【解析】由 ,不妨设 ,则 ,所以 ,
可变形化简为 ,
构造函数 ,则 ,
所以 在 上是单调递增函数,
所以 恒成立,
即 在 上恒成立,
当 时, ,
学科网(北京)股份有限公司又 时, ,而 ,所以 ,
所以 ,
所以 的取值范围为 .
故答案为:
17.【解析】(1)设购买24元的个人用户数为 ,则购买24元的公司用户数为 ,
设购买6元的公司用户数为 ,则购买6元的个人用户数为 ,
则有 ,解得 ,
所以用户类别与购买意向 列联表如下:
购买6元 购买24元 总计
个人用户 40 60 100
公司用户 20 80 100
总计 60 140 200
(2)由(1)中 列联表得
所以有 的把握认为用户类别与购买意向有关系.
18.【解析】(1)由 ,得
化简得
因为 三边均不相等,所以 ,即
由余弦定理得
在 中,由 ,得
(2)在 中, ,故
学科网(北京)股份有限公司由 得 ,易得
在 中, ,所以
在 中,由 ,得
19.【解析】(1)证明:因为底面 为正方形,所以 ,又因为
平面 ,
所以 平面
因为 平面 ,所以 ,
同理 ,又因为 平面 ,所以 平面 ,
(2)解:显然由(1)可得 ,在直角 中, 同理, 点 分别为
的中点,所以在 中,
所以 ,
在直角 中,
由(1)得 平面 ,所以 平面 ,所以点 到平面 的距离为
设点 到平面 的距离为 ,由
学科网(北京)股份有限公司得 ,解得 .所以点 到平面 的距离为 .
20.【解析】(1)函数 的反函数为
则 ,所以
所以曲线 在 处的切线的方程为 ,即 .
(2)证明:由(1)可知 ,显然 为 上的增函数.
因为 ,所以存在唯一的 ,使 .
从而有 .
因为 时, 时, ,
所以 在区间 上单调递减,在区间 上单调递增.
所以
当且仅当 时,等号成立,而 ,即 .
21.【解析】(1)由题可知双曲线的渐近线方程为 ,
因为 ,所以 ,所以直线 的斜率大于1.
由两条渐近线的夹角为 可得 ,因为 ,所以 即双曲线方程为 ,
因为 的面积为 ,所以 ,所以 .
学科网(北京)股份有限公司因为点 在双曲线上,所以将点的坐标代人方程可得 ,解得 ,或 .因
为
条件 ,所以 ,即双曲线的方程为 .
(2)因为以 为直径的圆过坐标原点,所以 ,所以 ,即:
①当直线 的斜率不存在时,设直线 的方程为 ,设 ,由 可得
,
又点 在双曲线上,代人可得 ,解得 .
所以 .
②当直线 的斜率存在时,设直线 的方程为 ,
由 联立消去 整理得 ,
因为直线 与双曲线交于 两点,所以 ,
即判别式 .
设 ,
则 ,
由 得到: ,所以 ,即
,
即 ,
学科网(北京)股份有限公司所以 ,
化简得 .
所以 。
当 时上式取等号,且方程(*)有解.
综上可得 的最小值是 .
22.【解析】(1)由 可得 ,代入
消去参数 ,可得 的直角坐标方程为:
化简 可得 ,所以 .
将 代入 的极坐标方程,可得 的直角坐标方程为: .
(2)曲线 是抛物线,其焦点 ,准线 ,
直线 ,恰好过抛物线的焦点.
由 消去 并整理得 ,
设 ,
则 ,线段 的中点 的横坐标 ,中点 的纵坐标 ,
过点 作 轴的平行线交 于一点 ,则点 的纵坐标也等于 ,所以点 的横坐标为 .
学科网(北京)股份有限公司23.【解析】(1) ,
在 上单调递减,在 上单调递增,
所以 ,即当 时,函数 取得最小值1
(2)由(1)可得当 为正实数时, ,
则由 可得: ,
所以
当且仅当 时,又 ,即当 时,等号成立.
所以 的最小值为9
学科网(北京)股份有限公司