陕西省商洛市2024届高三尖子生学情诊断考试（第二次）数学（理科）试卷(1)_2024年3月_013月合集_2024届陕西省商洛市高三尖子生学情诊断考试(第二次)

商洛市 2024 届高三尖子生学情诊断考试（第二次） 数学试卷（理科） 考生注意： 1.本试卷分选择题和非选择题两部分.满分 150分，考试时间 120分钟. 2.答题前，考生务必用直径 0.5毫米黑色墨水签字笔将密封线内项目填写清楚. 3.考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用 2B铅笔把答题卡上对应 题目的答案标号涂黑；非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题区域 内作答，超出答题区域书写的答案无效，在试题卷､草稿纸上作答无效. 4.本卷命题范围：高考范围. 一､选择题：本题共 12小题，每小题 5分，共 60 分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.已知集合M   x∣x2 2x0  ,N   x∣x2 10  ，则M N （ ） A. 1,2 B. 1,1 C. 0,2 D. 0,1 2.法国数学家棣莫弗（1667-1754年）发现了棣莫弗定理：设两个复数z r cosisin ， 1 1 1 1 1 3 z 2 r 2 cos 2 isin 2 r 1 ,r 2 0 ，则z 1 z 2 r 1 r 2   cos 1  2 isin 1  2  .设z   i，则z2024 2 2 的虚部为（ ） 3 3 A. B. C.1 D.0 2 2 3.已知等比数列 a  的前n项和S 32n1m，则m （ ） n n A.3 B.9 C.-9 D.-3 r r 1 r r  r r  r 4.设向量a,b 的夹角的余弦值为 ,|a|4,|b |1，则 2a3b b （ ） 4 A.-1 B.1 C.-5 D.5 5.执行如图所示的程序框图，输出S的值为（ ） 学科网（北京）股份有限公司A.70 B.112 C.168 D.240 9π  6.已知sin5π5sin   ，则sin2sin2（ ）  2  9 11 15 20 A. B. C. D. 26 26 26 13 7.在平面直角坐标系xOy中，抛物线C: y2 16x的焦点为F,P是C上的一点，点M 是y轴上的一点，且 uuur uuur MF 2PF ，则VOMF 的面积为（ ） A.24 3 B.16 3 C.24 2 D.16 2 3  8.已知函数 f x,gx 的定义域均为R，若 f  2x  ,g2x 均为偶函数，则（ ） 2  A. f 1 f 2 B.g21 C. f 1 f 2 D.g1 g5 9.小张每天早上在7:008:00任一时刻随机出门上班，他订购的报纸每天在7:308:10任一时刻随机送 到，则小张在出门时能拿到报纸的概率为（ ） 3 13 1 2 A. B. C. D. 16 16 3 3 10.数学家斐波那契在研究兔子繁殖问题时，发现有这样一个数列 a :1,1,2,3,5,8,L ，其中从第3项起，每 n 一项都等于它前面两项之和，即a a 1,a a a ，这样的数列称为“斐波那契数列”.若 1 2 n2 n1 n a 2a a a L a 1，则m （ ） m 3 6 9 174 A.175 B.176 C.177 D.178 11.某圆柱的轴截面是面积为12的正方形ABCD,P为圆柱底面圆弧CD的中点，在圆柱内放置一个球O，则 当球O的体积最大时，平面PAB与球O的交线长为（ ） 15π 2 15π 4 5π 4 15π A. B. C. D. 12 5 5 5 12.已知aea eblnbcec(a 1)，则（ ） A.abc B.bac C.cab D.cba 二､填空题：本题共 4小题，每小题 5分，共 20分.  π  π 13.已知x  0,  ，设函数 f xsin  3x ，则 f x 的单调递减区间是__________.  3  3 学科网（北京）股份有限公司7  1  14.  2x2 3x   2  的展开式中含x的项的系数为__________.  x  x2 y2 15.已知双曲线  1(a0,b0)的离心率为 2，其中一条渐近线与圆(x2)2 (y3)2 1交于 a2 b2 A,B两点，则 AB __________. 16.如图1，已知VABC是边长为2 3的等边三角形，E,F分别在线段AB,AC上滑动，且EF∥ BC，将 VAEF沿EF折起，使得点A翻折到点P的位置，连接PB,PC，如图2所示，则四棱锥PBCFE的体积 的最大值为__________. 三､解答题：共 70分.解答应写出文字说明､证明过程或演算步骤.第 17~21 题为必考题，每个试 题考生都必须作答.第 22､23题为选考题，考生根据要求作答. （一）必考题：共 60分. 17.（本小题满分12分） 已知某校高一有600名学生（其中男生320名，女生280名）.为了给学生提供更为丰富的校园文化生活，学 校增设了两门全新的校本课程A,B，学生根据自己的兴趣爱好在这两门课程中任选一门进行学习.学校统计 了学生的选课情况，得到如下的22列联表. 选择课程A 选择课程B 总计 男生 200 女生 60 总计 （1）请将22列联表补充完整，并判断是否有99.9%的把握认为选择课程与性别有关？说明你的理由； （2）在所有男生中按列联表中的选课情况采用分层抽样的方法抽出8名男生，再从这8名男生中抽取3人做 问卷调查，设这3人中选择课程A的人数为X ，求X 的分布列及数学期望. n(ad bc)2 附：K2  ,nabcd . abcdacbd 学科网（北京）股份有限公司P  K2…k  0.01 0.005 0.001 0 k 6.635 7.879 10.828 0 18.（本小题满分12分） 在VABC中，角A,B,C所对的边分别为a,b,c,2ac2bcosC. （1）求角B的大小； 3 （2）若VABC的面积为 ，周长为3b，求AC边上的高. 4 19.（本小题满分12分） 如图所示，四棱锥SABCD中，底面ABCD为矩形，AC与BD交于点O，点E在线段SD上，且OE ∥平面SAB，二面角SABC，二面角S ADC 均为直二面角. （1）求证：SE  DE； 3 5 （2）若SA AD2，且平面ABE与平面CBE夹角的余弦值为 ，求AB的长度. 10 20.（本小题满分12分） x2 y2 3 设F,F 分别是椭圆D:  1(a b0)的左､右焦点， FF 2 3，椭圆的离心率为 . 1 2 a2 b2 1 2 2 （1）求椭圆D的方程； （2）作直线l 与椭圆D交于不同的两点P,Q，其中点P的坐标为 2,0 ，若点N0,t 是线段PQ垂直平 1 uuur uuur 分线上一点，且满足NPNQ4，求实数t的值. 21.（本小题满分12分） x 已知函数 f x ,gxlnxa，其中a 0，曲线y  f x 在点  m, f m 处的切线与曲线 eax y  gx 相切于点  n,gn . （1）若n1，求a； 学科网（北京）股份有限公司（2）证明： a1m„ 0m1. （二）选考题：共 10分.请考生在第 22，23两题中任选一题作答.如果多做，则按所做的第一 题计分. 22.（本小题满分10分）选修4-4：坐标系与参数方程  x 3cos, 在平面直角坐标系xOy中，曲线C的参数方程为 （为参数），以原点O为极点，x轴  y  31sin 的正半轴为极轴建立极坐标系. （1）求曲线C的普通方程和极坐标方程； π （2）在平面直角坐标系xOy中，过点P3,0 且倾斜角为 的直线l与曲线C交于A,B两点，证明： 6 2 AB  PA  PB . 23.（本小题满分10分）选修4-5：不等式选讲 已知函数 f x 2x6  3x6 . （1）求不等式 f x1的解集； （2）若不等式 f x„ k x3 恒成立，求实数k 的取值范围. 学科网（北京）股份有限公司商洛市 2024 届高三尖子生学情诊断考试（第二次）•数学试卷（理科） 参考答案､提示及评分细则 1.A 因为M   x∣x2 2x0  {x∣0 x2},N   x∣x2 10  {x∣1 x1}，所以 M N {x∣1 x2}.故选A. 1 3 4π 4π 2.B z   icos isin ，所以 2 2 3 3 4π2024 4π2024 2π 2π 1 3 3 z2024 cos isin cos isin   i，所以z2024的虚部为 .故选B. 3 3 3 3 2 2 2 3.D 当n1时，a S 321m27m；当n…2时，a S S 32n1m32n11m 24. 1 1 n n n1   9n1，又 a  是等比数列，所以a 2427m，解得m3.故选D. n 1 r r r r 1 1 r r 4.B 设a与b 的夹角为，因为a与b 的夹角的余弦值为 ，即cos ，又|a|4,|b |1，所以 4 4 r r r r  1  r r  r r r r ab |a||b |cos14    1，所以 2a3b b 2ab 3b2 231.故选B.  4 5.C 第一次执行，由i 1,S 0，则S 01112，又由i 17，则进入循环；第一次循环，由 i 2,S 2，则S 22218，又由i 27，则进入循环；第二次循环，由i 3,S 8，则 S 833120，又由i 37，则进入循环；第三次循环，由i 4,S 20，则 S 2044140，又由i 47，则进入循环；第四次循环，由i 5,S 40，则 S 4055170，又由i 57，则进入循环；第五次循环，由i 6,S 70，则 S 70661112，又由i 67，则进入循环；第六次循环，由i 7,S 112，则 S 112771168，又由i 77，不成立，退出循环，则输出S 168.故选C. 9π  6.C 由sin5π5sin   ，可得sin5cos，即tan5，所以  2  sin2sin2 2sincossin2 2tantan2 25(5)2 15 sin2sin2     .故选C. sin2cos2 sin2cos2 1tan2 1(5)2 26 uuur uuur 7.D 由题意知F4,0 ，设M 0,m,Px ,y  ，所以MF 4,m,PF 4x ,y ，又 0 0 0 0 学科网（北京）股份有限公司uuur uuur m m 2 MF 2PF ，所以 4,m24x 0 ,y 0  ，所以x 0 2,y 0  2 ，所以   2   162，解得 1 m8 2，所以VOMF 的面积S  OF  m 16 2 .故选D. 2 3  3  3  3  3  8.C 因为 f  2x 为偶函数，所以 f  2x   f  2x ，即 f  x   f  x ，所以 2  2  2  2  2  f 3x f x ，令x  2得 f 1 f 2 ，故C正确，A无法判断是否正确；因为g2x 为偶函数， g2x g2x ，所以g4x gx ，令x5得g1 g5 ，故D无法判断是否正确；因为无 法判断g2 的取值情况，故B错误.故选C. 9.A 设小张离开家的时间距离7:00为x分钟，送报的时间距离7:00为y分钟， 0„ x„ 60, 则 小张能拿到报纸，则x…y.画出 x,y 区域，为如图中的矩形ABCD,x,y 中x…y对应区域 30„ y„ 70, 如图VEBF 所示，设矩形ABCD的面积为S，则小张在出门时能拿到报纸的概率为 1 3030 S 2 3 .故选A. VBEF   S 4060 16 10.B 由从第三项起，每个数等于它前面两个数的和，a a 1，由a a a  nN* ，得 1 2 n2 n1 n a a a ，所以a a a ,a a a ,L ,a a a ，将这n个式子左､右两边分别相加可得 n n2 n1 1 3 2 2 4 3 n n2 n1 S a a L a a 1，所以S 1a .所以 n 1 2 n n2 n n2 2a a a L a 1a a a a a a a a a L a a a 1S 1a 3 6 9 174 1 2 3 4 5 6 7 8 9 172 173 174 174 176 ，所以m176.故选B. 11.D 由题意知，当球O的体积最大时，球与圆柱的上下底面及母线均相切，因为正方形ABCD的面积为 12，所以AB BC 2 3，如图1，记AB所在底面的圆心为O,CD所在底面的圆心为O ，平面APB与 1 2 球O的交线为圆形，如图2,OE即为截面圆的直径，易知OP 123  15,OO 2 3，易知Rt 1 1 1 2 学科网（北京）股份有限公司OE OO OO2 12 4 15 VOO P∽RtVOEO ，故 1  1 2 ，所以OE  1 2   ，所以交线长为 1 2 1 2 OO OP 1 OP 15 5 1 2 1 1 4 15π πOE  .故选D. 1 5 a lnb c x1 12.D 由题意得   ，又a1，所以b1,c0.令 f x xlnx，则 fx ，所以当 ea eb ec x 0 x1时， fx0，当x1时， fx0，所以 f x 在 0,1 上单调递减，在 1, 上单调递 lnb b a lnb 增，所以 f x…f 11，所以xlnx…1，所以lnx„ x1 x，所以  ，又  ，所以 eb eb ea eb a b x 1x  ，设hx ,hx ，当x1时，hx0，所以hx 在 1, 上单调递减，又 ea eb ex ex a 1,b1，且hahb ，所以a b，所以cba.故选D. 5π π π  π 2π π π 2π 13. ,  （开区间，半开半闭区间也正确） 依题意3x    ,  ，令 „ 3x „ ，解得 18 3 3  3 3  2 3 3 5π π 5π π „ x„ ，所以 f x 的单调递减区间是  , . 18 3 18 3 7 7 14.960   2 1   的展开式的通项为 T Cr27r(1)rx  2 r ，故令r 0，2，可得  2x2 3x    2 1    x  r1 7  x  的展开式中含x的项的系数为 3C027 2C225 3841344960. 7 7 x2 y2 15. 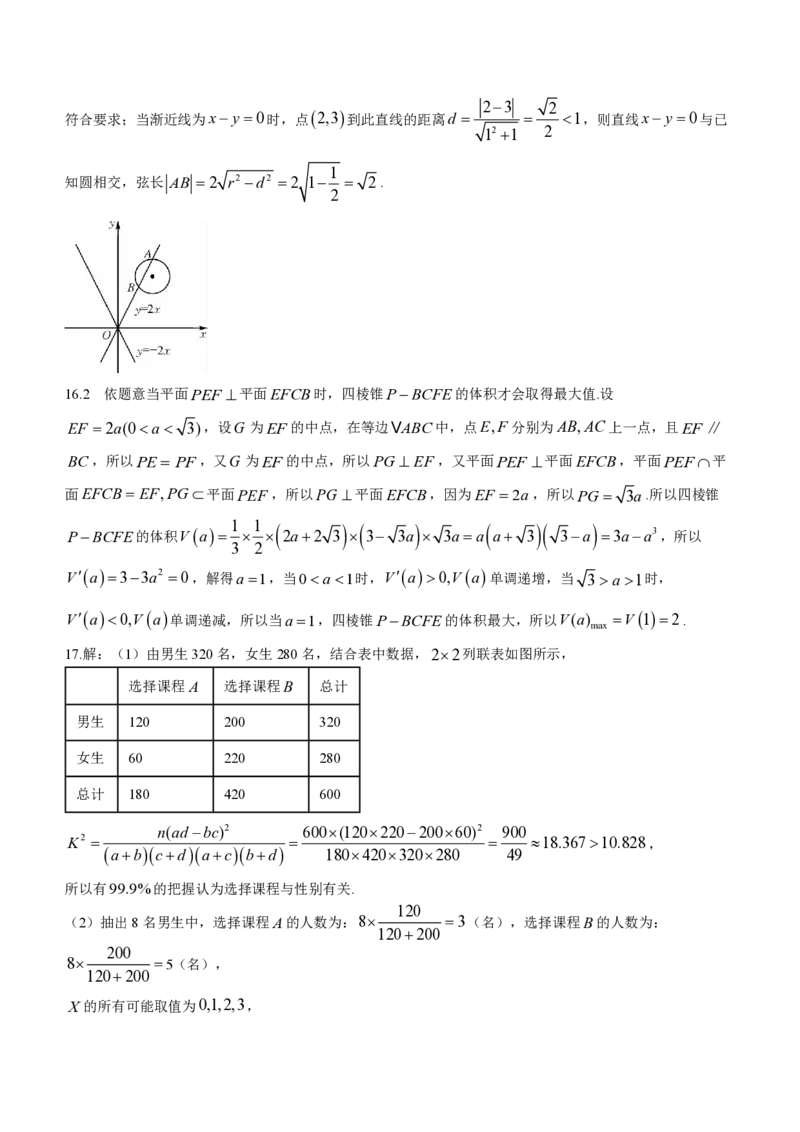2 圆(x2)2 (y3)2 1的圆心 2,3 ，半径r 1，由双曲线  1(a0,b0)的离心率为 a2 b2 a2 b2 b 2 b 2，得 1   ( 2)2，解得 1，于是双曲线的渐近线方程为y x，即x y 0.当渐 a2 a a 23 5 近线为x y 0时，点 2,3 到此直线的距离d  1，即直线x y 0与已知圆相离，不 12 12 2 学科网（北京）股份有限公司23 2 符合要求；当渐近线为x y 0时，点 2,3 到此直线的距离d   1，则直线x y 0与已 12 1 2 1 知圆相交，弦长 AB 2 r2 d2 2 1  2. 2 16.2 依题意当平面PEF 平面EFCB时，四棱锥PBCFE的体积才会取得最大值.设 EF 2a(0a 3)，设G 为EF的中点，在等边VABC中，点E,F分别为AB,AC上一点，且EF∥ BC，所以PE PF，又G 为EF的中点，所以PG  EF，又平面PEF 平面EFCB，平面PEF平 面EFCB EF,PG平面PEF，所以PG 平面EFCB，因为EF 2a，所以PG  3a.所以四棱锥 1 1        PBCFE的体积Va   2a2 3  3 3a  3a a a 3 3a 3aa3，所以 3 2 Va33a2 0，解得a1，当0a1时，Va0,Va 单调递增，当 3 a 1时， Va0,Va 单调递减，所以当a1，四棱锥PBCFE的体积最大，所以V(a) V12. max 17.解：（1）由男生320名，女生280名，结合表中数据，22列联表如图所示， 选择课程A 选择课程B 总计 男生 120 200 320 女生 60 220 280 总计 180 420 600 n(ad bc)2 600(12022020060)2 900 K2    18.36710.828， abcdacbd 180420320280 49 所以有99.9%的把握认为选择课程与性别有关. 120 （2）抽出8名男生中，选择课程A的人数为：8 3（名），选择课程B的人数为： 120200 200 8 5（名）， 120200 X 的所有可能取值为0,1,2,3， 学科网（北京）股份有限公司C3 5 C1C2 15 PX 0 5  ,PX 1 3 5  ， C3 28 C3 28 8 8 C2C1 15 C3 1 PX 2 3 5  ,PX 3 3  ， C3 56 C3 56 8 8 则X 的分布列为 X 0 1 2 3 5 15 15 1 P 28 28 56 56 5 15 15 1 9 所以EX0 1 2 3  . 28 28 56 56 8 18.解：（1）由已知结合正弦定理边化角可得2sinAsinC 2sinBcosC . 又sinAsinBCsinBcosCcosBsinC， 代入整理可得2cosBsinCsinC 0. 1 因为sinC 0，所以cosB . 2 π 又0 Bπ，所以B . 3 1 3 π （2）由S  acsinB 及B 可得，ac 1. 2 4 3 又周长为3b，则abc3b，所以ac2b. π 根据余弦定理可得，b2 a2 c2 2accos (ac)2 3ac(2b)2 3， 3 整理可得b 1. 1 3 3 设AC边上的高为h，则S  bh ，解得h ， 2 4 2 3 所以AC边上的高为 . 2 19.（1）证明：因为OE∥平面SAB,OE 平面SBD，平面SAB平面SBDSB， 所以OE∥SB. 又因为四边形ABCD为矩形，所以BO DO，则SE  DE. （2）解：因为四边形ABCD为矩形，所以AB AD. 又因为平面SAD平面ABCD，平面SAD平面ABCD AD,AB平面ABCD， 所以AB平面SAD. 因为SA平面SAD，所以ABSA. 学科网（北京）股份有限公司同理，ADSA. 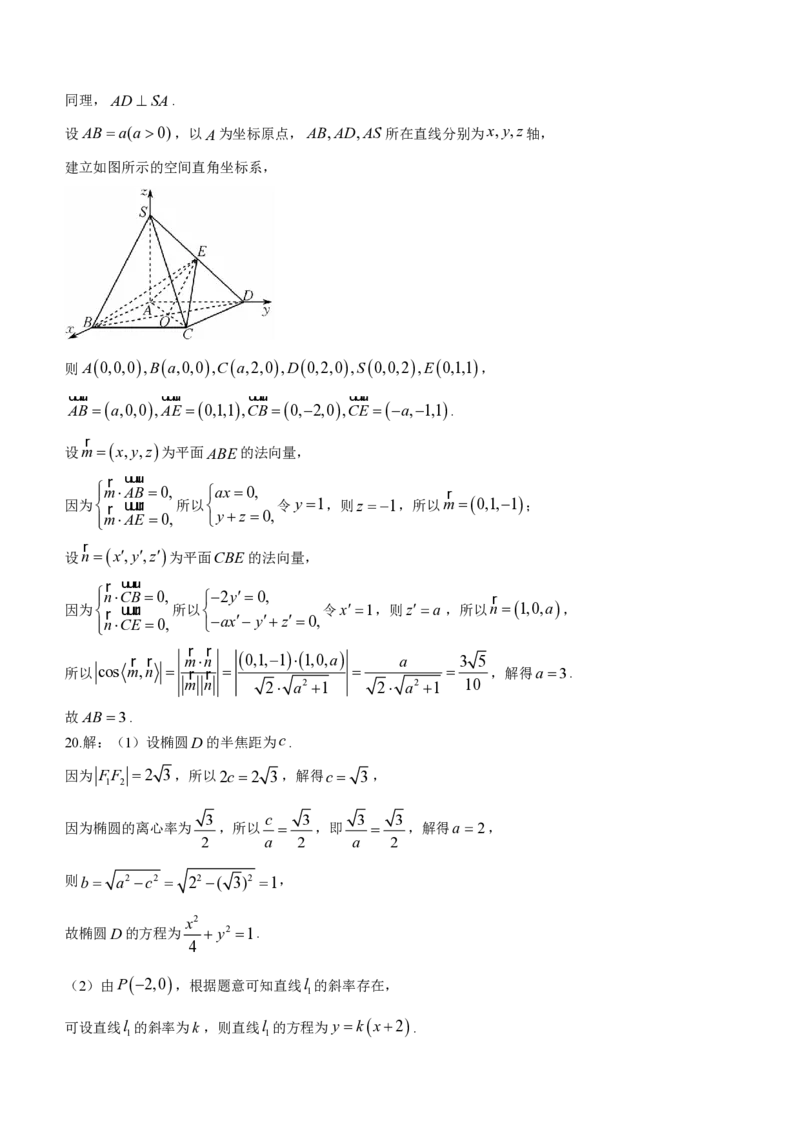设ABa(a0)，以A为坐标原点，AB,AD,AS 所在直线分别为x,y,z轴， 建立如图所示的空间直角坐标系， 则A0,0,0,Ba,0,0,Ca,2,0,D0,2,0,S0,0,2,E0,1,1 ， uuur uuur uuur uuur ABa,0,0,AE 0,1,1,CB0,2,0,CE a,1,1 . r 设mx,y,z 为平面ABE的法向量， uuur r  mAB0, ax0, r 因为r uuur 所以 令y1，则z 1，所以m0,1,1 ； mAE 0, yz 0, r 设n x,y,z 为平面CBE的法向量， uuur r  nCB0, 2y0, r 因为r uuur 所以 令x1，则z a ，所以n 1,0,a ， nCE 0, ax yz0, r r r r mn 0,1,11,0,a a 3 5 所以 cos m,n  r r    ，解得a3. m n 2 a2 1 2 a2 1 10 故AB3. 20.解：（1）设椭圆D的半焦距为c. 因为 FF 2 3，所以2c2 3，解得c 3， 1 2 3 c 3 3 3 因为椭圆的离心率为 ，所以  ，即  ，解得a  2， 2 a 2 a 2 则b a2 c2  22 ( 3)2 1， x2 故椭圆D的方程为  y2 1. 4 （2）由P2,0 ，根据题意可知直线l 的斜率存在， 1 可设直线l 的斜率为k ，则直线l 的方程为y kx2 . 1 1 学科网（北京）股份有限公司把y kx2 代入椭圆D的方程，消去y整理得  14k2 x2 16k2x  16k2 4  0. 16k2 28k2 4k 设Qx ,y  ，则2x  ，则x  ,y kx 2 ， 1 1 1 14k2 1 14k2 1 1 14k2  8k2 2k  所以线段PQ的中点坐标为 , . 14k2 14k2   uuur uuur ①当k 0时，Q2,0 ，线段PQ的垂直平分线为y轴，于是NP2,t,NQ2,t . uuur uuur 由NPNQ4t2 4，解得t 2 2； 2k 1 8k2  ②当k  0时，线段PQ的垂直平分线的方程为y  x . 14k2 k 14k2   6k 由点N0,t 是线段PQ的垂直平分线上一点，令x 0，得t  . 14k2 uuur uuur uuur uuur 因为NP2,t,NQx ,y t,NPNQ4， 1 1 uuur uuur 416k2 6k  4k 6k  4  16k4 15k2 1  所以NPNQ2x ty t      4， 1 1 14k2 14k2 14k2 14k2   14k22 14 解得k  ， 7 6k 2 14 所以t   . 14k2 5 2 14 综上所述，实数t的值为2 2, . 5 1 21.（1）解：gx ，所以g11，又g1a，所以曲线y  gx 在点  1,g1 处的切线方程为 x y  xa1， 1ax 1am 因为 fx ，所以 fm 1，即eam am10， eax eam 设amt,htet t1，则htet 10，即ht 单调递增， 又h00，所以em0，又a 0，所以m0， 因为 f 00，所以曲线 f x 在 0,0 处的切线方程为yx，所以xa1 x，解得a1. 1am m （2）证明：因为 fm , f m ， eam eam 学科网（北京）股份有限公司所以曲线y  f x 在  m, f m 处的切线方程为y  1am xm m  1am x am2 ， ean ean eam eam 1 同理可知曲线y  gx 在  n,gn 处的切线方程为y  xlnna1， n 1 1am am2 所以  ,lnna1 ， n eam ean 1 1t t2 设amt，则 t 0，所以t 1，所以t 0，即t 单调递减，且01， n et et 当m0时，t 0，所以n1，由（1）可知a1，此时 a1m0； 1 当m0时，t 0，则 t1，即0n1， n am2 又lnna1 0，所以a1lnn0，所以a1，此时 a1m0； ean am2 1 t2 当m0时，0t 1，所以a1 lnn  tln1t. ean a et t2 2t aet t2 t  设t tln1t,t0,1，则t ， aet at1et 若a1，则aet t2 t t2 t10，所以t0,t 单调递减，所以t0,1 时， t00a1，与a1t 矛盾，故a1不符题意， 所以应有a1，此时 a1m0. 综上所述， a1m„ 0. 当m…0时，m10， t2 2t aet t2 t  当m0时，t 0且a1，设t tln1t(t 0)，此时t 0，所 aet at1et 以t 单调递减，所以aaea alna1a1t ，所以t ama，即m10. 综上所述， a1m„ 0m1.  x 3cos, 22.（1）解：由 得到x2 (y 3)2 ( 3cos)2 ( 3sin)2 3，  y  31sin, 即x2 (y 3)2 3，所以曲线C的普通方程为x2  y2 2 3y 0. 学科网（北京）股份有限公司又因为2  x2  y2,y sin，则2 2 3sin0， 整理得2 3sin，即曲线C的极坐标方程为2 3sin，  3 x3 t,  2 （2）证明：由题意可得直线l的参数方程为 （t为参数）， 1  y  t  2 代入x2  y2 2 3y 0，整理得t2 4 3t90， 所以Δ4836120,t t 4 3,t t 9. A B A B 则 PA  PB  t t 4 3, AB  t t  t t 2 4t t 2 3， A B A B A B A B 所以 PA  PB 2 AB . x,x2,  23.解：（1） f x 2x6  3x6 5x12,2„ x„ 3,  x,x3,  当x  2时，x1，即1 x2； 11 11 当2„ x„ 3时，5x121，解得x ，即2„ x ； 5 5 当x3时，x1，解得x1，此时无解.  11 综上，不等式 f x1的解集为 1, .  5  （2）因为不等式 f x„ k x3 恒成立， 所以k…f x x3 ，即k… 2x6  3x6  x3  3x9  3x6 恒成立， 因为 3x9  3x6„ 3x93x6 3，当且仅当2„ x„ 3时取等号， 所以k…3，即实数k 的取值范围为 3, . 学科网（北京）股份有限公司