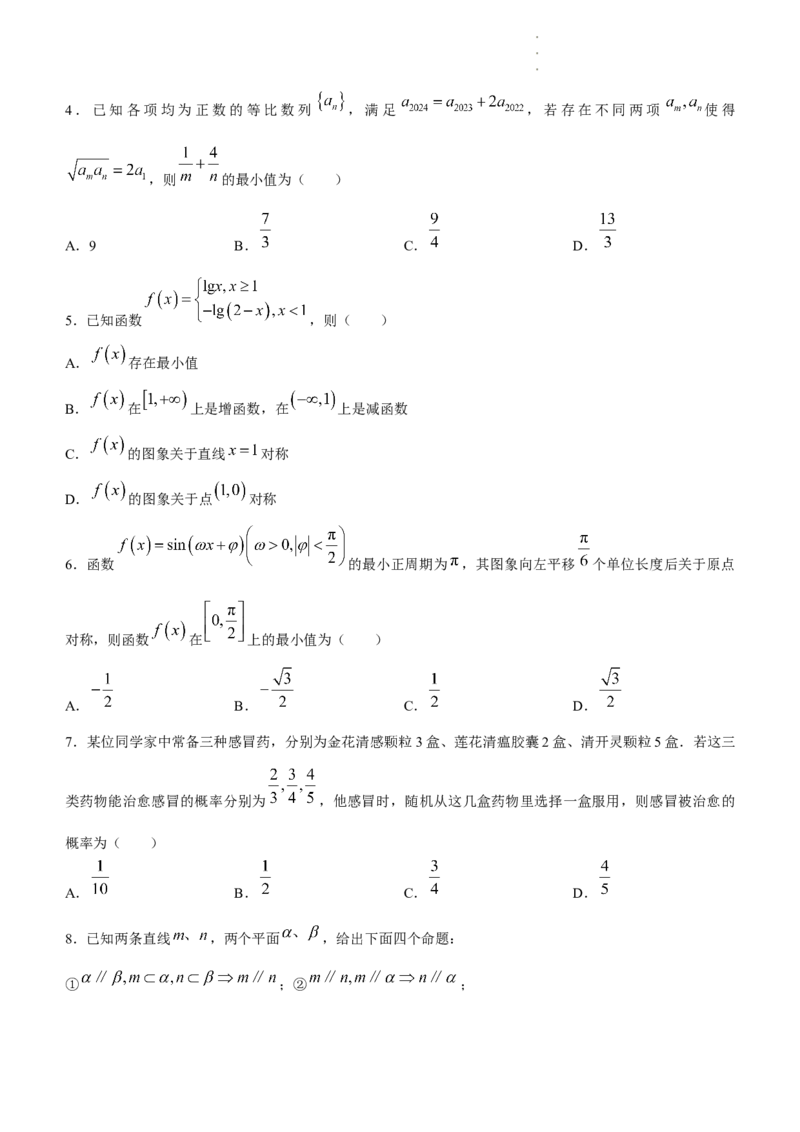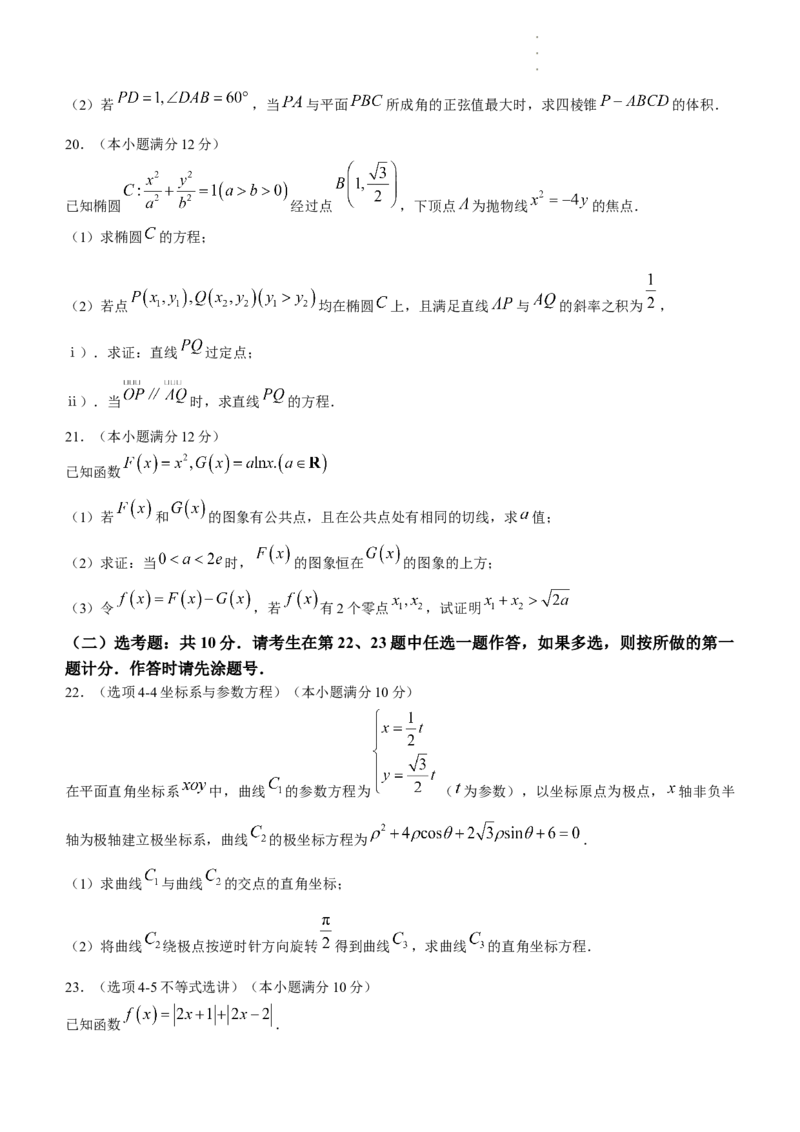文档内容
2024 年宝鸡市高考模拟检测(二)
数学(理科)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.其中第Ⅱ卷解答题又分必考题和选
考题两部分,选考题为二选一.考生作答时,将所有答案写在答题卡上,在本试卷上答题无效.
本试卷满分150分.考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择
题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书
写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷(选择题共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个
是符合题目要求的.
1.若集合 ,则 ( )
A. B. C. D.
2.在复平面内,复数 对应的点的坐标是 为虚数单位,则 ( )
A. B. C. D.
3.2023年3月11日,“探索一号”科考船搭载着“奋斗者”号载人潜水器圆满完成国际首次环大洋洲载人
深潜科考任务,顺利返回三亚.本次航行有两个突出的成就,一是到达了东南印度洋的蒂阿曼蒂那深渊,二
是到达了瓦莱比—热恩斯深渊,并且在这两个海底深渊都进行了勘探和采集.如图 1是“奋斗者”号模型图,
其球舱可以抽象为圆锥和圆柱的组合体,其轴截面如图2所示,则该模型球舱体积为( ) .
A. B. C. D.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司4.已知各项均为正数的等比数列 ,满足 ,若存在不同两项 使得
,则 的最小值为( )
A.9 B. C. D.
5.已知函数 ,则( )
A. 存在最小值
B. 在 上是增函数,在 上是减函数
C. 的图象关于直线 对称
D. 的图象关于点 对称
6.函数 的最小正周期为 ,其图象向左平移 个单位长度后关于原点
对称,则函数 在 上的最小值为( )
A. B. C. D.
7.某位同学家中常备三种感冒药,分别为金花清感颗粒3盒、莲花清瘟胶囊2盒、清开灵颗粒5盒.若这三
类药物能治愈感冒的概率分别为 ,他感冒时,随机从这几盒药物里选择一盒服用,则感冒被治愈的
概率为( )
A. B. C. D.
8.已知两条直线 ,两个平面 ,给出下面四个命题:
① ;② ;
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司③ ;④ .
其中真命题的序号有:( )
A.①③ B.③④ C.①④ D.②③
9.已知直线 与双曲线 交于 两点,点 是弦 的中点,
则双曲线 的离心率为( )
A.2 B. C. D.3
10.在 中, 分别是角 的对边,若 ,则 的值为(
)
A.2022 B.2023 C.2024 D.2025
11.记 为等差数列 的前 项和,若 ,且 ,则数列 中最大的负数为(
)
A. B. C. D.
12.已知函数 ,若 至多有一个零点,则实数 的取值范围是( )
A. B. C. D.
第Ⅱ卷(非选择题共90分)
二、填空题:本题共4小题,每小题5分,满分20分.
13.已知向量 ,且 ,则向量 与 的夹角为______.
14.已知样本 ,的平均数为10,则该样本方差的最小值为______.
15.直线 与圆 相交于 两点,若 ,则 ______.
16.已知定义在 上的奇函数 ,满足 为数列 的前 项和,且
,则 ______.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
(一)必考题:共60分
17.(本小题满分12分)
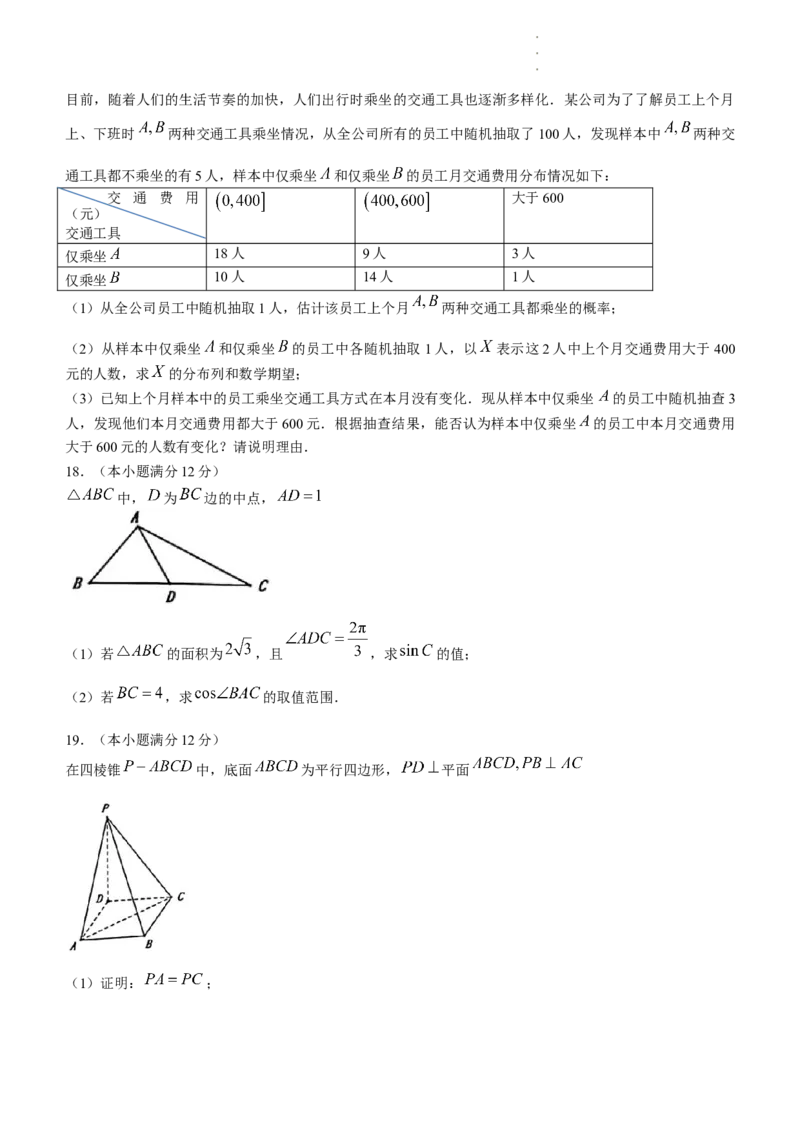
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司目前,随着人们的生活节奏的加快,人们出行时乘坐的交通工具也逐渐多样化.某公司为了了解员工上个月
上、下班时 两种交通工具乘坐情况,从全公司所有的员工中随机抽取了100人,发现样本中 两种交
通工具都不乘坐的有5人,样本中仅乘坐 和仅乘坐 的员工月交通费用分布情况如下:
交 通 费 用 大于600
(元)
交通工具
仅乘坐 18人 9人 3人
仅乘坐 10人 14人 1人
(1)从全公司员工中随机抽取1人,估计该员工上个月 两种交通工具都乘坐的概率;
(2)从样本中仅乘坐 和仅乘坐 的员工中各随机抽取1人,以 表示这2人中上个月交通费用大于400
元的人数,求 的分布列和数学期望;
(3)已知上个月样本中的员工乘坐交通工具方式在本月没有变化.现从样本中仅乘坐 的员工中随机抽查3
人,发现他们本月交通费用都大于600元.根据抽查结果,能否认为样本中仅乘坐 的员工中本月交通费用
大于600元的人数有变化?请说明理由.
18.(本小题满分12分)
中, 为 边的中点,
(1)若 的面积为 ,且 ,求 的值;
(2)若 ,求 的取值范围.
19.(本小题满分12分)
在四棱锥 中,底面 为平行四边形, 平面
(1)证明: ;
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司(2)若 ,当 与平面 所成角的正弦值最大时,求四棱锥 的体积.
20.(本小题满分12分)
已知椭圆 经过点 ,下顶点 为抛物线 的焦点.
(1)求椭圆 的方程;
(2)若点 均在椭圆 上,且满足直线 与 的斜率之积为 ,
ⅰ).求证:直线 过定点;
ⅱ).当 时,求直线 的方程.
21.(本小题满分12分)
已知函数
(1)若 和 的图象有公共点,且在公共点处有相同的切线,求 值;
(2)求证:当 时, 的图象恒在 的图象的上方;
(3)令 ,若 有2个零点 ,试证明
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多选,则按所做的第一
题计分.作答时请先涂题号.
22.(选项4-4坐标系与参数方程)(本小题满分10分)
在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点, 轴非负半
轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求曲线 与曲线 的交点的直角坐标;
(2)将曲线 绕极点按逆时针方向旋转 得到曲线 ,求曲线 的直角坐标方程.
23.(选项4-5不等式选讲)(本小题满分10分)
已知函数 .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司(1)求 的最小值;
(2)若 时, 恒成立,求 的最小值.
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司