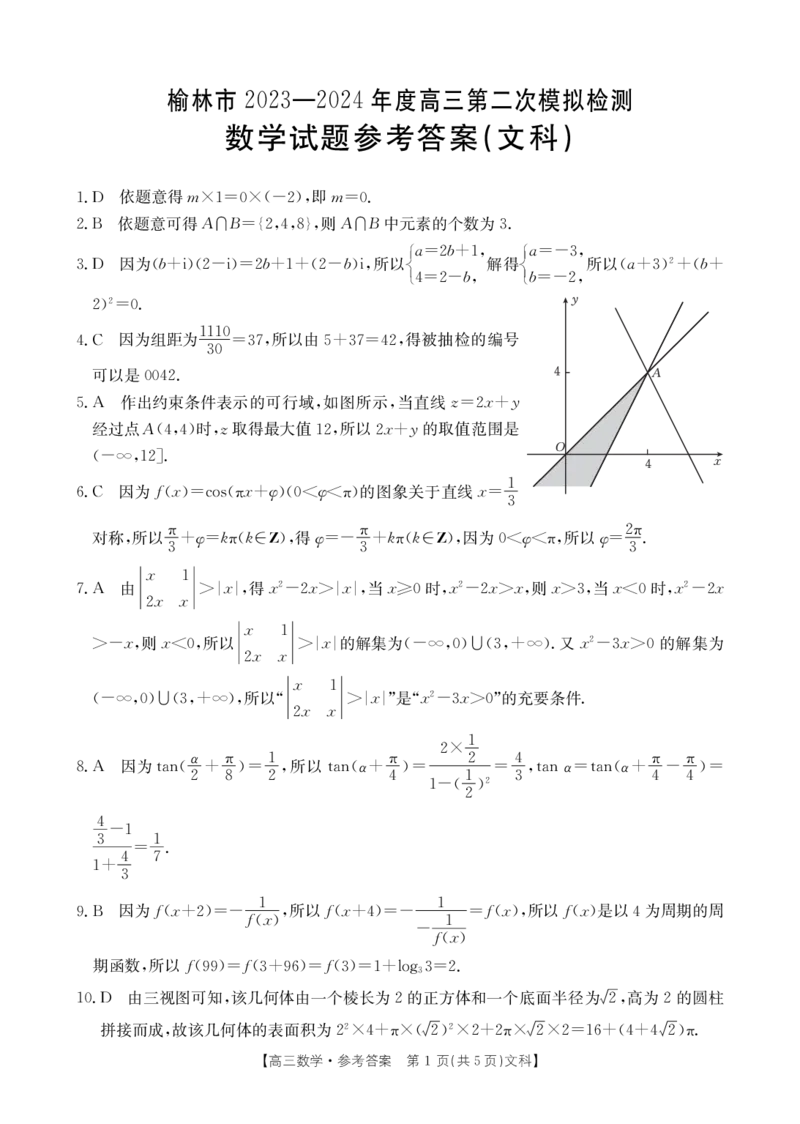文档内容
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}榆林市#$#%!#$#&年度高三第二次模拟检测
数学试题参考答案"文科#
!!’!依题意得"(!)$(!*#"#即")$!
#!+!依题意可得#"$)$##&#,%#则#"$中元素的个数为%!
$&)#%-!# $&)*%#
%!’!因为!%-."!#*.")#%-!-!#*%".#所以# 解得# 所以!&-%"#-!%-
%&)#*%# %%)*##
#"#)$!
!!!$
&!/!因为组距为 )%0#所以由"-%0)&##得被抽检的编号
%$
可以是$$&#!
"!1!作出约束条件表示的可行域#如图所示#当直线’)#(-)
经过点#!&#&"时#’取得最大值!##所以#(-)的取值范围是
!*2#!#&!
!
3!/!因为*!(")456!!(-! "!$&!&!"的图象关于直线()
%
! ! #!
对称#所以 -!)+!!+’!"#得 !)* -+!!+’!"#因为$&!&!#所以 !) !
% % %
(!!
0!1!由 ()()#得(#*#(()()#当(*$时#(#*#(((#则((%#当(&$时#(#*#(
#(!(
(!!
(*(#则(&$#所以 ()()的解集为!*2#$"+!%#-2"!又(#*%(($的解集为
#(!(
(!!
!*2#$"+!%#-2"#所以’ ()()(是’(#*%(($(的充要条件!
#(!(
!
#(
" ! ! ! # & ! !
,!1!因为789! - ") #所以789!"- ") ) #789")789!"- * ")
# , # & ! % & &
!*! "#
#
&
*!
% !
) !
& 0
!-
%
! !
:!+!因为*!(-#")* #所以*!(-&")* )*!("#所以*!("是以&为周期的周
*!(" !
*
*!("
期函数#所以*!::")*!%-:3")*!%")!-;5<%)#!
%
!$!’!由三视图可知#该几何体由一个棱长为#的正方体和一个底面半径为槡##高为#的圆柱
拼接而成#故该几何体的表面积为##(&-!(!槡#"#(#-#!(槡#(#)!3-!&-&槡#"!!
!高三数学"参考答案!第!!!!!页#共"页$文科%
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}
书书书!!!/!因为),-)=),-))"=%#所以可设),-))"+!+($"#),-))%+#
! # ! #
依题意可得),-))"+#),-)))--))%+或),-))%+#),-)))--))"+#
! # ! # # ! ! #
#0 )--) % "
故.的离心率/) ) ! # ) 或 !
#& ),-)*),-) # #
! #
!#!+!令*!(")!(#*&(-""!& ( %*"*!")$#得")*(#
-&(或")& ( %*!!作出1!(")*(#-&(#2!(")& ( %*!
的大致图象#如图所示#这两个函数的图象的交点为!$#
$"#!%#%"#因为1!(" )!("(*!#所以由图可知"
>8?
的取值范围是!*!#$"+!$#%"+!%#&"!故整数")!或
##个数为#!
!%!槡0!由余弦定理#得$.#)#$#-#.#*##$)#.456#)"-#)0#所以$.)槡0!
!&!)#)%(!或(#)%)"!依题意可得.的标准方程可设为)#)#3(!3($"或(#)#3)!3($"#
%
将点#的坐标代入得3) #则.的标准方程为)#)%(或(#)%)!
#
&&槡!!
!"! !!设切点为$#则#$,4$#所以4$)槡#4#*#$#)槡!!#则球4的半径为
%
& &&槡!!
槡!!#所以球4的体积为 !(!槡!!"%) !!
% %
*5!#" *5!#"
!3!$*!*2#!"+!!#-2"!因为*!(")@(* (#所以*5!(")@(* #则*5!#")@#*
@*! @*!
*5!#"
#解得*5!#")@#*@#则*!(")@(*@(#*5!(")@(*@#则*5!!")$!当(’!*2#!"
@*!
时#*5!("&$#*!("单调递减#当(’!!#-2"时#*5!("($#*!("单调递增!因为*!!")$#
所以*!("($的解集为!*2#!"+!!#-2"!
!0!解+!!"由#(&槡##得(&$!"#………………………………………………………………#分
$!"*$ !
所以由几何概型可知#甲获奖的概率为 ) !……………………………………&分
#*$ &
!#"从装有编号为!###%#&#"#3的3个小球的箱子内随机抽取#个小球#所有的抽取情况为
!!##"#!!#%"#!!#&"#!!#""#!!#3"#!##%"#!##&"#!##""#!##3"#!%#&"#!%#""#!%#3"#!&#""#
!"#!"#3"#共!"种情况# ………………………………………………………………,分
% !
其中#均为偶数的有%种#所以乙获奖的概率为 ) !………………………………!!分
!" "
! !
因为 ( #所以甲获奖的概率更大!……………………………………………………!#分
& "
!,!!!"证明+因为& *#&)#6-&#所以& )#&-#6-&#
6-! 6 6-! 6
& & #&-#6-& & & &
所以 6-!* 6) 6 * 6) 6-,* 6),#…………………………………………%分
#6-! #6 #6-! #6 #6 #6
&
所以$6%为公差是,的等差数列!…………………………………………………………&分
#6
!高三数学"参考答案!第!!!!#页#共"页$文科%
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}& &
!#"解+因为 !),#所以 6),-,!6*!"),6#……………………………………………3分
# #6
& !36)##6
所以&),6)#6#则 #6) )!3)&6# ……………………………………………,分
6 6 6
&*&6(& !3 &6-%*3&
所以7)!3(!&-&#-,-&6")!3( ) !&6-!*&"!或 "!………!#分
6 !*& % %
!:!!!"证明+因为$.)!#..)%#$.)槡!$#
! !
所以$.#-..#)$.##则$.,..!………………………………………………………#分
! ! !
又.8,平面$..$#所以.8,..#……………………………………………………%分
! ! !
因为$.".8).#所以..,平面#$.8!………………………………………………&分
!
又底面#$.8为正方形#所以四棱柱#$.89#$.8 为正四棱柱!…………………"分
! ! ! !
!#"解+连接$8#交#.于点4#………………………………………3分 "
!
$
!
因为底面#$.8为正方形#所以#.,$8!…………………………0分
%
!
由!!"知#..,平面#$.8#则..,$8!…………………………,分 & !
! !
因为.."#.).#所以$8,平面#..#!………………………:分
! ! !
! 槡#
因为$.)!#所以$4) $8) # ………………………………!$分
# #
" $
! 槡# ’
所以四棱锥$9#..# 的体积:) ( (槡#(%)!!…………!#分
! ! % #
!
#
#$!解+!!"因为*!(")@&(*#(#所以*5!(")&@&(*#!…………………!分
又*!("的图象在点!$#*!$""处的切线与直线;+)-%)$平行#所以*5!$")&*#)$#则&
)##*5!(")#@#(*#!………………………………………………………………………%分
当(’!*2#$"时#*5!("&$#*!("单调递减*当(’!$#-2"时#*5!("($#*!("单调递增!
………………………………………………………………………………………………&分
由*!(")@#(*#(#得*!*!")@*#-##*!$")!#*!#")@&*&(@*#-## ……………3分
故*!("在-*!##&上的最大值为@&*&#最小值为!!……………………………………0分
!#"设切点为!(
$
#@#($*#(
$
"#则切线的斜率+)#@#($*##所以切线方程为)*!@#($*#(
$
")
!#@#($*#"!(*(
$
"!…………………………………………………………………………:分
! !
因为切线经过点!
#
#*!"#所以*!*!@#($*#(
$
")!#@#($*#"!
#
*(
$
"#整理得*!*@#($-
#(
$
)@#($*#(
$
@#($*!-#(
$
#即(
$
@#($)@#($ #解得(
$
)!! ……………………………!!分
故切线方程为)*@#-#)!#@#*#"!(*!"#即!#@#*#"(*)*@#)$! ………………!#分
#!!解+!!"因为.的长轴长为,#
所以#&),#…………………………………………………………………………………!分
所以&)&!……………………………………………………………………………………#分
!*#"# %#
又 - )!#所以%#)!##……………………………………………………………%分
&# %#
!高三数学"参考答案!第!!!!%页#共"页$文科%
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}(# )#
所以.的方程为 - )!!………………………………………………………………&分
!3 !#
!#"易知#!&#$"#则直线;的斜率存在#设其方程为))+(-"#,!(#)"# (*& (*& (*& (*&
! # ! #
3!(-("*&,
)*&-#+- ! # &
((*&!(-("-!3
! # ! #
3(!*,+""*&,(!&+#-%"
)*&-#+- &
!&"#*&,"*&(!*,+""-!3(!&+#-%"
+"-&+#-% +!3*&+"-&+#-%
)*&!#+*!#( ")*&-#+*!#( &*&-#+-!*#+*!"&
"#-,+"-!3+# !3*&+-&+"#
)&#…………………………………………………………………………………………!!分
所以线段=>的中点为!$##"#为定点!…………………………………………………!#分
##!解+!!"由曲线=的参数方程#得))(*##………………………………………………#分
由?#-?)?#*?*##得?)*!# ……………………………………………………………%分
$()?#*?)##
则# ……………………………………………………………………………&分
%))?#-?)$#
故曲线=与曲线>的交点坐标为!##$"!…………………………………………………"分
$()?#*?#
!#"由# 得)*()#?# ……………………………………………………………3分
%))?#-?#
)*( )*( )*(
则?) #代入))?#-?#得))! "#- # ……………………………………0分
# # #
整理得)#*#()-(#*#(*#))$# ………………………………………………………,分
! ! !
因为()?#*?)!?* "#* ** #……………………………………………………:分
# & &
!
所以曲线>的普通方程为)#*#()-(#*#(*#))$!(** "!……………………!$分
&
#%!解+!!"当&)#时#*!("-!&可化为)()-#)(*#)-!&!………………………………!分
!高三数学"参考答案!第!!!!&页#共"页$文科%
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}$(-$#
!$
当(-$时## 解得* -(-$* ……………………………………#分
%*(*#!(*#"-!&# %
$$&(&##
当$&(&#时## 解得$&(&#*………………………………………%分
%(*#!(*#"-!&#
$(*##
当(*#时## 解得#-(-3!……………………………………………&分
%(-#!(*#"-!&#
!$
故当&)#时#不等式*!("-!&的解集为-* #3&!……………………………………"分
%
!#"因为槡(#-,)()-!3)槡!)()-&"#))()-&#
所以*!("*槡(#-,)()-!3等价于)(*#)-)(*&)*&!………………………………3分
因为)(*#)-)(*&)*)(*#*!(*&")))&*#)# ……………………………………0分
所以)(*#)-)(*&)的最小值为)&*#)#所以)&*#)*&#………………………………,分
解得&-*#或&*3#故&的取值范围是!*2#*#&+-3#-2"!……………………!$分
!高三数学"参考答案!第!!!!"页#共"页$文科%
{#{QQABSYQAoggIAIIAAQgCAQ0QCEMQkBCCAKoOQBAIoAAASANABAA=}#}