文档内容
2021 年柳州市初中学业水平考试与高中阶段学校招生考试
数学
(考试时间:120分钟 满分:120分)
第Ⅰ卷
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符
合要求的)
1. 在实数3, ,0, 中,最大的数为( )
A. 3 B. C. 0 D.
2. 如下摆放的几何体中,主视图为圆的是( )
A. B. C. D.
3. 柳州市大力发展新能源汽车业,仅今年二月宏光MINIEV销量就达17000辆,用科学记数法将数据17000
表示为( )
A. B. C. D.
4. 以下四个标志,每个标志都有图案和文字说明,其中的图案是轴对称图形是( )
A. B.
C. D.
5. 以下调查中,最适合用来全面调查的是( )
A. 调查柳江流域水质情况 B. 了解全国中学生的心理健康状况
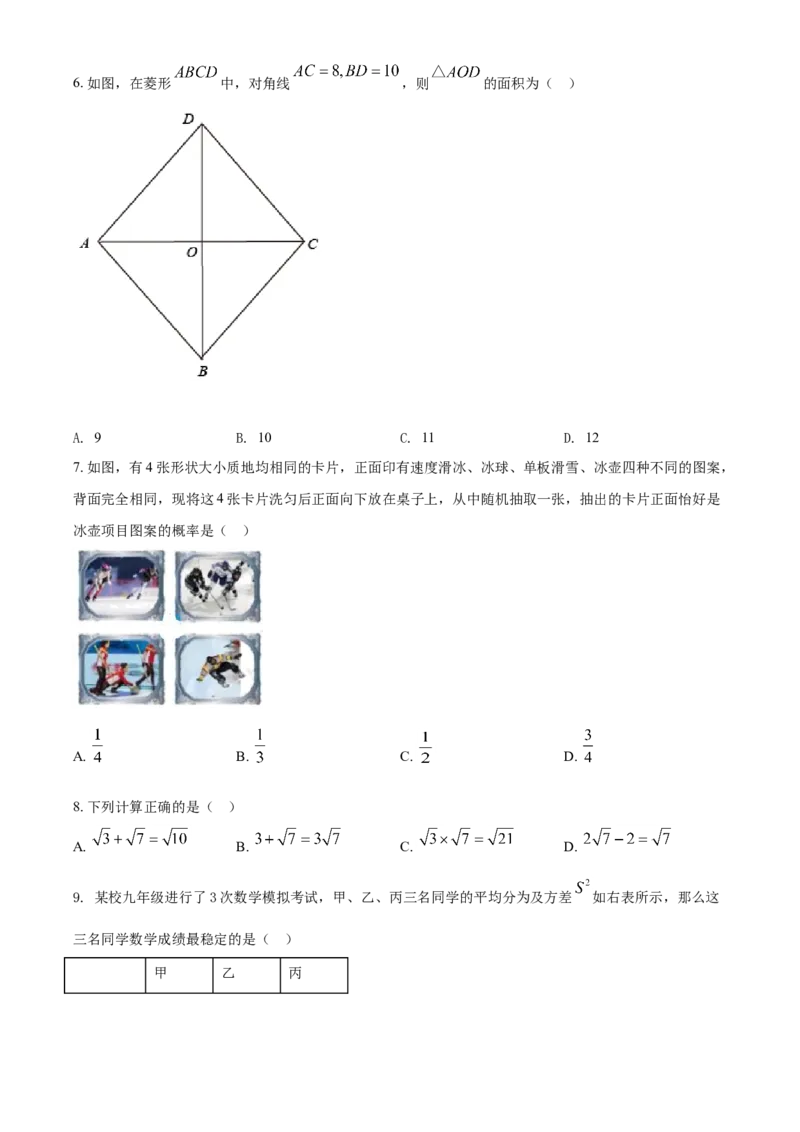
C. 了解全班学生的身高情况 D. 调查春节联欢晚会收视率6. 如图,在菱形 中,对角线 ,则 的面积为( )
A. 9 B. 10 C. 11 D. 12
7. 如图,有4张形状大小质地均相同的卡片,正面印有速度滑冰、冰球、单板滑雪、冰壶四种不同的图案,
背面完全相同,现将这4张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面怡好是
冰壶项目图案的概率是( )
A. B. C. D.
8. 下列计算正确的是( )
A. B. C. D.
9. 某校九年级进行了3次数学模拟考试,甲、乙、丙三名同学的平均分为及方差 如右表所示,那么这
三名同学数学成绩最稳定的是( )
甲 乙 丙91 91 91
6 24 54
A. 甲 B. 乙 C. 丙 D. 无法确定
的
10. 若一次函数 图像如图所示,则下列说法正确的是( )
A. B. C. y随x的增大而增大 D. 时,
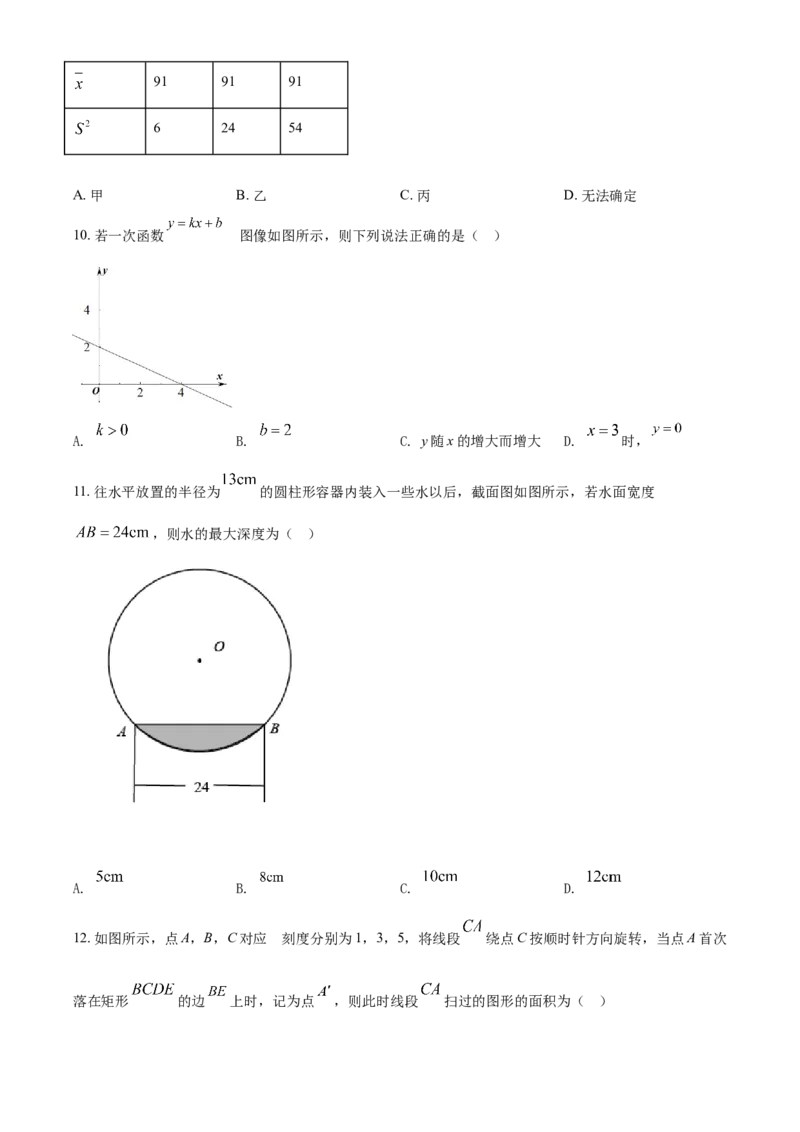
11. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度
,则水的最大深度为( )
A. B. C. D.
的
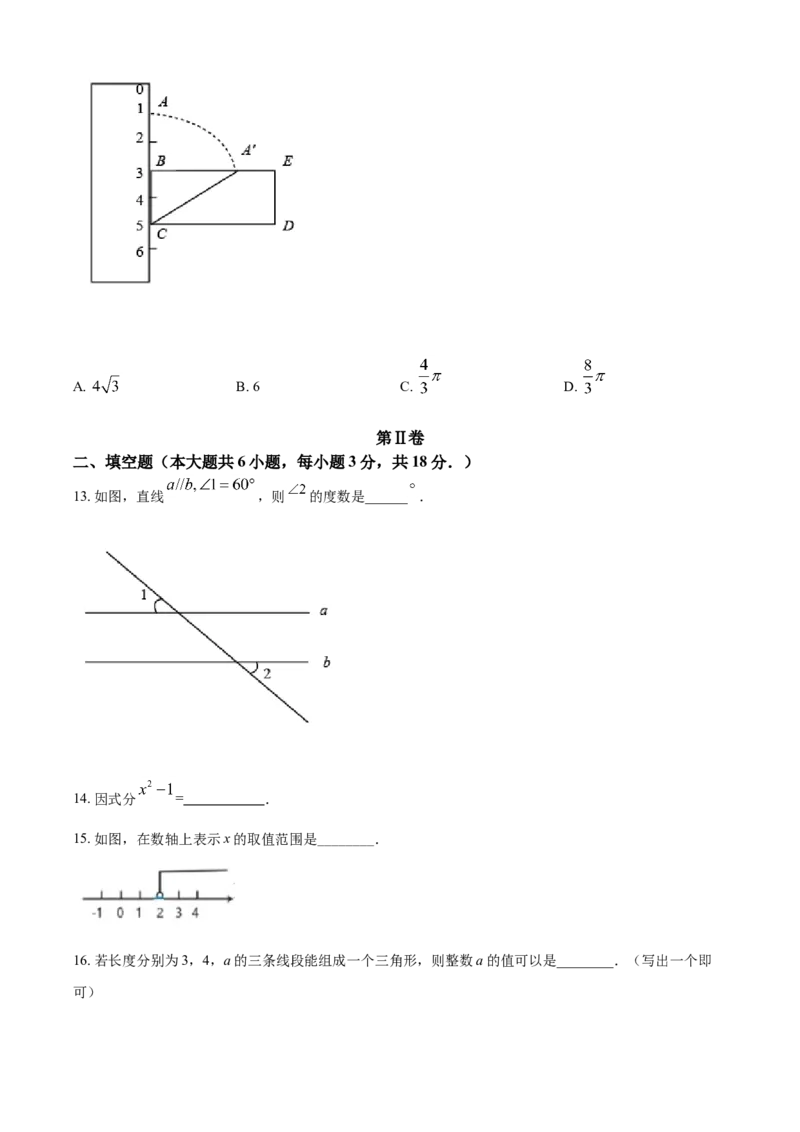
12. 如图所示,点A,B,C对应 刻度分别为1,3,5,将线段 绕点C按顺时针方向旋转,当点A首次
落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为( )A. B. 6 C. D.
第Ⅱ卷
二、填空题(本大题共6小题,每小题3分,共18分.)
13. 如图,直线 ,则 的度数是______ .
14. 因式分 = .
15. 如图,在数轴上表示x的取值范围是________.
16. 若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是________.(写出一个即
可)17. 在x轴,y轴上分别截取 ,再分别以点A,B为圆心,以大于 长为半径画弧,两弧交于
点P,若点P的坐标为 ,则a的值是_______.
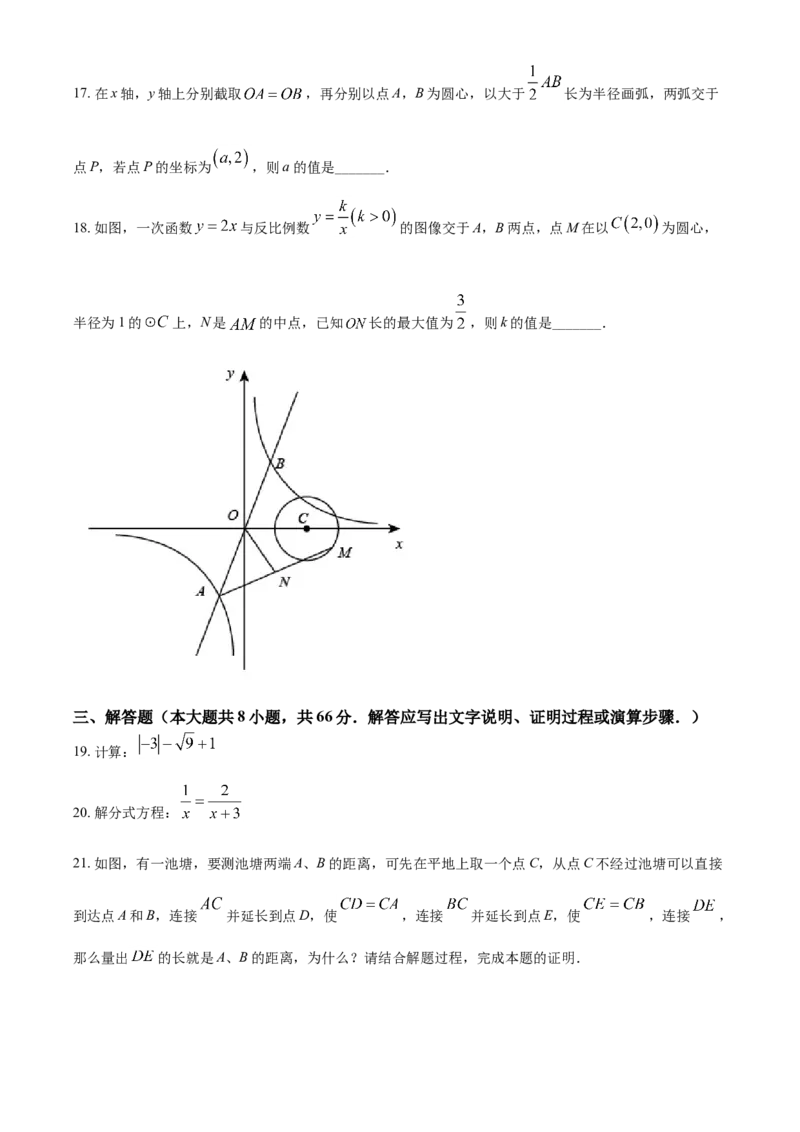
18. 如图,一次函数 与反比例数 的图像交于A,B两点,点M在以 为圆心,
半径为1的 上,N是 的中点,已知 长的最大值为 ,则k的值是_______.
三、解答题(本大题共8小题,共66分.解答应写岀文字说明、证明过程或演算步骤.)
19. 计算:
20. 解分式方程:
21. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接
到达点A和B,连接 并延长到点D,使 ,连接 并延长到点E,使 ,连接 ,
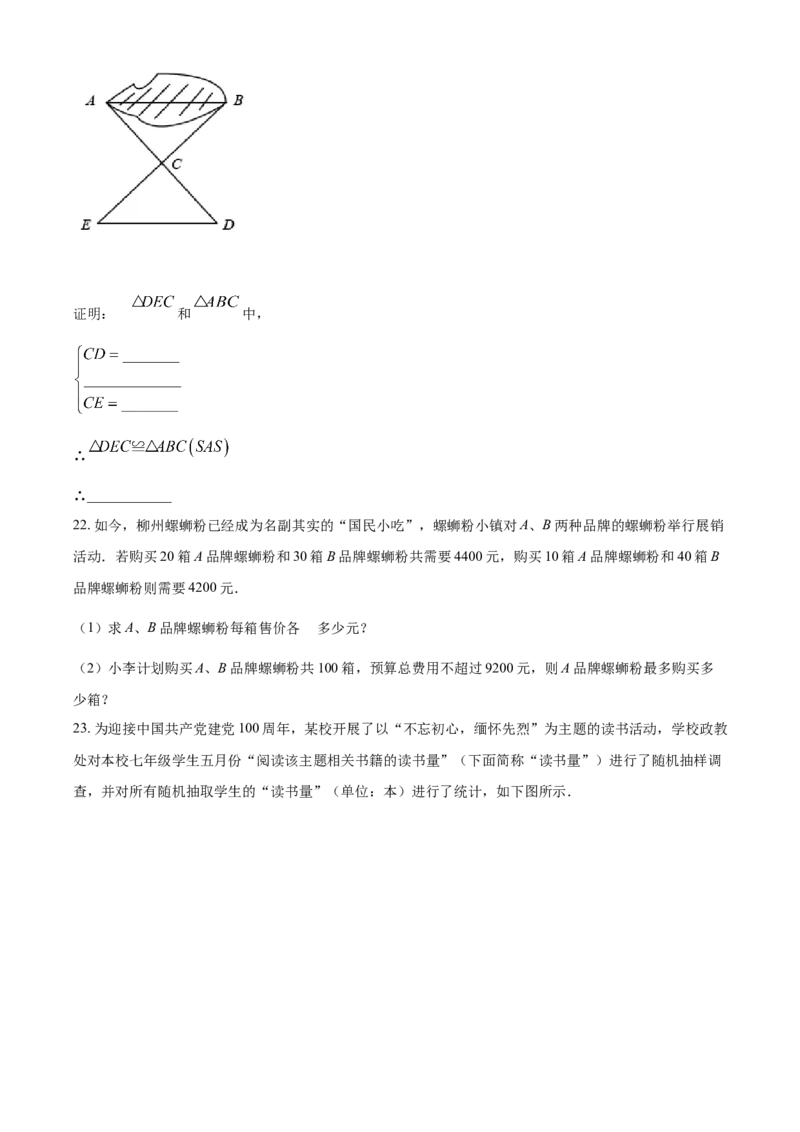
那么量出 的长就是A、B的距离,为什么?请结合解题过程,完成本题的证明.证明: 在和 中,
∴
∴____________
22. 如今,柳州螺蛳粉已经成为名副其实的“国民小吃”,螺蛳粉小镇对A、B两种品牌的螺蛳粉举行展销
活动.若购买20箱A品牌螺蛳粉和30箱B品牌螺蛳粉共需要4400元,购买10箱A品牌螺蛳粉和40箱B
品牌螺蛳粉则需要4200元.
为
(1)求A、B品牌螺蛳粉每箱售价各 多少元?
(2)小李计划购买A、B品牌螺蛳粉共100箱,预算总费用不超过9200元,则A品牌螺蛳粉最多购买多
少箱?
23. 为迎接中国共产党建党100周年,某校开展了以“不忘初心,缅怀先烈”为主题的读书活动,学校政教
处对本校七年级学生五月份“阅读该主题相关书籍的读书量”(下面简称“读书量”)进行了随机抽样调
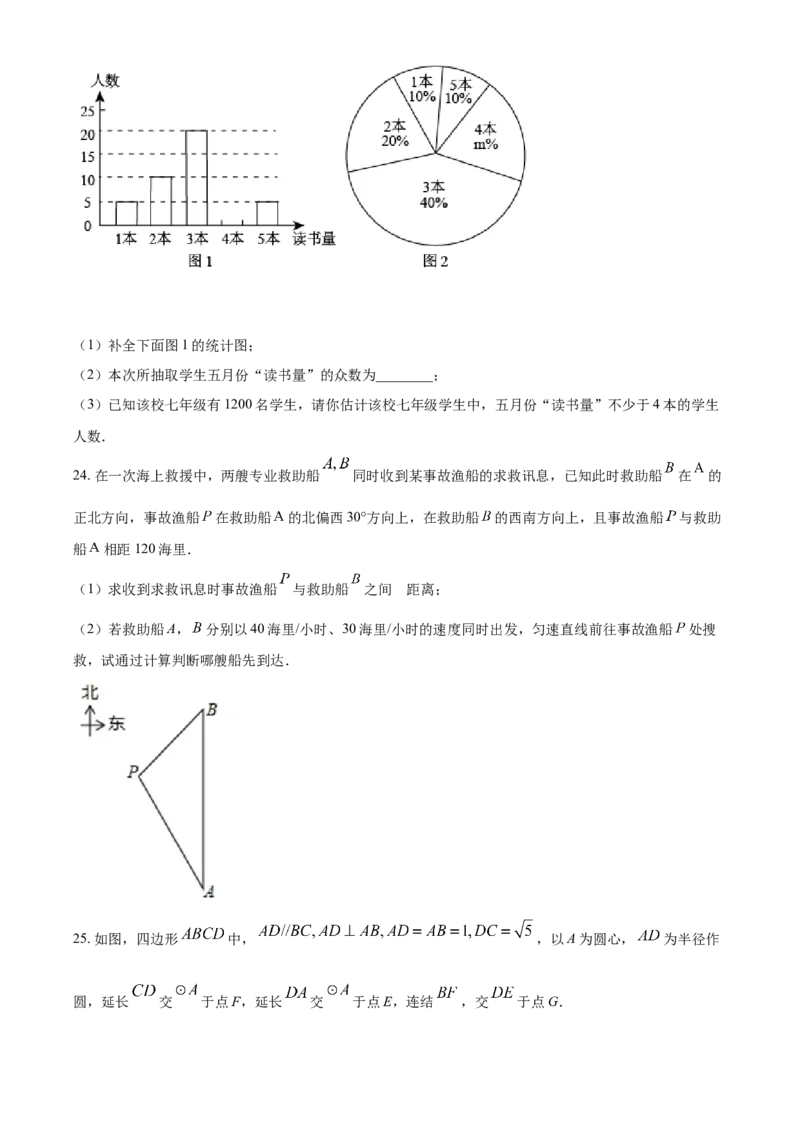
查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示.(1)补全下面图1的统计图;
(2)本次所抽取学生五月份“读书量”的众数为________;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,五月份“读书量”不少于4本的学生
人数.
24. 在一次海上救援中,两艘专业救助船 同时收到某事故渔船的求救讯息,已知此时救助船 在 的
正北方向,事故渔船 在救助船 的北偏西30°方向上,在救助船 的西南方向上,且事故渔船 与救助
船 相距120海里.
的
(1)求收到求救讯息时事故渔船 与救助船 之间 距离;
(2)若救助船A, 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船 处搜
救,试通过计算判断哪艘船先到达.
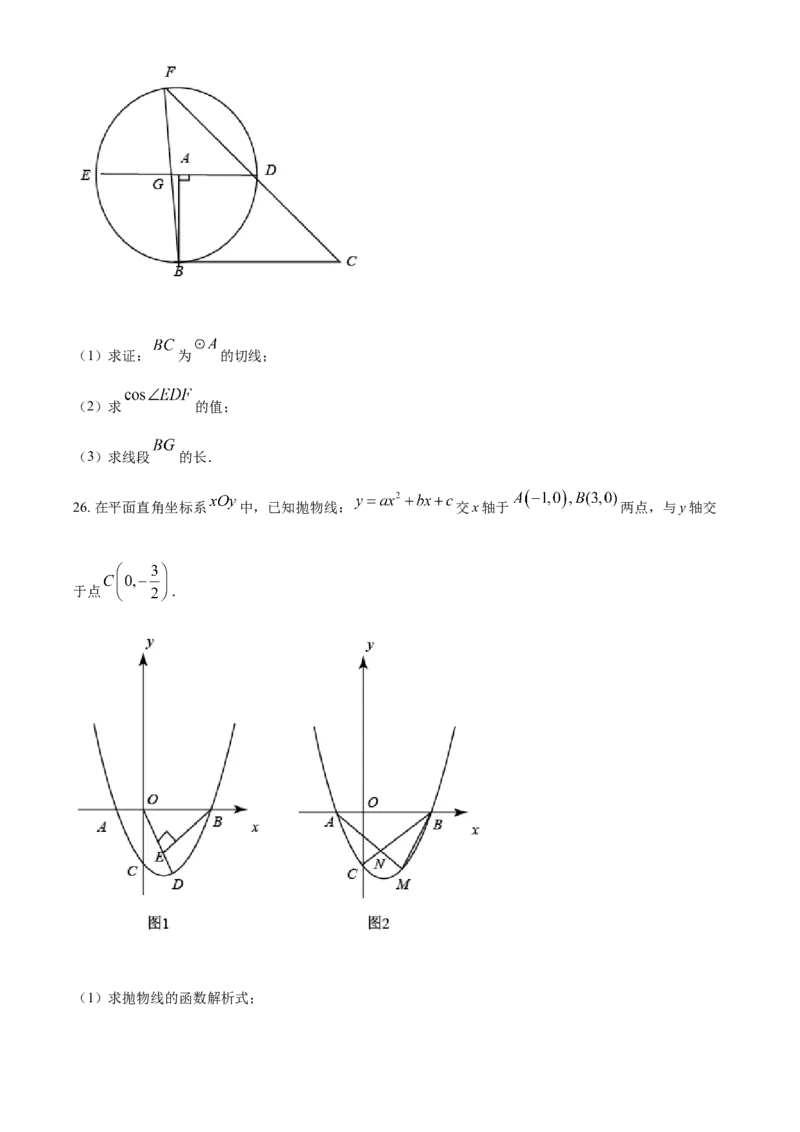
25. 如图,四边形 中, ,以A为圆心, 为半径作
圆,延长 交 于点F,延长 交 于点E,连结 ,交 于点G.(1)求证: 为 的切线;
(2)求 的值;
(3)求线段 的长.
26. 在平面直角坐标系 中,已知抛物线: 交x轴于 两点,与y轴交
于点 .
(1)求抛物线的函数解析式;(2)如图1,点D为第四象限抛物线上一点,连接 ,过点B作 ,垂足为E,若 ,
求点D的坐标;
(3)如图2,点M为第四象限抛物线上一动点,连接 ,交 于点N,连接 ,记 的面
积为 , 的面程为 ,求 的最大值.