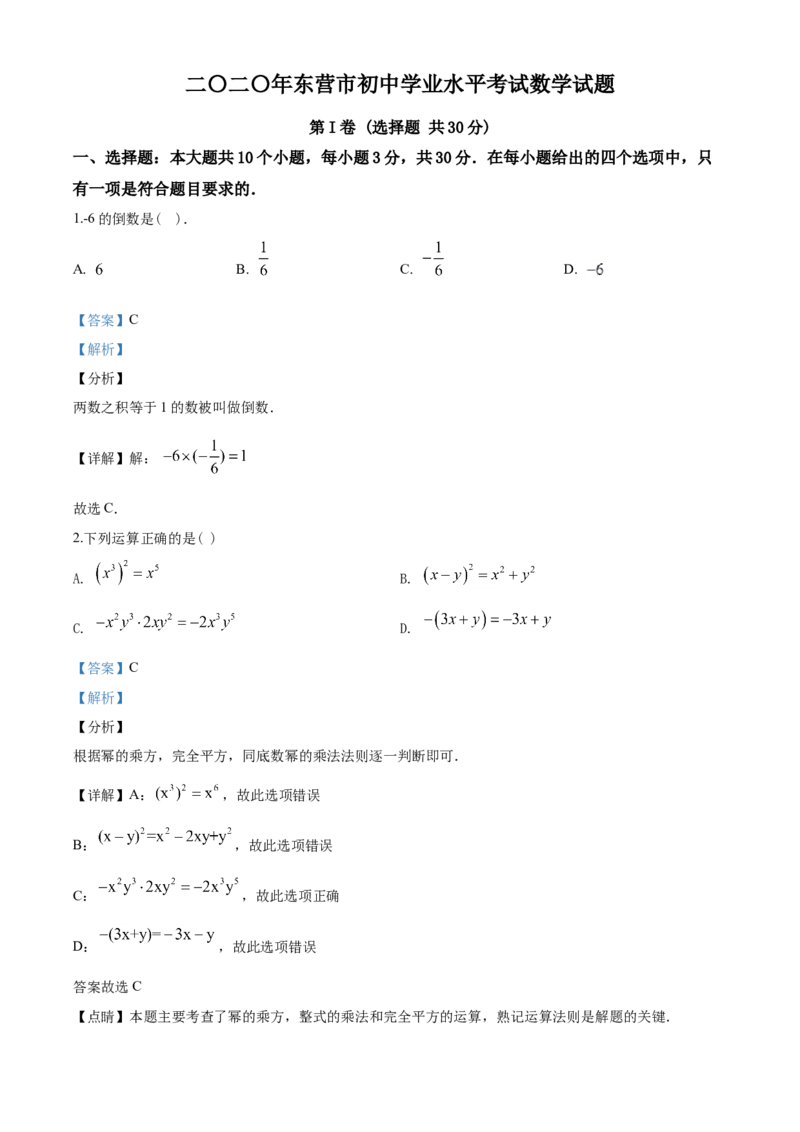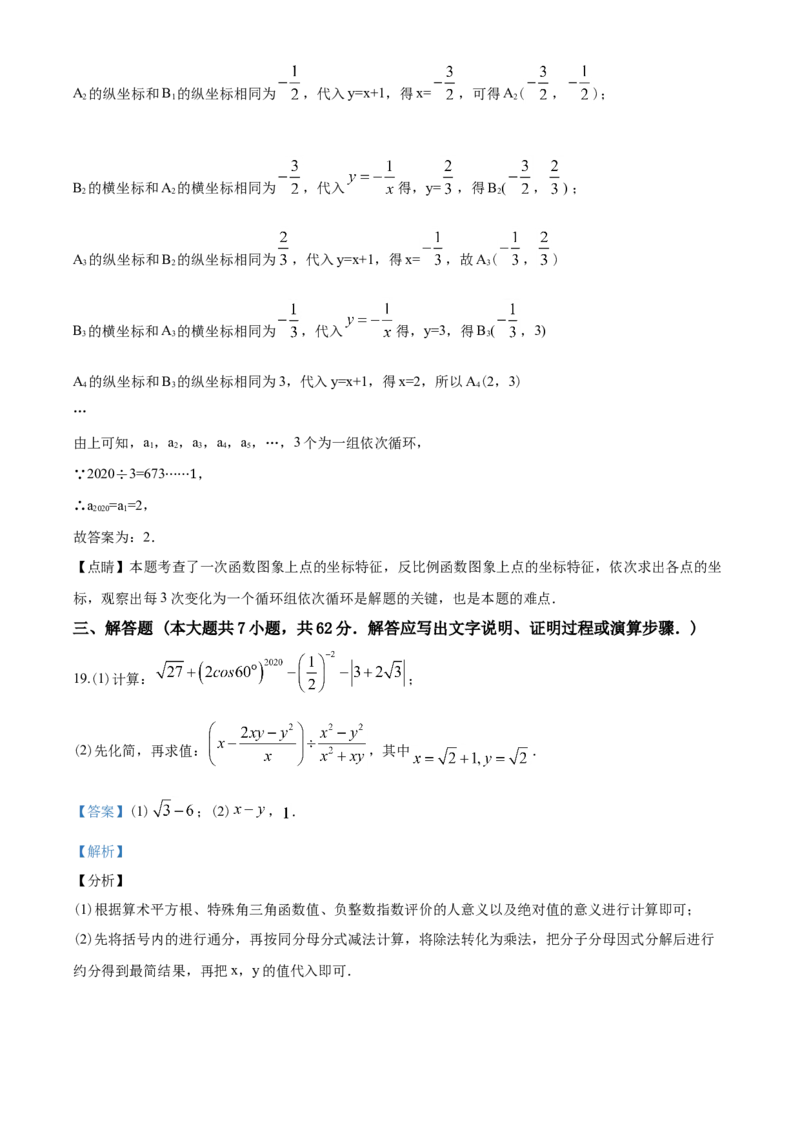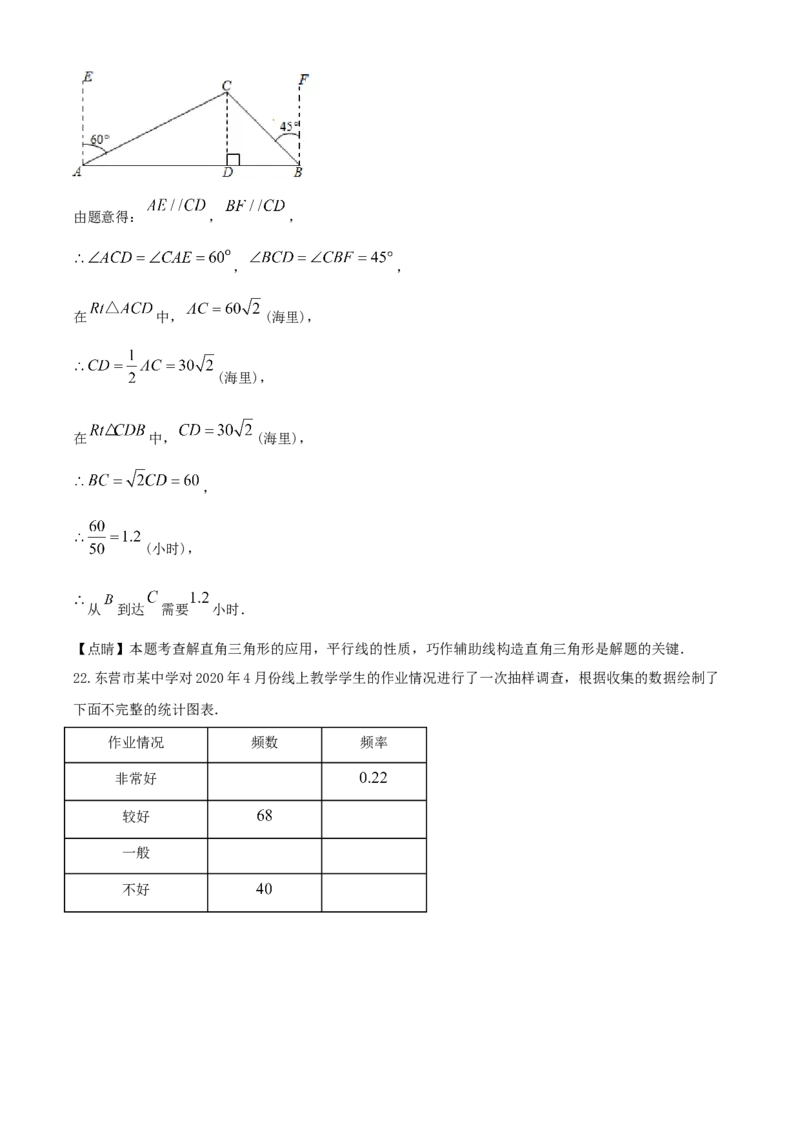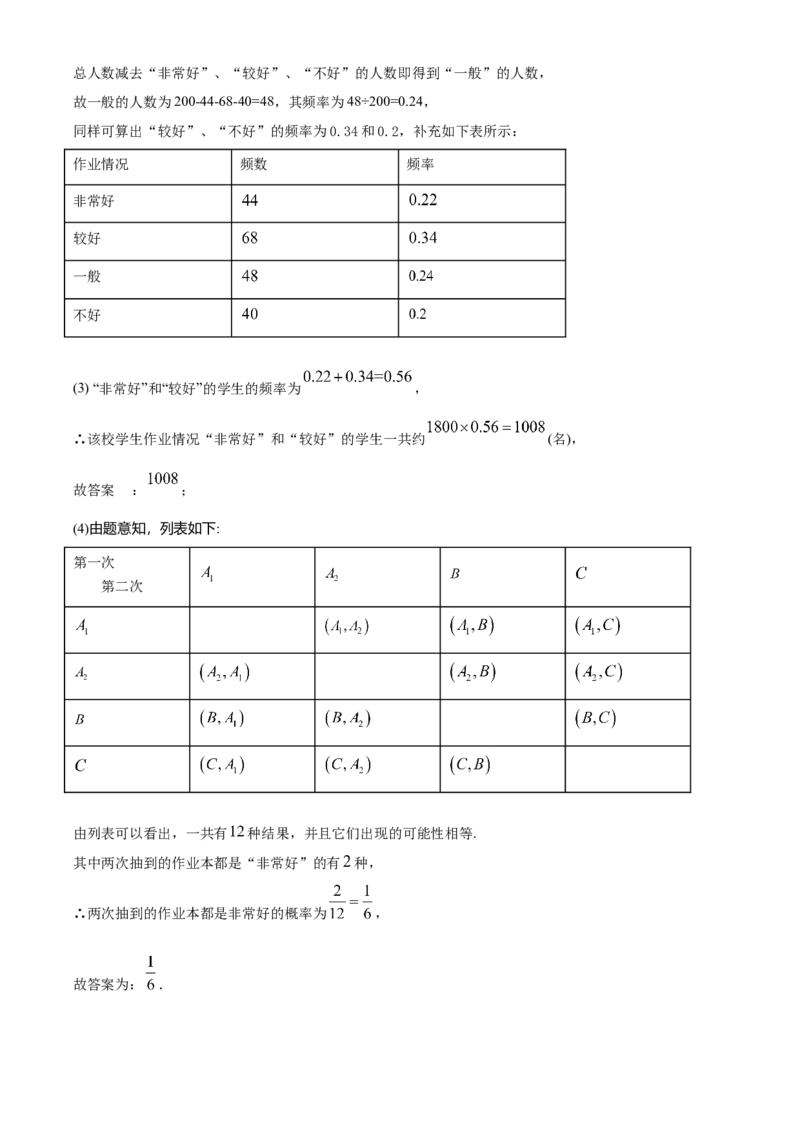文档内容
二〇二〇年东营市初中学业水平考试数学试题
第I卷 (选择题 共30分)
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.-6的倒数是( ).
A. B. C. D.
2.下列运算正确的是( )
A. B.
C. D.
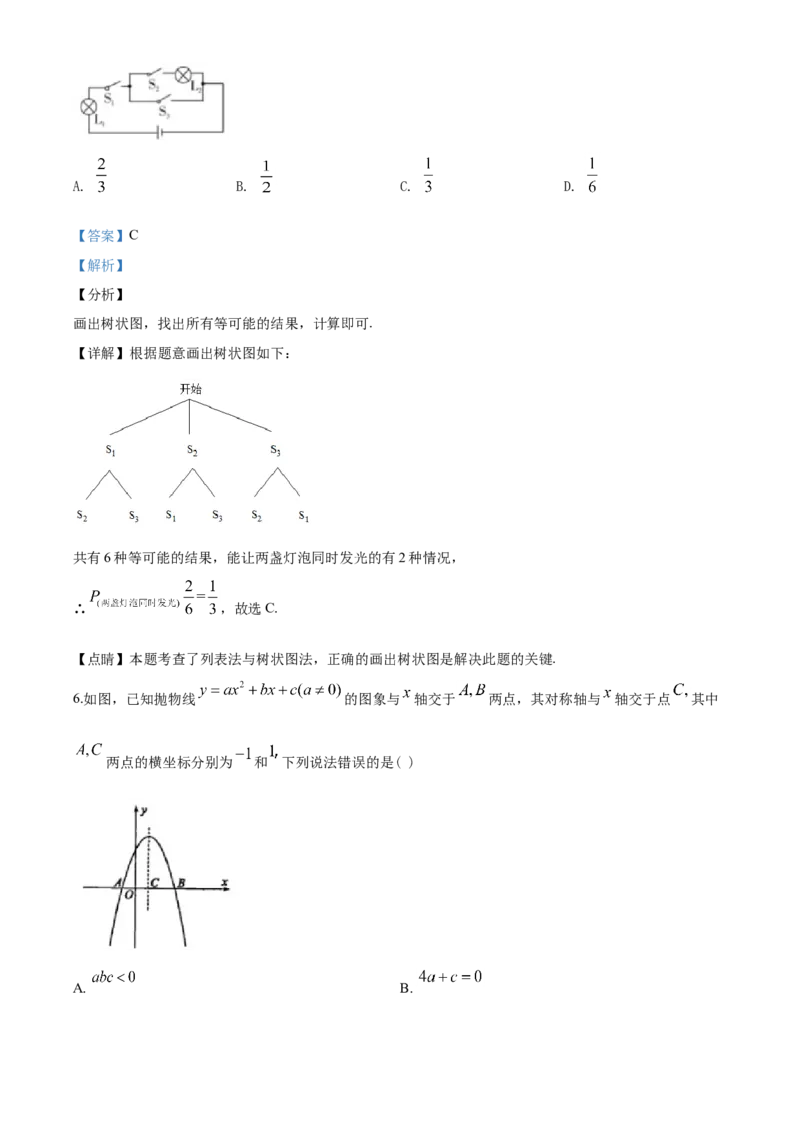
3.利用科学计算器求值时,小明的按键顺序为 ,则计算器面板显示的结果为( )
A. B. C. D.
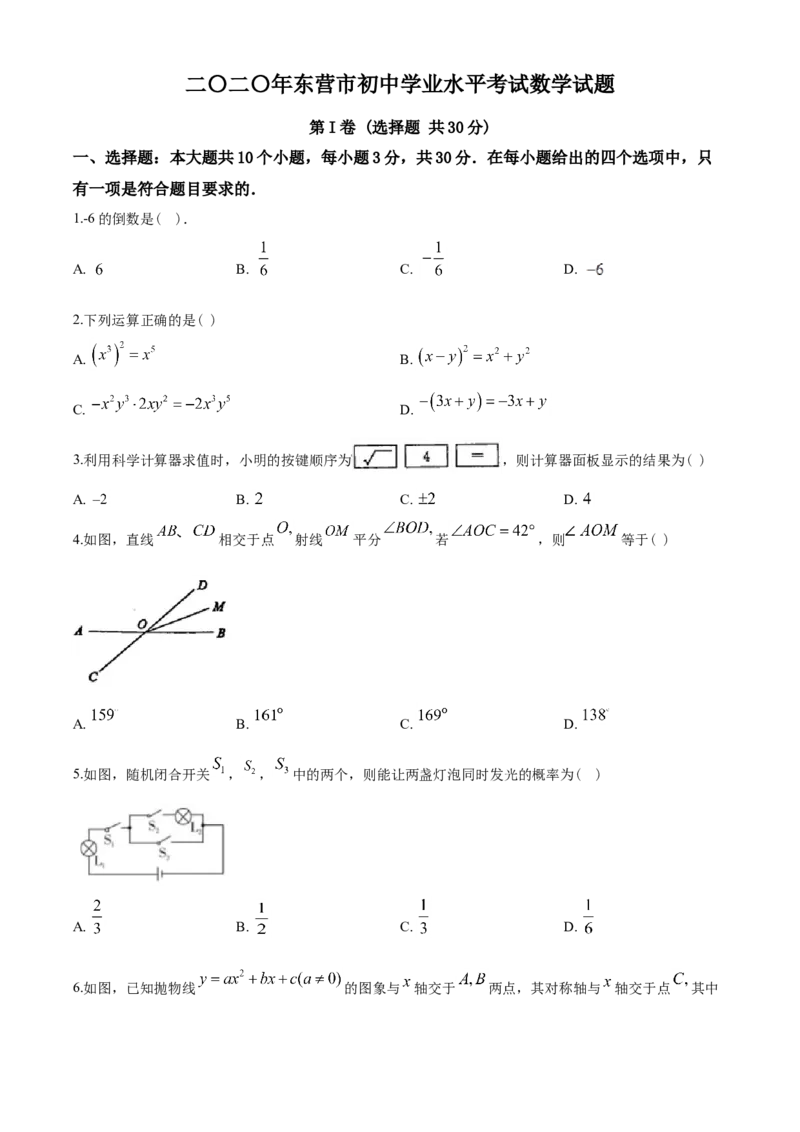
4.如图,直线 相交于点 射线 平分 若 ,则 等于( )
A. B. C. D.
5.如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )
A. B. C. D.
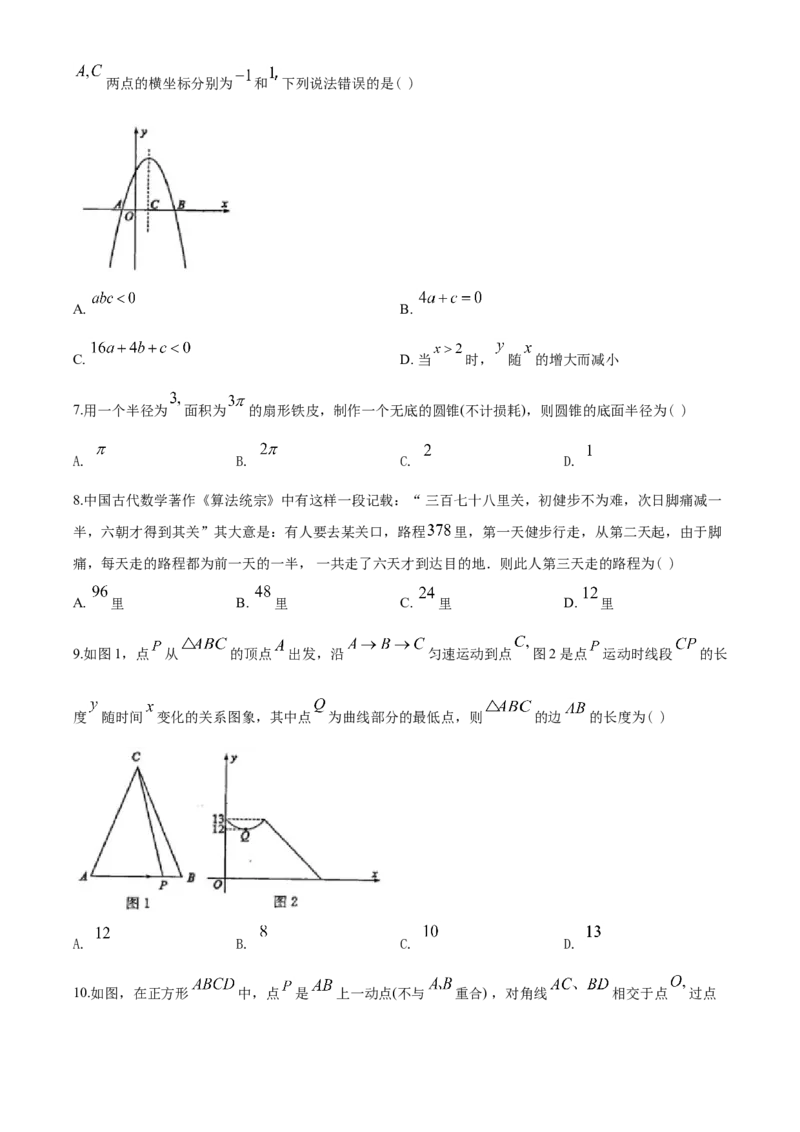
6.如图,已知抛物线 的图象与 轴交于 两点,其对称轴与 轴交于点 其中两点的横坐标分别为 和 下列说法错误的是( )
A. B.
C. D. 当 时, 随 的增大而减小
7.用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )
A. B. C. D.
8.中国古代数学著作《算法统宗》中有这样一段记载:“ 三百七十八里关,初健步不为难,次日脚痛减一
半,六朝才得到其关”其大意是:有人要去某关口,路程 里,第一天健步行走,从第二天起,由于脚
痛,每天走的路程都为前一天的一半, 一共走了六天才到达目的地.则此人第三天走的路程为( )
A. 里 B. 里 C. 里 D. 里
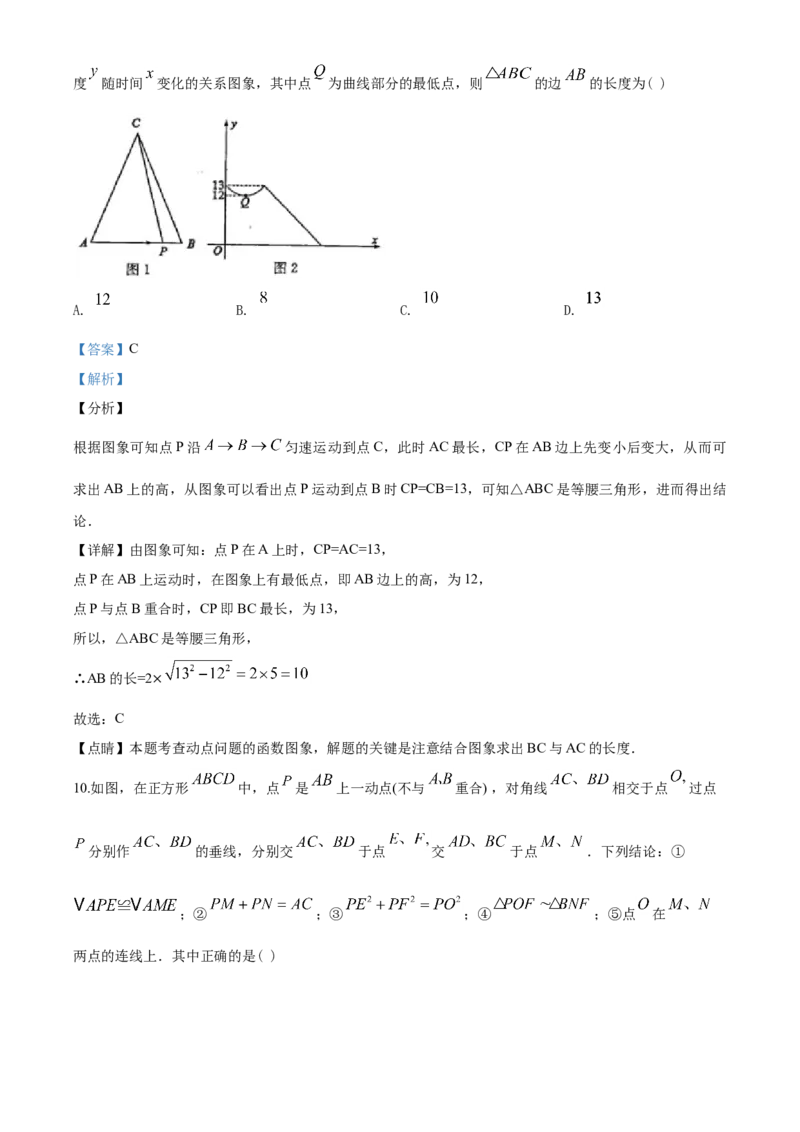
9.如图1,点 从 的顶点 出发,沿 匀速运动到点 图2是点 运动时线段 的长
度 随时间 变化的关系图象,其中点 为曲线部分的最低点,则 的边 的长度为( )
A. B. C. D.
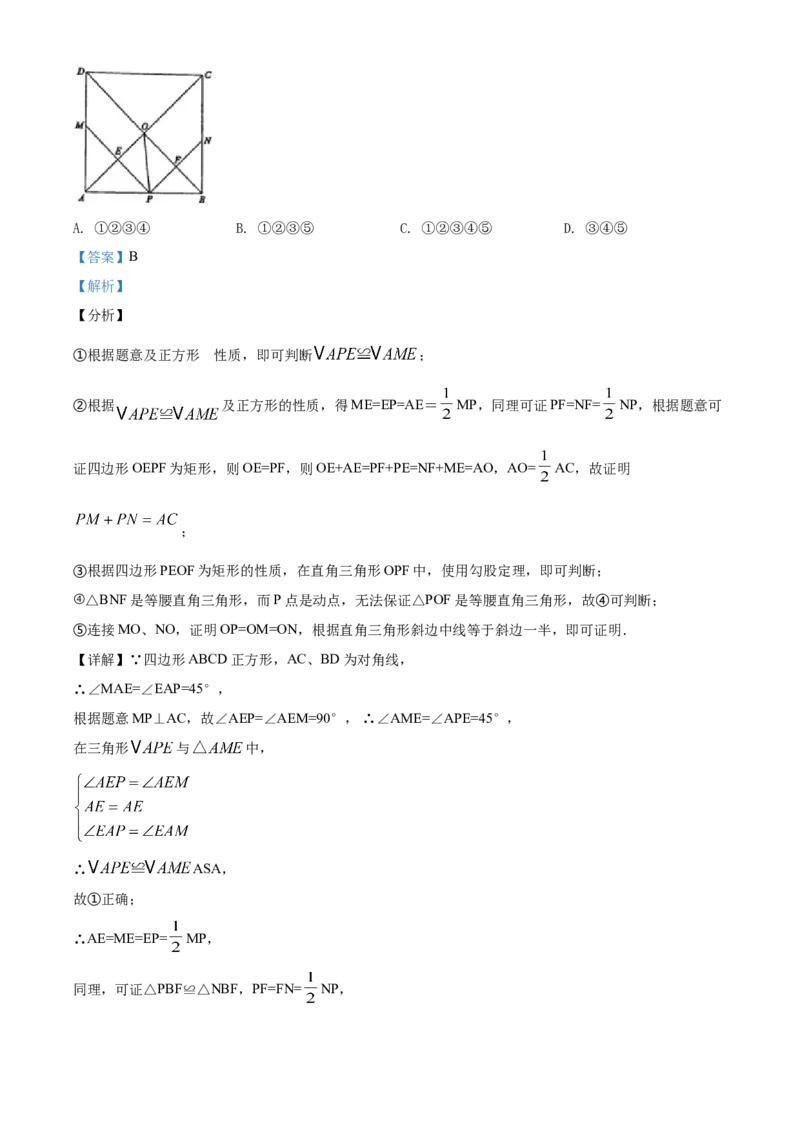
10.如图,在正方形 中,点 是 上一动点(不与 重合) ,对角线 相交于点 过点的
分别作 垂线,分别交 于点 交 于点 .下列结论:①
;② ;③ ;④ ;⑤点 在
两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
第II卷 (非选择题共90分)
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分只
要求填写最后结果.
11.2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于
秒,则 用科学记数法表示为___.
12.因式分解: ___.
13. 某校女子排球队队员的年龄分布如下表:
年龄 13 14 15
人数 4 7 4
则该校女子排球队队员的平均年龄是 岁.
14.已知一次函数y=kx+b的图象经过A(1,﹣1),B(﹣1,3)两点,则k 0(填“>”或“<”)
15.如果关于 的一元二次方程 有实数根,那么 的取值范围是___.
的
16.如图, 为平行四边形 边 上一点, 分别为 上 点,且
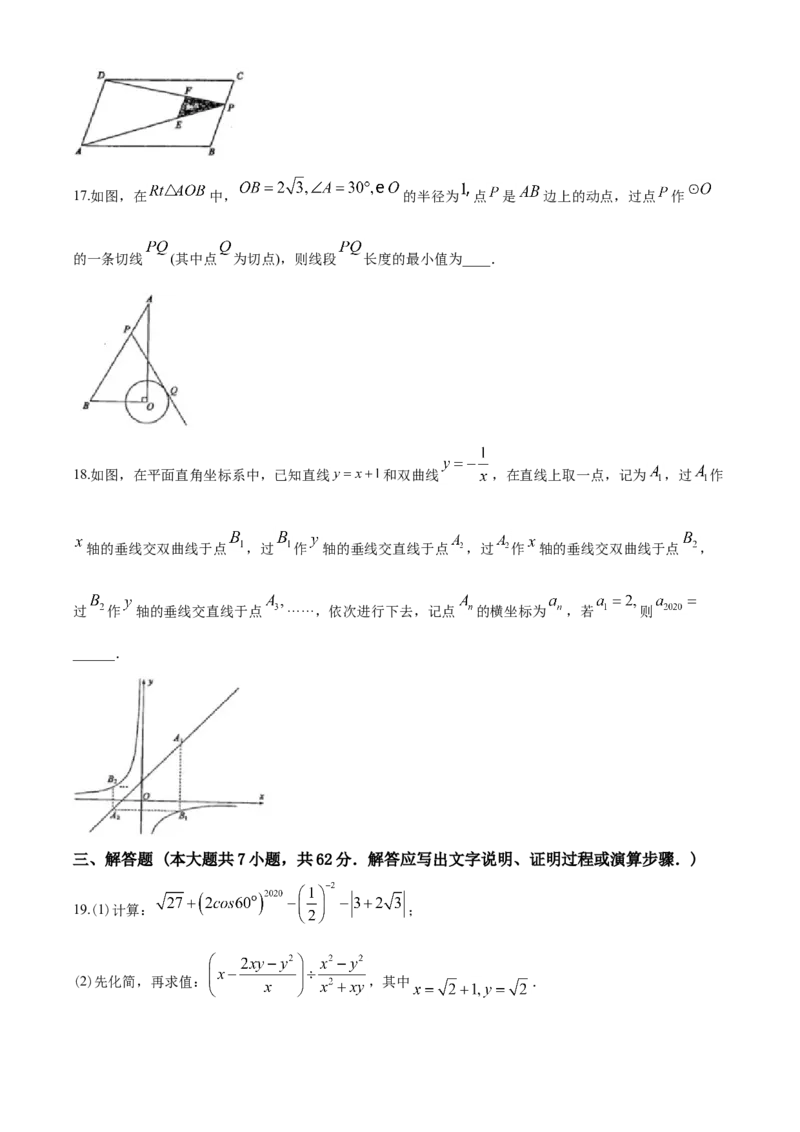
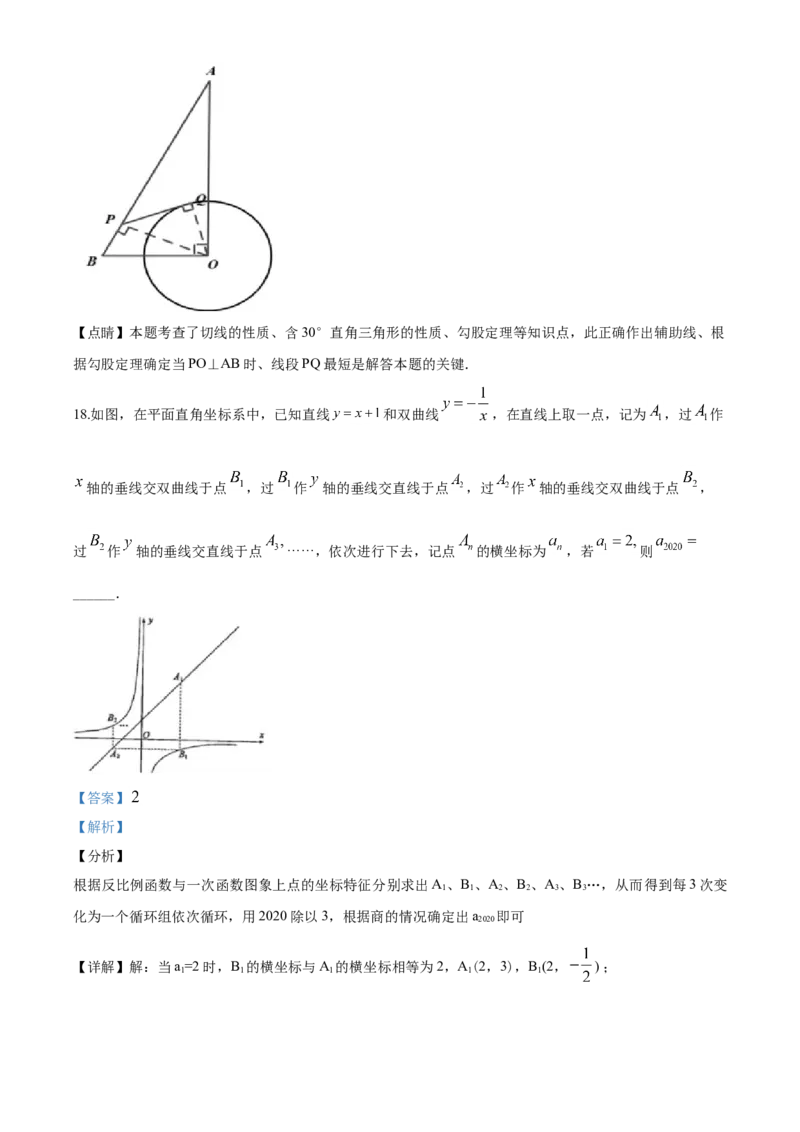
的面积分别记为 .若 则 ____.17.如图,在 中, 的半径为 点 是 边上的动点,过点 作
的一条切线 (其中点 为切点),则线段 长度的最小值为____.
18.如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过 作
轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ,过 作 轴的垂线交双曲线于点 ,
过 作 轴的垂线交直线于点 ······,依次进行下去,记点 的横坐标为 ,若 则
______.
三、解答题 (本大题共7小题,共62分.解答应写出文字说明、证明过程或演算步骤.)
19.(1)计算: ;
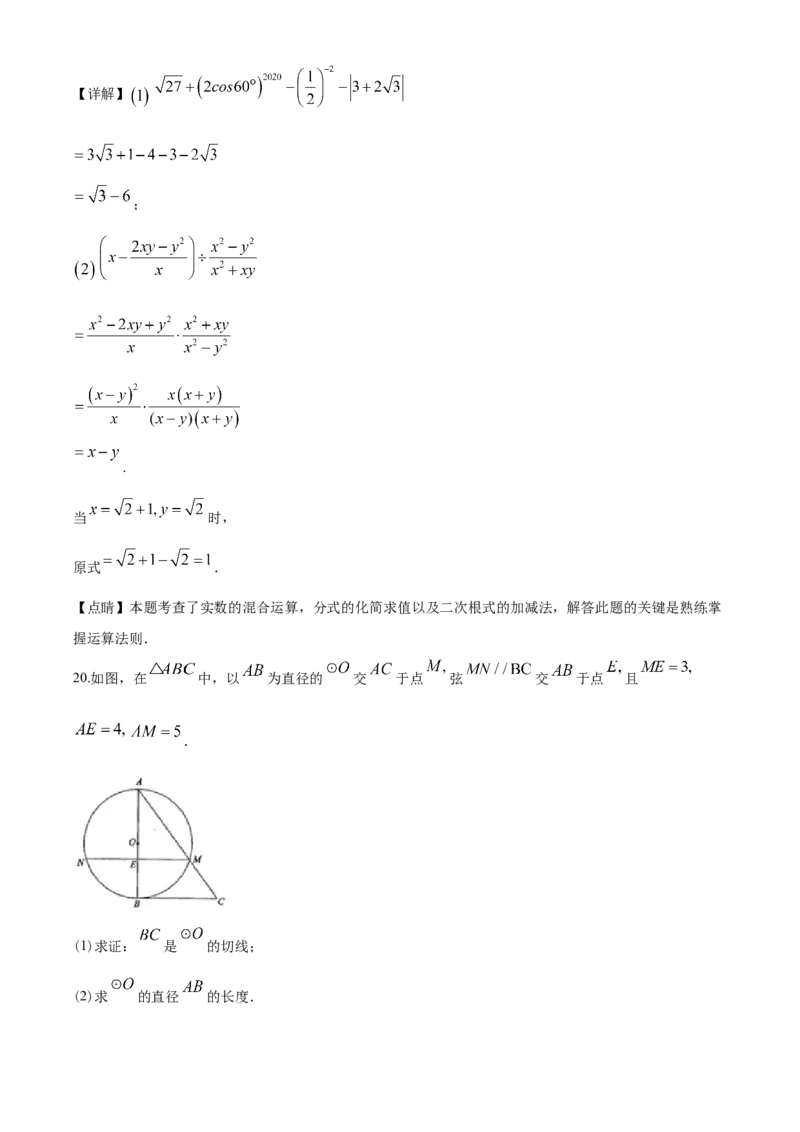
(2)先化简,再求值: ,其中 .20.如图,在 中,以 为直径的 交 于点 弦 交 于点 且
.
(1)求证: 是 的切线;
(2)求 的直径 的长度.
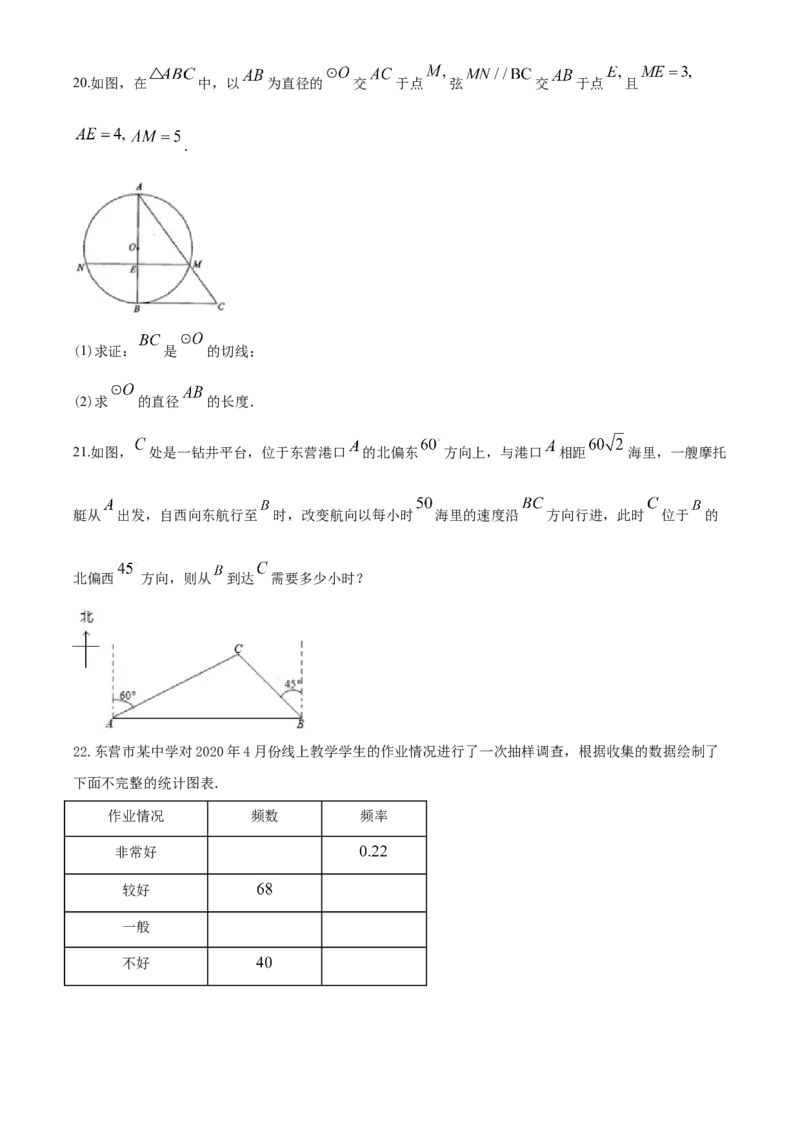
21.如图, 处是一钻井平台,位于东营港口 的北偏东 方向上,与港口 相距 海里,一艘摩托
艇从 出发,自西向东航行至 时,改变航向以每小时 海里的速度沿 方向行进,此时 位于 的
北偏西 方向,则从 到达 需要多少小时?
22.东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了
下面不完整的统计图表.
作业情况 频数 频率
非常好
较好
一般
不好请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了多少名学生?
(2)将统计表中所缺的数据填在表中横线上;
(3)若该中学有 名学生,估计该校学生作业情况“非常好”和“较好”的学生一共约多少名?
的
(4)某学习小组 名学生 作业本中,有 本“非常好”(记为 ), 本“较好”(记为 ), 本“一
般”(记为 ),这些作业本封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不
放回, 从余下的 本中再抽取一本 ,请用“列表法”或“画树状图”的方法求出两次抽到的作业本都是
“非常好”的概率.
23.2020年初,新冠肺炎疫情爆发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号 的防疫口
罩共 万只,且所有口罩当月全部售出,其中成本、售价如下表:
型号
价格(元/只) 甲 乙
项目
成本
售价
(1)若该公司三月份的销售收入为 万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果公司四月份投入成本不超过 万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公
司所获利润最大?并求出最大利润.
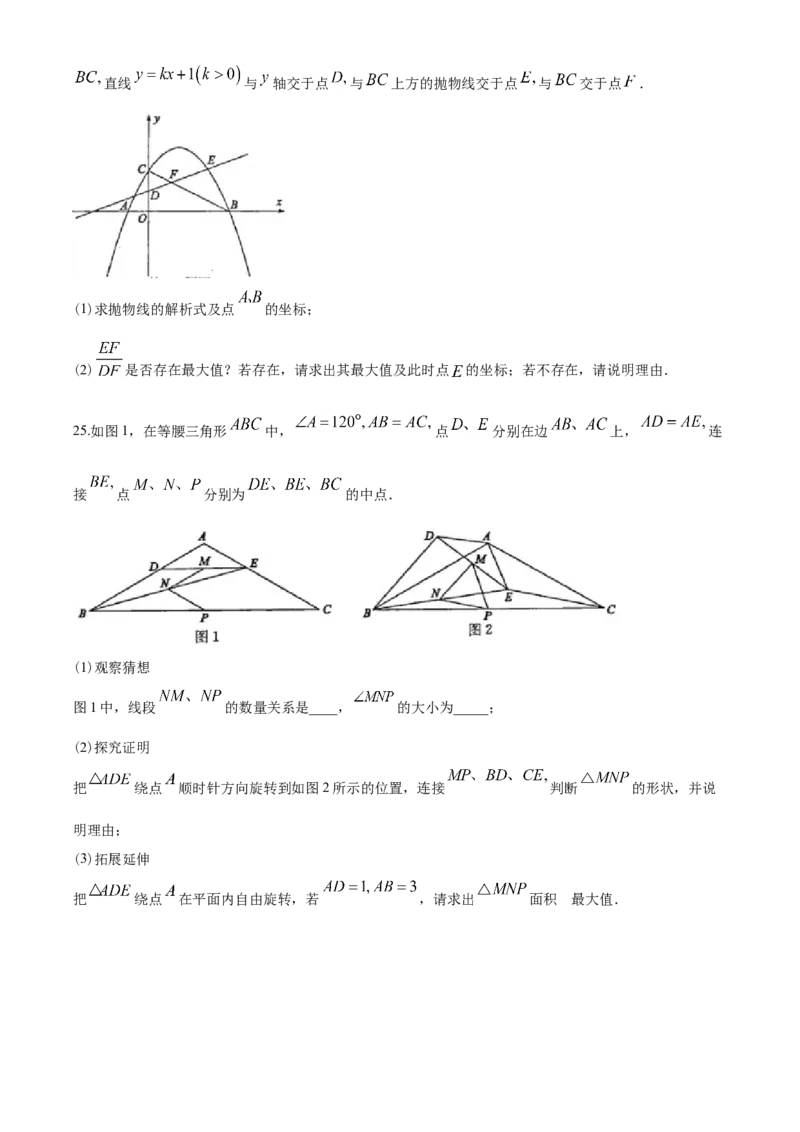
24.如图,抛物线 的图象经过点 ,交 轴于点 (点 在点 左侧),连接直线 与 轴交于点 与 上方的抛物线交于点 与 交于点 .
(1)求抛物线的解析式及点 的坐标;
(2) 是否存在最大值?若存在,请求出其最大值及此时点 的坐标;若不存在,请说明理由.
25.如图1,在等腰三角形 中, 点 分别在边 上, 连
接 点 分别为 的中点.
(1)观察猜想
图1中,线段 的数量关系是____, 的大小为_____;
(2)探究证明
把 绕点 顺时针方向旋转到如图2所示的位置,连接 判断 的形状,并说
明理由;
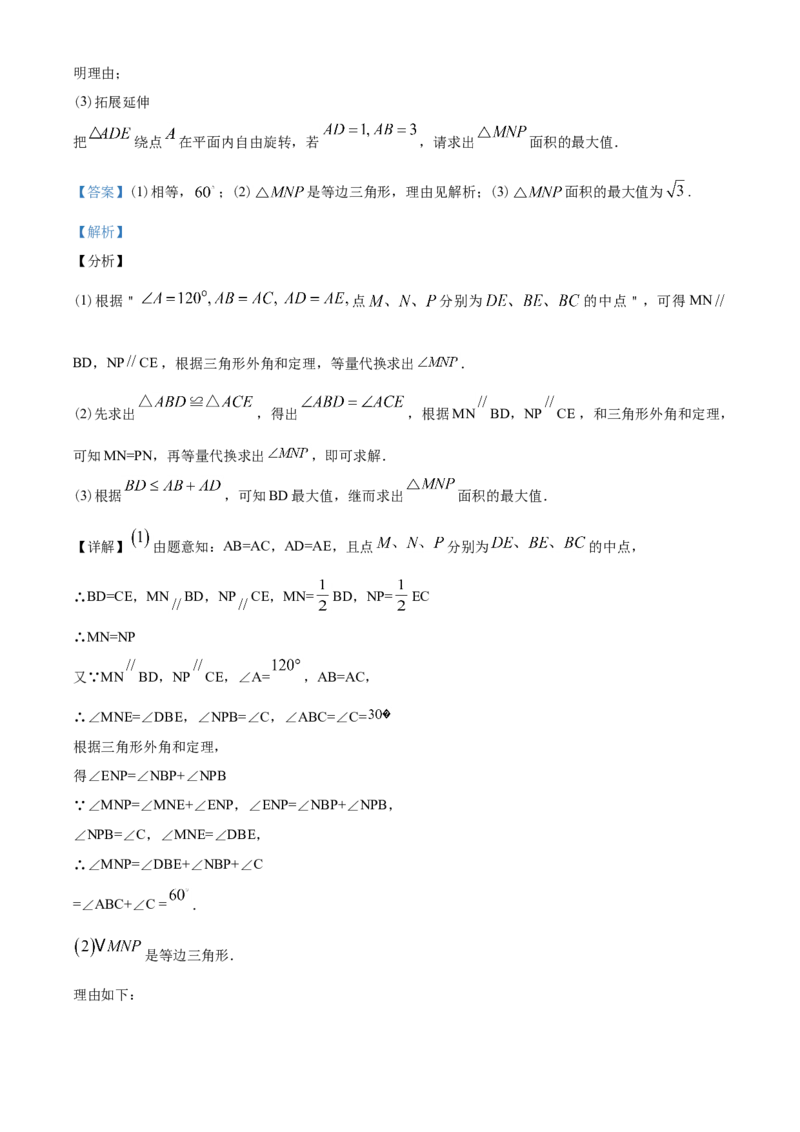
(3)拓展延伸
的
把 绕点 在平面内自由旋转,若 ,请求出 面积 最大值.二〇二〇年东营市初中学业水平考试数学试题
第I卷 (选择题 共30分)
一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.-6的倒数是( ).
A. B. C. D.
【答案】C
【解析】
【分析】
两数之积等于1的数被叫做倒数.
【详解】解:
故选C.
2.下列运算正确的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】
根据幂的乘方,完全平方,同底数幂的乘法法则逐一判断即可.
【详解】A: ,故此选项错误
B: ,故此选项错误
C: ,故此选项正确
D: ,故此选项错误
答案故选C
【点睛】本题主要考查了幂的乘方,整式的乘法和完全平方的运算,熟记运算法则是解题的关键.3.利用科学计算器求值时,小明的按键顺序为 ,则计算器面板显示的结果为( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据算术平方根的求解方法进行计算即可得解.
【详解】4的算术平方根 ,
故选:B.
【点睛】本题主要考查了算术平方根的求解方法,考生需要将其与平方根进行对比掌握.
4.如图,直线 相交于点 射线 平分 若 ,则 等于( )
A. B. C. D.
【答案】A
【解析】
【分析】
先求出∠AOD=180°-∠AOC,再求出∠BOD=180°-∠AOD,最后根据角平分线平分角即可求解.
【详解】解:由题意可知:∠AOD=180°-∠AOC=180°-42°=138°,
∴∠BOD=180°-∠AOD=42°,
又OM是∠BOD的角平分线,
∴∠DOM= ∠BOD=21°,
∴∠AOM=∠DOM+∠AOD=21°+138°=159°.
故选:A.
【点睛】本题考查了角平分线的性质及平角的定义,熟练掌握角平分线的性质和平角的定义是解决此类题
的关键.
5.如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )A. B. C. D.
【答案】C
【解析】
【分析】
画出树状图,找出所有等可能的结果,计算即可.
【详解】根据题意画出树状图如下:
共有6种等可能的结果,能让两盏灯泡同时发光的有2种情况,
∴ ,故选C.
【点睛】本题考查了列表法与树状图法,正确的画出树状图是解决此题的关键.
6.如图,已知抛物线 的图象与 轴交于 两点,其对称轴与 轴交于点 其中
两点的横坐标分别为 和 下列说法错误的是( )
A. B.C. D. 当 时, 随 的增大而减小
【答案】B
【解析】
【分析】
根据开口方向、对称轴、与 轴交点即可分别判断 符号,进而判断A选项;由 两点的横坐
标分别为 和 可得两个方程,判断B选项;由当 时 判断C选项;由二次函数
对称轴及增减性判断D选项.
【详解】∵开口向下,与 轴交点在正半轴
∴
∵ 两点的横坐标分别为 和
∴
∴
∴ ,故A选项正确,B选项错误
∵ 两点的横坐标分别为 和
∴B点横坐标为3
∴当 时 ,故C选项正确
∵当 时, 随 的增大而减小
∴当 时, 随 的增大而减小,故D选项正确
故选:B.
【点睛】本题考查二次函数的图像和性质,重点考查二次函数系数符号与图象的关系,熟记二次函数图象
性质是解题的关键.
7.用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )
A. B. C. D.【答案】D
【解析】
【分析】
根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和
扇形面积公式得到 •2π•r•3=3π,然后解方程即可.
【详解】解:根据题意得 •2π•r•3=3π,
解得r=1.
故选:D.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇
形的半径等于圆锥的母线长.
8.中国古代数学著作《算法统宗》中有这样一段记载:“ 三百七十八里关,初健步不为难,次日脚痛减一
半,六朝才得到其关”其大意是:有人要去某关口,路程 里,第一天健步行走,从第二天起,由于脚
痛,每天走的路程都为前一天的一半, 一共走了六天才到达目的地.则此人第三天走的路程为( )
A. 里 B. 里 C. 里 D. 里
【答案】B
【解析】
【分析】
根据题意可设第一天所走的路程为 ,用含 的式子分别把这六天的路程表示出来,相加等于总路程
378,解此方程即可.
【详解】解:设第一天的路程为 里
∴
解得
∴第三天的路程为
故答案选B
【点睛】本题主要考查了一元一次方程的应用,通过每日路程之和等于总路程建立一元一次方程是解题的
关键.
的
9.如图1,点 从 顶点 出发,沿 匀速运动到点 图2是点 运动时线段 的长度 随时间 变化的关系图象,其中点 为曲线部分的最低点,则 的边 的长度为( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据图象可知点P沿 匀速运动到点C,此时AC最长,CP在AB边上先变小后变大,从而可
求出AB上的高,从图象可以看出点P运动到点B时CP=CB=13,可知△ABC是等腰三角形,进而得出结
论.
【详解】由图象可知:点P在A上时,CP=AC=13,
点P在AB上运动时,在图象上有最低点,即AB边上的高,为12,
点P与点B重合时,CP即 BC最长,为13,
所以,△ABC是等腰三角形,
∴AB的长=2
×
故选:C
【点睛】本题考查动点问题的函数图象,解题的关键是注意结合图象求出BC与AC的长度.
10.如图,在正方形 中,点 是 上一动点(不与 重合) ,对角线 相交于点 过点
分别作 的垂线,分别交 于点 交 于点 .下列结论:①
;② ;③ ;④ ;⑤点 在
两点的连线上.其中正确的是( )A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
【答案】B
【解析】
【分析】
①根据题意及正方形 的性质,即可判断 ;
②根据 及正方形的性质,得ME=EP=AE= MP,同理可证PF=NF= NP,根据题意可
证四边形OEPF为矩形,则OE=PF,则OE+AE=PF+PE=NF+ME=AO,AO= AC,故证明
;
③根据四边形PEOF为矩形的性质,在直角三角形OPF中,使用勾股定理,即可判断;
④△BNF是等腰直角三角形,而P点是动点,无法保证△POF是等腰直角三角形,故④可判断;
⑤连接MO、NO,证明OP=OM=ON,根据直角三角形斜边中线等于斜边一半,即可证明.
【详解】∵四边形ABCD正方形,AC、BD为对角线,
∴∠MAE=∠EAP=45°,
根据题意MP⊥AC,故∠AEP=∠AEM=90°, ∴∠AME=∠APE=45°,
在三角形 与 中,
∴ ASA,
故①正确;
∴AE=ME=EP= MP,
同理,可证△PBF≌△NBF,PF=FN= NP,∵正方形ABCD中,AC⊥BD,
又∵PM⊥AC,PN⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,
∴四边形PEOF为矩形,
∴PF=OE,
∴OE+AE=PF+PE=NF+ME=AO,
又∵ME=PE= MP,
FP=FN= NP,OA= AC,
∴ PM+PN=AC,
故②正确;
∵四边形PEOF为矩形,
∴PE=OF,
在直角三角形OPF中, ,
∴ ,
故③正确;
∵△BNF是等腰直角三角形,而P点是动点,无法保证△POF是等腰直角三角形,
故④错误;
连接MO、NO,
在△OEM和△OEP中,
∴△OEM≌△OEP,OM=OP,
同理可证△OFP≌△OFN,OP=ON,
又∵∠MPN=90°,
OM=OP=ON,OP=12MO+NO,
根据直角三角形斜边中线等于斜边一半,OP= MN,
∴MO+NO=MN,点 在 两点的连线上.故⑤正确.
故选择B.
【点睛】本题主要考查几何综合问题,掌握正方形、矩形的判定和性质,全等三角形的判定和性质,勾股
定理是解答本题的关键.
第II卷 (非选择题共90分)
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分只
要求填写最后结果.
11.2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于
秒,则 用科学记数法表示为___.
【答案】
【解析】
【分析】
根据科学记数法表示较小的数,一般形式为 ,其中1≤|a|<10,n为由原数左边起第一个不为零的
数字前面的0的个数所决定,进而求解.
【详解】因为 ,
故答案为: .
【点睛】本题考查了用科学记数法表示较小的数,一般形式为 ,其中1≤|a|<10,正确确定a与n
的值是解题的关键.
12.因式分解: ___.
【答案】
【解析】
【分析】
先提公因式,再按照平方差公式分解即可.
【详解】解:
故答案为: .【点睛】本题考查的是提公因式与公式法分解因式,掌握以上知识是解题的关键.
13. 某校女子排球队队员的年龄分布如下表:
年龄 13 14 15
人数 4 7 4
则该校女子排球队队员的平均年龄是 岁.
【答案】14.
【解析】
【详解】平均数是指在一组数据中所有数据之和再除以数据的个数,因此,
该校女子排球队队员的平均年龄是 (岁).
故答案为:14.
的
14.已知一次函数y=kx+b 图象经过A(1,﹣1),B(﹣1,3)两点,则k 0(填“>”或“<”)
【答案】<.
【解析】
【分析】
根据A(1,-1),B(-1,3),利用横坐标和纵坐标的增减性判断出k的符号.
【详解】∵A点横坐标为1,B点横坐标为-1,
根据-1<1,3>-1,
可知,随着横坐标的增大,纵坐标减小了,
∴k<0.
故答案为<.
15.如果关于 的一元二次方程 有实数根,那么 的取值范围是___.
【答案】
【解析】
【分析】
由一元二次方程根与系数的关键可得: 从而列不等式可得答案.【详解】解: 关于 的一元二次方程 有实数根,
故答案为:
【点睛】本题考查的是一元二次方程根的判别式,掌握一元二次方程根的判别式是解题的关键.
16.如图, 为平行四边形 边 上一点, 分别为 上的点,且
的面积分别记为 .若 则 ____.
【答案】
【解析】
【分析】
证明△PEF∽△PAD,再结合△PEF的面积为2可求出△PAD的面积,进而求出平行四边形ABCD的面积,
再用平行四边形ABCD的面积减去△PAD的面积即可求解.
【详解】解:∵
∴ ,且∠APD=∠EPF,
∴△PEF∽△PAD,
根据相似三角形面积比等于相似比的平方,且△PEF的面积为2可知,,
∴ ,
过P点作平行四边形ABCD的底AD上的高PH,
∴ ,
∴ ,
即平行四边形ABCD的面积为 ,
∴ .
故答案为: .
【点睛】本题考查了平行四边形 的性质,相似三角形的判定及性质等,熟练掌握其性质是解决本题的关键.
17.如图,在 中, 的半径为 点 是 边上的动点,过点 作
的一条切线 (其中点 为切点),则线段 长度的最小值为____.【答案】
【解析】
【分析】
如图:连接OP、OQ,根据 ,可得当OP⊥AB时,PQ最短;在 中运用含30°的
直角三角形的性质和勾股定理求得AB、AQ的长,然后再运用等面积法求得OP的长,最后运用勾股定理
解答即可.
【详解】解:如图:连接OP、OQ,
∵ 是 的一条切线
∴PQ⊥OQ
∴
∴当OP⊥AB时,PQ最短
在Rt△ABC中,
∴AB=2OB= ,AO=cos∠A·AB=
∵S =
△AOB
∴ ,即OP=3
在Rt△OPQ中,OP=3,OQ=1
∴PQ= .
故答案为 .【点睛】本题考查了切线的性质、含30°直角三角形的性质、勾股定理等知识点,此正确作出辅助线、根
据勾股定理确定当PO⊥AB时、线段PQ最短是解答本题的关键.
18.如图,在平面直角坐标系中,已知直线 和双曲线 ,在直线上取一点,记为 ,过 作
轴的垂线交双曲线于点 ,过 作 轴的垂线交直线于点 ,过 作 轴的垂线交双曲线于点 ,
过 作 轴的垂线交直线于点 ······,依次进行下去,记点 的横坐标为 ,若 则
______.
【答案】
【解析】
【分析】
根据反比例函数与一次函数图象上点的坐标特征分别求出A 、B 、A 、B 、A 、B …,从而得到每3次变
1 1 2 2 3 3
化为一个循环组依次循环,用2020除以3,根据商的情况确定出a 即可
2020
【详解】解:当a=2时,B 的横坐标与A 的横坐标相等为2,A(2,3),B (2, ) ;
1 1 1 1 1A 的纵坐标和B 的纵坐标相同为 ,代入y=x+1,得x= ,可得A( , );
2 1 2
B 的横坐标和A 的横坐标相同为 ,代入 得,y= ,得B ( , ) ;
2 2 2
A 的纵坐标和B 的纵坐标相同为 ,代入y=x+1,得x= ,故A( , )
3 2 3
B 的横坐标和A 的横坐标相同为 ,代入 得,y=3,得B ( ,3)
3 3 3
A 的纵坐标和B 的纵坐标相同为3,代入y=x+1,得x=2,所以A(2,3)
4 3 4
…
由上可知,a,a,a,a,a,…,3个为一组依次循环,
1 2 3 4 5
∵2020÷3=673 ,
∴a =a=2, ⋯⋯1
2020 1
故答案为:2.
【点睛】本题考查了一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征,依次求出各点的坐
标,观察出每3次变化为一个循环组依次循环是解题的关键,也是本题的难点.
三、解答题 (本大题共7小题,共62分.解答应写出文字说明、证明过程或演算步骤.)
19.(1)计算: ;
(2)先化简,再求值: ,其中 .
【答案】(1) ;(2) , .
【解析】
【分析】
(1)根据算术平方根、特殊角三角函数值、负整数指数评价的人意义以及绝对值的意义进行计算即可;
(2)先将括号内的进行通分,再按同分母分式减法计算,将除法转化为乘法,把分子分母因式分解后进行
约分得到最简结果,再把x,y的值代入即可.【详解】
;
.
当 时,
原式 .
【点睛】本题考查了实数的混合运算,分式的化简求值以及二次根式的加减法,解答此题的关键是熟练掌
握运算法则.
20.如图,在 中,以 为直径的 交 于点 弦 交 于点 且
.
(1)求证: 是 的切线;
(2)求 的直径 的长度.【答案】(1)见解析;(2) 的直径 的长度为
【解析】
【分析】
(1)先用勾股定理的逆定理证明△AEM 为直角三角形,且∠AEM=90°,再根据 MN∥BC 即可证明
∠ABC=90°进而求解;
(2)连接BM,由AB是直径得到∠AMB=90°,再分别在Rt△AMB和Rt△AEM中使用∠A的余弦即可求解.
【详解】解:(1) ,
,
为 的直径,
是 的切线.
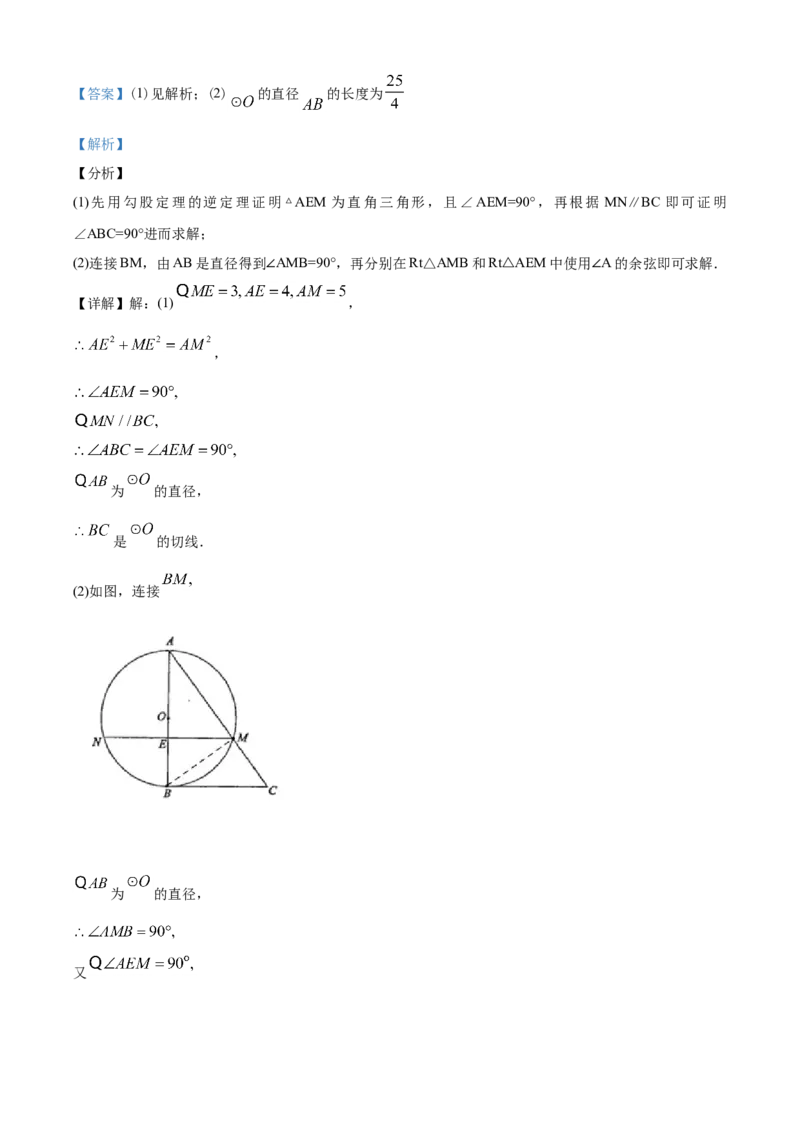
(2)如图,连接
为 的直径,
又,
即 ,
,
∴ 的直径 的长度为 .
故答案为: .
【点睛】本题考查了圆中切线的证明,圆周角定理,直角三角形中锐角的三角函数的求法,熟练掌握切线
的性质和判定及锐角三角函数的定义是解决此类题的关键.
21.如图, 处是一钻井平台,位于东营港口 的北偏东 方向上,与港口 相距 海里,一艘摩托
艇从 出发,自西向东航行至 时,改变航向以每小时 海里的速度沿 方向行进,此时 位于 的
北偏西 方向,则从 到达 需要多少小时?
【答案】从 到达 需要 小时.
【解析】
【分析】
过点 作 于点 ,在 与 中,利用锐角三角函数的定义求出CD与BC的长,
进而求解.
【详解】解:如图,过点 作 于点 ,由题意得: , ,
, ,
在 中, (海里),
(海里),
在 中, (海里),
,
(小时),
从 到达 需要 小时.
【点睛】本题考查解直角三角形的应用,平行线的性质,巧作辅助线构造直角三角形是解题的关键.
22.东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了
下面不完整的统计图表.
作业情况 频数 频率
非常好
较好
一般
不好请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了多少名学生?
(2)将统计表中所缺的数据填在表中横线上;
(3)若该中学有 名学生,估计该校学生作业情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组 名学生的作业本中,有 本“非常好”(记为 ), 本“较好”(记为 ), 本“一
般”(记为 ),这些作业本封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不
放回, 从余下的 本中再抽取一本 ,请用“列表法”或“画树状图”的方法求出两次抽到的作业本都是
“非常好”的概率.
【答案】(1) ;(2)见解析;(3)约 名;(4) .
【解析】
【分析】
(1)用72°除360°得到“不好”的学生人数的占比,然后再用40除以该百分比即可得到总共调查的学生人数;
(2)先算出“非常好”的人数,然后再用总分数减去“非常好”、“较好”、“不好”的人数即得到“一
般”的人数,最后分别用求出其人数除总人数得到其频率;
(3)先算出“非常好”和“较好”的学生的频率,再乘以1800即可求解;
(4)采用列表法将所有可能的情况列出,然后再用概率公式求解即可.
【详解】解:(1)由图形可知:72°占360°的百分比为 ,
故调查的总的学生人数为 (名),
故答案为:200(名) .
(2)“非常好”的学生人数为:0.22×200=44(人),总人数减去“非常好”、“较好”、“不好”的人数即得到“一般”的人数,
故一般的人数为200-44-68-40=48,其频率为48÷200=0.24,
同样可算出“较好”、“不好”的频率为0.34和0.2,补充如下表所示:
作业情况 频数 频率
非常好
较好
一般
不好
(3) “非常好”和“较好”的学生的频率为 ,
∴该校学生作业情况“非常好”和“较好”的学生一共约 (名),
为
故答案 : ;
(4)由题意知,列表如下:
第一次
第二次
由列表可以看出,一共有 种结果,并且它们出现的可能性相等.
其中两次抽到的作业本都是“非常好”的有 种,
∴两次抽到的作业本都是非常好的概率为 ,
故答案为: .【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适
合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放
回实验.用到的知识点为:概率=所求情况数与总情况数之比.
23.2020年初,新冠肺炎疫情爆发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号的防疫口
罩共 万只,且所有口罩当月全部售出,其中成本、售价如下表:
型号
价格(元/只) 甲 乙
项目
成本
售价
(1)若该公司三月份的销售收入为 万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果公司四月份投入成本不超过 万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公
司所获利润最大?并求出最大利润.
【答案】(1)甲、乙两种型号口罩的产量分别为 万只和 万只;(2)从而安排生产甲种型号的口罩 万
只,乙种型号的口罩 万只时,获得最大利润,最大利润为 万元.
【解析】
【分析】
(1)设甲种型号口罩的产量是 万只,则乙种型号口罩的产量是 万只,根据该公司三月份的销售
收入为 万元列出一元一次方程,从而可以得到甲、乙两种型号的产品分别是多少万只;
(2)根据题意,可以得到利润和生产甲种产品数量的函数关系式,再根据公司四月份投入总成本(原料总成
本+生产提成总额)不超过216万元,可以得到生产甲种产品数量的取值范围,然后根据一次函数的性质,
即可得到应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大,并求出最大利润.
【详解】 设甲种型号口罩的产量是 万只,则乙种型号口罩的产量是 万只,
根据题意得:解得:
则
则甲、乙两种型号口罩的产量分别为 万只和 万只;
设甲种型号口罩的产量是 万只,则乙种型号口罩的产量是 万只,
根据题意得:
解得: .
设所获利润为 万元,
则
由于 ,所以 随 的增大而增大,
即当 时, 最大,
此时 .
从而安排生产甲种型号的口罩 万只,乙种型号的口罩 万只时,获得最大利润,最大利润为 万元
【点睛】本题考查一次函数的应用、一元一次方程的应用、一元一次不等式的应用,解答本题的关键是明
确题意,利用一次函数的性质和不等式的性质解答.
24.如图,抛物线 的图象经过点 ,交 轴于点 (点 在点 左侧),连接
直线 与 轴交于点 与 上方的抛物线交于点 与 交于点 .
(1)求抛物线的解析式及点 的坐标;(2) 是否存在最大值?若存在,请求出其最大值及此时点 的坐标;若不存在,请说明理由.
【答案】(1) , ;(2)存在,当 时,有最大值且最大值为 ,
此时点 的坐标为 .
【解析】
【分析】
(1)直接将 代入 求出a,即可确定抛物线解析式;然后令y=0求得x的值,再结
合已知即可确定A、B的坐标;
(2)作 轴,交 于点 ,由平行线等分线段定理可得 ;再根据题意求出D点坐标和
CD的长,可得 ;然后再根据B、C的坐标求出直线BC的解析式;再设 ,
则 ,运用两点间距离公式求得EG,然后再代入 ,根据二次函数的性质即可说明
【详解】解: 把 代入 ,即 ,解得
∴抛物线的解析式为
令
可得:
∴ ;
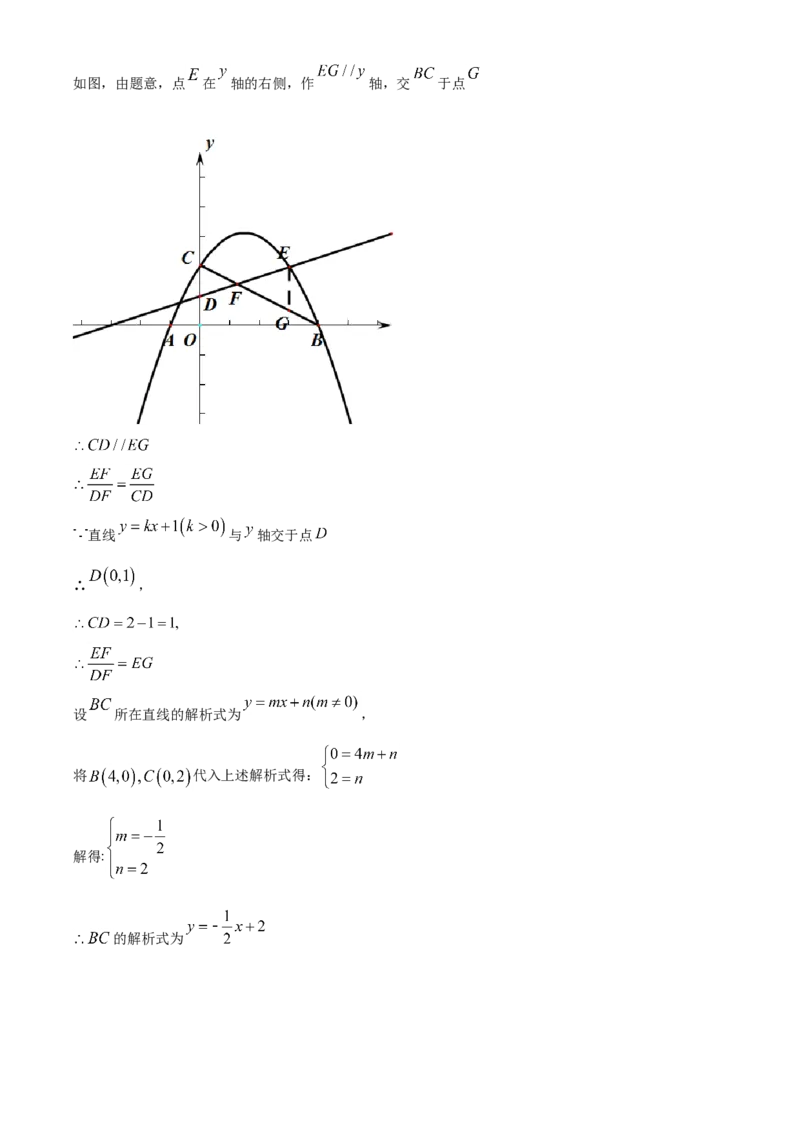
存在,如图,由题意,点 在 轴的右侧,作 轴,交 于点
直线 与 轴交于点
∴ ,
设 所在直线的解析式为 ,
将 代入上述解析式得:
解得:
的解析式为设
则 ,其中 .
∴抛物线开口方向朝下
∴当 时,有最大值,最大值为 .
将t=2代入 =-2+3+2=3
∴点 的坐标为 .
【点睛】本题主要考查了求一次函数和二次函数解析式、平行线等分线段定理以及运用二次函数的性质求
最值,掌握平行线等分线段定理是解答本题的关键.
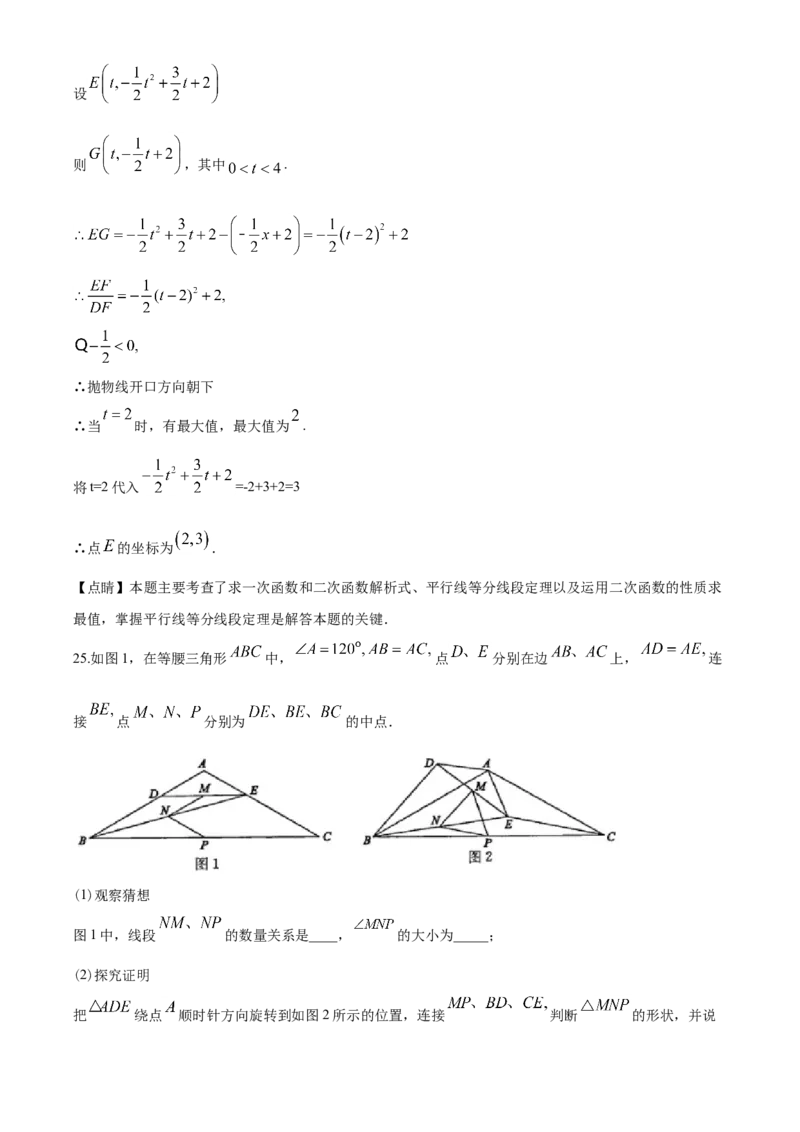
25.如图1,在等腰三角形 中, 点 分别在边 上, 连
接 点 分别为 的中点.
(1)观察猜想
图1中,线段 的数量关系是____, 的大小为_____;
(2)探究证明
把 绕点 顺时针方向旋转到如图2所示的位置,连接 判断 的形状,并说明理由;
(3)拓展延伸
把 绕点 在平面内自由旋转,若 ,请求出 面积的最大值.
【答案】(1)相等, ;(2) 是等边三角形,理由见解析;(3) 面积的最大值为 .
【解析】
【分析】
(1)根据" 点 分别为 的中点",可得MN
BD,NP CE ,根据三角形外角和定理,等量代换求出 .
(2)先求出 ,得出 ,根据MN BD,NP CE ,和三角形外角和定理,
可知MN=PN,再等量代换求出 ,即可求解.
(3)根据 ,可知BD最大值,继而求出 面积的最大值.
【详解】 由题意知:AB=AC,AD=AE,且点 分别为 的中点,
∴BD=CE,MN BD,NP CE,MN= BD,NP= EC
∴MN=NP
又∵MN BD,NP CE,∠A= ,AB=AC,
∴∠MNE=∠DBE,∠NPB=∠C,∠ABC=∠C=
根据三角形外角和定理,
得∠ENP=∠NBP+∠NPB
∵∠MNP=∠MNE+∠ENP,∠ENP=∠NBP+∠NPB,
∠NPB=∠C,∠MNE=∠DBE,
∴∠MNP=∠DBE+∠NBP+∠C
=∠ABC+∠C = .
是等边三角形.
理由如下:如图,由旋转可得
在 ABD和 ACE中
.
点 分别为 的中点,
是 的中位线,
且
同理可证 且
.
在 中
∵∠MNP= ,MN=PN
是等边三角形.
根据题意得:
即 ,从而
的面积 .
∴ 面积的最大值为 .【点睛】本题主要考查了三角形中点的性质、三角形相似的判定定理、三角形外角和定理以及图形旋转的
相关知识;正确掌握三角形相似的判定定理、三角形外角和定理以及图形旋转的相关知识是解题的关键.