文档内容
【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
2020年山东省日照市中考数学试卷
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合要求的,请把符
合要求的的选项选出来.
1. 2020的相反数是( )
1 1
A.− B. C.−2020 D.2020
2020 2020
2. 单项式−3ab的系数是( )
A.3 B.−3 C.3a D.−3a
3. “扶贫”是新时期党和国家的重点工作之一,为落实习近平总书记提出的“精准扶贫”战略构想,某省预计三年内
脱贫1020000人,数字1020000用科学记数法可表示为( )
A.1.02×106 B.1.02×105 C.10.2×105 D.102×104
4. 下列调查中,适宜采用全面调查的是( )
A.调查全国初中学生视力情况
B.了解某班同学“三级跳远”的成绩情况
C.调查某品牌汽车的抗撞击情况
D.调查2019年央视“主持人大赛”节目的收视率
5. 将函数y=2x的图象向上平移3个单位,则平移后的函数解析式是( )
A.y=2x+3 B.y=2x−3 C.y=2(x+3) D.y=2(x−3)
6. 下列各式中,运算正确的是( )
A. = B. = C. = D.
x3+x3 x6 x2 ⋅x3 x5 (x+3) 2 x2+9 √5−√3=√2
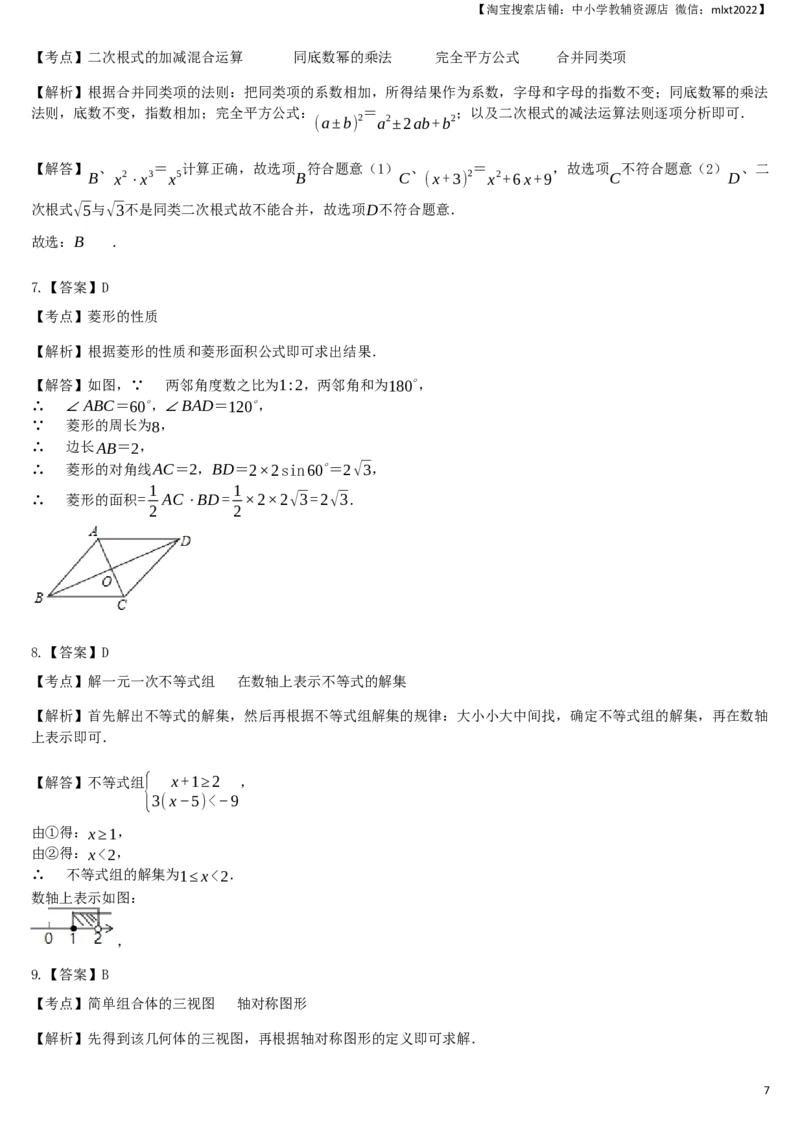
7. 已知菱形的周长为8,两邻角的度数比为1:2,则菱形的面积为( )
A.8√3 B.8 C.4√3 D.2√3
8. 不等式组{ x+1≥2 的解集在数轴上表示为( )
3(x−5)<−9
A. B. C. D.
9. 如图,几何体由5个相同的小正方体构成,该几何体三视图中为轴对称图形的是( )
A.主视图 B.左视图
C.俯视图 D.主视图和俯视图
1【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
10. 如图,AB是⊙O的直径,CD为⊙O的弦,AB⊥CD于点E,若CD=6√3,AE=9,则阴影部分的面积为
( )
9 9
A.6π− √3 B.12π−9√3 C.3π− √3 D.9√3
2 4
11. 用大小相同的圆点摆成如图所示的图案,按照这样的规律摆放,则第10个图案中共有圆点的个数是( )
A.59 B.65 C.70 D.71
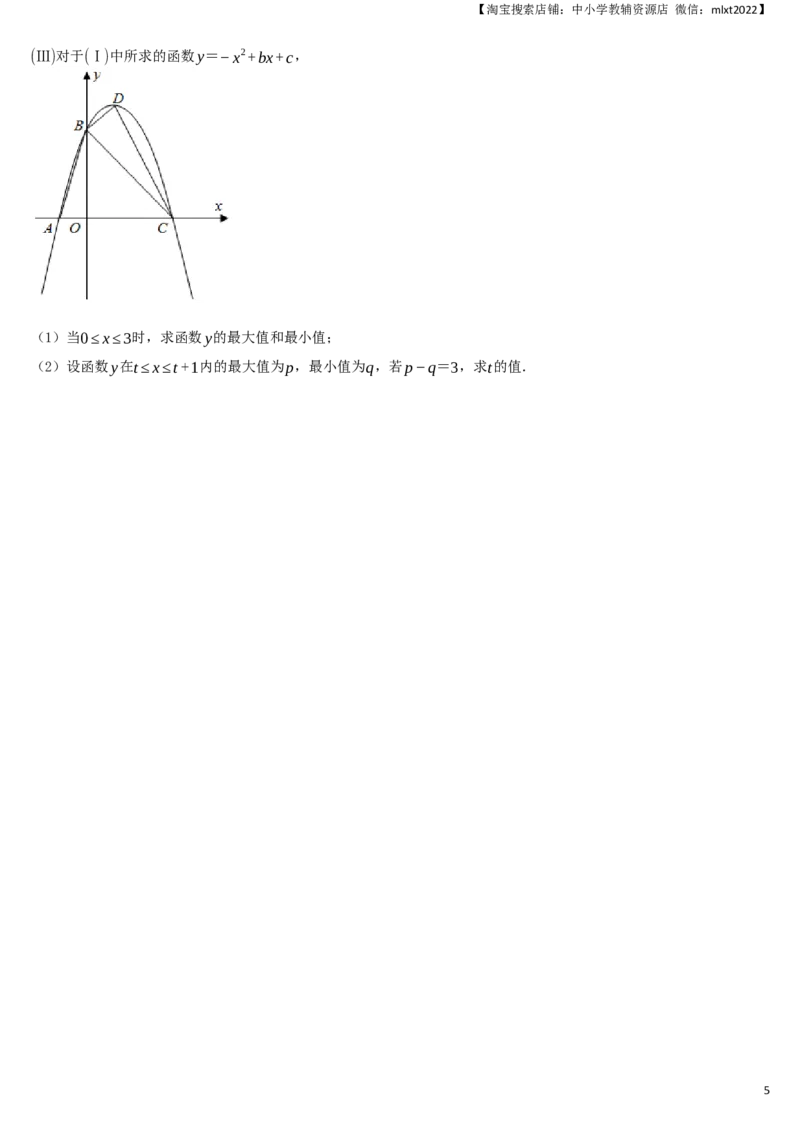
12. 如图,二次函数 = 图象的对称轴为直线 = ,下列结论:
y ax2+bx+c(a≠0) x −1
①abc<0;②3a<−c;③若m为任意实数,则有a−bm≤am2+b; ④若图象经过点(−3,−2),方程ax2+bx+c+2
=0的两根为x ,x (|x |<|x |),则2x −x =5.其中正确的结论的个数是( )
1 2 1 2 1 2
A.4个 B.3个 C.2个 D.1个
二、填空题:本大题共4小题,每小题4分,共16分.不需写解答过程,只要求填写最后结果.
13.分解因式:mn+4n=________.
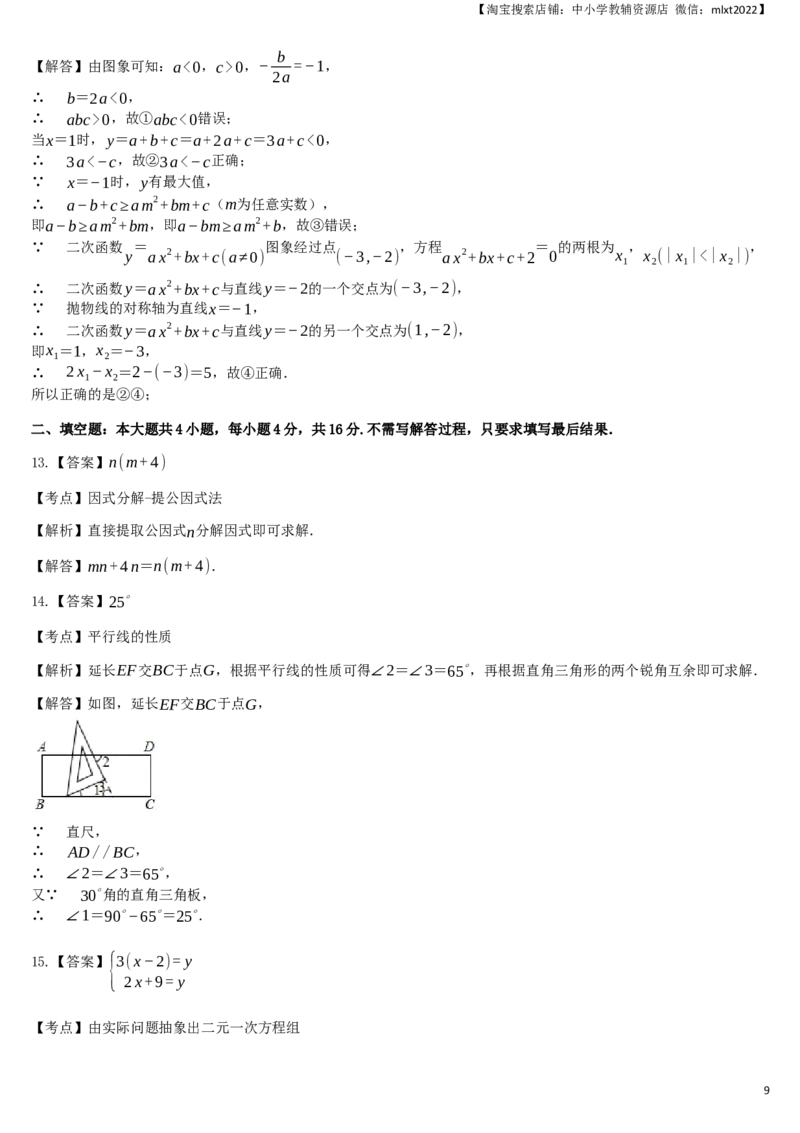
14. 如图,有一个含有30∘角的直角三角板,一顶点放在直尺的一条边上,若∠2=65∘,则∠1的度数是________.
15.《孙子算经》记载:今有3人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每
三人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x
人,则可列方程组为________.
16.如图,在平面直角坐标系中, ▱ABCD的顶点B位于y轴的正半轴上,顶点C,D位于x轴的负半轴上,双曲线
k
y= (k<0,x<0)与 ▱ABCD的边AB,AD交于点E、F,点A的纵坐标为10,F(−12,5),把△BOC沿着BC所在
x
2【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
直线翻折,使原点O落在点G处,连接EG,若EG// y轴,则△BOC的面积是________.
三、解答题:本大题共6小题,共68分.解答要写出必要的文字说明、证明过程或演算步骤.
2
17. (1)计算:√3−8+( ) −1−√3×cos30∘;
3
x−3 3
(2)解方程: +1= .
x−2 2−x
18.如图,某小区有一块靠墙(墙的长度不限)的矩形空地ABCD,为美化环境,用总长为100m的篱笆围成四块矩形
花圃(靠墙一侧不用篱笆,篱笆的厚度不计).
(1)若四块矩形花圃的面积相等,求证:AE=3BE;
(2)在(1)的条件下,设BC的长度为xm,矩形区域ABCD的面积为ym2,求y与x之间的函数关系式,并写出自变
量x的取值范围.
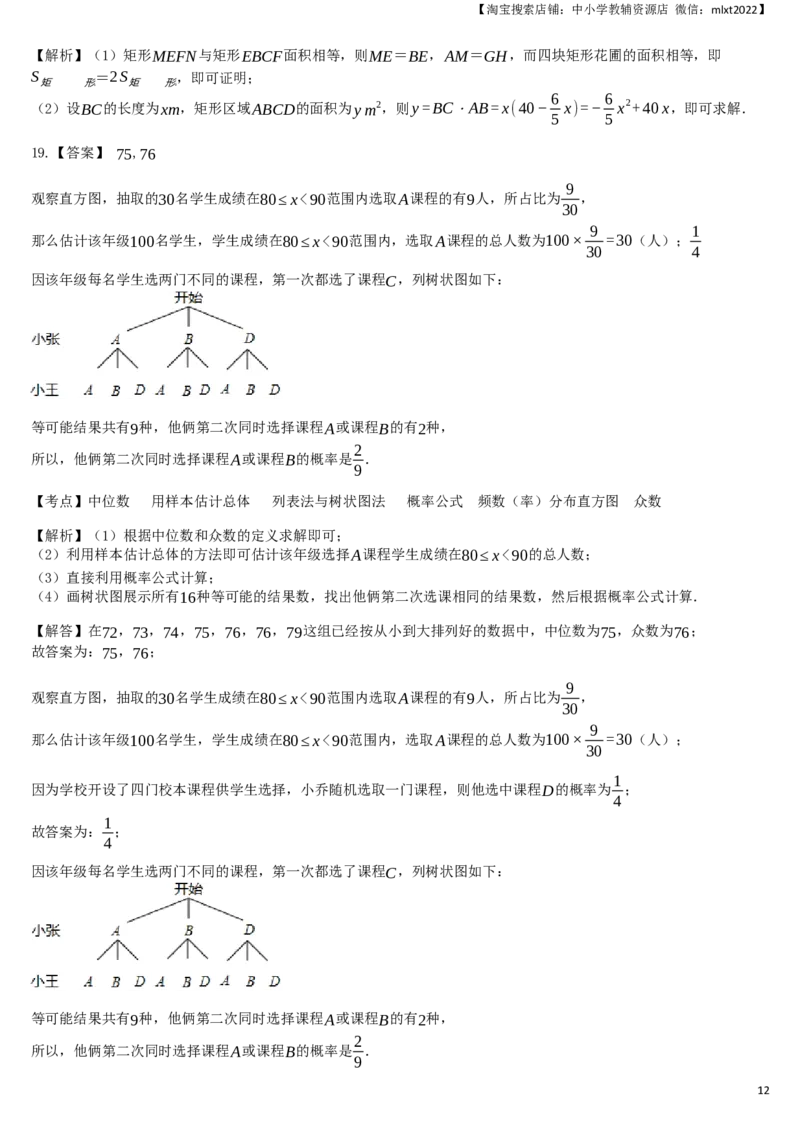
19. 为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A.趣味数学;B.博
乐阅读;C.快乐英语;D.硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情
况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)已知70≤x<80这组的数据为:72,73,74,75,76,76,79.则这组数据的中位数是________;众数是
________;
(2)根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数;
(3)该年级学生小乔随机选取了一门课程,则小乔选中课程D的概率是________;
3【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
(4)该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同
时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.
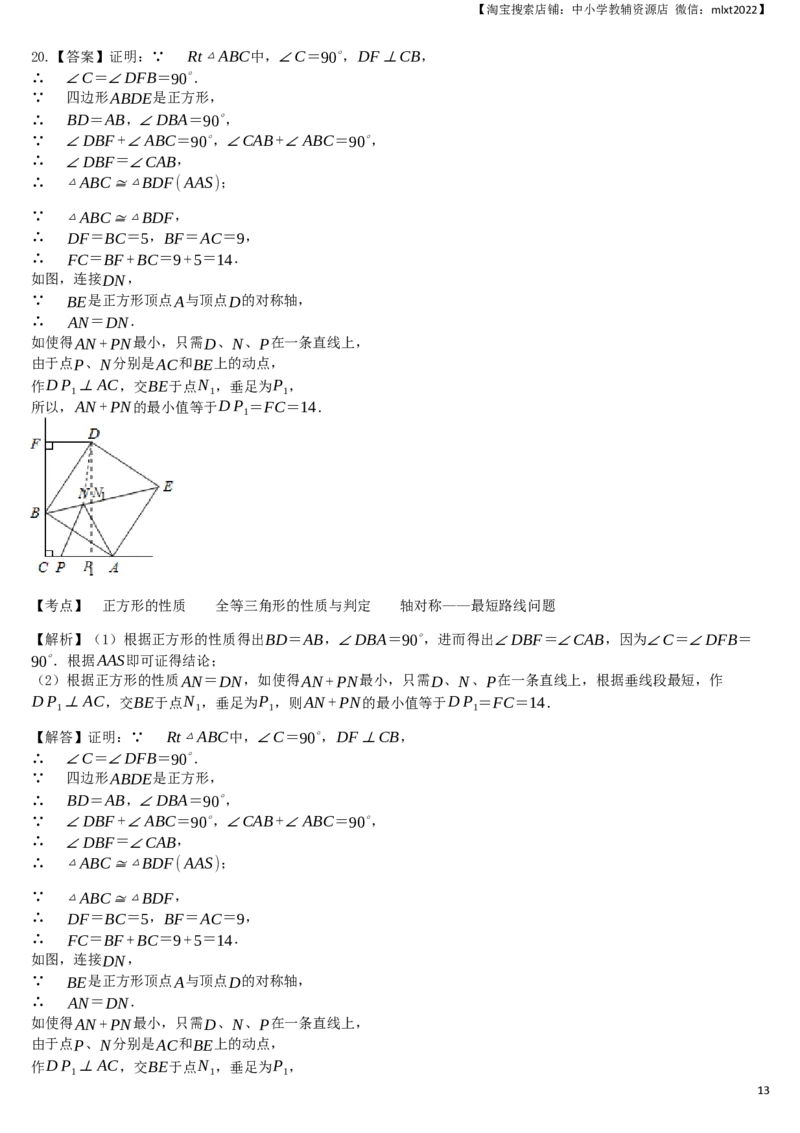
20. 如图,Rt△ABC中,∠C=90∘,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线
于点F,连接BE.
(1)求证:△ABC≅△BDF;
(2)P,N分别为AC,BE上的动点,连接AN,PN,若DF=5,AC=9,求AN+PN的最小值.
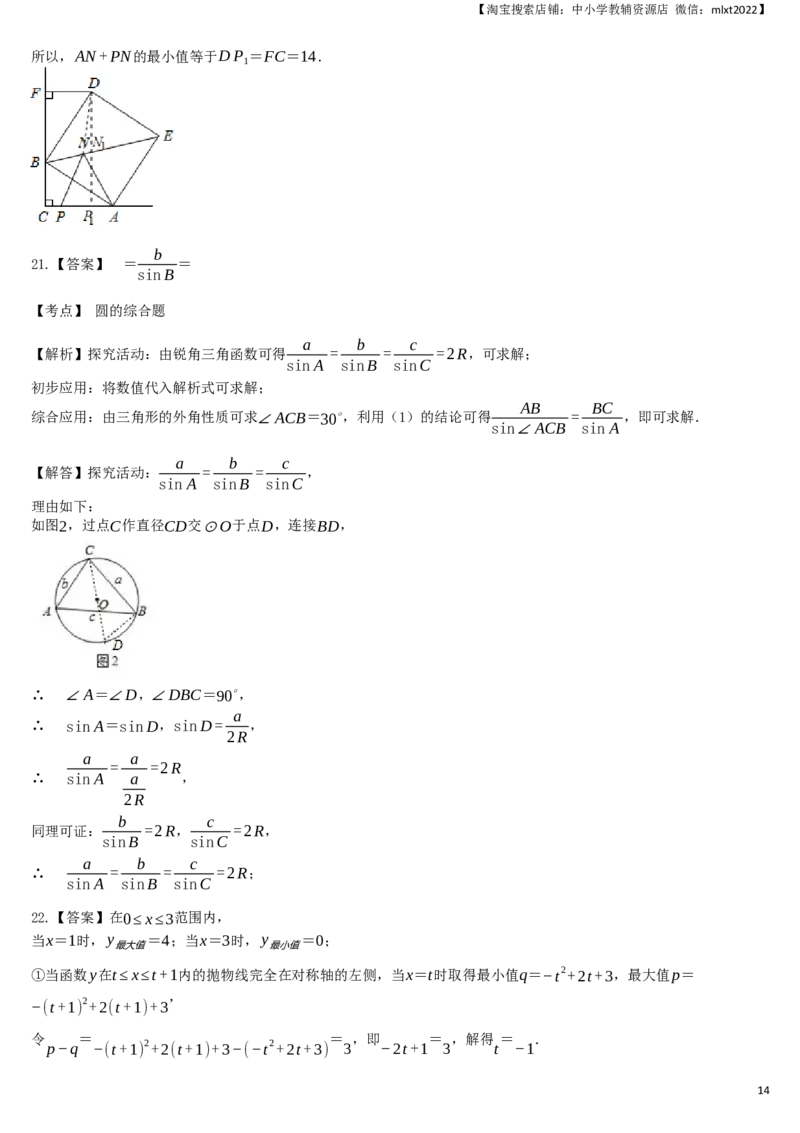
21.阅读理解:
如图1,Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90∘,其外接圆半径为R.根据锐角三角函数的
a b a b
定义:sinA= ,sinB= ,可得 = =c=2R,
c c sinA sinB
a b c
即: = = =2R,(规定sin90∘=1).
sinA sinB sinC
探究活动:
a
如图2,在锐角△ABC中,a,b,c分别是∠A,∠B,∠C的对边,其外接圆半径为R,那么: ________
sinA
c
(用>、=或<连接),并说明理由.
sinC
事实上,以上结论适用于任意三角形.
初步应用:
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠A=60∘,∠B=45∘,a=8,求b.
综合应用:
如图3,在某次数学活动中,小凤同学测量一古塔CD的高度,在A处用测角仪测得塔顶C的仰角为15∘,又沿古塔的方
向前行了100m到达B处,此时A,B,D三点在一条直线上,在B处测得塔顶C的仰角为45∘,求古塔CD的高度(结果
√6−√2
保留小数点后一位).(√3≈1.732,sin15∘= )
4
22. 如图,函数y=−x2+bx+c的图象经过点A(m,0),B(0,n)两点,m,n分别是方程x2−2x−3=0的两个实数
根,且m0,由对称轴得b=2a<0,则abc>0,故①错误;当x=1时,y=a+b+c=a+2a+c=
3a+c<0,得②正确;由x=−1时,y有最大值,得a−b+c≥am2+bm+c,得③错误;由题意得二次函数y=
ax2+bx+c与直线y=−2的一个交点为(−3,−2),另一个交点为(1,−2),即x =1,x =−3,进而得出④正确,即
1 2
可得出结论.
8【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
b
【解答】由图象可知:a<0,c>0,− =−1,
2a
∴ b=2a<0,
∴ abc>0,故①abc<0错误;
当x=1时,y=a+b+c=a+2a+c=3a+c<0,
∴ 3a<−c,故②3a<−c正确;
∵ x=−1时,y有最大值,
∴ a−b+c≥am2+bm+c(m为任意实数),
即a−b≥am2+bm,即a−bm≥am2+b,故③错误;
∵ 二次函数 = 图象经过点 ,方程 = 的两根为 , ,
y ax2+bx+c(a≠0) (−3,−2) ax2+bx+c+2 0 x x (|x |<|x |)
1 2 1 2
∴ 二次函数y=ax2+bx+c与直线y=−2的一个交点为(−3,−2),
∵ 抛物线的对称轴为直线x=−1,
∴ 二次函数y=ax2+bx+c与直线y=−2的另一个交点为(1,−2),
即x =1,x =−3,
1 2
∴ 2x −x =2−(−3)=5,故④正确.
1 2
所以正确的是②④;
二、填空题:本大题共4小题,每小题4分,共16分.不需写解答过程,只要求填写最后结果.
13.【答案】n(m+4)
【考点】因式分解-提公因式法
【解析】直接提取公因式n分解因式即可求解.
【解答】mn+4n=n(m+4).
14.【答案】25∘
【考点】平行线的性质
【解析】延长EF交BC于点G,根据平行线的性质可得∠2=∠3=65∘,再根据直角三角形的两个锐角互余即可求解.
【解答】如图,延长EF交BC于点G,
∵ 直尺,
∴ AD//BC,
∴ ∠2=∠3=65∘,
又∵ 30∘角的直角三角板,
∴ ∠1=90∘−65∘=25∘.
15.【答案】{3(x−2)= y
2x+9= y
【考点】由实际问题抽象出二元一次方程组
9【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
【解析】根据“每3人乘一车,最终剩余2辆空车;若每2人同乘一车,最终剩下9人因无车可乘而步行”,即可得出关
于x,y的二元一次方程组,此题得解.
【解答】依题意,得:{3(x−2)= y.
2x+9= y
50
16.【答案】
3
【考点】反比例函数系数k的几何意义 坐标与图形变化-对称 反比例函数的性质
平行四边形的性质 反比例函数图象上点的坐标特征
60
【解析】将点F坐标代入解析式,可求双曲线解析式为y=− ,由平行四边形的性质可得OB=10,BE=6,由勾股
x
定理可求EG的长,由勾股定理可求CO的长,即可求解.
k
【解答】∵ 双曲线y= (k<0,x<0)经过点F(−12,5),
x
∴ k=−60,
60
∴ 双曲线解析式为y=− .
x
∵ ▱ABCD的顶点A的纵坐标为10,
60
∴ BO=10,点E的纵坐标为10,且在双曲线y=− 上,
x
∴ 点E的横坐标为−6,即BE=6.
∵ △BOC和△BGC关于BC对称,
∴ BG=BO=10,GC=OC.
∵ EG// y轴,在Rt△BEG中,BE=6,BG=10,
∴ .
EG=√102−62=8
延长EG交x轴于点H,
∵ EG// y轴,
∴ ∠GHC是直角,
在Rt△GHC中,设GC=m,则有CH=OH−OC=BE−GC=6−m,GH=EH−EG=10−8=2,
则有 = ,
m2 22+(6−m) 2
10
∴ m= ,
3
10
∴ GC= =OC,
3
1 10 50
∴ S = × ×10= ,
△BOC 2 3 3
10【淘宝搜索店铺:中小学教辅资源店 微信:mlxt2022】
三、解答题:本大题共6小题,共68分.解答要写出必要的文字说明、证明过程或演算步骤.
3 √3 3 3
17.【答案】 原式=−2+ −√3× =−2+ − =−2.
2 2 2 2
x−3 3
+1= ,
x−2 2−x
两边同乘以(x−2)得,x−3+(x−2)=−3,
解得,x=1.
经检验x=1是原分式方程的解.
【考点】特殊角的三角函数值 实数的运算 负整数指数幂 解分式方程
【解析】(1)原式利用立方根的定义,负整数指数幂的意义以及特殊角的三角形函数进行计算即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
3 √3 3 3
【解答】原式=−2+ −√3× =−2+ − =−2.
2 2 2 2
x−3 3
+1= ,
x−2 2−x
两边同乘以(x−2)得,x−3+(x−2)=−3,
解得,x=1.
经检验x=1是原分式方程的解.
18.【答案】证明:∵ 矩形MEFN与矩形EBCF面积相等,
∴ ME=BE,AM=GH.
∵ 四块矩形花圃的面积相等,即S =2S ,
矩 形AMDND矩 形MEFN
∴ AM=2ME,
∴ AE=3BE;
∵ 篱笆总长为100m,
∴ 2AB+GH+3BC=100,
1
即2AB+ AB+3BC=100,
2
6
∴ AB=40− BC.
5
设BC的长度为xm,矩形区域ABCD的面积为ym2,
6 6
则y=BC⋅AB=x(40− x)=− x2+40x,
5 5
6
∵ AB=40− BC,
5
40 2
∴ BE= − x>0,
3 5
100
解得x< ,
3
6 100
∴ y=− x2+40x(0