文档内容
2020 年广东省初中学业水平考试
数 学
说明:1.全卷共4页,满分为120分,考试用时为90分钟.
2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准
考证号、姓名、考场号、座位号.用2B铅笔把对应该号码的标号涂
黑.
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答
案信息点涂黑,如需改动,用像皮檫干净后,再选涂其他答案,答案
不能答在试题上.
4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各
题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再
写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无
效.
5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交
回.
一、选择题(本大题10小题,每小题 3分,共30分)在每小题列出的四个选
项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.
1.9的相反数是
A.﹣9 B.9 C. D.﹣
2.一组数据2、4、3、5、2的中位数是
数学试卷 第 1 页 (共 34 页)A.5 B.3.5 C.3 D.2.5
3.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为
A.(﹣3 ,2) B.(﹣2 ,3) C.(2 ,﹣3) D.
(3 ,﹣2)
4.若一个多边形的内角和是540°,则该多边形的边数为
A.4 B.5 C.6 D.7
5.若式子 在实数范围内有意义,则x的取值范围是
A.x≠2 B.x≥2 C.x≤2 D.x≠﹣2
6.已知△ABC 的周长为 16,点 D、E、F 分别为△ABC 三条边的中点,则
△DEF的周长为
A.8 B. C.16 D.4
7.把函数y=(x﹣1)2+2的图象向右平移1个单位长度,平移后图象的函数解
析式为
A.y=x2+2 B.y=(x﹣1)2+1
C.y=(x﹣2)2+2 D.y=(x﹣1)2+3
8.不等式组 的解集为
A.无解 B.x≤1 C.x≥﹣1 D.﹣1≤x≤1
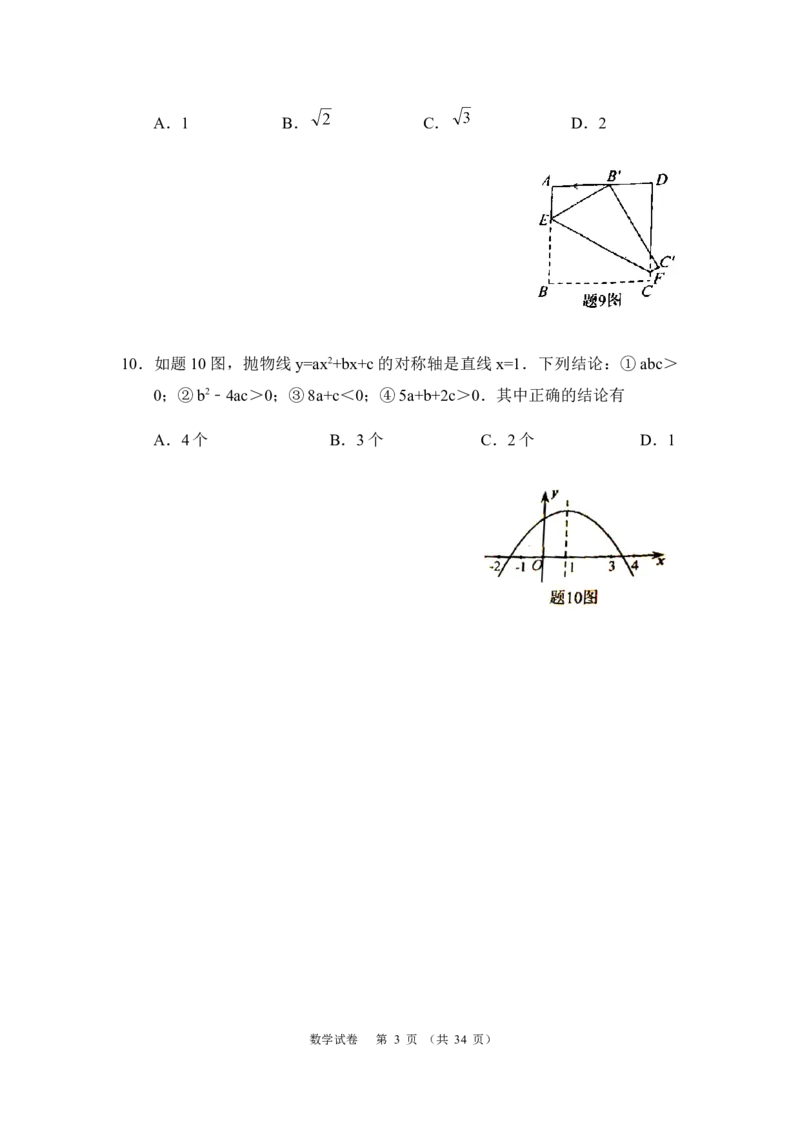
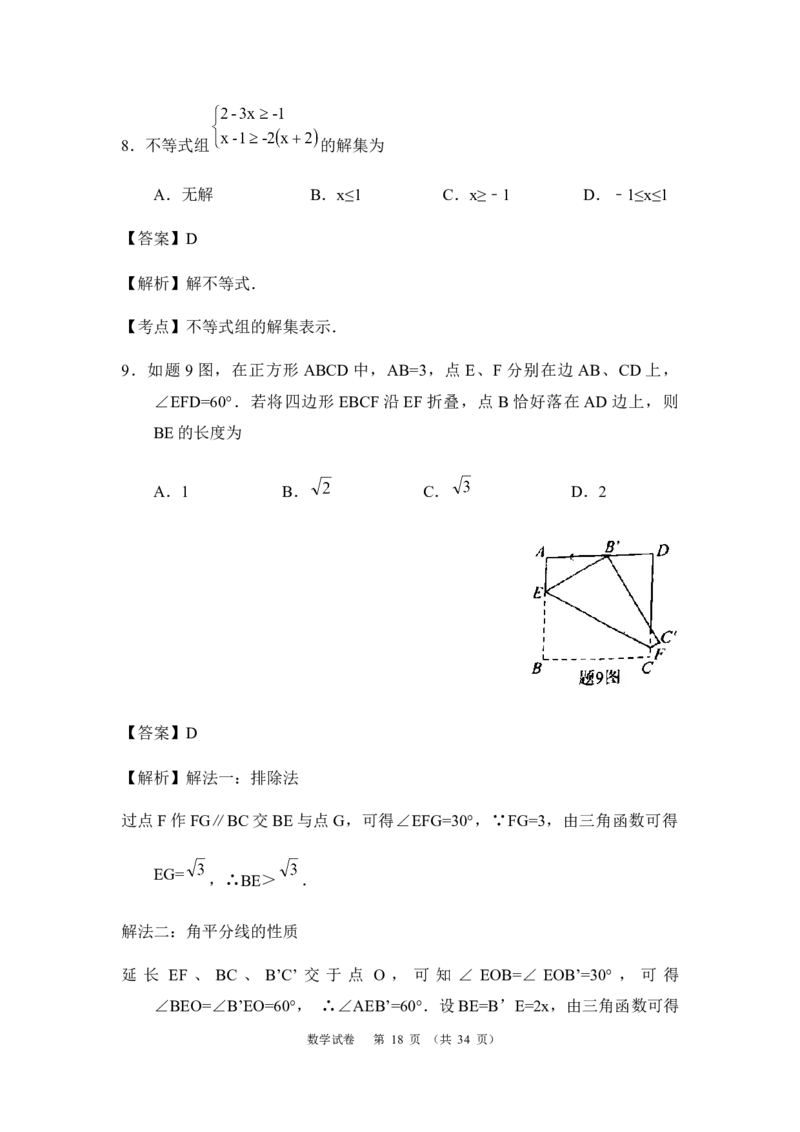
9.如题 9 图,在正方形 ABCD 中,AB=3,点 E、F 分别在边 AB、CD 上,
∠EFD=60°.若将四边形 EBCF 沿 EF 折叠,点 B 恰好落在 AD 边上,则
BE的长度为
数学试卷 第 2 页 (共 34 页)A.1 B. C. D.2
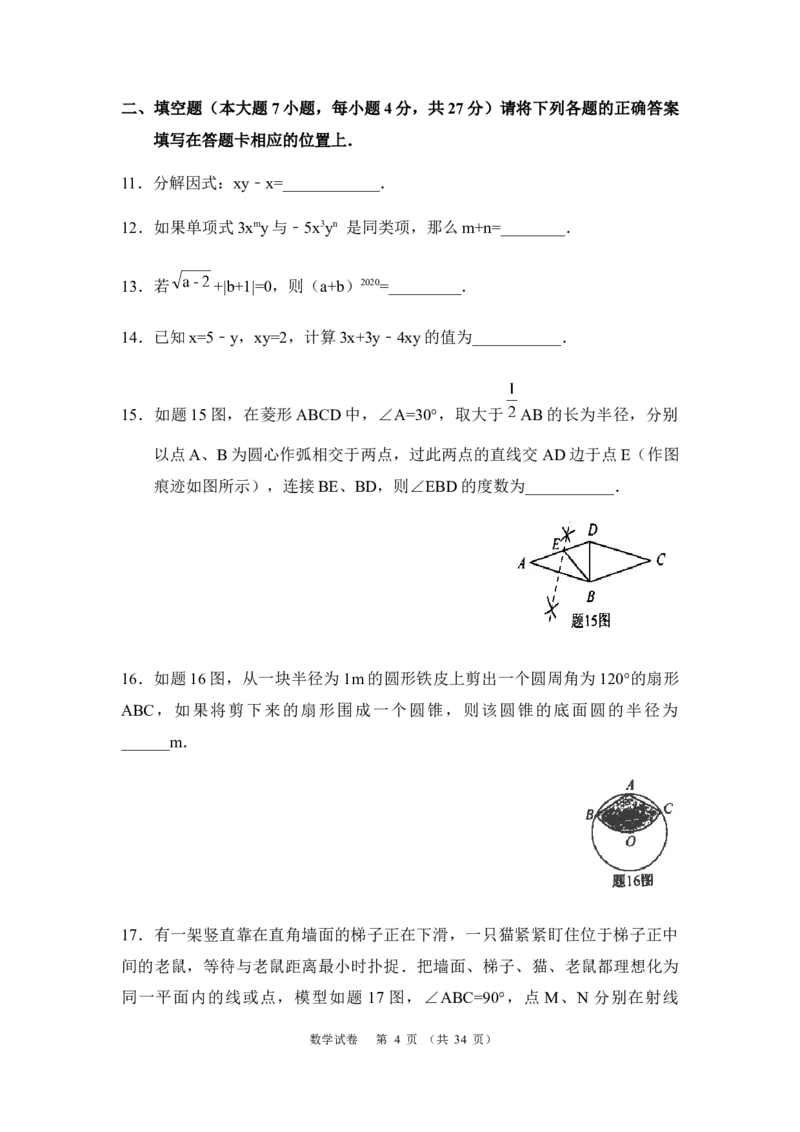
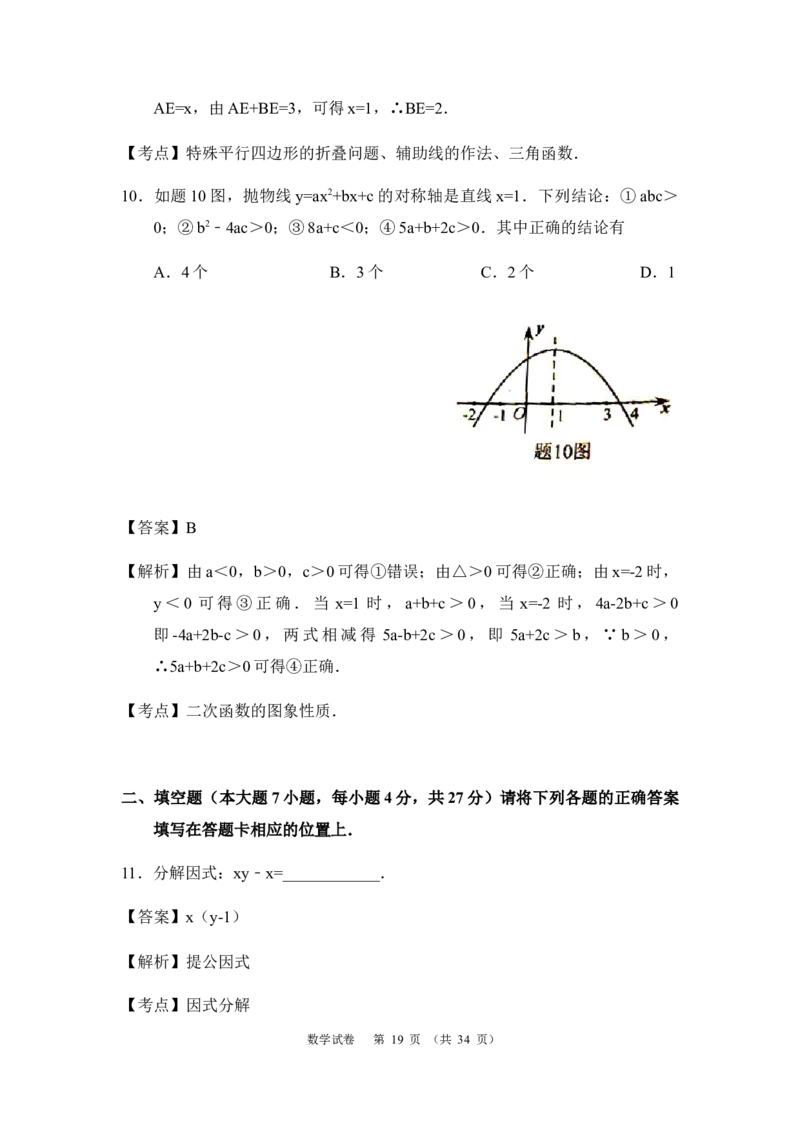
10.如题10图,抛物线y=ax2+bx+c的对称轴是直线x=1.下列结论:①abc>
0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0.其中正确的结论有
A.4个 B.3个 C.2个 D.1
数学试卷 第 3 页 (共 34 页)二、填空题(本大题7小题,每小题4分,共27分)请将下列各题的正确答案
填写在答题卡相应的位置上.
11.分解因式:xy﹣x=____________.
12.如果单项式3xmy与﹣5x3yn 是同类项,那么m+n=________.
13.若 +|b+1|=0,则(a+b)2020=_________.
14.已知x=5﹣y,xy=2,计算3x+3y﹣4xy的值为___________.
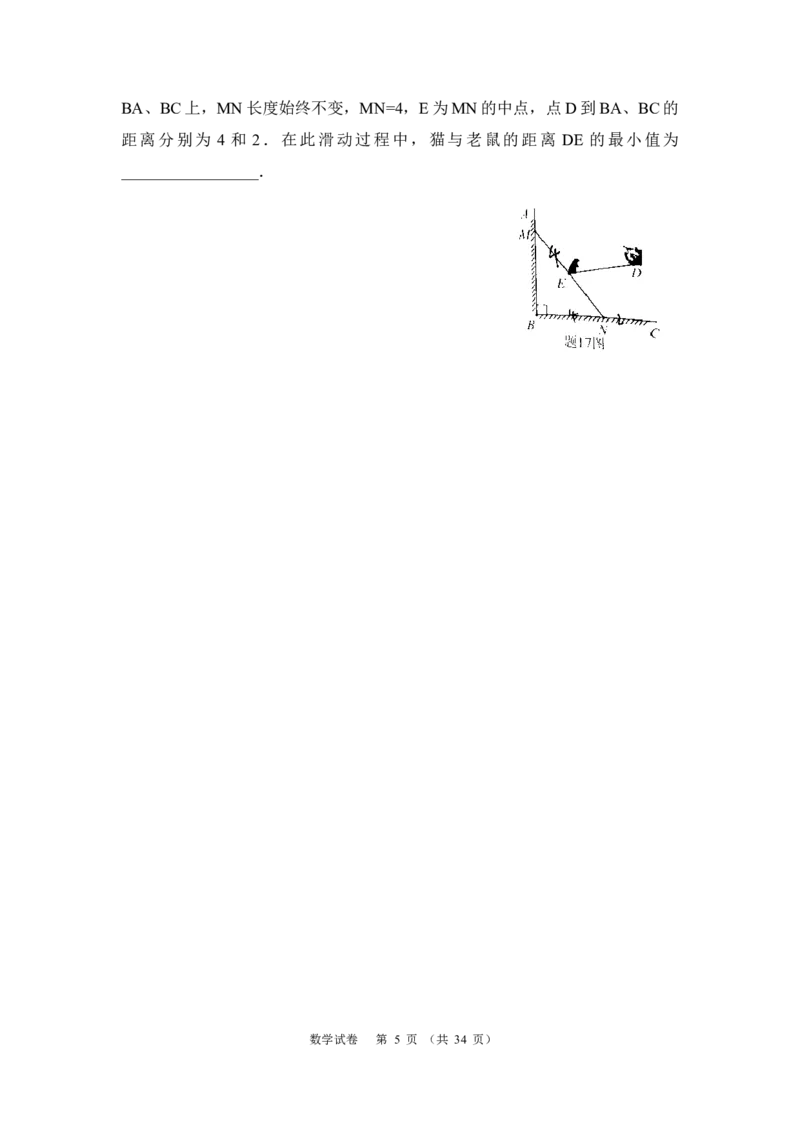
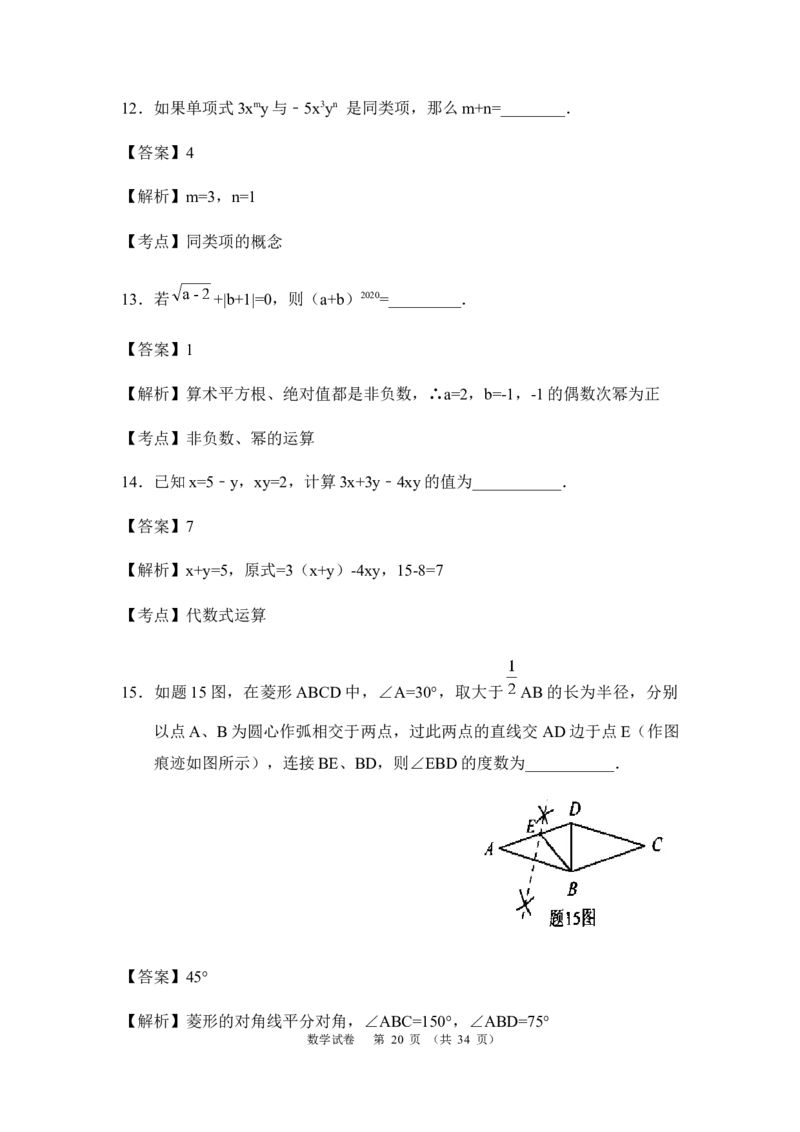
15.如题15图,在菱形ABCD中,∠A=30°,取大于 AB的长为半径,分别
以点A、B为圆心作弧相交于两点,过此两点的直线交 AD边于点E(作图
痕迹如图所示),连接BE、BD,则∠EBD的度数为___________.
16.如题16图,从一块半径为1m的圆形铁皮上剪出一个圆周角为120°的扇形
ABC,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为
______m.
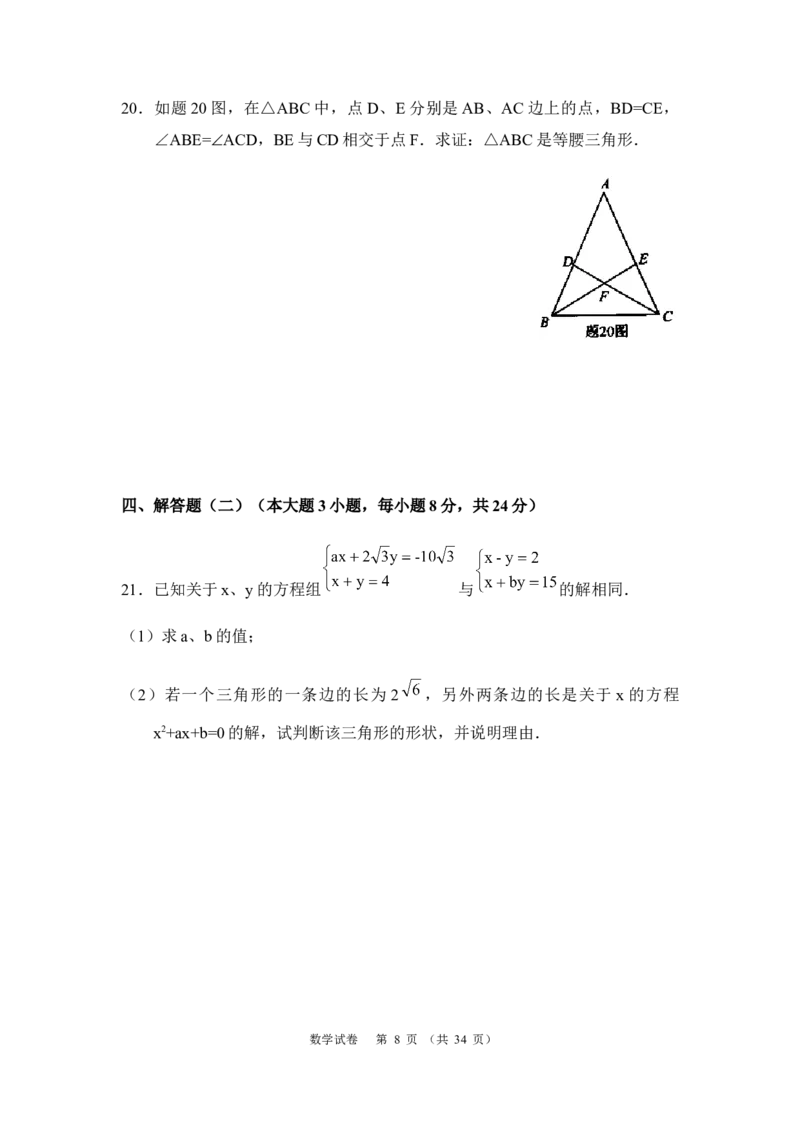
17.有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中
间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫、老鼠都理想化为
同一平面内的线或点,模型如题 17 图,∠ABC=90°,点 M、N 分别在射线
数学试卷 第 4 页 (共 34 页)BA、BC上,MN长度始终不变,MN=4,E为MN的中点,点D到BA、BC的
距离分别为 4 和 2.在此滑动过程中,猫与老鼠的距离 DE 的最小值为
_________________.
数学试卷 第 5 页 (共 34 页)三、解答题(一)(本大题3小题,每小题6分,共18分)
18.先化简,再求值:(x+y)2+(x+y)(x﹣y) ﹣2x2,其中x= ,y= .
19.某中学展开主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非
常了解”、“比较了解”、“基本了解”“不太了解”四个等级,要求每
名学生选且只能选其中一个等级 .随机抽取了120名学生的有效问卷,
数据整理如下:
等级 非常了解 比较了解 基本了解 不太了解
人数(人) 24 72 18 x
(1)求x的值;
(2)若该校有学生 1800 人,请根据抽样调查结果估算该校“非常了解”和
“比较了解”垃圾分类知识的学生共有多少人?
数学试卷 第 6 页 (共 34 页)数学试卷 第 7 页 (共 34 页)20.如题20图,在△ABC中,点D、E分别是AB、AC边上的点,BD=CE,
∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
四、解答题(二)(本大题3小题,毎小题8分,共24分)
21.已知关于x、y的方程组 与 的解相同.
(1)求a、b的值;
(2)若一个三角形的一条边的长为 2 ,另外两条边的长是关于 x 的方程
x2+ax+b=0的解,试判断该三角形的形状,并说明理由.
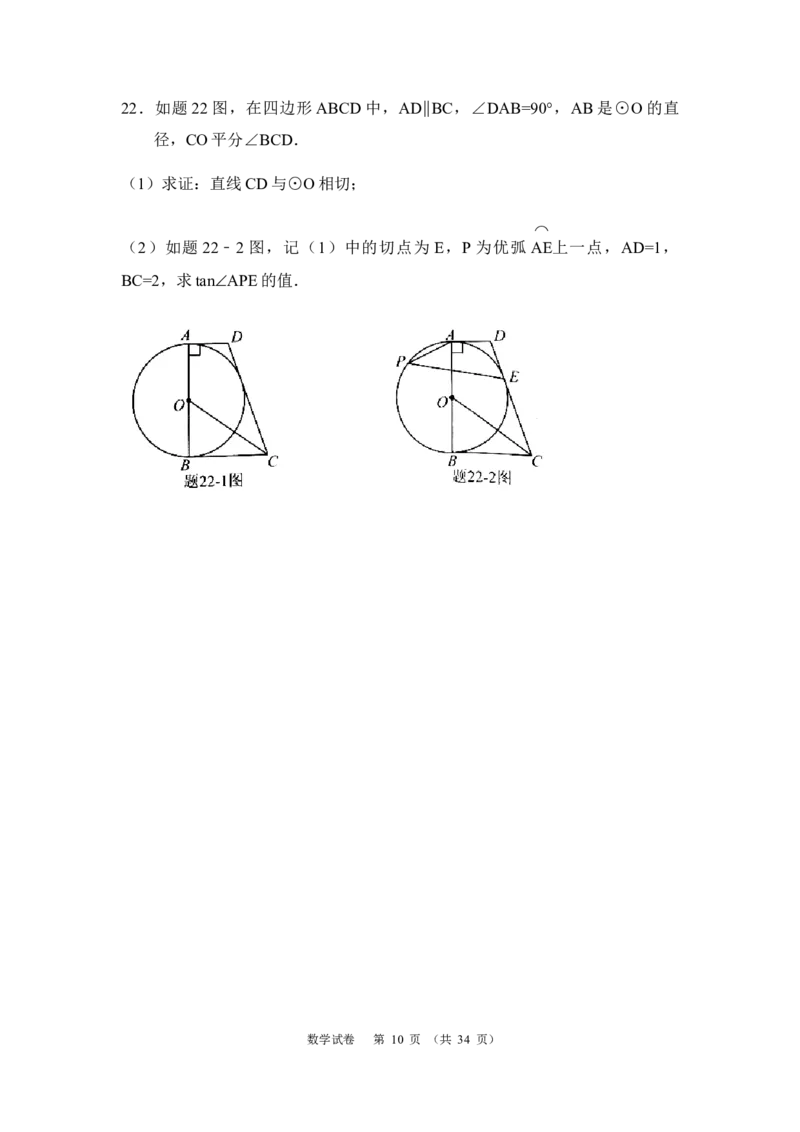
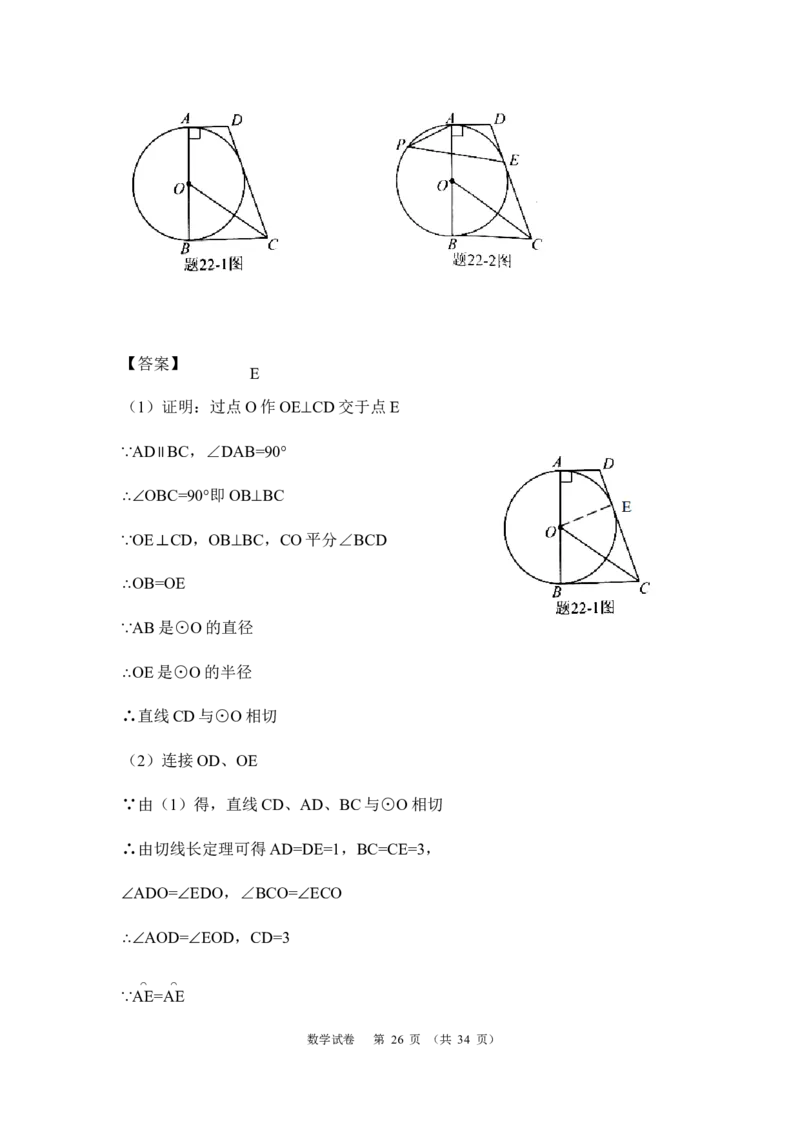
数学试卷 第 8 页 (共 34 页)数学试卷 第 9 页 (共 34 页)22.如题22图,在四边形ABCD中,AD∥BC,∠DAB=90°,AB是⊙O的直
径,CO平分∠BCD.
(1)求证:直线CD与⊙O相切;
⌒
(2)如题 22﹣2 图,记(1)中的切点为 E,P 为优弧 AE上一点,AD=1,
BC=2,求tan∠APE的值.
数学试卷 第 10 页 (共 34 页)23.某社区拟建A、B两类摊位以搞活“地摊经济”,每个A类摊位的占地面
积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,
建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用
同样面积建B类摊位个数的 .
(1)求每个A、B类摊位占地面积各为多少平方米?
(2)该社区拟建A、B两类摊位共90个,且B类摊位的数量不少于A类摊位
数量的3倍.求建造这90个摊位的最大费用.
数学试卷 第 11 页 (共 34 页)五、解答题(三)(本大题2小题,毎小题10分,共20分)
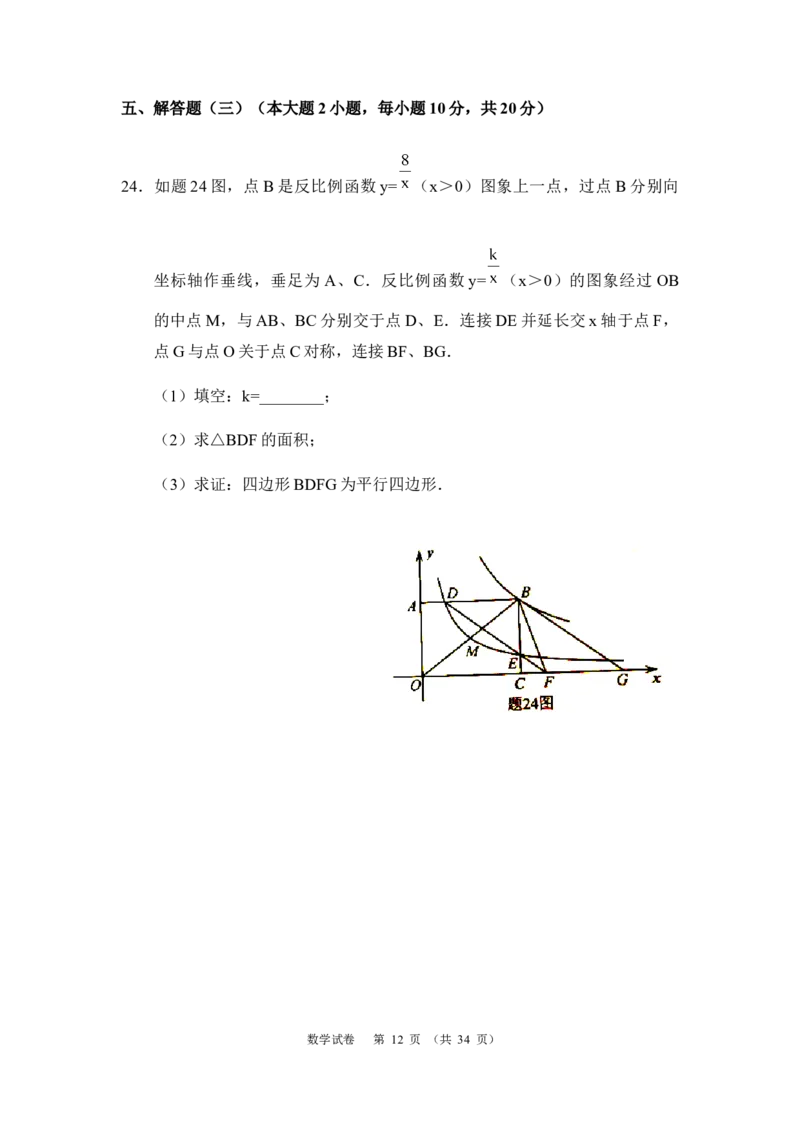
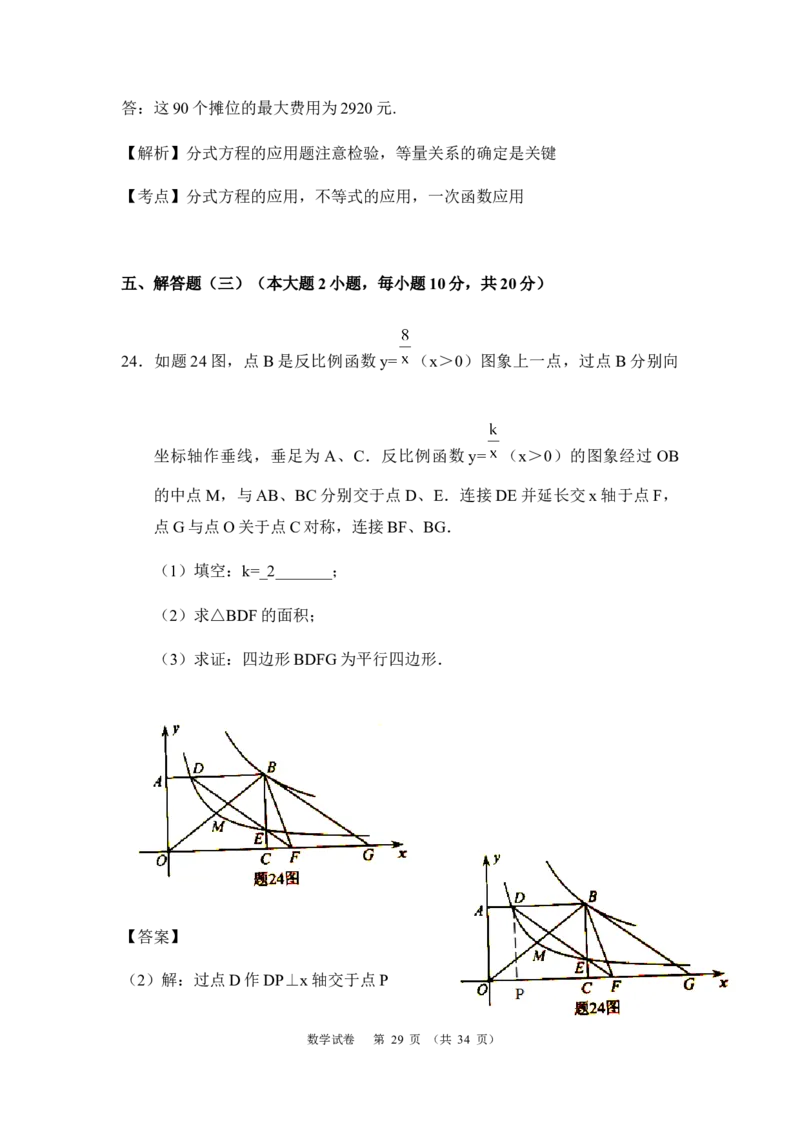
24.如题24图,点B是反比例函数y= (x>0)图象上一点,过点B分别向
坐标轴作垂线,垂足为 A、C.反比例函数 y= (x>0)的图象经过 OB
的中点M,与AB、BC分别交于点D、E.连接DE并延长交x轴于点F,
点G与点O关于点C对称,连接BF、BG.
(1)填空:k=________;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
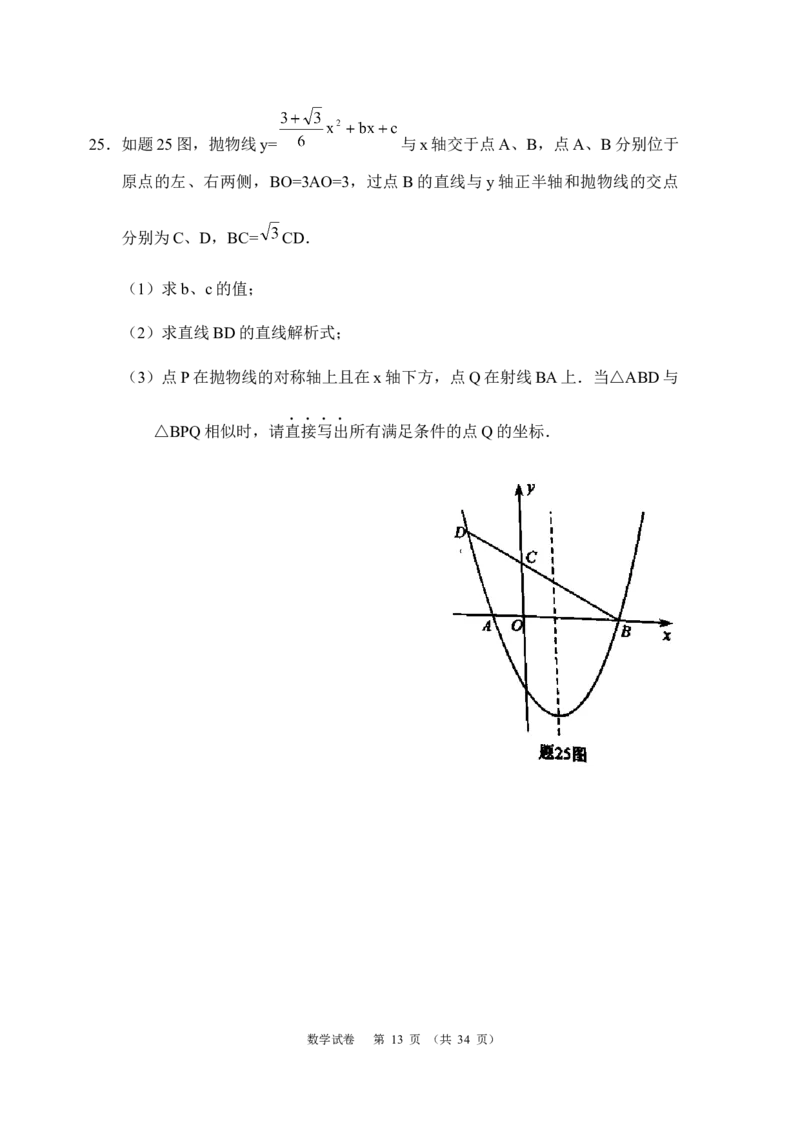
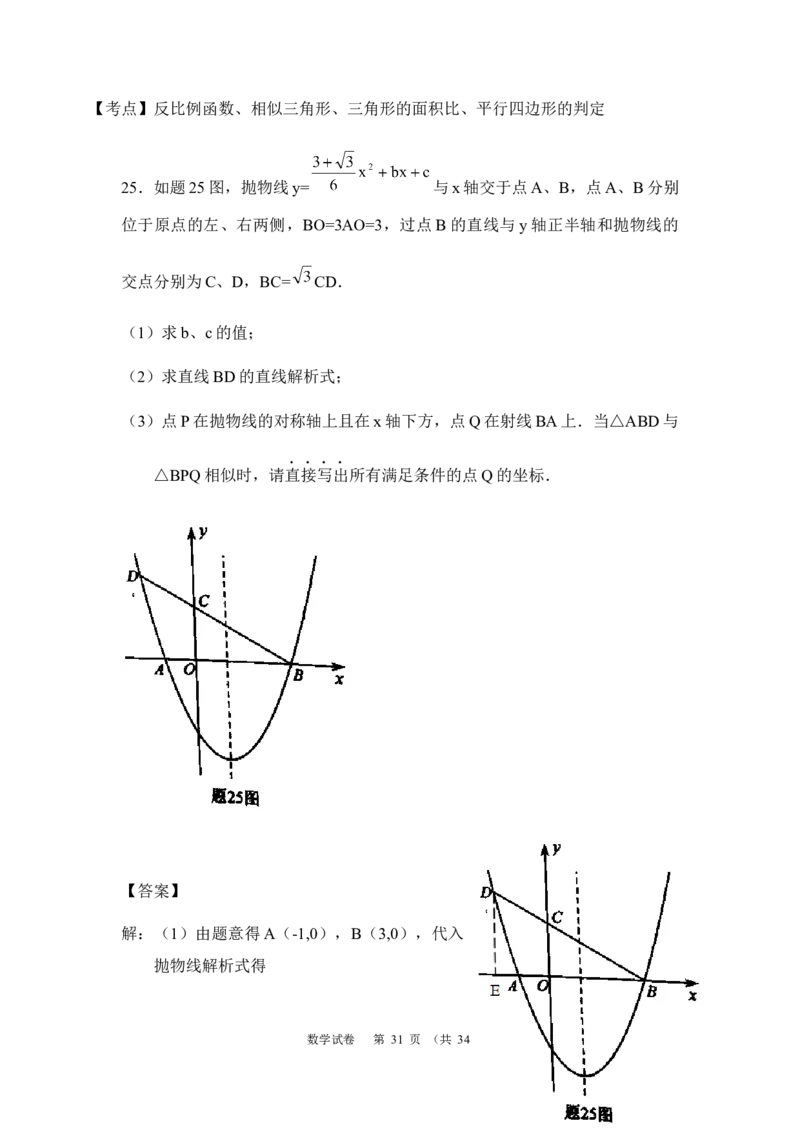
数学试卷 第 12 页 (共 34 页)25.如题25图,抛物线y= 与x轴交于点A、B,点A、B分别位于
原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点
分别为C、D,BC= CD.
(1)求b、c的值;
(2)求直线BD的直线解析式;
(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与
△BPQ相似时,请直接写出所有满足条件的点Q的坐标.
数学试卷 第 13 页 (共 34 页)2020 年广东省初中学业水平考试
数 学
说明:1.全卷共4页,满分为120分,考试用时为90分钟.
2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准
考证号、姓名、考场号、座位号.用2B铅笔把对应该号码的标号涂
黑.
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答
案信息点涂黑,如需改动,用像皮檫干净后,再选涂其他答案,答案
不能答在试题上.
4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各
题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再
写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无
效.
5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交
回.
一、选择题(本大题10小题,每小题 3分,共30分)在每小题列出的四个选
项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.
1.9的相反数是
A.﹣9 B.9 C. D.﹣
【答案】A
数学试卷 第 14 页 (共 34 页)【解析】正数的相反数是负数.
【考点】相反数
2.一组数据2、4、3、5、2的中位数是
A.5 B.3.5 C.3 D.2.5
【答案】C
【解析】按顺序排列,中间的数或者中间两个数的平均数.
【考点】中位数
数学试卷 第 15 页 (共 34 页)3.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为
A.(﹣3 ,2) B.(﹣2 ,3) C.(2 ,﹣3) D.
(3 ,﹣2)
【答案】D
【解析】关于x轴对称:横坐标不变,纵坐标互为相反数.
【考点】对称性
4.若一个多边形的内角和是540°,则该多边形的边数为
A.4 B.5 C.6 D.7
【答案】B
【解析】(n-2)×180°=540°,解得n=5.
【考点】n边形的内角和
5.若式子 在实数范围内有意义,则x的取值范围是
A.x≠2 B.x≥2 C.x≤2 D.x≠﹣2
【答案】B
【解析】偶数次方根的被开方数是非负数.
【考点】二次根式
6.已知△ABC 的周长为 16,点 D、E、F 分别为△ABC 三条边的中点,则
△DEF的周长为
A.8 B. C.16 D.4
【答案】A
【解析】三角形的中位线等于第三边的一半.
数学试卷 第 16 页 (共 34 页)【考点】三角形中位线的性质.
7.把函数y=(x﹣1)2+2的图象向右平移1个单位长度,平移后图象的函数解
析式为
A.y=x2+2 B.y=(x﹣1)2+1
C.y=(x﹣2)2+2 D.y=(x﹣1)2+3
【答案】C
【解析】左加右减,向右x变为x-1,y=(x﹣1﹣1)2+2y=(x﹣2)2+2 .
【考点】函数的平移问题.
数学试卷 第 17 页 (共 34 页)8.不等式组 的解集为
A.无解 B.x≤1 C.x≥﹣1 D.﹣1≤x≤1
【答案】D
【解析】解不等式.
【考点】不等式组的解集表示.
9.如题 9 图,在正方形 ABCD 中,AB=3,点 E、F 分别在边 AB、CD 上,
∠EFD=60°.若将四边形 EBCF 沿 EF 折叠,点 B 恰好落在 AD 边上,则
BE的长度为
A.1 B. C. D.2
【答案】D
【解析】解法一:排除法
过点F作FG∥BC交BE与点G,可得∠EFG=30°,∵FG=3,由三角函数可得
EG=
,∴BE> .
解法二:角平分线的性质
延 长 EF 、 BC 、 B’C’ 交 于 点 O , 可 知 ∠ EOB=∠ EOB’=30° , 可 得
∠BEO=∠B’EO=60°, ∴∠AEB’=60°.设BE=B’E=2x,由三角函数可得
数学试卷 第 18 页 (共 34 页)AE=x,由AE+BE=3,可得x=1,∴BE=2.
【考点】特殊平行四边形的折叠问题、辅助线的作法、三角函数.
10.如题10图,抛物线y=ax2+bx+c的对称轴是直线x=1.下列结论:①abc>
0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0.其中正确的结论有
A.4个 B.3个 C.2个 D.1
【答案】B
【解析】由a<0,b>0,c>0可得①错误;由△>0可得②正确;由x=-2时,
y<0 可得③正确.当 x=1 时,a+b+c>0,当 x=-2 时,4a-2b+c>0
即-4a+2b-c>0,两式相减得 5a-b+2c>0,即 5a+2c>b,∵b>0,
∴5a+b+2c>0可得④正确.
【考点】二次函数的图象性质.
二、填空题(本大题7小题,每小题4分,共27分)请将下列各题的正确答案
填写在答题卡相应的位置上.
11.分解因式:xy﹣x=____________.
【答案】x(y-1)
【解析】提公因式
【考点】因式分解
数学试卷 第 19 页 (共 34 页)12.如果单项式3xmy与﹣5x3yn 是同类项,那么m+n=________.
【答案】4
【解析】m=3,n=1
【考点】同类项的概念
13.若 +|b+1|=0,则(a+b)2020=_________.
【答案】1
【解析】算术平方根、绝对值都是非负数,∴a=2,b=-1,-1的偶数次幂为正
【考点】非负数、幂的运算
14.已知x=5﹣y,xy=2,计算3x+3y﹣4xy的值为___________.
【答案】7
【解析】x+y=5,原式=3(x+y)-4xy,15-8=7
【考点】代数式运算
15.如题15图,在菱形ABCD中,∠A=30°,取大于 AB的长为半径,分别
以点A、B为圆心作弧相交于两点,过此两点的直线交 AD边于点E(作图
痕迹如图所示),连接BE、BD,则∠EBD的度数为___________.
【答案】45°
【解析】菱形的对角线平分对角,∠ABC=150°,∠ABD=75°
数学试卷 第 20 页 (共 34 页)【考点】垂直平分线的性质、菱形的性质
16.如题16图,从一块半径为1m的圆形铁皮上剪出一个圆周角为120°的扇形
ABC,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为
______m.
【答案】
【解析】连接BO、AO可得△ABO为等边,可知AB=1,l= ,2πr= 得r=
【考点】弧长公式、圆锥
17.有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中
间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫、老鼠都理想化为
同一平面内的线或点,模型如题 17 图,∠ABC=90°,点 M、N 分别在射线
BA、BC上,MN长度始终不变,MN=4,E为MN的中点,点D到BA、BC的
距离分别为 4 和 2.在此滑动过程中,猫与老鼠的距离 DE 的最小值为
_________________.
数学试卷 第 21 页 (共 34 页)【答案】
【解析】 点B到点E的距离不变,点E在以B为圆心的圆上,线段BD与圆的
交点即为所求最短距离的E点,BD= ,BE=2
【考点】直角三角形的性质、数学建模思想、最短距离问题
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.先化简,再求值:(x+y)2+(x+y)(x﹣y) ﹣2x2,其中x= ,y= .
【答案】
解:
原式=x2+2xy+y2+x2-y2-2x2
=2xy
把x= ,y= 代入,
原式=2× × =2
【解析】完全平方公式、平方差公式,合并同类项
数学试卷 第 22 页 (共 34 页)【考点】整式乘除,二次根式
19.某中学展开主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非
常了解”、“比较了解”、“基本了解”“不太了解”四个等级,要求每
名学生选且只能选其中一个等级 .随机抽取了120名学生的有效问卷,
数据整理如下:
等级 非常了解 比较了解 基本了解 不太了解
人数(人) 24 72 18 x
(1)求x的值;
(2)若该校有学生 1800 人,请根据抽样调查结果估算该校“非常了解”和
“比较了解”垃圾分类知识的学生共有多少人?
【答案】
解:
(1)由题意得24+72+18+x=120,解得x=6
(2)1800× =1440(人)
答:估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有1440人.
【解析】统计表的分析
【考点】概率统计
20.如题20图,在△ABC中,点D、E分别是AB、AC边上的点,BD=CE,
∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
数学试卷 第 23 页 (共 34 页)【答案】
证明:
∵BD=CE,∠ABE=∠ACD,∠DFB=∠CFE
∴△BFDF≌△CFE(AAS)
∴∠DBF=∠ECF
∵∠DBF+∠ABE=∠ECF+∠ACD
∴∠ABC=∠ACB
∴AB=AC
∴△ABC是等腰三角形
【解析】等式的性质、等角对等边
【考点】全等三角形的判定方法、等腰三角形的判定方法
四、解答题(二)(本大题3小题,毎小题8分,共24分)
21.已知关于x、y的方程组 与 的解相同.
(1)求a、b的值;
(2)若一个三角形的一条边的长为 2 ,另外两条边的长是关于 x 的方程
x2+ax+b=0的解,试判断该三角形的形状,并说明理由.
【答案】
解:
数学试卷 第 24 页 (共 34 页)(1)由题意得 ,解得
由 ,解得
(2)该三角形的形状是等腰直角三角形,理由如下:
由(1)得x2﹣4 x+12=0
(x- )2=0
x =x =
1 2
∴该三角形的形状是等腰三角形
∵(2 )2=24,( )2=12
∴(2 )2=( )2+( )2
∴该三角形的形状是等腰直角三角形
【解析】理解方程组同解的概念,一元二次方程的解法、三角形形状的判断
【考点】二元一次方程组、一元二次方程、勾股定理逆定理
22.如题22图,在四边形ABCD中,AD∥BC,∠DAB=90°,AB是⊙O的直径,
CO平分∠BCD.
(1)求证:直线CD与⊙O相切;
⌒
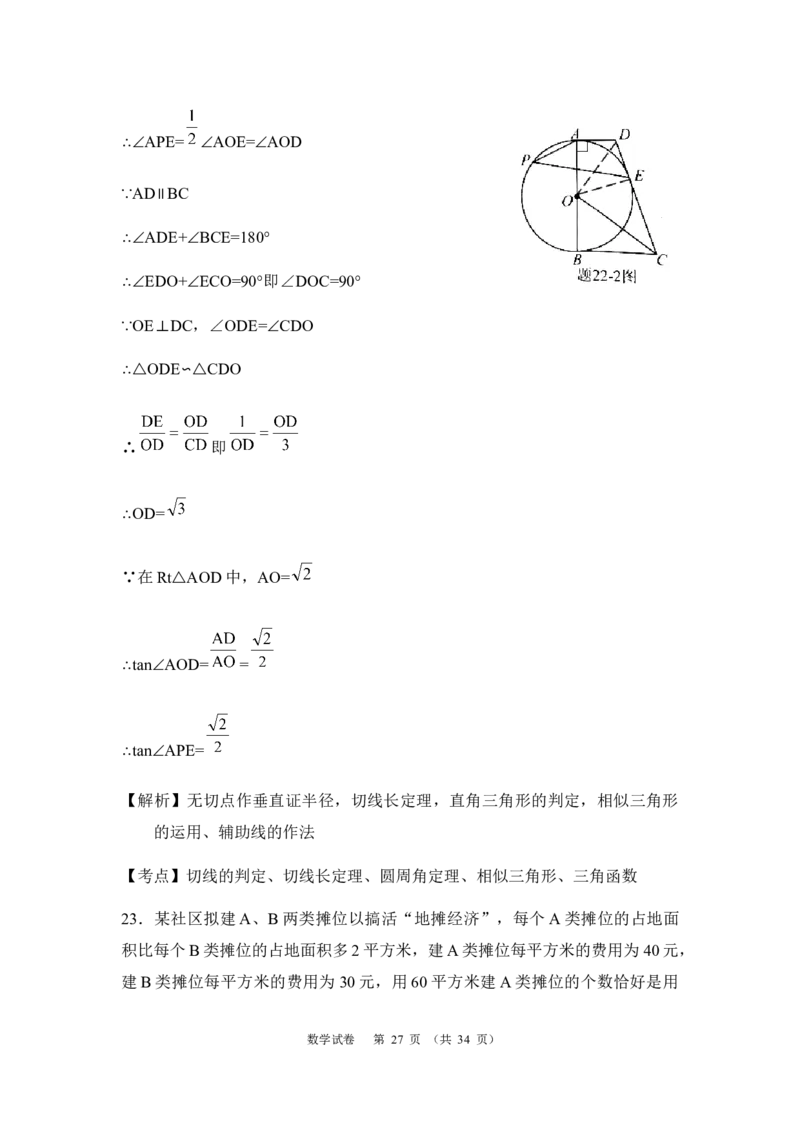
(2)如题 22﹣2 图,记(1)中的切点为 E,P 为优弧 AE上一点,AD=1,
BC=2,求tan∠APE的值.
数学试卷 第 25 页 (共 34 页)【答案】
E
(1)证明:过点O作OE⊥CD交于点E
∵AD∥BC,∠DAB=90°
∴∠OBC=90°即OB⊥BC
∵OE⊥CD,OB⊥BC,CO平分∠BCD
∴OB=OE
∵AB是⊙O的直径
∴OE是⊙O的半径
∴直线CD与⊙O相切
(2)连接OD、OE
∵由(1)得,直线CD、AD、BC与⊙O相切
∴由切线长定理可得AD=DE=1,BC=CE=3,
∠ADO=∠EDO,∠BCO=∠ECO
∴∠AOD=∠EOD,CD=3
⌒ ⌒
∵AE=AE
数学试卷 第 26 页 (共 34 页)∴∠APE= ∠AOE=∠AOD
∵AD∥BC
∴∠ADE+∠BCE=180°
∴∠EDO+∠ECO=90°即∠DOC=90°
∵OE⊥DC,∠ODE=∠CDO
∴△ODE∽△CDO
∴ 即
∴OD=
∵在Rt△AOD中,AO=
∴tan∠AOD= =
∴tan∠APE=
【解析】无切点作垂直证半径,切线长定理,直角三角形的判定,相似三角形
的运用、辅助线的作法
【考点】切线的判定、切线长定理、圆周角定理、相似三角形、三角函数
23.某社区拟建A、B两类摊位以搞活“地摊经济”,每个A类摊位的占地面
积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,
建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用
数学试卷 第 27 页 (共 34 页)同样面积建B类摊位个数的 .
(1)求每个A、B类摊位占地面积各为多少平方米?
(2)该社区拟建A、B两类摊位共90个,且B类摊位的数量不少于A类摊位
数量的3倍.求建造这90个摊位的最大费用.
【答案】
解:(1)设每个B类摊位占地面积为x平方米,则每个A类摊位占地面积为
(x+2)平方米.
解得x=3
经检验x=3是原方程的解
∴x+2=5(平方米)
答:每个A、B类摊位占地面积各为5平方米和3平方米.
(2)设A类摊位数量为a个,则B类摊位数量为(90-a)个,最大费用为y元.
由90-a≥3a,解得a≤22.5
∵a为正整数
∴a的最大值为22
y=40a+30(90-a)=10a+2700
∵10>0
∴y随a的增大而增大
∴当a=22时,y=10×22+2700=2920(元)
数学试卷 第 28 页 (共 34 页)答:这90个摊位的最大费用为2920元.
【解析】分式方程的应用题注意检验,等量关系的确定是关键
【考点】分式方程的应用,不等式的应用,一次函数应用
五、解答题(三)(本大题2小题,毎小题10分,共20分)
24.如题24图,点B是反比例函数y= (x>0)图象上一点,过点B分别向
坐标轴作垂线,垂足为 A、C.反比例函数 y= (x>0)的图象经过 OB
的中点M,与AB、BC分别交于点D、E.连接DE并延长交x轴于点F,
点G与点O关于点C对称,连接BF、BG.
(1)填空:k=_2_______;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
【答案】
(2)解:过点D作DP⊥x轴交于点P
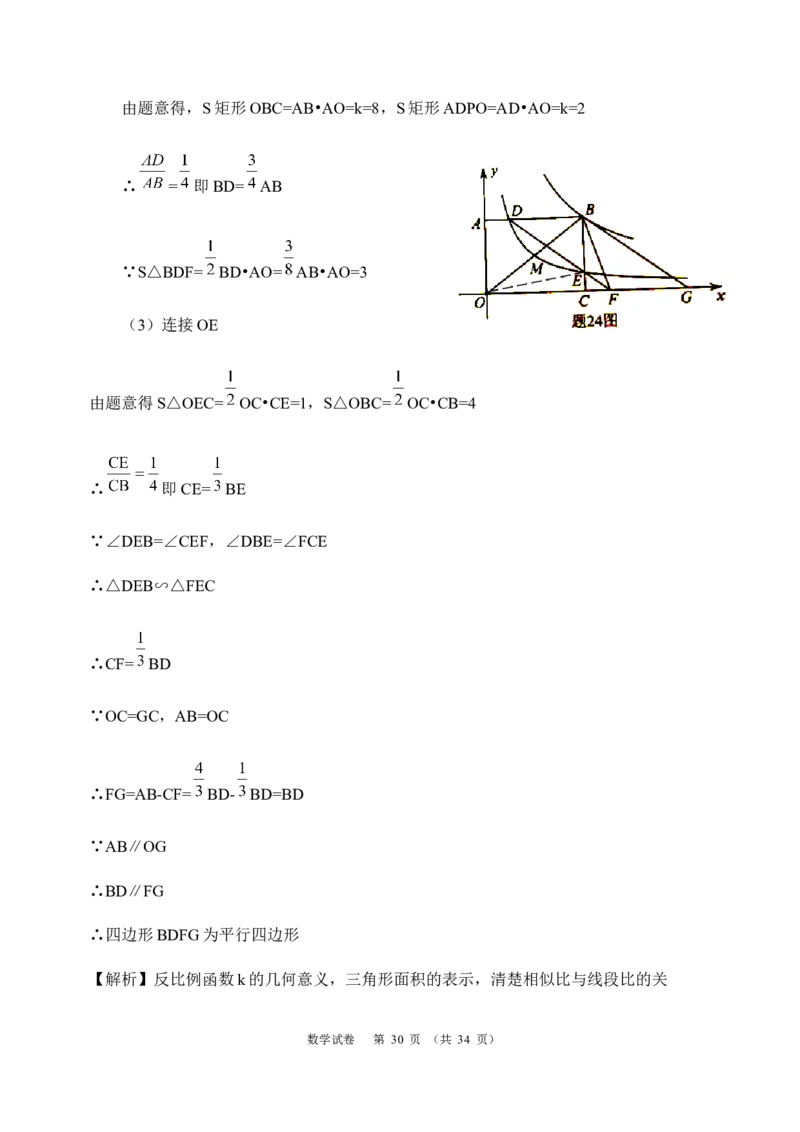
数学试卷 第 29 页 (共 34 页)由题意得,S矩形OBC=AB•AO=k=8,S矩形ADPO=AD•AO=k=2
∴ = 即BD= AB
∵S△BDF= BD•AO= AB•AO=3
(3)连接OE
由题意得S△OEC= OC•CE=1,S△OBC= OC•CB=4
∴ 即CE= BE
∵∠DEB=∠CEF,∠DBE=∠FCE
∴△DEB∽△FEC
∴CF= BD
∵OC=GC,AB=OC
∴FG=AB-CF= BD- BD=BD
∵AB∥OG
∴BD∥FG
∴四边形BDFG为平行四边形
【解析】反比例函数k的几何意义,三角形面积的表示,清楚相似比与线段比的关
数学试卷 第 30 页 (共 34 页)【考点】反比例函数、相似三角形、三角形的面积比、平行四边形的判定
25.如题25图,抛物线y= 与x轴交于点A、B,点A、B分别
位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的
交点分别为C、D,BC= CD.
(1)求b、c的值;
(2)求直线BD的直线解析式;
(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与
△BPQ相似时,请直接写出所有满足条件的点Q的坐标.
【答案】
解:(1)由题意得A(-1,0),B(3,0),代入
抛物线解析式得
数学试卷 第 31 页 (共 34 页),解得
(2)过点D作DE⊥x轴交于点E
∵OC∥OC,BC= CD,OB=3
∴
∴OE=
∴点D的横坐标为xD=-
∵点D是射线BC与抛物线的交点
∴把xD=- 代入抛物线解析式得yD= +1
∴D(- , +1)
设直线BD解析式为y=kx+m,将B(3,0)、D(- , +1)代入
,解得
直线BD的直线解析式为y=
∴
数学试卷 第 32 页 (共 34 页)(3)由题意得tan∠ABD= ,tan∠ADB=1
由题意得抛物线的对称轴为直线x=1,设对称轴与x轴交点为M,P(1,n)且
n<0,Q(x,0)且x<3
①当△PBQ∽△ABD时,tan∠PBQ=tan∠ABD即 = ,解得-n=
tan∠PQB=tan∠ADB,即 =1,解得x=
②当△PQB∽△ABD时,tan∠PBQ=tan∠ADB即 =1,解得-n=2
tan∠QPB=tan∠ABD,即 = ,解得x=
③当△PQB∽△DAB时,tan∠PBQ=tan∠ABD即 = ,解得-n=
tan∠PQM=tan∠DAE,即 = ,解得x=
④当△PQB∽△ABD时,tan∠PBQ=tan∠ABD即 =1,解得-n=2
= ,解得x=
tan∠PQM=tan∠DAE,即
综上所述,Q ( ,0)、Q ( ,0)、Q ( ,0)、Q (
1 2 3 4
数学试卷 第 33 页 (共 34 页),0)
【解析】分类讨论不重不漏,计算能力要求高
【考点】一次函数、二次函数、平面直角坐标系、相似三角形、三角函数、分类讨
论、二次根式计算
数学试卷 第 34 页 (共 34 页)