2007年山东高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_山东

2007 年山东高考文科数学真题及答案 第Ⅰ卷（共60分） 一、选择题：本大题共12小题，每小题5分，共50分，在每小题给出的四个选项中，选 择一个符合题目要求的选项． 43i 1．复数 的实部是（ ） 1+2i A．2 B．2 C．3 D．4  1  2．已知集合M {1，1}，N x| 2x1 4，xZ，则M  N （ ）  2  A．{1，1} B．{0} C．{1} D．{1，0} 3．下列几何体各自的三视图中，有且仅有两个视图相同的是（ ） ①正方形 ②圆锥 ③三棱台 ④正四棱锥 A．①② B．①③ C．①④ D．②④   4．要得到函数y sinx的图象，只需将函数y cos  x 的图象（ ）     A．向右平移 个单位 B．向右平移 个单位     C．向左平移 个单位 D．向左平移 个单位   5．已知向量a (1，n)，b(1，n)，若2ab与b垂直，则 a （ ） A．1 B． 2 C．2 D．4 6 ． 给 出 下 列 三 个 等 式 ： f(xy) f(x) f(y)，f(x y) f(x)f(y)， f(x) f(y) f(x y) ．下列函数中不满足其中任何一个等式的是（ ） 1 f(x)f(y) A． f(x)3x B． f(x)sinx C． f(x)log x D． f(x)tanx 2 7．命题“对任意的xR，x3 x2 1≤0”的否定是（ ） A．不存在xR，x3x2 1≤0 B．存在xR，x3x2 1≤0 第1页 | 共11页C．存在xR，x3x2 10 D．对任意的xR，x3x2 10 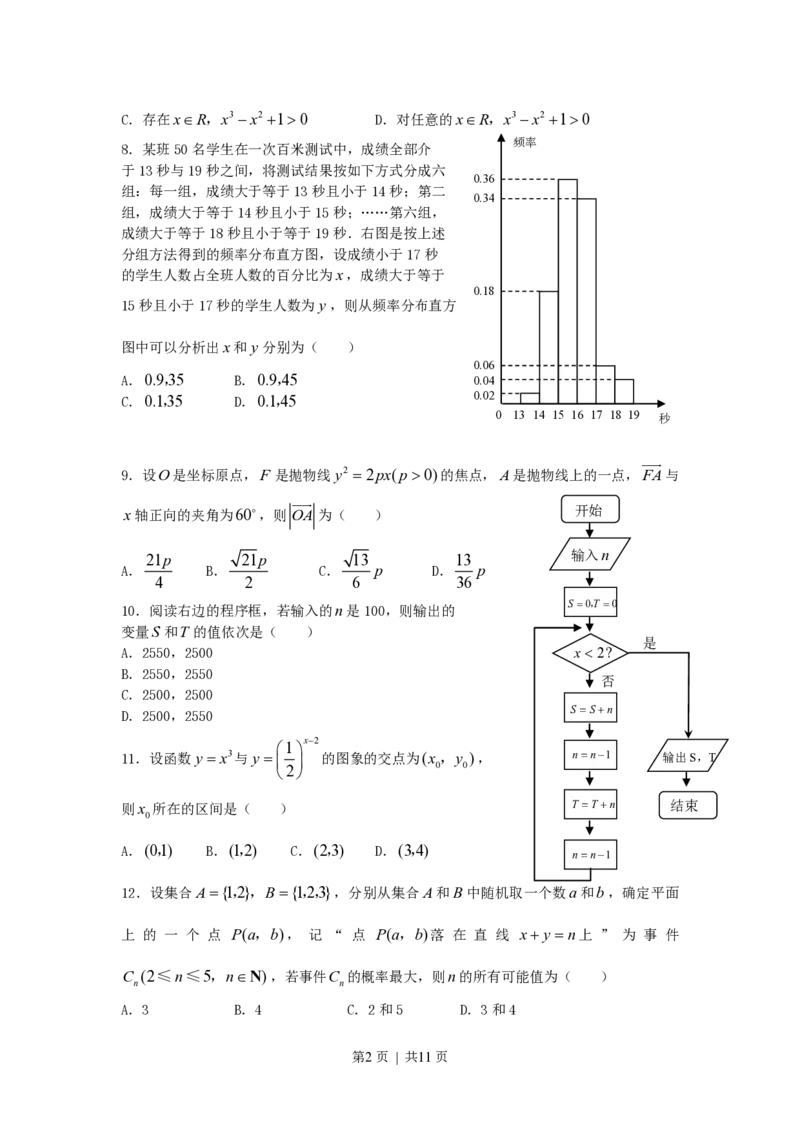频率 8．某班50名学生在一次百米测试中，成绩全部介 于13秒与19秒之间，将测试结果按如下方式分成六 0.36 组：每一组，成绩大于等于13秒且小于14秒；第二 0.34 组，成绩大于等于14秒且小于15秒；……第六组， 成绩大于等于18秒且小于等于19秒．右图是按上述 分组方法得到的频率分布直方图，设成绩小于17秒 的学生人数占全班人数的百分比为x，成绩大于等于 0.18 15秒且小于17秒的学生人数为y，则从频率分布直方 图中可以分析出x和y分别为（ ） 0.06 A．0.9，35 B．0.9，45 0.04 C．0.1，35 D．0.1，45 0.02 0 13 14 15 16 17 18 19 秒  9．设O是坐标原点，F 是抛物线y2 2px(p 0)的焦点，A是抛物线上的一点，FA与  开始 x轴正向的夹角为60，则 OA 为（ ） 输入n 21p 21p 13 13 A． B． C． p D． p 4 2 6 36 S0，T 0 10．阅读右边的程序框，若输入的n是100，则输出的 变量S 和T 的值依次是（ ） 是 A．2550，2500 x2? B．2550，2550 否 C．2500，2500 SSn D．2500，2550 x2 1 11．设函数y  x3与y    的图象的交点为(x，y )， nn1 输出S，T 2 0 0 则x 所在的区间是（ ） T Tn 结束 0 A．(0，1) B．(1，2) C．(2，3) D．(3，4) nn1 12．设集合A{1，2}，B{1，2，3}，分别从集合A和B中随机取一个数a和b，确定平面 上 的 一 个 点 P(a，b)， 记 “ 点 P(a，b)落 在 直 线 x y n上 ” 为 事 件 C (2≤n≤5，nN)，若事件C 的概率最大，则n的所有可能值为（ ） n n A．3 B．4 C．2和5 D．3和4 第2页 | 共11页第Ⅱ卷（共90分） 二、填空题：本大题共4小题，每小题4分，共16分，答案须填在题中横线上． 13．设函数 f (x) x2，f (x) x1，f (x) x3，则 f (f (f (2007))) ． 1 2 3 1 2 3 14．函数y a1x(a 0，a 1)的图象恒过定点A，若点A在直线mxny10(mn0) 1 1 上，则  的最小值为 ． m n 15．当x(1，2)时，不等式x2 mx40恒成立，则m的取值范围是 ． 16．与直线x y20和曲线x2  y2 12x12y540都相切的半径最小的圆的标准 方程是 ． 三、解答题：本大题共5小题，共74分．解答写出文字说明、证明过程或演算步骤． 17．（本小题满分12分） 在△ABC中，角A，B，C的对边分别为a，b，c，tanC 3 7 ． （1）求cosC ；   5 （2）若CB CA ，且ab9，求c．  2 18．（本小题满分12分） 设{a }是公比大于 1 的等比数列， S 为数列{a }的前 n项和．已知 S 7，且 n n n 3 a 3，3a，a 4构成等差数列． 1 2 3 （1）求数列{a }的等差数列． n （2）令b lna ，n1，2， ，求数列{b }的前n项和T ． n 3n1  n 19．（本小题满分12分） 本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用 不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、 乙两个电视台为该公司所做的每分钟广告，能给公司事来的收益分别为0.3万元和0.2万 元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益 是多少万元？ D C 1 1 20．（本小题满分12分） A 1 B 如图，在直四棱柱ABCDABC D 中， 1 1 1 1 1 已知DC  DD 2AD2AB，AD⊥DC，AB∥DC． 1 （1）求证：DC⊥AC ； 1 1 （2）设E是DC 上一点，试确定E的位置，使DE∥平面 C 1 D A B 第3页 | 共11页ABD，并说明理由． 1 21．（本小题满分12分） 设函数 f(x)ax2 blnx，其中ab0． 证明：当ab0时，函数 f(x)没有极值点；当ab0时，函数 f(x)有且只有一个极 值点，并求出极值． 22．（本小题满分14分） 已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为 3，最小值为1． （1）求椭圆C的标准方程； （2）若直线l: y kxm与椭圆C相交于 A，B两点（ A，B不是左右顶点），且以 AB 为直径的图过椭圆C的右顶点．求证：直线l过定点，并求出该定点的坐标． 第4页 | 共11页答案 一、选择题 1．B 2．C 3．D 4．A 5．C 6．B 7．C 8．A 9．B 10．A 11．B 12．D 二、填空题 1 13． 14．1 15．m≤5 16．(x2)2 (y2)2 2 2007 三、解答题 sinC 17．解：（1） tanC 3 7， 3 7  cosC 又 sin2Ccos2C 1  1 解得cosC  ． 8 tanC 0，C是锐角．  1 cosC  ． 8   5 （2） CB CA ，   2 5 abcosC  ， 2 ab20． 又 ab9  a2 2abb2 81． a2 b2 41． c2 a2 b2 2abcosC 36． c6． a a a 7，  1 2 3 18．解：（1）由已知得:(a 3)(a 4) 1 3 3a .   2 2 解得a 2． 2 2 设数列{a }的公比为q，由a 2，可得a  ，a 2q． n 2 1 q 3 2 又S 7，可知 22q7， 3 q 即2q2 5q20， 第5页 | 共11页1 解得q 2，q  ． 1 2 2 由题意得q1，q2． a 1． 1 故数列{a }的通项为a 2n1． n n （2）由于b lna ，n1，2， ， n 3n1  由（1）得a 23n 3n1 b ln23n 3nln2 n 又b b 3ln2 n1 n n {b }是等差数列． n T b b  b n 1 2  n n(b b )  1 n 2 n(3ln23ln2)  2 3n(n1)  ln2. 2 3n(n1) 故T  ln2． n 2 19．解：设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟，总收益为z元， y x y≤300， 500  由题意得500x200y≤90000，  400 x≥0，y≥0.  目标函数为z 3000x2000y． 300 x y≤300， M l 200  二元一次不等式组等价于5x2y≤900，  100 x≥0，y≥0.  作出二元一次不等式组所表示的平面区域，即可行域． 如图： 0 100 200300 x 作直线l:3000x2000y 0， 第6页 | 共11页即3x2y 0． 平移直线l，从图中可知，当直线l过M 点时，目标函数取得最大值． x y 300， 联立 解得x100，y 200． 5x2y 900. 点M 的坐标为(100，200)． z 3000x2000y 700000（元） max 答：该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最 大收益是70万元． 20．（1）证明：在直四棱柱ABCDABC D 中， 1 1 1 1 D C 1 1 连结C D， 1 A 1 B 1 DC  DD ，  1 四边形DCC D 是正方形． 1 1 DC ⊥DC． 1 1 又AD⊥DC，AD⊥DD，DC⊥DD  D， D C 1 1 A B AD⊥平面DCC D ， 1 1 DC 平面DCC D ， 1 1 1 AD⊥DC． 1 AD，DC 平面ADC ，  1 1 D C 1 1 且AD⊥DC  D， A 1 B DC⊥平面ADC ， 1 1 1 又AC 平面ADC ， 1 1 M DC⊥AC ． 1 1 （2）连结AD 1 ，连结AE， D E C A B 设AD ADM ， 1 1 BD AE  N，连结MN ，  第7页 | 共11页平面ADE 平面ABDMN ，  1  1 要使DE∥平面ABD， 1 1 须使MN∥DE， 1 又M 是AD 的中点． 1 N 是AE的中点． 又易知△ABN≌△EDN ， AB DE． 即E是DC 的中点． 综上所述，当E是DC 的中点时，可使DE∥平面ABD． 1 1 21．证明：因为 f(x)ax2 blnx，ab0，所以 f(x)的定义域为(0，)． b 2ax2 b f(x) 2ax  ． x x 当ab0时，如果a0，b0，f(x)0，f(x)在(0，)上单调递增； 如果a0，b0，f(x)0，f(x)在(0，)上单调递减． 所以当ab0，函数 f(x)没有极值点． 当ab0时，  b  b  2ax  x   2a 2a    f(x) x 令 f(x)0， b b 将x   (0，)（舍去），x   (0，)， 1 2a 2 2a 当a0，b0时， f(x)，f(x)随x的变化情况如下表： 第8页 | 共11页 b  b  b  x 0，     ，      2a  2a  2a  f(x)  0  f(x) 极小值   从上表可看出，  b  b  b  函数 f(x)有且只有一个极小值点，极小值为 f        1ln    ．  2a  2  2a 当a0，b0时， f(x)，f(x)随x的变化情况如下表：  b  b  b  x 0，     ，      2a  2a  2a  f(x)  0  f(x) 极大值   从上表可看出，  b  b  b  函数 f(x)有且只有一个极大值点，极大值为 f        1ln    ．  2a  2  2a 综上所述， 当ab0时，函数 f(x)没有极值点； 当ab0时， 若 a0，b0时 ， 函 数 f(x)有 且 只 有 一 个 极 小 值 点 ， 极 小 值 为 b  b    1ln    ． 2  2a 若 a0，b0时 ， 函 数 f(x)有 且 只 有 一 个 极 大 值 点 ， 极 大 值 为 b  b    1ln    ． 2  2a x2 y2 22．解：（1）由题意设椭圆的标准方程为  1(ab0)， a2 b2 由已知得：ac3，ac1， 第9页 | 共11页a2，c1， b2 a2 c2 3 x2 y2 椭圆的标准方程为  1． 4 3 （2）设A(x，y )，B(x，y )． 1 1 2 2 y kxm，  联立x2 y2  1.   4 3 得 (34k2)x2 8mkx4(m2 3)0，则  64m2k2 16(34k2)(m2 3)0，即34k2 m2 0，   8mk x x  ， 1 2 34k2   4(m2 3) x x  .  1 2 34k2 3(m2 4k2) 又y y (kx m)(kx m)k2x x mk(x x )m2  ． 1 2 1 2 1 2 1 2 34k2 因为以AB为直径的圆过椭圆的右顶点D(2，0)， y y k k 1，即 1 2 1． AD BD x 2  x 2 1 2 y y x x 2(x x )40． 1 2 1 2 1 2 3(m2 4k2) 4(m2 3) 15mk    40． 34k2 34k2 34k2 7m2 16mk4k2 0． 2k 解得：m 2k，m  ，且均满足34k2 m2 0． 1 2 7 当m 2k 时，l的方程y k(x2)，直线过点(2，0)，与已知矛盾； 1 2k  2 2  当m  时，l的方程为y k  x ，直线过定点 ，0 ． 2 7  7 7  第10页 | 共11页2  所以，直线l过定点，定点坐标为 ，0 ． 7  第11页 | 共11页