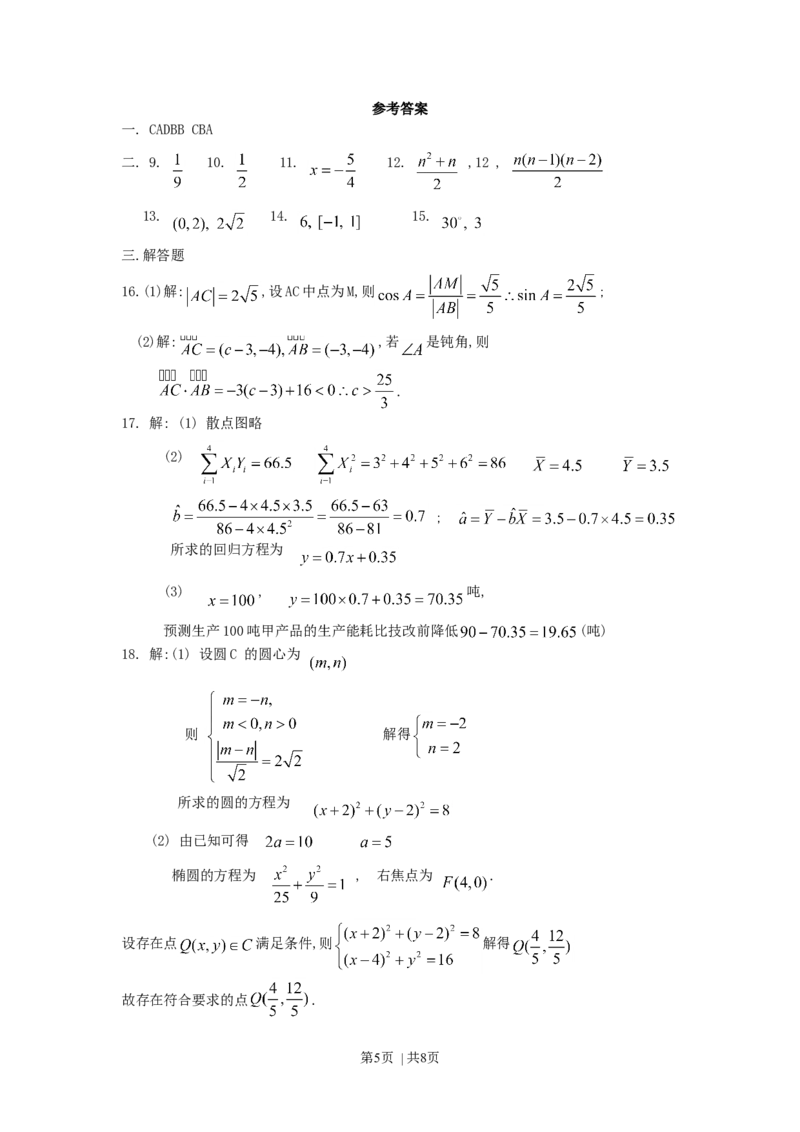文档内容
2007 年广东高考理科数学真题及答案
本试卷共4页,21小题,满分150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的铅笔或签字笔将自己的姓名和考生号、试室
号、座位号填写在答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应
位置上、将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点
涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指
定区域内相应位置上,如需改动,先划掉原来的答案,然后再写上新的答案;
不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题号(或题组号)对应的信息点,
再作答。漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式 ,其中 是锥体的底面积, 是锥体的高。
如果事件 、 互斥,那么 .
如果事件 、 相互独立,那么 .
用最小二乘法求线性回归方程系数公式 .
一、 选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,
只
有一项符合要求的.
1.已知函数 的定义域为 , 的定义域为 ,则
A. B. C. D.
2.若复数 是纯虚数( 是虚数单位, 是实数)则 =
A.2 B. C. D.
3.若函数
A.最小正周期为 的奇函数 B.最小正周期为 的奇函数
C.最小正周期为 的偶函数 D.最小正周期为 的偶函数
4.客车从甲地以60 km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以
80 km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达
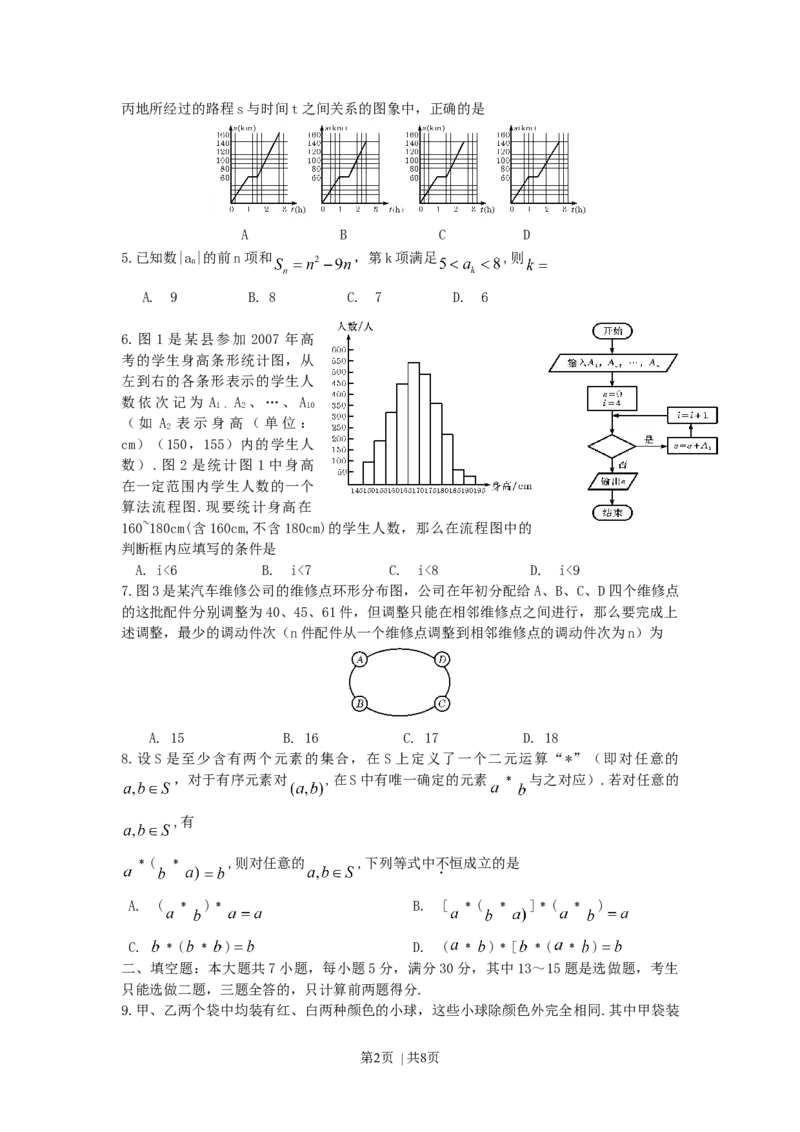
第1页 | 共8页丙地所经过的路程s与时间t之间关系的图象中,正确的是
A B C D
5.已知数|a|的前n项和 ,第k项满足 ,则
n
A. 9 B. 8 C. 7 D. 6
6.图 1 是某县参加 2007 年高
考的学生身高条形统计图,从
左到右的各条形表示的学生人
数依次记为 A A 、…、A
1、 2 10
(如 A 表示身高(单位:
2
cm)(150,155)内的学生人
数).图 2 是统计图 1 中身高
在一定范围内学生人数的一个
算法流程图.现要统计身高在
160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的
判断框内应填写的条件是
A. i<6 B. i<7 C. i<8 D. i<9
7.图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点
的这批配件分别调整为40、45、61件,但调整只能在相邻维修点之间进行,那么要完成上
述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A. 15 B. 16 C. 17 D. 18
8.设 S 是至少含有两个元素的集合,在 S 上定义了一个二元运算“*”(即对任意的
,对于有序元素对 ,在S中有唯一确定的元素 ﹡ 与之对应).若对任意的
,有
﹡( ﹡ ,则对任意的 ,下列等式中不恒成立的是
A. ( ﹡ )﹡ B. [ ﹡( ﹡ ]﹡( ﹡ )
C. ﹡( ﹡ ) D. ( ﹡ )﹡[ ﹡( ﹡ )
二、填空题:本大题共7小题,每小题5分,满分30分,其中13~15题是选做题,考生
只能选做二题,三题全答的,只计算前两题得分.
9.甲、乙两个袋中均装有红、白两种颜色的小球,这些小球除颜色外完全相同.其中甲袋装
第2页 | 共8页有4个红球,2个白球,乙袋装有1个红球,5个白球. 现分别从甲、乙两袋中各随机取
出一个球,则取出的两球都是红球的概率为 .(答案用分数表示)
10.若向量 满足 与 的夹角为120°,则 .
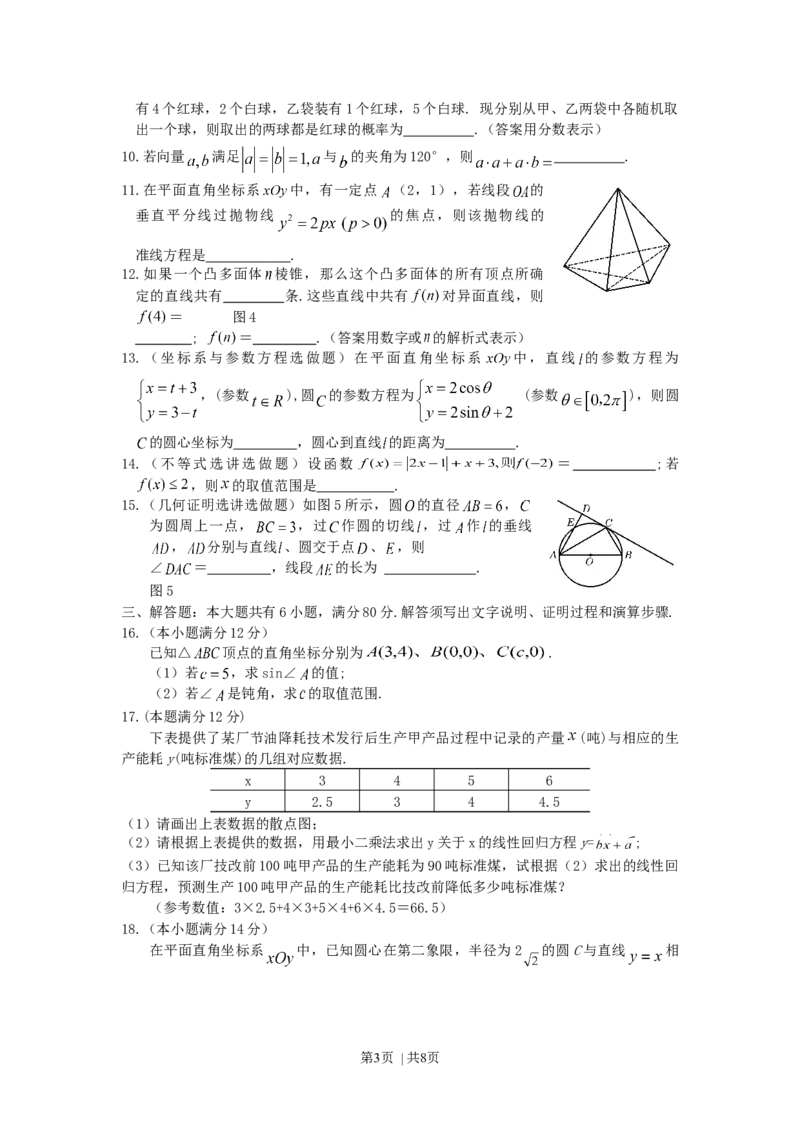
11.在平面直角坐标系 中,有一定点 (2,1),若线段 的
垂直平分线过抛物线 的焦点,则该抛物线的
准线方程是 .
12.如果一个凸多面体 棱锥,那么这个凸多面体的所有顶点所确
定的直线共有 条.这些直线中共有 对异面直线,则
= 图4
; = .(答案用数字或 的解析式表示)
13.(坐标系与参数方程选做题)在平面直角坐标系 中,直线 的参数方程为
,(参数 ),圆 的参数方程为 (参数 ),则圆
的圆心坐标为 ,圆心到直线 的距离为 .
14.(不等式选讲选做题)设函数 = ;若
,则 的取值范围是 .
15.(几何证明选讲选做题)如图5所示,圆 的直径 ,
为圆周上一点, ,过 作圆的切线 ,过 作 的垂线
, 分别与直线 、圆交于点 、 ,则
∠ = ,线段 的长为 .
图5
三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知△ 顶点的直角坐标分别为 .
(1)若 ,求sin∠ 的值;
(2)若∠ 是钝角,求 的取值范围.
17.(本题满分12分)
下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量 (吨)与相应的生
产能耗y(吨标准煤)的几组对应数据.
x 3 4 5 6
y 2.5 3 4 4.5
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= ;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回
归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
18.(本小题满分14分)
在平面直角坐标系 中,已知圆心在第二象限,半径为2 的圆C与直线 相
第3页 | 共8页切于坐标原点O.椭圆 =1与圆C的一个交点到椭圆两点的距离之和为10.
(1)求圆C的方程.
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆右焦点F的距离等于线段OF的长.
若存在,请求出点Q的坐标;若不存在,请说明理由.
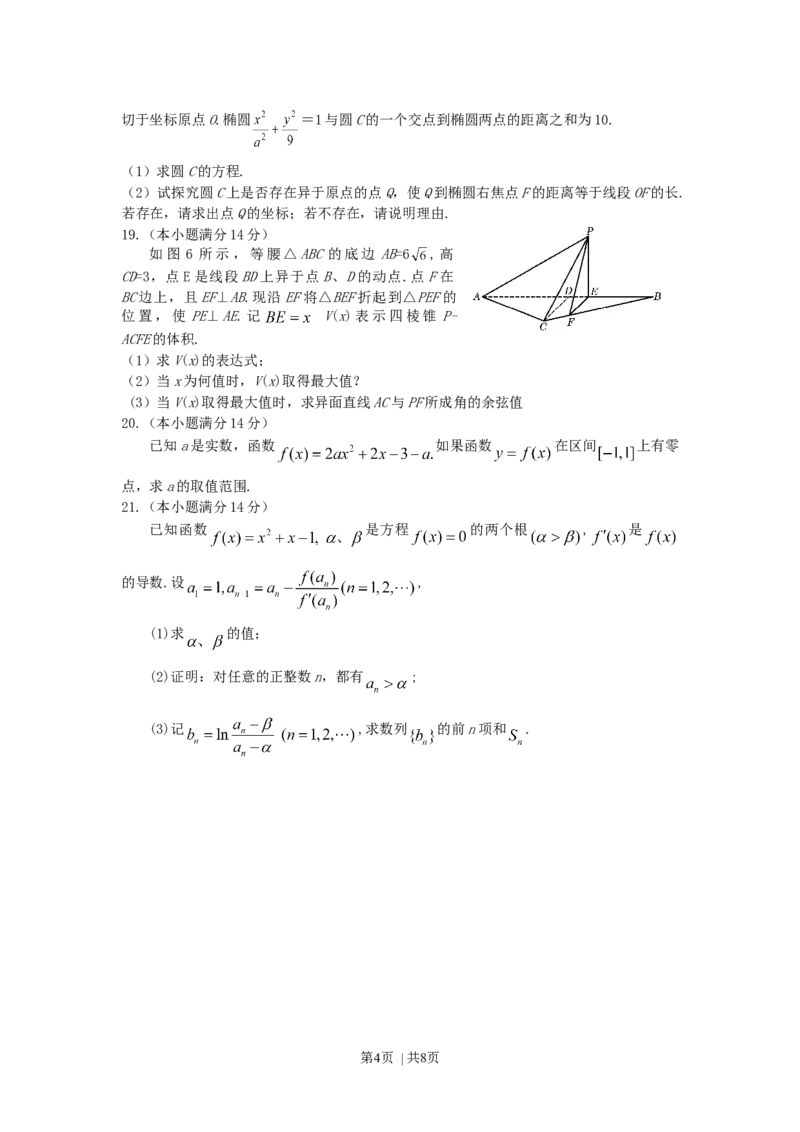
19.(本小题满分14分)
如图 6 所示,等腰△ABC的底边 AB=6 ,高
CD=3,点E是线段BD上异于点B、D的动点.点F在
BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的
位置,使 PE⊥AE.记 V(x)表示四棱锥 P-
ACFE的体积.
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
20.(本小题满分14分)
已知a是实数,函数 如果函数 在区间 上有零
点,求a的取值范围.
21.(本小题满分14分)
已知函数 是方程 的两个根 , 是
的导数.设 ,
(1)求 的值;
(2)证明:对任意的正整数n,都有 ;
(3)记 ,求数列 的前n项和 .
第4页 | 共8页参考答案
一. CADBB CBA
二. 9. 10. 11. 12. ,12 ,
13. 14. 15.
三.解答题
16.(1)解: ,设AC中点为M,则 ;
(2)解: ,若 是钝角,则
.
17. 解: (1) 散点图略
(2)
;
所求的回归方程为
(3) , 吨,
预测生产100吨甲产品的生产能耗比技改前降低 (吨)
18. 解:(1) 设圆C 的圆心为
则 解得
所求的圆的方程为
(2) 由已知可得
椭圆的方程为 , 右焦点为 .
设存在点 满足条件,则 解得
故存在符合要求的点 .
第5页 | 共8页19. 解 : (1) 即
;
z
(2) ,
P
时 , 时 ,
D E B
A
y
时 取得最大值.
C F
x
(3)以E为空间坐标原点,直线EF为 轴,直线
EB 为 轴 , 直 线 EP 为 轴 建 立 空 间 直 角 坐 标 系 , 则
;
,设异面直线AC与PF夹角是
20.解:若 ,则 有唯一零点为 ,故 不符合要求;
由 , 且
. 由 当 时 ,
,
当 时, , 在两个区间上分别递增;
当 时, , 在两个区间上分别递减;
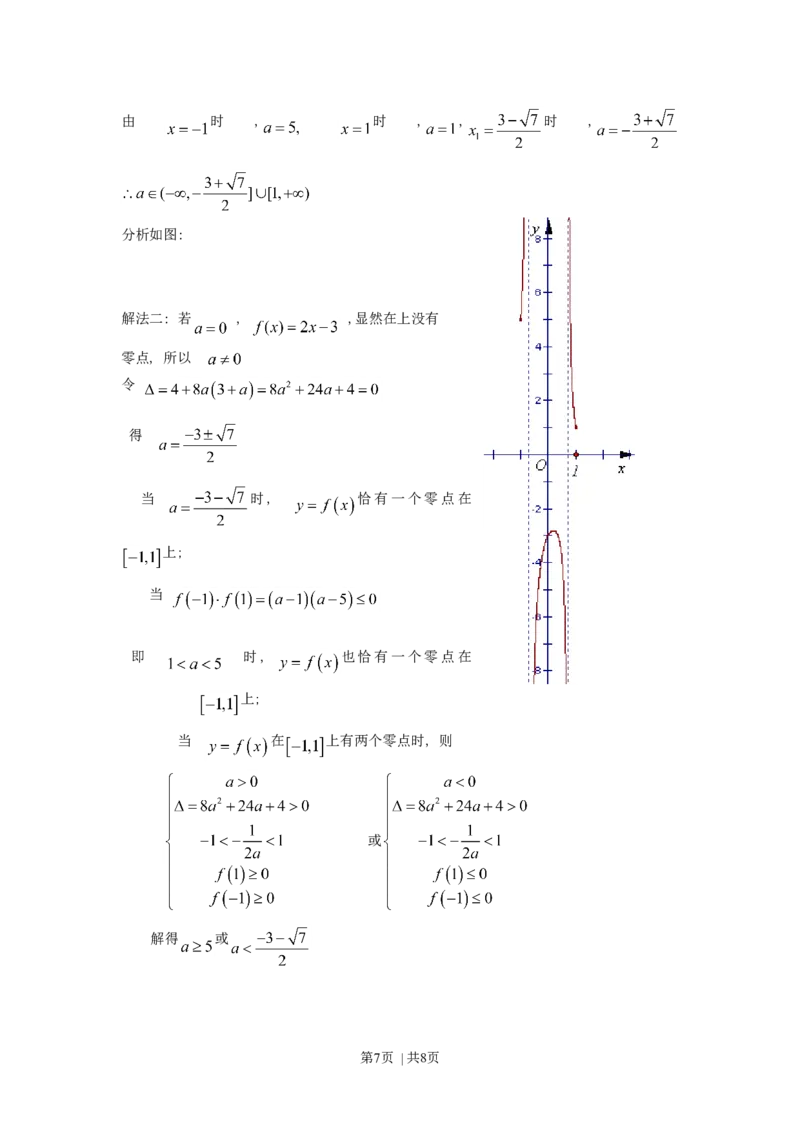
第6页 | 共8页由 时 , 时 , , 时 ,
分析如图:
解法二: 若 , ,显然在上没有
零点, 所以
令
得
当 时, 恰有一个零点在
上;
当
即 时, 也恰有一个零点在
上;
当 在 上有两个零点时, 则
或
解得 或
第7页 | 共8页因此 的取值范围是 或 ;
21解:(1) 由 得
(2)(数学归纳法)①当 时, 命题成立;
②假设当 时命题成立,即
,又等号成立时
时, 时命题成立;由①②知对任意 均有 .
(3)
同理
又
数列 是一个首项为 ,公比为2的等比数列;
.
第8页 | 共8页