文档内容
参考答案
1.A 【解析】|﹣6|=6,故选:A.
2.C 【解析】从上面看易得俯视图:
.故选:C.
1 3
3.B 【解析】A、x2•x3=x5,原计算错误,故此选项不符合题意;B、xy2- xy2= xy2,
4 4
原计算正确,故此选项符合题意;C、(x+y)2=x2+2xy+y2,原计算错误,故此选项不
符合题意;D、(2xy2)2=4xy4,原计算错误,故此选项不符合题意.故选:B.
4.D 【解析】∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠BEF=180°﹣64°=116°;
∵EG平分∠BEF,
∴∠GEB=58°.故选:D.
1
5.C 【解析】∵反比例函数y= (x<0)中,k=1>0,
x
∴该函数图象在第三象限,故选:C.
6.A 【解析】∵DE∥AB,
CE CD 3
∴ = = ,
AE BD 2
CE 3
∴ 的值为 ,故选:A.
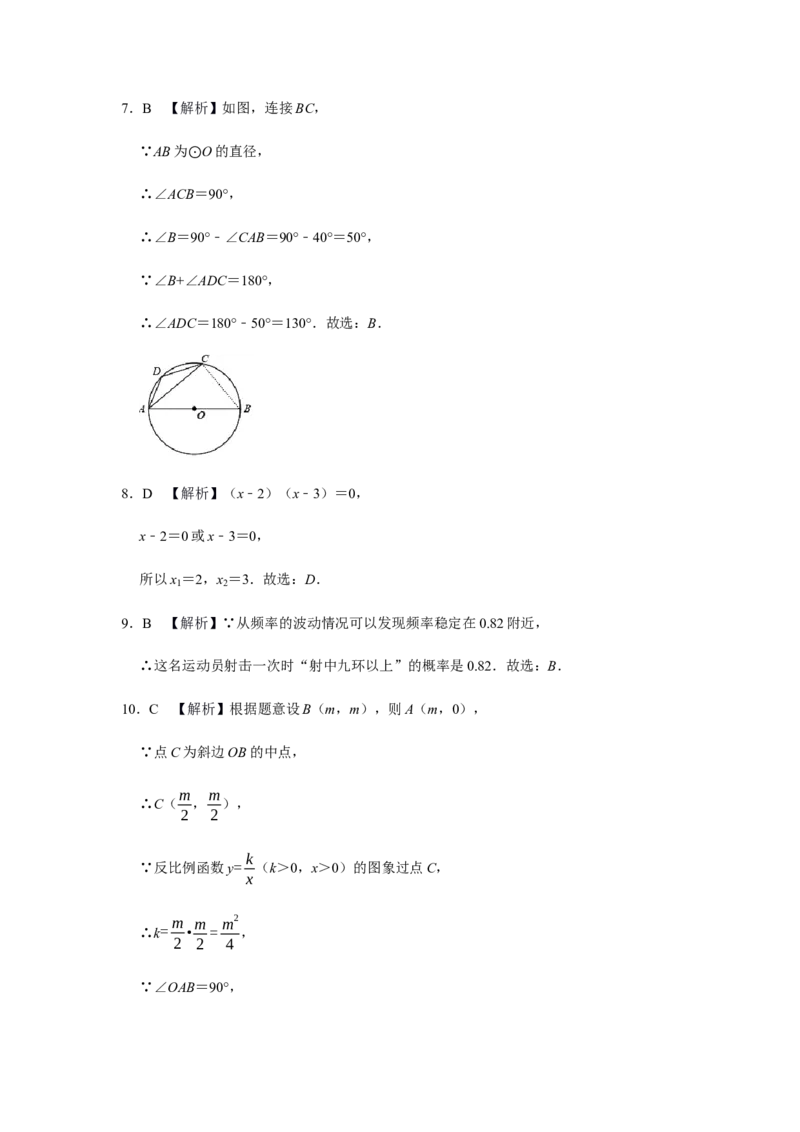
CA 57.B 【解析】如图,连接BC,
∵AB为 O的直径,
⊙
∴∠ACB=90°,
∴∠B=90°﹣∠CAB=90°﹣40°=50°,
∵∠B+∠ADC=180°,
∴∠ADC=180°﹣50°=130°.故选:B.
8.D 【解析】(x﹣2)(x﹣3)=0,
x﹣2=0或x﹣3=0,
所以x =2,x =3.故选:D.
1 2
9.B 【解析】∵从频率的波动情况可以发现频率稳定在0.82附近,
∴这名运动员射击一次时“射中九环以上”的概率是0.82.故选:B.
10.C 【解析】根据题意设B(m,m),则A(m,0),
∵点C为斜边OB的中点,
m m
∴C( , ),
2 2
k
∵反比例函数y= (k>0,x>0)的图象过点C,
x
m m m2
∴k= • = ,
2 2 4
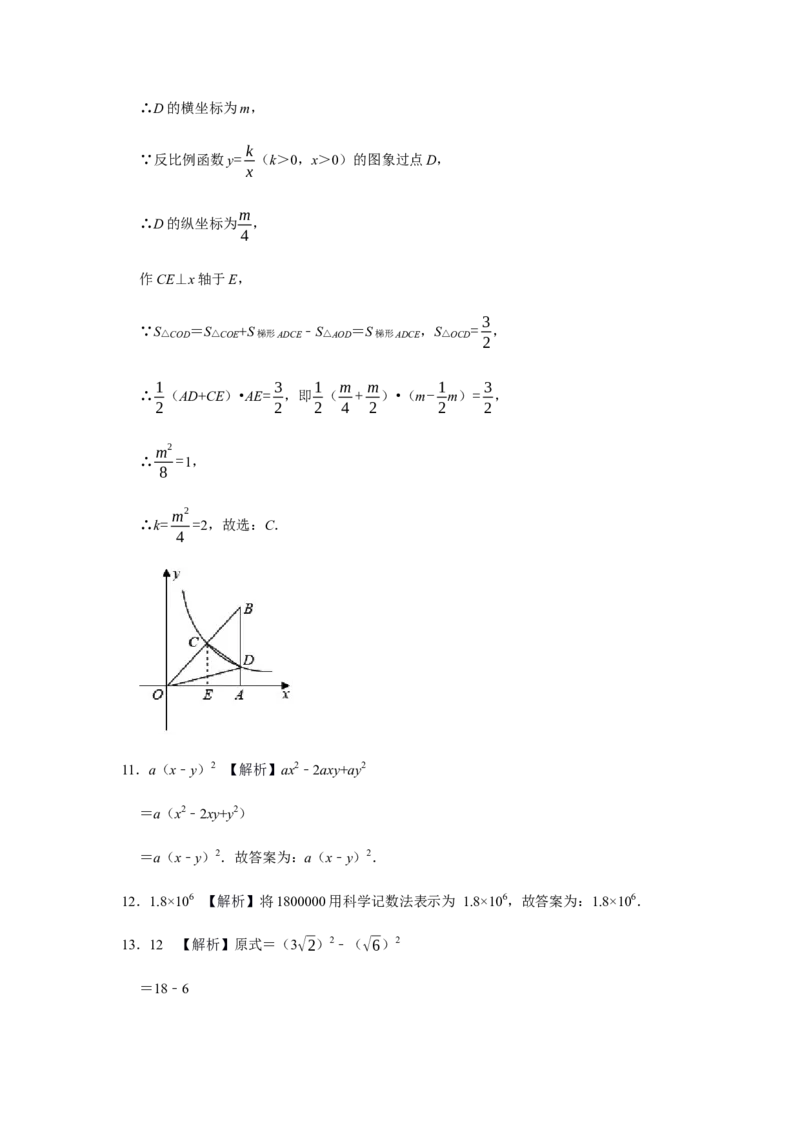
∵∠OAB=90°,∴D的横坐标为m,
k
∵反比例函数y= (k>0,x>0)的图象过点D,
x
m
∴D的纵坐标为 ,
4
作CE⊥x轴于E,
3
∵S△COD =S△COE +S梯形ADCE ﹣S△AOD =S梯形ADCE ,S△OCD = ,
2
1 3 1 m m 1 3
∴ (AD+CE)•AE= ,即 ( + )•(m- m)= ,
2 2 2 4 2 2 2
m2
∴ =1,
8
m2
∴k= =2,故选:C.
4
11.a(x﹣y)2 【解析】ax2﹣2axy+ay2
=a(x2﹣2xy+y2)
=a(x﹣y)2.故答案为:a(x﹣y)2.
12.1.8×106 【解析】将1800000用科学记数法表示为 1.8×106,故答案为:1.8×106.
13.12 【解析】原式=(3√2)2﹣(√6)2
=18﹣6=12.故答案为:12.
14.丙 【解析】∵平均成绩都是87.9分,S甲 2=3.83,S乙 2=2.71,S丙 2=1.52,
∴S丙 2<S乙 2<S甲 2,
∴丙选手的成绩更加稳定,
∴适合参加比赛的选手是丙,故答案为:丙.
15.15 【解析】∵圆锥的底面半径为3,高为4,
π
∴母线长为5,
∴圆锥的侧面积为: rl= ×3×5=15 ,故答案为:15
π π π π
16.4 【解析】∵OA=1,OB=2,
∴AC=2,BD=4,
1
∴菱形ABCD的面积为 ×2×4=4.故答案为:4.
2
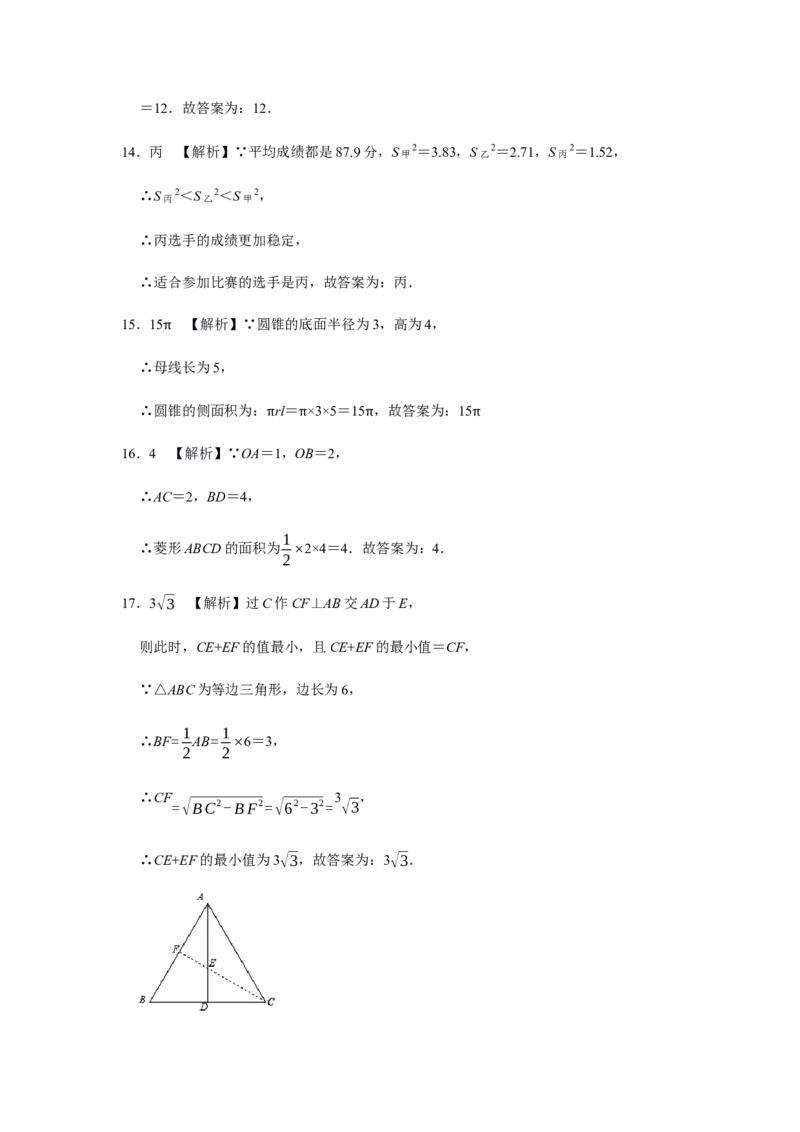
17.3√3 【解析】过C作CF⊥AB交AD于E,
则此时,CE+EF的值最小,且CE+EF的最小值=CF,
∵△ABC为等边三角形,边长为6,
1 1
∴BF= AB= ×6=3,
2 2
∴CF 3 ,
=√BC2-BF2=√62-32= √3
∴CE+EF的最小值为3√3,故答案为:3√3.18.√3(1+√3)2019 【解析】在Rt△OA B 中,∵∠OA B =90°,∠MON=60°,OA =
1 1 1 1 1
1,
∴A B =A A =OA •tan60°=√3,
1 1 1 2 1
∵A B ∥A B ,
1 1 2 2
∴A B OA ,
2 2= 2
A B OA
1 1 1
∴A B 1+√3,
2 2=
√3 1
∴A B =√3(1+√3),
2 2
同法可得,A B =√3(1+√3)2,
3 3
…
由此规律可知,A B =√3(1+√3)2019,故答案为√3(1+√3)2019.
2020 2020
4-x-x2+x x-1
19.【解答】原式= •
x-1 x-2
(2-x)(2+x) x-1
= •
x-1 x-2
=﹣2﹣x.
∵x≠1,x≠2,
∴在0≤x≤2的范围内的整数选x=0.
当x=0时,原式=﹣2﹣0=﹣2.
1
20.【解答】(1)李老师被分配到“洗手监督岗”的概率= ;
4
1
故答案为: ;
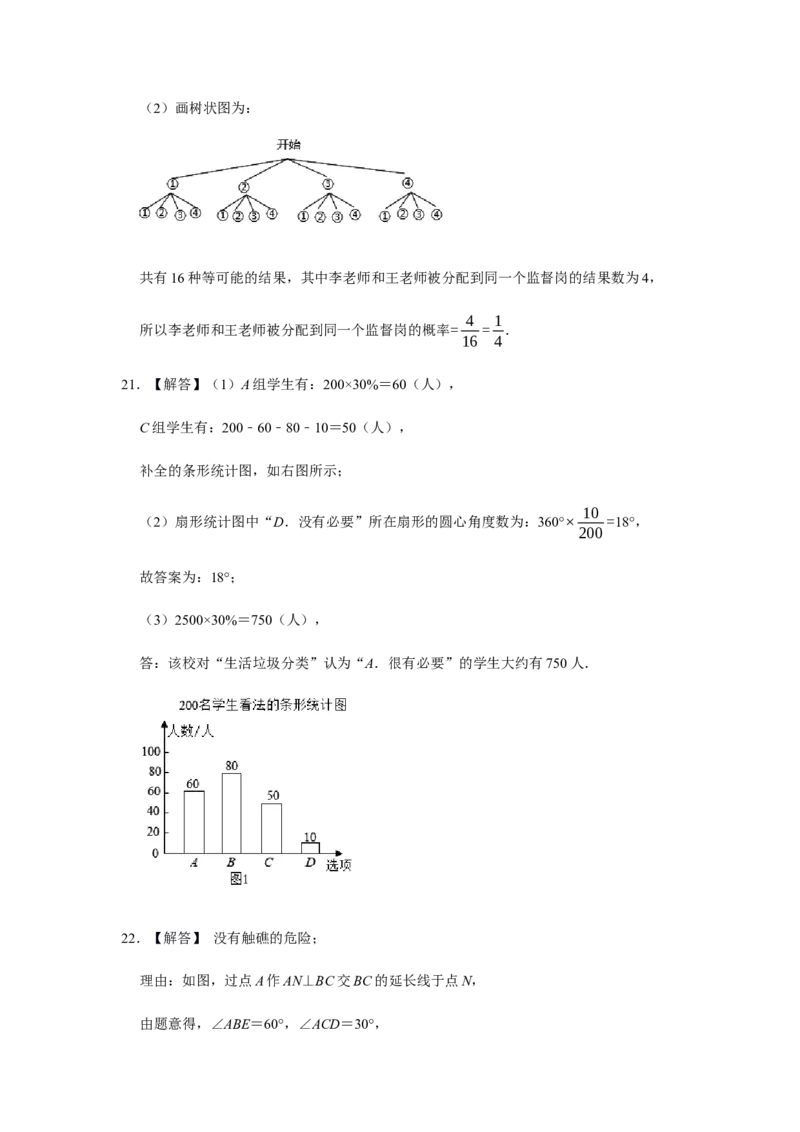
4(2)画树状图为:
共有16种等可能的结果,其中李老师和王老师被分配到同一个监督岗的结果数为4,
4 1
所以李老师和王老师被分配到同一个监督岗的概率= = .
16 4
21.【解答】(1)A组学生有:200×30%=60(人),
C组学生有:200﹣60﹣80﹣10=50(人),
补全的条形统计图,如右图所示;
10
(2)扇形统计图中“D.没有必要”所在扇形的圆心角度数为:360°× =18°,
200
故答案为:18°;
(3)2500×30%=750(人),
答:该校对“生活垃圾分类”认为“A.很有必要”的学生大约有750人.
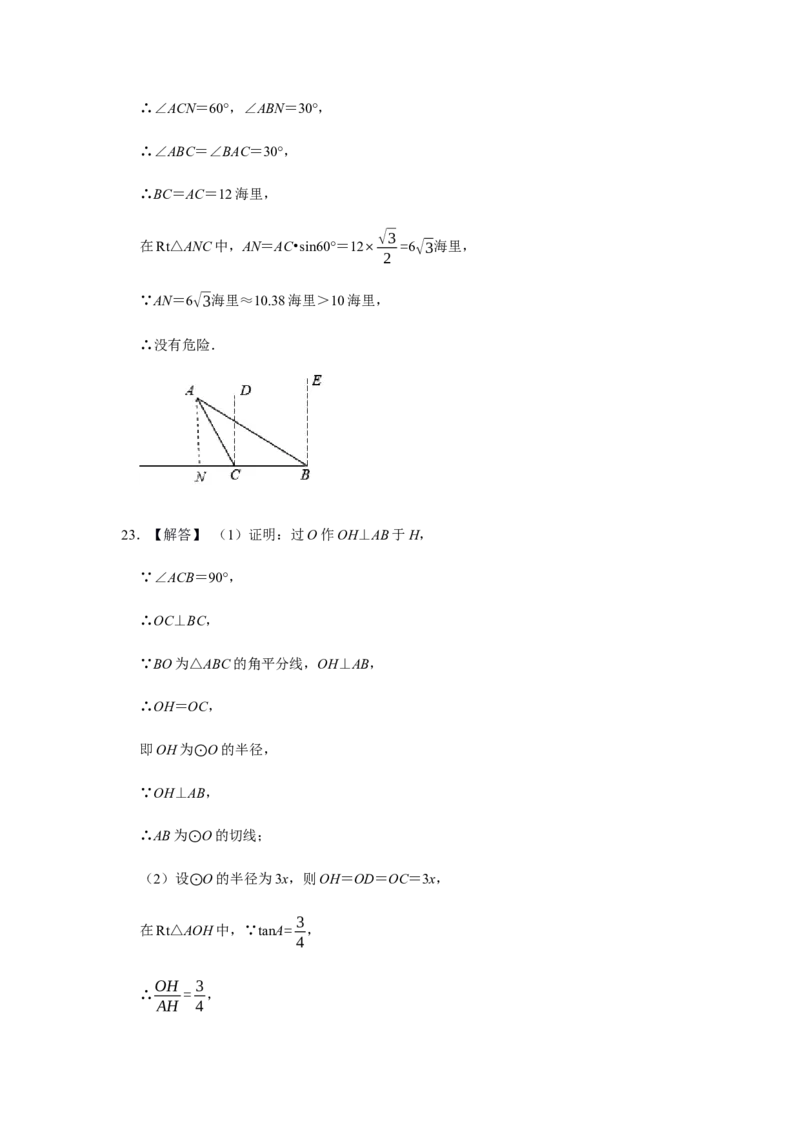
22.【解答】 没有触礁的危险;
理由:如图,过点A作AN⊥BC交BC的延长线于点N,
由题意得,∠ABE=60°,∠ACD=30°,∴∠ACN=60°,∠ABN=30°,
∴∠ABC=∠BAC=30°,
∴BC=AC=12海里,
√3
在Rt△ANC中,AN=AC•sin60°=12× =6√3海里,
2
∵AN=6√3海里≈10.38海里>10海里,
∴没有危险.
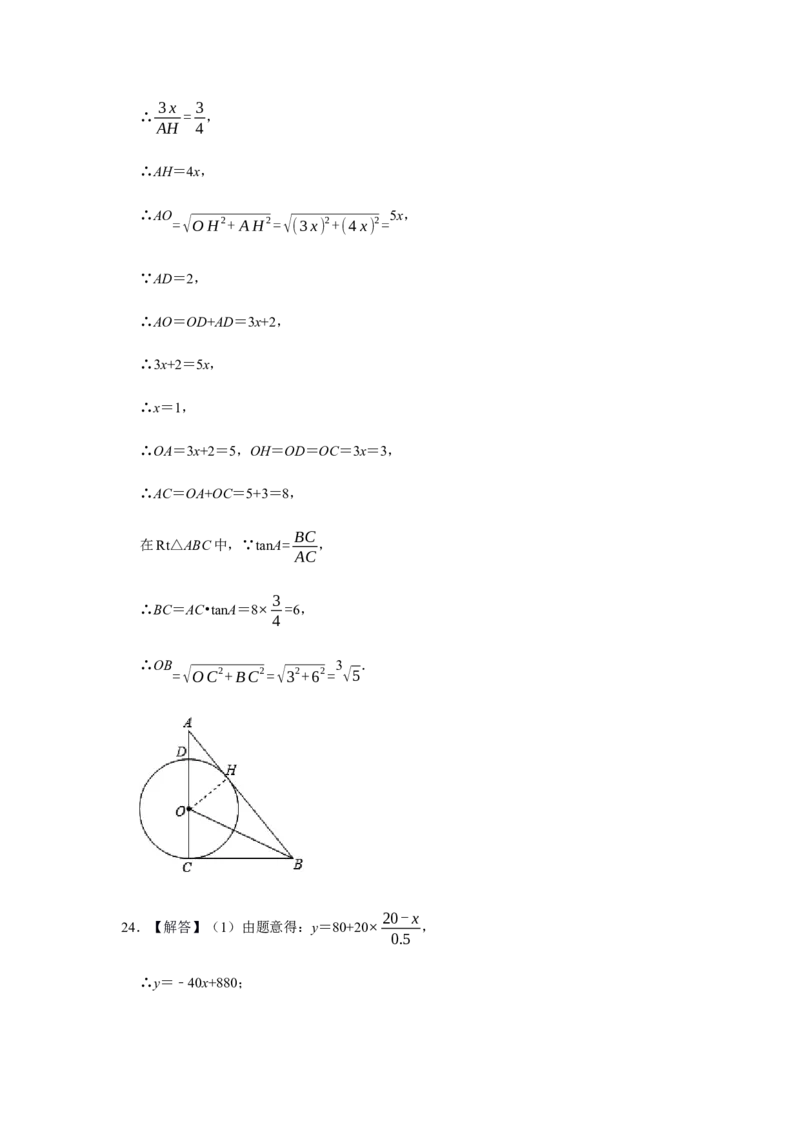
23.【解答】 (1)证明:过O作OH⊥AB于H,
∵∠ACB=90°,
∴OC⊥BC,
∵BO为△ABC的角平分线,OH⊥AB,
∴OH=OC,
即OH为 O的半径,
⊙
∵OH⊥AB,
∴AB为 O的切线;
⊙
(2)设 O的半径为3x,则OH=OD=OC=3x,
⊙
3
在Rt△AOH中,∵tanA= ,
4
OH 3
∴ = ,
AH 43x 3
∴ = ,
AH 4
∴AH=4x,
∴AO 5x,
=√OH2+AH2=√(3x) 2+(4x) 2=
∵AD=2,
∴AO=OD+AD=3x+2,
∴3x+2=5x,
∴x=1,
∴OA=3x+2=5,OH=OD=OC=3x=3,
∴AC=OA+OC=5+3=8,
BC
在Rt△ABC中,∵tanA= ,
AC
3
∴BC=AC•tanA=8× =6,
4
∴OB 3 .
=√OC2+BC2=√32+62= √5
20-x
24.【解答】(1)由题意得:y=80+20× ,
0.5
∴y=﹣40x+880;(2)设每天的销售利润为w元,则有:
w=(﹣40x+880)(x﹣16)
=﹣40(x﹣19)2+360,
∵a=﹣40<0,
∴二次函数图象开口向下,
∴当x=19时,w有最大值,最大值为360元.
答:当销售单价为19元时,销售这款“免洗洗手液”每天的销售利润最大,最大利润
为880元.
25.【解答】(1)AE=AF.
∵AD=AB,四边形ABCD矩形,
∴四边形ABCD是正方形,
∴∠BAD=90°,
∵AF⊥AE,
∴∠EAF=90°,
∴∠EAB=∠FAD,
∴△EAB≌△FAD(AAS),
∴AF=AE;
故答案为:AF=AE.
(2)AF=kAE.
证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠ADF=90°,
∴∠FAD+∠FAB=90°,∵AF⊥AE,
∴∠EAF=90°,
∴∠EAB+∠FAB=90°,
∴∠EAB=∠FAD,
∵∠ABE+∠ABC=180°,
∴∠ABE=180°﹣∠ABC=180°﹣90°=90°,
∴∠ABE=∠ADF.
∴△ABE∽△ADF,
AB AE
∴ = ,
AD AF
∵AD=kAB,
AB 1
∴ = ,
AD k
AE 1
∴ = ,
AF k
∴AF=kAE.
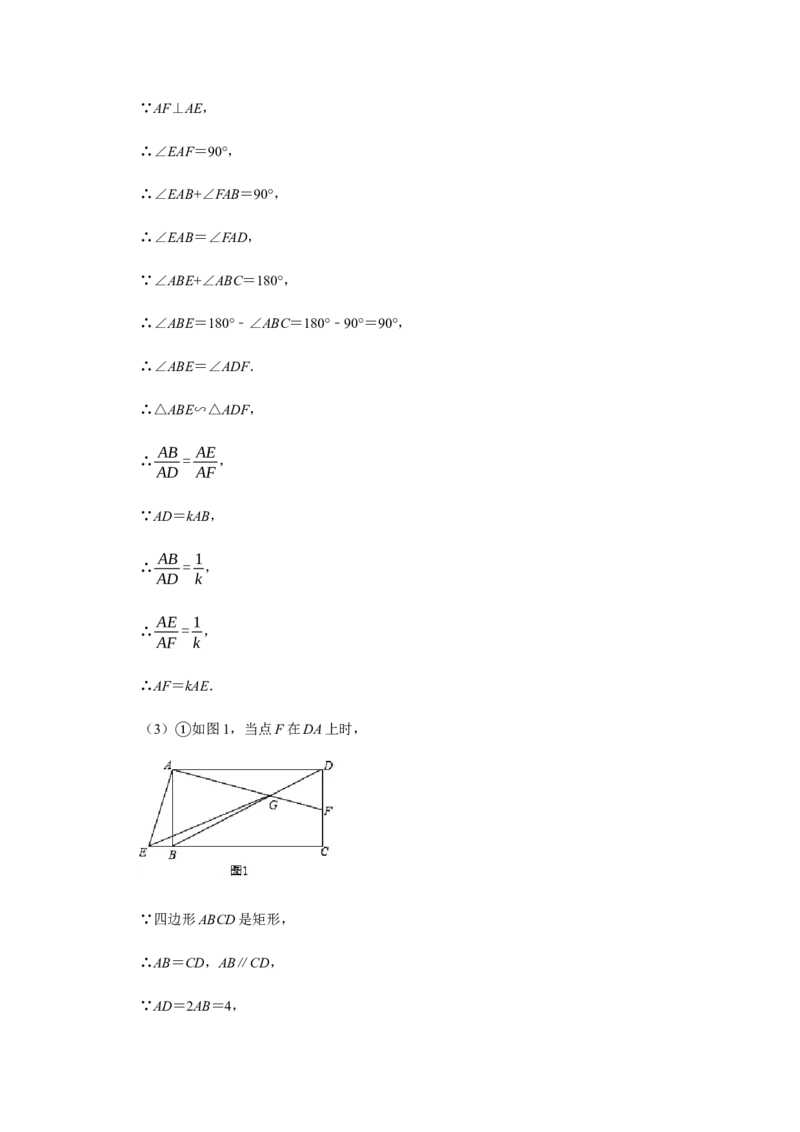
(3) 如图1,当点F在DA上时,
①
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AD=2AB=4,∴AB=2,
∴CD=2,
∵CF=1,
∴DF=CD﹣CF=2﹣1=1.
在Rt△ADF中,∠ADF=90°,
∴AF ,
=√AD2+DF2=√42+12=√17
∵DF∥AB,
∴∠GDF=∠GBA,∠GFD=∠GAB,
∴△GDF∽△GBA,
GF DF 1
∴ = = ,
GA BA 2
∵AF=GF+AG,
2 2
∴AG= AF= √17.
3 3
∵△ABE∽△ADF,
AE AB 2 1
∴ = = = ,
AF AD 4 2
1 1 √17
∴AE= AF= ×√17= .
2 2 2
在Rt△EAG中,∠EAG=90°,
∴EG √ √17 2√17 5√17,
=√AE2+AG2=
( )
2+(
)
2=
2 3 6
如图2,当点F在DC的延长线上时,DF=CD+CF=2+1=3,
②在Rt△ADF中,∠ADF=90°,
∴AF 5.
=√AD2+DF2=√42+32=
∵DF∥AB,
∵∠GAB=∠GFD,∠GBA=∠GDF,
∴△AGB∽△FGD,
AG AB 2
∴ = = ,
FG FD 3
∵GF+AG=AF=5,
∴AG=2,
∵△ABE∽△ADF,
AE AB 2 1
∴ = = = ,
AF AD 4 2
1 1 5
∴AE= AF= ×5= ,
2 2 2
在Rt△EAG中,∠EAG=90°,
√ 5 √41
∴EG=√AE2+AG2= ( ) 2+22= .
2 2
5√17 √41
综上所述,EG的长为 或 .
6 2
26.【解答】(1)y=ax2+bx﹣3=a(x+3)(x﹣1),解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3 ;
①
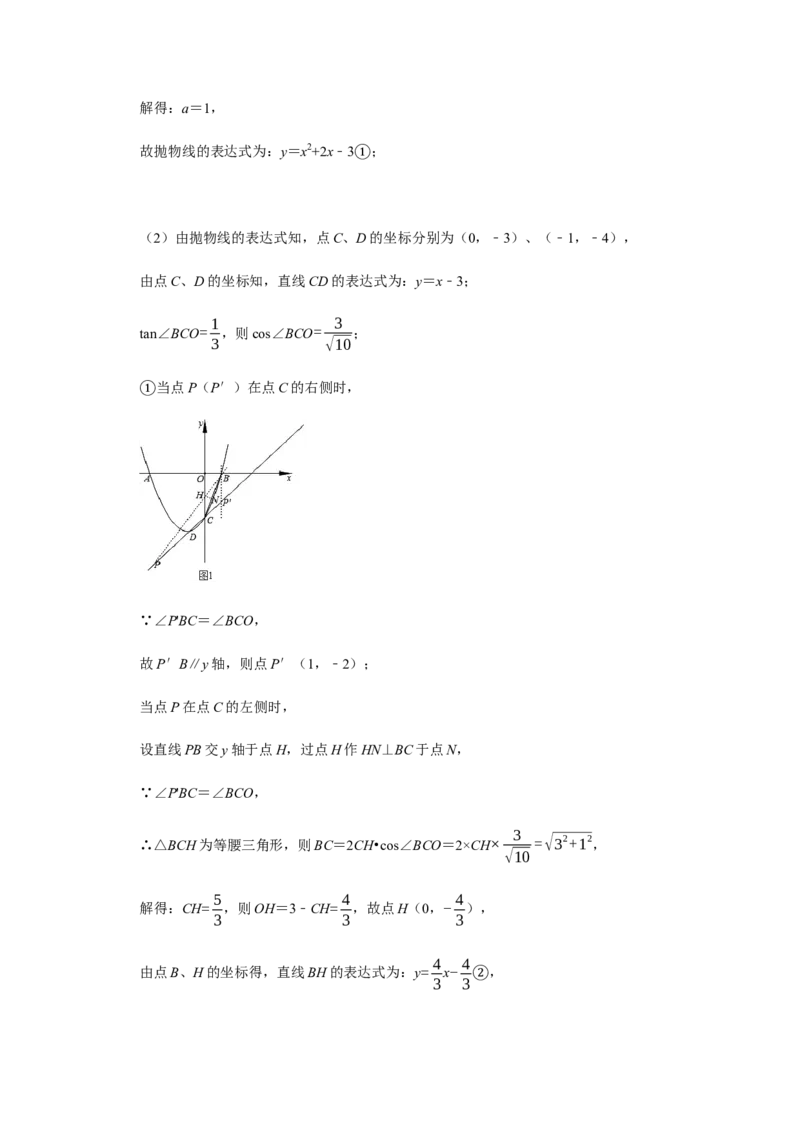
(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),
由点C、D的坐标知,直线CD的表达式为:y=x﹣3;
1 3
tan∠BCO= ,则cos∠BCO= ;
3 √10
当点P(P′)在点C的右侧时,
①
∵∠P'BC=∠BCO,
故P′B∥y轴,则点P′(1,﹣2);
当点P在点C的左侧时,
设直线PB交y轴于点H,过点H作HN⊥BC于点N,
∵∠P'BC=∠BCO,
3
∴△BCH为等腰三角形,则BC=2CH•cos∠BCO=2×CH× =√32+12 ,
√10
5 4 4
解得:CH= ,则OH=3﹣CH= ,故点H(0,- ),
3 3 3
4 4
由点B、H的坐标得,直线BH的表达式为:y= x- ,
3 3
②{x=-5
联立 并解得: ,
y=-8
①②
故点P的坐标为(1,﹣2)或(﹣5,﹣8);
1
∵∠PAB=∠BCO,而tan∠BCO= ,
3
②
1
故设直线AP的表达式为:y= x+s,将点A的坐标代入上式并解得:s=1,
3
1
故直线AP的表达式为:y= x+1,
3
4
{x=
联立 并解得: 3 ,故点N(4,13);
13 3 9
y=
①③
9
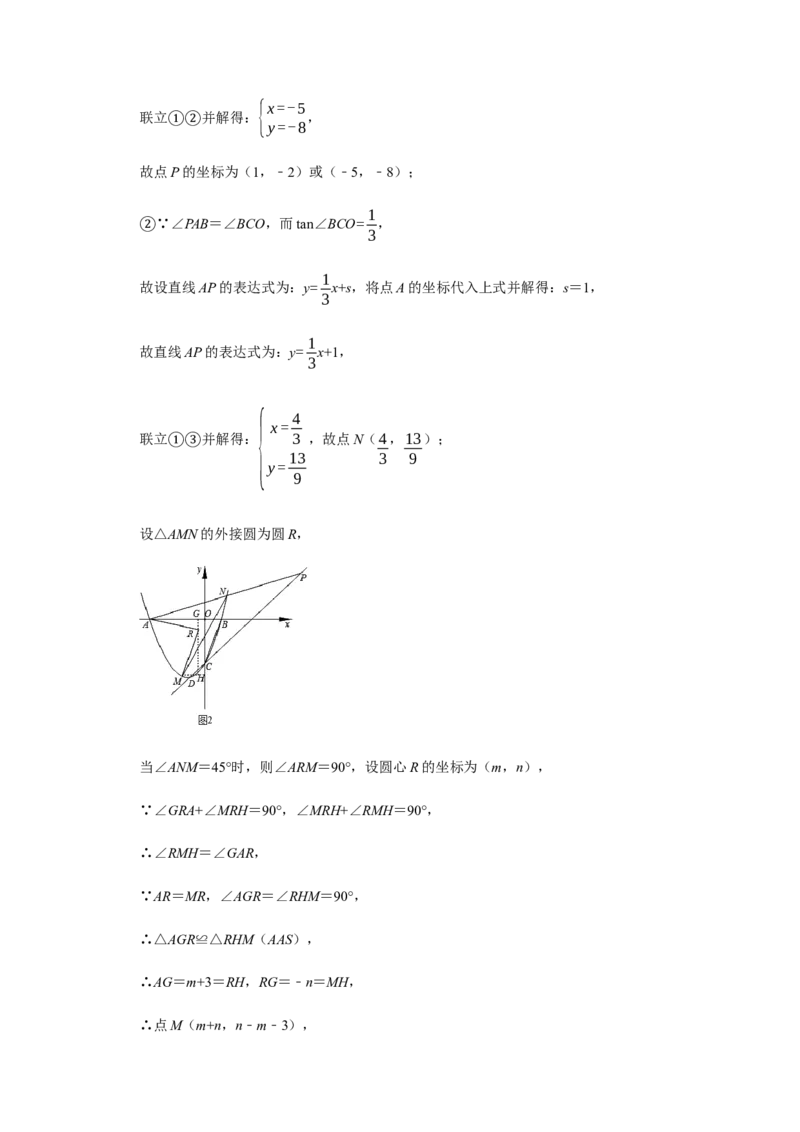
设△AMN的外接圆为圆R,
当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),
∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,
∴∠RMH=∠GAR,
∵AR=MR,∠AGR=∠RHM=90°,
∴△AGR≌△RHM(AAS),
∴AG=m+3=RH,RG=﹣n=MH,
∴点M(m+n,n﹣m﹣3),将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3 ,
③
4 13
由题意得:AR=NR,即(m+3)2=(m- )2+( )2 ,
3 9
④
2
{m=-
联立 并解得: 9 ,
10
n=-
③④
9
4 35
故点M(- ,- ).
3 9