文档内容
2021年新疆生产建设兵团中考数学试卷
一、单项选择题(本大题共9小题,每小题5分,共45分,请按答题卷中的要求作答)
1.下列实数是无理数的是( )
A.﹣2 B.1 C. D.2
2.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
3.不透明的袋子中有3个白球和2个红球,这些球除颜色外无其他差别,从袋子中随机摸
出1个球,恰好是白球的概率为( )
A. B. C. D.
4.下列运算正确的是( )
A.2x2+3x2=5x2 B.x2•x4=x8
C.x6÷x2=x3 D.(xy2)2=xy4
5.如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
6.一元二次方程x2﹣4x+3=0的解为( )
A.x =﹣1,x =3 B.x =1,x =3
1 2 1 2
C.x =1,x =﹣3 D.x =﹣1,x =﹣3
1 2 1 2
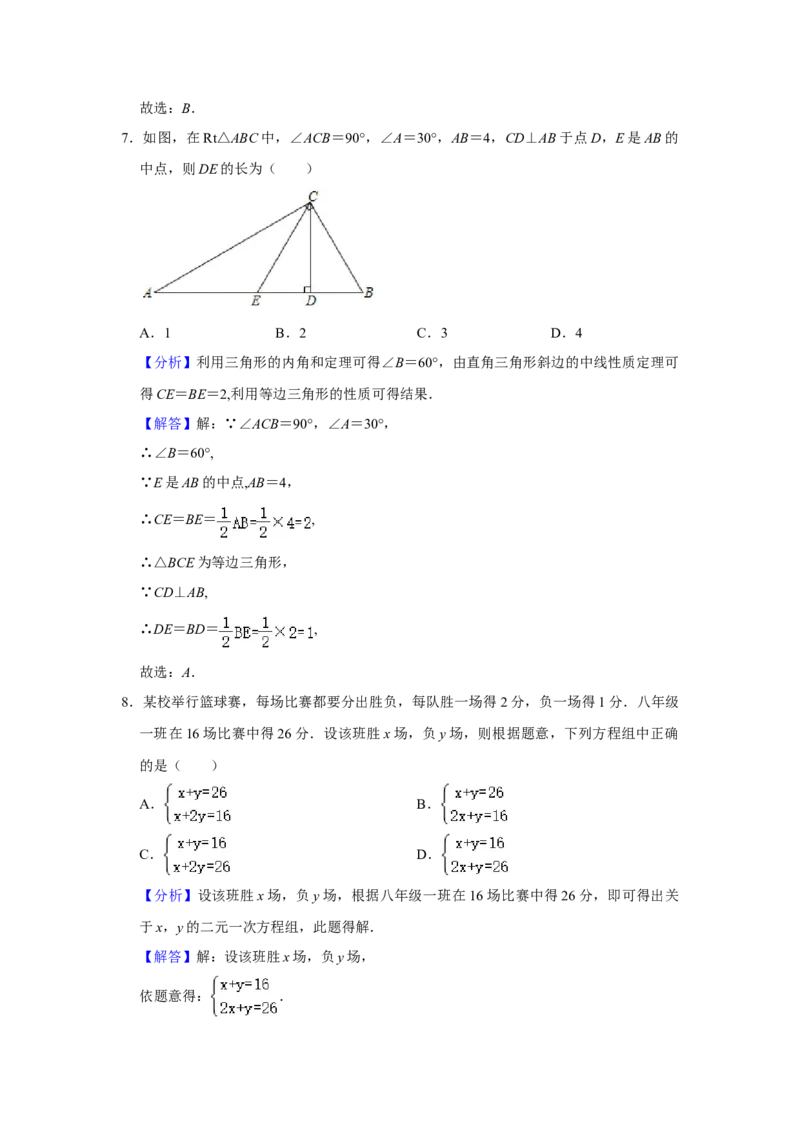
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的
中点,则DE的长为( )A.1 B.2 C.3 D.4
8.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级
一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确
的是( )
A. B.
C. D.
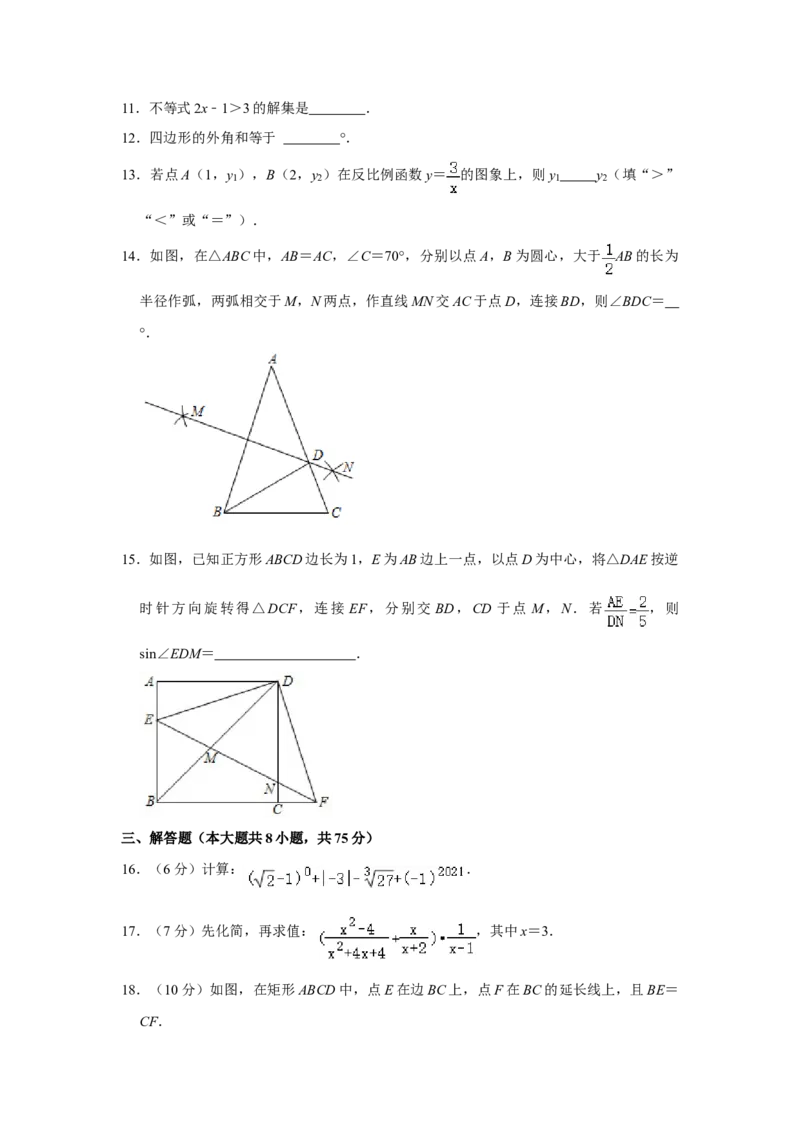
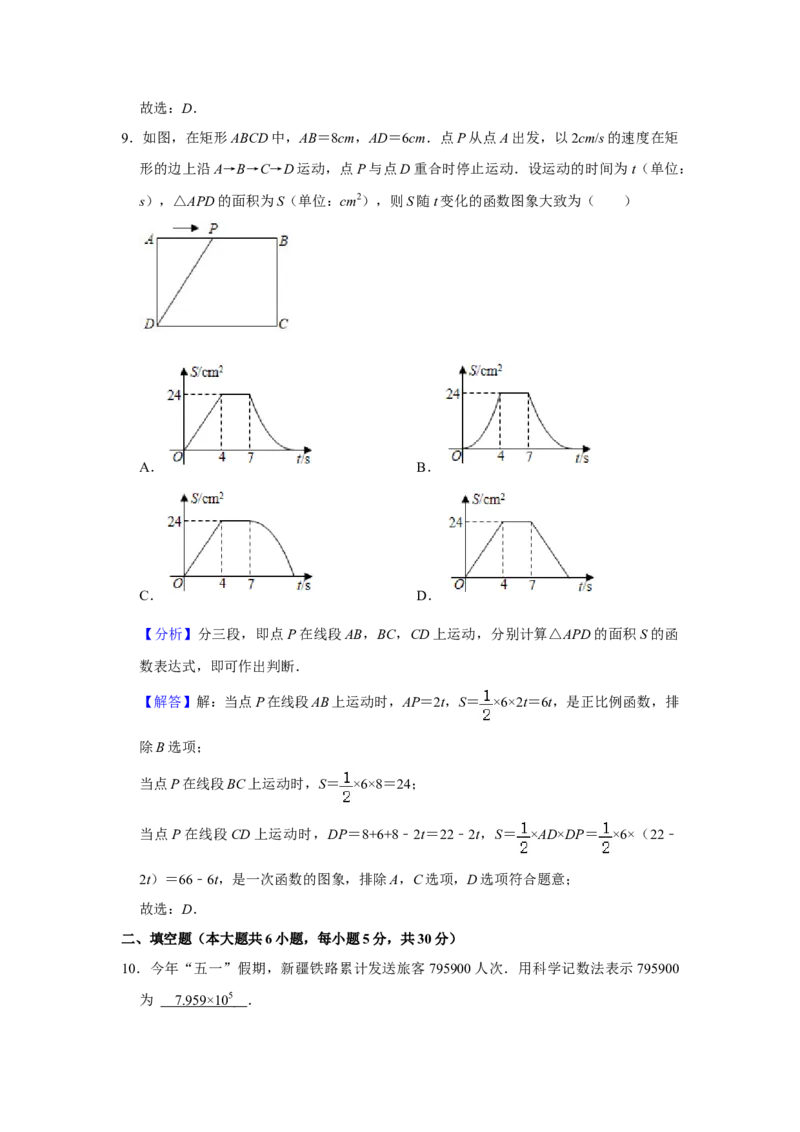
9.如图,在矩形ABCD中,AB=8cm,AD=6cm.点P从点A出发,以2cm/s的速度在矩
形的边上沿A→B→C→D运动,点P与点D重合时停止运动.设运动的时间为t(单位:
s),△APD的面积为S(单位:cm2),则S随t变化的函数图象大致为( )
A. B.
C. D.
二、填空题(本大题共6小题,每小题5分,共30分)
10.今年“五一”假期,新疆铁路累计发送旅客795900人次.用科学记数法表示795900
为 .11.不等式2x﹣1>3的解集是 .
12.四边形的外角和等于 °.
13.若点A(1,y ),B(2,y )在反比例函数y= 的图象上,则y y (填“>”
1 2 1 2
“<”或“=”).
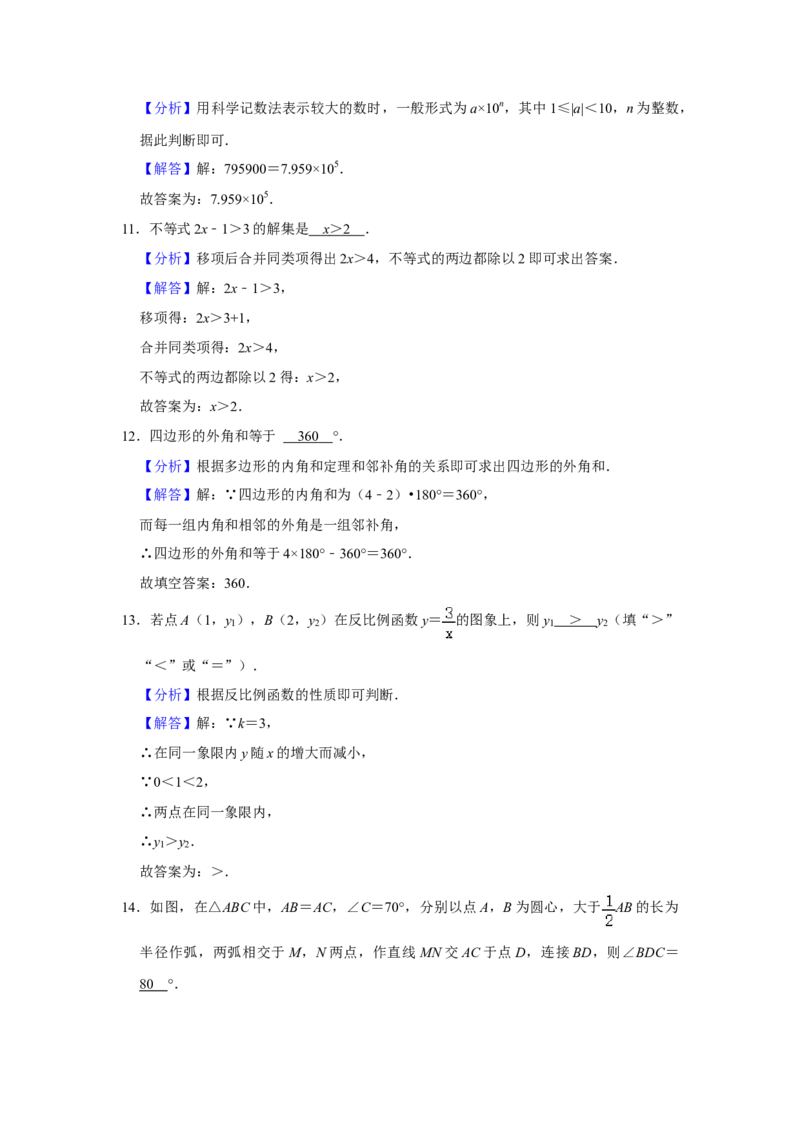
14.如图,在△ABC中,AB=AC,∠C=70°,分别以点A,B为圆心,大于 AB的长为
半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则∠BDC=
°.
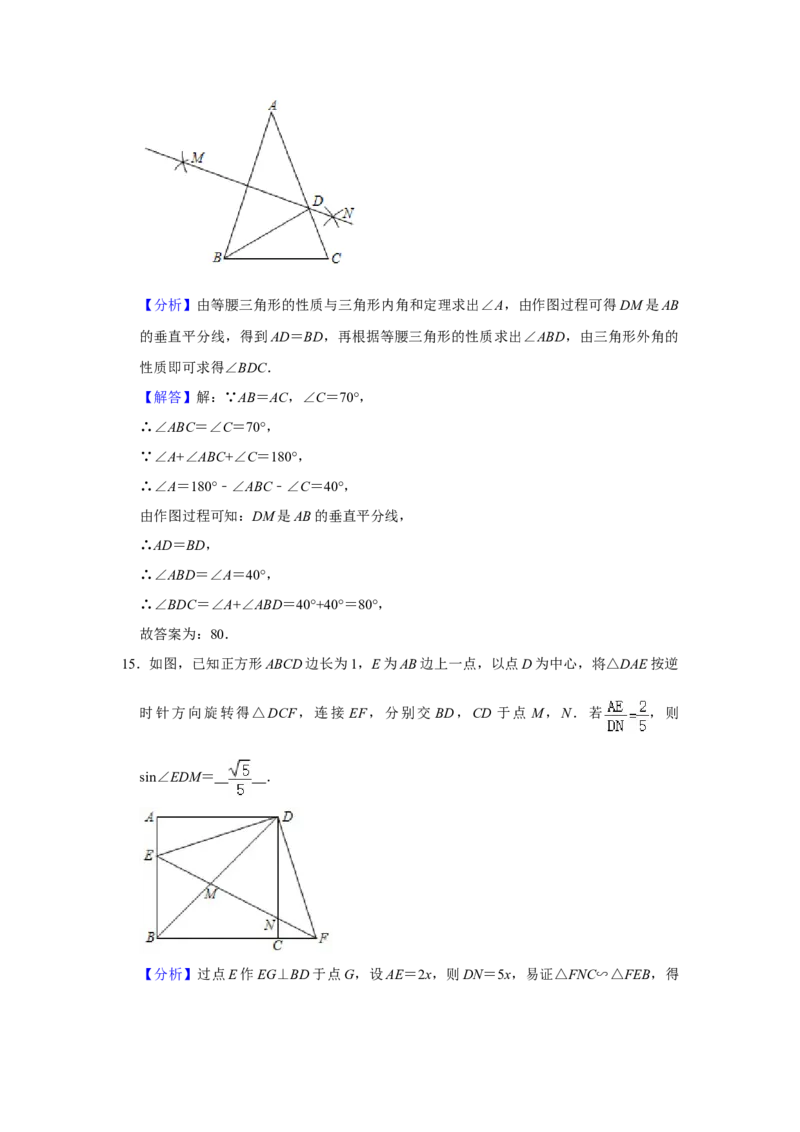
15.如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将△DAE按逆
时针方向旋转得△DCF,连接 EF,分别交 BD,CD 于点 M,N.若 ,则
sin∠EDM= .
三、解答题(本大题共8小题,共75分)
16.(6分)计算: .
17.(7分)先化简,再求值: ,其中x=3.
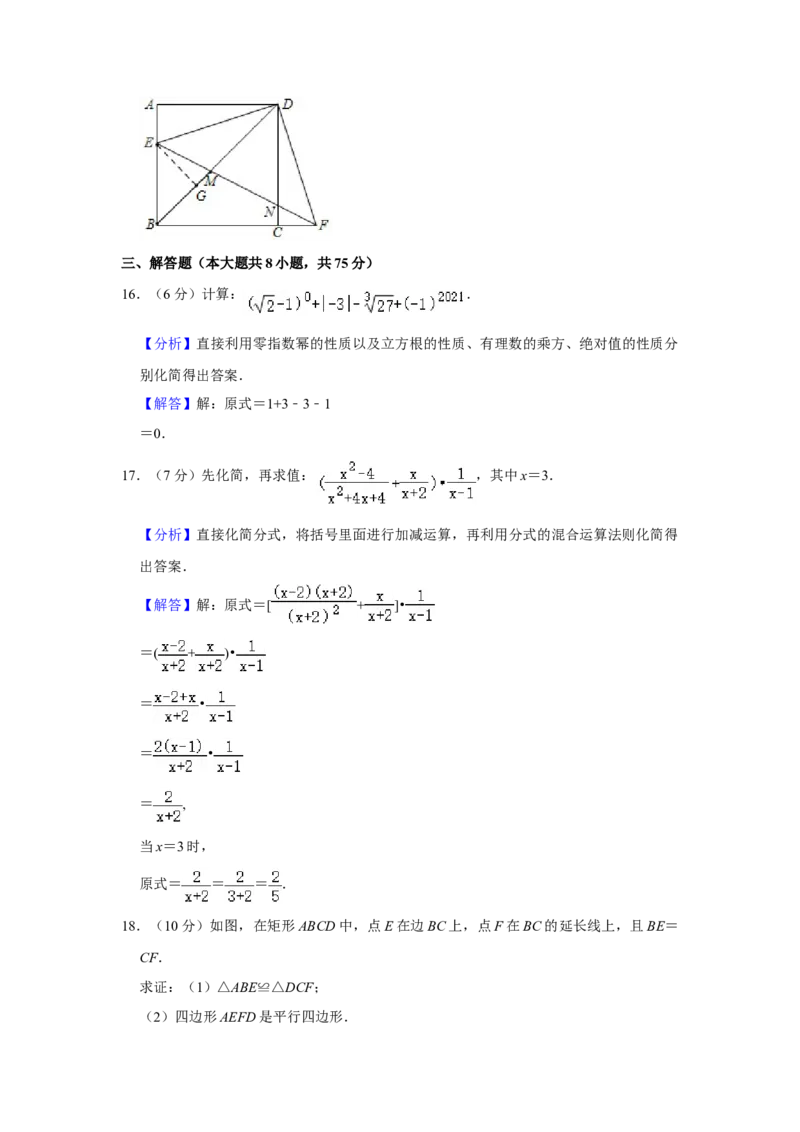
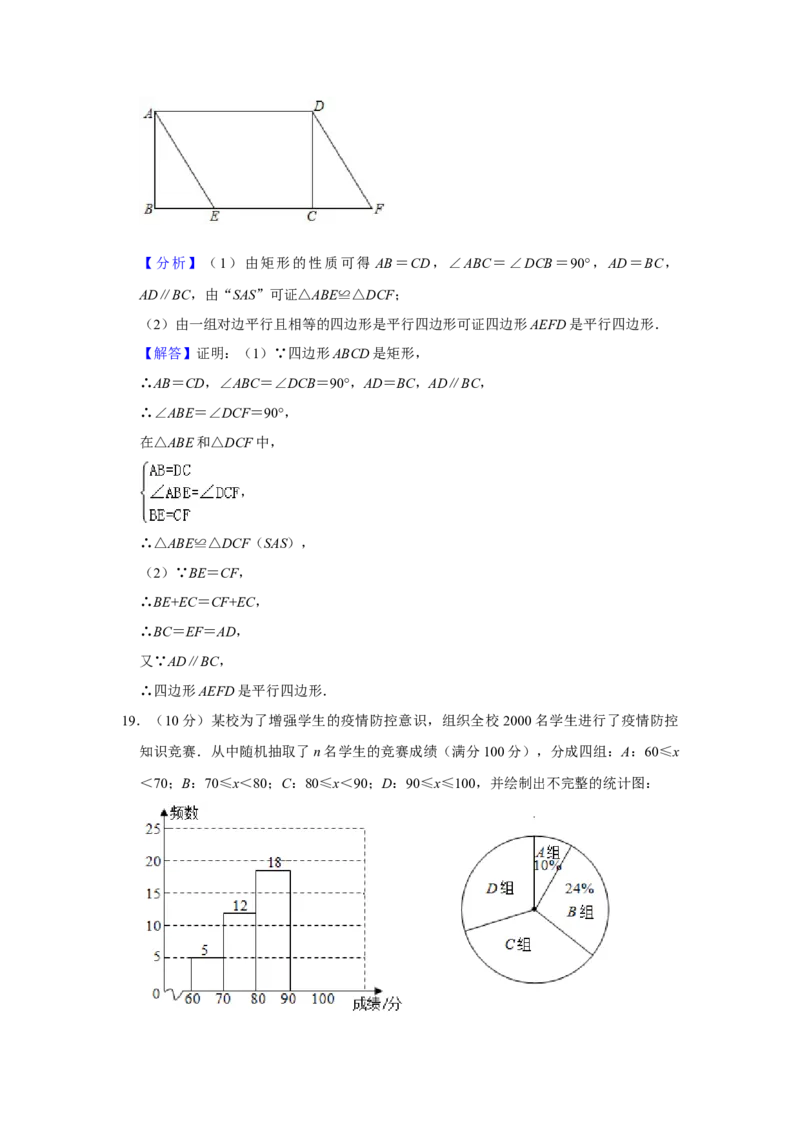
18.(10分)如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且BE=
CF.求证:(1)△ABE≌△DCF;
(2)四边形AEFD是平行四边形.
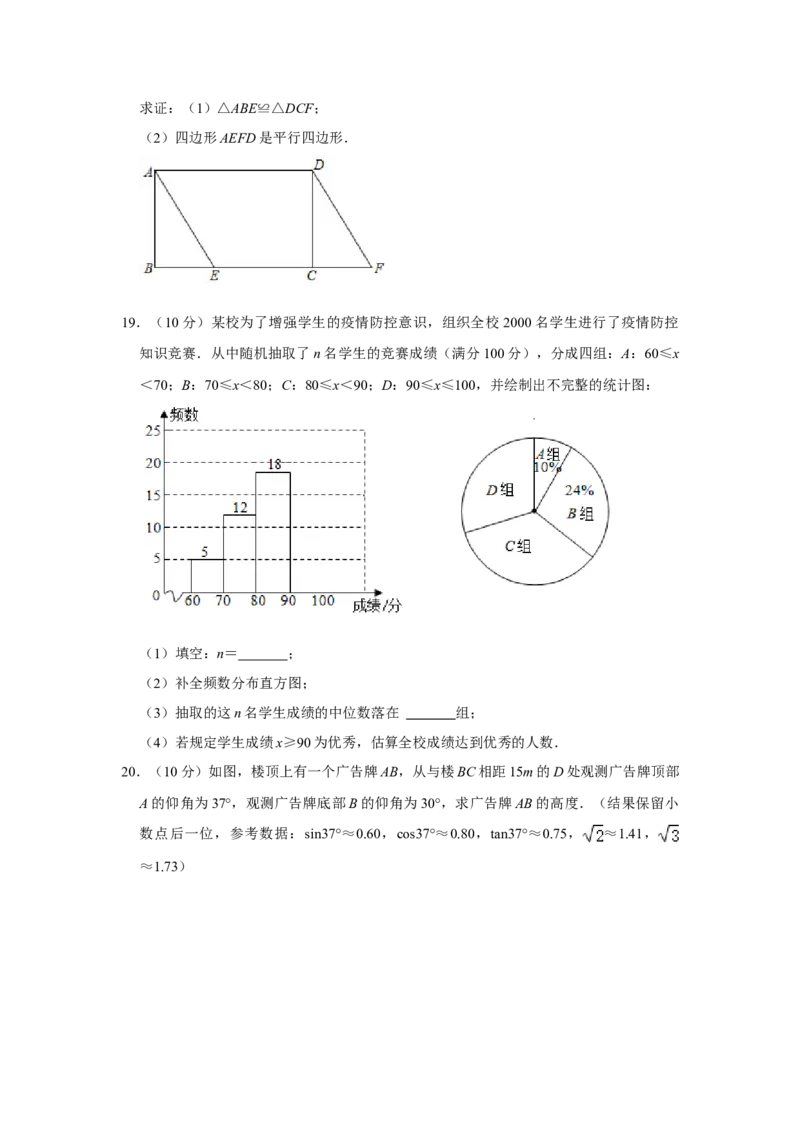
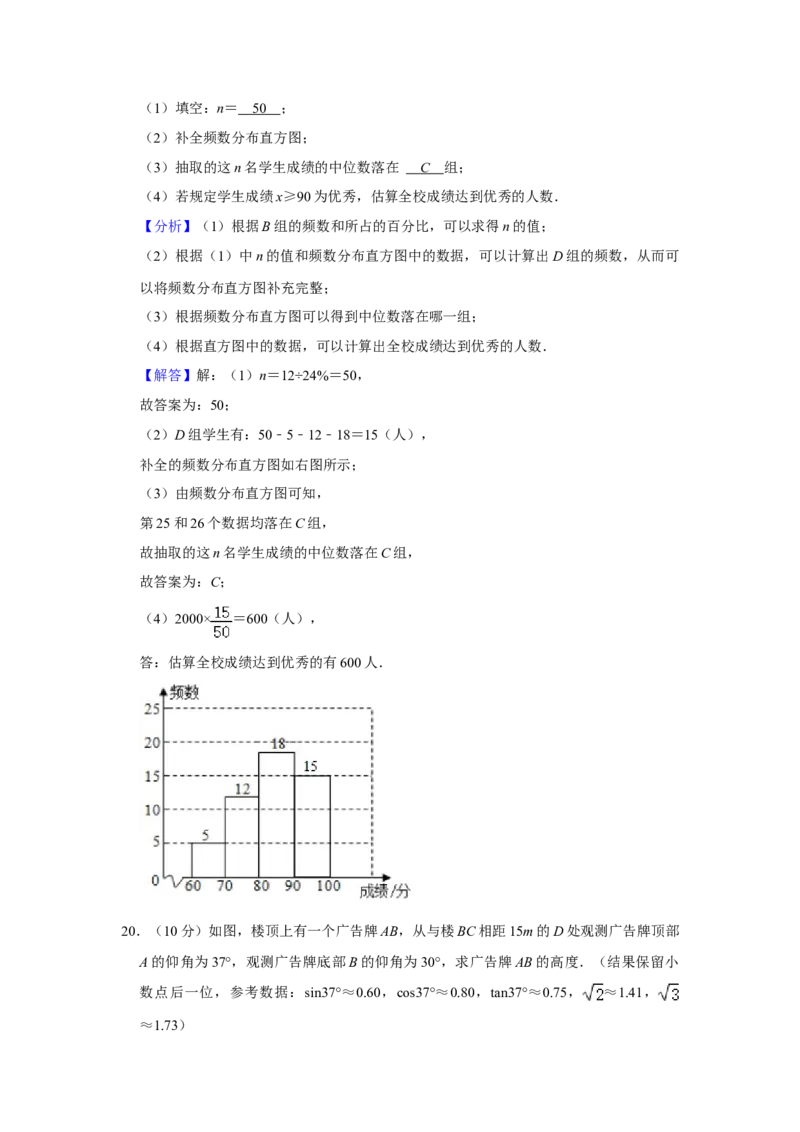
19.(10分)某校为了增强学生的疫情防控意识,组织全校 2000名学生进行了疫情防控
知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A:60≤x
<70;B:70≤x<80;C:80≤x<90;D:90≤x≤100,并绘制出不完整的统计图:
(1)填空:n= ;
(2)补全频数分布直方图;
(3)抽取的这n名学生成绩的中位数落在 组;
(4)若规定学生成绩x≥90为优秀,估算全校成绩达到优秀的人数.
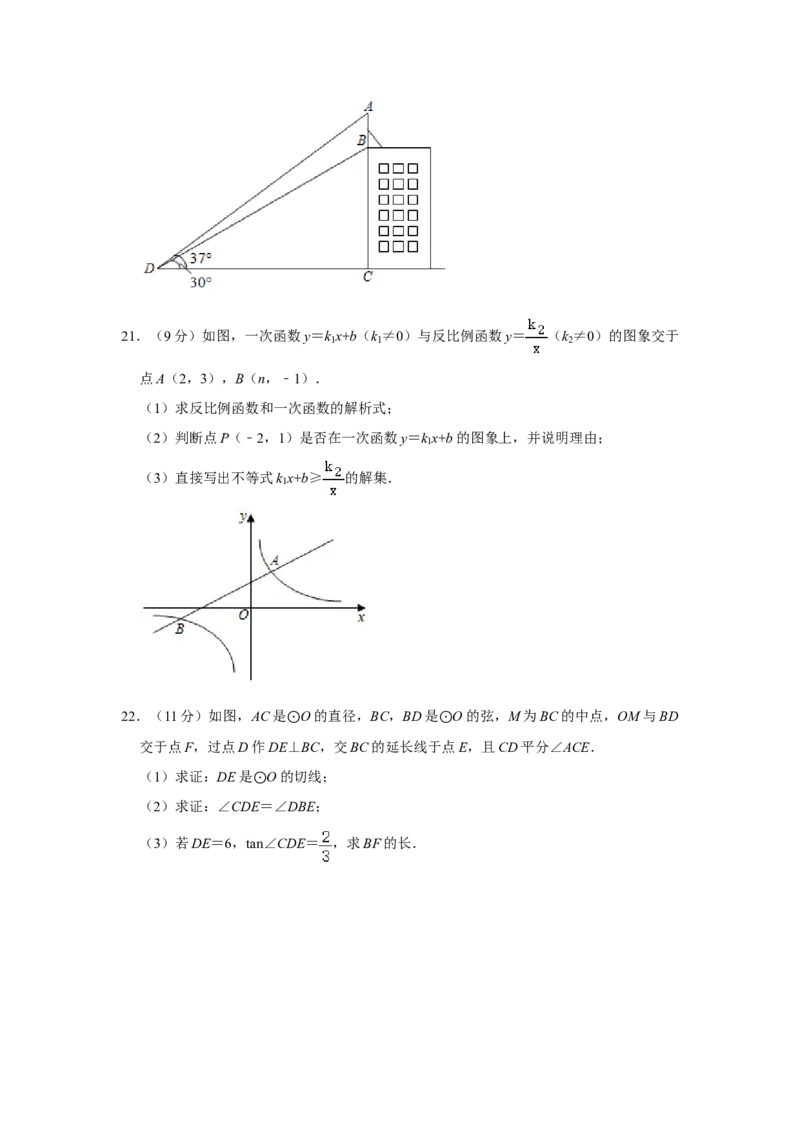
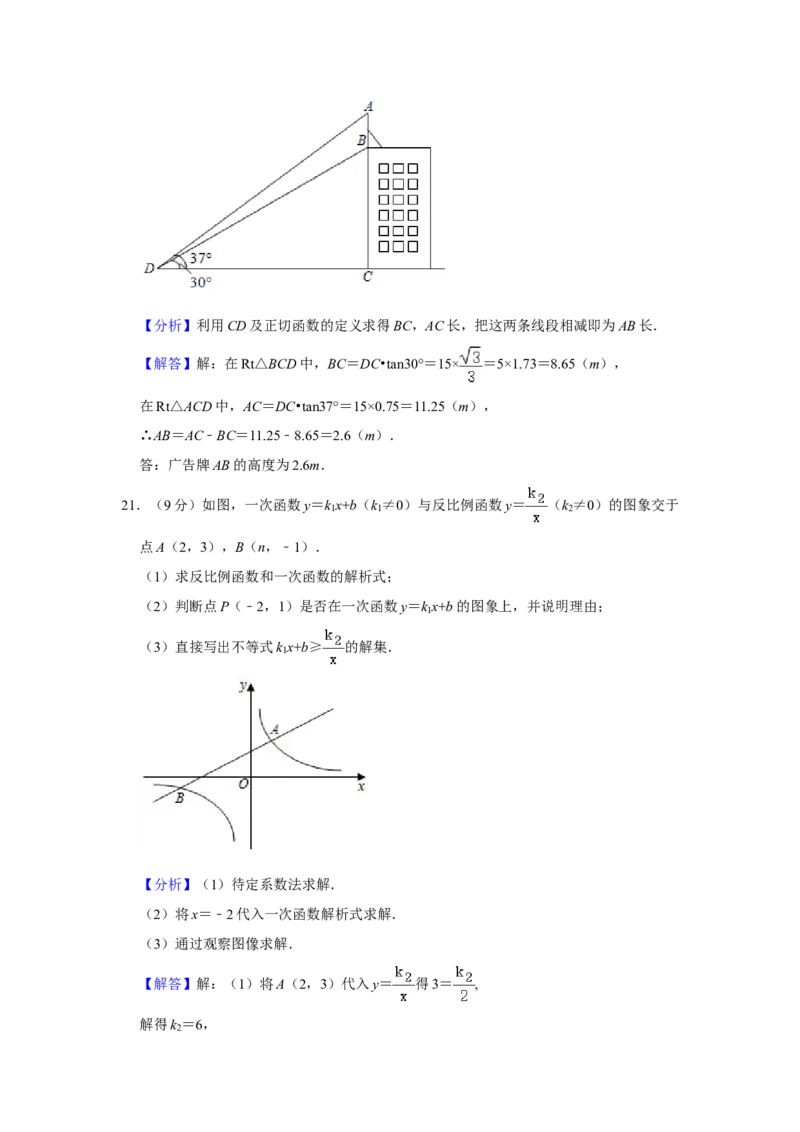
20.(10分)如图,楼顶上有一个广告牌AB,从与楼BC相距15m的D处观测广告牌顶部
A的仰角为37°,观测广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留小
数点后一位,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
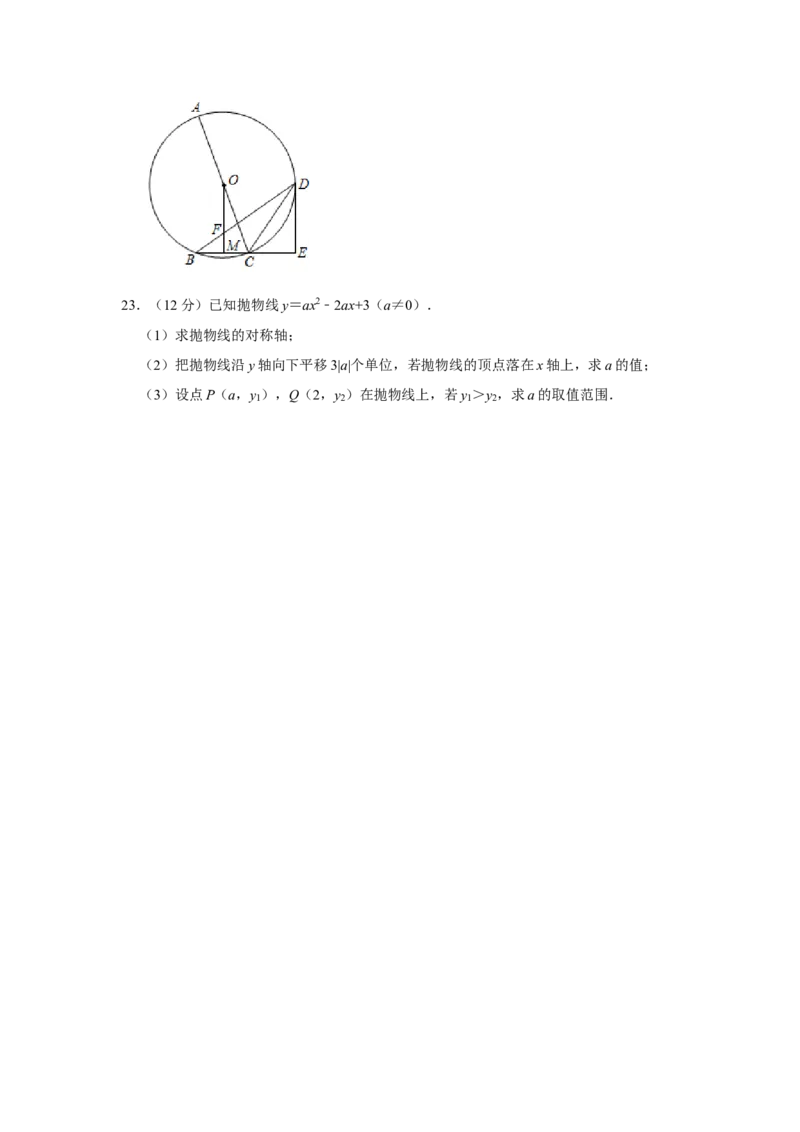
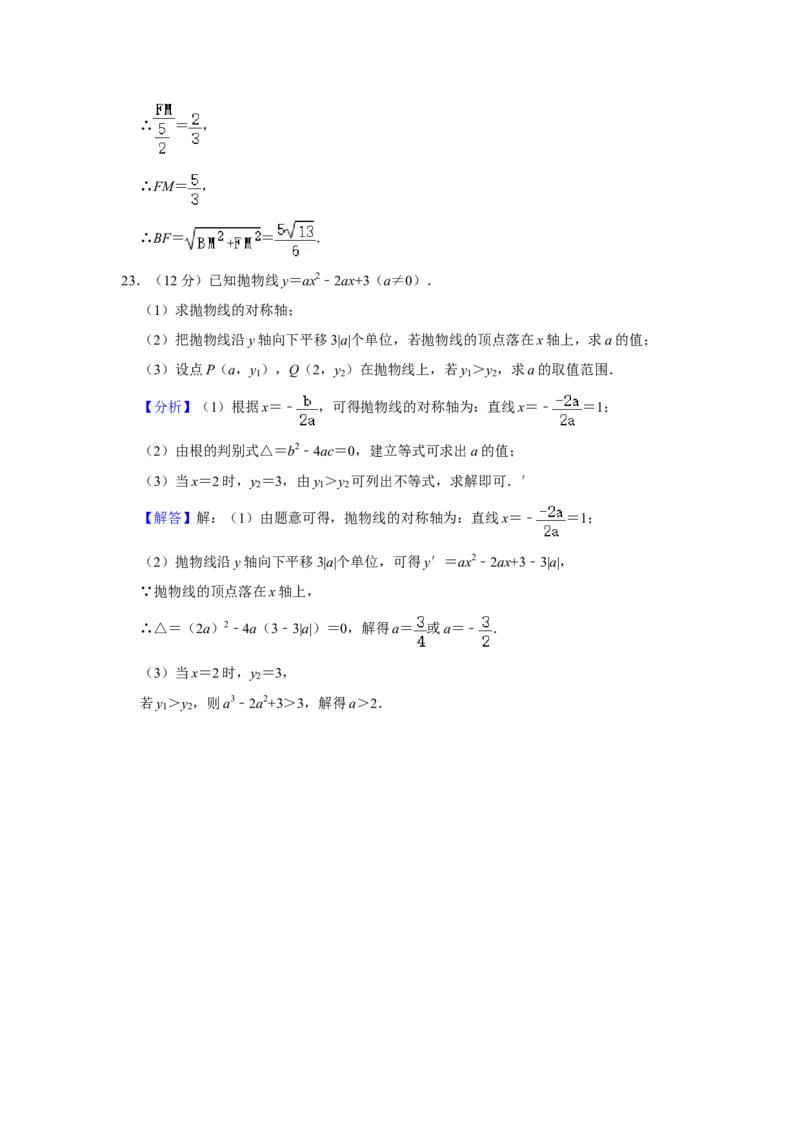
≈1.73)21.(9分)如图,一次函数y=k x+b(k ≠0)与反比例函数y= (k ≠0)的图象交于
1 1 2
点A(2,3),B(n,﹣1).
(1)求反比例函数和一次函数的解析式;
(2)判断点P(﹣2,1)是否在一次函数y=k x+b的图象上,并说明理由;
1
(3)直接写出不等式k x+b≥ 的解集.
1
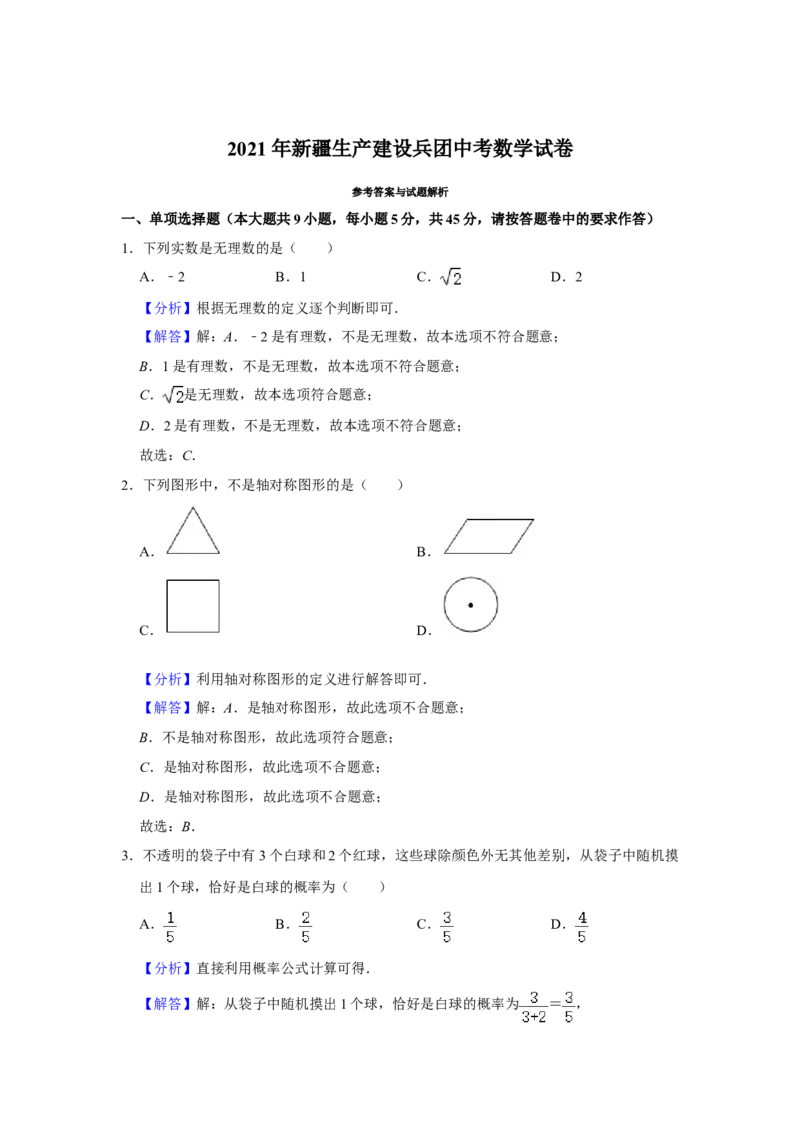
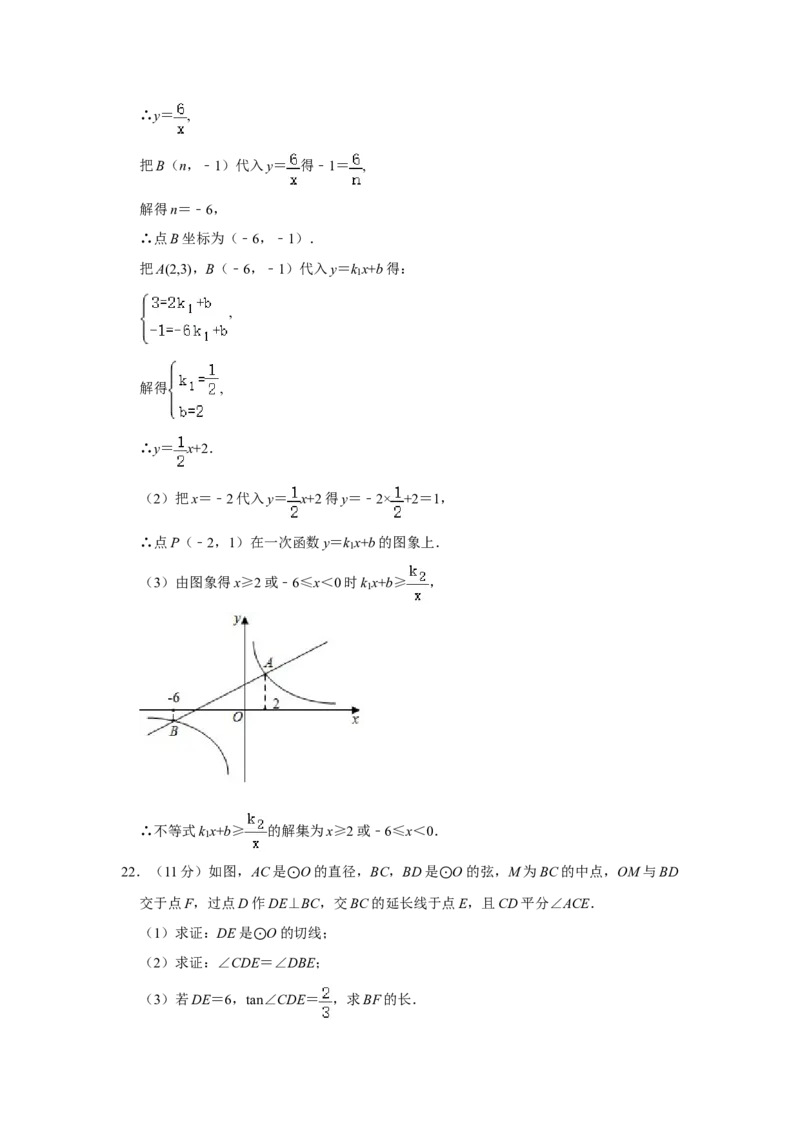
22.(11分)如图,AC是 O的直径,BC,BD是 O的弦,M为BC的中点,OM与BD
交于点F,过点D作DE⊙⊥BC,交BC的延长线于⊙点E,且CD平分∠ACE.
(1)求证:DE是 O的切线;
(2)求证:∠CDE⊙=∠DBE;
(3)若DE=6,tan∠CDE= ,求BF的长.23.(12分)已知抛物线y=ax2﹣2ax+3(a≠0).
(1)求抛物线的对称轴;
(2)把抛物线沿y轴向下平移3|a|个单位,若抛物线的顶点落在x轴上,求a的值;
(3)设点P(a,y ),Q(2,y )在抛物线上,若y >y ,求a的取值范围.
1 2 1 22021年新疆生产建设兵团中考数学试卷
参考答案与试题解析
一、单项选择题(本大题共9小题,每小题5分,共45分,请按答题卷中的要求作答)
1.下列实数是无理数的是( )
A.﹣2 B.1 C. D.2
【分析】根据无理数的定义逐个判断即可.
【解答】解:A.﹣2是有理数,不是无理数,故本选项不符合题意;
B.1是有理数,不是无理数,故本选项不符合题意;
C. 是无理数,故本选项符合题意;
D.2是有理数,不是无理数,故本选项不符合题意;
故选:C.
2.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
【分析】利用轴对称图形的定义进行解答即可.
【解答】解:A.是轴对称图形,故此选项不合题意;
B.不是轴对称图形,故此选项符合题意;
C.是轴对称图形,故此选项不合题意;
D.是轴对称图形,故此选项不合题意;
故选:B.
3.不透明的袋子中有3个白球和2个红球,这些球除颜色外无其他差别,从袋子中随机摸
出1个球,恰好是白球的概率为( )
A. B. C. D.
【分析】直接利用概率公式计算可得.
【解答】解:从袋子中随机摸出1个球,恰好是白球的概率为 = ,故选:C.
4.下列运算正确的是( )
A.2x2+3x2=5x2 B.x2•x4=x8
C.x6÷x2=x3 D.(xy2)2=xy4
【分析】直接利用同底数幂的乘除运算法则以及合并同类项法则、幂的乘方运算法则分
别判断得出答案.
【解答】解:A.2x2+3x2=5x2,故此选项符合题意;
B.x2•x4=x6,故此选项不合题意;
C.x6÷x2=x4,故此选项不合题意;
D.(xy2)2=x2y4,故此选项不合题意;
故选:A.
5.如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
【分析】先根据平行线的性质,得出∠DAB的度数,再根据平角的定义,即可得出∠2
的度数.
【解答】解:∵DE∥BC,
∴∠DAB=∠B=60°,
∴∠2=180°﹣∠DAB﹣∠1=180°﹣60°﹣50°=70°.
故选:C.
6.一元二次方程x2﹣4x+3=0的解为( )
A.x =﹣1,x =3 B.x =1,x =3
1 2 1 2
C.x =1,x =﹣3 D.x =﹣1,x =﹣3
1 2 1 2
【分析】利用因式分解法求解即可.
【解答】解:∵x2﹣4x+3=0,
∴(x﹣1)(x﹣3)=0,
则x﹣1=0或x﹣3=0,
解得x =1,x =3,
1 2故选:B.
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的
中点,则DE的长为( )
A.1 B.2 C.3 D.4
【分析】利用三角形的内角和定理可得∠B=60°,由直角三角形斜边的中线性质定理可
得CE=BE=2,利用等边三角形的性质可得结果.
【解答】解:∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵E是AB的中点,AB=4,
∴CE=BE= ,
∴△BCE为等边三角形,
∵CD⊥AB,
∴DE=BD= ,
故选:A.
8.某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级
一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确
的是( )
A. B.
C. D.
【分析】设该班胜x场,负y场,根据八年级一班在16场比赛中得26分,即可得出关
于x,y的二元一次方程组,此题得解.
【解答】解:设该班胜x场,负y场,
依题意得: .故选:D.
9.如图,在矩形ABCD中,AB=8cm,AD=6cm.点P从点A出发,以2cm/s的速度在矩
形的边上沿A→B→C→D运动,点P与点D重合时停止运动.设运动的时间为t(单位:
s),△APD的面积为S(单位:cm2),则S随t变化的函数图象大致为( )
A. B.
C. D.
【分析】分三段,即点P在线段AB,BC,CD上运动,分别计算△APD的面积S的函
数表达式,即可作出判断.
【解答】解:当点P在线段AB上运动时,AP=2t,S= ×6×2t=6t,是正比例函数,排
除B选项;
当点P在线段BC上运动时,S= ×6×8=24;
当点P在线段CD上运动时,DP=8+6+8﹣2t=22﹣2t,S= ×AD×DP= ×6×(22﹣
2t)=66﹣6t,是一次函数的图象,排除A,C选项,D选项符合题意;
故选:D.
二、填空题(本大题共6小题,每小题5分,共30分)
10.今年“五一”假期,新疆铁路累计发送旅客795900人次.用科学记数法表示795900
为 7.959×1 0 5 .【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,
据此判断即可.
【解答】解:795900=7.959×105.
故答案为:7.959×105.
11.不等式2x﹣1>3的解集是 x > 2 .
【分析】移项后合并同类项得出2x>4,不等式的两边都除以2即可求出答案.
【解答】解:2x﹣1>3,
移项得:2x>3+1,
合并同类项得:2x>4,
不等式的两边都除以2得:x>2,
故答案为:x>2.
12.四边形的外角和等于 36 0 °.
【分析】根据多边形的内角和定理和邻补角的关系即可求出四边形的外角和.
【解答】解:∵四边形的内角和为(4﹣2)•180°=360°,
而每一组内角和相邻的外角是一组邻补角,
∴四边形的外角和等于4×180°﹣360°=360°.
故填空答案:360.
13.若点A(1,y ),B(2,y )在反比例函数y= 的图象上,则y > y (填“>”
1 2 1 2
“<”或“=”).
【分析】根据反比例函数的性质即可判断.
【解答】解:∵k=3,
∴在同一象限内y随x的增大而减小,
∵0<1<2,
∴两点在同一象限内,
∴y >y .
1 2
故答案为:>.
14.如图,在△ABC中,AB=AC,∠C=70°,分别以点A,B为圆心,大于 AB的长为
半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则∠BDC=
80 °.【分析】由等腰三角形的性质与三角形内角和定理求出∠A,由作图过程可得DM是AB
的垂直平分线,得到AD=BD,再根据等腰三角形的性质求出∠ABD,由三角形外角的
性质即可求得∠BDC.
【解答】解:∵AB=AC,∠C=70°,
∴∠ABC=∠C=70°,
∵∠A+∠ABC+∠C=180°,
∴∠A=180°﹣∠ABC﹣∠C=40°,
由作图过程可知:DM是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠BDC=∠A+∠ABD=40°+40°=80°,
故答案为:80.
15.如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将△DAE按逆
时针方向旋转得△DCF,连接 EF,分别交 BD,CD 于点 M,N.若 ,则
sin∠EDM= .
【分析】过点E作EG⊥BD于点G,设AE=2x,则DN=5x,易证△FNC∽△FEB,得,求出x的值,进而得到AE,EB的值,根据勾股定理求出ED,在Rt△EBG中
求出EG,根据正弦的定义即可求解.
【解答】解:如图,过点E作EG⊥BD于点G,
设AE=2x,则DN=5x,
由旋转性质得:CF=AE=2x,∠DCF=∠A=90°,
∵四边形ABCD是正方形,
∴∠DCB=90°,∠ABC=90°,∠ABD=45°,
∴∠DCB+∠DCF=180°,∠DCB=∠ABC,
∴点B,C,F在同一条直线上,
∵∠DCB=∠ABC,∠NFC=∠EFB,
∴△FNC∽△FEB,
∴ ,
∴ ,
解得:x =﹣1(舍去),x = ,
1 2
∴AE=2× = ,
∴ED= = = ,
EB=AB﹣AE=1﹣ = ,
在Rt△EBG中,EG=BE•sin45°= × = ,
∴sin∠EDM= = = ,
故答案为: .三、解答题(本大题共8小题,共75分)
16.(6分)计算: .
【分析】直接利用零指数幂的性质以及立方根的性质、有理数的乘方、绝对值的性质分
别化简得出答案.
【解答】解:原式=1+3﹣3﹣1
=0.
17.(7分)先化简,再求值: ,其中x=3.
【分析】直接化简分式,将括号里面进行加减运算,再利用分式的混合运算法则化简得
出答案.
【解答】解:原式=[ + ]•
=( + )•
= •
= •
= ,
当x=3时,
原式= = = .
18.(10分)如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且BE=
CF.
求证:(1)△ABE≌△DCF;
(2)四边形AEFD是平行四边形.【分析】(1)由矩形的性质可得 AB=CD,∠ABC=∠DCB=90°,AD=BC,
AD∥BC,由“SAS”可证△ABE≌△DCF;
(2)由一组对边平行且相等的四边形是平行四边形可证四边形AEFD是平行四边形.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°,AD=BC,AD∥BC,
∴∠ABE=∠DCF=90°,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
(2)∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF=AD,
又∵AD∥BC,
∴四边形AEFD是平行四边形.
19.(10分)某校为了增强学生的疫情防控意识,组织全校 2000名学生进行了疫情防控
知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A:60≤x
<70;B:70≤x<80;C:80≤x<90;D:90≤x≤100,并绘制出不完整的统计图:(1)填空:n= 5 0 ;
(2)补全频数分布直方图;
(3)抽取的这n名学生成绩的中位数落在 C 组;
(4)若规定学生成绩x≥90为优秀,估算全校成绩达到优秀的人数.
【分析】(1)根据B组的频数和所占的百分比,可以求得n的值;
(2)根据(1)中n的值和频数分布直方图中的数据,可以计算出D组的频数,从而可
以将频数分布直方图补充完整;
(3)根据频数分布直方图可以得到中位数落在哪一组;
(4)根据直方图中的数据,可以计算出全校成绩达到优秀的人数.
【解答】解:(1)n=12÷24%=50,
故答案为:50;
(2)D组学生有:50﹣5﹣12﹣18=15(人),
补全的频数分布直方图如右图所示;
(3)由频数分布直方图可知,
第25和26个数据均落在C组,
故抽取的这n名学生成绩的中位数落在C组,
故答案为:C;
(4)2000× =600(人),
答:估算全校成绩达到优秀的有600人.
20.(10分)如图,楼顶上有一个广告牌AB,从与楼BC相距15m的D处观测广告牌顶部
A的仰角为37°,观测广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留小
数点后一位,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
≈1.73)【分析】利用CD及正切函数的定义求得BC,AC长,把这两条线段相减即为AB长.
【解答】解:在Rt△BCD中,BC=DC•tan30°=15× =5×1.73=8.65(m),
在Rt△ACD中,AC=DC•tan37°=15×0.75=11.25(m),
∴AB=AC﹣BC=11.25﹣8.65=2.6(m).
答:广告牌AB的高度为2.6m.
21.(9分)如图,一次函数y=k x+b(k ≠0)与反比例函数y= (k ≠0)的图象交于
1 1 2
点A(2,3),B(n,﹣1).
(1)求反比例函数和一次函数的解析式;
(2)判断点P(﹣2,1)是否在一次函数y=k x+b的图象上,并说明理由;
1
(3)直接写出不等式k x+b≥ 的解集.
1
【分析】(1)待定系数法求解.
(2)将x=﹣2代入一次函数解析式求解.
(3)通过观察图像求解.
【解答】解:(1)将A(2,3)代入y= 得3= ,
解得k =6,
2∴y= ,
把B(n,﹣1)代入y= 得﹣1= ,
解得n=﹣6,
∴点B坐标为(﹣6,﹣1).
把A(2,3),B(﹣6,﹣1)代入y=k x+b得:
1
,
解得 ,
∴y= x+2.
(2)把x=﹣2代入y= x+2得y=﹣2× +2=1,
∴点P(﹣2,1)在一次函数y=k x+b的图象上.
1
(3)由图象得x≥2或﹣6≤x<0时k x+b≥ ,
1
∴不等式k x+b≥ 的解集为x≥2或﹣6≤x<0.
1
22.(11分)如图,AC是 O的直径,BC,BD是 O的弦,M为BC的中点,OM与BD
交于点F,过点D作DE⊙⊥BC,交BC的延长线于⊙点E,且CD平分∠ACE.
(1)求证:DE是 O的切线;
(2)求证:∠CDE⊙=∠DBE;
(3)若DE=6,tan∠CDE= ,求BF的长.【分析】(1)连接 OD,由 CD 平分∠ACE,OC=OD,可得∠DCE=∠ODC,
OD∥BC,从而可证DE是 O的切线;
(2)连接AB,由AC是⊙O的直径,得∠ABD+∠DBC=90°,又∠ABD=∠ACD,
∠ABD=∠ODC,可得∠O⊙DC+∠DBC=90°,结合∠ODC+∠CDE=90°,即可得∠CDE
=∠DBE;
(3)求出CE=4,BE=9,即可得BC=5,由M为BC的中点,可得OM⊥BC,BM=
,Rt△BFM中,求出FM= ,再用勾股定理即得答案,BF= = .
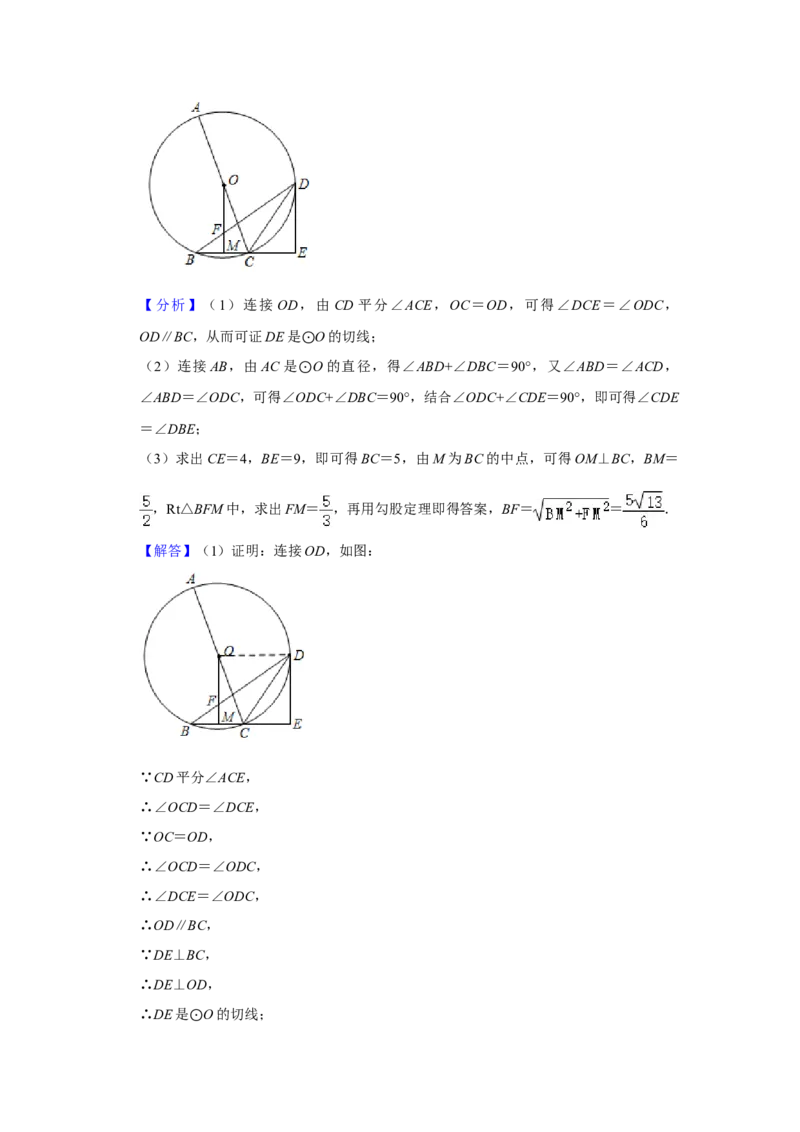
【解答】(1)证明:连接OD,如图:
∵CD平分∠ACE,
∴∠OCD=∠DCE,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠DCE=∠ODC,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∴DE是 O的切线;
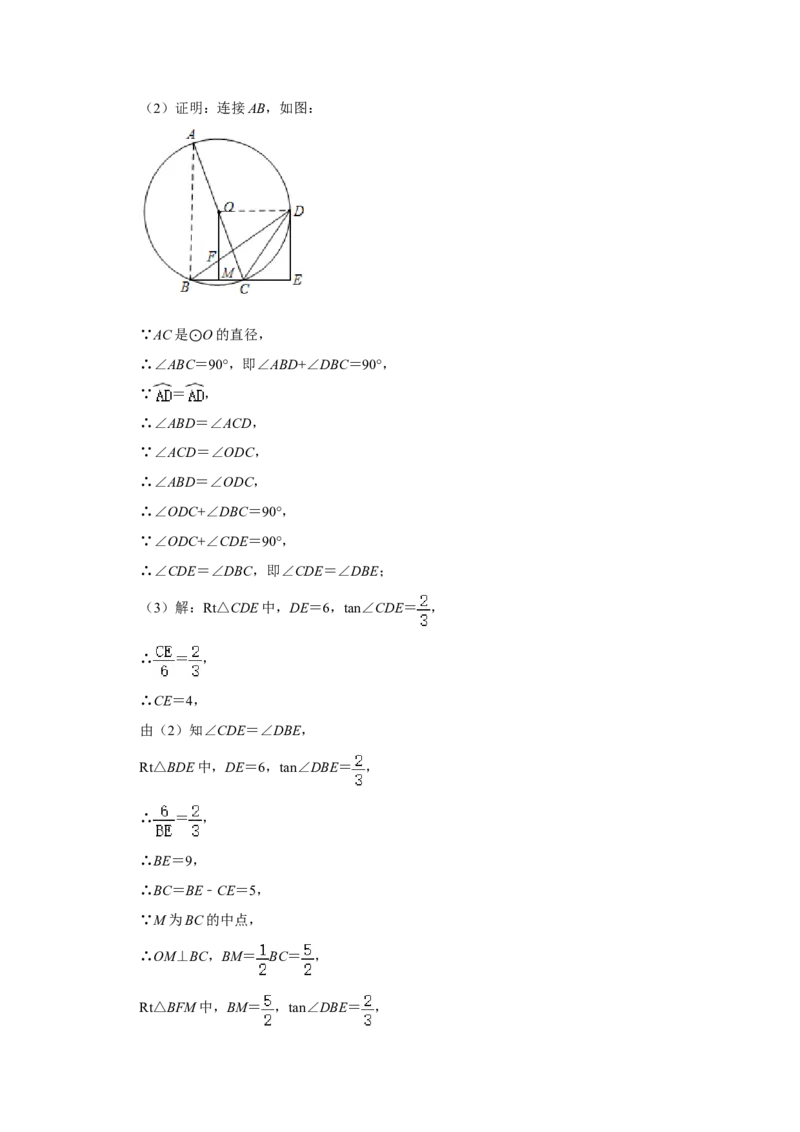
⊙(2)证明:连接AB,如图:
∵AC是 O的直径,
∴∠ABC⊙=90°,即∠ABD+∠DBC=90°,
∵ = ,
∴∠ABD=∠ACD,
∵∠ACD=∠ODC,
∴∠ABD=∠ODC,
∴∠ODC+∠DBC=90°,
∵∠ODC+∠CDE=90°,
∴∠CDE=∠DBC,即∠CDE=∠DBE;
(3)解:Rt△CDE中,DE=6,tan∠CDE= ,
∴ = ,
∴CE=4,
由(2)知∠CDE=∠DBE,
Rt△BDE中,DE=6,tan∠DBE= ,
∴ = ,
∴BE=9,
∴BC=BE﹣CE=5,
∵M为BC的中点,
∴OM⊥BC,BM= BC= ,
Rt△BFM中,BM= ,tan∠DBE= ,∴ = ,
∴FM= ,
∴BF= = .
23.(12分)已知抛物线y=ax2﹣2ax+3(a≠0).
(1)求抛物线的对称轴;
(2)把抛物线沿y轴向下平移3|a|个单位,若抛物线的顶点落在x轴上,求a的值;
(3)设点P(a,y ),Q(2,y )在抛物线上,若y >y ,求a的取值范围.
1 2 1 2
【分析】(1)根据x=﹣ ,可得抛物线的对称轴为:直线x=﹣ =1;
(2)由根的判别式△=b2﹣4ac=0,建立等式可求出a的值;
(3)当x=2时,y =3,由y >y 可列出不等式,求解即可.′
2 1 2
【解答】解:(1)由题意可得,抛物线的对称轴为:直线x=﹣ =1;
(2)抛物线沿y轴向下平移3|a|个单位,可得y′=ax2﹣2ax+3﹣3|a|,
∵抛物线的顶点落在x轴上,
∴△=(2a)2﹣4a(3﹣3|a|)=0,解得a= 或a=﹣ .
(3)当x=2时,y =3,
2
若y >y ,则a3﹣2a2+3>3,解得a>2.
1 2