文档内容
2021年内蒙古呼和浩特市中考数学试卷
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.几种气体的液化温度(标准大气压)如下表:
气体 氧气 氢气 氮气 氦气
液化温度℃ ﹣183 ﹣253 ﹣195.8 ﹣268
其中液化温度最低的气体是( )
A.氦气 B.氮气 C.氢气 D.氧气
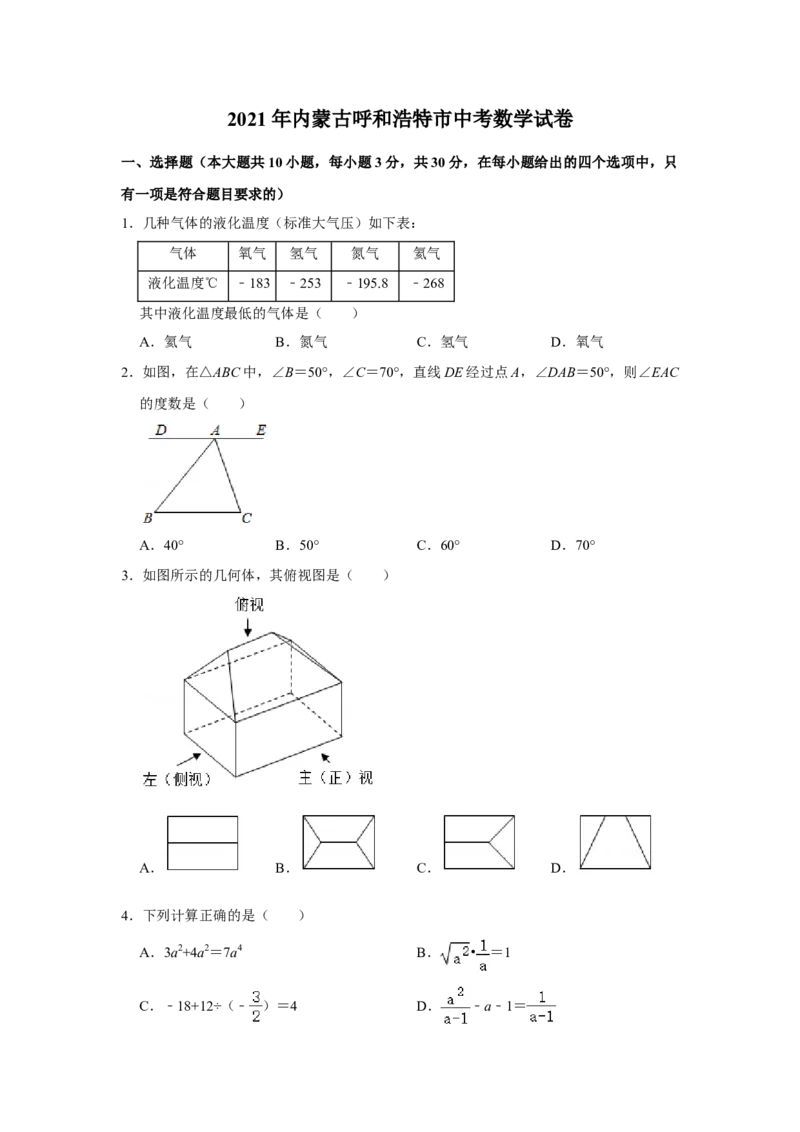
2.如图,在△ABC中,∠B=50°,∠C=70°,直线DE经过点A,∠DAB=50°,则∠EAC
的度数是( )
A.40° B.50° C.60° D.70°
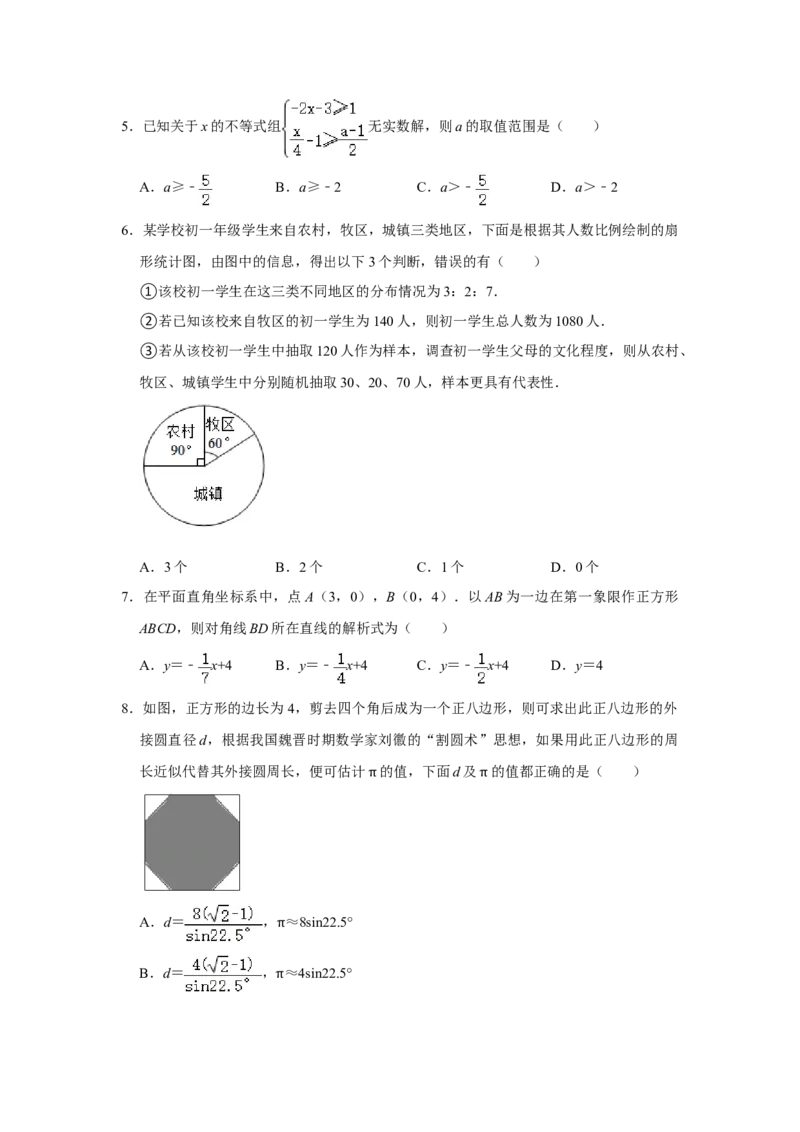
3.如图所示的几何体,其俯视图是( )
A. B. C. D.
4.下列计算正确的是( )
A.3a2+4a2=7a4 B. • =1
C.﹣18+12÷(﹣ )=4 D. ﹣a﹣1=5.已知关于x的不等式组 无实数解,则a的取值范围是( )
A.a≥﹣ B.a≥﹣2 C.a>﹣ D.a>﹣2
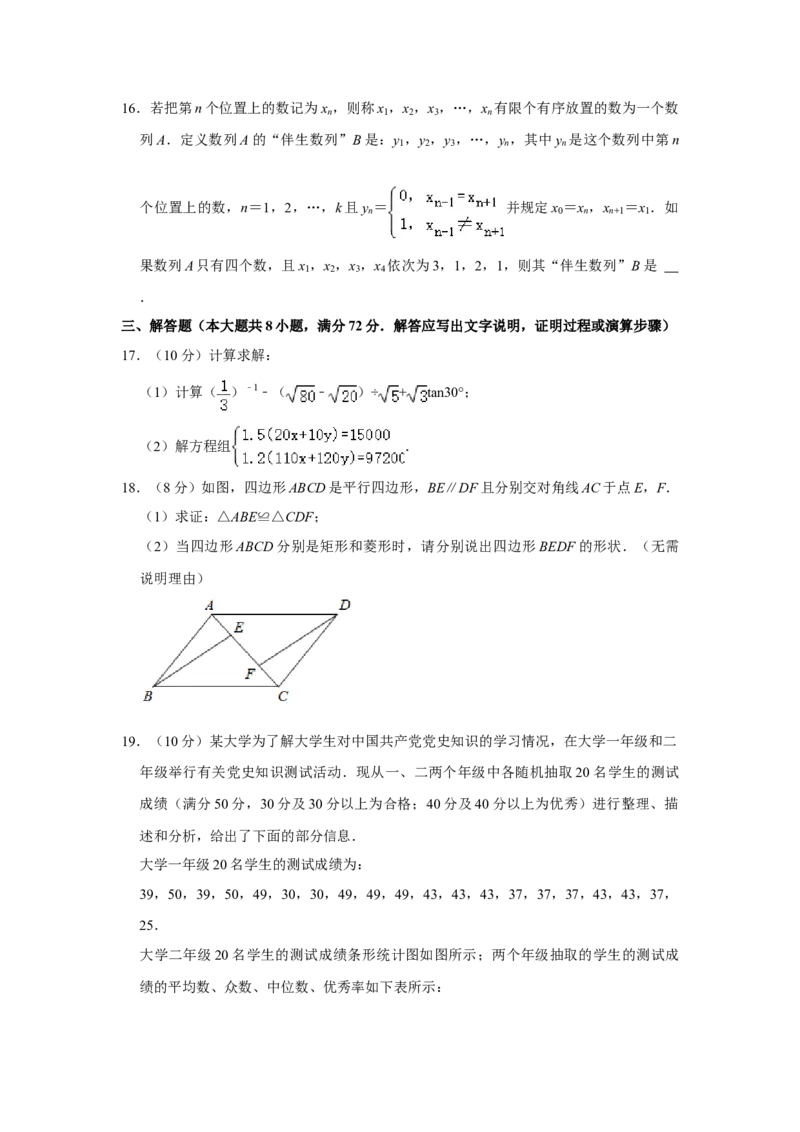
6.某学校初一年级学生来自农村,牧区,城镇三类地区,下面是根据其人数比例绘制的扇
形统计图,由图中的信息,得出以下3个判断,错误的有( )
①该校初一学生在这三类不同地区的分布情况为3:2:7.
②若已知该校来自牧区的初一学生为140人,则初一学生总人数为1080人.
③若从该校初一学生中抽取120人作为样本,调查初一学生父母的文化程度,则从农村、
牧区、城镇学生中分别随机抽取30、20、70人,样本更具有代表性.
A.3个 B.2个 C.1个 D.0个
7.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形
ABCD,则对角线BD所在直线的解析式为( )
A.y=﹣ x+4 B.y=﹣ x+4 C.y=﹣ x+4 D.y=4
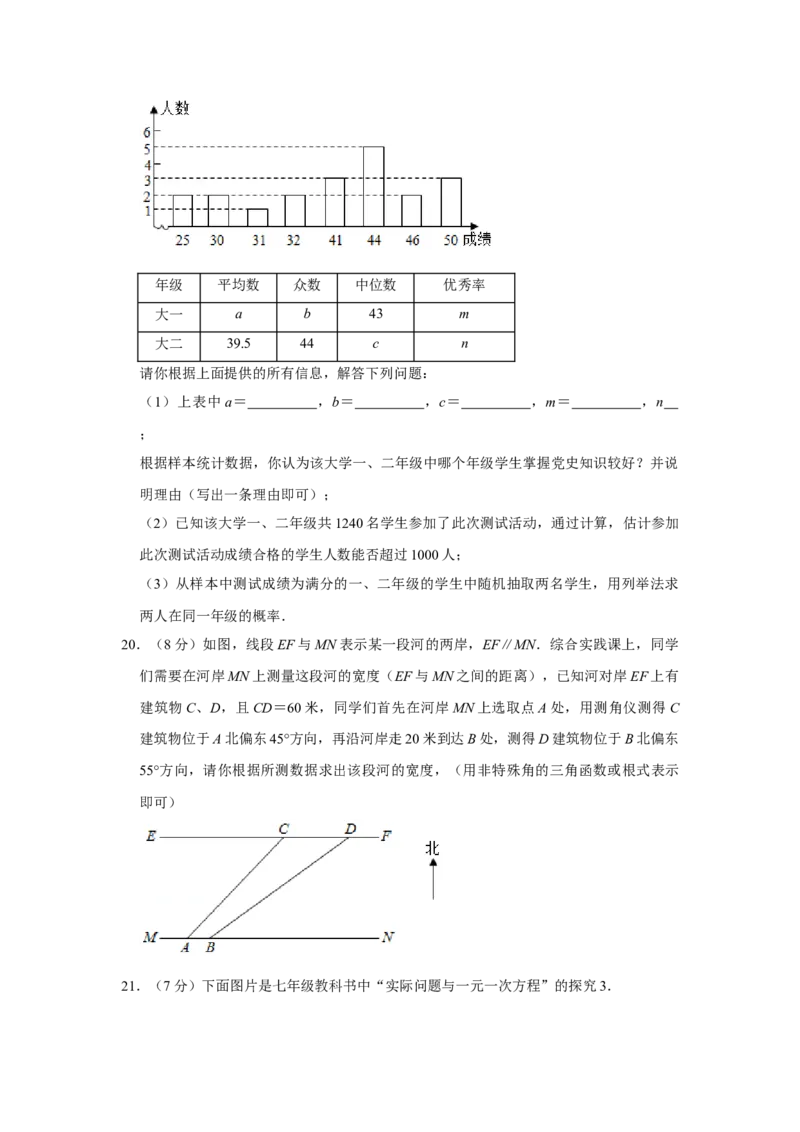
8.如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外
接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周
长近似代替其外接圆周长,便可估计 的值,下面d及 的值都正确的是( )
π π
A.d= , ≈8sin22.5°
π
B.d= , ≈4sin22.5°
πC.d= , ≈8sin22.5°
π
D.d= , ≈4sin22.5°
π
9.以下四个命题:
①任意三角形的一条中位线与第三边上的中线互相平分;
②A,B,C,D,E,F六个足球队进行单循环赛,若A,B,C,D,E分别赛了5,
4,3,2,1场,则由此可知,还没有与B队比赛的球队可能是D队;
③两个正六边形一定位似;
④有13人参加捐款,其中小王的捐款数比13人捐款的平均数多2元,则小王的捐款数
不可能最少,但可能只比最少的多,比其他的都少.
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
10.已知二次项系数等于1的一个二次函数,其图象与 x轴交于两点(m,0),(n,
0),且过A(0,b),B(3,a)两点(b,a是实数),若0<m<n<2,则ab的取值
范围是( )
A.0<ab< B.0<ab< C.0<ab< D.0<ab<
二、填空题(本大题共6小题,每小题3分,共18分.本题要求把正确结果填在答题卡规
定的横线上,不需要解答过程)
11.因式分解:x3y﹣4xy= .
12.正比例函数y=k x与反比例函数y= 的图象交于A,B两点,若A点坐标为( ,
1
﹣2 ),则k +k = .
1 2
13.已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 .
(用含 的代数式表示),圆心角为 度.
14.动物学π家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为
0.5,据此若设刚出生的这种动物共有a只,则20年后存活的有 只,现年20
岁的这种动物活到25岁的概率是 .
15.已知菱形ABCD的面积为2 ,点E是一边BC上的中点,点P是对角线BD上的动
点.连接AE,若AE平分∠BAC,则线段PE与PC的和的最小值为 ,
最大值为 .16.若把第n个位置上的数记为x ,则称x ,x ,x ,…,x 有限个有序放置的数为一个数
n 1 2 3 n
列A.定义数列A的“伴生数列”B是:y ,y ,y ,…,y ,其中y 是这个数列中第n
1 2 3 n n
个位置上的数,n=1,2,…,k且y = 并规定x =x ,x =x .如
n 0 n n+1 1
果数列A只有四个数,且x ,x ,x ,x 依次为3,1,2,1,则其“伴生数列”B是
1 2 3 4
.
三、解答题(本大题共8小题,满分72分.解答应写出文字说明,证明过程或演算步骤)
17.(10分)计算求解:
(1)计算( )﹣1﹣( ﹣ )÷ + tan30°;
(2)解方程组 .
18.(8分)如图,四边形ABCD是平行四边形,BE∥DF且分别交对角线AC于点E,F.
(1)求证:△ABE≌△CDF;
(2)当四边形ABCD分别是矩形和菱形时,请分别说出四边形BEDF的形状.(无需
说明理由)
19.(10分)某大学为了解大学生对中国共产党党史知识的学习情况,在大学一年级和二
年级举行有关党史知识测试活动.现从一、二两个年级中各随机抽取20名学生的测试
成绩(满分50分,30分及30分以上为合格;40分及40分以上为优秀)进行整理、描
述和分析,给出了下面的部分信息.
大学一年级20名学生的测试成绩为:
39,50,39,50,49,30,30,49,49,49,43,43,43,37,37,37,43,43,37,
25.
大学二年级20名学生的测试成绩条形统计图如图所示;两个年级抽取的学生的测试成
绩的平均数、众数、中位数、优秀率如下表所示:年级 平均数 众数 中位数 优秀率
大一 a b 43 m
大二 39.5 44 c n
请你根据上面提供的所有信息,解答下列问题:
(1)上表中a= ,b= ,c= ,m= ,n
;
根据样本统计数据,你认为该大学一、二年级中哪个年级学生掌握党史知识较好?并说
明理由(写出一条理由即可);
(2)已知该大学一、二年级共1240名学生参加了此次测试活动,通过计算,估计参加
此次测试活动成绩合格的学生人数能否超过1000人;
(3)从样本中测试成绩为满分的一、二年级的学生中随机抽取两名学生,用列举法求
两人在同一年级的概率.
20.(8分)如图,线段EF与MN表示某一段河的两岸,EF∥MN.综合实践课上,同学
们需要在河岸MN上测量这段河的宽度(EF与MN之间的距离),已知河对岸EF上有
建筑物C、D,且CD=60米,同学们首先在河岸MN上选取点A处,用测角仪测得C
建筑物位于A北偏东45°方向,再沿河岸走20米到达B处,测得D建筑物位于B北偏东
55°方向,请你根据所测数据求出该段河的宽度,(用非特殊角的三角函数或根式表示
即可)
21.(7分)下面图片是七年级教科书中“实际问题与一元一次方程”的探究3.探究3
电话计费问题
下表中有两种移动电话计费方式.
月使用费/元 主叫限定时间/ 主叫超时 被叫
min 费/(元/min)
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
考虑下列问题:
月使用费固定收:
主叫不超限定时间不再收费,主叫超时部分加收超时费,被叫免费.
(1)设一个月内用移动电话主叫为tmin(t是正整数).根据上表,列表说明:当t在
不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计
算验证你的看法.
小明升入初三再看这个问题,发现两种计费方式,每一种都是因主叫时间的变化而引起
计费的变化,他把主叫时间视为在正实数范围内变化,决定用函数来解决这个问题.
(1)根据函数的概念,小明首先将问题中的两个变量分别设为自变量x和自变量的函
数y,请你帮小明写出:
x表示问题中的 ,y表示问题中的 .
并写出计费方式一和二分别对应的函数解析式;
(2)在给出的正方形网格纸上画出(1)中两个函数的大致图象,并依据图象直接写出
如何根据主叫时间选择省钱的计费方式.(注:坐标轴单位长度可根据需要自己确定)22.(7分)为了促进学生加强体育锻炼,某中学从去年开始,每周除体育课外,又开展
了“足球俱乐部1小时”活动.去年学校通过采购平台在某体育用品店购买 A品牌足球
共花费2880元,B品牌足球共花费2400元,且购买A品牌足球数量是B品牌数量的1.5
倍,每个足球的售价,A品牌比B品牌便宜12元.今年由于参加俱乐部人数增加,需要
从该店再购买A、B两种足球共50个,已知该店对每个足球的售价,今年进行了调整,
A品牌比去年提高了5%,B品牌比去年降低了10%,如果今年购买A、B两种足球的总
费用不超过去年总费用的一半,那么学校最多可购买多少个B品牌足球?
23.(10分)已知AB是 O的任意一条直径.
(1)用图1,求证: ⊙O是以直径AB所在直线为对称轴的轴对称图形;
(2)已知 O的面积⊙为4 ,直线CD与 O相切于点C,过点B作BD⊥CD,垂足为
D,如图2.⊙ π ⊙
求证:① BC2=2BD;
②改变图2中切点C的位置,使得线段OD⊥BC时,OD=2 .
24.(12分)已知抛物线y=ax2+kx+h(a>0).
(1)通过配方可以将其化成顶点式为 ,根据该抛物线在对称轴
两侧从左到右图象的特征,可以判断,当顶点在x轴 (填上方
或下方),即4ah﹣k2 0(填大于或小于)时,该抛物线与x轴必
有两个交点;
(2)若抛物线上存在两点A(x ,y ),B(x ,y ),分布在x轴的两侧,则抛物线顶
1 1 2 2点必在x轴下方,请你结合A、B两点在抛物线上的可能位置,根据二次函数的性质,
对这个结论的正确性给以说明;(为了便于说明,不妨设x <x 且都不等于顶点的横坐
1 2
标;另如果需要借助图象辅助说明,可自己画出简单示意图)
(3)利用二次函数(1)(2)结论,求证:当a>0,(a+c)(a+b+c)<0时,(b﹣
c)2>4a(a+b+c).