文档内容
2021年山东省临沂市中考数学试卷
一.选择题(本大题共14小题,每小题3分,共42分)在每小题所给出的四个选项中,
只有一项是符合题目要求的。
1.﹣ 的相反数是( )
A.﹣ B.﹣2 C.2 D.
2.2021年5月15日,天问一号探测器成功着陆火星,中国成为全世界第二个实现火星着
陆的国家.据测算,地球到火星的最近距离约为 55000000km,将数据55000000用科学
记数法表示为( )
A.5.5×106 B.0.55×108 C.5.5×107 D.55×106
3.计算2a3•5a3的结果是( )
A.10a6 B.10a9 C.7a3 D.7a6
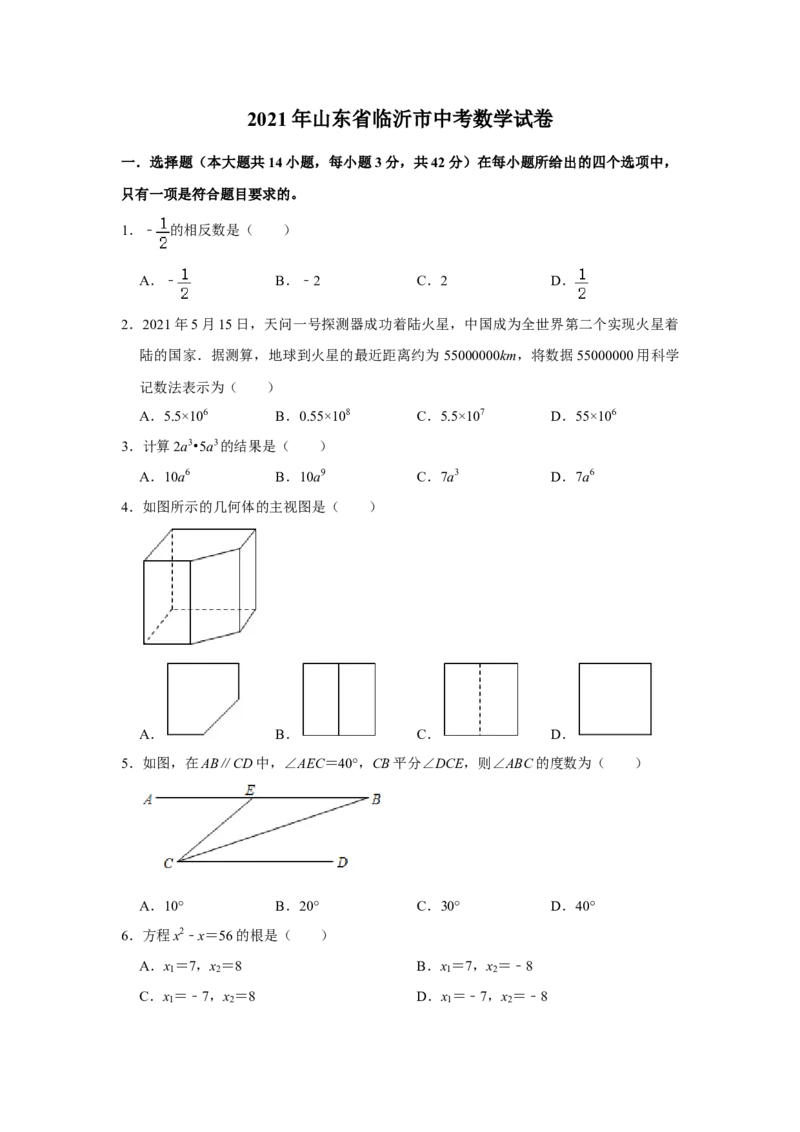
4.如图所示的几何体的主视图是( )
A. B. C. D.
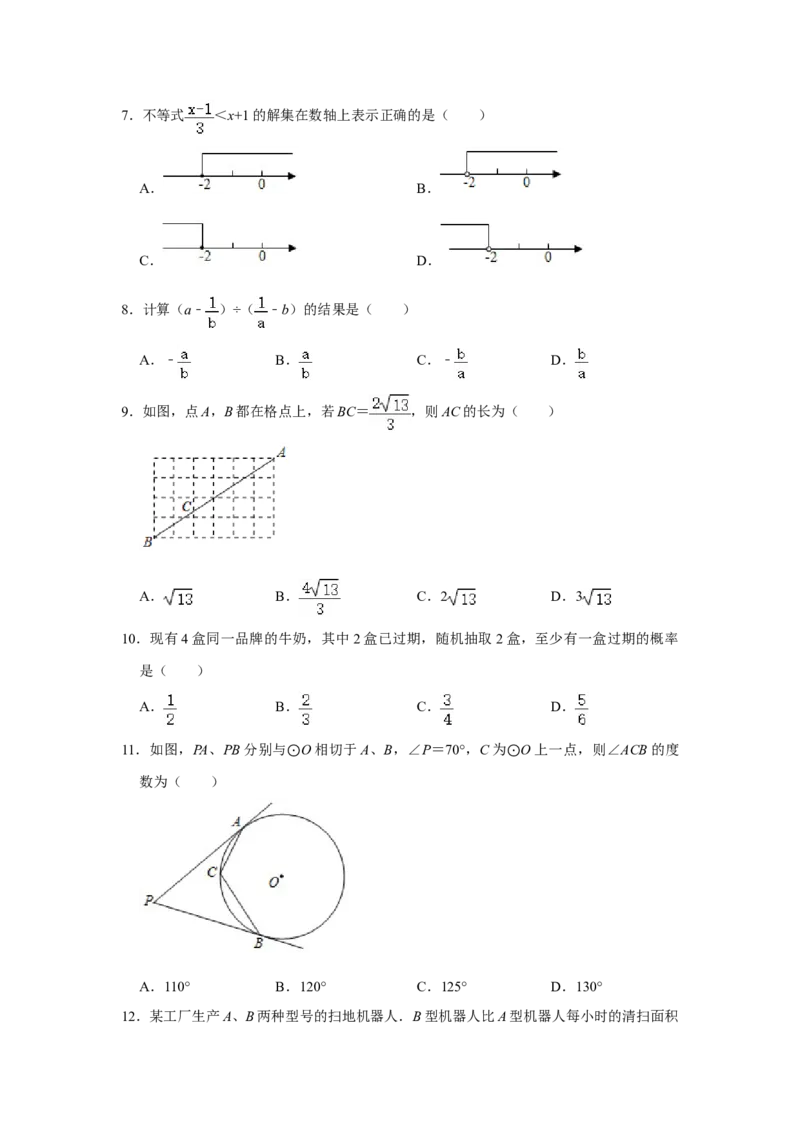
5.如图,在AB∥CD中,∠AEC=40°,CB平分∠DCE,则∠ABC的度数为( )
A.10° B.20° C.30° D.40°
6.方程x2﹣x=56的根是( )
A.x =7,x =8 B.x =7,x =﹣8
1 2 1 2
C.x =﹣7,x =8 D.x =﹣7,x =﹣8
1 2 1 27.不等式 <x+1的解集在数轴上表示正确的是( )
A. B.
C. D.
8.计算(a﹣ )÷( ﹣b)的结果是( )
A.﹣ B. C.﹣ D.
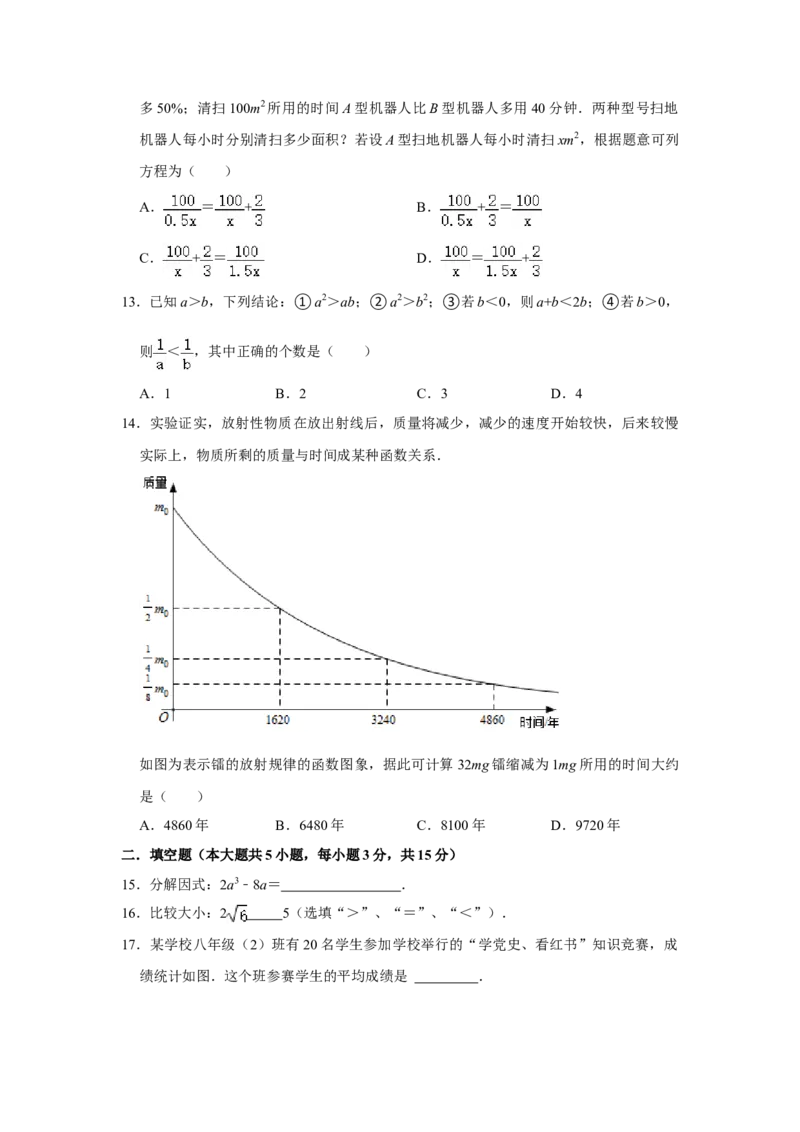
9.如图,点A,B都在格点上,若BC= ,则AC的长为( )
A. B. C.2 D.3
10.现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率
是( )
A. B. C. D.
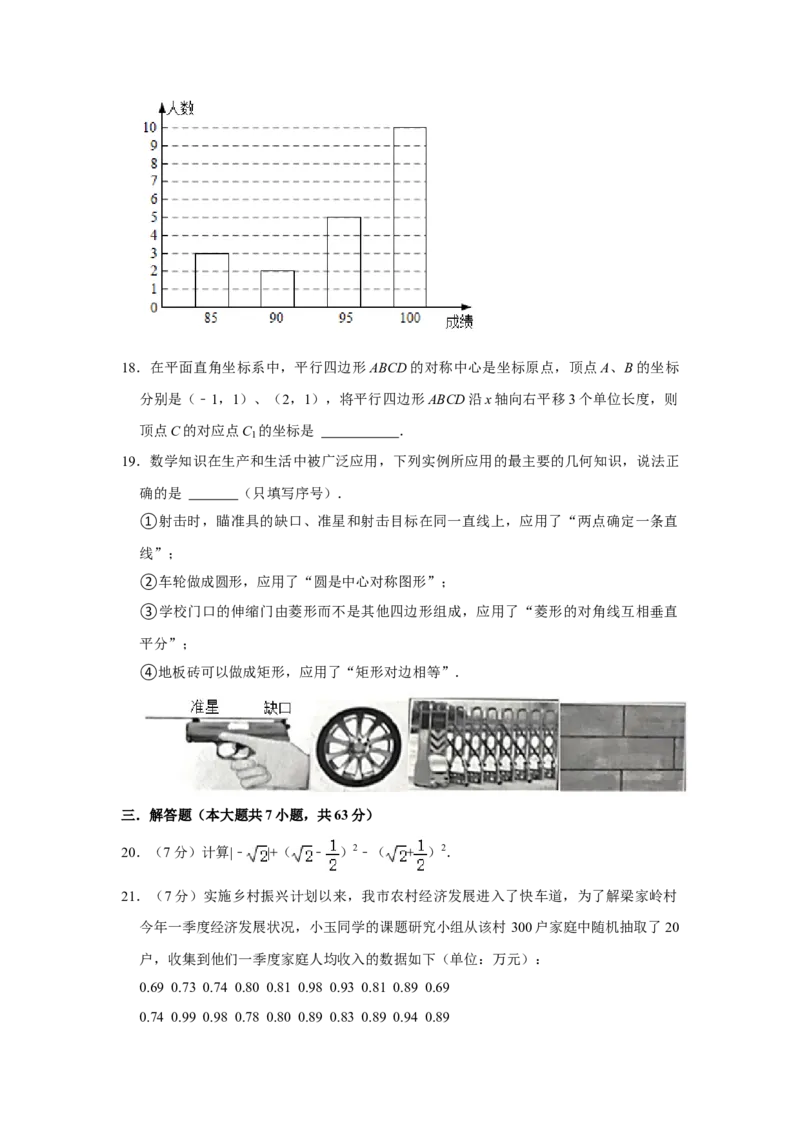
11.如图,PA、PB分别与 O相切于A、B,∠P=70°,C为 O上一点,则∠ACB的度
数为( ) ⊙ ⊙
A.110° B.120° C.125° D.130°
12.某工厂生产A、B两种型号的扫地机器人.B型机器人比A型机器人每小时的清扫面积多50%;清扫100m2所用的时间A型机器人比B型机器人多用40分钟.两种型号扫地
机器人每小时分别清扫多少面积?若设A型扫地机器人每小时清扫xm2,根据题意可列
方程为( )
A. = + B. + =
C. + = D. = +
13.已知a>b,下列结论:①a2>ab;②a2>b2;③若b<0,则a+b<2b;④若b>0,
则 < ,其中正确的个数是( )
A.1 B.2 C.3 D.4
14.实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢
实际上,物质所剩的质量与时间成某种函数关系.
如图为表示镭的放射规律的函数图象,据此可计算32mg镭缩减为1mg所用的时间大约
是( )
A.4860年 B.6480年 C.8100年 D.9720年
二.填空题(本大题共5小题,每小题3分,共15分)
15.分解因式:2a3﹣8a= .
16.比较大小:2 5(选填“>”、“=”、“<”).
17.某学校八年级(2)班有20名学生参加学校举行的“学党史、看红书”知识竞赛,成
绩统计如图.这个班参赛学生的平均成绩是 .18.在平面直角坐标系中,平行四边形ABCD的对称中心是坐标原点,顶点A、B的坐标
分别是(﹣1,1)、(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则
顶点C的对应点C 的坐标是 .
1
19.数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正
确的是 (只填写序号).
①射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直
线”;
②车轮做成圆形,应用了“圆是中心对称图形”;
③学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直
平分”;
④地板砖可以做成矩形,应用了“矩形对边相等”.
三.解答题(本大题共7小题,共63分)
20.(7分)计算|﹣ |+( ﹣ )2﹣( + )2.
21.(7分)实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了解梁家岭村
今年一季度经济发展状况,小玉同学的课题研究小组从该村 300户家庭中随机抽取了20
户,收集到他们一季度家庭人均收入的数据如下(单位:万元):
0.69 0.73 0.74 0.80 0.81 0.98 0.93 0.81 0.89 0.69
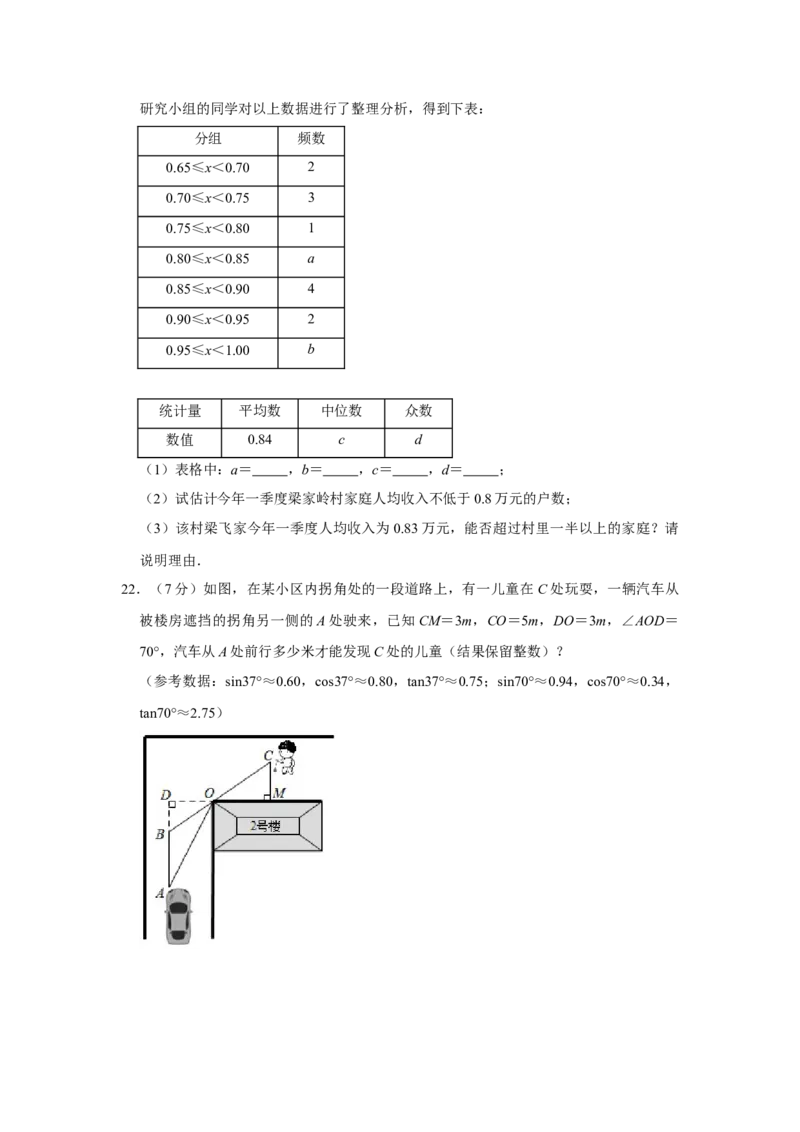
0.74 0.99 0.98 0.78 0.80 0.89 0.83 0.89 0.94 0.89研究小组的同学对以上数据进行了整理分析,得到下表:
分组 频数
0.65≤x<0.70 2
0.70≤x<0.75 3
0.75≤x<0.80 1
0.80≤x<0.85 a
0.85≤x<0.90 4
0.90≤x<0.95 2
0.95≤x<1.00 b
统计量 平均数 中位数 众数
数值 0.84 c d
(1)表格中:a= ,b= ,c= ,d= ;
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数;
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请
说明理由.
22.(7分)如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从
被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=
70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,
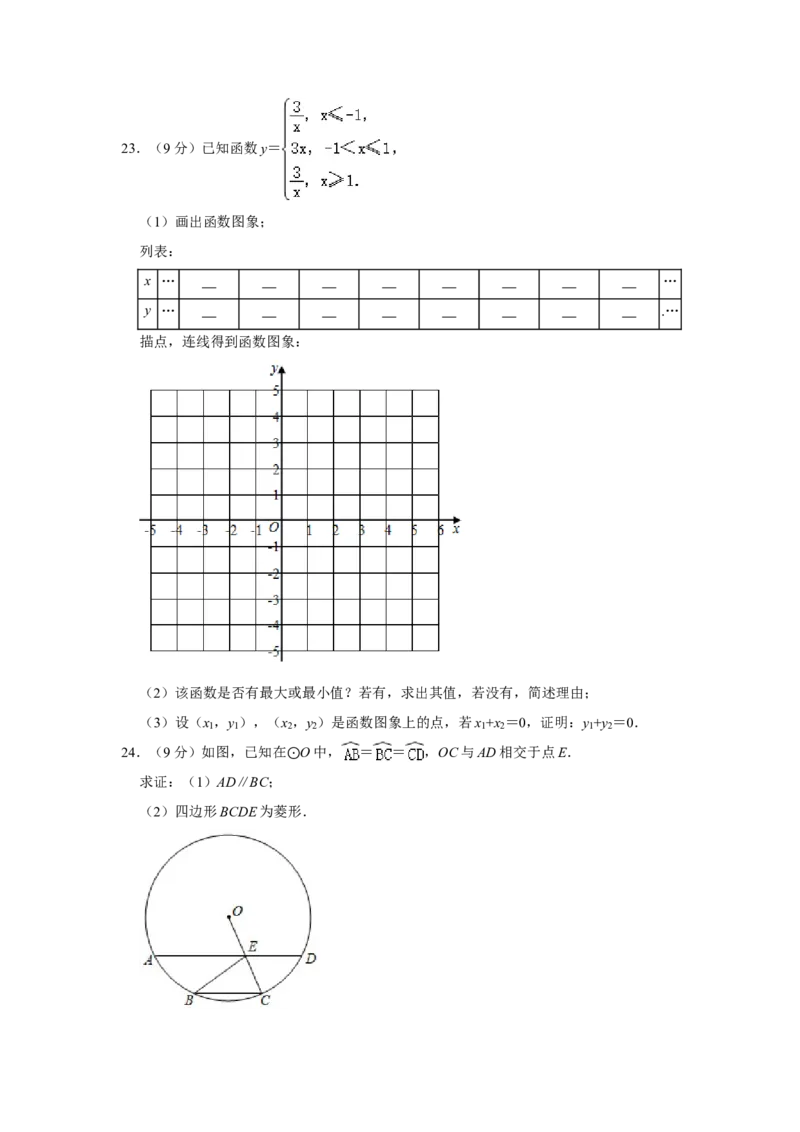
tan70°≈2.75)23.(9分)已知函数y=
(1)画出函数图象;
列表:
x … …
y … .…
描点,连线得到函数图象:
(2)该函数是否有最大或最小值?若有,求出其值,若没有,简述理由;
(3)设(x ,y ),(x ,y )是函数图象上的点,若x +x =0,证明:y +y =0.
1 1 2 2 1 2 1 2
24.(9分)如图,已知在 O中, = = ,OC与AD相交于点E.
求证:(1)AD∥BC; ⊙
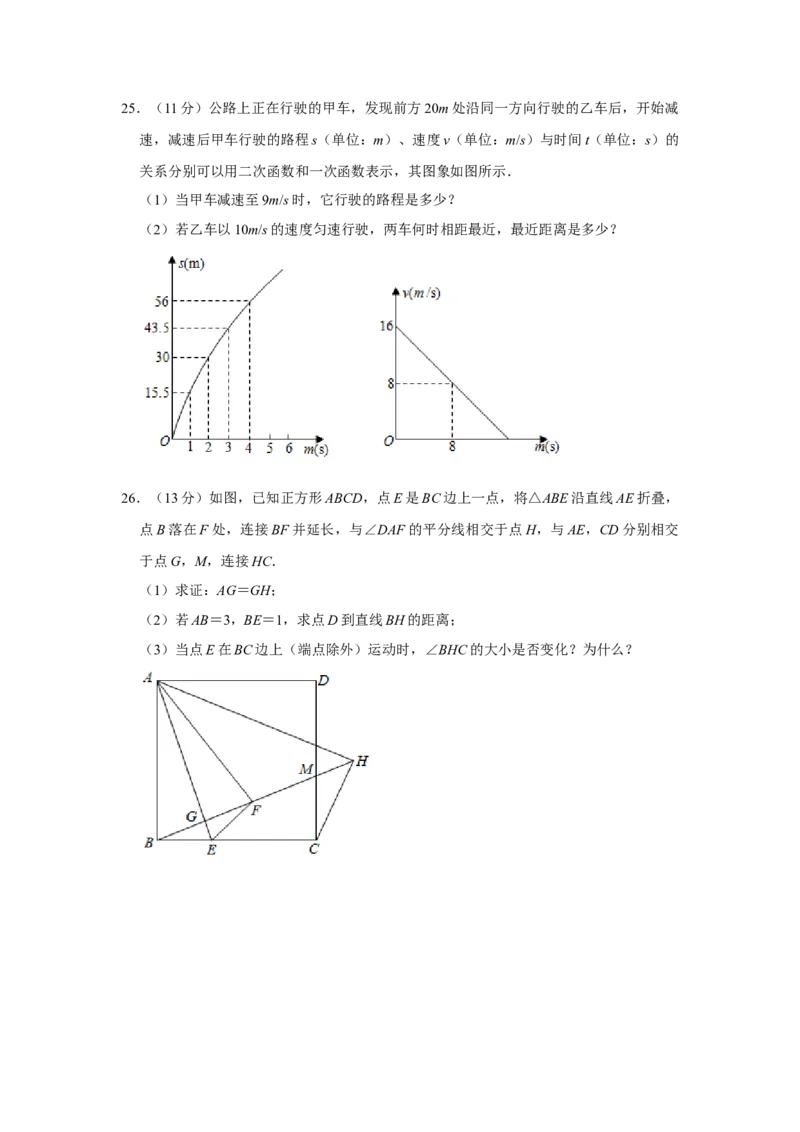
(2)四边形BCDE为菱形.25.(11分)公路上正在行驶的甲车,发现前方20m处沿同一方向行驶的乙车后,开始减
速,减速后甲车行驶的路程s(单位:m)、速度v(单位:m/s)与时间t(单位:s)的
关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)当甲车减速至9m/s时,它行驶的路程是多少?
(2)若乙车以10m/s的速度匀速行驶,两车何时相距最近,最近距离是多少?
26.(13分)如图,已知正方形ABCD,点E是BC边上一点,将△ABE沿直线AE折叠,
点B落在F处,连接BF并延长,与∠DAF的平分线相交于点H,与AE,CD分别相交
于点G,M,连接HC.
(1)求证:AG=GH;
(2)若AB=3,BE=1,求点D到直线BH的距离;
(3)当点E在BC边上(端点除外)运动时,∠BHC的大小是否变化?为什么?