文档内容
2021年湖南省株洲市中考数学试卷
一、选择题(本大题共10小题,每小题有且只有一个正确答案,每小题4分,共40分)
1.若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
2.方程 ﹣1=2的解是( )
A.x=2 B.x=3 C.x=5 D.x=6
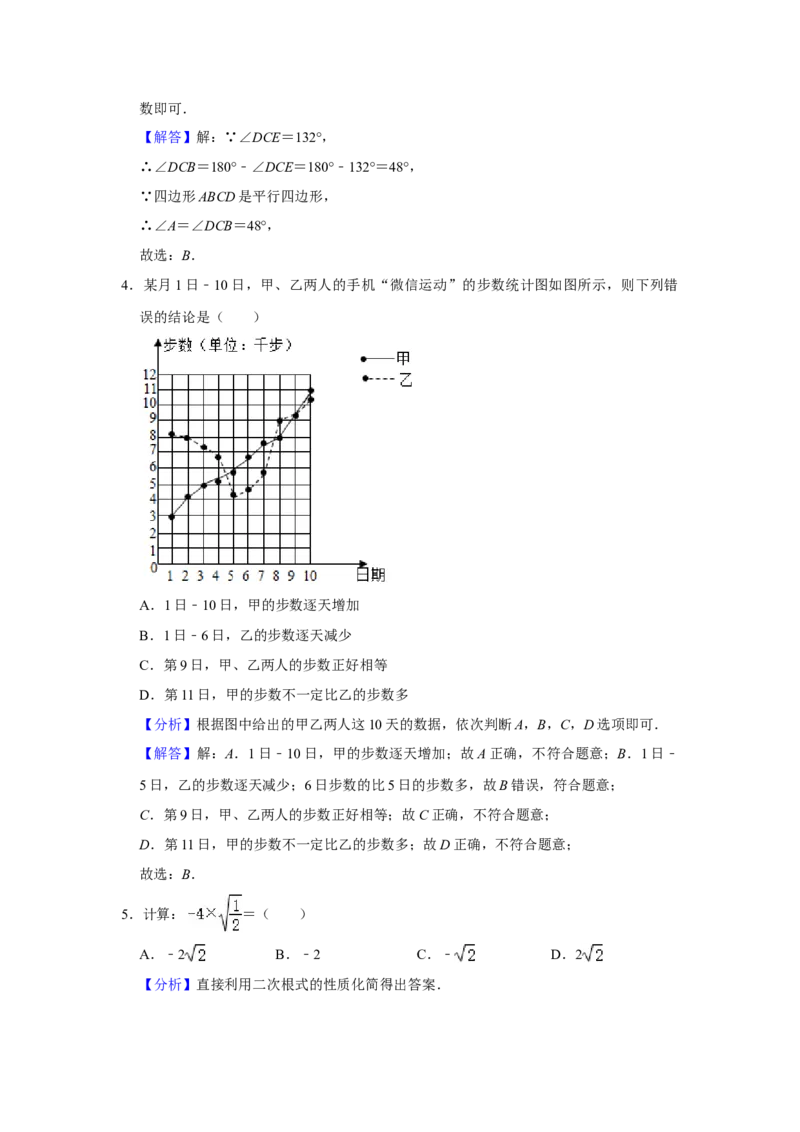
3.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=
132°,则∠A=( )
A.38° B.48° C.58° D.66°
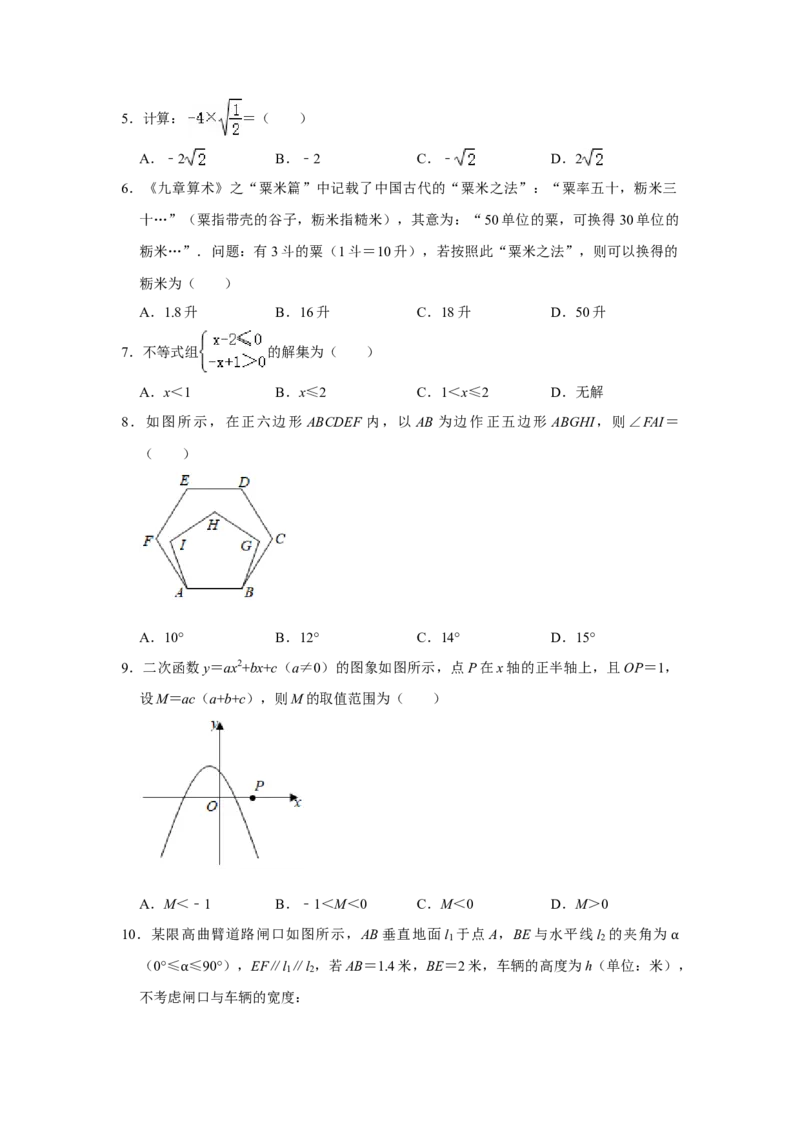
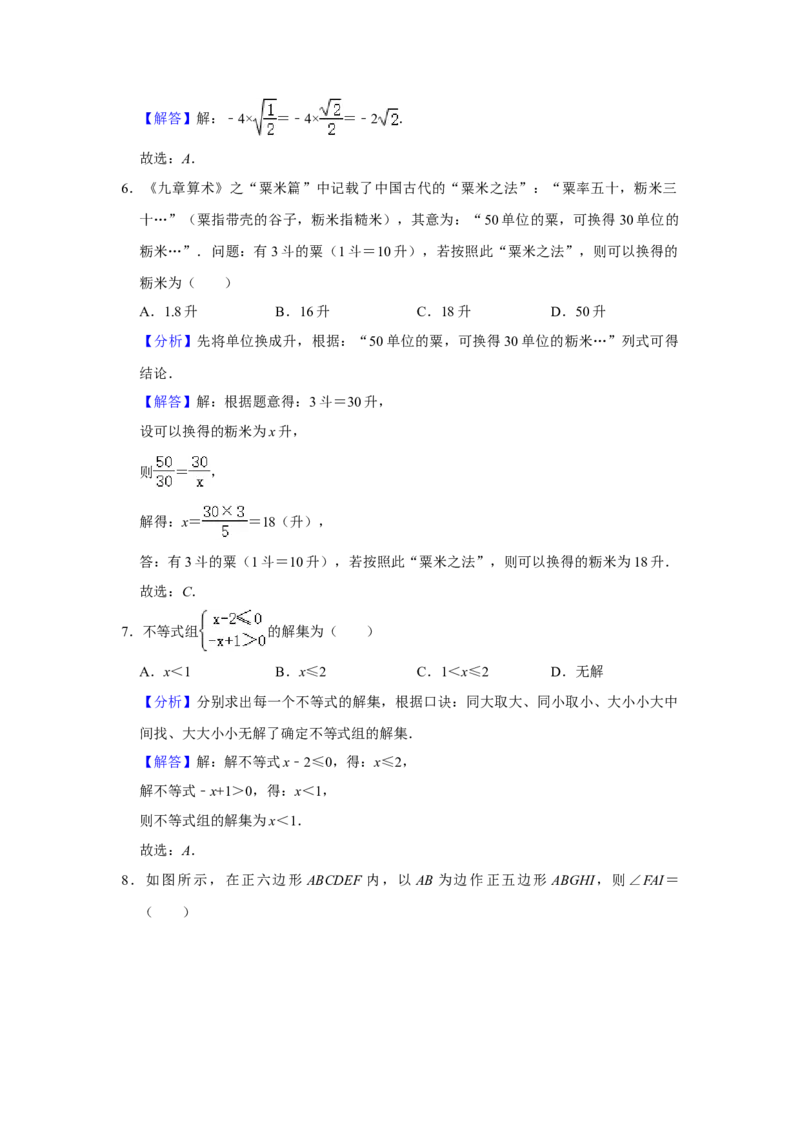
4.某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错
误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多5.计算: =( )
A.﹣2 B.﹣2 C.﹣ D.2
6.《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”:“粟率五十,粝米三
十…”(粟指带壳的谷子,粝米指糙米),其意为:“50单位的粟,可换得30单位的
粝米…”.问题:有3斗的粟(1斗=10升),若按照此“粟米之法”,则可以换得的
粝米为( )
A.1.8升 B.16升 C.18升 D.50升
7.不等式组 的解集为( )
A.x<1 B.x≤2 C.1<x≤2 D.无解
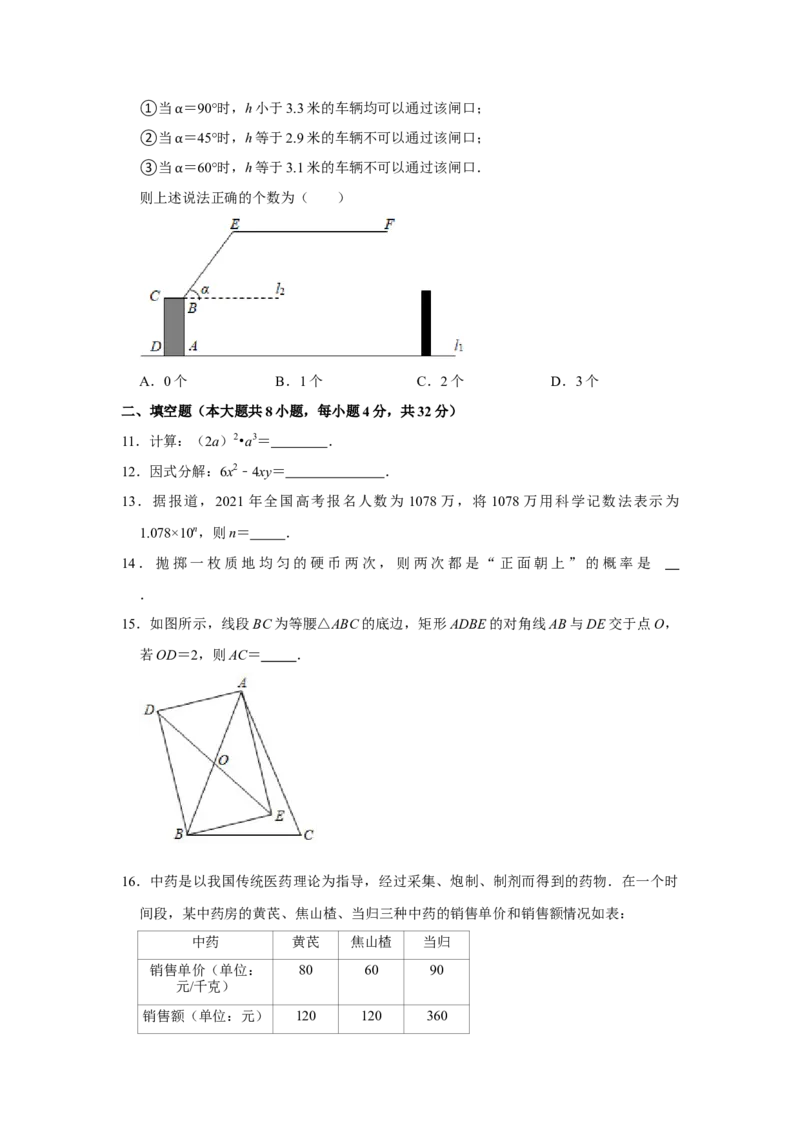
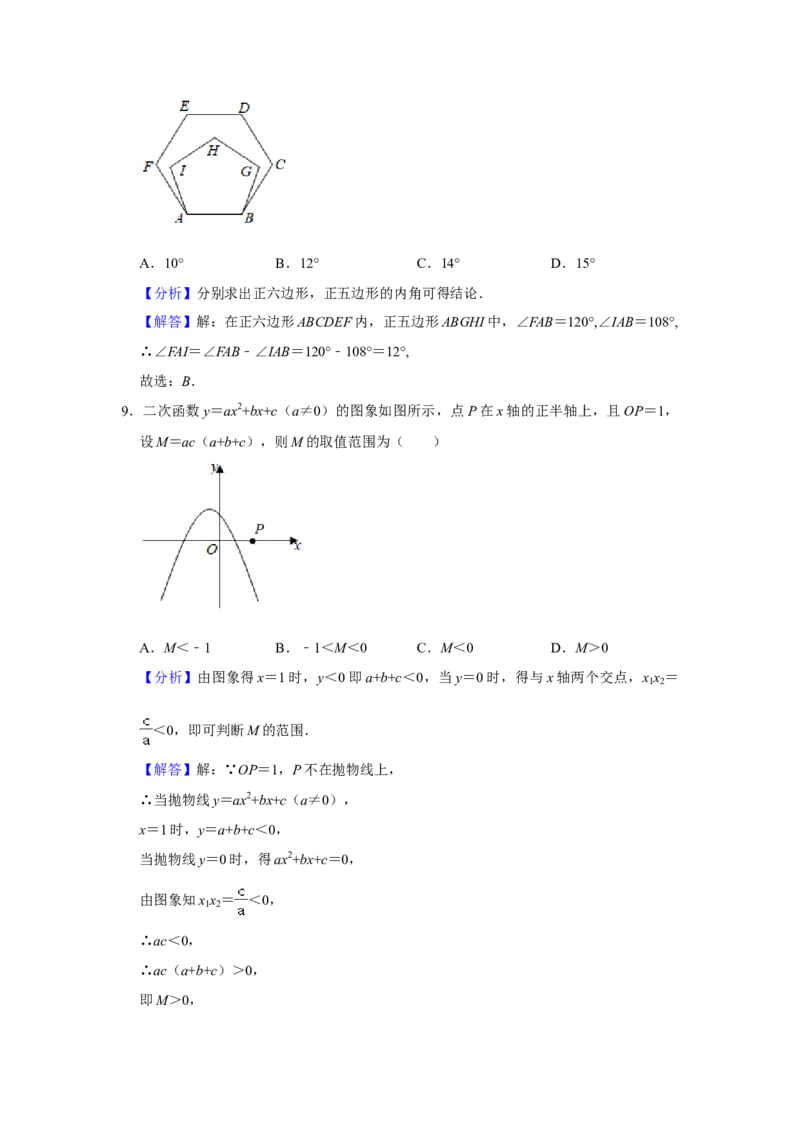
8.如图所示,在正六边形 ABCDEF 内,以 AB 为边作正五边形 ABGHI,则∠FAI=
( )
A.10° B.12° C.14° D.15°
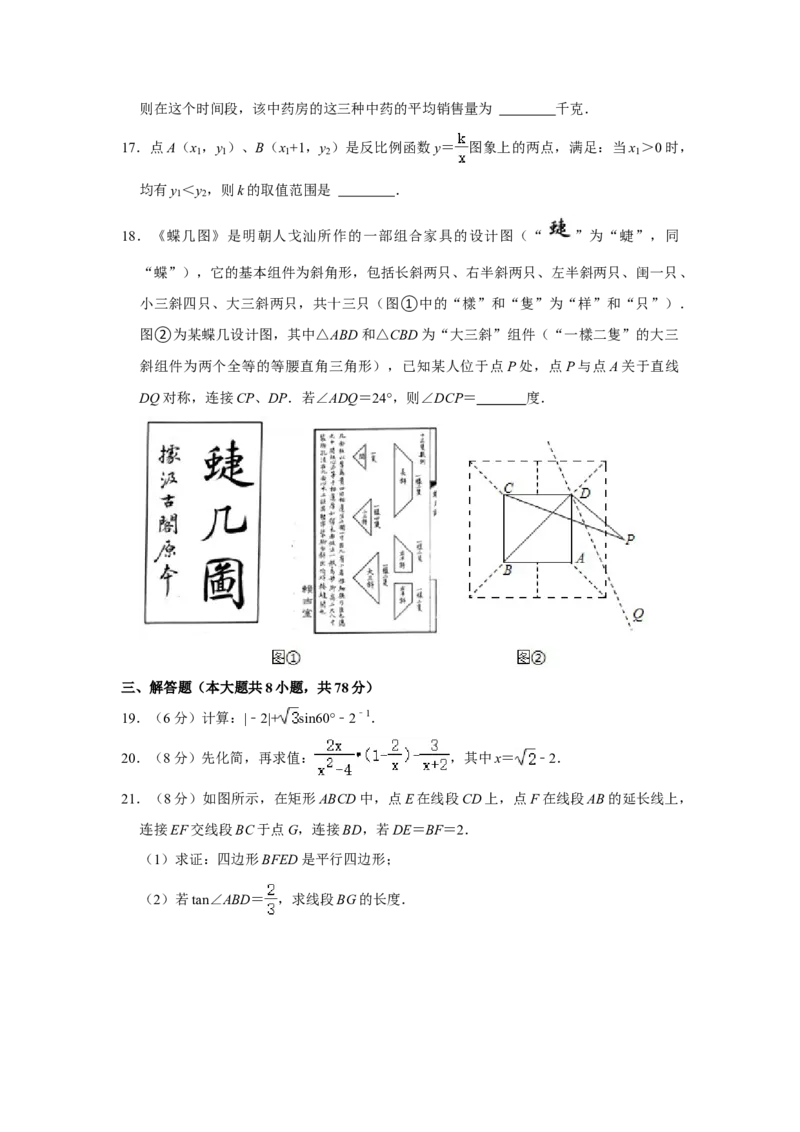
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,点P在x轴的正半轴上,且OP=1,
设M=ac(a+b+c),则M的取值范围为( )
A.M<﹣1 B.﹣1<M<0 C.M<0 D.M>0
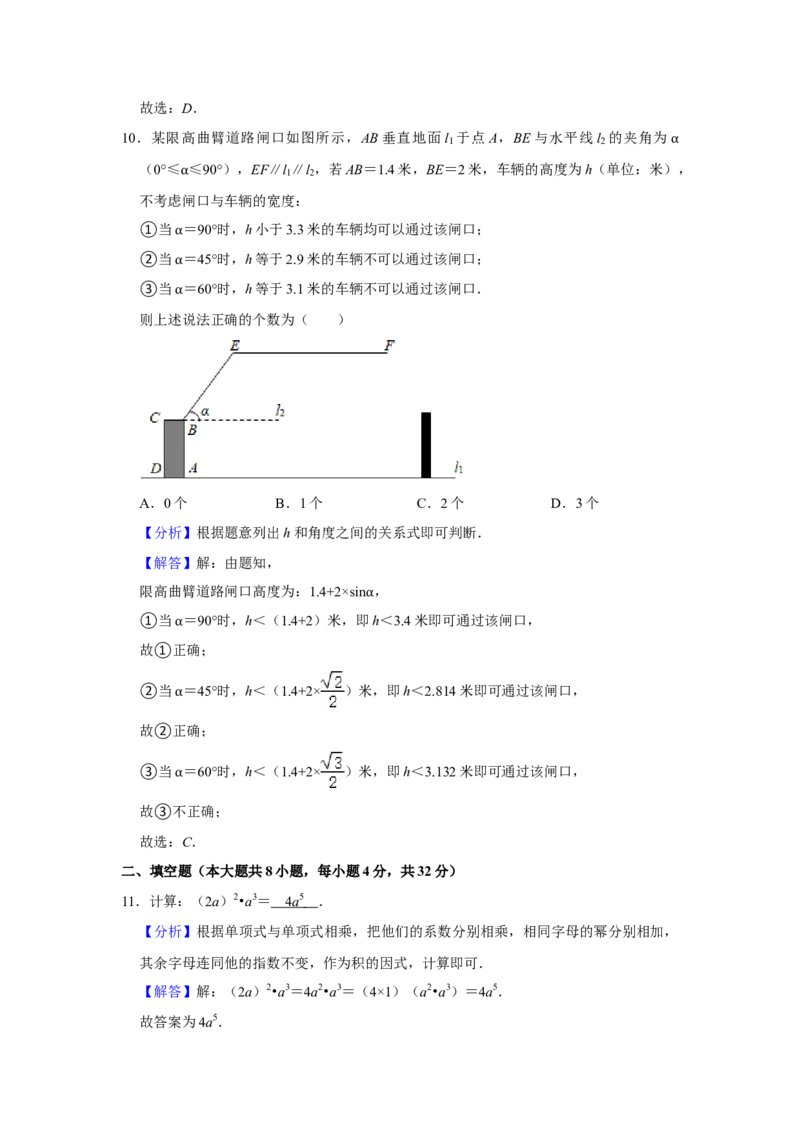
10.某限高曲臂道路闸口如图所示,AB垂直地面l 于点A,BE与水平线l 的夹角为
1 2
(0°≤ ≤90°),EF∥l ∥l ,若AB=1.4米,BE=2米,车辆的高度为h(单位:米)α,
1 2
不考虑α闸口与车辆的宽度:①当 =90°时,h小于3.3米的车辆均可以通过该闸口;
②当α=45°时,h等于2.9米的车辆不可以通过该闸口;
③当α=60°时,h等于3.1米的车辆不可以通过该闸口.
则上述α说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共8小题,每小题4分,共32分)
11.计算:(2a)2•a3= .
12.因式分解:6x2﹣4xy= .
13.据报道,2021 年全国高考报名人数为 1078 万,将 1078 万用科学记数法表示为
1.078×10n,则n= .
14.抛掷一枚质地均匀的硬币两次,则两次都是“正面朝上”的概率是
.
15.如图所示,线段BC为等腰△ABC的底边,矩形ADBE的对角线AB与DE交于点O,
若OD=2,则AC= .
16.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时
间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价(单位: 80 60 90
元/千克)
销售额(单位:元) 120 120 360则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
17.点A(x ,y )、B(x +1,y )是反比例函数y= 图象上的两点,满足:当x >0时,
1 1 1 2 1
均有y <y ,则k的取值范围是 .
1 2
18.《蝶几图》是明朝人戈汕所作的一部组合家具的设计图(“ ”为“蜨”,同
“蝶”),它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、
小三斜四只、大三斜两只,共十三只(图①中的“樣”和“隻”为“样”和“只”).
图②为某蝶几设计图,其中△ABD和△CBD为“大三斜”组件(“一樣二隻”的大三
斜组件为两个全等的等腰直角三角形),已知某人位于点P处,点P与点A关于直线
DQ对称,连接CP、DP.若∠ADQ=24°,则∠DCP= 度.
三、解答题(本大题共8小题,共78分)
19.(6分)计算:|﹣2|+ sin60°﹣2﹣1.
20.(8分)先化简,再求值: ,其中x= ﹣2.
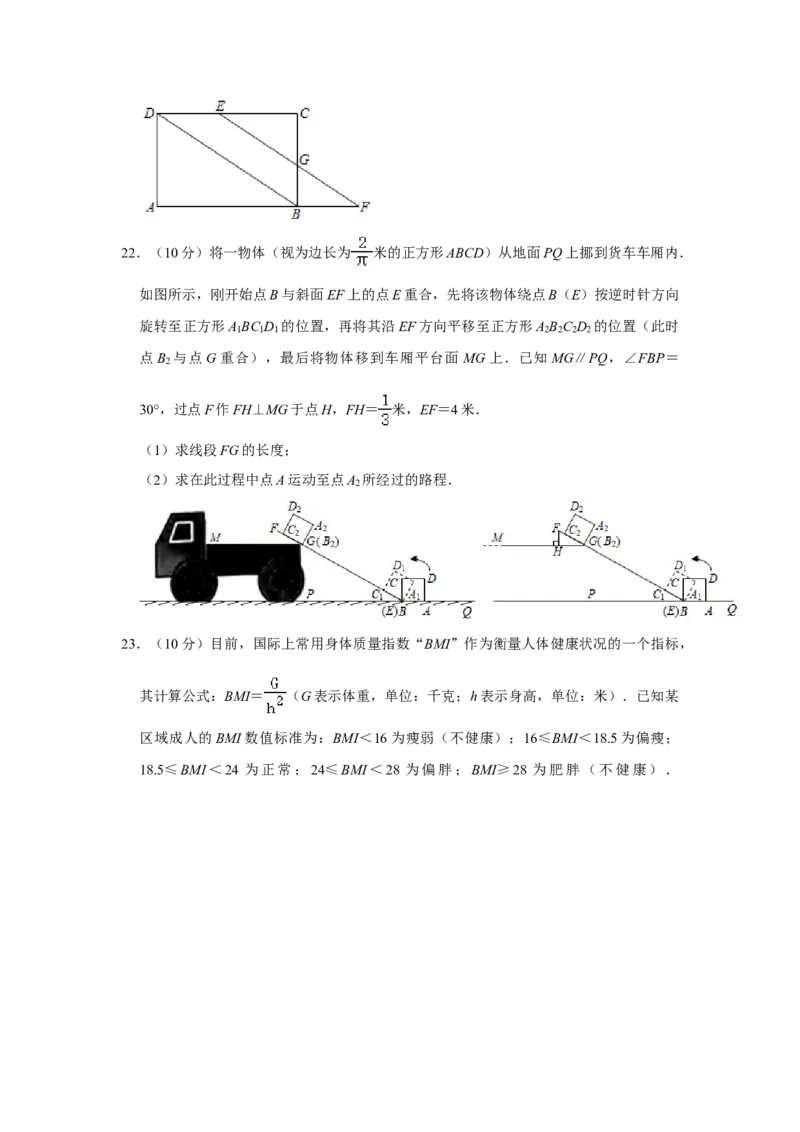
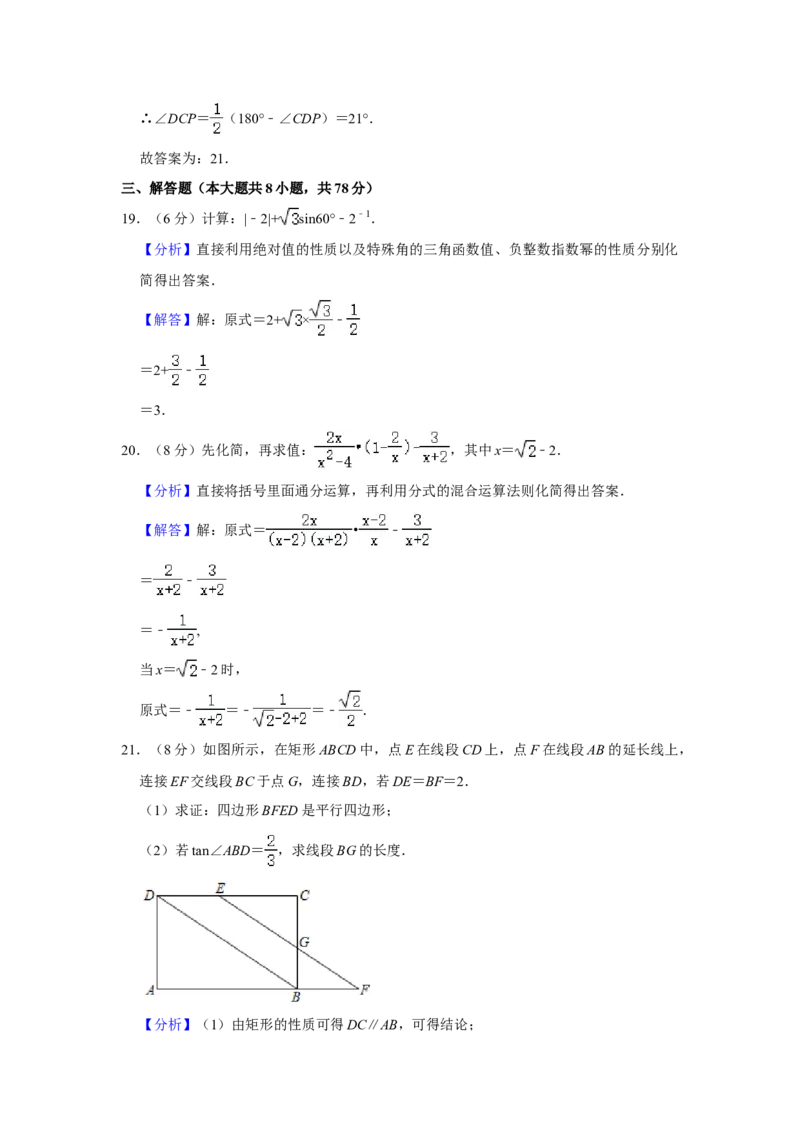
21.(8分)如图所示,在矩形ABCD中,点E在线段CD上,点F在线段AB的延长线上,
连接EF交线段BC于点G,连接BD,若DE=BF=2.
(1)求证:四边形BFED是平行四边形;
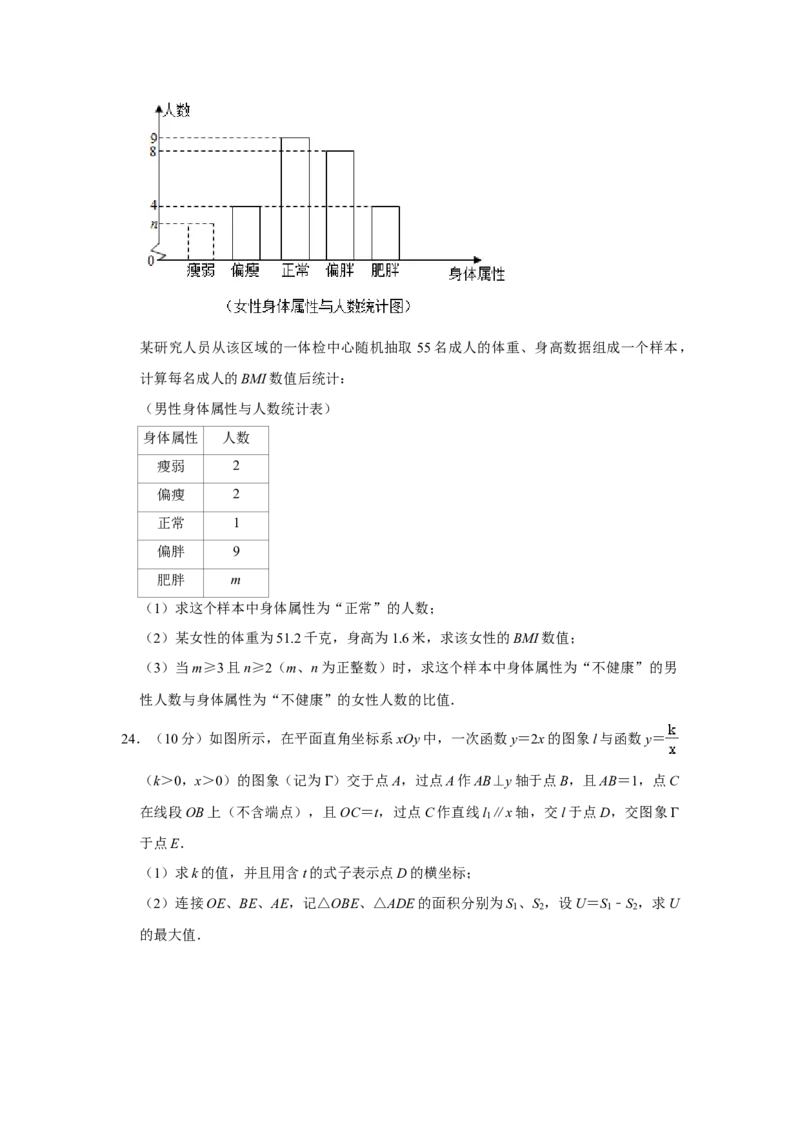
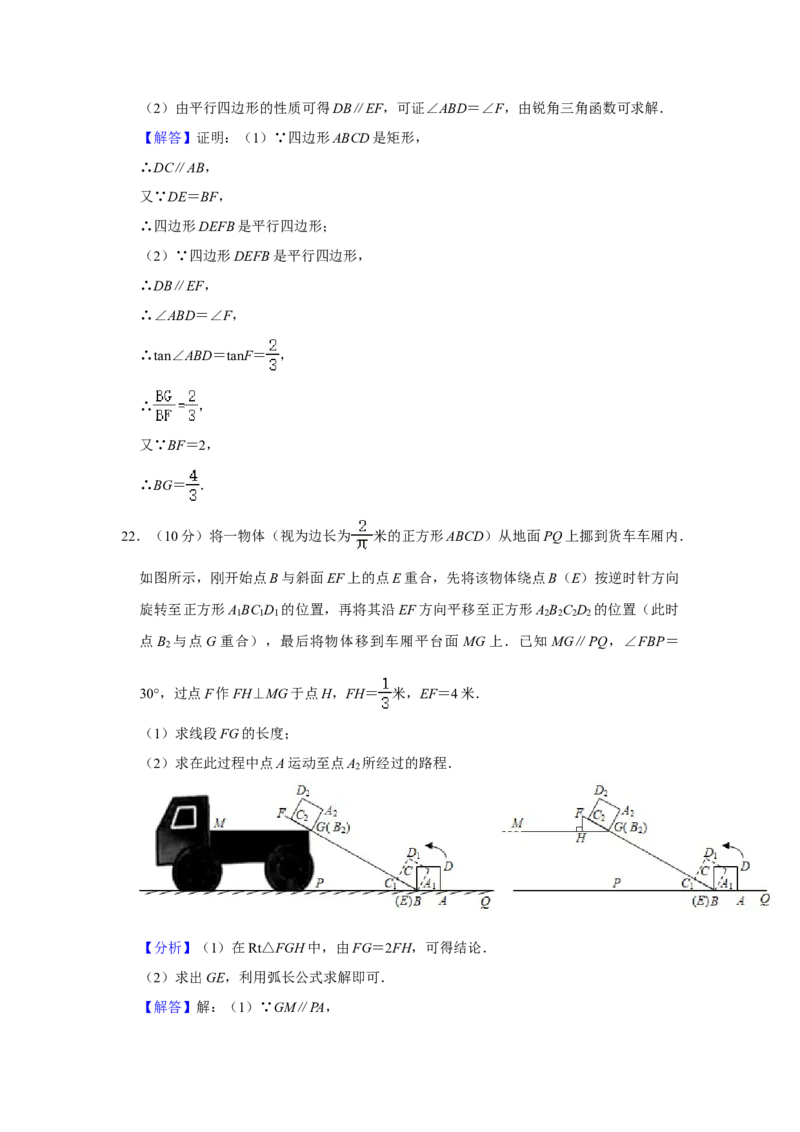
(2)若tan∠ABD= ,求线段BG的长度.22.(10分)将一物体(视为边长为 米的正方形ABCD)从地面PQ上挪到货车车厢内.
如图所示,刚开始点B与斜面EF上的点E重合,先将该物体绕点B(E)按逆时针方向
旋转至正方形A BC D 的位置,再将其沿EF方向平移至正方形A B C D 的位置(此时
1 1 1 2 2 2 2
点B 与点G重合),最后将物体移到车厢平台面 MG上.已知MG∥PQ,∠FBP=
2
30°,过点F作FH⊥MG于点H,FH= 米,EF=4米.
(1)求线段FG的长度;
(2)求在此过程中点A运动至点A 所经过的路程.
2
23.(10分)目前,国际上常用身体质量指数“BMI”作为衡量人体健康状况的一个指标,
其计算公式:BMI= (G表示体重,单位:千克;h表示身高,单位:米).已知某
区域成人的BMI数值标准为:BMI<16为瘦弱(不健康);16≤BMI<18.5为偏瘦;
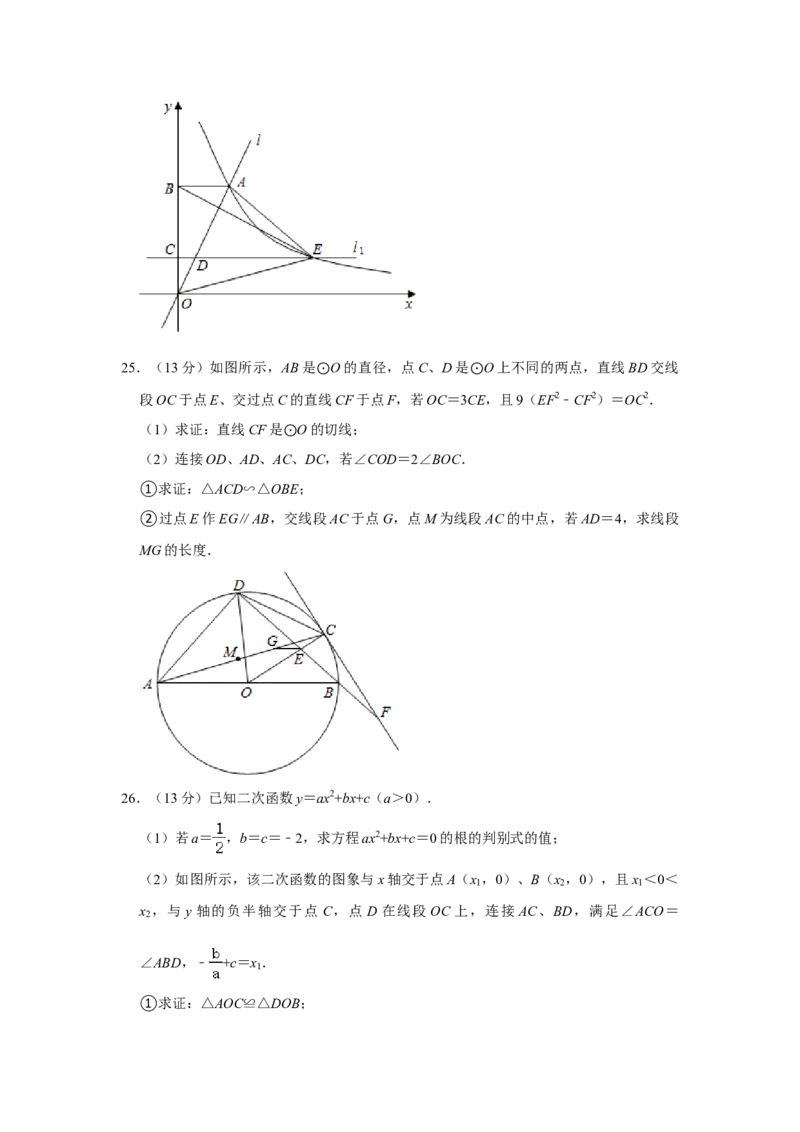
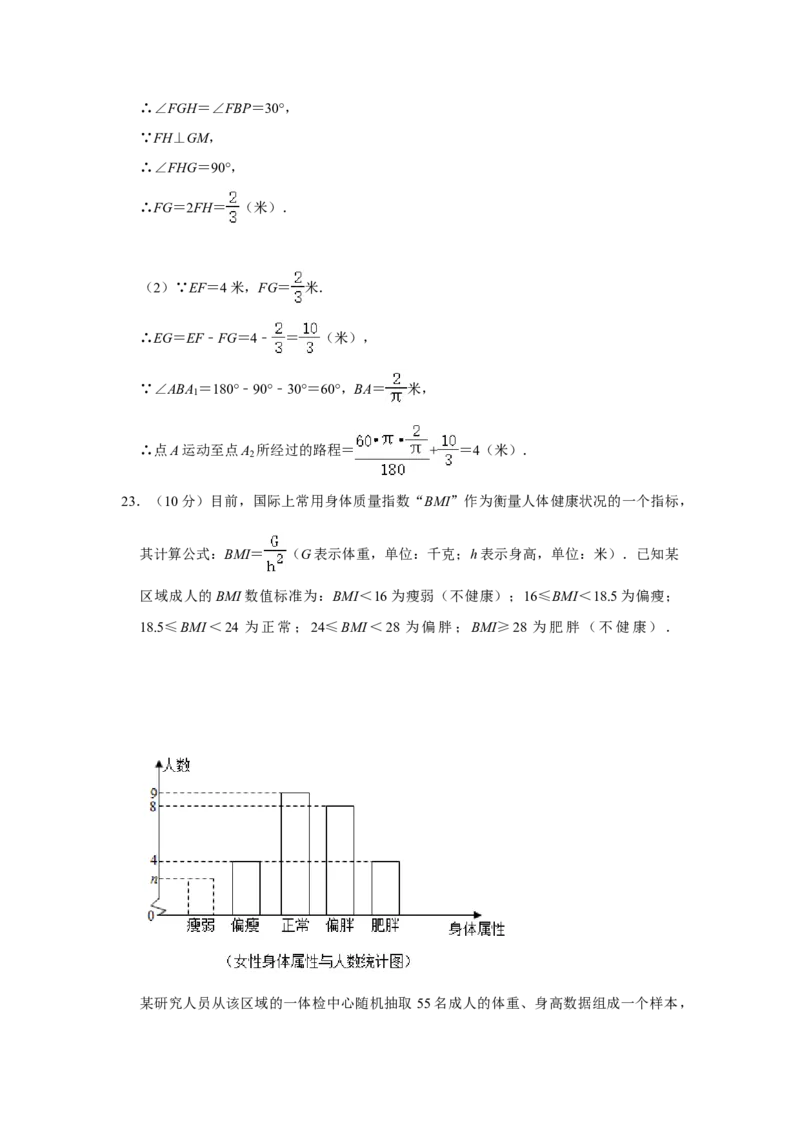
18.5≤BMI<24 为正常;24≤BMI<28 为偏胖;BMI≥28 为肥胖(不健康).某研究人员从该区域的一体检中心随机抽取 55名成人的体重、身高数据组成一个样本,
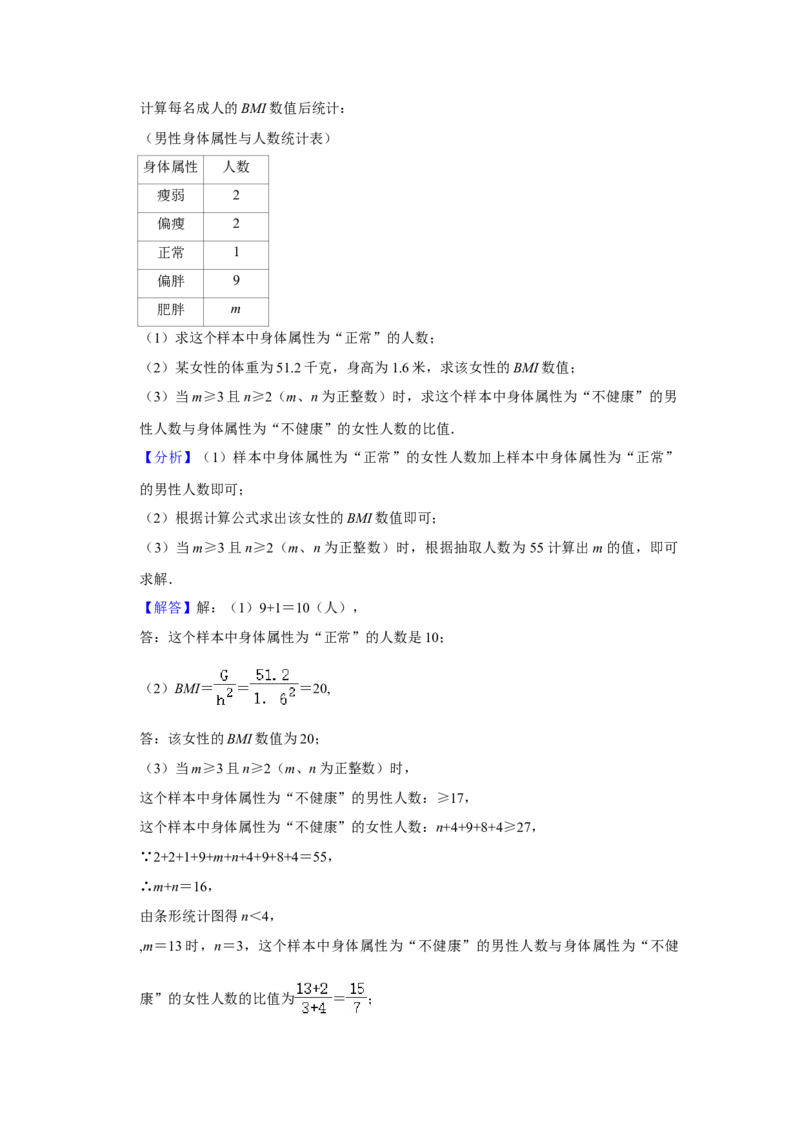
计算每名成人的BMI数值后统计:
(男性身体属性与人数统计表)
身体属性 人数
瘦弱 2
偏瘦 2
正常 1
偏胖 9
肥胖 m
(1)求这个样本中身体属性为“正常”的人数;
(2)某女性的体重为51.2千克,身高为1.6米,求该女性的BMI数值;
(3)当m≥3且n≥2(m、n为正整数)时,求这个样本中身体属性为“不健康”的男
性人数与身体属性为“不健康”的女性人数的比值.
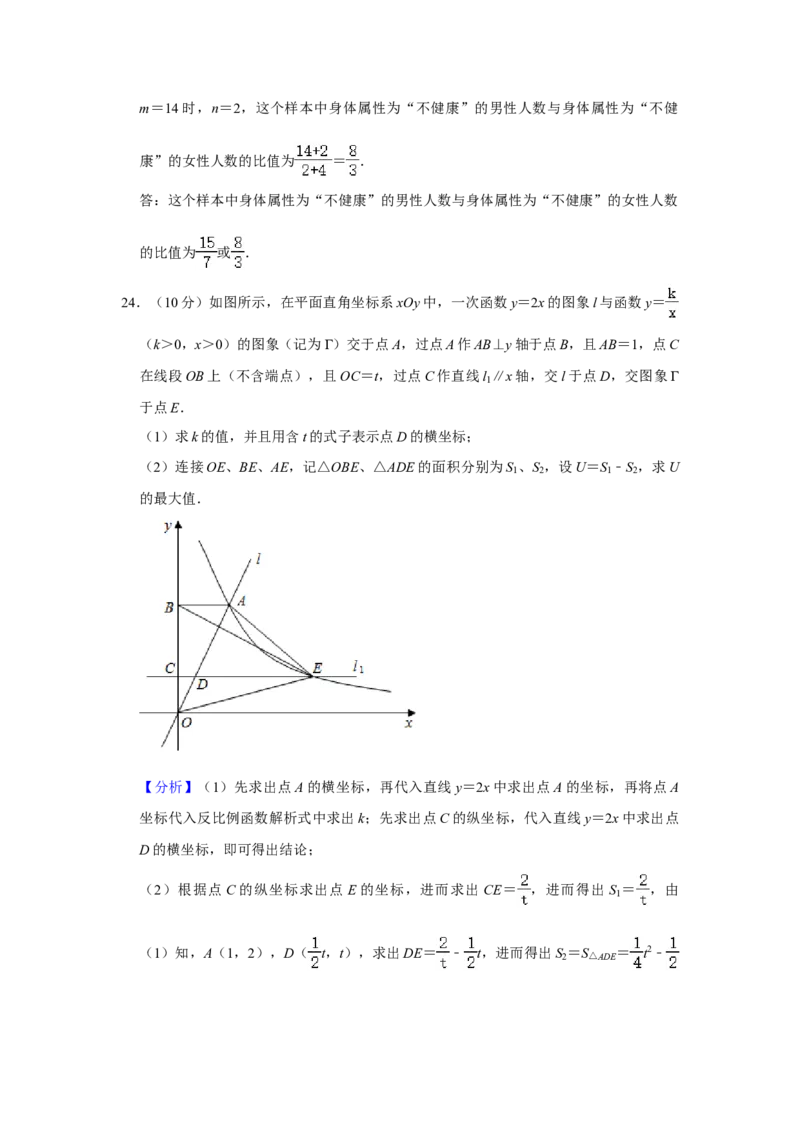
24.(10分)如图所示,在平面直角坐标系xOy中,一次函数y=2x的图象l与函数y=
(k>0,x>0)的图象(记为Г)交于点A,过点A作AB⊥y轴于点B,且AB=1,点C
在线段OB上(不含端点),且OC=t,过点C作直线l ∥x轴,交l于点D,交图象Г
1
于点E.
(1)求k的值,并且用含t的式子表示点D的横坐标;
(2)连接OE、BE、AE,记△OBE、△ADE的面积分别为S 、S ,设U=S ﹣S ,求U
1 2 1 2
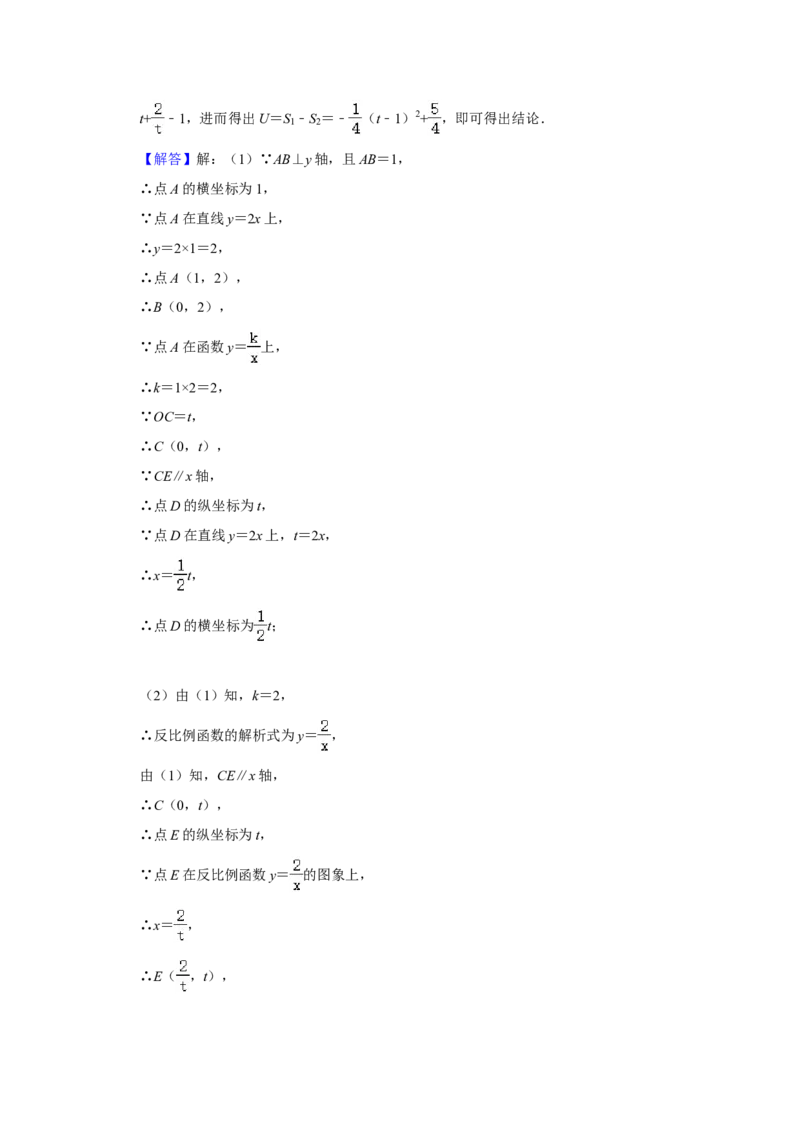
的最大值.25.(13分)如图所示,AB是 O的直径,点C、D是 O上不同的两点,直线BD交线
段OC于点E、交过点C的直⊙线CF于点F,若OC=3C⊙E,且9(EF2﹣CF2)=OC2.
(1)求证:直线CF是 O的切线;
(2)连接OD、AD、AC⊙、DC,若∠COD=2∠BOC.
①求证:△ACD∽△OBE;
②过点E作EG∥AB,交线段AC于点G,点M为线段AC的中点,若AD=4,求线段
MG的长度.
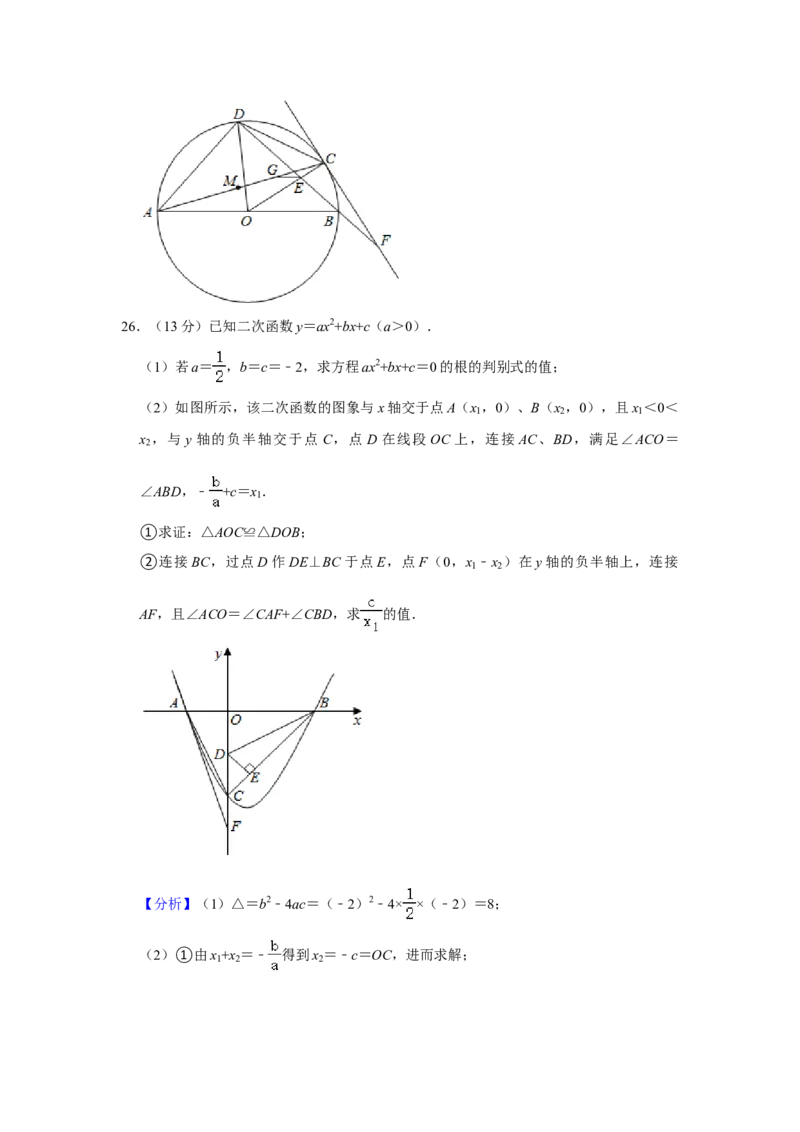
26.(13分)已知二次函数y=ax2+bx+c(a>0).
(1)若a= ,b=c=﹣2,求方程ax2+bx+c=0的根的判别式的值;
(2)如图所示,该二次函数的图象与x轴交于点A(x ,0)、B(x ,0),且x <0<
1 2 1
x ,与 y 轴的负半轴交于点 C,点 D 在线段 OC 上,连接 AC、BD,满足∠ACO=
2
∠ABD,﹣ +c=x .
1
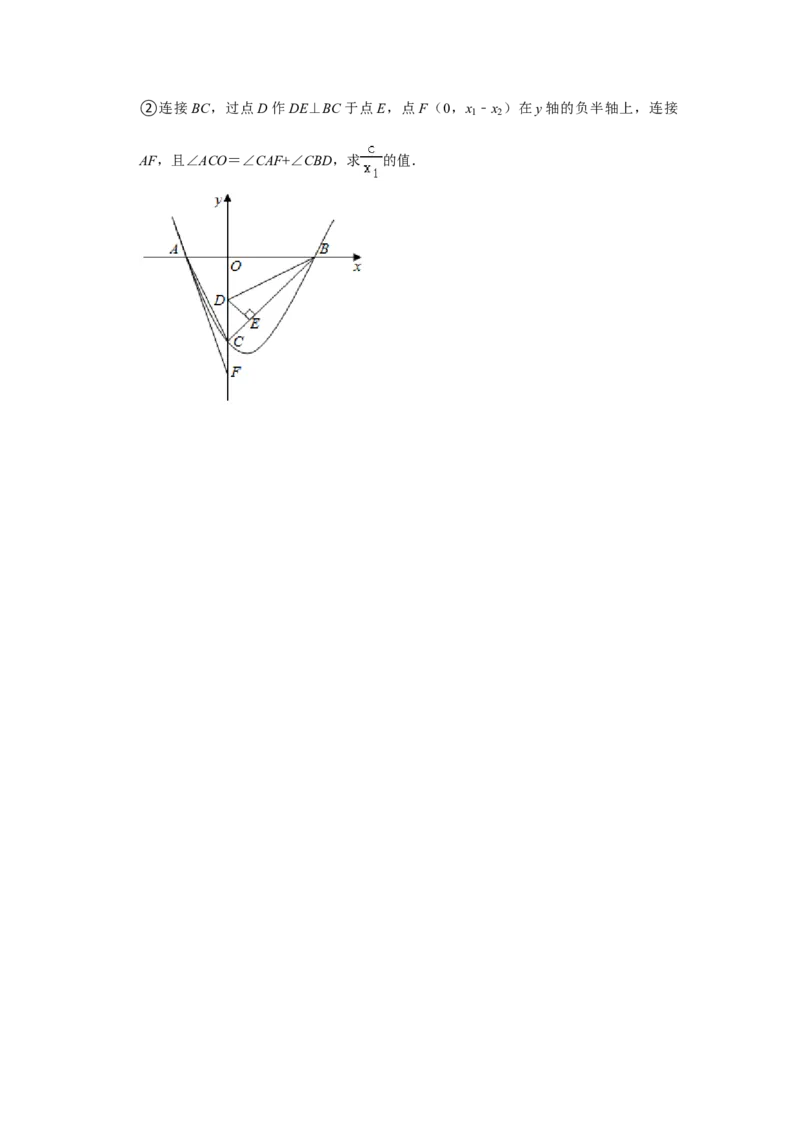
①求证:△AOC≌△DOB;②连接BC,过点D作DE⊥BC于点E,点F(0,x ﹣x )在y轴的负半轴上,连接
1 2
AF,且∠ACO=∠CAF+∠CBD,求 的值.2021年湖南省株洲市中考数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题有且只有一个正确答案,每小题4分,共40分)
1.若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
【分析】根据倒数的定义:乘积是1的两数互为倒数,即可得出答案.
【解答】解:∵a的倒数为2,
∴a= .
故选:A.
2.方程 ﹣1=2的解是( )
A.x=2 B.x=3 C.x=5 D.x=6
【分析】移项,合并同类项,系数化成1即可.
【解答】解: ﹣1=2,
移项,得 =2+1,
合并同类项,得 =3,
系数化成1,得x=6,
故选:D.
3.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=
132°,则∠A=( )
A.38° B.48° C.58° D.66°
【分析】根据平行四边形的外角的度数求得其相邻的内角的度数,然后求得其对角的度数即可.
【解答】解:∵∠DCE=132°,
∴∠DCB=180°﹣∠DCE=180°﹣132°=48°,
∵四边形ABCD是平行四边形,
∴∠A=∠DCB=48°,
故选:B.
4.某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错
误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多
【分析】根据图中给出的甲乙两人这10天的数据,依次判断A,B,C,D选项即可.
【解答】解:A.1日﹣10日,甲的步数逐天增加;故A正确,不符合题意;B.1日﹣
5日,乙的步数逐天减少;6日步数的比5日的步数多,故B错误,符合题意;
C.第9日,甲、乙两人的步数正好相等;故C正确,不符合题意;
D.第11日,甲的步数不一定比乙的步数多;故D正确,不符合题意;
故选:B.
5.计算: =( )
A.﹣2 B.﹣2 C.﹣ D.2
【分析】直接利用二次根式的性质化简得出答案.【解答】解:﹣4× =﹣4× =﹣2 .
故选:A.
6.《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”:“粟率五十,粝米三
十…”(粟指带壳的谷子,粝米指糙米),其意为:“50单位的粟,可换得30单位的
粝米…”.问题:有3斗的粟(1斗=10升),若按照此“粟米之法”,则可以换得的
粝米为( )
A.1.8升 B.16升 C.18升 D.50升
【分析】先将单位换成升,根据:“50单位的粟,可换得30单位的粝米…”列式可得
结论.
【解答】解:根据题意得:3斗=30升,
设可以换得的粝米为x升,
则 = ,
解得:x= =18(升),
答:有3斗的粟(1斗=10升),若按照此“粟米之法”,则可以换得的粝米为18升.
故选:C.
7.不等式组 的解集为( )
A.x<1 B.x≤2 C.1<x≤2 D.无解
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中
间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式x﹣2≤0,得:x≤2,
解不等式﹣x+1>0,得:x<1,
则不等式组的解集为x<1.
故选:A.
8.如图所示,在正六边形 ABCDEF 内,以 AB 为边作正五边形 ABGHI,则∠FAI=
( )A.10° B.12° C.14° D.15°
【分析】分别求出正六边形,正五边形的内角可得结论.
【解答】解:在正六边形ABCDEF内,正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB﹣∠IAB=120°﹣108°=12°,
故选:B.
9.二次函数y=ax2+bx+c(a≠0)的图象如图所示,点P在x轴的正半轴上,且OP=1,
设M=ac(a+b+c),则M的取值范围为( )
A.M<﹣1 B.﹣1<M<0 C.M<0 D.M>0
【分析】由图象得x=1时,y<0即a+b+c<0,当y=0时,得与x轴两个交点,x x =
1 2
<0,即可判断M的范围.
【解答】解:∵OP=1,P不在抛物线上,
∴当抛物线y=ax2+bx+c(a≠0),
x=1时,y=a+b+c<0,
当抛物线y=0时,得ax2+bx+c=0,
由图象知x x = <0,
1 2
∴ac<0,
∴ac(a+b+c)>0,
即M>0,故选:D.
10.某限高曲臂道路闸口如图所示,AB垂直地面l 于点A,BE与水平线l 的夹角为
1 2
(0°≤ ≤90°),EF∥l ∥l ,若AB=1.4米,BE=2米,车辆的高度为h(单位:米)α,
1 2
不考虑α闸口与车辆的宽度:
①当 =90°时,h小于3.3米的车辆均可以通过该闸口;
②当α=45°时,h等于2.9米的车辆不可以通过该闸口;
③当α=60°时,h等于3.1米的车辆不可以通过该闸口.
则上述α说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
【分析】根据题意列出h和角度之间的关系式即可判断.
【解答】解:由题知,
限高曲臂道路闸口高度为:1.4+2×sin ,
①当 =90°时,h<(1.4+2)米,即αh<3.4米即可通过该闸口,
故①正α确;
②当 =45°时,h<(1.4+2× )米,即h<2.814米即可通过该闸口,
α
故②正确;
③当 =60°时,h<(1.4+2× )米,即h<3.132米即可通过该闸口,
α
故③不正确;
故选:C.
二、填空题(本大题共8小题,每小题4分,共32分)
11.计算:(2a)2•a3= 4 a 5 .
【分析】根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,
其余字母连同他的指数不变,作为积的因式,计算即可.
【解答】解:(2a)2•a3=4a2•a3=(4×1)(a2•a3)=4a5.
故答案为4a5.12.因式分解:6x2﹣4xy= 2 x ( 3 x ﹣ 2 y ) .
【分析】直接提取公因式2x,即可分解因式得出答案.
【解答】解:6x2﹣4xy=2x(3x﹣2y).
故答案为:2x(3x﹣2y).
13.据报道,2021 年全国高考报名人数为 1078 万,将 1078 万用科学记数法表示为
1.078×10n,则n= 7 .
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,
据此判断即可.
【解答】解:1078万=10780000=1.078×107,
则n=7.
故答案为:7.
14.抛掷一枚质地均匀的硬币两次,则两次都是“正面朝上”的概率是 .
【分析】画树状图展示所有4种等可能的结果数,再找出两次都是“正面朝上”的结果
数,然后根据概率公式求解.
【解答】解:画树状图如下:
共有4种等可能的结果数,其中两次都是“正面朝上”的结果有1种,
∴两次都是“正面朝上”的概率= .
故答案为: .
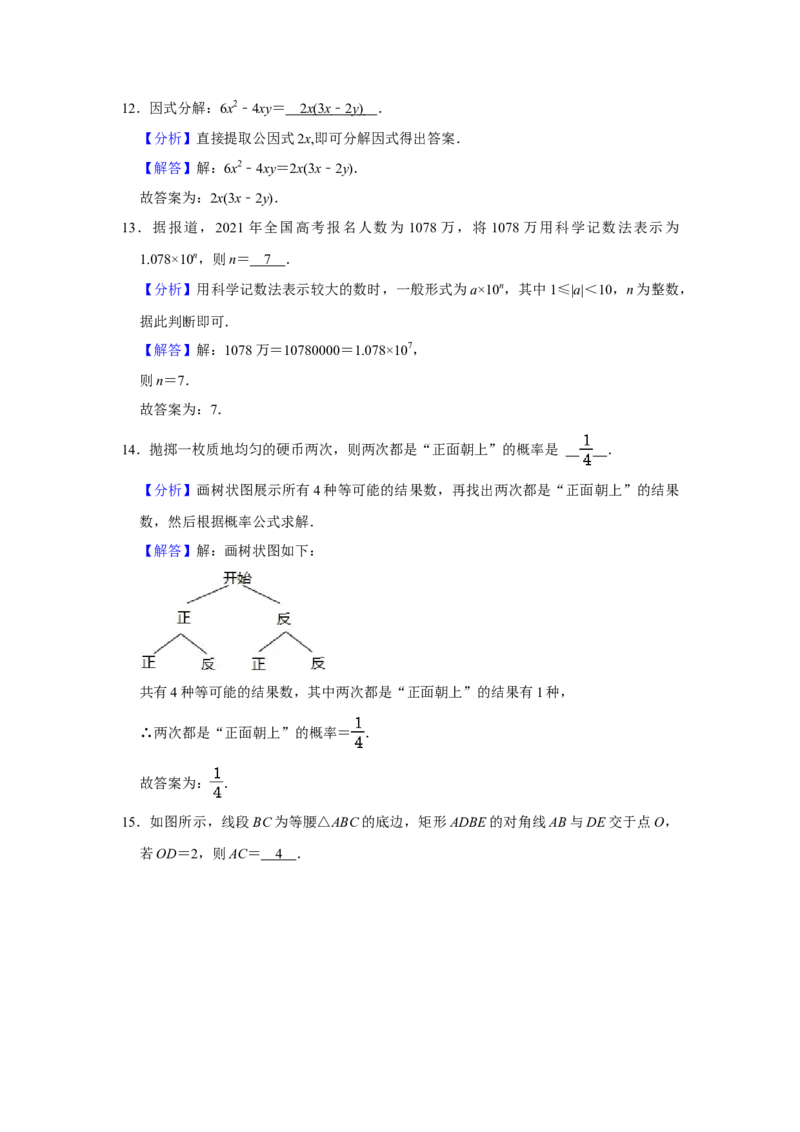
15.如图所示,线段BC为等腰△ABC的底边,矩形ADBE的对角线AB与DE交于点O,
若OD=2,则AC= 4 .【分析】由矩形的性质可得AB=2OD=4,由等腰三角形的性质可求解.
【解答】解:∵四边形ADBE是矩形,
∴AB=DE,AO=BO,DO=OE,
∴AB=DE=2OD=4,
∵AB=AC,
∴AC=4,
故答案为4.
16.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时
间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价(单位: 80 60 90
元/千克)
销售额(单位:元) 120 120 360
则在这个时间段,该中药房的这三种中药的平均销售量为 2. 5 千克.
【分析】利用销售数量=销售额÷销售单价,可分别求出黄芪、焦山楂、当归三种中药
的销售数量,再求出三者的算术平均数即可得出结论.
【解答】解:黄芪的销售量为120÷80=1.5(千克),
焦山楂的销售量为120÷60=2(千克),
当归的销售量为360÷90=4(千克).
该中药房的这三种中药的平均销售量为 =2.5(千克).
故答案为:2.5.
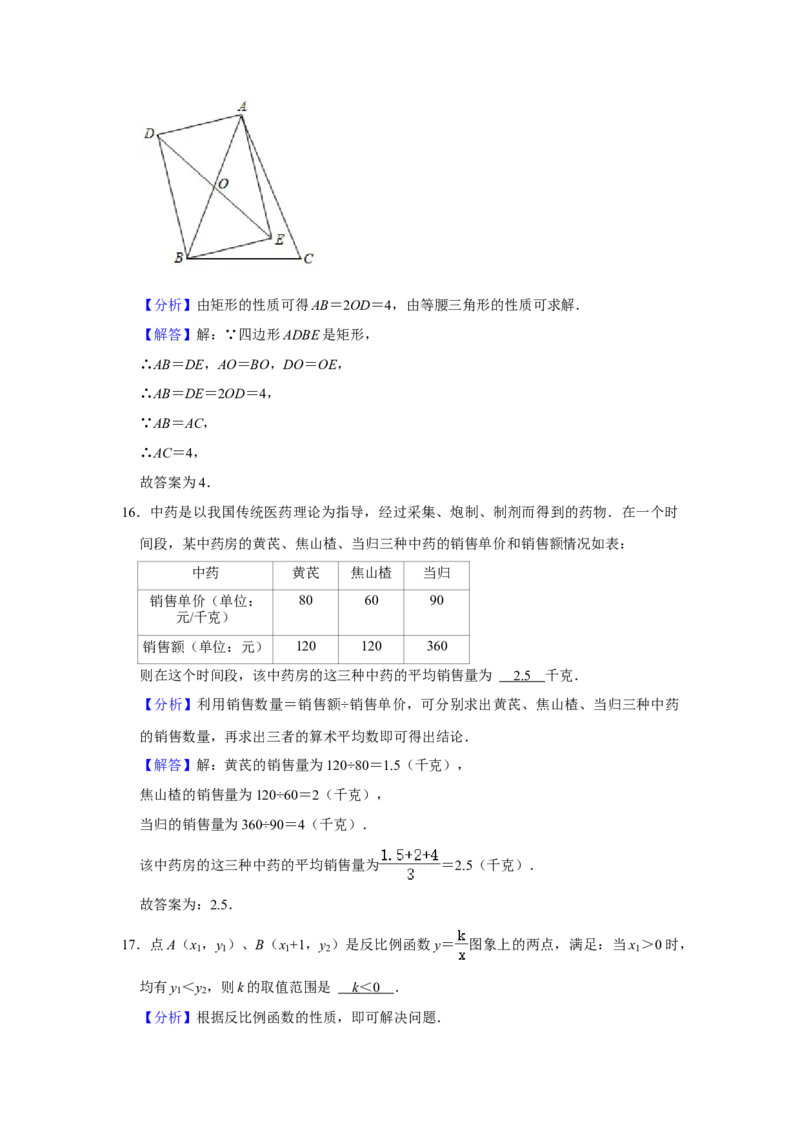
17.点A(x ,y )、B(x +1,y )是反比例函数y= 图象上的两点,满足:当x >0时,
1 1 1 2 1
均有y <y ,则k的取值范围是 k < 0 .
1 2
【分析】根据反比例函数的性质,即可解决问题.【解答】解:∵点A(x ,y )、B(x +1,y )是反比例函数y= 图象上的两点,
1 1 1 2
又∵0<x <x +1时,y <y ,
1 1 1 2
∴函数图象在二四象限,
∴k<0,
故答案为k<0.
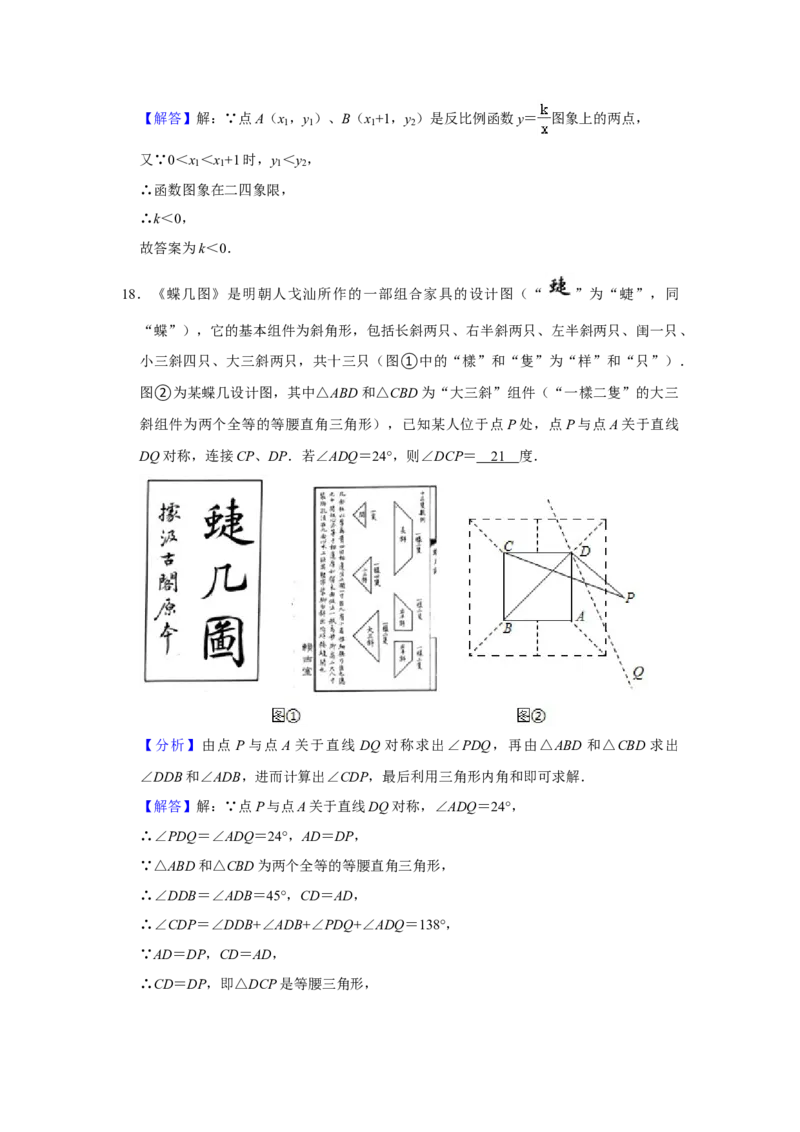
18.《蝶几图》是明朝人戈汕所作的一部组合家具的设计图(“ ”为“蜨”,同
“蝶”),它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、
小三斜四只、大三斜两只,共十三只(图①中的“樣”和“隻”为“样”和“只”).
图②为某蝶几设计图,其中△ABD和△CBD为“大三斜”组件(“一樣二隻”的大三
斜组件为两个全等的等腰直角三角形),已知某人位于点P处,点P与点A关于直线
DQ对称,连接CP、DP.若∠ADQ=24°,则∠DCP= 2 1 度.
【分析】由点 P 与点 A 关于直线 DQ 对称求出∠PDQ,再由△ABD 和△CBD 求出
∠DDB和∠ADB,进而计算出∠CDP,最后利用三角形内角和即可求解.
【解答】解:∵点P与点A关于直线DQ对称,∠ADQ=24°,
∴∠PDQ=∠ADQ=24°,AD=DP,
∵△ABD和△CBD为两个全等的等腰直角三角形,
∴∠DDB=∠ADB=45°,CD=AD,
∴∠CDP=∠DDB+∠ADB+∠PDQ+∠ADQ=138°,
∵AD=DP,CD=AD,
∴CD=DP,即△DCP是等腰三角形,∴∠DCP= (180°﹣∠CDP)=21°.
故答案为:21.
三、解答题(本大题共8小题,共78分)
19.(6分)计算:|﹣2|+ sin60°﹣2﹣1.
【分析】直接利用绝对值的性质以及特殊角的三角函数值、负整数指数幂的性质分别化
简得出答案.
【解答】解:原式=2+ × ﹣
=2+ ﹣
=3.
20.(8分)先化简,再求值: ,其中x= ﹣2.
【分析】直接将括号里面通分运算,再利用分式的混合运算法则化简得出答案.
【解答】解:原式= • ﹣
= ﹣
=﹣ ,
当x= ﹣2时,
原式=﹣ =﹣ =﹣ .
21.(8分)如图所示,在矩形ABCD中,点E在线段CD上,点F在线段AB的延长线上,
连接EF交线段BC于点G,连接BD,若DE=BF=2.
(1)求证:四边形BFED是平行四边形;
(2)若tan∠ABD= ,求线段BG的长度.
【分析】(1)由矩形的性质可得DC∥AB,可得结论;(2)由平行四边形的性质可得DB∥EF,可证∠ABD=∠F,由锐角三角函数可求解.
【解答】证明:(1)∵四边形ABCD是矩形,
∴DC∥AB,
又∵DE=BF,
∴四边形DEFB是平行四边形;
(2)∵四边形DEFB是平行四边形,
∴DB∥EF,
∴∠ABD=∠F,
∴tan∠ABD=tanF= ,
∴ ,
又∵BF=2,
∴BG= .
22.(10分)将一物体(视为边长为 米的正方形ABCD)从地面PQ上挪到货车车厢内.
如图所示,刚开始点B与斜面EF上的点E重合,先将该物体绕点B(E)按逆时针方向
旋转至正方形A BC D 的位置,再将其沿EF方向平移至正方形A B C D 的位置(此时
1 1 1 2 2 2 2
点B 与点G重合),最后将物体移到车厢平台面 MG上.已知MG∥PQ,∠FBP=
2
30°,过点F作FH⊥MG于点H,FH= 米,EF=4米.
(1)求线段FG的长度;
(2)求在此过程中点A运动至点A 所经过的路程.
2
【分析】(1)在Rt△FGH中,由FG=2FH,可得结论.
(2)求出GE,利用弧长公式求解即可.
【解答】解:(1)∵GM∥PA,∴∠FGH=∠FBP=30°,
∵FH⊥GM,
∴∠FHG=90°,
∴FG=2FH= (米).
(2)∵EF=4米,FG= 米.
∴EG=EF﹣FG=4﹣ = (米),
∵∠ABA =180°﹣90°﹣30°=60°,BA= 米,
1
∴点A运动至点A 所经过的路程= + =4(米).
2
23.(10分)目前,国际上常用身体质量指数“BMI”作为衡量人体健康状况的一个指标,
其计算公式:BMI= (G表示体重,单位:千克;h表示身高,单位:米).已知某
区域成人的BMI数值标准为:BMI<16为瘦弱(不健康);16≤BMI<18.5为偏瘦;
18.5≤BMI<24 为正常;24≤BMI<28 为偏胖;BMI≥28 为肥胖(不健康).
某研究人员从该区域的一体检中心随机抽取 55名成人的体重、身高数据组成一个样本,计算每名成人的BMI数值后统计:
(男性身体属性与人数统计表)
身体属性 人数
瘦弱 2
偏瘦 2
正常 1
偏胖 9
肥胖 m
(1)求这个样本中身体属性为“正常”的人数;
(2)某女性的体重为51.2千克,身高为1.6米,求该女性的BMI数值;
(3)当m≥3且n≥2(m、n为正整数)时,求这个样本中身体属性为“不健康”的男
性人数与身体属性为“不健康”的女性人数的比值.
【分析】(1)样本中身体属性为“正常”的女性人数加上样本中身体属性为“正常”
的男性人数即可;
(2)根据计算公式求出该女性的BMI数值即可;
(3)当m≥3且n≥2(m、n为正整数)时,根据抽取人数为55计算出m的值,即可
求解.
【解答】解:(1)9+1=10(人),
答:这个样本中身体属性为“正常”的人数是10;
(2)BMI= = =20,
答:该女性的BMI数值为20;
(3)当m≥3且n≥2(m、n为正整数)时,
这个样本中身体属性为“不健康”的男性人数:≥17,
这个样本中身体属性为“不健康”的女性人数:n+4+9+8+4≥27,
∵2+2+1+9+m+n+4+9+8+4=55,
∴m+n=16,
由条形统计图得n<4,
,m=13时,n=3,这个样本中身体属性为“不健康”的男性人数与身体属性为“不健
康”的女性人数的比值为 = ;m=14时,n=2,这个样本中身体属性为“不健康”的男性人数与身体属性为“不健
康”的女性人数的比值为 = .
答:这个样本中身体属性为“不健康”的男性人数与身体属性为“不健康”的女性人数
的比值为 或 .
24.(10分)如图所示,在平面直角坐标系xOy中,一次函数y=2x的图象l与函数y=
(k>0,x>0)的图象(记为Г)交于点A,过点A作AB⊥y轴于点B,且AB=1,点C
在线段OB上(不含端点),且OC=t,过点C作直线l ∥x轴,交l于点D,交图象Г
1
于点E.
(1)求k的值,并且用含t的式子表示点D的横坐标;
(2)连接OE、BE、AE,记△OBE、△ADE的面积分别为S 、S ,设U=S ﹣S ,求U
1 2 1 2
的最大值.
【分析】(1)先求出点A的横坐标,再代入直线y=2x中求出点A的坐标,再将点A
坐标代入反比例函数解析式中求出k;先求出点C的纵坐标,代入直线y=2x中求出点
D的横坐标,即可得出结论;
(2)根据点C的纵坐标求出点 E的坐标,进而求出 CE= ,进而得出S = ,由
1
(1)知,A(1,2),D( t,t),求出DE= ﹣ t,进而得出S
2
=S△ADE = t2﹣t+ ﹣1,进而得出U=S ﹣S =﹣ (t﹣1)2+ ,即可得出结论.
1 2
【解答】解:(1)∵AB⊥y轴,且AB=1,
∴点A的横坐标为1,
∵点A在直线y=2x上,
∴y=2×1=2,
∴点A(1,2),
∴B(0,2),
∵点A在函数y= 上,
∴k=1×2=2,
∵OC=t,
∴C(0,t),
∵CE∥x轴,
∴点D的纵坐标为t,
∵点D在直线y=2x上,t=2x,
∴x= t,
∴点D的横坐标为 t;
(2)由(1)知,k=2,
∴反比例函数的解析式为y= ,
由(1)知,CE∥x轴,
∴C(0,t),
∴点E的纵坐标为t,
∵点E在反比例函数y= 的图象上,
∴x= ,
∴E( ,t),∴CE= ,
∵B(0,2),
∴OB=2.
∴S
1
=S△OBE = OB•CE= ×2× =
由(1)知,A(1,2),D( t,t),
∴DE= ﹣ t,
∵CE∥x轴,
∴S
2
=S△ADE = DE(y
A
﹣y
D
)= ( ﹣ t)(2﹣t)= t2﹣ t+ ﹣1,
∴U=S ﹣S = ﹣( t2﹣ t+ ﹣1)=﹣ t2+ t+1=﹣ (t﹣1)2+ ,
1 2
∵点C在线段OB上(不含端点),
∴0<t<2,
∴当t=1时,U最大= .
25.(13分)如图所示,AB是 O的直径,点C、D是 O上不同的两点,直线BD交线
段OC于点E、交过点C的直⊙线CF于点F,若OC=3C⊙E,且9(EF2﹣CF2)=OC2.
(1)求证:直线CF是 O的切线;
(2)连接OD、AD、AC⊙、DC,若∠COD=2∠BOC.
①求证:△ACD∽△OBE;
②过点E作EG∥AB,交线段AC于点G,点M为线段AC的中点,若AD=4,求线段
MG的长度.【分析】(1)利用勾股定理的逆定理证明∠ECF=90°,可得结论.
(2)①证明∠DAC=∠EOB,∠DCA=∠EBO,可得结论.
②利用相似三角形的性质求出AC,再求出CM,CG,可得结论.
【解答】(1)证明:∵9(EF2﹣CF2)=OC2,OC=3OE,
∴9(EF2﹣CF2)=9EC2,
∴EF2=EC2+CF2,
∴∠ECF=90°,
∴OC⊥CF,
∴直线CF是 O的切线.
⊙
(2)①证明:∵∠COD=2∠DAC,∠COD=2∠BOC,
∴∠DAC=∠EOB,
∵∠DCA=∠EBO,
∴△ACD∽△OBE.
②解:∵OB=OC,OC=3EC,
∴OB:OE=3:2,
∵△ACD∽△OBE,
∴ = ,
∴ = = ,
∵AD=4,
∴AC=6,
∵M是AC的中点,
∴CM=MA=3,
∵EG∥OA,
∴ = = ,
∴CG=2,
∴MG=CM﹣CG=3﹣2=1.26.(13分)已知二次函数y=ax2+bx+c(a>0).
(1)若a= ,b=c=﹣2,求方程ax2+bx+c=0的根的判别式的值;
(2)如图所示,该二次函数的图象与x轴交于点A(x ,0)、B(x ,0),且x <0<
1 2 1
x ,与 y 轴的负半轴交于点 C,点 D 在线段 OC 上,连接 AC、BD,满足∠ACO=
2
∠ABD,﹣ +c=x .
1
①求证:△AOC≌△DOB;
②连接BC,过点D作DE⊥BC于点E,点F(0,x ﹣x )在y轴的负半轴上,连接
1 2
AF,且∠ACO=∠CAF+∠CBD,求 的值.
【分析】(1)△=b2﹣4ac=(﹣2)2﹣4× ×(﹣2)=8;
(2)①由x +x =﹣ 得到x =﹣c=OC,进而求解;
1 2 2②证明∠CBD=∠AFO,而tan∠CBD= = = ,tan∠AFO=
= = =tan∠CBD= ,即可求解.
【解答】解:(1)当若a= ,b=c=﹣2时,△=b2﹣4ac=(﹣2)2﹣4× ×(﹣2)
=8;
(2)①设ax2+bx+c=0,则x +x =﹣ ,x x = ,
1 2 1 2
则 +x =﹣x =c,即x =﹣c=OC,x = ÷x =﹣ ,
1 2 2 1 2
∵OB=x =CO,∠ACO=∠ABD,∠COA=∠BOD=90°,
2
∴△AOC≌△DOB(AAS);
②∵∠OCA=∠CAF+∠CFA,∠ACO=∠CAF+∠CBD,
∴∠CBD=∠AFO,
∵OB=OC,故∠OCD=45°,
∵CD=OC﹣OD=OC﹣OA=﹣c﹣ ,
则DE= CD=﹣ (c+ )=CE,
则BE=BC﹣CE= OB﹣CE=﹣ c+ (﹣c+ ),
则tan∠CBD= = = ,而tan∠AFO= = = =tan∠CBD= ,
解得ca=﹣2,
而 = =﹣ac=2,
故 的值为2.