文档内容
2022 年湖南省岳阳市中考数学试卷
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,共24分)
8的相反数是()
1. 1 1
A. B. 8 C. − D. −8
8 8
某个立体图形的侧面展开图如图所示,它的底面是正三
2. 角形,那么这个立体图形是()
A. 圆柱
B. 圆锥
C. 三棱柱
D. 四棱柱
下列运算结果正确的是()
3.
A. a+2a=3a B. a5÷a=a5 C. a2 ⋅a3=a6 D. (a4 ) 3=a7
某村通过直播带货对产出的稻虾米进行线上销售,连续7天的销量(单位:袋)分别
4. 为:105,103,105,110,108,105,108,这组数据的众数和中位数分别是
()
A. 105,108 B. 105,105 C. 108,105 D. 108,108
如图,已知l//AB,CD⊥l于点D,若
5. ∠C=40°,则∠1的度数是()
A. 30°
B. 40°
C. 50°
D. 60°
下列命题是真命题的是()
6A.. 对顶角相等
B. 平行四边形的对角线互相垂直
C. 三角形的内心是它的三条边的垂直平分线的交点
D. 三角分别相等的两个三角形是全等三角形
第 页,共 页
学科网(北京)股份有限公司
1 1我国古代数学著作《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家
7. 取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?大意为:今有100头鹿
进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中
有多少户人家?在这个问题中,城中人家的户数为()
A. 25 B. 75 C. 81 D. 90
已知二次函数y=mx2−4m2x−3(m为常数,m≠0),点P(x ,y )是该函数图
p p
8.
象上一点,当0≤x ≤4时,y ≤−3,则m的取值范围是()
p p
A. m≥1或m<0 B. m≥1
C. m≤−1或m>0 D. m≤−1
二、填空题(本大题共8小题,共32分)
要使√x−1有意义,则x的取值范围是______.
9. 2022年5月14日,编号为B−001J的C919大飞机首飞成功.数据显示,C919
10. 大飞机的单价约为653000000元,数据653000000用科学记数法表示为______.
如图,在△ABC中,AB=AC,AD⊥BC于点D,
11. 若BC=6,则CD=______.
3x
分式方程 =2的解为x=______.
x+1
12.
已知关于x的一元二次方程x2+2x+m=0有两个不相等的实数根,则实数m的取
13. 值范围是______.
聚焦“双减”政策落地,凸显寒假作业特色.某学校评选出的寒假优质特色作业
14. 共分为四类:A(节日文化篇),B(安全防疫篇),C(劳动实践篇),D(冬奥运动篇
).下面是根据统计结果绘制的两幅不完整的统计图,则B类作业有______份.
第 页,共 页
2 2喜迎二十大,“龙舟故里”赛龙舟.丹丹在汩罗江国际龙舟竞渡中心广场点P处
15. 观看200米直道竞速赛.如图所示,赛道AB为东西方向,赛道起点A位于点P的
北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200米,则点P到
赛道AB的距离约为______米(结果保留整数,参考数据:√3≈1.732).
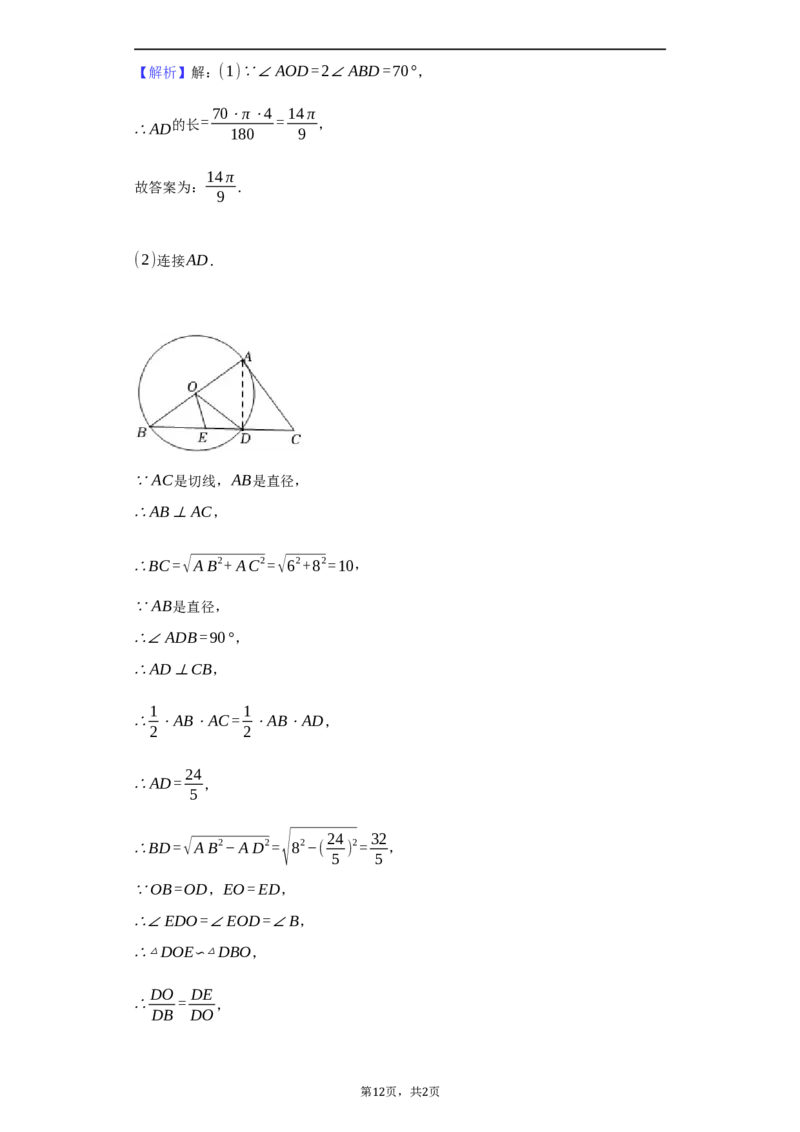
如图,在⊙O中,AB为直径,AB=8,BD为
16. 弦,过点A的切线与BD的延长线交于点C,E
为线段BD上一点(不与点B重合),且OE=DE.
⏜
(1)若∠B=35°,则 的长为______(结果保
AD
留π);
DE
(2)若AC=6,则 =______.
BE
三、解答题(本大题共8小题,共64分)
计算:|−3|−2tan45°+(−1) 2022−(√3−π) 0.
17.
已知a2−2a+1=0,求代数式a(a−4)+(a+1)(a−1)+1的值.
18.
如图,点E,F分别在▱ABCD的边AB,BC上,AE=CF,连接DE,DF.请从
19. 以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作
为已知条件,使▱ABCD为菱形.
(1)你添加的条件是______(填序号);
(2)添加了条件后,请证明▱ABCD为菱形.
第 页,共 页
学科网(北京)股份有限公司
3 1守护好一江碧水,打造长江最美岸线.江豚,麋鹿,天鹅已成为岳阳“吉祥三
20. 宝”的新名片.某校生物兴趣小组设计了3张环保宣传卡片,正面图案如图所示,
它们除此之外完全相同.
(1)将这3张卡片背面朝上,洗匀,从中随机抽取一张,则抽取的卡片正面图案恰
好是“麋鹿”的概率为______;
(2)将这3张卡片背面朝上,洗匀,从中随机抽取一张,不放回,再从剩余的两张
卡片中随机抽取一张,请用列表或画树状图的方法,求抽取的卡片正面图案恰好
是“江豚”和“天鹅”的概率.
k
如图,反比例函数y= (k≠0)与正比例函数y=mx(m≠0)的图象交于点
x
21.
A(−1,2)和点B,点C是点A关于y轴的对称点,连接AC,BC.
(1)求该反比例函数的解析式;
(2)求△ABC的面积;
k
(3)请结合函数图象,直接写出不等式 0时,对称轴x=2m>0,
此时,当x=4时,y≤−3,即m⋅42−4m2 ⋅4−3≤−3,
解得m≥1;
②当m<0时,对称轴x=2m<0,
当0≤x≤4时,y随x增大而减小,
第 页,共 页
8 2则当0≤x ≤4时,y ≤−3恒成立;
p p
综上,m的取值范围是:m≥1或m<0.
故选:A.
先求出抛物线的对称轴及抛物线与y轴的交点坐标,再分两种情况:m>0或m<0,根
据二次函数的性质求得m的不同取值范围便可.
本题考查了二次函数的性质,关键是分情况讨论.
9.【答案】x≥1
【解析】解:由题意得:x−1≥0,
解得:x≥1,
故答案为:x≥1.
根据二次根式的被开方数是非负数列出不等式,解不等式得到答案.
本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关
键.
10.【答案】6.53×108
【解析】解:653000000=6.53×108.
故答案为:6.53×108.
利用科学记数法的定义解决.
考查科学记数法的定义,关键是理解运用科学记数法.
11.【答案】3
【解析】解:∵AB=AC,AD⊥BC,
∴CD=BD,
∵BC=6,
∴CD=3,
故答案为:3.
根据等腰三角形的性质可知D是BC的中点,即可求出CD的长.
本题考查了等腰三角形的性质,熟练掌握等腰三角形三线合一是解题的关键.
12.【答案】2
第 页,共 页
学科网(北京)股份有限公司
9 13x
【解析】解: =2,
x+1
3x=2x+2,
x=2,
经检验x=2是方程的解,
故答案为:2.
去分母,移项、合并同类项,再求所求的根进行检验即可求解.
本题考查解分式方程,熟练掌握分式方程的解法,注意对所求的根进行检验是解题的
关键.
13.【答案】m<1
【解析】解:根据题意得Δ=22−4×1×m>0,
解得m<1,
所以实数m的取值范围是m<1.
故答案为:m<1.
根据判别式的意义得到Δ=22−4×1×m>0,然后解不等式求出m的取值即可.
本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如
下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数
根;当Δ<0时,方程无实数根.
14.【答案】20
【解析】解:∵C类作业有30份,且C类作业份数占总份数的30%,
∴总份数为:30÷30%=100(份),
∵A,D类作业分别有25份,25份,
∴B类作业的份数为:100−25−30−25=20(份),
故答案为:20.
由条形统计图可得A,C,D类作业分别有25份,30份,25份,由扇形统计图可得C
类作业份数占总份数的30%,可得总份数为100份,减去A,C,D类作业的份数即可
求解.
本题考查条形统计图,扇形统计图,解题的关键是能够根据统计图提取所需信息.
第 页,共 页
10 215.【答案】87
【解析】解:过点P作PC⊥AB,垂足为P,
设PC=x米,
在Rt△APC中,∠APC=30°,
√3
∴AC=PC⋅tan30°= x(米),
3
在Rt△CBP中,∠CPB=60°,
∴BC=CP⋅tan60°=√3x(米),
∵AB=200米,
∴AC+BC=200,
√3
∴ x+√3x=200,
3
∴x=50√3≈87,
∴PC=87米,
∴点P到赛道AB的距离约为87米,
故答案为:87.
过点P作PC⊥AB,垂足为P,设PC=x米,然后分别在Rt△APC和Rt△CBP中,
利用锐角三角函数的定义求出AC,BC的长,再根据AB=200米,列出关于x的方程,
进行计算即可解答.
本题考查了解直角三角形的应用−方向角问题,根据题目的已知条件并结合图形添加
适当的辅助线是解题的关键.
14π 25
16.【答案】
9 39
第 页,共 页
学科网(北京)股份有限公司
11 1【解析】解:(1)∵∠AOD=2∠ABD=70°,
⏜ 的长=
70⋅π⋅4
=
14π
,
∴AD
180 9
14π
故答案为: .
9
(2)连接AD.
∵AC是切线,AB是直径,
∴AB⊥AC,
∴BC=√AB2+AC2=√62+82=10,
∵AB是直径,
∴∠ADB=90°,
∴AD⊥CB,
1 1
∴ ⋅AB⋅AC= ⋅AB⋅AD,
2 2
24
∴AD= ,
5
√ 24 32
∴BD=√AB2−AD2= 82−( ) 2= ,
5 5
∵OB=OD,EO=ED,
∴∠EDO=∠EOD=∠B,
∴△DOE △DBO,
∽
DO DE
∴ = ,
DB DO
第 页,共 页
12 24 DE
∴ =
32 4 ,
5
5
∴DE= ,
2
32 5 39
∴BE=BD−DE= − = ,
5 2 10
5
DE 2 25
∴ = = .
BE 39 39
10
25
故答案为: .
39
(1)利用弧长公式求解;
(2)解直角三角形求出BC,AD,BD,再利用相似三角形的性质求出DE,BE,可得
结论.
本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找相
似三角形解决问题,属于中考常考题型.
17.【答案】解:|−3|−2tan45°+(−1) 2022−(√3−π) 0
=3−2×1+1−1
=3−2+1−1
=1.
【解析】先化简各式,然后再进行计算即可解答.
本题考查了特殊角的三角函数值,零指数幂,实数的运算,有理数的乘方,绝对值,
准确熟练地化简各式是解题的关键.
18.【答案】解:a(a−4)+(a+1)(a−1)+1
=a2−4a+a2−1+1
=2a2−4a
=2(a2−2a),
第 页,共 页
学科网(北京)股份有限公司
13 1∵a2−2a+1=0,
∴a2−2a=−1,
∴原式=2×(−1)=−2.
【解析】先化简所求的式子,再结合已知求解即可.
本题考查代数式的运算,熟练掌握单项式乘多项式,平方差公式是解题的关键.
19.【答案】①
【解析】(1)解:添加的条件是∠1=∠2,
故答案为:①;
(2)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△ADE和△CDF中,
{∠1=∠2
∠A=∠C,
AE=CF
∴△ADE △CDF(AAS),
∴AD=C≌D,
∴▱ABCD为菱形.
(1)添加合适的条件即可;
(2)证△ADE △CDF(AAS),得AD=CD,再由菱形的判定即可得出结论.
本题考查了菱≌形的判定、平行四边形的性质、全等三角形的判定与性质等知识,熟练
掌握菱形的判定,证明三角形全等是解题的关键.
1
20.【答案】
3
【解析】解:(1)将这3张卡片背面朝上,洗匀,从中随机抽取一张,
1
则抽取的卡片正面图案恰好是“麋鹿”的概率为 ,
3
1
故答案为: ;
3
(2)将江豚,麋鹿,天鹅三张卡片分别记作①、②、③,
列表如下:
第 页,共 页
14 2① ② ③
① (②,①) (③,①)
② (①,②) (③,②)
③ (①,③) (②,③)
由表知,共有6种等可能结果,其中抽取的卡片正面图案恰好是“江豚”和“天鹅”的
有2种结果,
2 1
所以抽取的卡片正面图案恰好是“江豚”和“天鹅”的概率为 = .
6 3
(1)直接利用概率公式求解即可;
(2)将江豚,麋鹿,天鹅三张卡片分别记作①、②、③,列表得出所有等可能结果,
从中找到符合条件的结果数,再根据概率公式求解即可.
此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数
之比.
k k
21.【答案】解:(1)把点A(−1,2)代入y= (k≠0)得:2= ,
x −1
∴k=−2,
2
∴反比例函数的解析式为y=− ;
x
k
(2)∵反比例函数y= (k≠0)与正比例函数y=mx(m≠0)的图象交于点A(−1,2)和
x
点B,
∴B(1,−2),
∵点C是点A关于y轴的对称点,
∴C(1,2),
∴CD=2,
1
∴S = ×2×(2+2)=4.
△ABC 2
k
(3)根据图象得:不等式