文档内容
2021年贵州省黔东南州中考数学试卷
一、选择题(每小题4分,10个小题共40分.)
1.2021的相反数是( )
A.2021 B.﹣2021 C. D.
2.下列运算正确的是( )
A. + = B.a3•a2= 6
C.(a3)2=a6 D.a2﹣b2=α(a﹣b)2
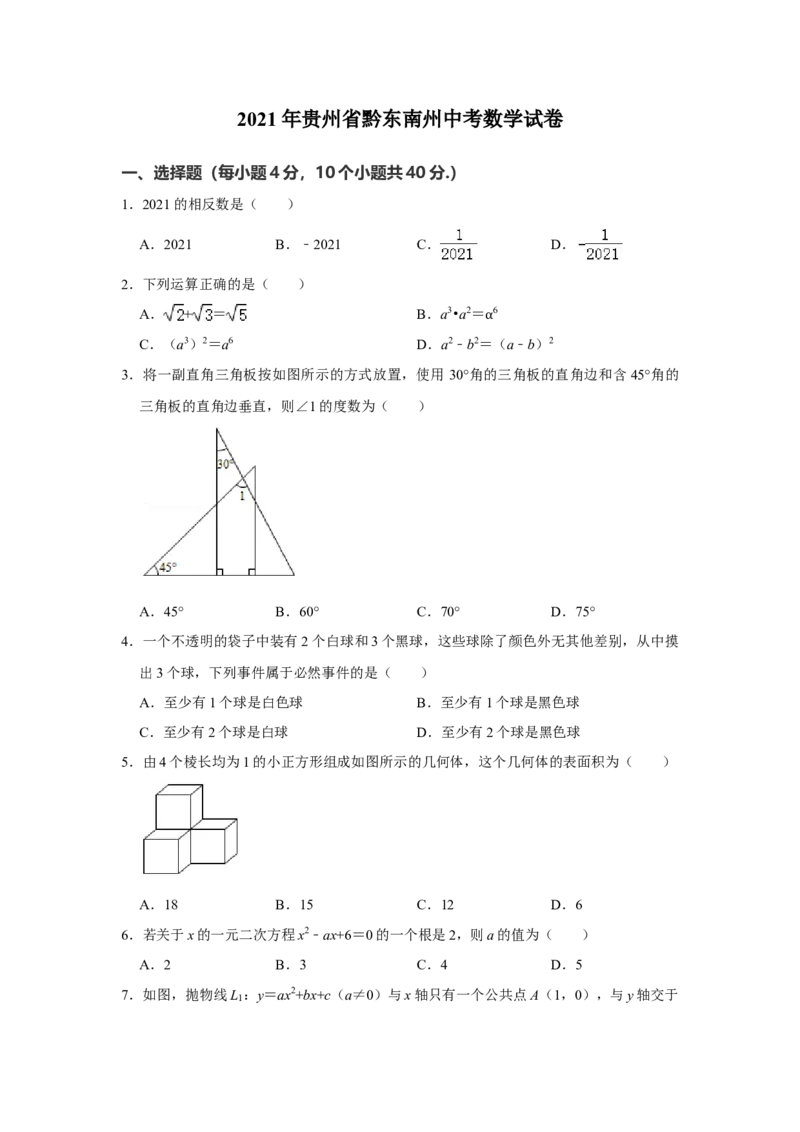
3.将一副直角三角板按如图所示的方式放置,使用 30°角的三角板的直角边和含45°角的
三角板的直角边垂直,则∠1的度数为( )
A.45° B.60° C.70° D.75°
4.一个不透明的袋子中装有2个白球和3个黑球,这些球除了颜色外无其他差别,从中摸
出3个球,下列事件属于必然事件的是( )
A.至少有1个球是白色球 B.至少有1个球是黑色球
C.至少有2个球是白球 D.至少有2个球是黑色球
5.由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )
A.18 B.15 C.12 D.6
6.若关于x的一元二次方程x2﹣ax+6=0的一个根是2,则a的值为( )
A.2 B.3 C.4 D.5
7.如图,抛物线L :y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于
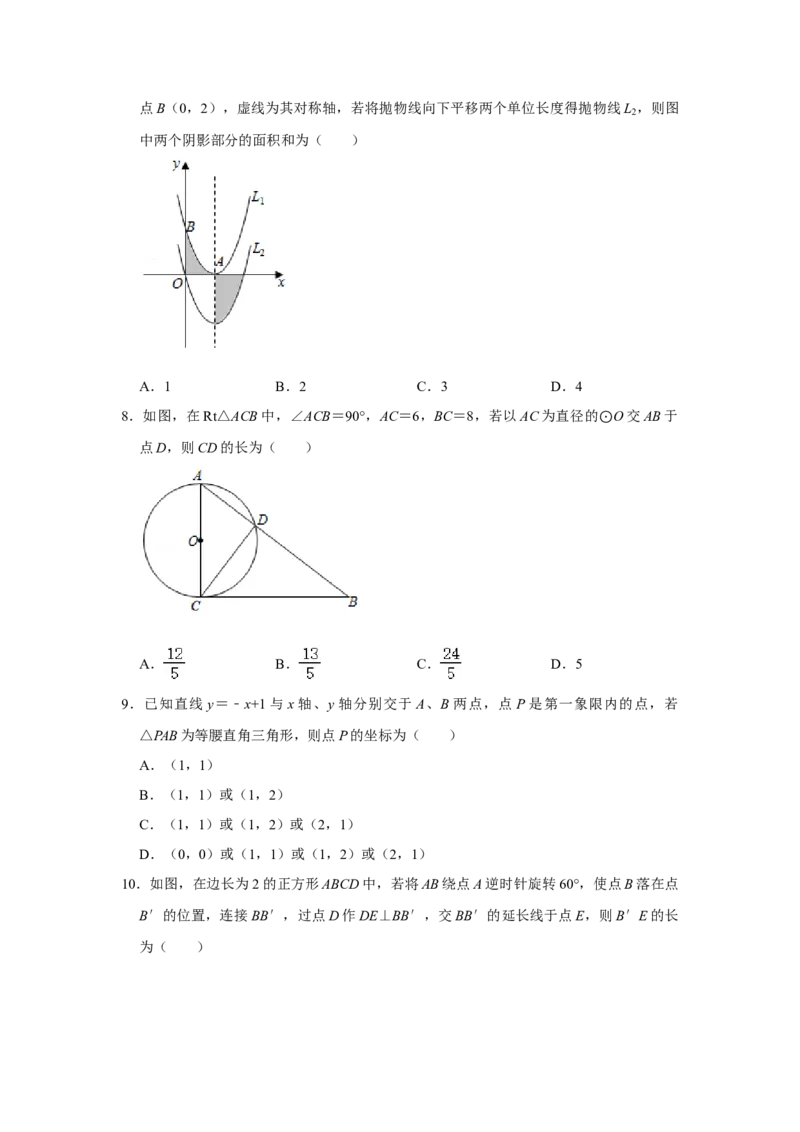
1点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L ,则图
2
中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
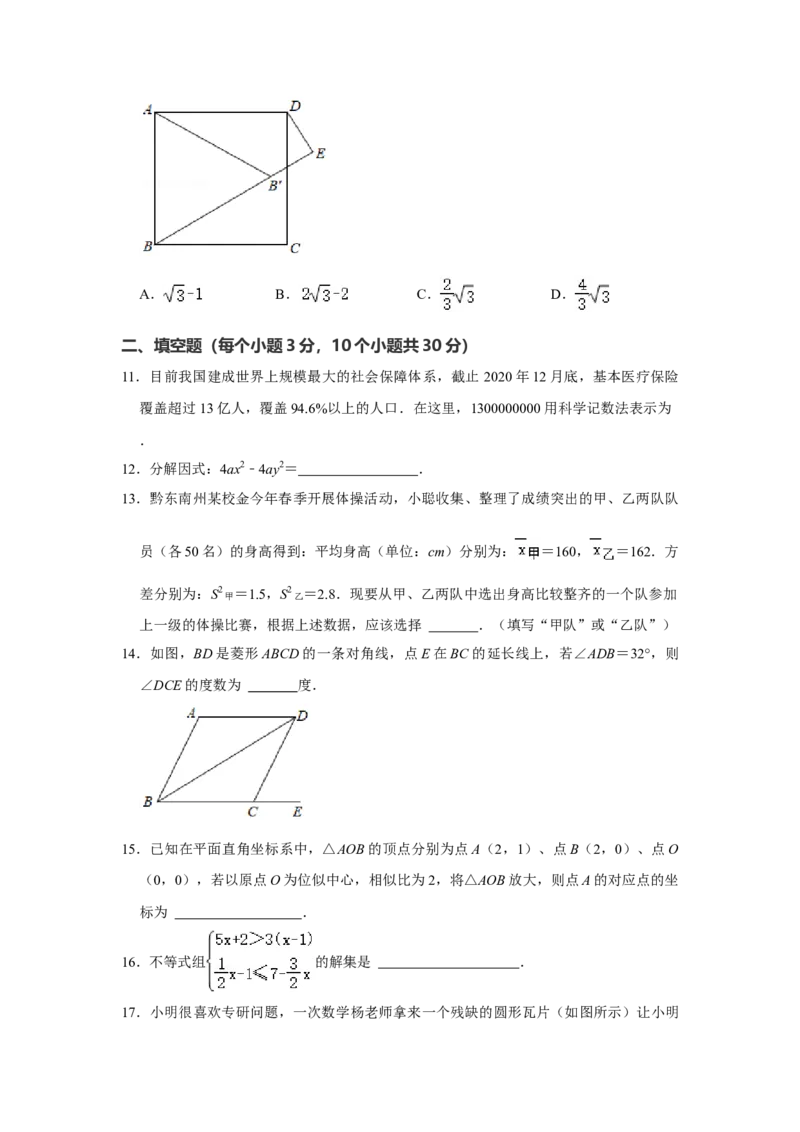
8.如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,若以AC为直径的 O交AB于
点D,则CD的长为( ) ⊙
A. B. C. D.5
9.已知直线y=﹣x+1与x轴、y轴分别交于A、B两点,点P是第一象限内的点,若
△PAB为等腰直角三角形,则点P的坐标为( )
A.(1,1)
B.(1,1)或(1,2)
C.(1,1)或(1,2)或(2,1)
D.(0,0)或(1,1)或(1,2)或(2,1)
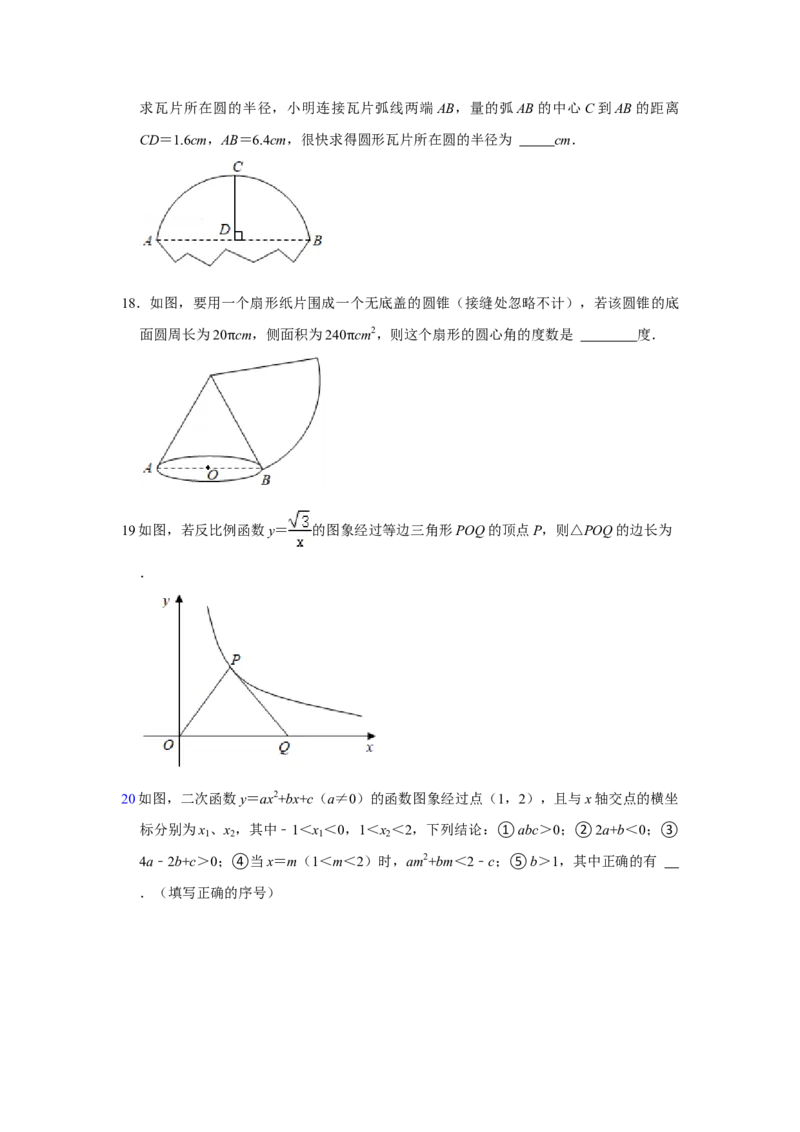
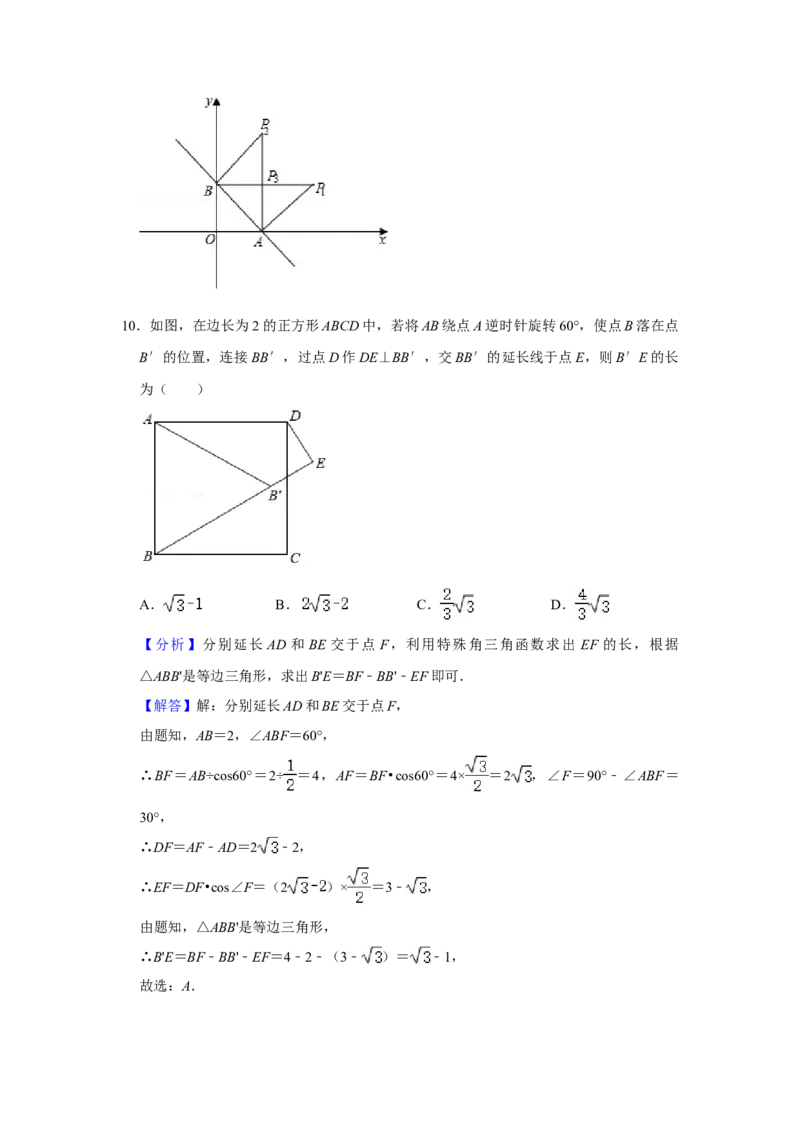
10.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点
B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长
为( )A. B. C. D.
二、填空题(每个小题3分,10个小题共30分)
11.目前我国建成世界上规模最大的社会保障体系,截止 2020年12月底,基本医疗保险
覆盖超过13亿人,覆盖94.6%以上的人口.在这里,1300000000用科学记数法表示为
.
12.分解因式:4ax2﹣4ay2= .
13.黔东南州某校金今年春季开展体操活动,小聪收集、整理了成绩突出的甲、乙两队队
员(各50名)的身高得到:平均身高(单位:cm)分别为: =160, =162.方
差分别为:S2
甲
=1.5,S2
乙
=2.8.现要从甲、乙两队中选出身高比较整齐的一个队参加
上一级的体操比赛,根据上述数据,应该选择 .(填写“甲队”或“乙队”)
14.如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若∠ADB=32°,则
∠DCE的度数为 度.
15.已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O
(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐
标为 .
16.不等式组 的解集是 .
17.小明很喜欢专研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离
CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在圆的半径为 cm.
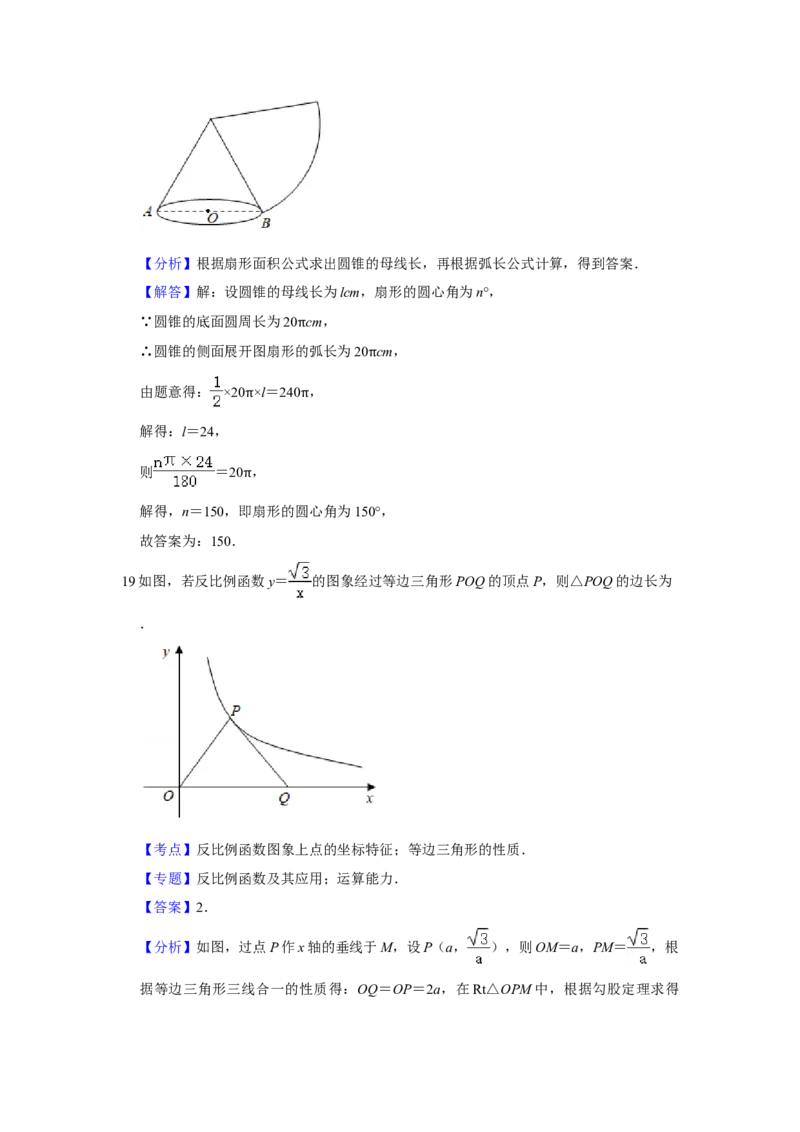
18.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底
面圆周长为20 cm,侧面积为240 cm2,则这个扇形的圆心角的度数是 度.
π π
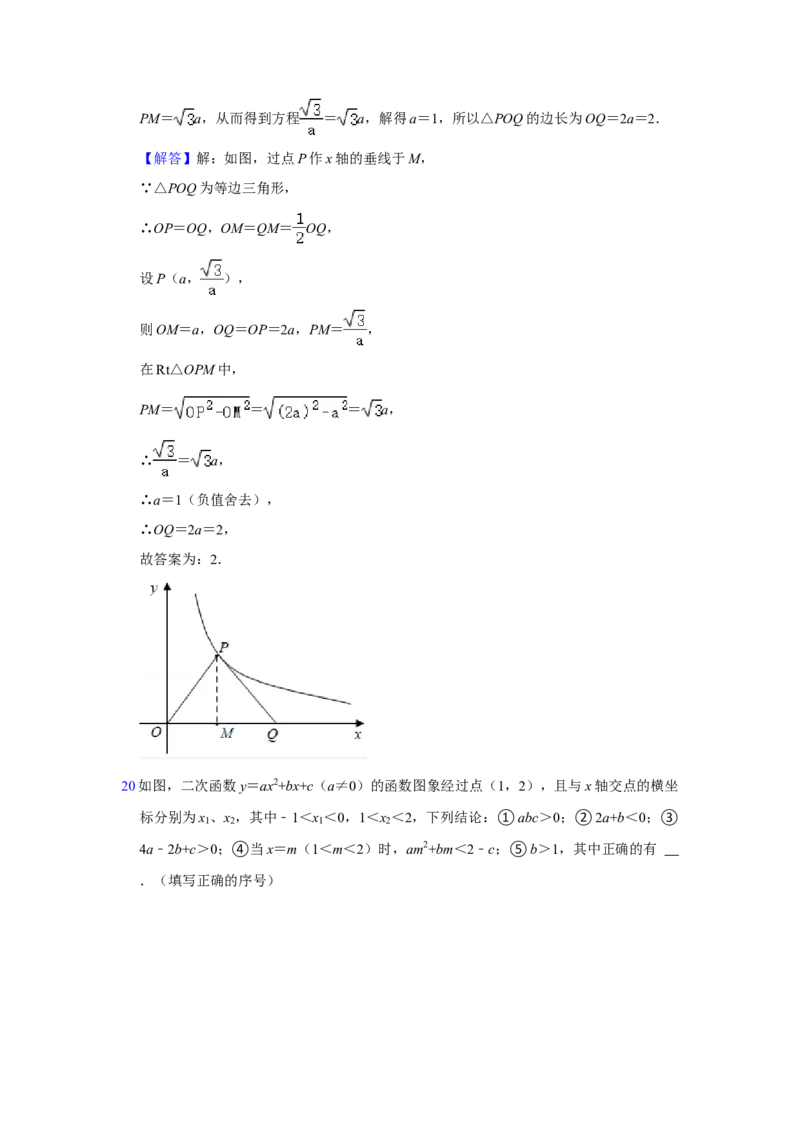
19如图,若反比例函数y= 的图象经过等边三角形POQ的顶点P,则△POQ的边长为
.
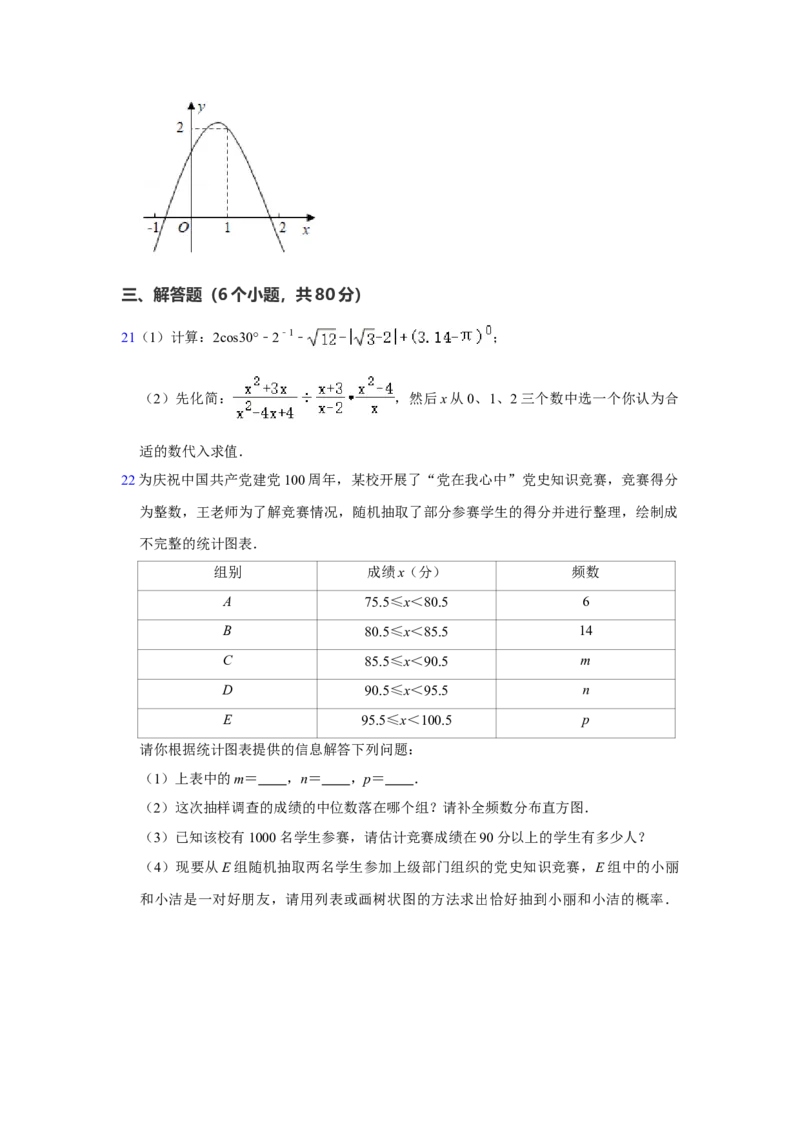
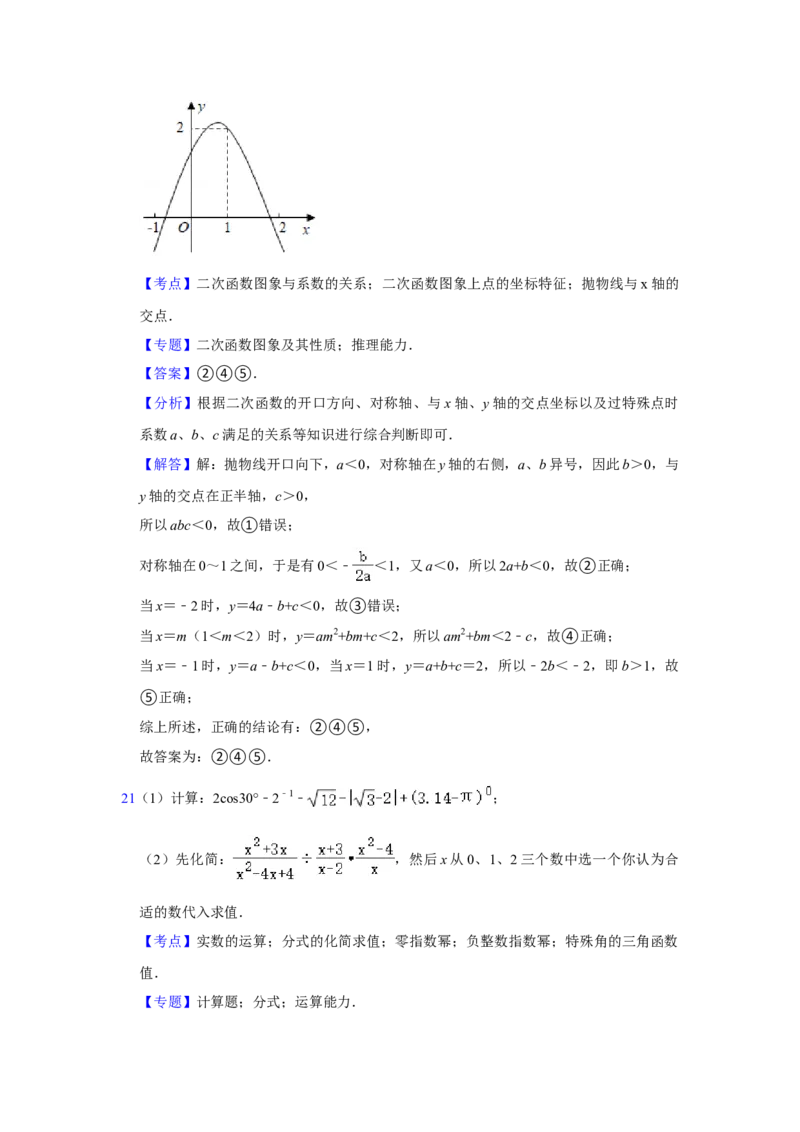
20如图,二次函数y=ax2+bx+c(a≠0)的函数图象经过点(1,2),且与x轴交点的横坐
标分别为x 、x ,其中﹣1<x <0,1<x <2,下列结论:①abc>0;②2a+b<0;③
1 2 1 2
4a﹣2b+c>0;④当x=m(1<m<2)时,am2+bm<2﹣c;⑤b>1,其中正确的有
.(填写正确的序号)三、解答题(6个小题,共80分)
21(1)计算:2cos30°﹣2﹣1﹣ ;
(2)先化简: ,然后x从0、1、2三个数中选一个你认为合
适的数代入求值.
22为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分
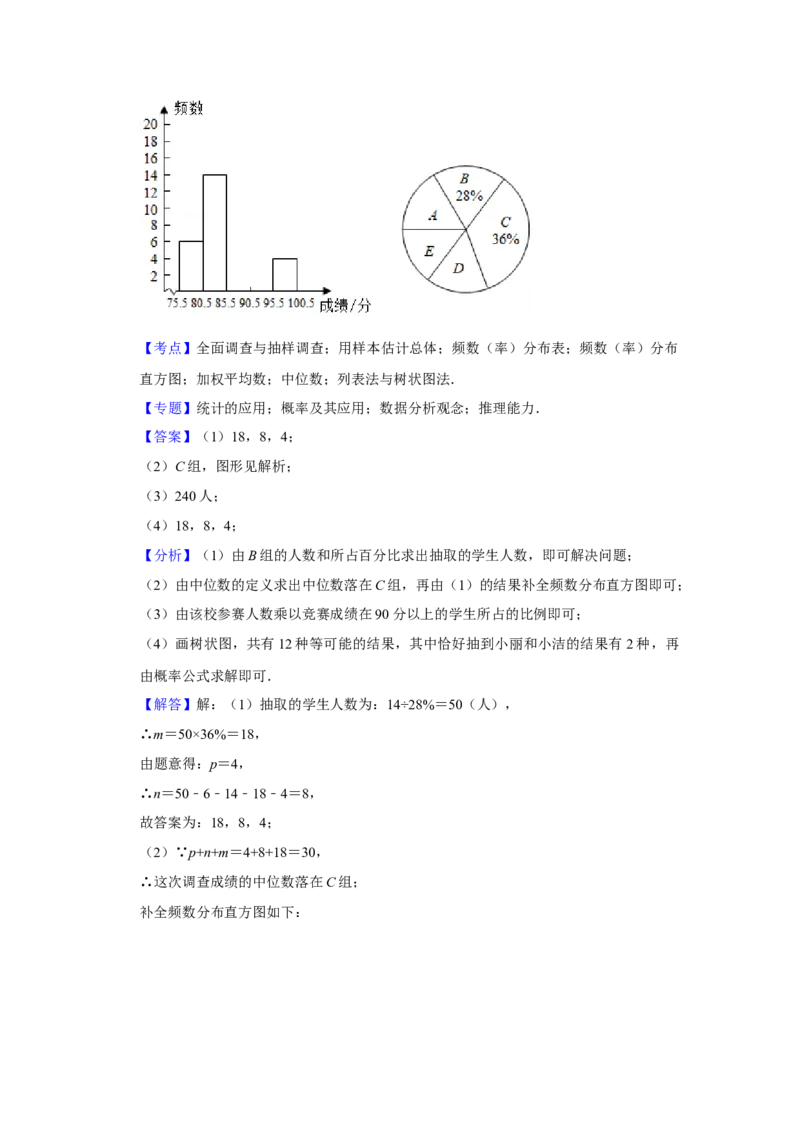
为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成
不完整的统计图表.
组别 成绩x(分) 频数
A 75.5≤x<80.5 6
B 80.5≤x<85.5 14
C 85.5≤x<90.5 m
D 90.5≤x<95.5 n
E 95.5≤x<100.5 p
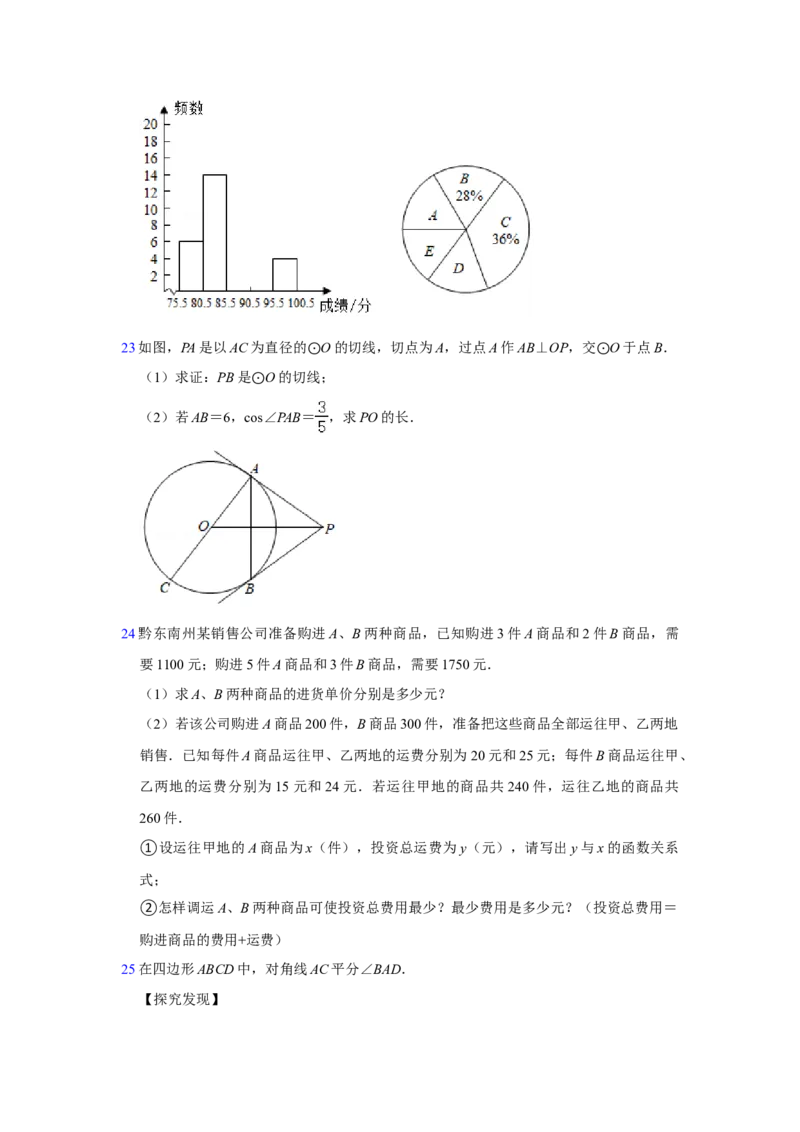
请你根据统计图表提供的信息解答下列问题:
(1)上表中的m= ,n= ,p= .
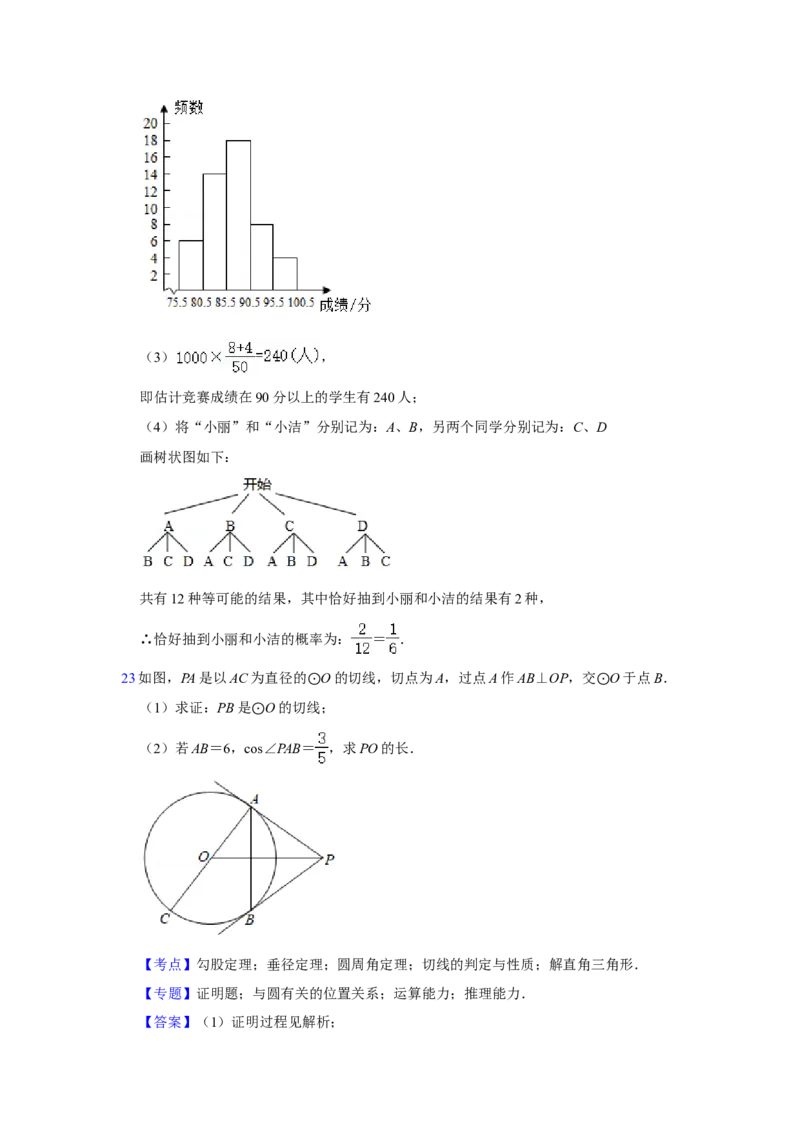
(2)这次抽样调查的成绩的中位数落在哪个组?请补全频数分布直方图.
(3)已知该校有1000名学生参赛,请估计竞赛成绩在90分以上的学生有多少人?
(4)现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛,E组中的小丽
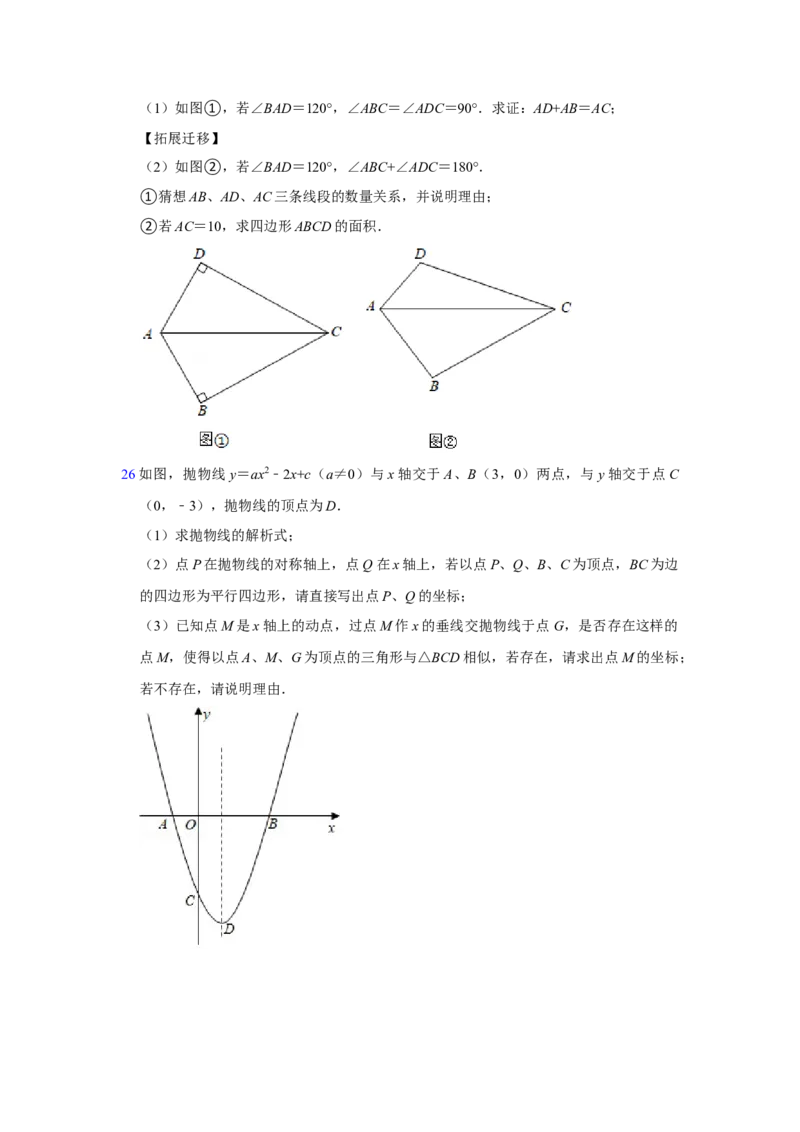
和小洁是一对好朋友,请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率.23如图,PA是以AC为直径的 O的切线,切点为A,过点A作AB⊥OP,交 O于点B.
(1)求证:PB是 O的切线⊙; ⊙
⊙
(2)若AB=6,cos∠PAB= ,求PO的长.
24黔东南州某销售公司准备购进A、B两种商品,已知购进3件A商品和2件B商品,需
要1100元;购进5件A商品和3件B商品,需要1750元.
(1)求A、B两种商品的进货单价分别是多少元?
(2)若该公司购进A商品200件,B商品300件,准备把这些商品全部运往甲、乙两地
销售.已知每件A商品运往甲、乙两地的运费分别为20元和25元;每件B商品运往甲、
乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共
260件.
①设运往甲地的A商品为x(件),投资总运费为y(元),请写出y与x的函数关系
式;
②怎样调运A、B两种商品可使投资总费用最少?最少费用是多少元?(投资总费用=
购进商品的费用+运费)
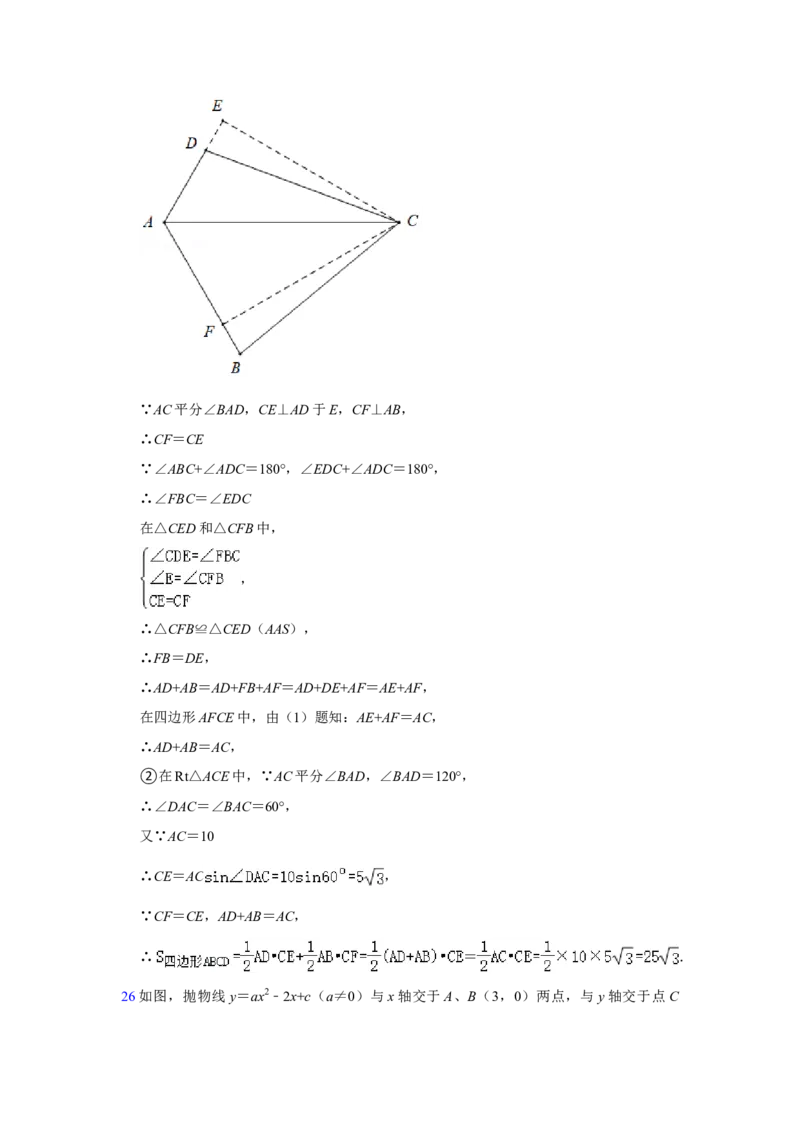
25在四边形ABCD中,对角线AC平分∠BAD.
【探究发现】(1)如图①,若∠BAD=120°,∠ABC=∠ADC=90°.求证:AD+AB=AC;
【拓展迁移】
(2)如图②,若∠BAD=120°,∠ABC+∠ADC=180°.
①猜想AB、AD、AC三条线段的数量关系,并说明理由;
②若AC=10,求四边形ABCD的面积.
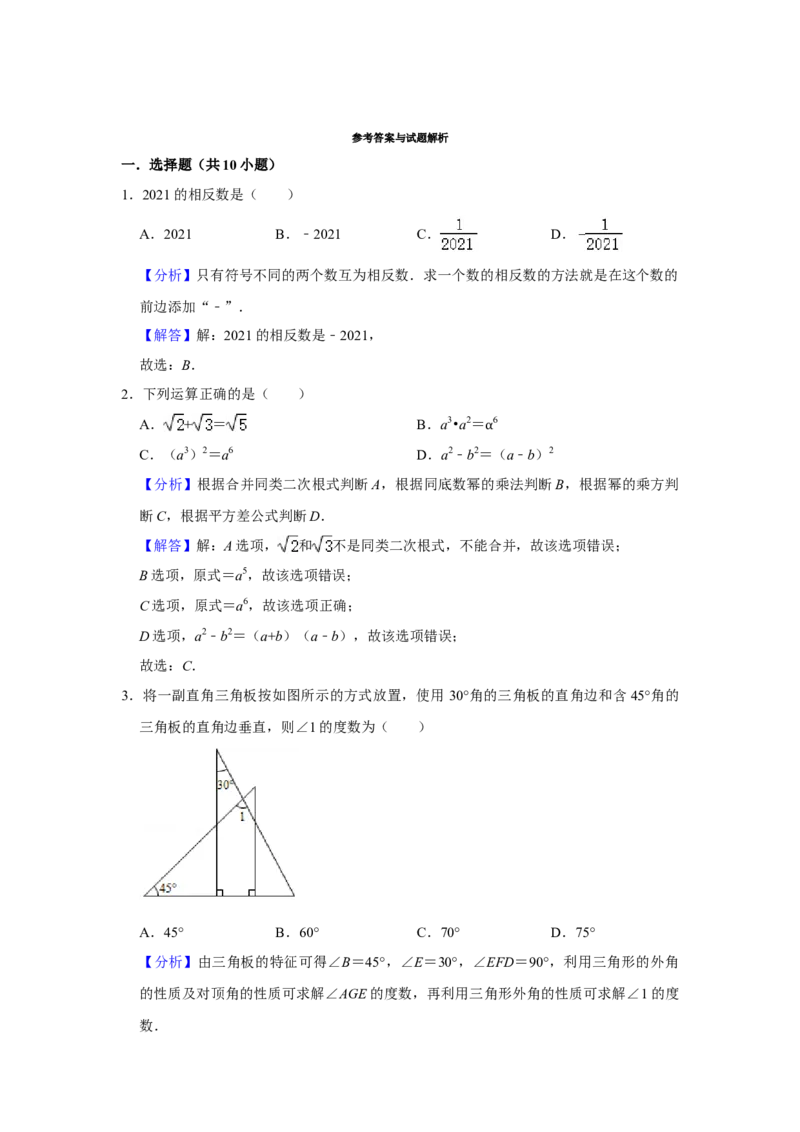
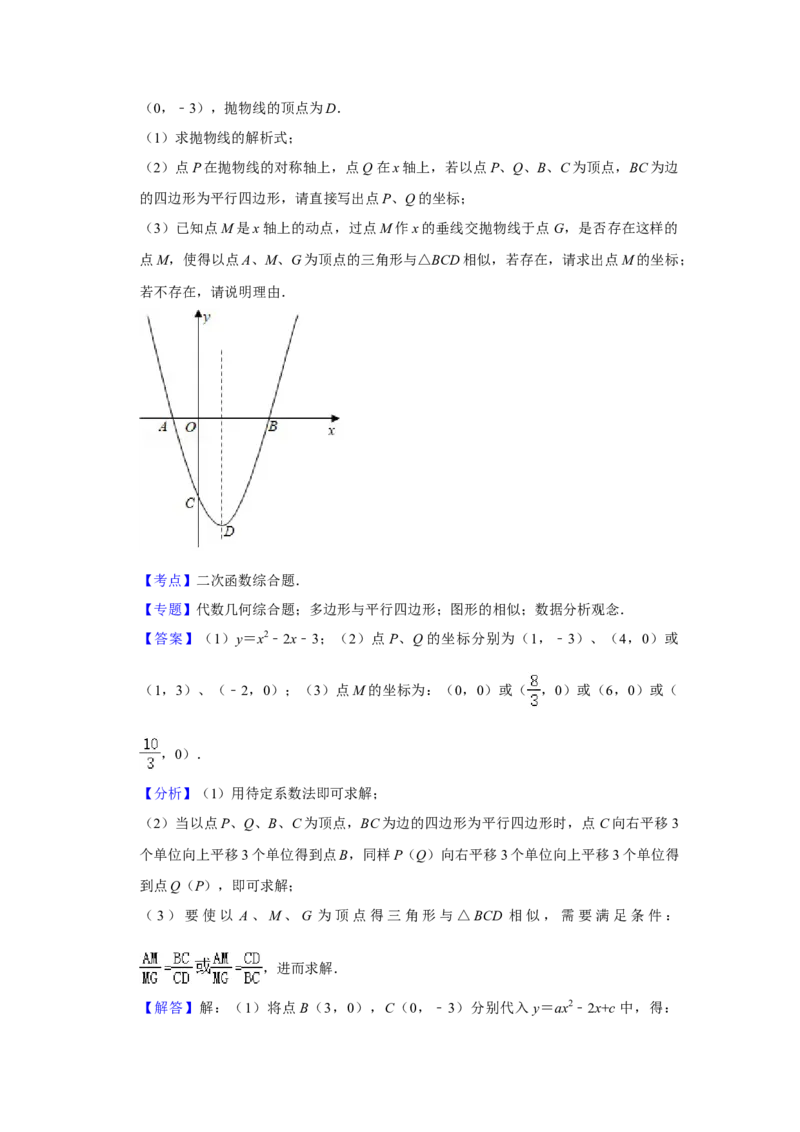
26如图,抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B(3,0)两点,与y轴交于点C
(0,﹣3),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)点P在抛物线的对称轴上,点Q在x轴上,若以点P、Q、B、C为顶点,BC为边
的四边形为平行四边形,请直接写出点P、Q的坐标;
(3)已知点M是x轴上的动点,过点M作x的垂线交抛物线于点G,是否存在这样的
点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;
若不存在,请说明理由.参考答案与试题解析
一.选择题(共10小题)
1.2021的相反数是( )
A.2021 B.﹣2021 C. D.
【分析】只有符号不同的两个数互为相反数.求一个数的相反数的方法就是在这个数的
前边添加“﹣”.
【解答】解:2021的相反数是﹣2021,
故选:B.
2.下列运算正确的是( )
A. + = B.a3•a2= 6
C.(a3)2=a6 D.a2﹣b2=α(a﹣b)2
【分析】根据合并同类二次根式判断A,根据同底数幂的乘法判断B,根据幂的乘方判
断C,根据平方差公式判断D.
【解答】解:A选项, 和 不是同类二次根式,不能合并,故该选项错误;
B选项,原式=a5,故该选项错误;
C选项,原式=a6,故该选项正确;
D选项,a2﹣b2=(a+b)(a﹣b),故该选项错误;
故选:C.
3.将一副直角三角板按如图所示的方式放置,使用 30°角的三角板的直角边和含45°角的
三角板的直角边垂直,则∠1的度数为( )
A.45° B.60° C.70° D.75°
【分析】由三角板的特征可得∠B=45°,∠E=30°,∠EFD=90°,利用三角形的外角
的性质及对顶角的性质可求解∠AGE的度数,再利用三角形外角的性质可求解∠1的度
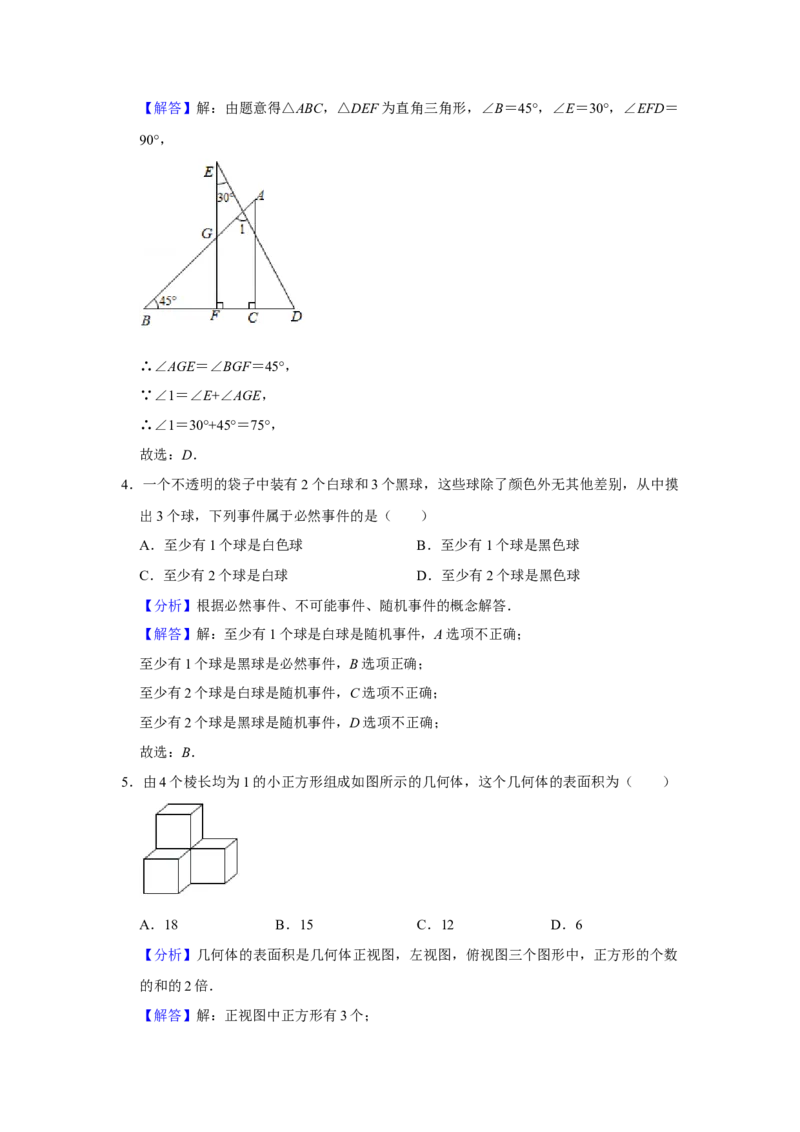
数.【解答】解:由题意得△ABC,△DEF为直角三角形,∠B=45°,∠E=30°,∠EFD=
90°,
∴∠AGE=∠BGF=45°,
∵∠1=∠E+∠AGE,
∴∠1=30°+45°=75°,
故选:D.
4.一个不透明的袋子中装有2个白球和3个黑球,这些球除了颜色外无其他差别,从中摸
出3个球,下列事件属于必然事件的是( )
A.至少有1个球是白色球 B.至少有1个球是黑色球
C.至少有2个球是白球 D.至少有2个球是黑色球
【分析】根据必然事件、不可能事件、随机事件的概念解答.
【解答】解:至少有1个球是白球是随机事件,A选项不正确;
至少有1个球是黑球是必然事件,B选项正确;
至少有2个球是白球是随机事件,C选项不正确;
至少有2个球是黑球是随机事件,D选项不正确;
故选:B.
5.由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )
A.18 B.15 C.12 D.6
【分析】几何体的表面积是几何体正视图,左视图,俯视图三个图形中,正方形的个数
的和的2倍.
【解答】解:正视图中正方形有3个;左视图中正方形有3个;
俯视图中正方形有3个.
则这个几何体中正方形的个数是:2×(3+3+3)=18个.
则几何体的表面积为18cm2.
故选:A.
6.若关于x的一元二次方程x2﹣ax+6=0的一个根是2,则a的值为( )
A.2 B.3 C.4 D.5
【分析】根据关于x的一元二次方程x2﹣ax+6=0的一个根是2,将x=2代入方程即可
求得a的值.
【解答】解:∵关于x的一元二次方程x2﹣ax+6=0的一个根是2,
∴22﹣2a+6=0,
解得a=5.
故选:D.
7.如图,抛物线L :y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于
1
点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L ,则图
2
中两个阴影部分的面积和为( )
A.1 B.2 C.3 D.4
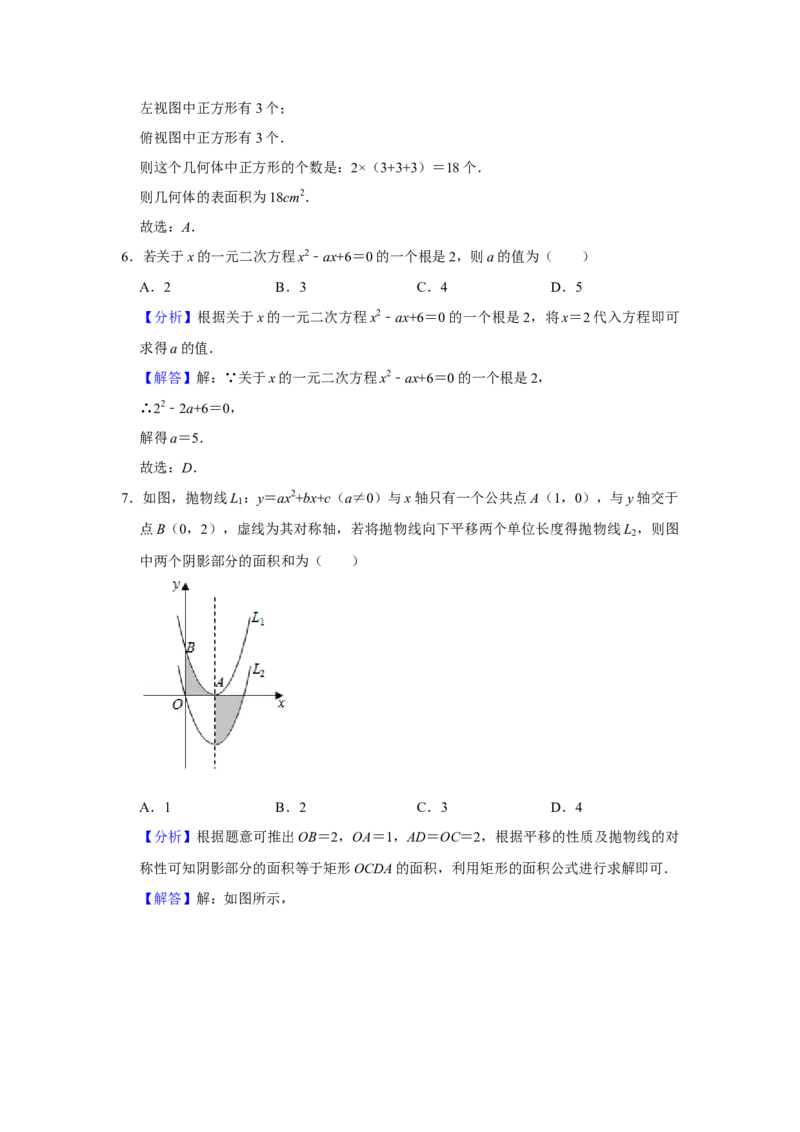
【分析】根据题意可推出OB=2,OA=1,AD=OC=2,根据平移的性质及抛物线的对
称性可知阴影部分的面积等于矩形OCDA的面积,利用矩形的面积公式进行求解即可.
【解答】解:如图所示,过抛物线L 的顶点D作CD∥x轴,与y轴交于点C,
2
则四边形OCDA是矩形,
∵抛物线L :y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B
1
(0,2),
∴OB=2,OA=1,
将抛物线L 向下平移两个单位长度得抛物线L ,则AD=OC=2,
1 2
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分 =S矩形OCDA =OA•AD=1×2=2.
故选:B.
8.如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,若以AC为直径的 O交AB于
点D,则CD的长为( ) ⊙
A. B. C. D.5
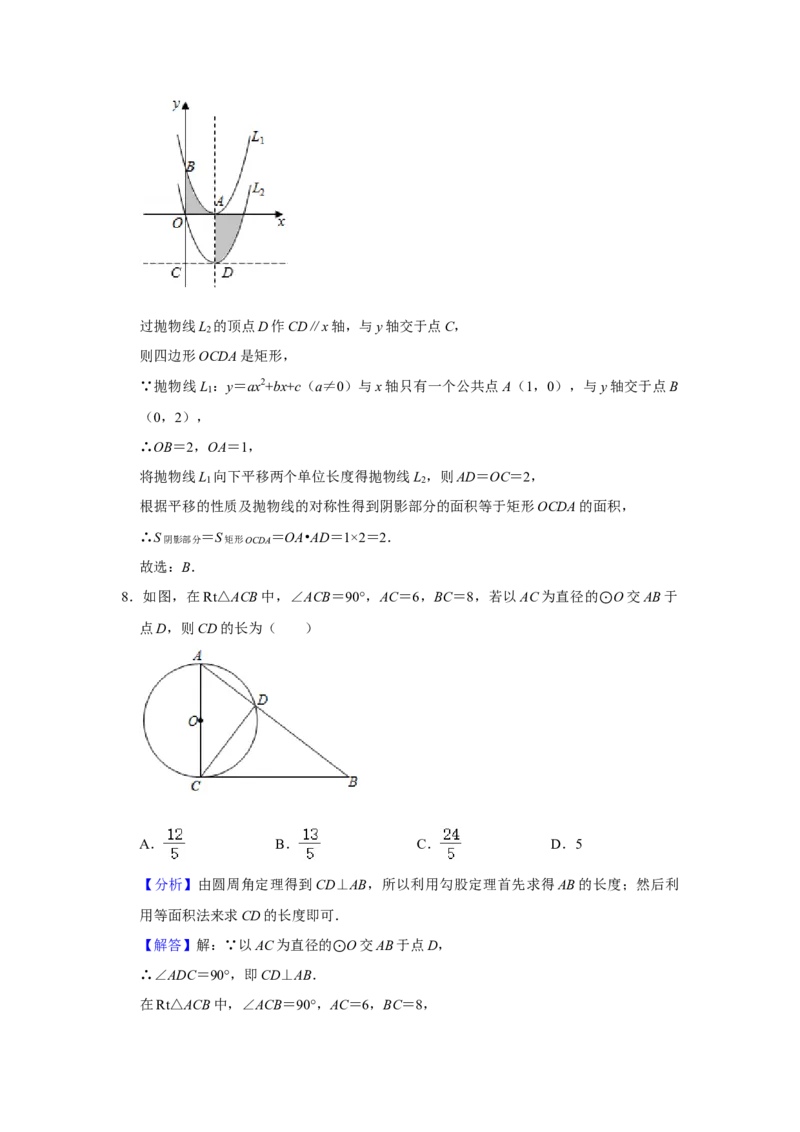
【分析】由圆周角定理得到CD⊥AB,所以利用勾股定理首先求得AB的长度;然后利
用等面积法来求CD的长度即可.
【解答】解:∵以AC为直径的 O交AB于点D,
∴∠ADC=90°,即CD⊥AB. ⊙
在Rt△ACB中,∠ACB=90°,AC=6,BC=8,则由勾股定理得到:AB= = =10.
∴ AC•BC= AB•CD,即 = .
故CD= .
故选:C.
9.已知直线y=﹣x+1与x轴、y轴分别交于A、B两点,点P是第一象限内的点,若
△PAB为等腰直角三角形,则点P的坐标为( )
A.(1,1)
B.(1,1)或(1,2)
C.(1,1)或(1,2)或(2,1)
D.(0,0)或(1,1)或(1,2)或(2,1)
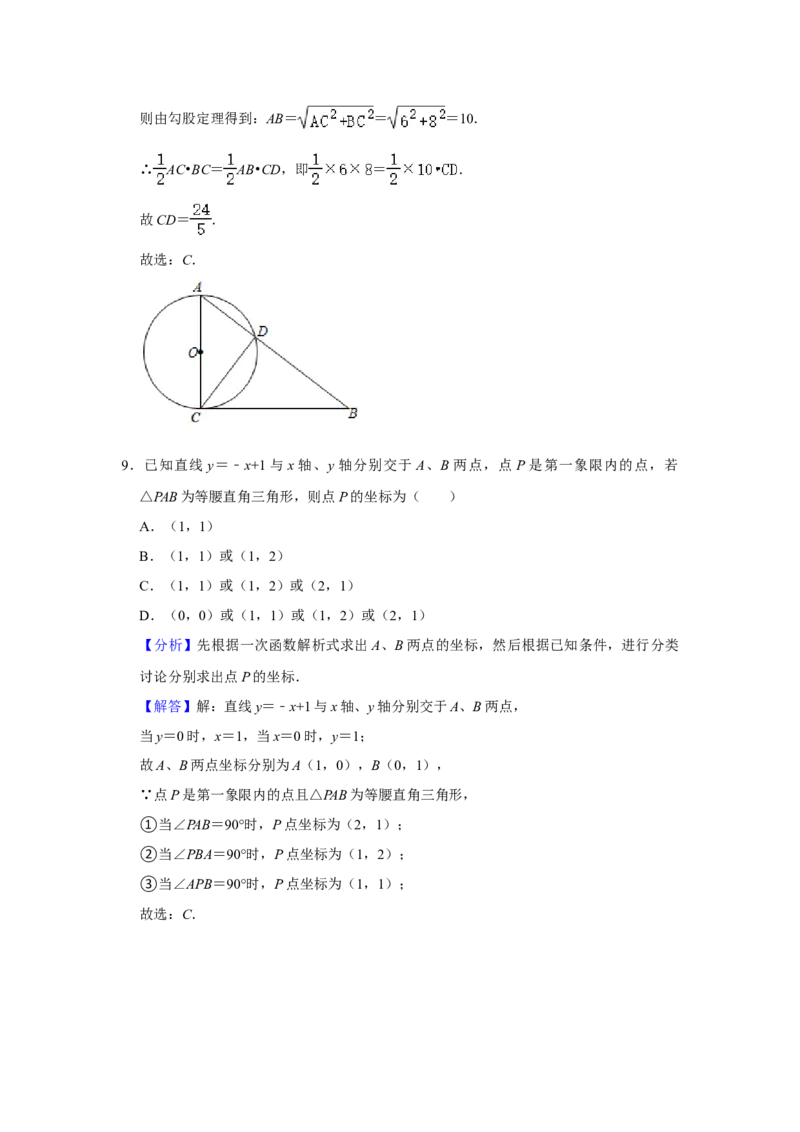
【分析】先根据一次函数解析式求出A、B两点的坐标,然后根据已知条件,进行分类
讨论分别求出点P的坐标.
【解答】解:直线y=﹣x+1与x轴、y轴分别交于A、B两点,
当y=0时,x=1,当x=0时,y=1;
故A、B两点坐标分别为A(1,0),B(0,1),
∵点P是第一象限内的点且△PAB为等腰直角三角形,
①当∠PAB=90°时,P点坐标为(2,1);
②当∠PBA=90°时,P点坐标为(1,2);
③当∠APB=90°时,P点坐标为(1,1);
故选:C.10.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点
B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长
为( )
A. B. C. D.
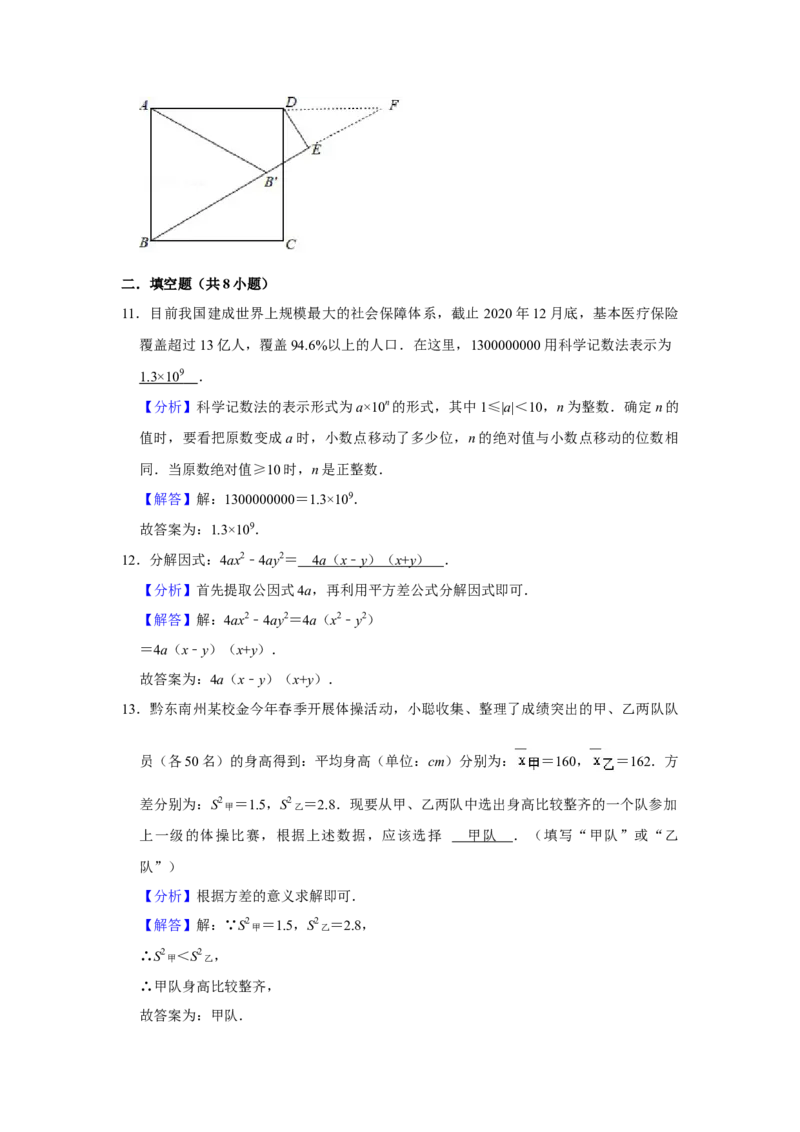
【分析】分别延长 AD 和 BE 交于点 F,利用特殊角三角函数求出 EF 的长,根据
△ABB'是等边三角形,求出B'E=BF﹣BB'﹣EF即可.
【解答】解:分别延长AD和BE交于点F,
由题知,AB=2,∠ABF=60°,
∴BF=AB÷cos60°=2÷ =4,AF=BF•cos60°=4× =2 ,∠F=90°﹣∠ABF=
30°,
∴DF=AF﹣AD=2 ﹣2,
∴EF=DF•cos∠F=(2 )× =3﹣ ,
由题知,△ABB'是等边三角形,
∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3﹣ )= ﹣1,
故选:A.二.填空题(共8小题)
11.目前我国建成世界上规模最大的社会保障体系,截止 2020年12月底,基本医疗保险
覆盖超过13亿人,覆盖94.6%以上的人口.在这里,1300000000用科学记数法表示为
1.3×10 9 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.当原数绝对值≥10时,n是正整数.
【解答】解:1300000000=1.3×109.
故答案为:1.3×109.
12.分解因式:4ax2﹣4ay2= 4 a ( x ﹣ y )( x + y ) .
【分析】首先提取公因式4a,再利用平方差公式分解因式即可.
【解答】解:4ax2﹣4ay2=4a(x2﹣y2)
=4a(x﹣y)(x+y).
故答案为:4a(x﹣y)(x+y).
13.黔东南州某校金今年春季开展体操活动,小聪收集、整理了成绩突出的甲、乙两队队
员(各50名)的身高得到:平均身高(单位:cm)分别为: =160, =162.方
差分别为:S2
甲
=1.5,S2
乙
=2.8.现要从甲、乙两队中选出身高比较整齐的一个队参加
上一级的体操比赛,根据上述数据,应该选择 甲队 .(填写“甲队”或“乙
队”)
【分析】根据方差的意义求解即可.
【解答】解:∵S2
甲
=1.5,S2
乙
=2.8,
∴S2
甲
<S2
乙
,
∴甲队身高比较整齐,
故答案为:甲队.14.如图,BD是菱形ABCD的一条对角线,点E在BC的延长线上,若∠ADB=32°,则
∠DCE的度数为 6 4 度.
【分析】根据菱形的性质可得BC=CD,AD∥BC,得到∠CBD=∠BDC=∠ADB,利
用外角性质可得.
【解答】解:∵四边形ABCD为菱形,
∴BC=CD,AD∥BC,
∴∠CBD=∠BDC,∠CBD=∠ADB=32°,
∴∠CBD=∠BDC=32°,
∴∠DCE=∠CBD+∠BDC=64°,
故答案为:64.
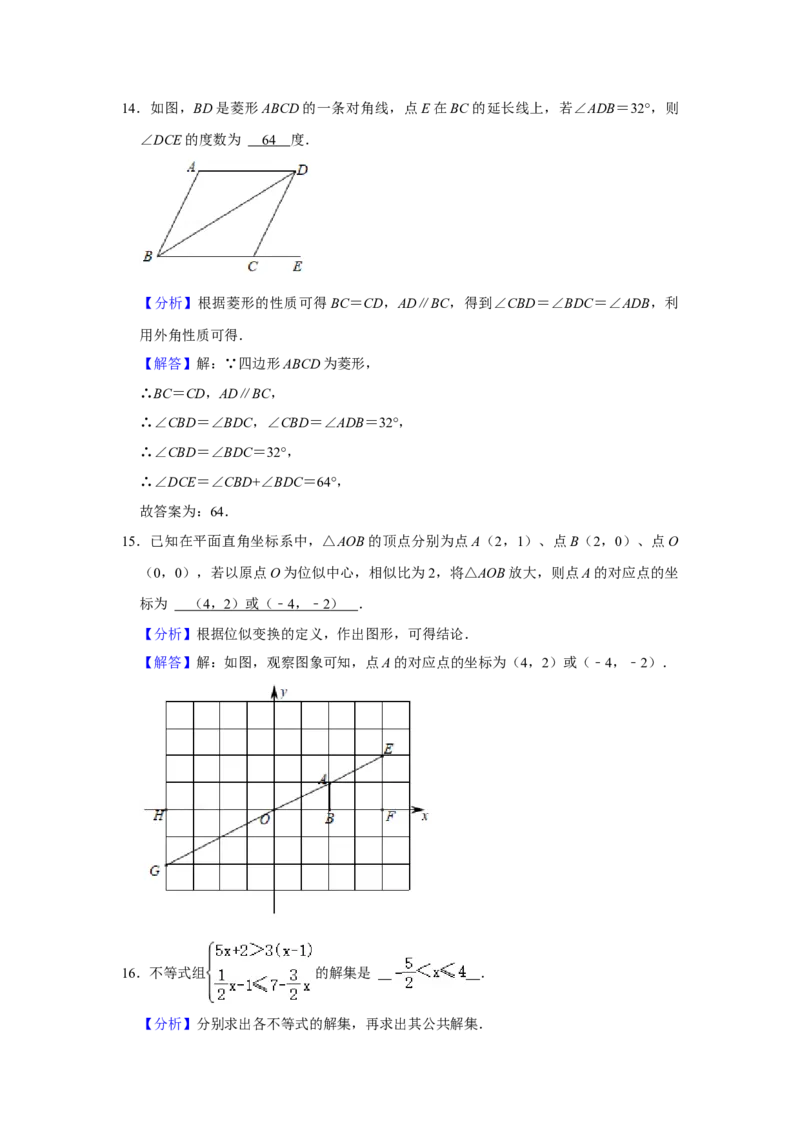
15.已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O
(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐
标为 ( 4 , 2 )或(﹣ 4 ,﹣ 2 ) .
【分析】根据位似变换的定义,作出图形,可得结论.
【解答】解:如图,观察图象可知,点A的对应点的坐标为(4,2)或(﹣4,﹣2).
16.不等式组 的解集是 .
【分析】分别求出各不等式的解集,再求出其公共解集.【解答】解:解不等式5x+2>3(x﹣1),得:x>﹣ ,
解不等式 ,得:x≤4,
则不等式组的解集为﹣ <x≤4,
故答案为﹣ <x≤4.
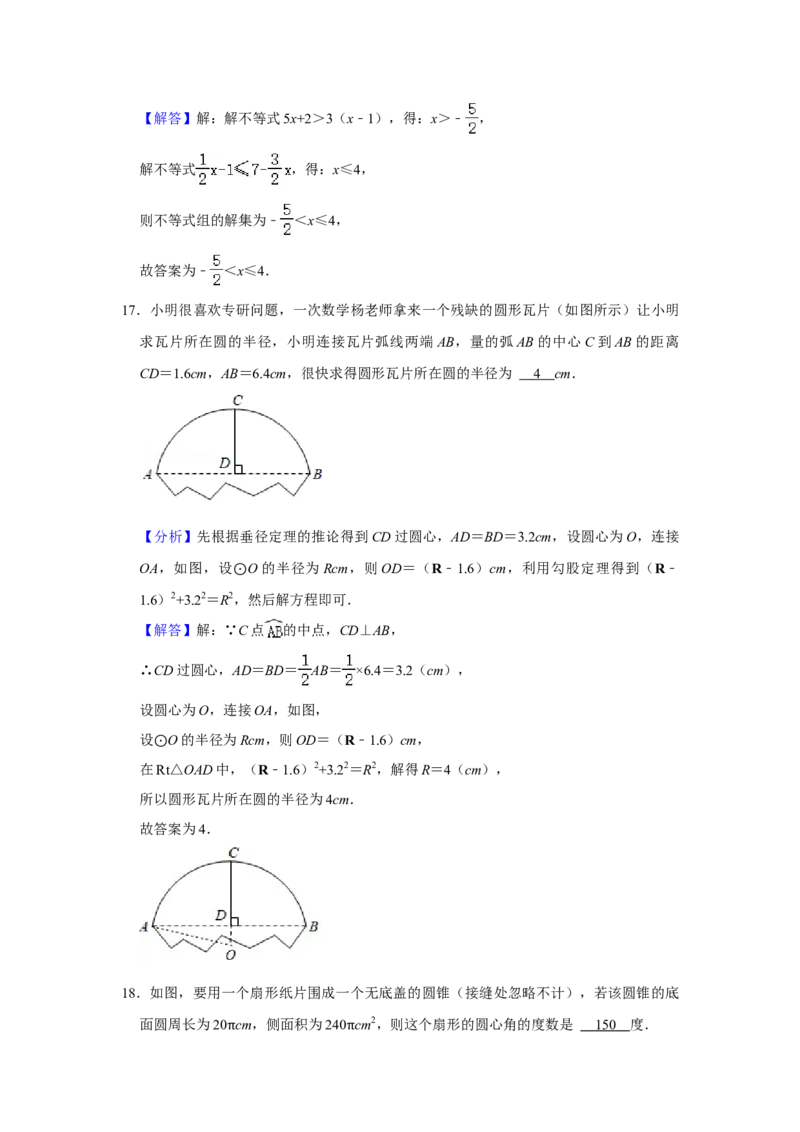
17.小明很喜欢专研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明
求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离
CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在圆的半径为 4 cm.
【分析】先根据垂径定理的推论得到CD过圆心,AD=BD=3.2cm,设圆心为O,连接
OA,如图,设 O的半径为Rcm,则OD=(R﹣1.6)cm,利用勾股定理得到(R﹣
1.6)2+3.22=R2⊙,然后解方程即可.
【解答】解:∵C点 的中点,CD⊥AB,
∴CD过圆心,AD=BD= AB= ×6.4=3.2(cm),
设圆心为O,连接OA,如图,
设 O的半径为Rcm,则OD=(R﹣1.6)cm,
在⊙Rt△OAD中,(R﹣1.6)2+3.22=R2,解得R=4(cm),
所以圆形瓦片所在圆的半径为4cm.
故答案为4.
18.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底
面圆周长为20 cm,侧面积为240 cm2,则这个扇形的圆心角的度数是 15 0 度.
π π【分析】根据扇形面积公式求出圆锥的母线长,再根据弧长公式计算,得到答案.
【解答】解:设圆锥的母线长为lcm,扇形的圆心角为n°,
∵圆锥的底面圆周长为20 cm,
∴圆锥的侧面展开图扇形的π弧长为20 cm,
π
由题意得: ×20 ×l=240 ,
π π
解得:l=24,
则 =20 ,
π
解得,n=150,即扇形的圆心角为150°,
故答案为:150.
19如图,若反比例函数y= 的图象经过等边三角形POQ的顶点P,则△POQ的边长为
.
【考点】反比例函数图象上点的坐标特征;等边三角形的性质.
【专题】反比例函数及其应用;运算能力.
【答案】2.
【分析】如图,过点P作x轴的垂线于M,设P(a, ),则OM=a,PM= ,根
据等边三角形三线合一的性质得:OQ=OP=2a,在Rt△OPM中,根据勾股定理求得PM= a,从而得到方程 = a,解得a=1,所以△POQ的边长为OQ=2a=2.
【解答】解:如图,过点P作x轴的垂线于M,
∵△POQ为等边三角形,
∴OP=OQ,OM=QM= OQ,
设P(a, ),
则OM=a,OQ=OP=2a,PM= ,
在Rt△OPM中,
PM= = = a,
∴ = a,
∴a=1(负值舍去),
∴OQ=2a=2,
故答案为:2.
20如图,二次函数y=ax2+bx+c(a≠0)的函数图象经过点(1,2),且与x轴交点的横坐
标分别为x 、x ,其中﹣1<x <0,1<x <2,下列结论:①abc>0;②2a+b<0;③
1 2 1 2
4a﹣2b+c>0;④当x=m(1<m<2)时,am2+bm<2﹣c;⑤b>1,其中正确的有
.(填写正确的序号)【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;抛物线与x轴的
交点.
【专题】二次函数图象及其性质;推理能力.
【答案】②④⑤.
【分析】根据二次函数的开口方向、对称轴、与x轴、y轴的交点坐标以及过特殊点时
系数a、b、c满足的关系等知识进行综合判断即可.
【解答】解:抛物线开口向下,a<0,对称轴在y轴的右侧,a、b异号,因此b>0,与
y轴的交点在正半轴,c>0,
所以abc<0,故①错误;
对称轴在0~1之间,于是有0<﹣ <1,又a<0,所以2a+b<0,故②正确;
当x=﹣2时,y=4a﹣b+c<0,故③错误;
当x=m(1<m<2)时,y=am2+bm+c<2,所以am2+bm<2﹣c,故④正确;
当x=﹣1时,y=a﹣b+c<0,当x=1时,y=a+b+c=2,所以﹣2b<﹣2,即b>1,故
⑤正确;
综上所述,正确的结论有:②④⑤,
故答案为:②④⑤.
21(1)计算:2cos30°﹣2﹣1﹣ ;
(2)先化简: ,然后x从0、1、2三个数中选一个你认为合
适的数代入求值.
【考点】实数的运算;分式的化简求值;零指数幂;负整数指数幂;特殊角的三角函数
值.
【专题】计算题;分式;运算能力.【答案】(1) ;
(2)x+2,3.
【分析】(1)根据实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值进行
计算即可;
(2)根据分式的化简求值即可得结果.
【解答】解:(1)原式= = ;
(2)原式=
=x+2,
∵x取0或2时,原式无意义,
∴x只能取1,
当x=1时,原式=3.
22为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分
为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成
不完整的统计图表.
组别 成绩x(分) 频数
A 75.5≤x<80.5 6
B 80.5≤x<85.5 14
C 85.5≤x<90.5 m
D 90.5≤x<95.5 n
E 95.5≤x<100.5 p
请你根据统计图表提供的信息解答下列问题:
(1)上表中的m= ,n= ,p= .
(2)这次抽样调查的成绩的中位数落在哪个组?请补全频数分布直方图.
(3)已知该校有1000名学生参赛,请估计竞赛成绩在90分以上的学生有多少人?
(4)现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛,E组中的小丽
和小洁是一对好朋友,请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率.【考点】全面调查与抽样调查;用样本估计总体;频数(率)分布表;频数(率)分布
直方图;加权平均数;中位数;列表法与树状图法.
【专题】统计的应用;概率及其应用;数据分析观念;推理能力.
【答案】(1)18,8,4;
(2)C组,图形见解析;
(3)240人;
(4)18,8,4;
【分析】(1)由B组的人数和所占百分比求出抽取的学生人数,即可解决问题;
(2)由中位数的定义求出中位数落在C组,再由(1)的结果补全频数分布直方图即可;
(3)由该校参赛人数乘以竞赛成绩在90分以上的学生所占的比例即可;
(4)画树状图,共有12种等可能的结果,其中恰好抽到小丽和小洁的结果有2种,再
由概率公式求解即可.
【解答】解:(1)抽取的学生人数为:14÷28%=50(人),
∴m=50×36%=18,
由题意得:p=4,
∴n=50﹣6﹣14﹣18﹣4=8,
故答案为:18,8,4;
(2)∵p+n+m=4+8+18=30,
∴这次调查成绩的中位数落在C组;
补全频数分布直方图如下:(3) ,
即估计竞赛成绩在90分以上的学生有240人;
(4)将“小丽”和“小洁”分别记为:A、B,另两个同学分别记为:C、D
画树状图如下:
共有12种等可能的结果,其中恰好抽到小丽和小洁的结果有2种,
∴恰好抽到小丽和小洁的概率为: = .
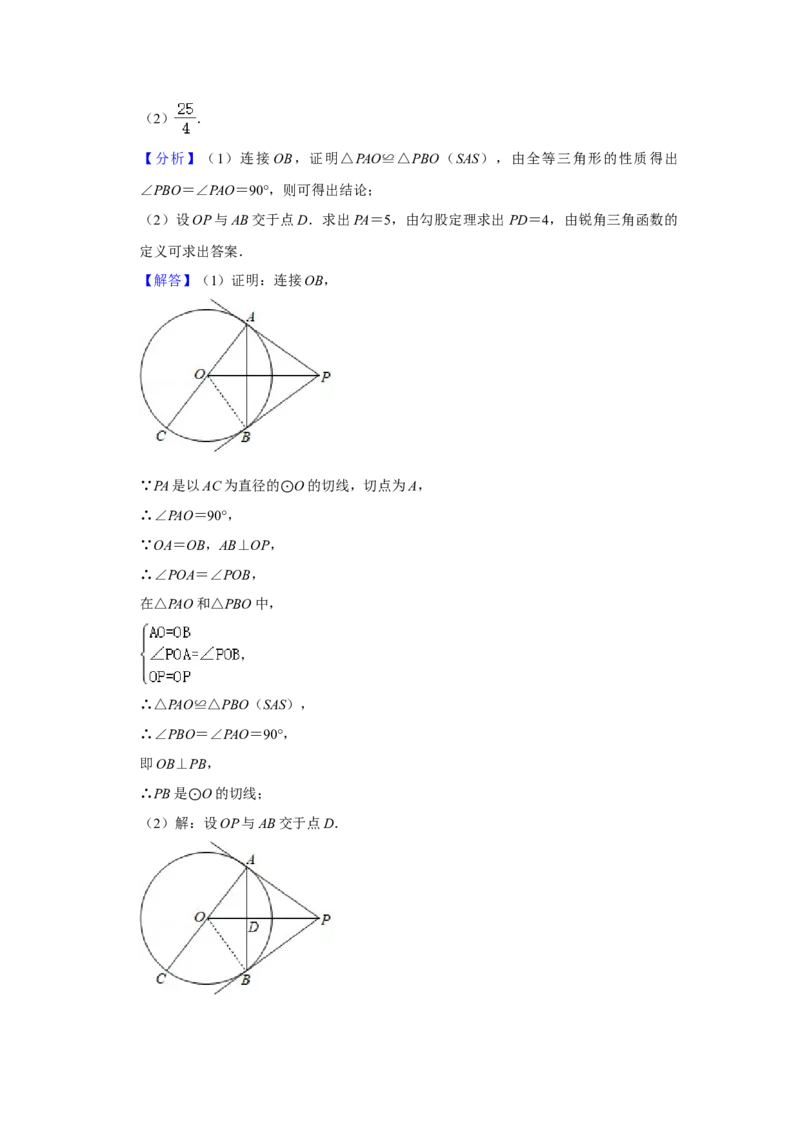
23如图,PA是以AC为直径的 O的切线,切点为A,过点A作AB⊥OP,交 O于点B.
(1)求证:PB是 O的切线⊙; ⊙
⊙
(2)若AB=6,cos∠PAB= ,求PO的长.
【考点】勾股定理;垂径定理;圆周角定理;切线的判定与性质;解直角三角形.
【专题】证明题;与圆有关的位置关系;运算能力;推理能力.
【答案】(1)证明过程见解析;(2) .
【分析】(1)连接 OB,证明△PAO≌△PBO(SAS),由全等三角形的性质得出
∠PBO=∠PAO=90°,则可得出结论;
(2)设OP与AB交于点D.求出PA=5,由勾股定理求出PD=4,由锐角三角函数的
定义可求出答案.
【解答】(1)证明:连接OB,
∵PA是以AC为直径的 O的切线,切点为A,
∴∠PAO=90°, ⊙
∵OA=OB,AB⊥OP,
∴∠POA=∠POB,
在△PAO和△PBO中,
,
∴△PAO≌△PBO(SAS),
∴∠PBO=∠PAO=90°,
即OB⊥PB,
∴PB是 O的切线;
(2)解⊙:设OP与AB交于点D.∵AB⊥OP,AB=6,
∴DA=DB=3,∠PDA=∠PDB=90°,
∵ ,
∴PA=5,
∴PD= = ,
在Rt△APD和Rt△APO中, , ,
∴ ,
∴PO= .
24黔东南州某销售公司准备购进A、B两种商品,已知购进3件A商品和2件B商品,需
要1100元;购进5件A商品和3件B商品,需要1750元.
(1)求A、B两种商品的进货单价分别是多少元?
(2)若该公司购进A商品200件,B商品300件,准备把这些商品全部运往甲、乙两地
销售.已知每件A商品运往甲、乙两地的运费分别为20元和25元;每件B商品运往甲、
乙两地的运费分别为15元和24元.若运往甲地的商品共240件,运往乙地的商品共
260件.
①设运往甲地的A商品为x(件),投资总运费为y(元),请写出y与x的函数关系
式;
②怎样调运A、B两种商品可使投资总费用最少?最少费用是多少元?(投资总费用=
购进商品的费用+运费)
【考点】二元一次方程组的应用;一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】(1)A商品的进货单价为200元,B商品的进货单价为250元;(2)①y与x
的函数关系式为y=4x+125040;②调运240件B商品到甲地,调运200件A商品、60
件B商品到乙地总费用最小,最小费用为125040元.
【分析】(1)设A商品的进货单价为x元,B商品的进货单价为y元,根据购进3件A
商品和2件B商品,需要1100元;购进5件A商品和3件B商品,需要1750元列出方
程组求解即可;(2)①设运往甲地的A商品为x件,则设运往乙地的A商品为(200﹣x)件,运往甲
地的B商品为(240﹣x)件,运往乙地的B商品为(60+x)件,根据投资总费用=购进
商品的费用+运费列出函数关系式即可;②由自变量的取值范围是:0≤x≤200,根据
函数的性质判断最佳运输方案并求出最低费用.
【解答】解:(1)设A商品的进货单价为x元,B商品的进货单价为y元,
根据题意,得 ,
解得: ,
答:A商品的进货单价为200元,B商品的进货单价为250元;
(2)①设运往甲地的A商品为x件,则设运往乙地的A商品为(200﹣x)件,
运往甲地的B商品为(240﹣x)件,运往乙地的B商品为(60+x)件,
则y=200×200+250×300+20x+25(200﹣x)+15(240﹣x)+24(60+x)=4x+125040,
∴y与x的函数关系式为y=4x+125040;
②在y=4x+125040中,
自变量的取值范围是:0≤x≤200,
∵k=4>0,
∴y随x增大而增大.
当x=0时,y取得最小值,y最小 =125040(元),
∴最佳调运方案为:调运240件B商品到甲地,调运200件A商品、60件B商品到乙地,
最小费用为125040元.
答:调运240件B商品到甲地,调运200件A商品、60件B商品到乙地总费用最小,最
小费用为125040元.
25在四边形ABCD中,对角线AC平分∠BAD.
【探究发现】
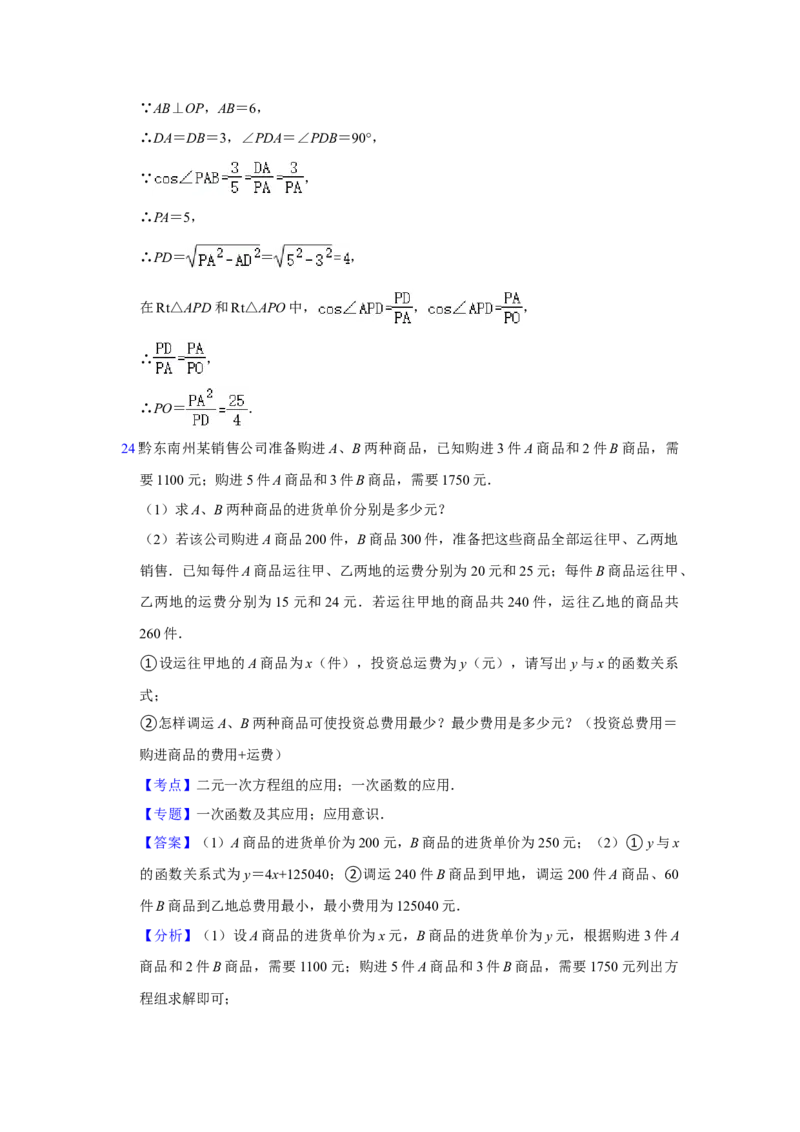
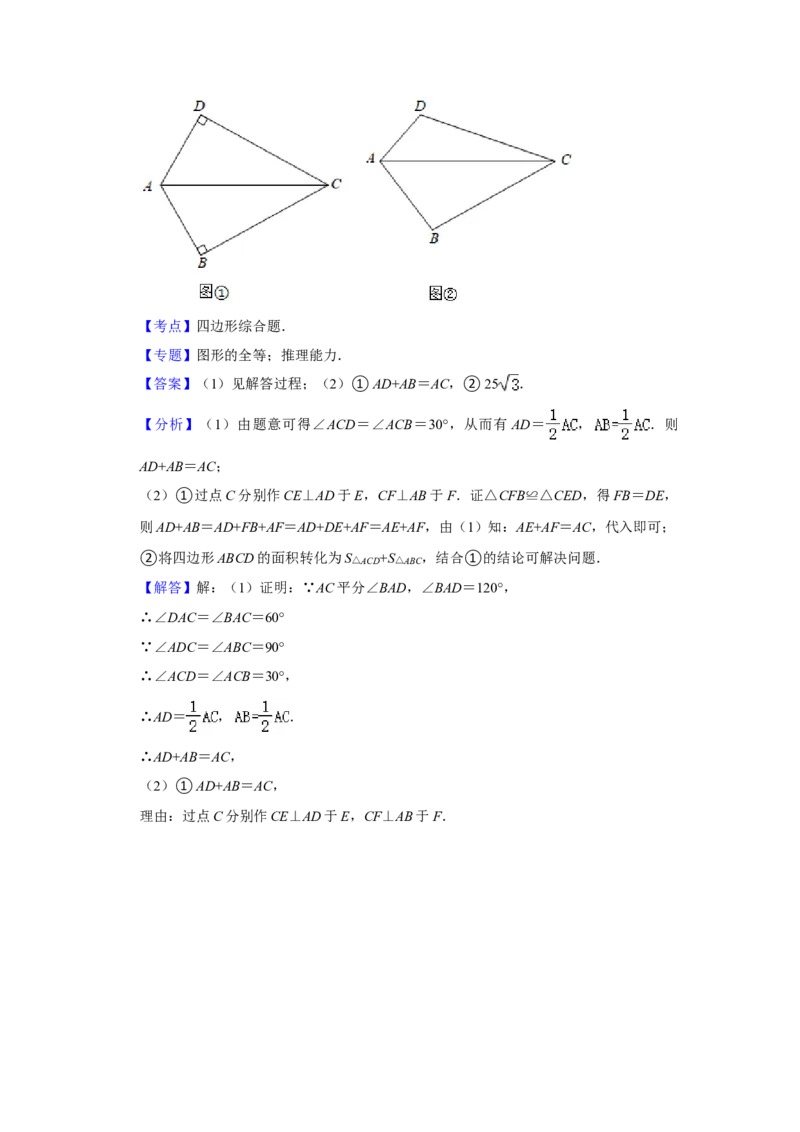
(1)如图①,若∠BAD=120°,∠ABC=∠ADC=90°.求证:AD+AB=AC;
【拓展迁移】
(2)如图②,若∠BAD=120°,∠ABC+∠ADC=180°.
①猜想AB、AD、AC三条线段的数量关系,并说明理由;
②若AC=10,求四边形ABCD的面积.【考点】四边形综合题.
【专题】图形的全等;推理能力.
【答案】(1)见解答过程;(2)①AD+AB=AC,②25 .
【分析】(1)由题意可得∠ACD=∠ACB=30°,从而有AD= , .则
AD+AB=AC;
(2)①过点C分别作CE⊥AD于E,CF⊥AB于F.证△CFB≌△CED,得FB=DE,
则AD+AB=AD+FB+AF=AD+DE+AF=AE+AF,由(1)知:AE+AF=AC,代入即可;
②将四边形ABCD的面积转化为S△ACD +S△ABC ,结合①的结论可解决问题.
【解答】解:(1)证明:∵AC平分∠BAD,∠BAD=120°,
∴∠DAC=∠BAC=60°
∵∠ADC=∠ABC=90°
∴∠ACD=∠ACB=30°,
∴AD= , .
∴AD+AB=AC,
(2)①AD+AB=AC,
理由:过点C分别作CE⊥AD于E,CF⊥AB于F.∵AC平分∠BAD,CE⊥AD于E,CF⊥AB,
∴CF=CE
∵∠ABC+∠ADC=180°,∠EDC+∠ADC=180°,
∴∠FBC=∠EDC
在△CED和△CFB中,
,
∴△CFB≌△CED(AAS),
∴FB=DE,
∴AD+AB=AD+FB+AF=AD+DE+AF=AE+AF,
在四边形AFCE中,由(1)题知:AE+AF=AC,
∴AD+AB=AC,
②在Rt△ACE中,∵AC平分∠BAD,∠BAD=120°,
∴∠DAC=∠BAC=60°,
又∵AC=10
∴CE=AC ,
∵CF=CE,AD+AB=AC,
∴ = .
26如图,抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B(3,0)两点,与y轴交于点C(0,﹣3),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)点P在抛物线的对称轴上,点Q在x轴上,若以点P、Q、B、C为顶点,BC为边
的四边形为平行四边形,请直接写出点P、Q的坐标;
(3)已知点M是x轴上的动点,过点M作x的垂线交抛物线于点G,是否存在这样的
点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;
若不存在,请说明理由.
【考点】二次函数综合题.
【专题】代数几何综合题;多边形与平行四边形;图形的相似;数据分析观念.
【答案】(1)y=x2﹣2x﹣3;(2)点P、Q的坐标分别为(1,﹣3)、(4,0)或
(1,3)、(﹣2,0);(3)点M的坐标为:(0,0)或( ,0)或(6,0)或(
,0).
【分析】(1)用待定系数法即可求解;
(2)当以点P、Q、B、C为顶点,BC为边的四边形为平行四边形时,点C向右平移3
个单位向上平移3个单位得到点B,同样P(Q)向右平移3个单位向上平移3个单位得
到点Q(P),即可求解;
(3)要使以 A、M、G 为顶点得三角形与△BCD 相似,需要满足条件:
,进而求解.
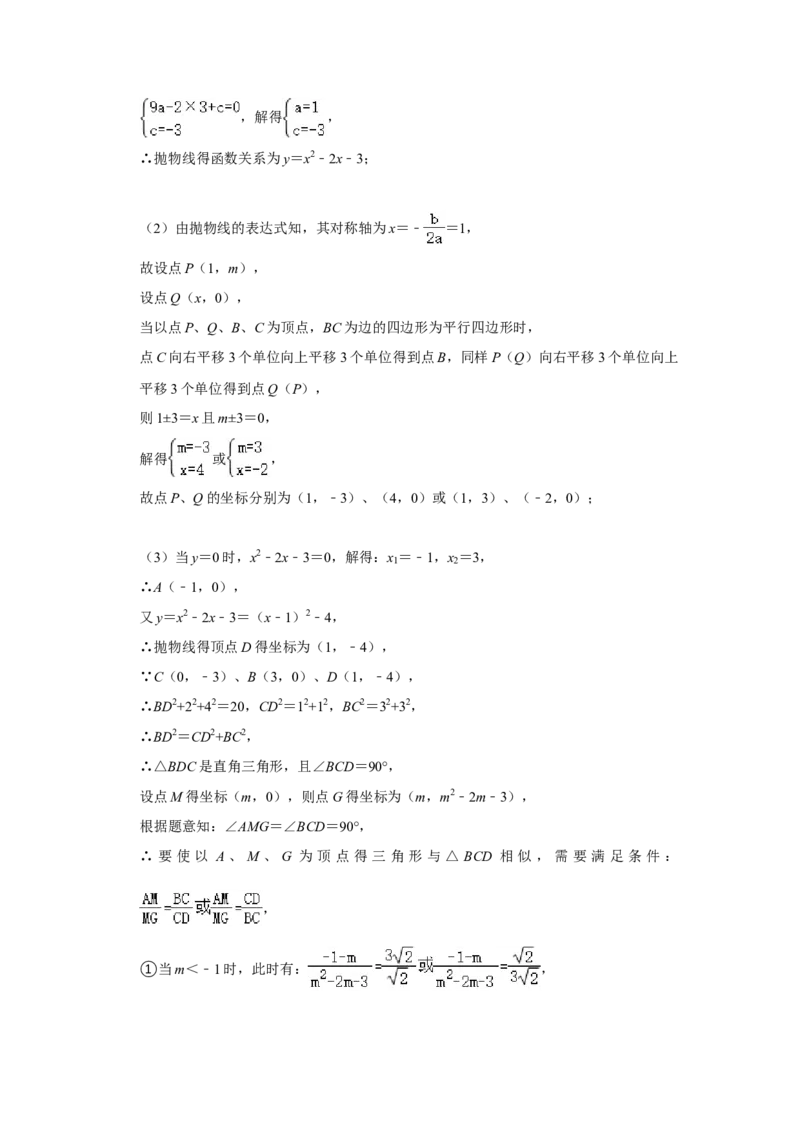
【解答】解:(1)将点B(3,0),C(0,﹣3)分别代入y=ax2﹣2x+c中,得:,解得 ,
∴抛物线得函数关系为y=x2﹣2x﹣3;
(2)由抛物线的表达式知,其对称轴为x=﹣ =1,
故设点P(1,m),
设点Q(x,0),
当以点P、Q、B、C为顶点,BC为边的四边形为平行四边形时,
点C向右平移3个单位向上平移3个单位得到点B,同样P(Q)向右平移3个单位向上
平移3个单位得到点Q(P),
则1±3=x且m±3=0,
解得 或 ,
故点P、Q的坐标分别为(1,﹣3)、(4,0)或(1,3)、(﹣2,0);
(3)当y=0时,x2﹣2x﹣3=0,解得:x =﹣1,x =3,
1 2
∴A(﹣1,0),
又y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线得顶点D得坐标为(1,﹣4),
∵C(0,﹣3)、B(3,0)、D(1,﹣4),
∴BD2+22+42=20,CD2=12+12,BC2=32+32,
∴BD2=CD2+BC2,
∴△BDC是直角三角形,且∠BCD=90°,
设点M得坐标(m,0),则点G得坐标为(m,m2﹣2m﹣3),
根据题意知:∠AMG=∠BCD=90°,
∴ 要 使 以 A 、 M 、 G 为 顶 点 得 三 角 形 与 △ BCD 相 似 , 需 要 满 足 条 件 :
,
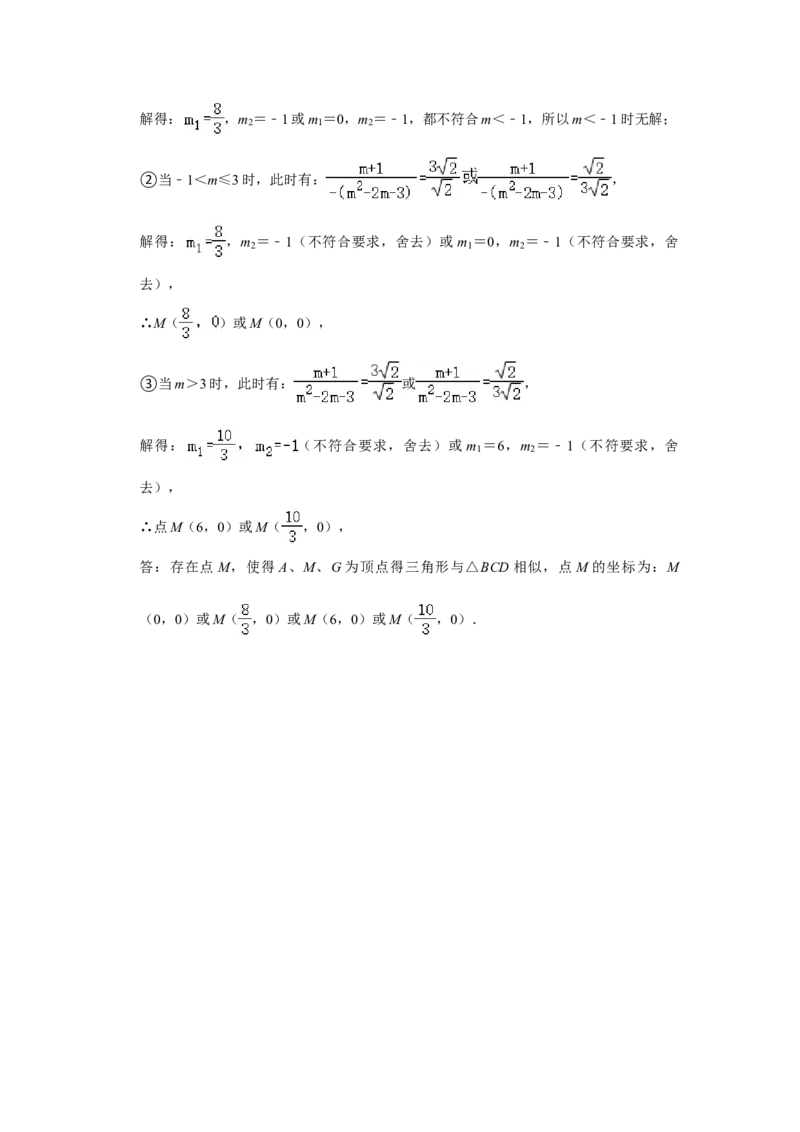
①当m<﹣1时,此时有: ,解得: ,m =﹣1或m =0,m =﹣1,都不符合m<﹣1,所以m<﹣1时无解;
2 1 2
②当﹣1<m≤3时,此时有: ,
解得: ,m =﹣1(不符合要求,舍去)或m =0,m =﹣1(不符合要求,舍
2 1 2
去),
∴M( )或M(0,0),
③当m>3时,此时有: 或 ,
解得: (不符合要求,舍去)或 m =6,m =﹣1(不符要求,舍
1 2
去),
∴点M(6,0)或M( ,0),
答:存在点 M,使得A、M、G为顶点得三角形与△BCD相似,点M的坐标为:M
(0,0)或M( ,0)或M(6,0)或M( ,0).