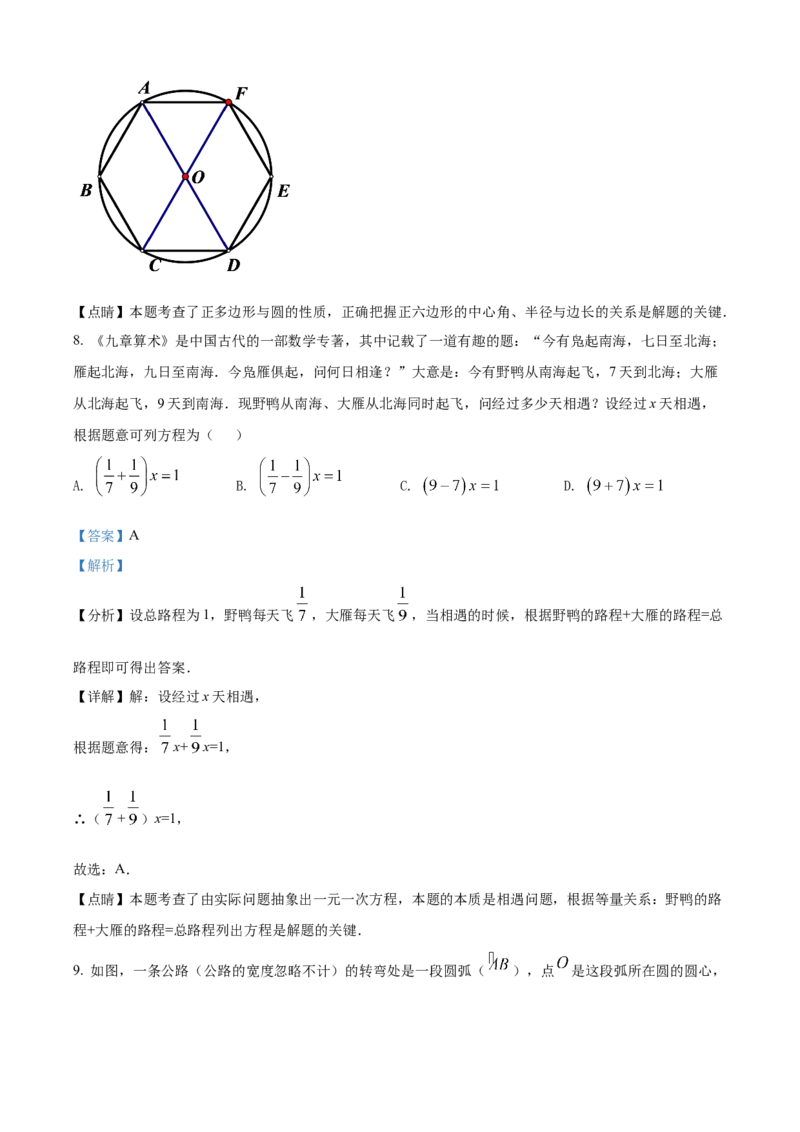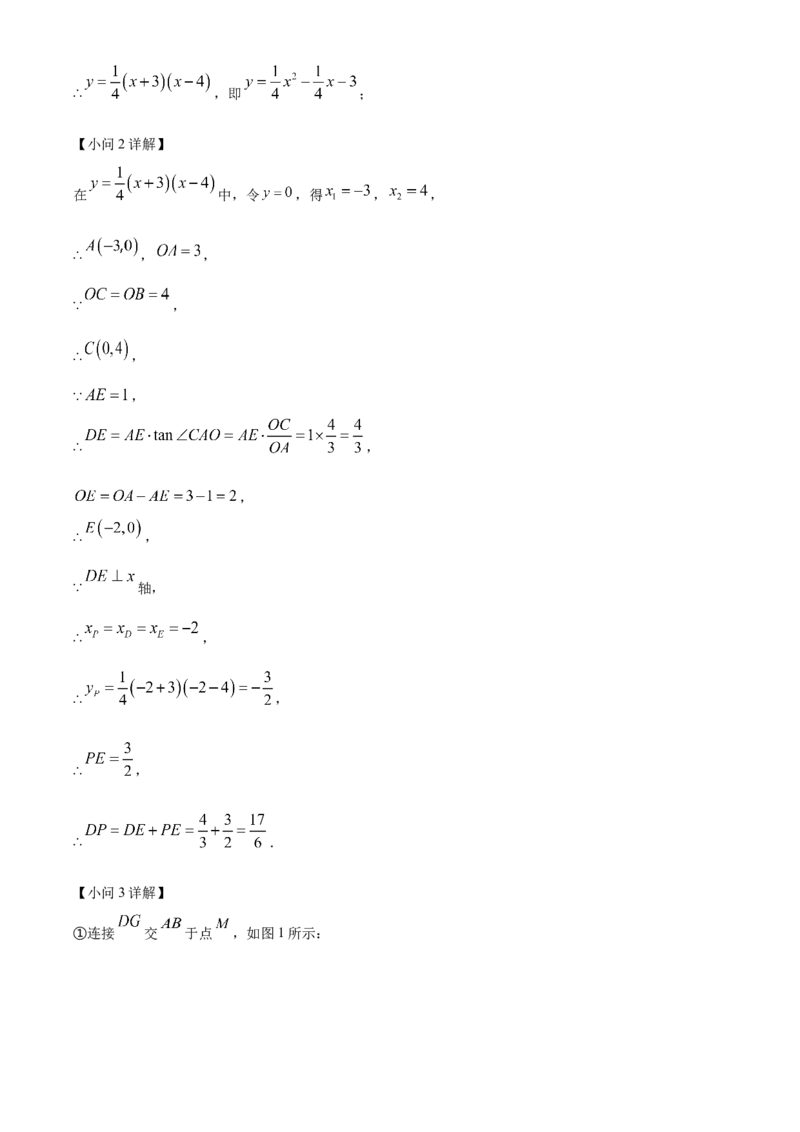文档内容
武威市 2022 年初中毕业、高中招生考试
数学试卷
考生注意:本试卷满分为120分,考试时间为120分钟.所有试题均在答题卡上作答,否则
无效.
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1. 的相反数为( )
A. B. 2 C. D.
【答案】B
【解析】
【分析】根据相反数的概念得出答案.
【详解】∵
∴ 的相反数为 .
故选:B
【点睛】本题考查了相反数的概念,熟练掌握相关概念是解本题的关键.
2. 若 ,则 的余角的大小是( )
A. 50° B. 60° C. 140° D. 160°
【答案】A
【解析】
【分析】用90°减去40°即可求解.
【详解】解:∵ ,
∴ 的余角= ,
故选A
【点睛】本题考查了求一个角的余角,掌握和为90° 的两角互为余角是解题的关键.
3. 不等式 的解集是( )
A. B. C. D.
【答案】C【解析】
的
【分析】按照解一元一次不等式 步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1即
可得出答案.
【详解】解:3x-2>4,
移项得:3x>4+2,
合并同类项得:3x>6,
系数化为1得:x>2.
故选:C.
【点睛】本题考查了解一元一次不等式,掌握解一元一次不等式的步骤:①去分母;②去括号;③移项;
④合并同类项;⑤化系数为1是解题的关键.
4. 用配方法解方程x2-2x=2时,配方后正确的是( )
A. B. C. D.
【答案】C
【解析】
【分析】方程左右两边都加上1,左边化为完全平方式,右边合并即可得到结果.
【详解】解:x2-2x=2,
x2-2x+1=2+1,即(x-1)2=3.
故选:C.
【点睛】本题考查了解一元二次方程-配方法,熟练掌握用配方法解一元二次方程的步骤是解决问题的关键.
5. 若 , , ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】根据△ABC∽△DEF,可以得到 然后根据BC=6,EF=4,即可求解.
【详解】解:∵∴
, ,
故选D
【点睛】本题考查了相似三角形的性质,掌握相似三角形的性质是解题的关键.
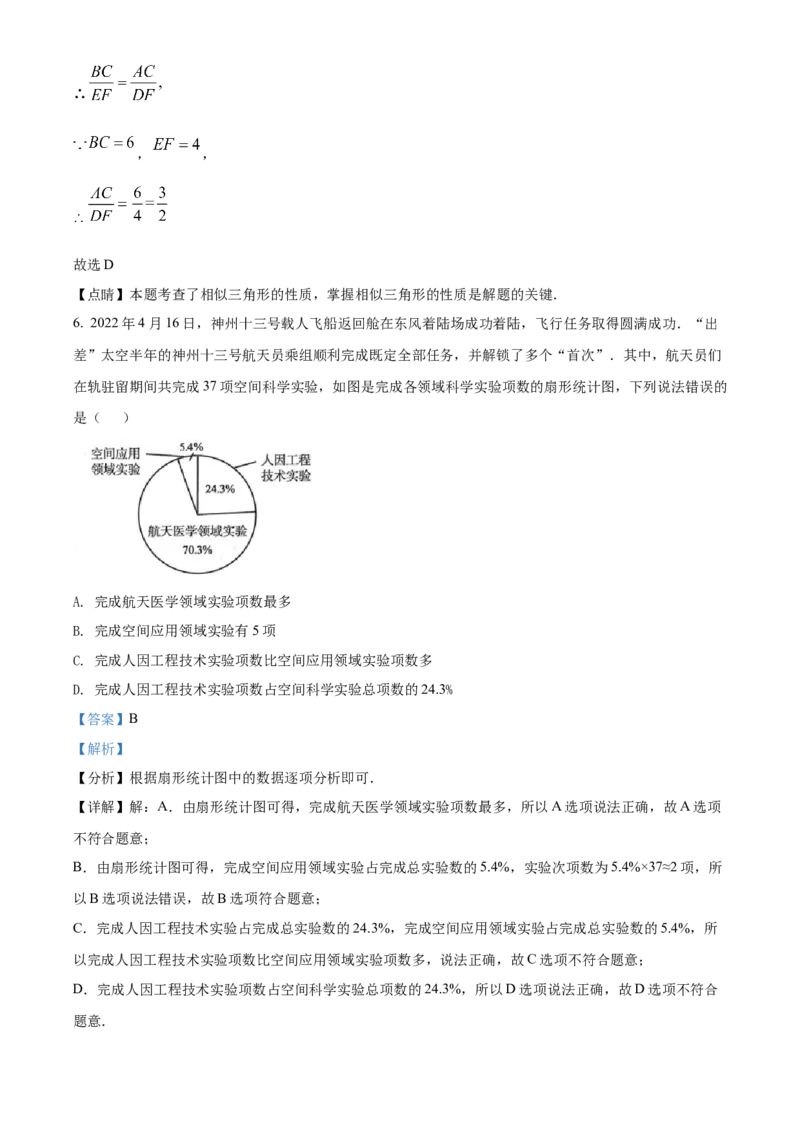
6. 2022年4月16日,神州十三号载人飞船返回舱在东风着陆场成功着陆,飞行任务取得圆满成功.“出
差”太空半年的神州十三号航天员乘组顺利完成既定全部任务,并解锁了多个“首次”.其中,航天员们
在轨驻留期间共完成37项空间科学实验,如图是完成各领域科学实验项数的扇形统计图,下列说法错误的
是( )
A. 完成航天医学领域实验项数最多
B. 完成空间应用领域实验有5项
C. 完成人因工程技术实验项数比空间应用领域实验项数多
D. 完成人因工程技术实验项数占空间科学实验总项数的24.3%
【答案】B
【解析】
【分析】根据扇形统计图中的数据逐项分析即可.
【详解】解:A.由扇形统计图可得,完成航天医学领域实验项数最多,所以A选项说法正确,故A选项
不符合题意;
B.由扇形统计图可得,完成空间应用领域实验占完成总实验数的5.4%,实验次项数为5.4%×37≈2项,所
以B选项说法错误,故B选项符合题意;
C.完成人因工程技术实验占完成总实验数的24.3%,完成空间应用领域实验占完成总实验数的5.4%,所
以完成人因工程技术实验项数比空间应用领域实验项数多,说法正确,故C选项不符合题意;
D.完成人因工程技术实验项数占空间科学实验总项数的24.3%,所以D选项说法正确,故D选项不符合
题意.故选:B.
【点睛】本题主要考查了扇形统计图,熟练掌握扇形统计图的应用是解决本题的关键.
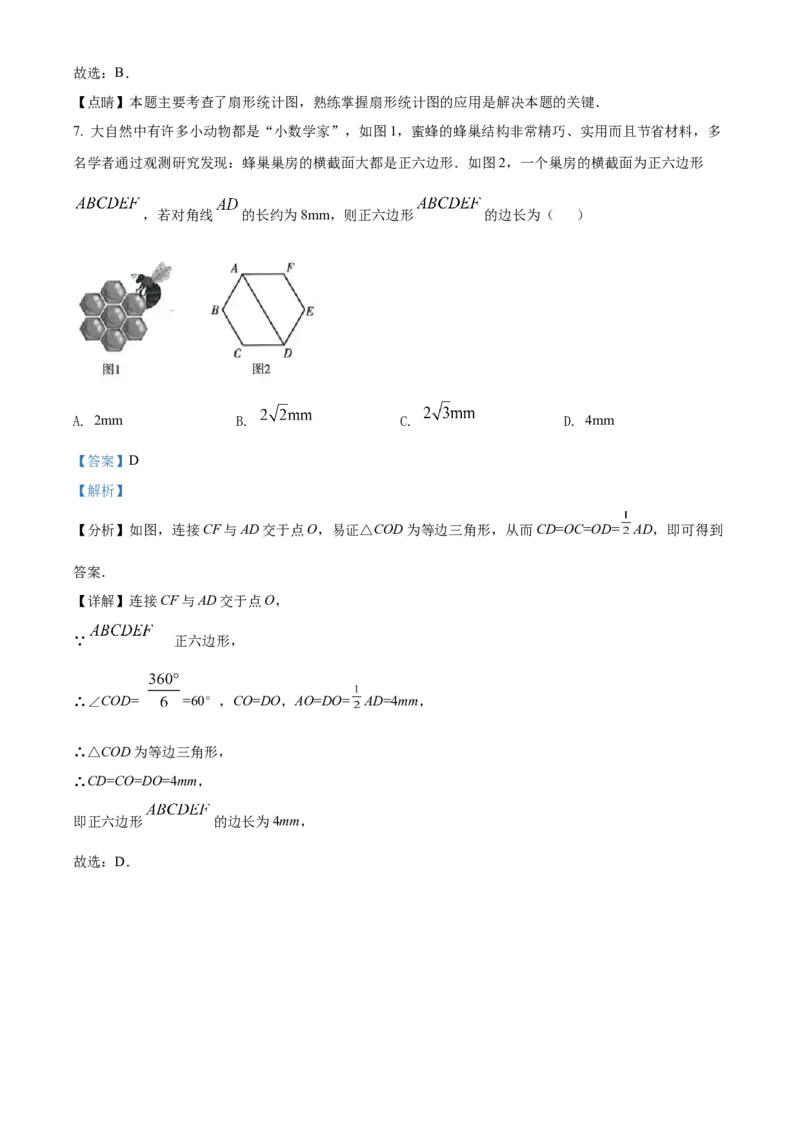
7. 大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多
名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形
,若对角线 的长约为8mm,则正六边形 的边长为( )
A. 2mm B. C. D. 4mm
【答案】D
【解析】
【分析】如图,连接CF与AD交于点O,易证△COD为等边三角形,从而CD=OC=OD= AD,即可得到
答案.
【详解】连接CF与AD交于点O,
为
∵ 正六边形,
∴∠COD= =60°,CO=DO,AO=DO= AD=4mm,
∴△COD为等边三角形,
∴CD=CO=DO=4mm,
即正六边形 的边长为4mm,
故选:D.【点睛】本题考查了正多边形与圆的性质,正确把握正六边形的中心角、半径与边长的关系是解题的关键.
8. 《九章算术》是中国古代的一部数学专著,其中记载了一道有趣的题:“今有凫起南海,七日至北海;
雁起北海,九日至南海.今凫雁俱起,问何日相逢?”大意是:今有野鸭从南海起飞,7天到北海;大雁
从北海起飞,9天到南海.现野鸭从南海、大雁从北海同时起飞,问经过多少天相遇?设经过x天相遇,
根据题意可列方程为( )
A. B. C. D.
【答案】A
【解析】
【分析】设总路程为1,野鸭每天飞 ,大雁每天飞 ,当相遇的时候,根据野鸭的路程+大雁的路程=总
路程即可得出答案.
【详解】解:设经过x天相遇,
根据题意得: x+ x=1,
∴( + )x=1,
故选:A.
【点睛】本题考查了由实际问题抽象出一元一次方程,本题的本质是相遇问题,根据等量关系:野鸭的路
程+大雁的路程=总路程列出方程是解题的关键.
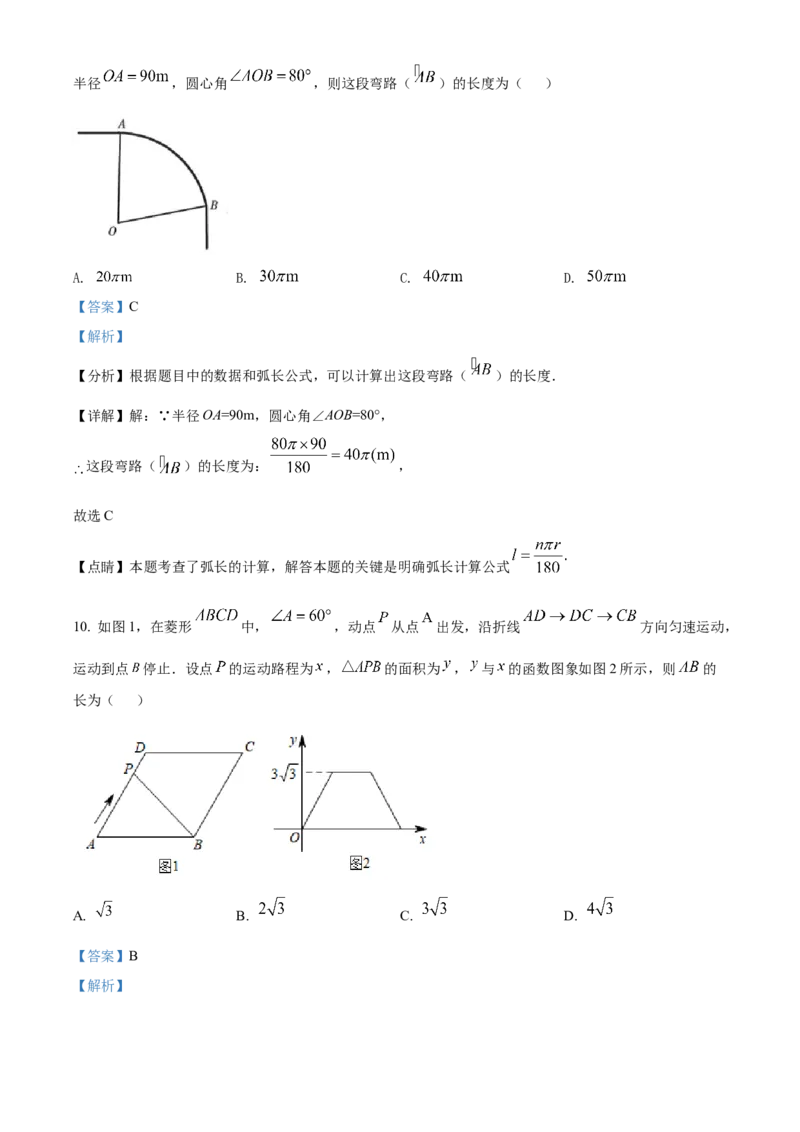
9. 如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧( ),点 是这段弧所在圆的圆心,半径 ,圆心角 ,则这段弯路( )的长度为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据题目中的数据和弧长公式,可以计算出这段弯路( )的长度.
【详解】解:∵半径OA=90m,圆心角∠AOB=80°,
这段弯路( )的长度为: ,
故选C
【点睛】本题考查了弧长的计算,解答本题的关键是明确弧长计算公式
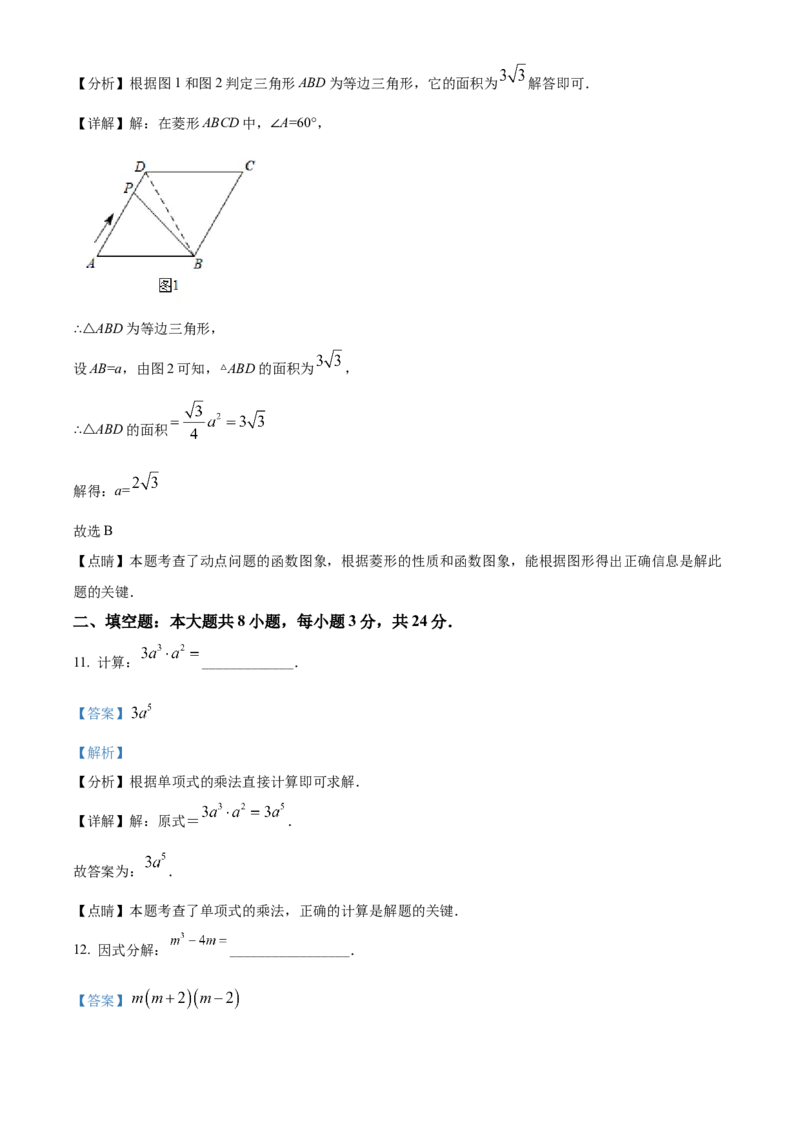
10. 如图1,在菱形 中, ,动点 从点 出发,沿折线 方向匀速运动,
运动到点 停止.设点 的运动路程为 , 的面积为 , 与 的函数图象如图2所示,则 的
长为( )
A. B. C. D.
【答案】B
【解析】【分析】根据图1和图2判定三角形ABD为等边三角形,它的面积为 解答即可.
【详解】解:在菱形ABCD中,∠A=60°,
∴△ABD为等边三角形,
设AB=a,由图2可知,△ABD的面积为 ,
∴△ABD的面积
解得:a=
故选B
【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此
题的关键.
二、填空题:本大题共8小题,每小题3分,共24分.
11. 计算: _____________.
【答案】
【解析】
【分析】根据单项式的乘法直接计算即可求解.
【详解】解:原式= .
故答案为: .
【点睛】本题考查了单项式的乘法,正确的计算是解题的关键.
12. 因式分解: _________________.
【答案】【解析】
【分析】原式提取m,再利用平方差公式分解即可.
【详解】解:原式=m(m2-4)=m(m+2)(m-2),
为
故答案 :m(m+2)(m-2)
【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
13. 若一次函数y=kx−2的函数值y随着自变量x值的增大而增大,则k=_________(写出一个满足条件的
值).
【答案】2(答案不唯一)
【解析】
【分析】根据函数值y随着自变量x值的增大而增大得到k>0,写出一个正数即可.
【详解】解:∵函数值y随着自变量x值的增大而增大,
∴k>0,
∴k=2(答案不唯一).
故答案为:2(答案不唯一).
【点睛】本题考查了一次函数的性质,掌握一次函数的性质:k>0,y随x的增大而增大;k<0,y随x的
增大而减小是解题的关键.
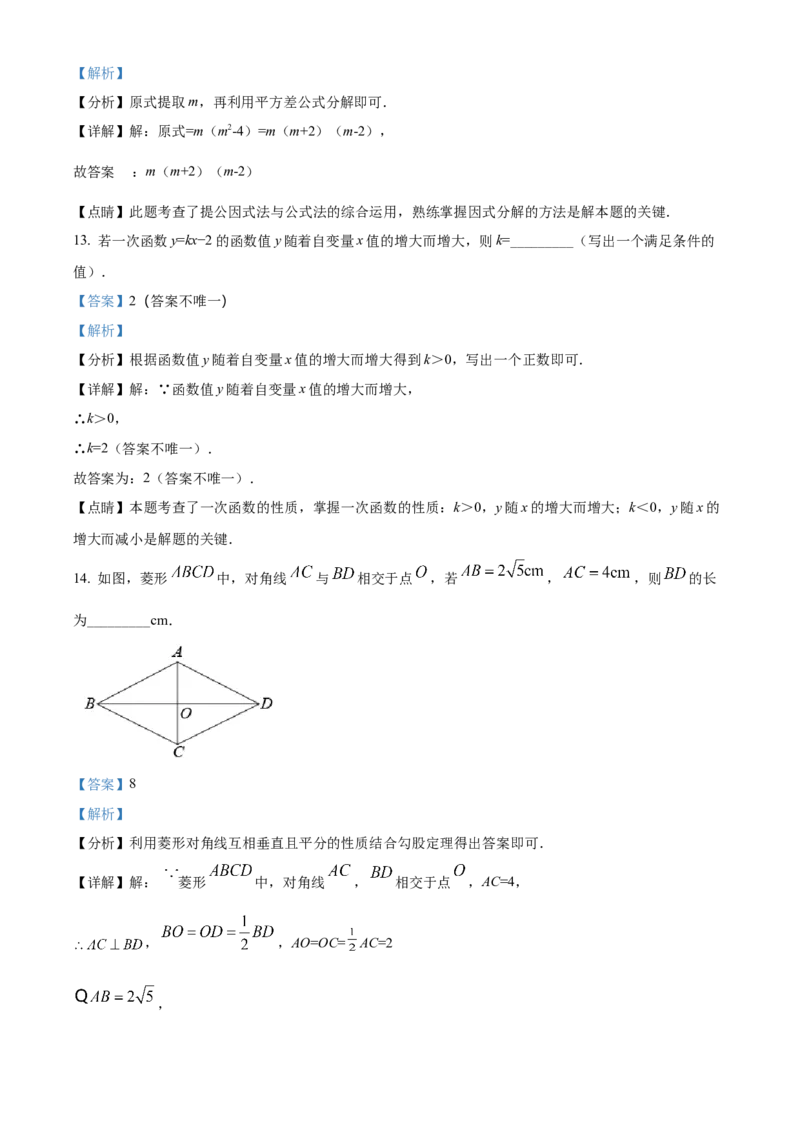
14. 如图,菱形 中,对角线 与 相交于点 ,若 , ,则 的长
为_________cm.
【答案】8
【解析】
【分析】利用菱形对角线互相垂直且平分的性质结合勾股定理得出答案即可.
【详解】解: 菱形 中,对角线 , 相交于点 ,AC=4,
, ,AO=OC= AC=2
,,
,
故答案为:8.
【点睛】此题主要考查了菱形的性质以及勾股定理的应用,熟练掌握菱形的性质,运用勾股定理解直角三
角形,是解题关键.
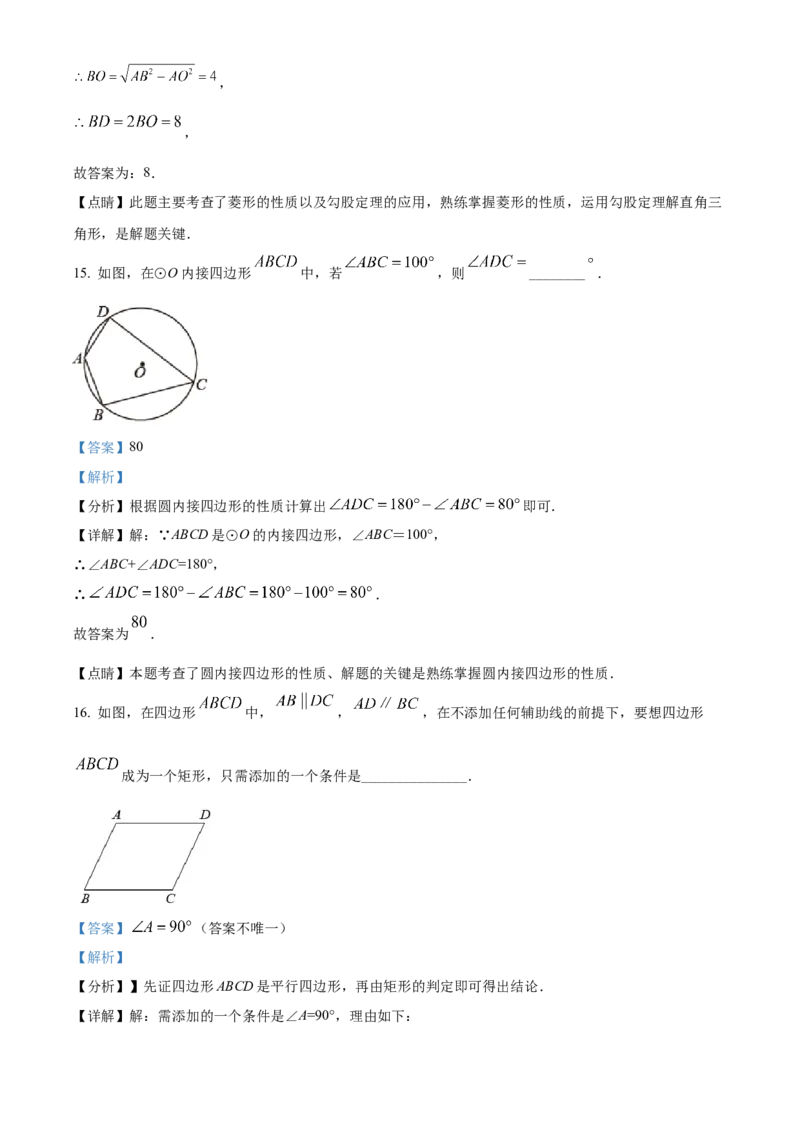
15. 如图,在⊙O内接四边形 中,若 ,则 ________ .
【答案】80
【解析】
【分析】根据圆内接四边形的性质计算出 即可.
【详解】解:∵ABCD是⊙O的内接四边形,∠ABC=100°,
∴∠ABC+∠ADC=180°,
∴ .
故答案为 .
【点睛】本题考查了圆内接四边形的性质、解题的关键是熟练掌握圆内接四边形的性质.
16. 如图,在四边形 中, , ,在不添加任何辅助线的前提下,要想四边形
成为一个矩形,只需添加的一个条件是_______________.
【答案】 (答案不唯一)
【解析】
【分析】】先证四边形ABCD是平行四边形,再由矩形的判定即可得出结论.
【详解】解:需添加的一个条件是∠A=90°,理由如下:∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°(答案不唯一).
【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定和平行四边形的
判定与性质是解题的关键.
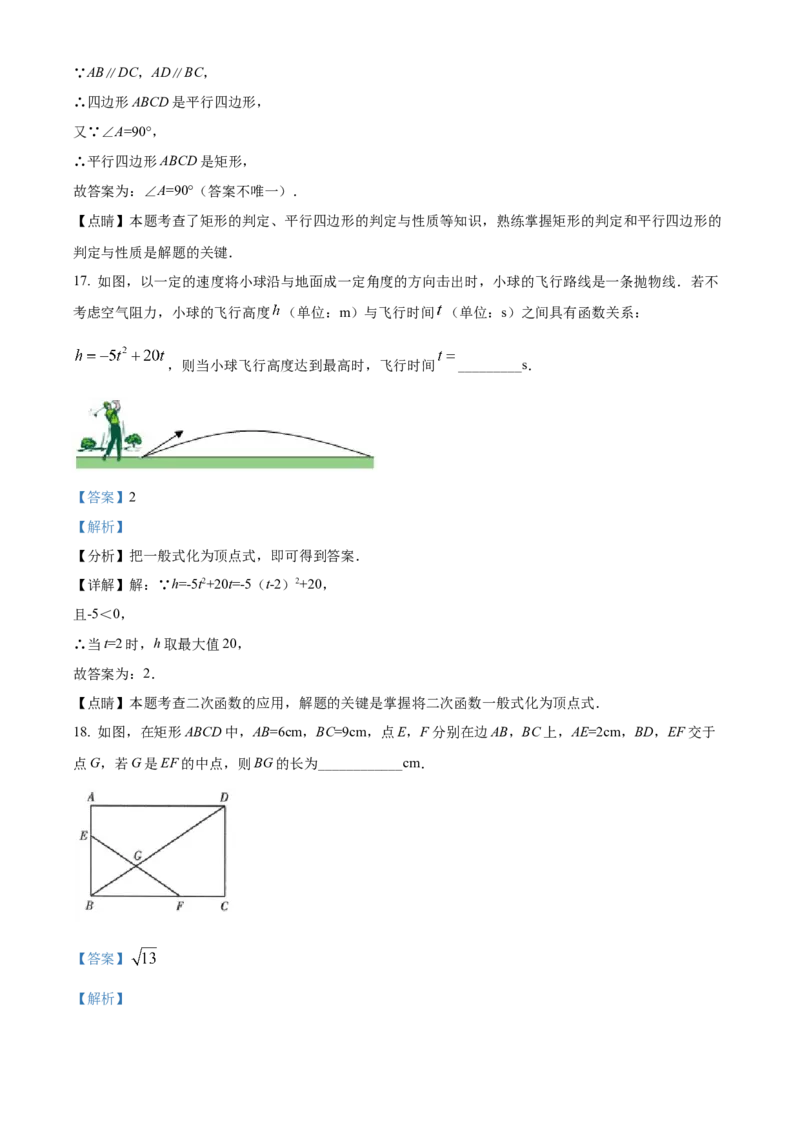
17. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不
考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系:
,则当小球飞行高度达到最高时,飞行时间 _________s.
【答案】2
【解析】
【分析】把一般式化为顶点式,即可得到答案.
【详解】解:∵h=-5t2+20t=-5(t-2)2+20,
且-5<0,
∴当t=2时,h取最大值20,
故答案为:2.
【点睛】本题考查二次函数的应用,解题的关键是掌握将二次函数一般式化为顶点式.
18. 如图,在矩形ABCD中,AB=6cm,BC=9cm,点E,F分别在边AB,BC上,AE=2cm,BD,EF交于
点G,若G是EF的中点,则BG的长为____________cm.
【答案】
【解析】【分析】根据矩形的性质可得AB=CD=6cm,∠ABC=∠C=90°,AB∥CD,从而可得∠ABD=∠BDC,然后
利用直角三角形斜边上的中线可得EG=BG,从而可得∠BEG=∠ABD,进而可得∠BEG=∠BDC,再证明
EBF∽△DCB,利用相似三角形的性质可求出BF的长,最后在Rt BEF中,利用勾股定理求出EF的长,
△即可解答. △
【详解】解:∵四边形ABCD是矩形,
∴AB=CD=6cm,∠ABC=∠C=90°,AB∥CD,
∴∠ABD=∠BDC,
∵AE=2cm,
∴BE=AB-AE=6-2=4(cm),
∵G是EF的中点,
∴EG=BG= EF,
∴∠BEG=∠ABD,
∴∠BEG=∠BDC,
∴△EBF∽△DCB,
∴ ,
∴ ,
∴BF=6,
∴EF= (cm),
∴BG= EF= (cm),
故答案为: .
【点睛】本题考查了相似三角形的判定与性质,勾股定理,矩形的性质,直角三角形斜边上的中线,熟练
掌握直角三角形斜边上的中线,以及相似三角形的判定与性质是解题的关键.
三、解答题:本大题共5小题,共26分.解答时,应写出必要的文字说明、证明过程或演算
步骤.
19. 计算: .【答案】
【解析】
【分析】根据二次根式的混合运算进行计算即可求解.
【详解】解:原式
.
【点睛】本题考查了次根式的混合运算,正确的计算是解题的关键.
20. 化简: .
【答案】1
【解析】
【分析】将除法转化为乘法,因式分解,约分,根据分式的加减法法则化简即可得出答案.
【详解】解:原式
=1.
【点睛】本题考查了分式的混合运算,考查学生运算能力,掌握运算的结果要化成最简分式或整式是解题
的关键.
21. 中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编(图1),书中记载了大量几
何作图题,所有内容均用浅近的文言文表述,第一编记载了这样一道几何作图题:
原文 释义
如图2, 为直角.
甲乙丙为定直角.
以乙为圆心,以任何半径作丁戊弧; 以点 为圆心,以任意长为半径画弧,交射线 , 分别于
点 , ;
以丁为圆心,以乙丁为半径画弧得交
点己;
以点 为圆心,以 长为半径画弧与 交于点 ;
再以戊为圆心,仍以原半径画弧得交
点庚; 再以点 为圆心,仍以 长为半径画弧与 交于点 ;
乙与己及庚相连作线.
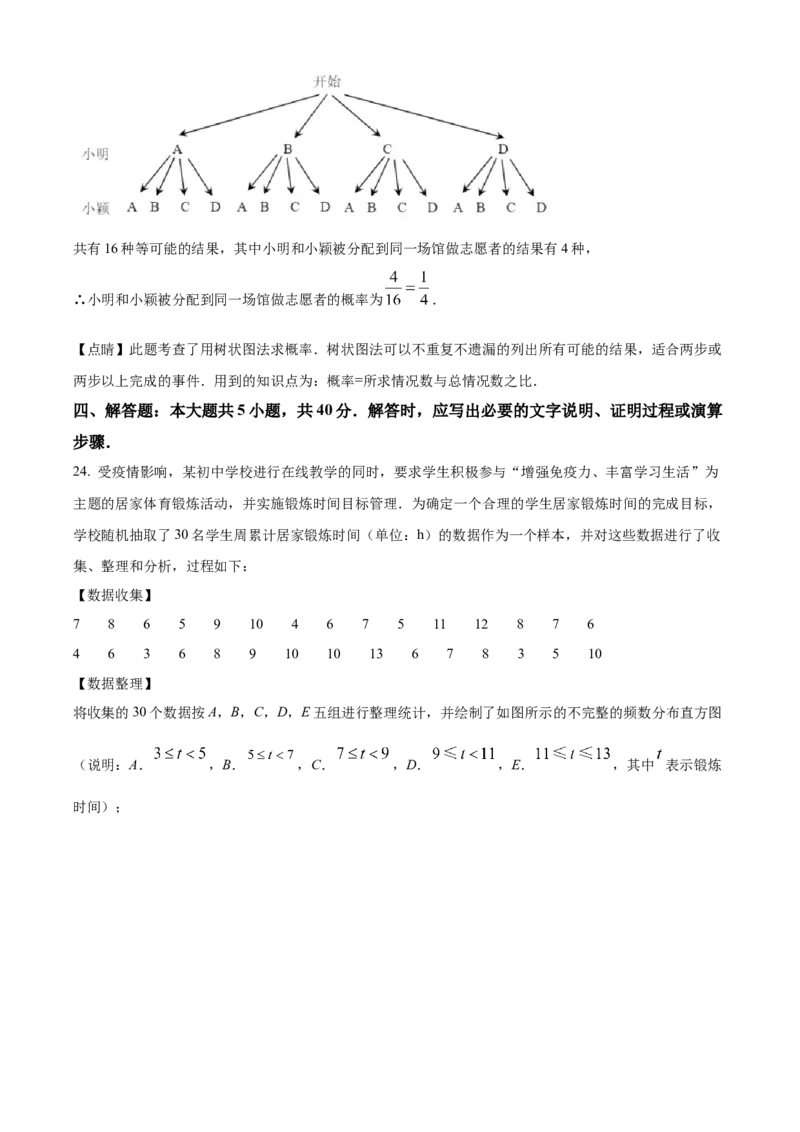
作射线 , .(1)根据以上信息,请你用不带刻度的直尺和圆规,在图2中完成这道作图题(保留作图痕迹,不写作
法);
(2)根据(1)完成的图,直接写出 , , 的大小关系.
【答案】(1)见解析 (2)
【解析】
【分析】(1)根据题意作出图形即可;
(2)连接DF,EG,可得 和 均为等边三角形, ,进而可得
.
【小问1详解】
解:(1)如图:
【小问2详解】
.
理由:连接DF,EG如图所示
则BD=BF=DF,BE=BG=EG即 和 均为等边三角形
∴
∵
∴
【点睛】本题考查了尺规作图,根据题意正确作出图形是解题的关键.
22. 灞陵桥位于甘肃省渭源县城南清源河(渭河上游)上,始建于明洪武初年,因“渭水绕长安,绕灞陵,
为玉石栏杆灞陵桥”之语,得名灞陵桥(图1),该桥为全国独一无二的纯木质叠梁拱桥.某综合实践研
究小组开展了测量汛期某天“灞陵桥拱梁顶部到水面的距离”的实践活动,过程如下:
方案设计:如图2,点C为桥拱梁顶部(最高点),在地面上选取A,B两处分别测得∠CAF和∠CBF的
度数(A,B,D,F在同一条直线上),河边D处测得地面AD到水面EG的距离DE(C,F,G在同一条
直线上,DF∥EG,CG⊥AF,FG=DE).
数据收集:实地测量地面上A,B两点的距离为8.8m,地面到水面的距离DE=1.5m,∠CAF=26.6°,
∠CBF=35°.
问题解决:求灞陵桥拱梁顶部C到水面的距离CG(结果保留一位小数).
.
参考数据:sin266°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.
根据上述方案及数据,请你完成求解过程.
【答案】16.9m
【解析】
【分析】设BF=x m,根据题意可得:DE=FG=1.5m,然后在Rt CBF中,利用锐角三角函数的定义求出
CF的长,再在Rt ACF中,利用锐角三角函数的定义列出关于△x的方程,进行计算即可解答.
【详解】解:设B△F=x m,
由题意得:
DE=FG=1.5m,
在Rt CBF中,∠CBF=35°,
△∴CF=BF•tan35°≈0.7x(m),
∵AB=8.8m,
∴AF=AB+BF=(8.8+x)m,
在Rt ACF中,∠CAF=26.6°,
△
∴tan26.6°= ≈0.5,
∴x=22,
经检验:x=22是原方程的根,
∴CG=CF+FG=0.7x+1.5=16.9(m),
∴灞陵桥拱梁顶部C到水面的距离CG约为16.9m.
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
23. 第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京-张家口成功举办,其中张家口赛区设
有四个冬奥会竞赛场馆,分别为:A.云顶滑雪公园、B.国家跳台滑雪中心、C.国家越野滑雪中心、
D.国家冬季两项中心.小明和小颖都是志愿者,他们被随机分配到这四个竞赛场馆中的任意一个场馆的
可能性相同.
(1)小明被分配到D.国家冬季两项中心场馆做志愿者的概率是多少?
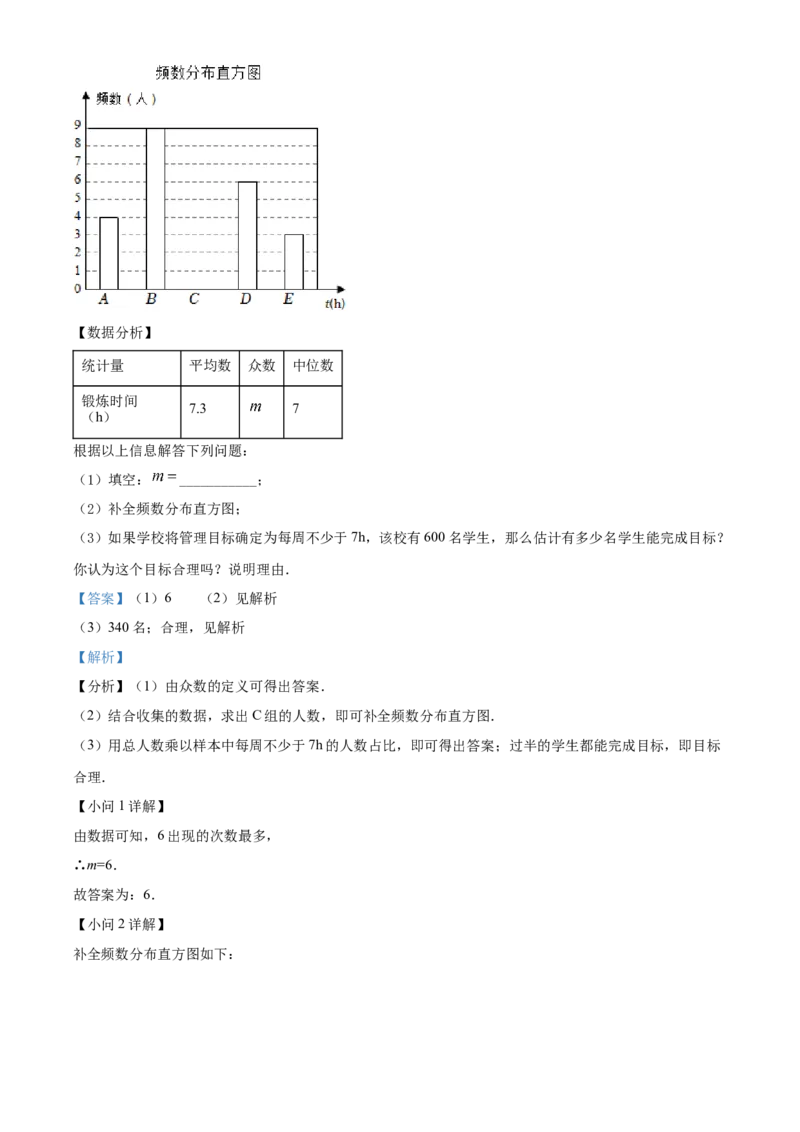
(2)利用画树状图或列表的方法,求小明和小颖被分配到同一场馆做志愿者的概率.
【答案】(1)
(2)
【解析】
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有16种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有4种,再
由概率公式求解即可.
【小问1详解】
解:小明被分配到D.国家冬季两项中心场馆做志愿者的概率是 ;
【小问2详解】
解:画树状图如下:共有16种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有4种,
∴小明和小颖被分配到同一场馆做志愿者的概率为 .
【点睛】此题考查了用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或
两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
四、解答题:本大题共5小题,共40分.解答时,应写出必要的文字说明、证明过程或演算
步骤.
24. 受疫情影响,某初中学校进行在线教学的同时,要求学生积极参与“增强免疫力、丰富学习生活”为
主题的居家体育锻炼活动,并实施锻炼时间目标管理.为确定一个合理的学生居家锻炼时间的完成目标,
学校随机抽取了30名学生周累计居家锻炼时间(单位:h)的数据作为一个样本,并对这些数据进行了收
集、整理和分析,过程如下:
【数据收集】
7 8 6 5 9 10 4 6 7 5 11 12 8 7 6
4 6 3 6 8 9 10 10 13 6 7 8 3 5 10
【数据整理】
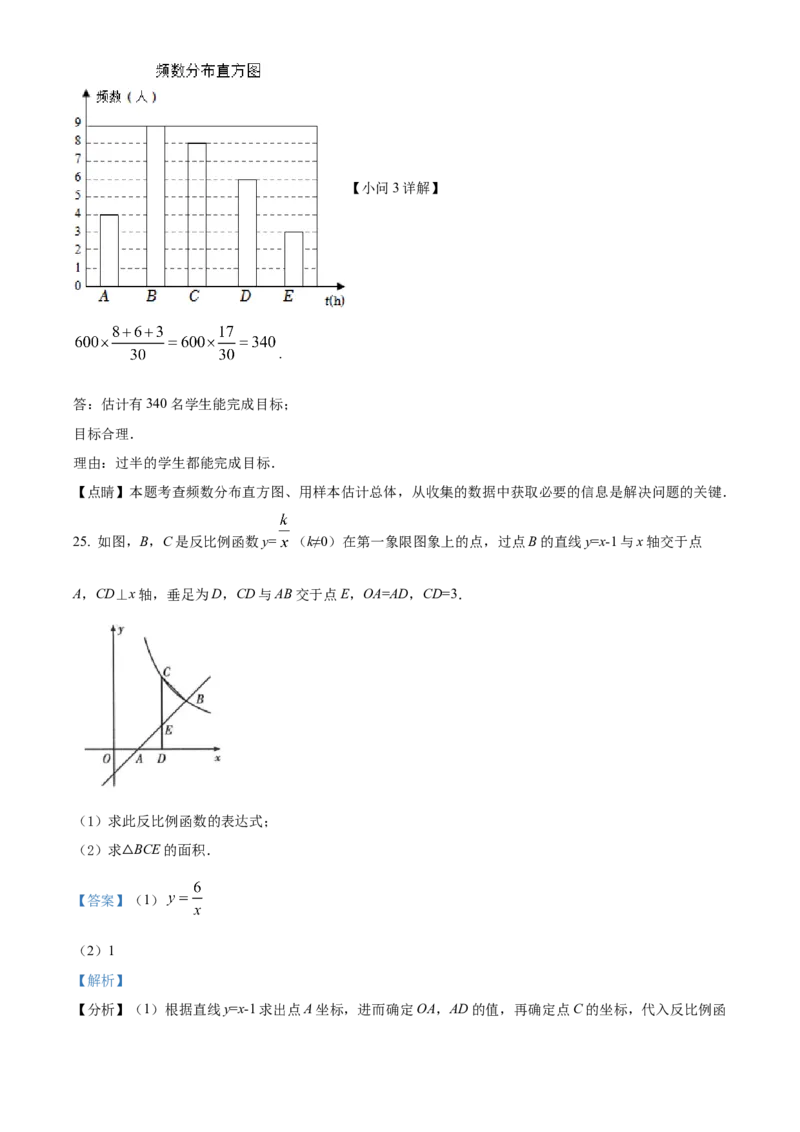
将收集的30个数据按A,B,C,D,E五组进行整理统计,并绘制了如图所示的不完整的频数分布直方图
(说明:A. ,B. ,C. ,D. ,E. ,其中 表示锻炼
时间);【数据分析】
统计量 平均数 众数 中位数
锻炼时间
7.3 7
(h)
根据以上信息解答下列问题:
(1)填空: ___________;
(2)补全频数分布直方图;
(3)如果学校将管理目标确定为每周不少于7h,该校有600名学生,那么估计有多少名学生能完成目标?
你认为这个目标合理吗?说明理由.
【答案】(1)6 (2)见解析
(3)340名;合理,见解析
【解析】
【分析】(1)由众数的定义可得出答案.
(2)结合收集的数据,求出C组的人数,即可补全频数分布直方图.
(3)用总人数乘以样本中每周不少于7h的人数占比,即可得出答案;过半的学生都能完成目标,即目标
合理.
【小问1详解】
由数据可知,6出现的次数最多,
∴m=6.
故答案为:6.
【小问2详解】
补全频数分布直方图如下:【小问3详解】
.
答:估计有340名学生能完成目标;
目标合理.
理由:过半的学生都能完成目标.
【点睛】本题考查频数分布直方图、用样本估计总体,从收集的数据中获取必要的信息是解决问题的关键.
25. 如图,B,C是反比例函数y= (k≠0)在第一象限图象上的点,过点B的直线y=x-1与x轴交于点
A,CD⊥x轴,垂足为D,CD与AB交于点E,OA=AD,CD=3.
(1)求此反比例函数的表达式;
(2)求 BCE的面积.
△
【答案】(1)
(2)1
【解析】
【分析】(1)根据直线y=x-1求出点A坐标,进而确定OA,AD的值,再确定点C的坐标,代入反比例函数的关系式即可;
(2)求出点E坐标,进而求出EC,再求出一次函数与反比例函数在第一象限的交点B的坐标,由三角形
的面积的计算方法进行计算即可.
【小问1详解】
解:当y=0时,即x-1=0,
∴x=1,
即直线y=x-1与x轴交于点A的坐标为(1,0),
∴OA=1=AD,
又∵CD=3,
∴点C的坐标为(2,3),
而点C(2,3)在反比例函数y= 的图象上,
∴k=2×3=6,
∴反比例函数的图象为y= ;
【小问2详解】
解:方程组 的正数解为 ,
的
∴点B 坐标为(3,2),
当x=2时,y=2-1=1,
∴点E的坐标为(2,1),即DE=1,
∴EC=3-1=2,
∴S = ×2×(3-2)=1,
BCE
△
答: BCE的面积为1.
【点△睛】本题考查反比例函数、一次函数交点坐标以及待定系数法求函数关系式,将一次函数、反比例函
数的关系式联立方程组是求出交点坐标的基本方法,将点的坐标转化为线段的长是正确解答的关键.
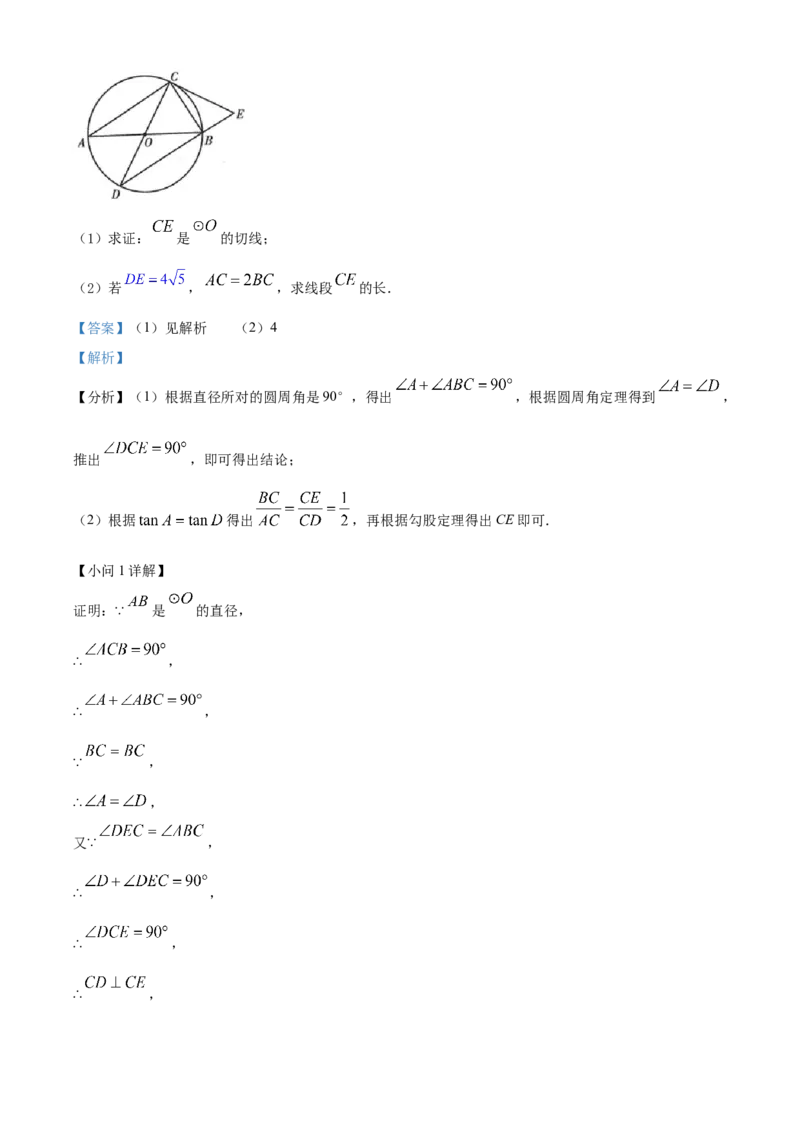
26. 如图, 内接于 , , 是 的直径, 是 延长线上一点,且 .(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
【答案】(1)见解析 (2)4
【解析】
【分析】(1)根据直径所对的圆周角是90°,得出 ,根据圆周角定理得到 ,
推出 ,即可得出结论;
(2)根据 得出 ,再根据勾股定理得出CE即可.
【小问1详解】
证明:∵ 是 的直径,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,∵ 为 的半径,
∴ 是 的切线;
【小问2详解】
由(1)知 ,
在 和 中,∵ , ,
∴ ,即 ,
∴ ,
在 中, , ,
∴ ,解得 .
【点睛】本题主要考查圆的综合题,熟练掌握圆周角定理,切线的判定,勾股定理等知识是解题的关键.
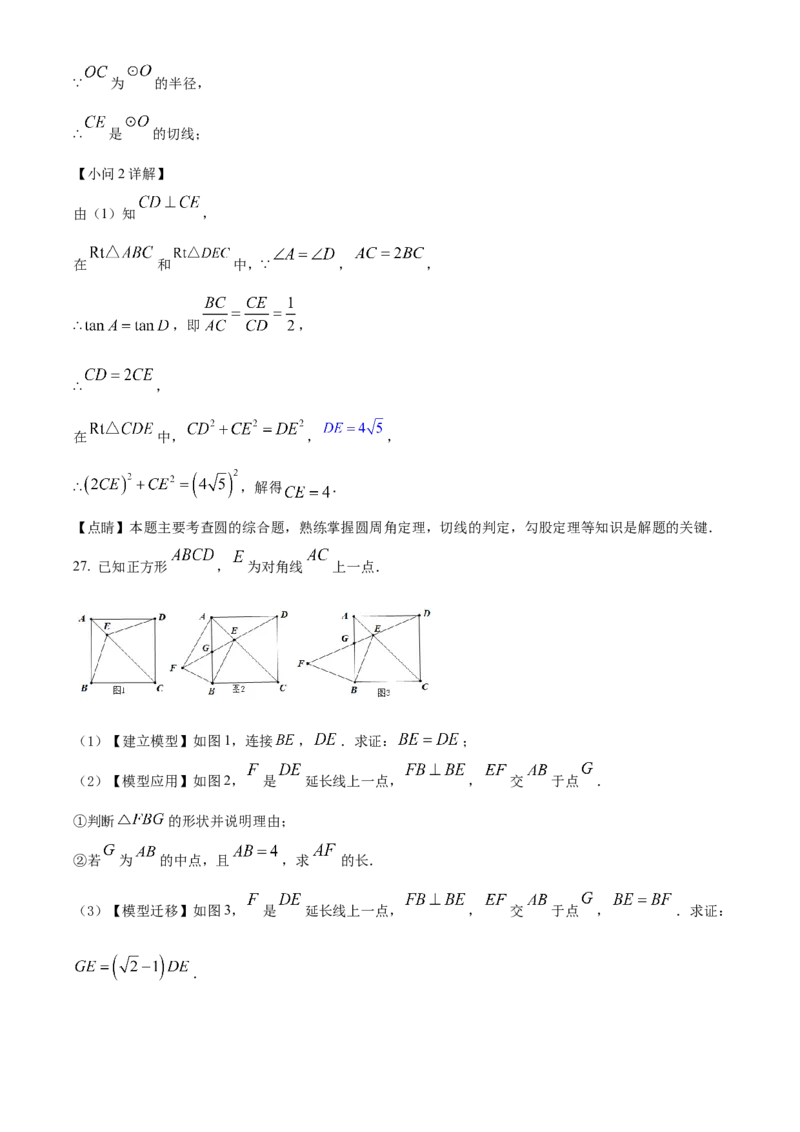
27. 已知正方形 , 为对角线 上一点.
(1)【建立模型】如图1,连接 , .求证: ;
(2)【模型应用】如图2, 是 延长线上一点, , 交 于点 .
①判断 的形状并说明理由;
②若 为 的中点,且 ,求 的长.
(3)【模型迁移】如图3, 是 延长线上一点, , 交 于点 , .求证:
.【答案】(1)见解析 (2)①等腰三角形,见解析;②
(3)见解析
【解析】
【分析】(1)根据正方形的性质,证明 即可.
(2)①根据(1)的证明,证明∠FBG=∠FGB即可.
②过点 作 ,垂足为 .利用三角函数求得FH,AH的长度即可.
(3)证明 即可.
【小问1详解】
)证明:∵四边形 为正方形, 为对角线,
∴ , .
∵ ,
∴ ,
∴ .
【小问2详解】
① 为等腰三角形.理由如下:
∵四边形 为正方形,
∴ ,
∴ .
∵ ,
∴ ,
由(1)得 ,
∴ ,
又∵ ,
∴ ,∴ 为等腰三角形.
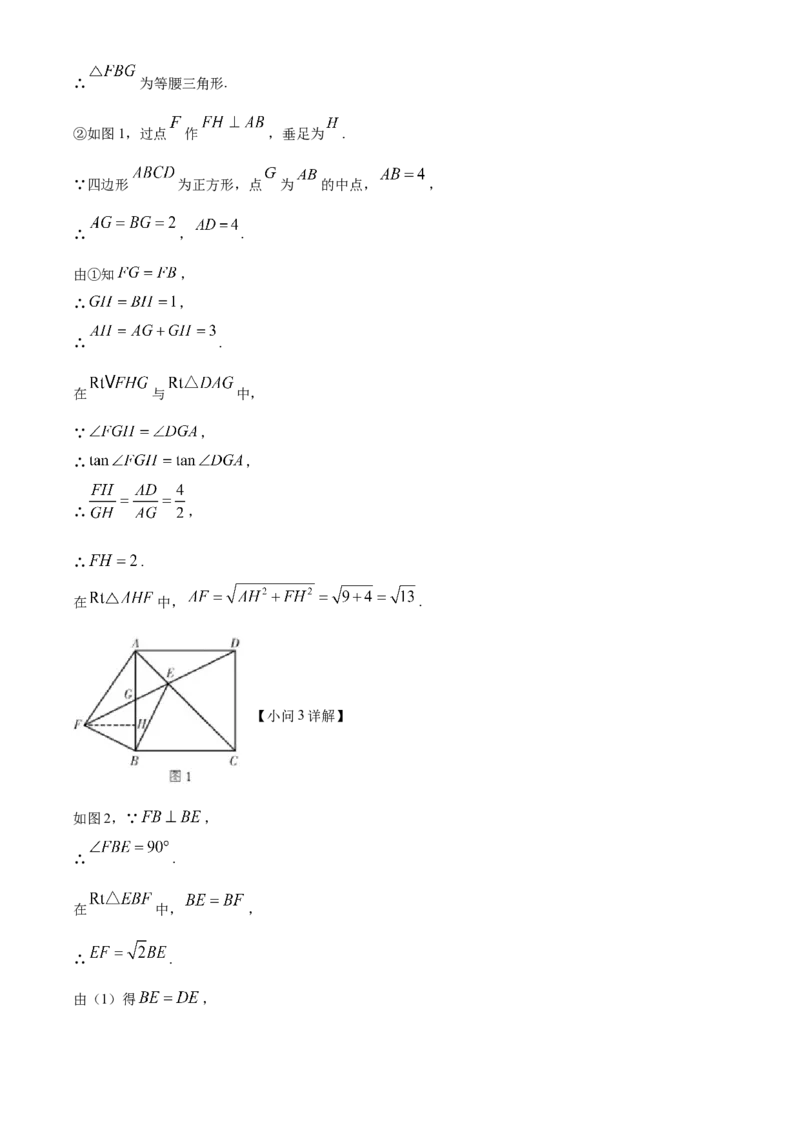
②如图1,过点 作 ,垂足为 .
∵四边形 为正方形,点 为 的中点, ,
∴ , .
由①知 ,
∴ ,
∴ .
在 与 中,
∵ ,
∴ ,
∴ ,
∴ .
在 中, .
【小问3详解】
如图2,∵ ,
∴ .
在 中, ,
∴ .
由(1)得 ,由(2)得 ,
∴ .
【点睛】本题考查了正方形的性质,等腰三角形的判定和性质,三角函数的应用,勾股定理,熟练掌握正
方形的性质,勾股定理和三角函数是解题的关键.
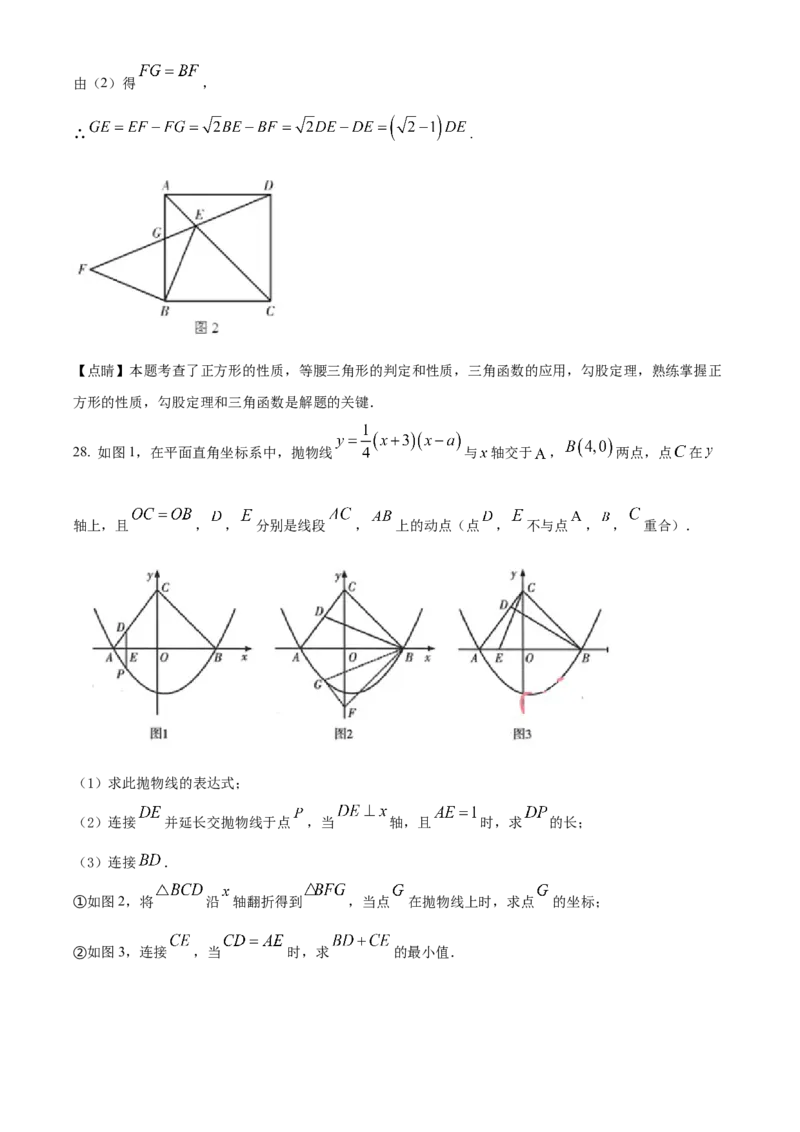
28. 如图1,在平面直角坐标系中,抛物线 与 轴交于 , 两点,点 在
轴上,且 , , 分别是线段 , 上的动点(点 , 不与点 , , 重合).
(1)求此抛物线的表达式;
(2)连接 并延长交抛物线于点 ,当 轴,且 时,求 的长;
(3)连接 .
①如图2,将 沿 轴翻折得到 ,当点 在抛物线上时,求点 的坐标;
②如图3,连接 ,当 时,求 的最小值.【答案】(1)
(2)
(3)① ;②
【解析】
【分析】(1)把点B代入抛物线关系式,求出a的值,即可得出抛物线的关系式;
(2)根据抛物线 可求出点A的坐标,点C的坐标,根据 ,利用三角函数,求
出DE的长,再求出点E的坐标,根据点P与点E的横坐标相同,得出点P的横坐标,代入抛物线的关系
式,求出点P的纵坐标,即可得出EP的值,最后求出DP的值即可;
(3)①连接 交 于点 ,设 ,则 ,求出
,得出点 ,将其代入抛物线关系式,列出关
于a的方程,解方程,求出a的值,即可得出G的坐标;
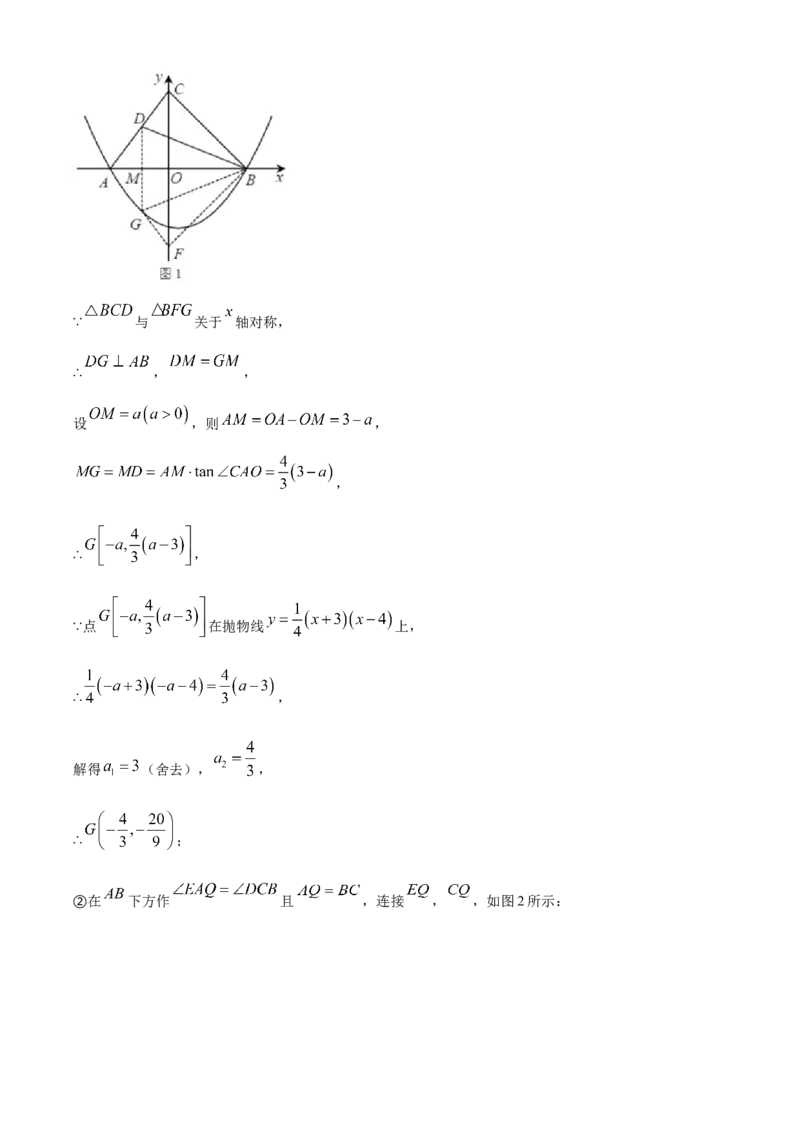
②在 下方作 且 ,连接 , ,证明 ,得出
,说明当 , , 三点共线时, 最小,最小为 ,过 作
,垂足为 ,先证明∠CAH=45°,算出AC长度,即可求出CH、AH,得出HQ,最后根据勾
股定理求出CQ的长度即可得出结果.
【小问1详解】
解:∵ 在抛物线 上,
∴ ,解得 ,∴ ,即 ;
【小问2详解】
在 中,令 ,得 , ,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
,
∴ ,
∵ 轴,
∴ ,
∴ ,
∴ ,
∴ .
【小问3详解】
①连接 交 于点 ,如图1所示:∵ 与 关于 轴对称,
∴ , ,
设 ,则 ,
,
∴ ,
∵点 在抛物线 上,
∴ ,
解得 (舍去), ,
∴ ;
②在 下方作 且 ,连接 , ,如图2所示:∵ ,
∴ ,
∴ ,
∴当 , , 三点共线时, 最小,最小为 ,
过 作 ,垂足为 ,
∵ , ,
∴ , ,
∵ ,
, ,
,
∴
,即 的最小值为 .
【点睛】本题主要考查了二次函数的综合应用,待定系数法求抛物线的关系式,全等三角形的判定和性质,
解直角三角形,三角函数的定义,作出辅助线,证明 ,得出当 , , 三点共线时,
最小,是解题的关键.