文档内容
2024年高考押题预测卷【全国卷】
数学·(文科01)参考答案
第一部分(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1 2 3 4 5 6 7 8 9 10 11 12
B A C D C A C B A C D A
二、填空题:本大题共4小题,每小题5分,共20分
13. / 14.3 15. 16.①③④
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
【答案】(1) (2)
【详解】(1)解法一 因为 ,所以 .................2分
在 中,由正弦定理得 ,........................................................................3分
所以 ,
所以 ,则 ..........................................................................................6分
解法二 设 ,则 ,
在 中,由余弦定理得 ,
....................................................................................................................................................2分
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 , 所以 ,................4分
所以 ,所以 ......................................6分
(2)由(1)中解法二可知 , ,
在 中,由余弦定理得 ,....................................8分
所以
,............................................................................................10分
当 时取等号,
故 面积的最大值为 ..................................................................................................12分
18.(12分)
【答案】(1)证明见解析 (2)
【详解】(1)在 中, ,
由正弦定理可得 ,即 ,
得 ,故 .......................................................................................2分
,
,故 .............................................4分
又 ,且 平面 ,
平面 ,.........................................................................................................5分
又 平面 平面 平面 ...............................................................6分
2
原创精品资源学科网独家享有版权,侵权必究!(2)由(1)可得 平面 ,且 ,
由 ,可得 ,............................................7分
则三棱锥 的体积为
,........................10分
故 ,即 , ...............................12分
19.(12分)
【答案】(1) ,平均值为 (2)
【详解】(1)由频率分布直方图可得:
,...................................................2分
即评分在 的频率为0.2,
故 ,........................................................................................................4分
故各组频率依次为: , , , , 。
所以平均值为 ......................6分
(2)由题可知:抽取的20份评分结果中,评分在 的份数为 ,分别记为 ,
评分在 的份数为 ,分别记为 . ....................................8分
则从这8份评分结果中任取2份,不同取法有:
,
,共28种,.....................................................................10分
记“这2份评分结果均不低于90分”为事件 ,
则事件 包含的基本事件有:
, ,共15种,
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故所求概率 .................................................................................................12分
20.(12分)
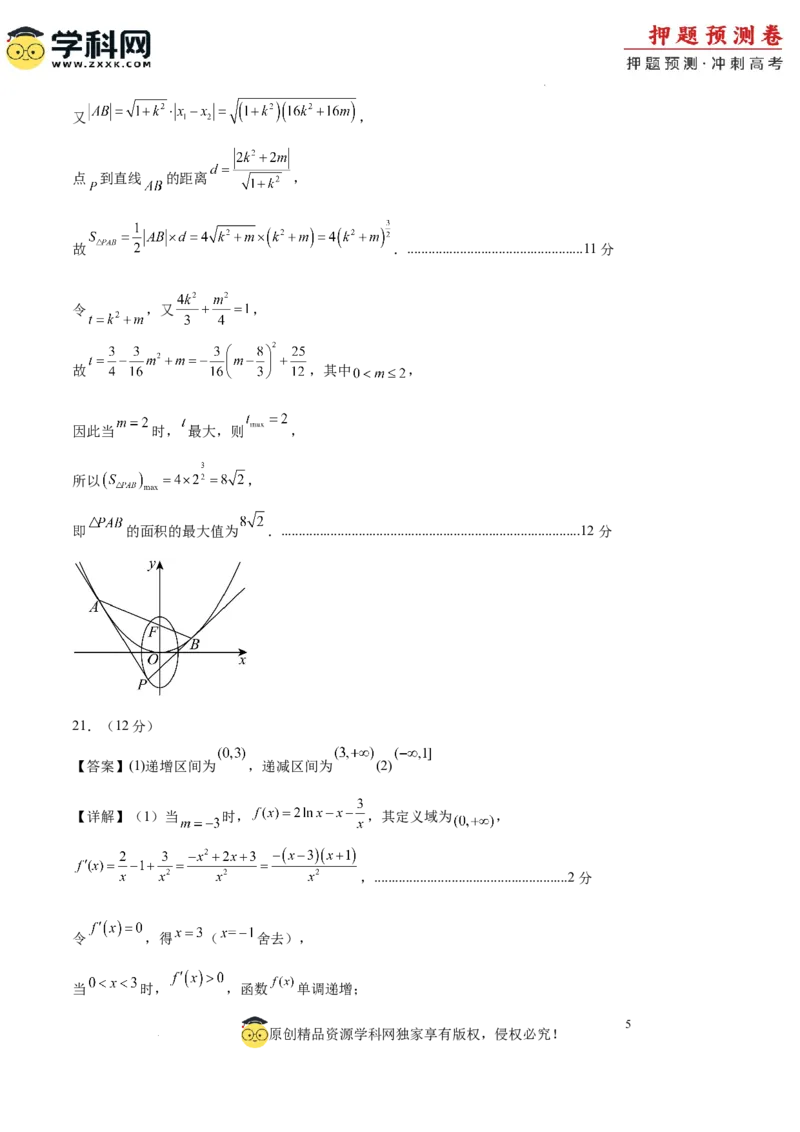
【答案】(1)椭圆 : ,抛物线 : (2)
【详解】(1)由 ,得 ,故抛物线 的标准方程为 ,.....................2分
由 ,得 ,得 ,
由椭圆 过点 ,得 ,
得 , ,
故椭圆 的标准方程为 ;..................................................................................5分
(2)设 , ,由 得 , ,
故抛物线在点 处的切线方程为 ,化简得 ,
同理可得抛物线在点 处的切线方程为 .
联立得 ,得 , ...............................................................7分
易得直线 的斜率存在,设直线 的方程为 ,
联立得 ,得 , ,
故 , , ............................................................................................9分
因此 ,由于点 在椭圆 上,故 .
4
原创精品资源学科网独家享有版权,侵权必究!又 ,
点 到直线 的距离 ,
故 ...................................................11分
令 ,又 ,
故 ,其中 ,
因此当 时, 最大,则 ,
所以 ,
即 的面积的最大值为 ......................................................................................12分
21.(12分)
【答案】(1)递增区间为 ,递减区间为 (2)
【详解】(1)当 时, ,其定义域为 ,
,.......................................................2分
令 ,得 ( 舍去),
当 时, ,函数 单调递增;
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司当 时, ,函数 单调递减.
所以函数 的单调递增区间为 ,单调递减区间为 ;............................5分
(2)方法1:由条件可知 ,于是 ,解得 .
当 时, ,
构造函数 , ,..........................................................................7分
,
所以函数 在 上单调递减,...........................................................................10分
于是 ,
因此实数m的取值范围是 ................................................................................12分
方法2:由条件可知 对任意的 恒成立,
令 , ,只需 即可..................................................7分
,
令 ,则 ,
所以函数 在 上单调递增,
于是 ,所以函数 在 上单调递增,.......................................10分
所以 ,于是 ,因此实数m的取值范围是 .................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)
6
原创精品资源学科网独家享有版权,侵权必究!【答案】(1) ;(2) .
【详解】(1)由 消去参数 ,得 ,即 ,.........2分
将 , 代入上式,
故曲线 的极坐标方程为 ,即 .....................................................5分
(2)解法一:设 ,
联立得 ,得 ,.....................................................7分
其中 ,
故 ,所以 或 ,故 或 ,所以 ,
所以 ,.............................................................................9分
所以 的面积为 ....................................10分
解法二: 由(1)得曲线 的直角坐标方程为 ,
则曲线 是以点 为圆心,2为半径的圆,.................................................................7分
把 代入 ,得直线 的直角坐标方程为 ,
所以圆心到直线 的距离为 ,所以 ,
因为直线 与 轴平行,所以点 到直线 的距离为 ,................................................9分
所以 ...............................................................................................10分
选修4-5:不等式选讲
23.(10分)
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【答案】(1) (2)
【详解】(1) ,
当 时, 即 ,解得 ;................................................1分
当 时, 即 ,无解;...........................................................2分
当 时, 即 ,解得 ;.........................................................3分
综上,不等式 的解集为 .......................................................5分
(2) 的解集为 ,
在 上恒成立, ................................................7分
由(1)可得 ........................................................9分
,解得 ,
实数 的取值范围为 .............................................................................................10分
8
原创精品资源学科网独家享有版权,侵权必究!