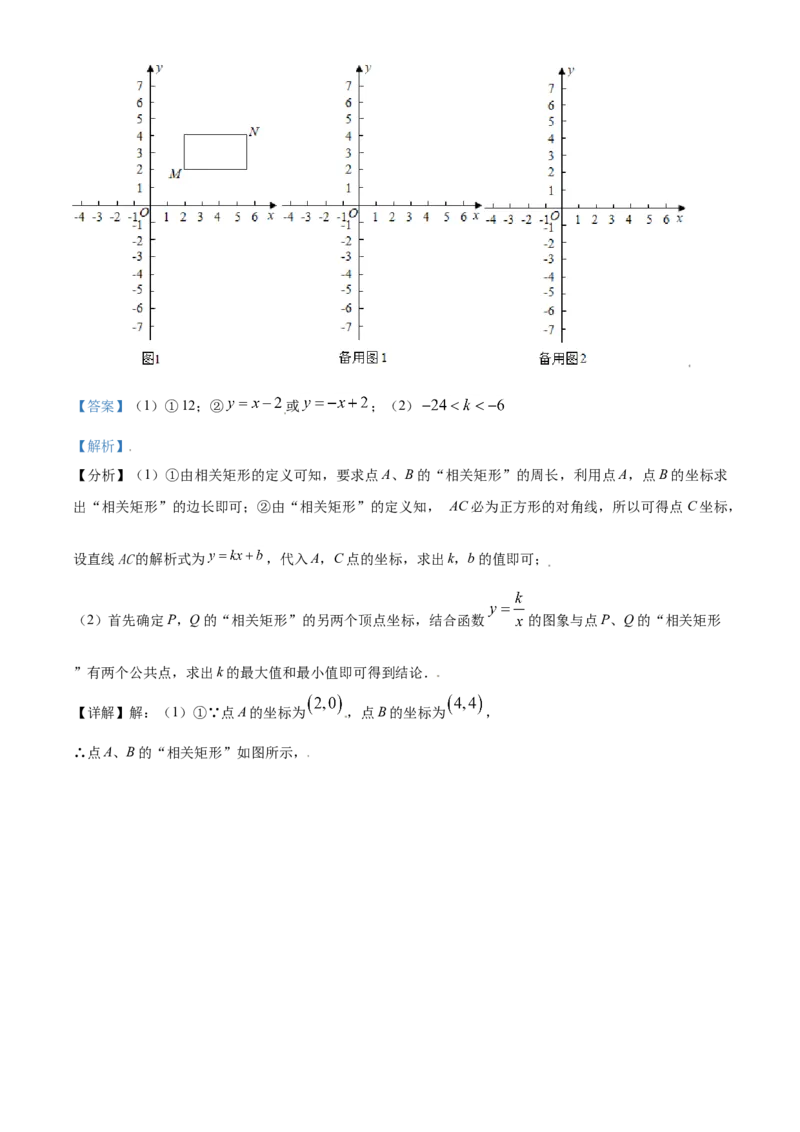
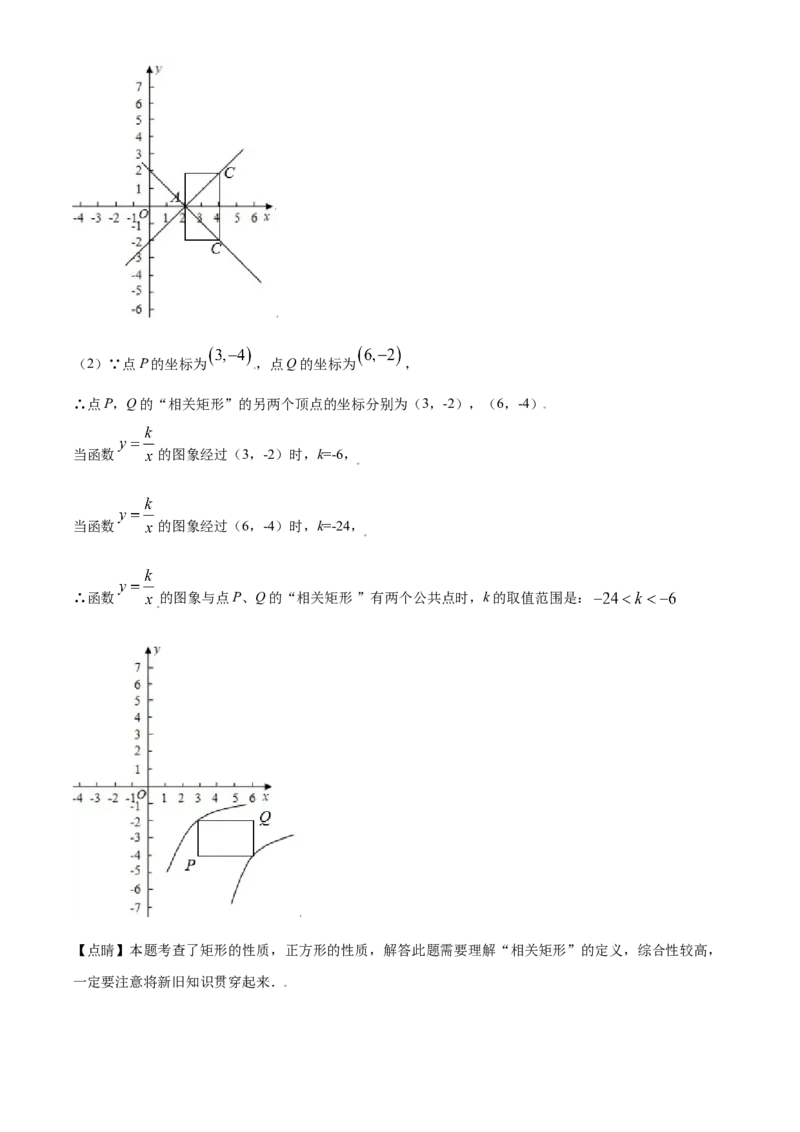
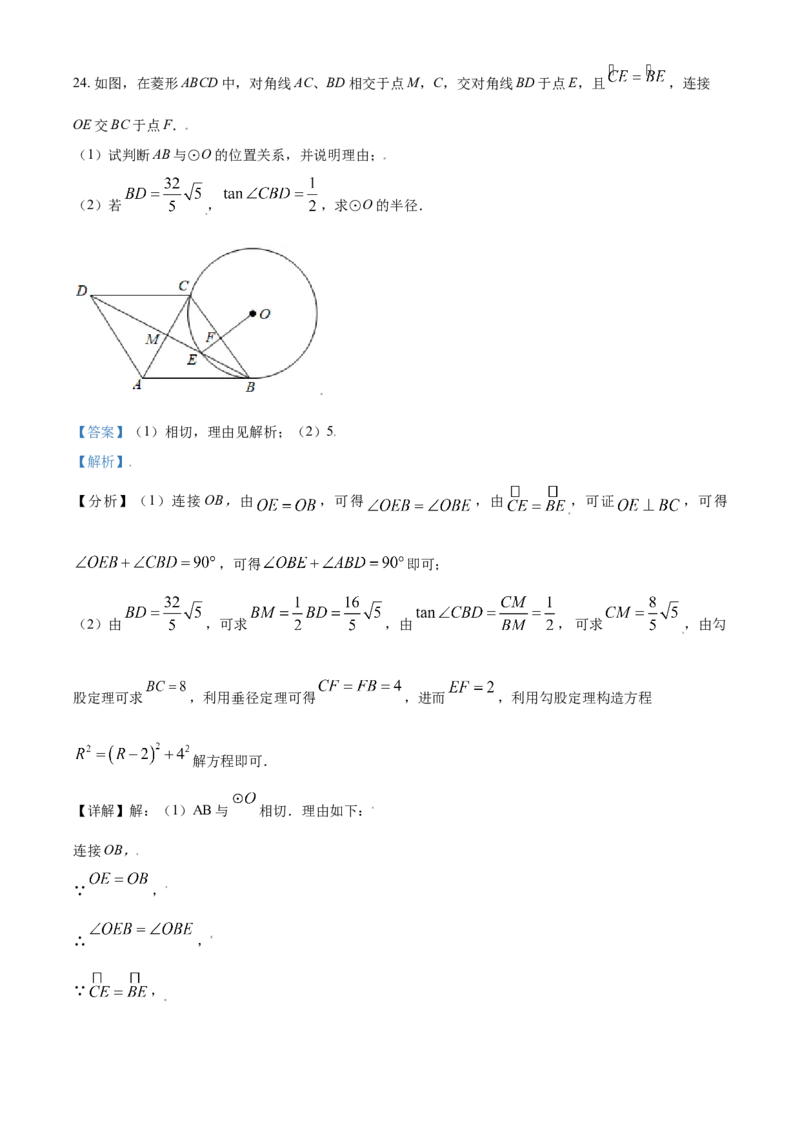
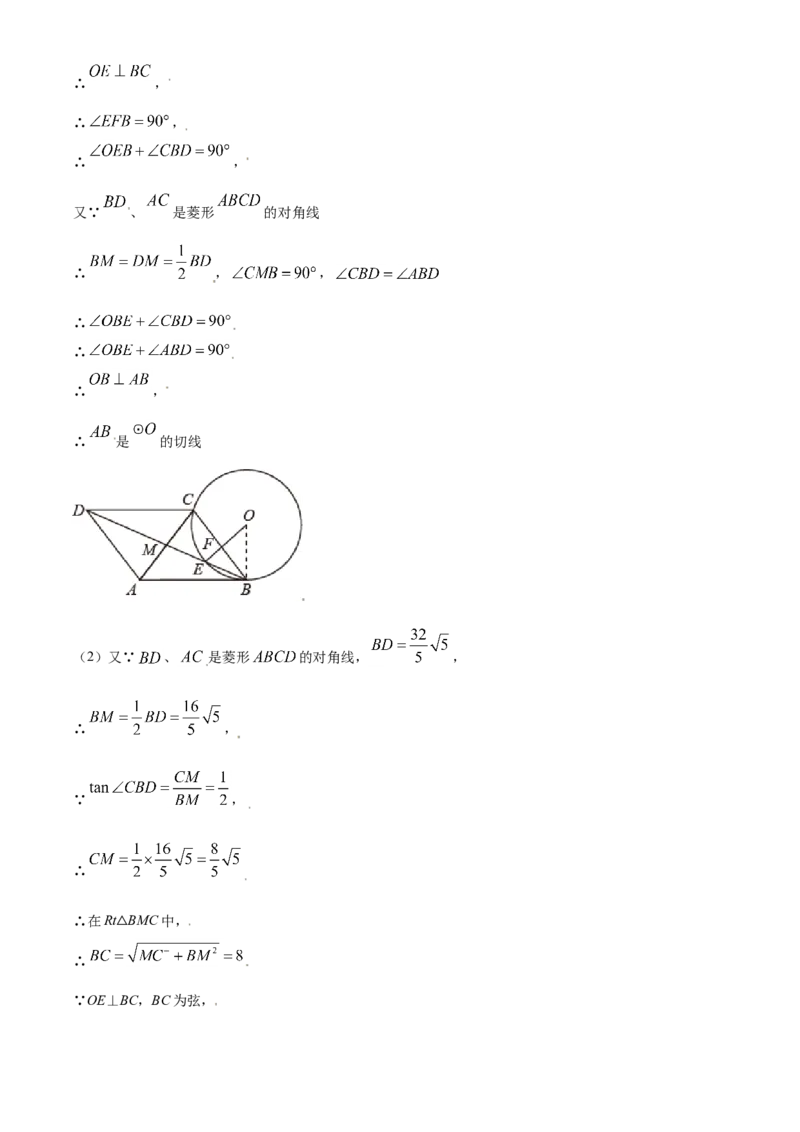
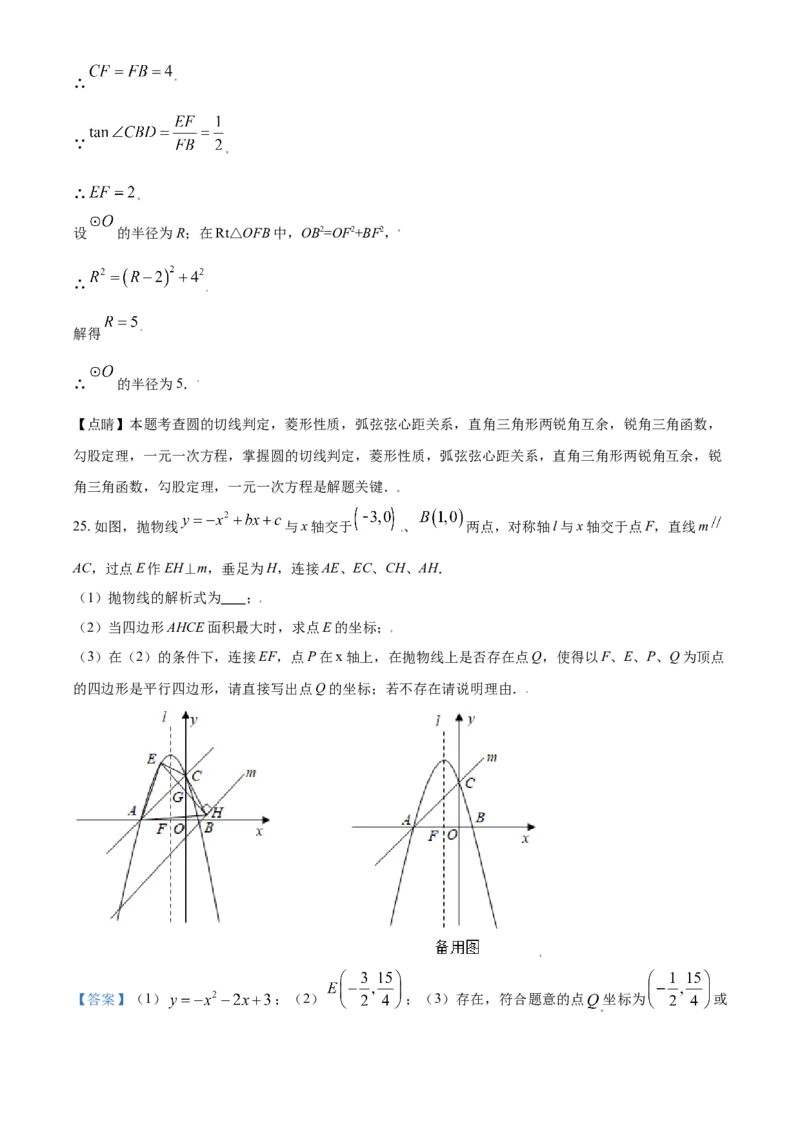
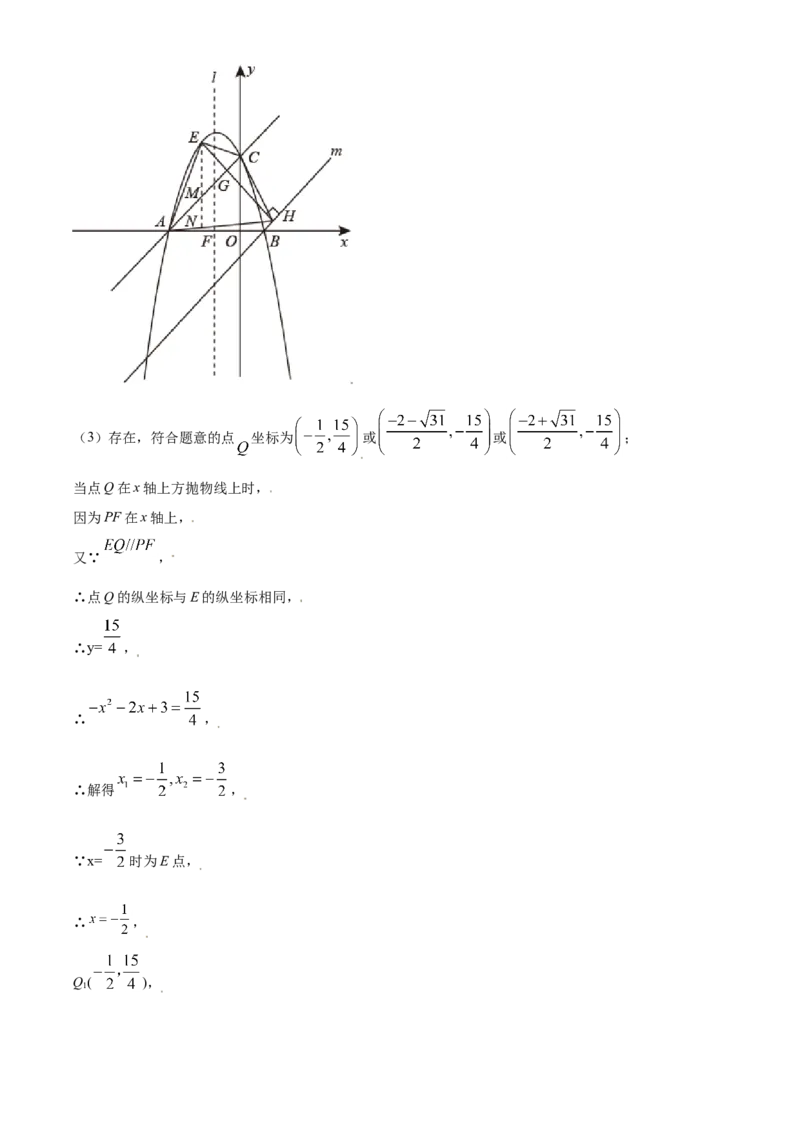
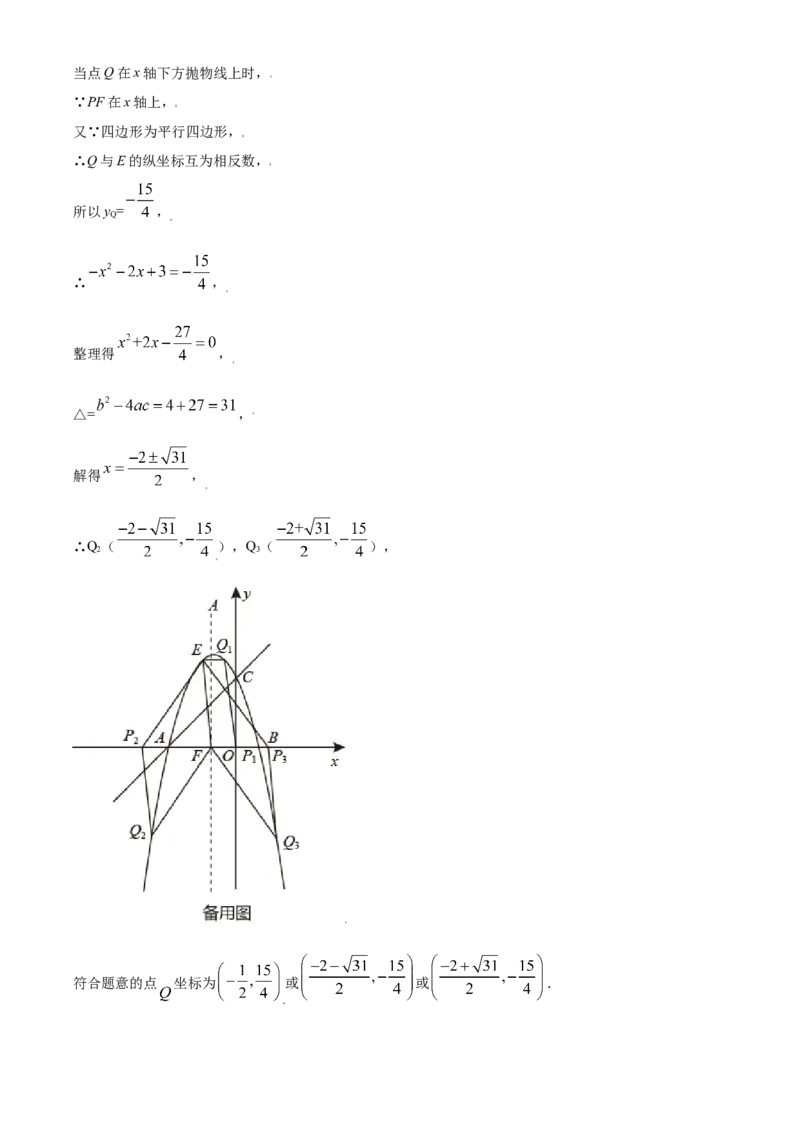
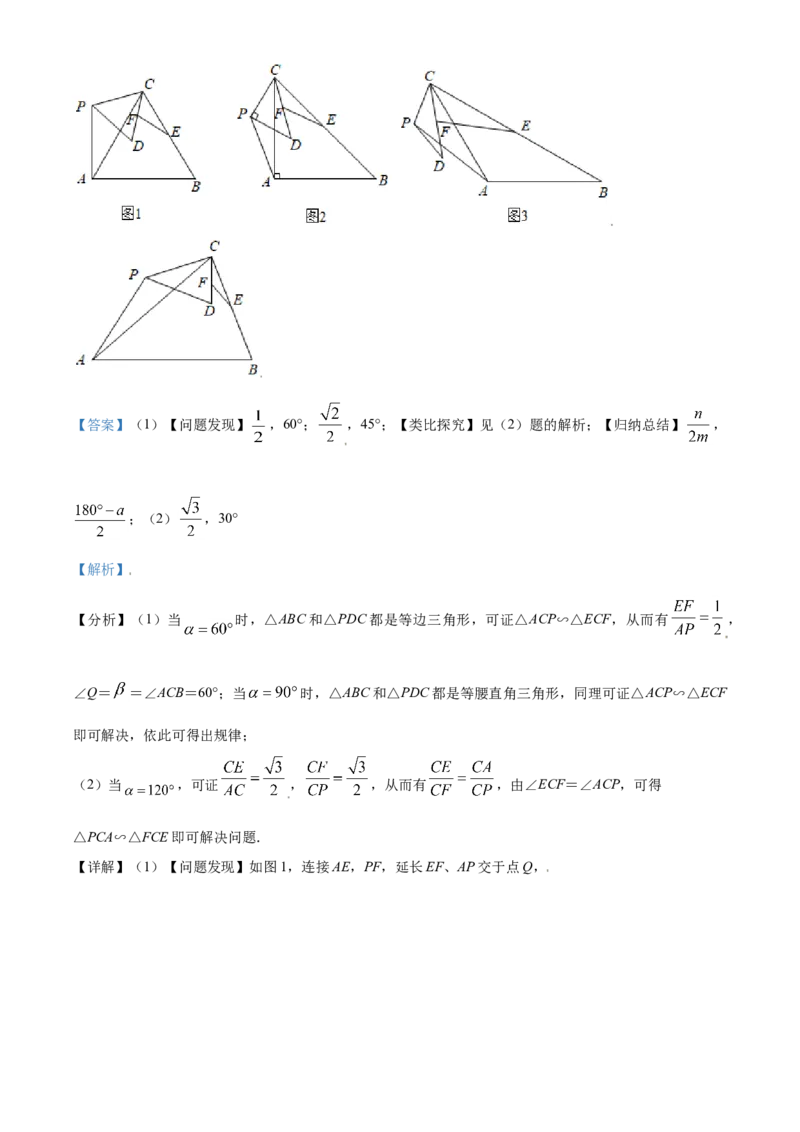
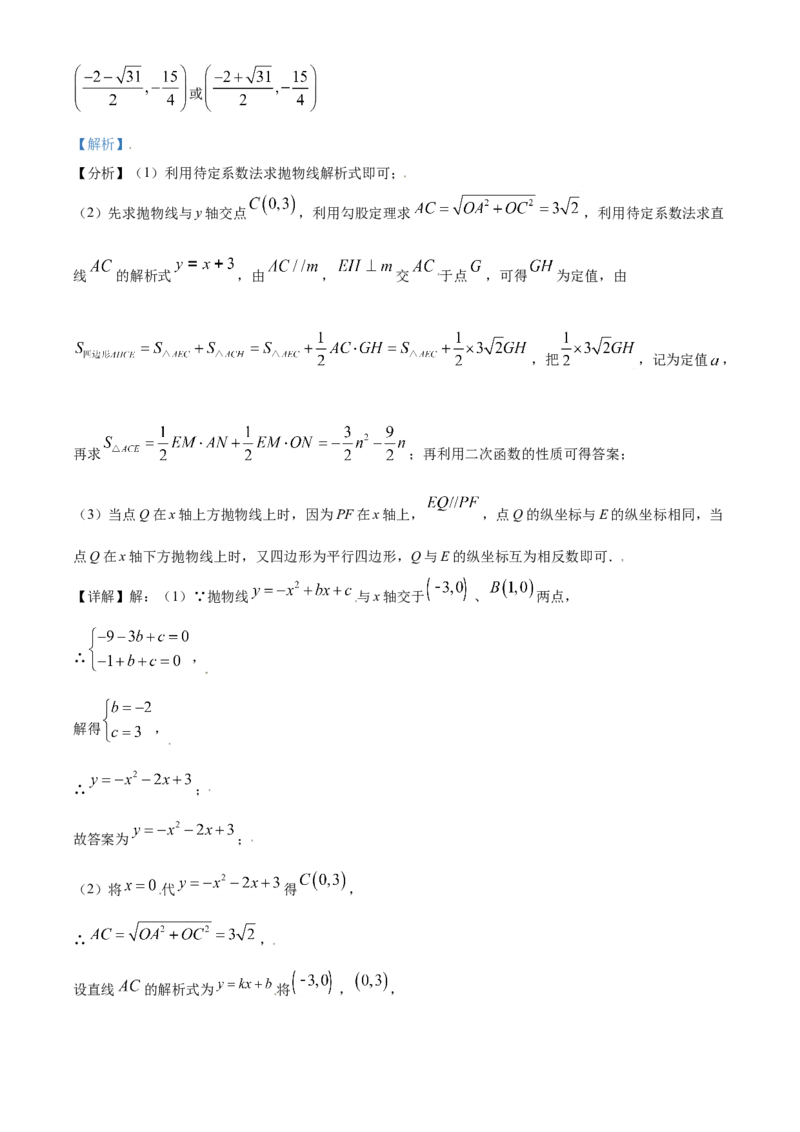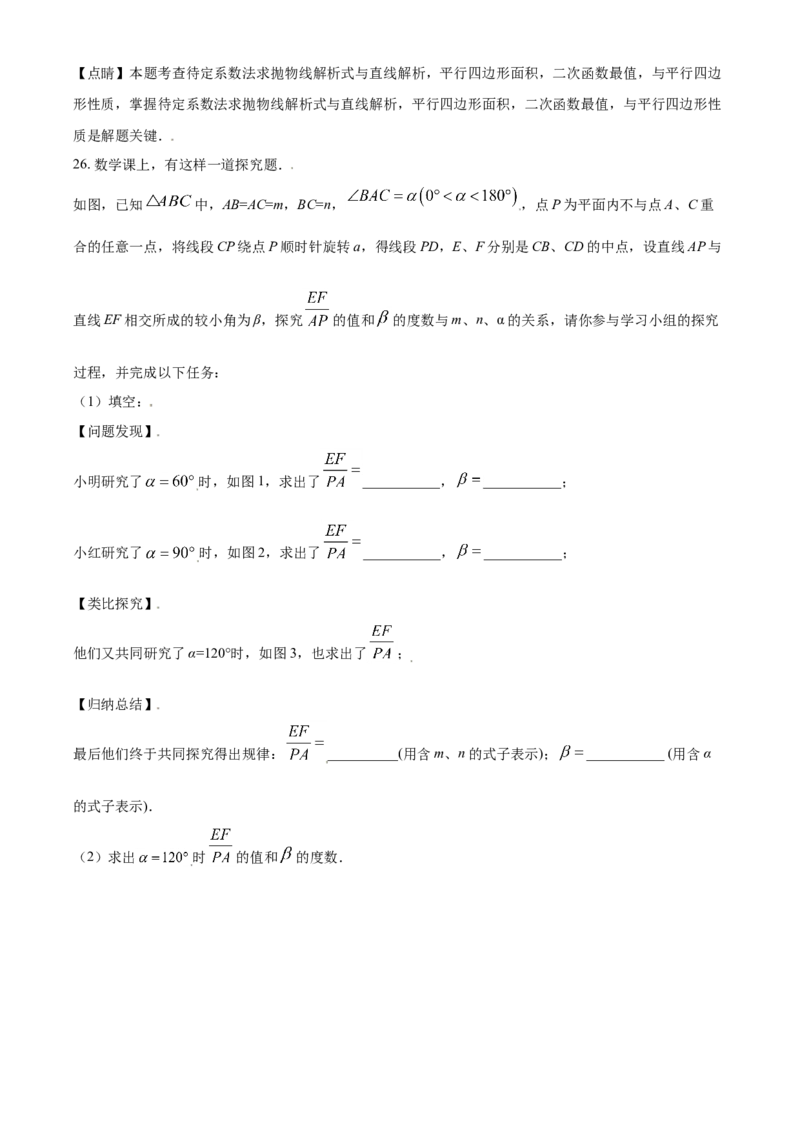文档内容
2021 年内蒙古赤峰市中考数学试卷
一、选择题(每小题出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的对
应位置上按要求涂黑,每小题3分,共2分)
1. -2021的相反数是( )
A. 2021 B. -2021 C. D.
【答案】A
【解析】
【分析】根据相反数的定义判断即可.
【详解】解:-2021的相反数是2021,
故选:A.
【点睛】本题考查了相反数的概念,解题关键是明确相反数的定义,准确求解.
2. 截至北京时间2021年1月3日6时,我国执行首次火星探测任务的“天问一号”火星探测器已经在轨飞行
约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里,数据8300000用科
学记数法表示为( )
A. 8.3×105 B. 8.3×106 C. 83×105 D. 0.83×107
【答案】B
【解析】
【分析】直接利用科学记数法的定义及表示形式 ,其中 , 为整数求解即可.
【详解】解:根据科学记数法的定义及表示形式 ,其中 , 为整数,
则数据8300000用科学记数法表示为: ,
故选:B.
【点睛】本题考查了科学记数法的表示方式,解题的关键是:掌握其定义和表达形式,根据题意确定
的值.
3. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【答案】C【解析】
【分析】根据轴对称图形和中心对称图形的概念逐项判断即可.
【详解】A.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.是轴对称图形,不是中心对称图形,故此选项不符合题意;
C. 是轴对称图形,也是中心对称图形,故此选项符合题意;
D.不是轴对称图形,也不是中心对称图形,故此选项不符合题意,
故选:C.
【点睛】本题考查轴对称图形、中心对称图形,理解轴对称图形和中心对称图形是解答的关键.
4. 下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 为了了解一批灯管的使用寿命,可以采用普查的方式进行
C. 一组数据2,5,4,5,6,7的众数、中位数和平均数都是5
D. 甲、乙两组队员身高数据的方差分别为 , ,那么乙组队员的身高比较整齐
【答案】D
【解析】
【分析】根据事件发生的可能性的大小判断即可.
【详解】解:A、“清明时节雨纷纷”是随机事件,故不符合题意;
B、为了了解一批灯管的使用寿命,不宜采用普查的方式进行,应采用抽查的方式进行,故不符合题意;
C、一组数据2,5,4,5,6,7的众数、中位数都是 ,平均数为 ,故选项
错误,不符合题意;
D、甲、乙两组队员身高数据的方差分别为 , ,
,
乙组队员的身高比较整齐,故选项正确,符合题意;
故选:D.
【点睛】本题考查了必然事件、随机事件、不可能事件、解题的关键是:理解几种事件的定义.
5. 下列计算正确的是( )
A. B.
C. D.【答案】B
【解析】
【分析】根据去括号法则可判断A,根据合并同类项法则可判断B,根据乘法公式可判断C,利用单项式
乘法法则与积的乘方法则可判断D.
【详解】解:A. ,故选项A去括号不正确,不符合题意;
B. ,故选项B合并同类项正确,符合题意;
C. ,故选项C公式展开不正确,不符合题意;
.
D ,故选项D单项式乘法计算不正确,不符合题意.
故选择B.
【点睛】本题考查去括号法则,同类项合并法则,乘法公式,积的乘方与单项式乘法,掌握去括号法则,
同类项合并法则,乘法公式,积的乘方与单项式乘法是解题关键.
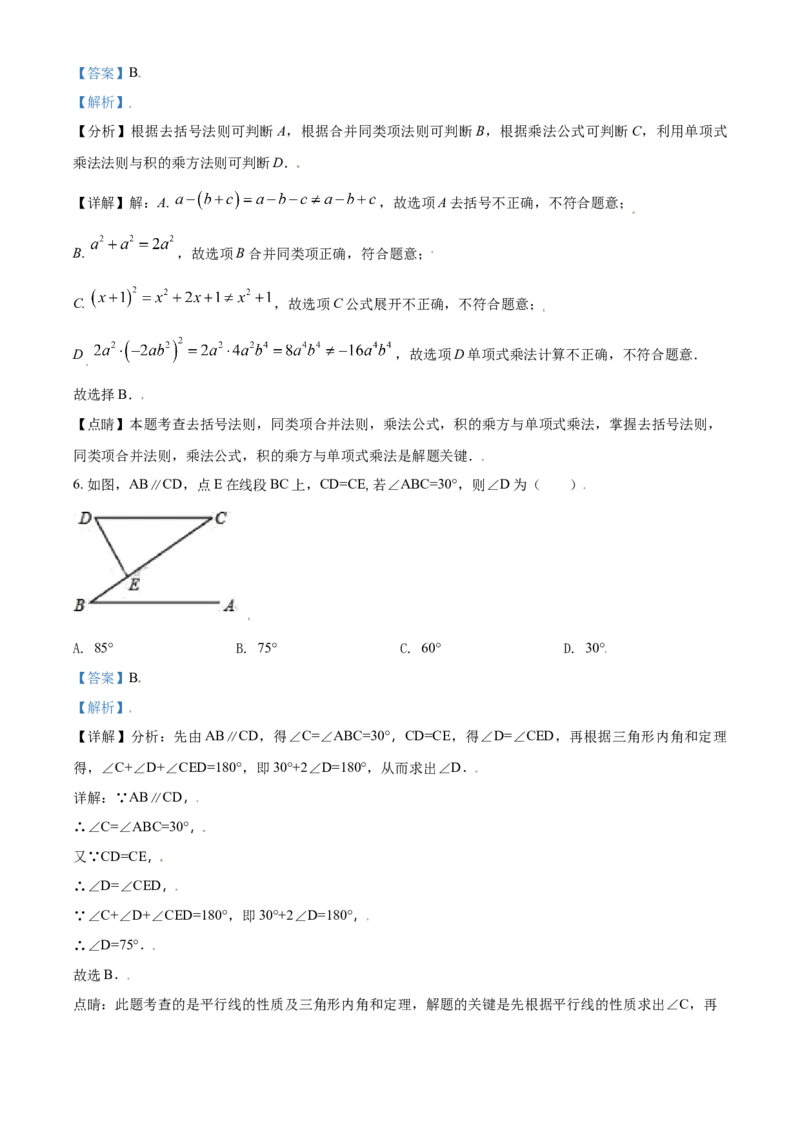
6. 如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D为( )
A. 85° B. 75° C. 60° D. 30°
【答案】B
【解析】
【详解】分析:先由AB∥CD,得∠C=∠ABC=30°,CD=CE,得∠D=∠CED,再根据三角形内角和定理
得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D.
详解:∵AB∥CD,
∴∠C=∠ABC=30°,
又∵CD=CE,
∴∠D=∠CED,
∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,
∴∠D=75°.
故选B.
点睛:此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.
7. 实数a、b、c在数轴上对应点的位置如图所示.如果 ,那么下列结论正确的是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据a+b=0,确定原点的位置,根据实数与数轴即可解答.
【详解】解:∵a+b=0,
∴原点在a,b的中间,
如图,
由图可得:|a|<|c|,a+c>0,abc<0, ,
故选:C.
【点睛】本题考查了实数与数轴,解决本题的关键是确定原点的位置.
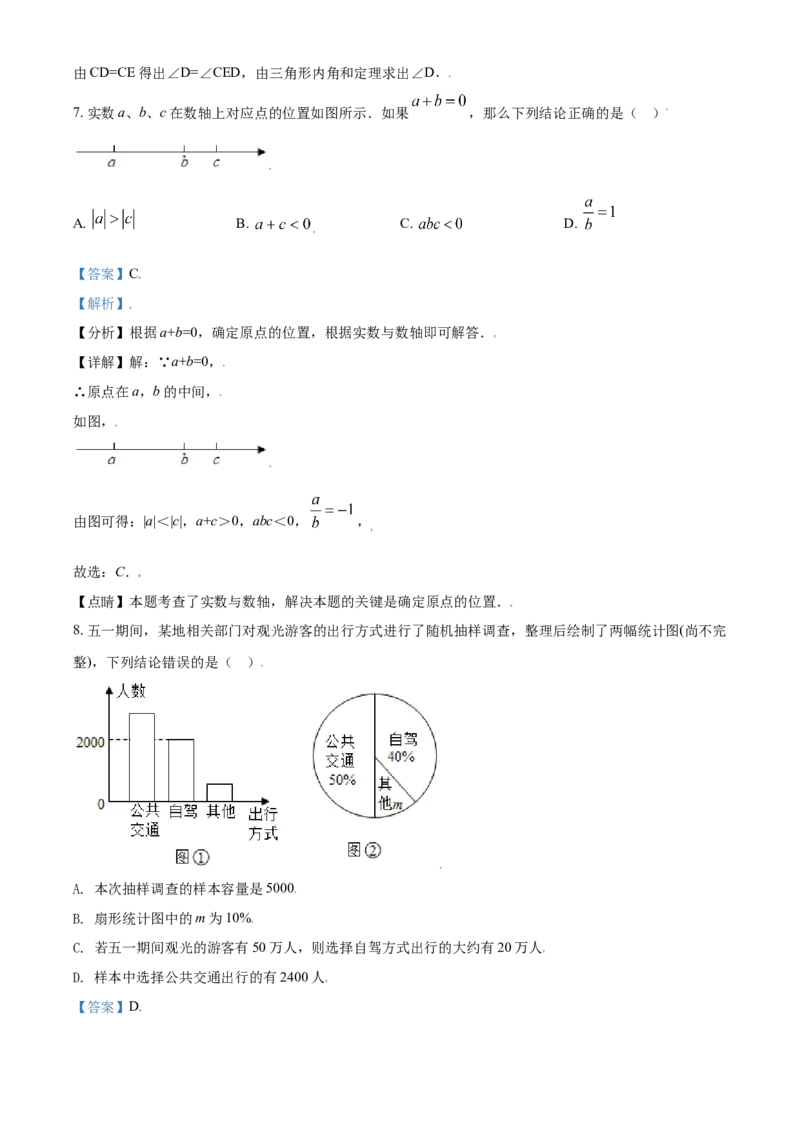
8. 五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完
整),下列结论错误的是( )
A. 本次抽样调查的样本容量是5000
B. 扇形统计图中的m为10%
C. 若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人
D. 样本中选择公共交通出行的有2400人
【答案】D【解析】
【分析】结合条形图和扇形图,求出样本人数,进而进行解答.
【详解】解:A、本次抽样调查的样本容量是 ,正确,不符合题意;
B、 故扇形图中的m为10%,正确,不符合题意;
C、若“五一”期间观光的游客有50万人,则选择自驾方式出行的有50×40%=20万人,正确,不符合题
意;
D、样本中选择公共交通出行的有5000×50%=2500人,错误,符合题意;
故选:D.
【点睛】本题考查了频数分布直方图、扇形统计图,熟悉样本、用样本估计总体是解题的关键,另外注意
学会分析图表.
9. 一元二次方程 ,配方后可形为( )
A. B.
C. D.
【答案】A
【解析】
【分析】把常数项移到方程右边,再把方程两边加上16,然后把方程作边写成完全平方形式即可
【详解】解:
x2-8x=2,
x2-8x+16=18,
(x-4)2=18.
故选:A.
【点睛】本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平
方法求解,这种解一元二次方程的方法叫配方法.
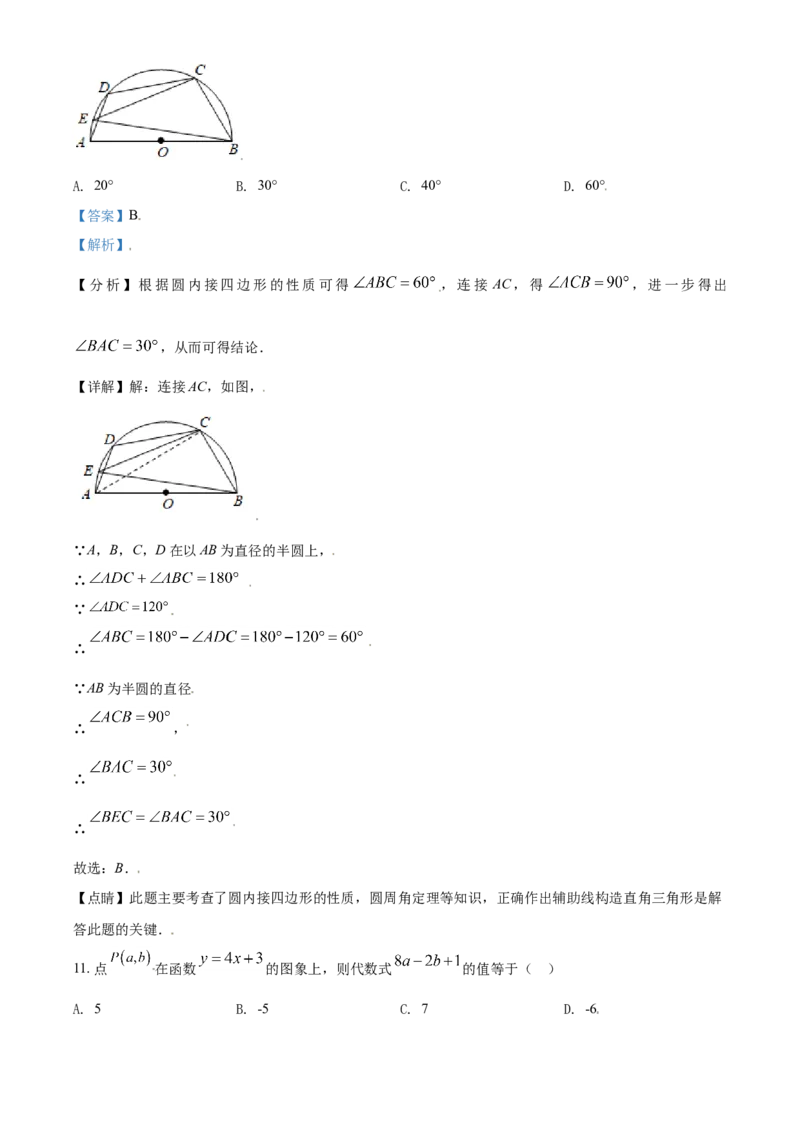
10. 如图,点C,D在以AB为直径的半圆上, ,点E是 上任意一点,连接BE,CE,
则 的度数为( )A. 20° B. 30° C. 40° D. 60°
【答案】B
【解析】
【分析】根据圆内接四边形的性质可得 ,连接 AC,得 ,进一步得出
,从而可得结论.
【详解】解:连接AC,如图,
∵A,B,C,D在以AB为直径的半圆上,
∴
∵
∴
∵AB为半圆的直径
∴ ,
∴
∴
故选:B.
【点睛】此题主要考查了圆内接四边形的性质,圆周角定理等知识,正确作出辅助线构造直角三角形是解
答此题的关键.
11. 点 在函数 的图象上,则代数式 的值等于( )
A. 5 B. -5 C. 7 D. -6【答案】B
【解析】
【分析】把点P的坐标代入一次函数解析式可以求得a、b间的数量关系,所以易求代数式8a-2b+1的值.
【详解】解:∵点P(a,b)在一次函数 的图象上,
∴b=4a+3,
8a-2b+1=8a-2(4a+3)+1=-5,即代数式 的值等于-5.
故选:B.
【点睛】本题考查了一次函数图象上点的坐标特征,熟知函数图象上的点的坐标满足图象的解析式是关键.
12. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:
x … -1 0 1 2 3 …
y … 3 0 -1 m 3 …
以下结论正确的是( )
A. 抛物线 的开口向下
B. 当 时,y随x增大而增大
C. 方程 的根为0和2
D. 当 时,x的取值范围是
【答案】C
【解析】
【分析】利用表中数据求出抛物线的解析式,根据解析式依次进行判断.
【详解】解:将 代入抛物线的解析式得;
,
解得: ,所以抛物线的解析式为: ,
A、 ,抛物线开口向上,故选项错误,不符合题;
B、抛物线的对称轴为直线 ,在 时,y随x增大而增大,故选项错误,不符合题意;
C、方程 的根为0和2,故选项正确,符合题意;
D、当 时,x的取值范围是 或 ,故选项错误,不符合题意;
故选:C.
【点睛】本题考查了二次函数的解析式的求法和函数的图象与性质,解题的关键是:利用待定系数法求出
解析式,然后利用函数的图象及性质解答.
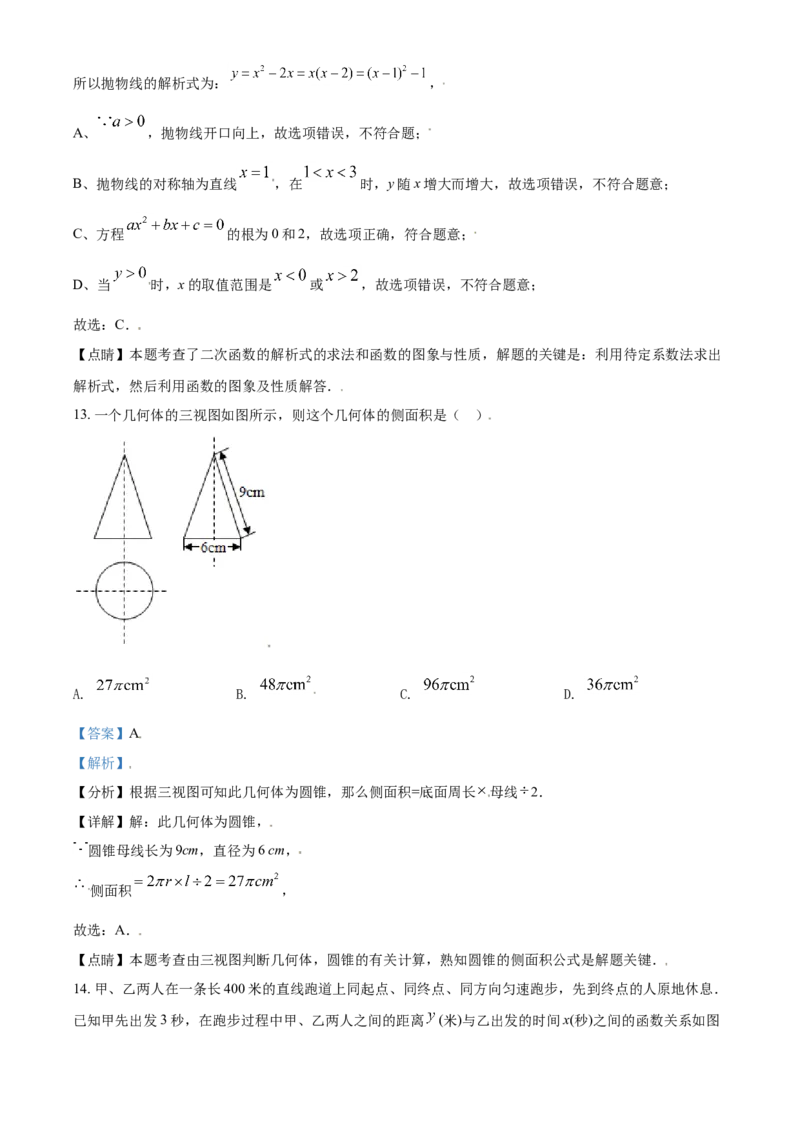
13. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据三视图可知此几何体为圆锥,那么侧面积=底面周长 母线 2.
【详解】解:此几何体为圆锥,
圆锥母线长为9cm,直径为6 cm,
侧面积 ,
故选:A.
【点睛】本题考查由三视图判断几何体,圆锥的有关计算,熟知圆锥的侧面积公式是解题关键.
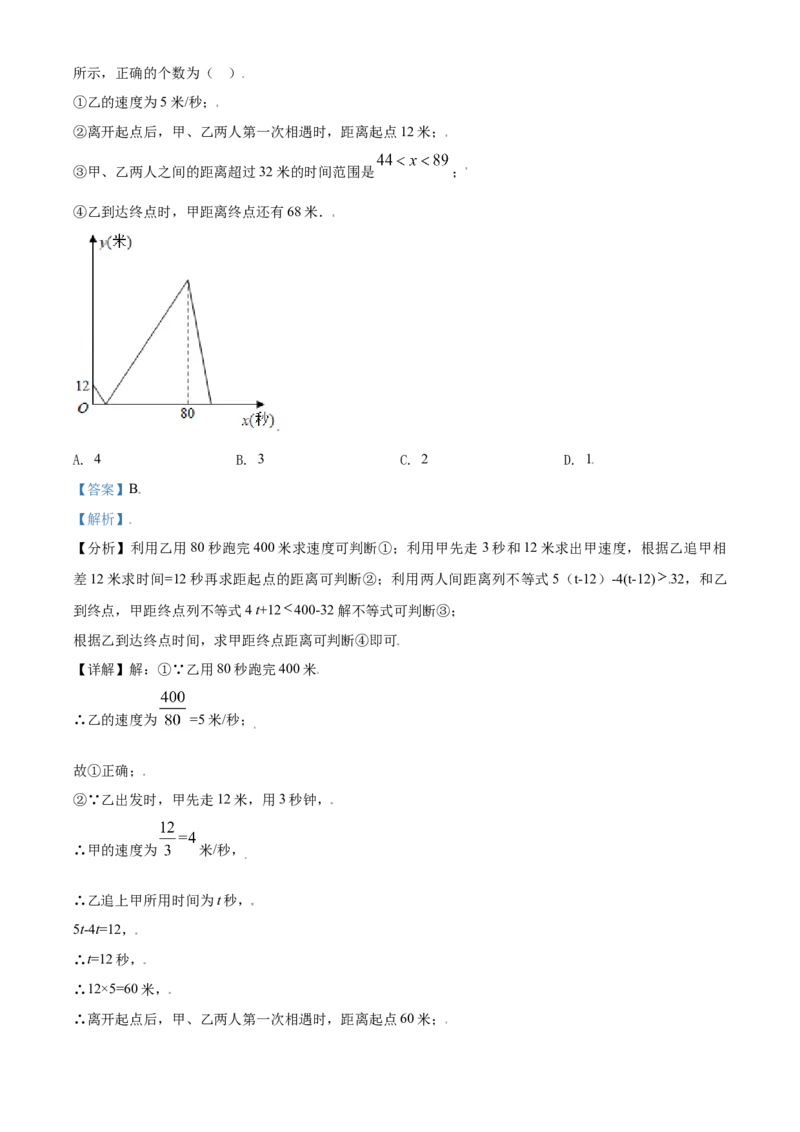
14. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.
已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离 (米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )
①乙的速度为5米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲、乙两人之间的距离超过32米的时间范围是 ;
④乙到达终点时,甲距离终点还有68米.
A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】
【分析】利用乙用80秒跑完400米求速度可判断①;利用甲先走3秒和12米求出甲速度,根据乙追甲相
差12米求时间=12秒再求距起点的距离可判断②;利用两人间距离列不等式5(t-12)-4(t-12) 32,和乙
到终点,甲距终点列不等式4 t+12 400-32解不等式可判断③;
根据乙到达终点时间,求甲距终点距离可判断④即可
【详解】解:①∵乙用80秒跑完400米
∴乙的速度为 =5米/秒;
故①正确;
②∵乙出发时,甲先走12米,用3秒钟,
∴甲的速度为 米/秒,
∴乙追上甲所用时间为t秒,
5t-4t=12,
∴t=12秒,
∴12×5=60米,
∴离开起点后,甲、乙两人第一次相遇时,距离起点60米;故②不正确;
③甲乙两人之间的距离超过32米设时间为t秒,
∴5(t-12)-4(t-12) 32,
∴t 44,
当乙到达终点停止运动后,
4 t+12 400-32,
∴t 89,
甲、乙两人之间的距离超过32米的时间范围是 ;
故③正确;
④乙到达终点时,
甲距终点距离为:400-12-4×80=400-332=68米,
甲距离终点还有68米.
故④正确;
正确的个数为3个.
故选择B.
【点睛】本题考查一次函数的图像应用问题,仔细阅读题目,认真观察图像,从图像中获取信息,掌握一
次函数的图像应用,列不等式与解不等式,关键是抓住图像纵轴是表示两人之间的距离,横坐标表示乙出
发时间,拐点的意义是解题关键.
二、填空题(请把答案填写在答题卡相应的横线上,每小题3分,共12分)
15. 在函数 中,自变量x 的取值范围是_____.
【答案】x≥-1且x≠
【解析】
【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,就可以求解.
详解】解:根据题意得:
【
解得:x≥-1且x≠
故答案为:x≥-1且x≠ .
【点睛】本题考查函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,
被开方数为非负数.
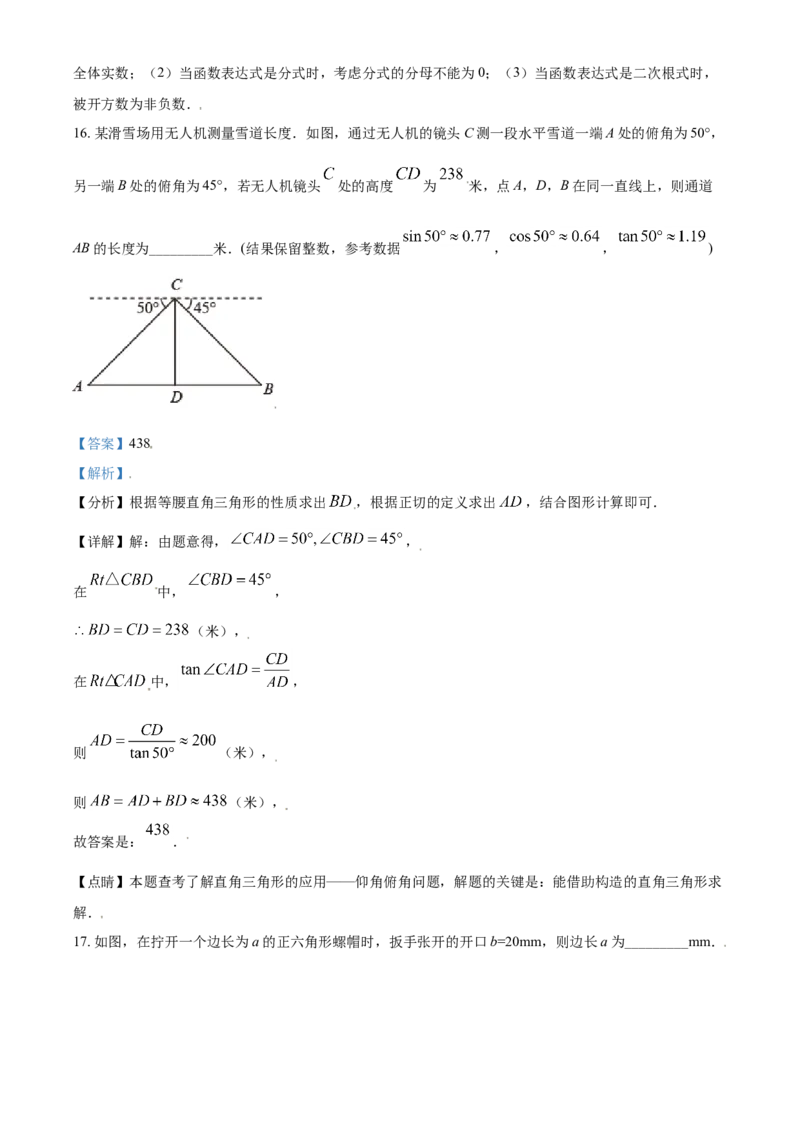
16. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,
另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A,D,B在同一直线上,则通道
AB的长度为_________米.(结果保留整数,参考数据 , , )
【答案】438
【解析】
【分析】根据等腰直角三角形的性质求出 ,根据正切的定义求出 ,结合图形计算即可.
【详解】解:由题意得, ,
在 中, ,
(米),
在 中, ,
则 (米),
则 (米),
故答案是: .
【点睛】本题查考了解直角三角形的应用——仰角俯角问题,解题的关键是:能借助构造的直角三角形求
解.
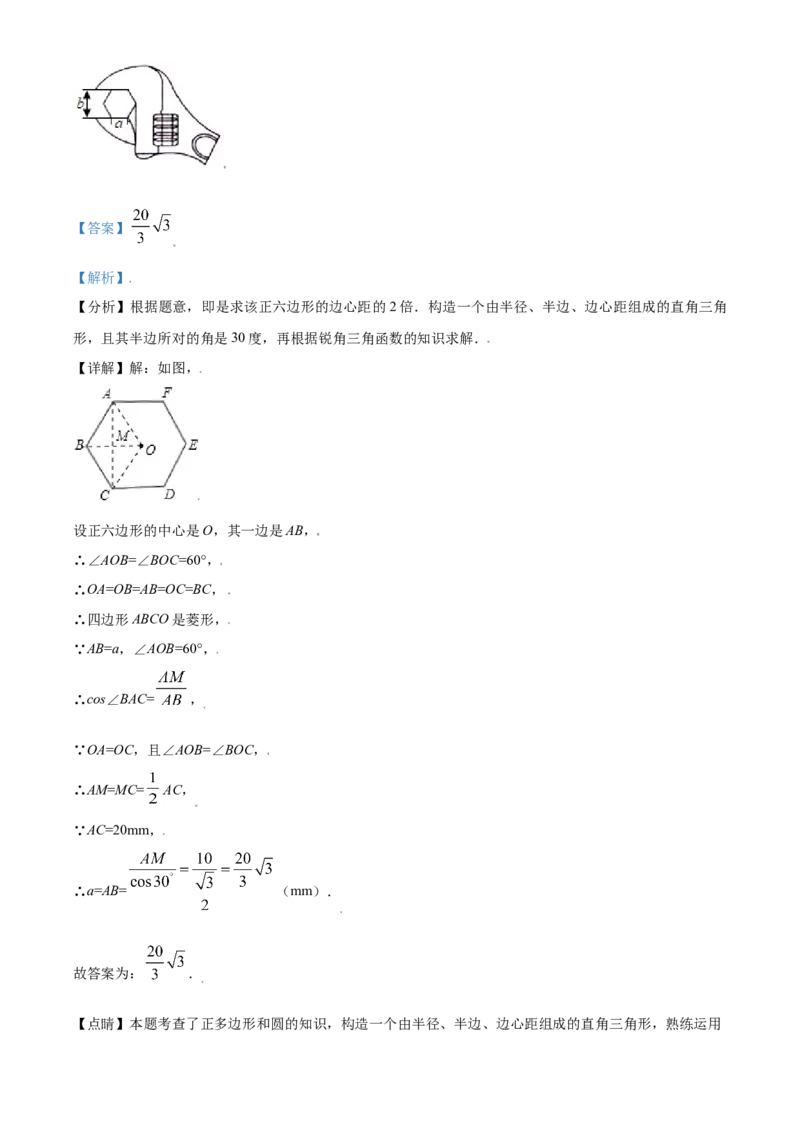
17. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为_________mm.【答案】
【解析】
【分析】根据题意,即是求该正六边形的边心距的2倍.构造一个由半径、半边、边心距组成的直角三角
形,且其半边所对的角是30度,再根据锐角三角函数的知识求解.
【详解】解:如图,
设正六边形的中心是O,其一边是AB,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∵AB=a,∠AOB=60°,
∴cos∠BAC= ,
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC= AC,
∵AC=20mm,
∴a=AB= (mm).
故答案为: .
【点睛】本题考查了正多边形和圆的知识,构造一个由半径、半边、边心距组成的直角三角形,熟练运用锐角三角函数进行求解是关键.
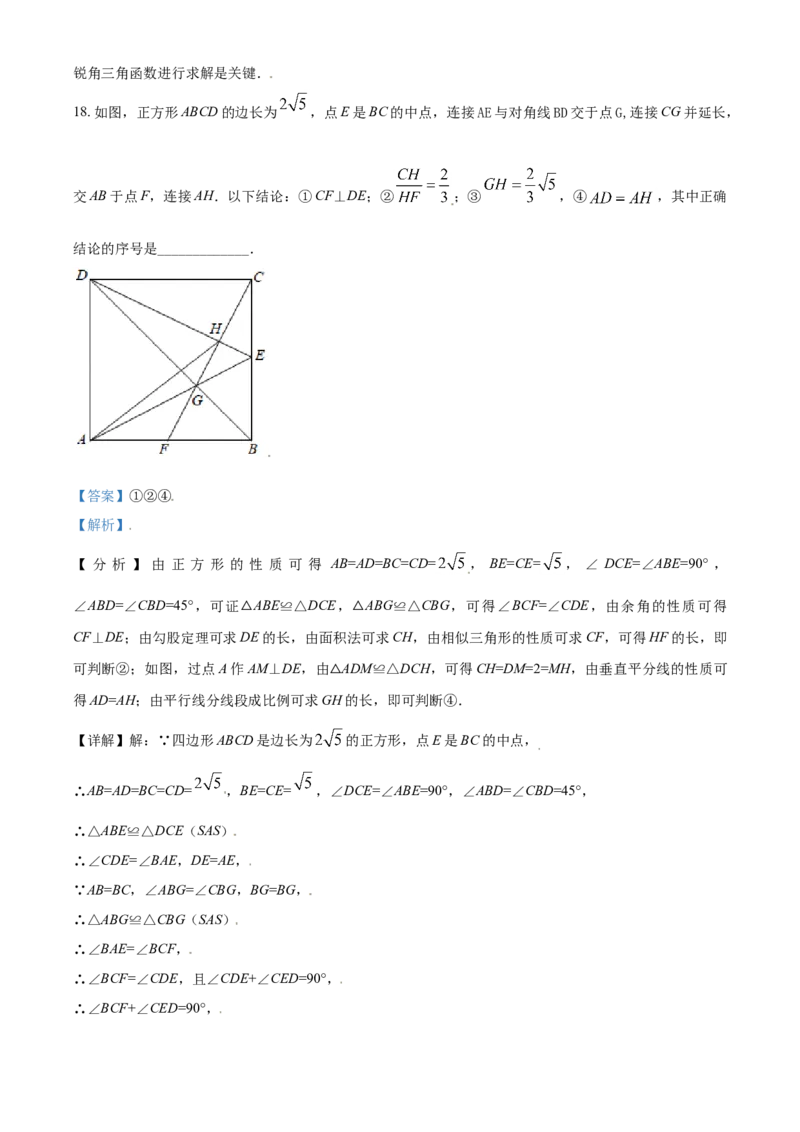
18. 如图,正方形ABCD的边长为 ,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,
交AB于点F,连接AH.以下结论:①CF⊥DE;② ;③ ,④ ,其中正确
结论的序号是_____________.
【答案】①②④
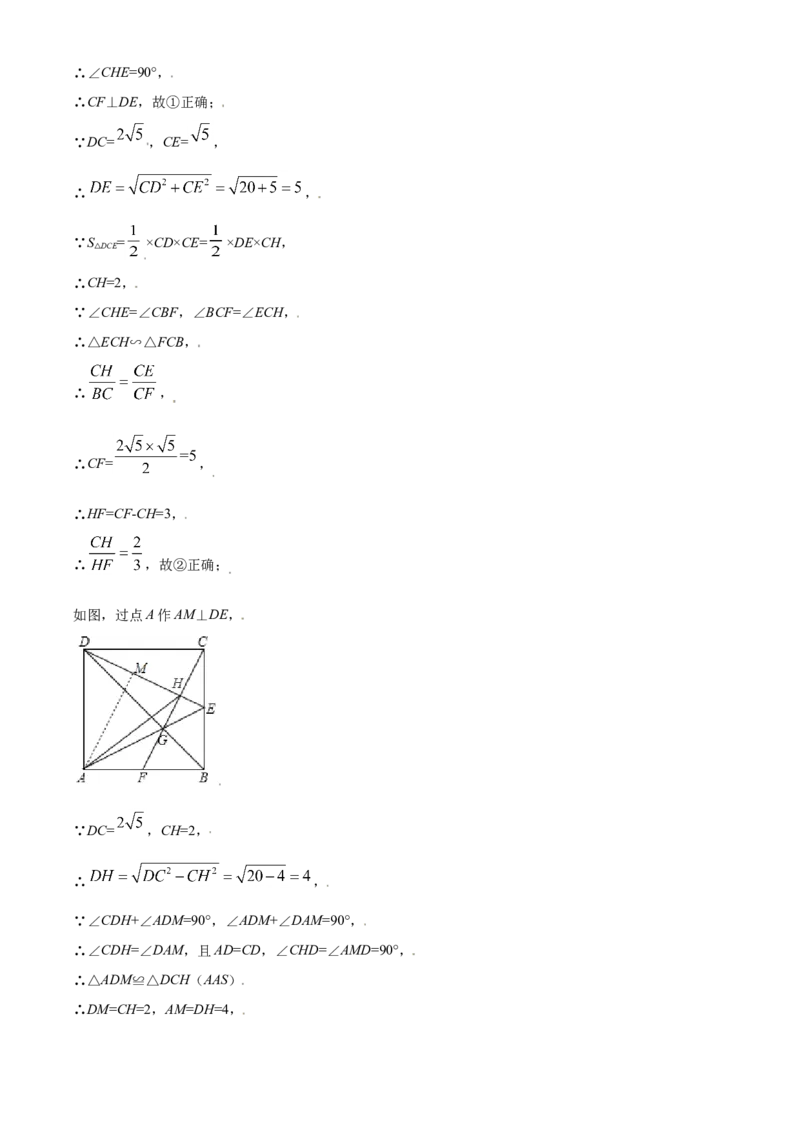
【解析】
【 分 析 】 由 正 方 形 的 性 质 可 得 AB=AD=BC=CD= , BE=CE= , ∠ DCE=∠ABE=90° ,
∠ABD=∠CBD=45°,可证 ABE≌△DCE, ABG≌△CBG,可得∠BCF=∠CDE,由余角的性质可得
CF⊥DE;由勾股定理可求D△E的长,由面积法△可求CH,由相似三角形的性质可求CF,可得HF的长,即
可判断②;如图,过点A作AM⊥DE,由 ADM≌△DCH,可得CH=DM=2=MH,由垂直平分线的性质可
得AD=AH;由平行线分线段成比例可求G△H的长,即可判断④.
【详解】解:∵四边形ABCD是边长为 的正方形,点E是BC的中点,
∴AB=AD=BC=CD= ,BE=CE= ,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠CDE=∠BAE,DE=AE,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,∴∠CHE=90°,
∴CF⊥DE,故①正确;
∵DC= ,CE= ,
∴ ,
∵S = ×CD×CE= ×DE×CH,
DCE
△
∴CH=2,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴ ,
∴CF= ,
∴HF=CF-CH=3,
∴ ,故②正确;
如图,过点A作AM⊥DE,
∵DC= ,CH=2,
∴ ,
∵∠CDH+∠ADM=90°,∠ADM+∠DAM=90°,
∴∠CDH=∠DAM,且AD=CD,∠CHD=∠AMD=90°,
∴△ADM≌△DCH(AAS)
∴DM=CH=2,AM=DH=4,∴MH=DM=2,且AM⊥DH,
∴AD=AH,故④正确;
∵DE=5,DH=4,
∴HE=1,ME=HE+MH=3,
∵AM⊥DE,CF⊥DE,
∴AM∥CF,
∴ ,
∴
∴HG= ,故③错误,
所以,正确结论是①②④
故答案为①②④.
【点睛】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性
质,直角三角形的性质,勾股定理等知识,熟练运用这些性质进行推理是本题的关键.
三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过或
演算步骤.共8题,满分96分)
19. 先化简,再求值: ,其中 .
【答案】
【解析】
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将计算m的值代入化简结果中求值可得.
【详解】解:∵
∴当 时,原式 .
【点睛】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.
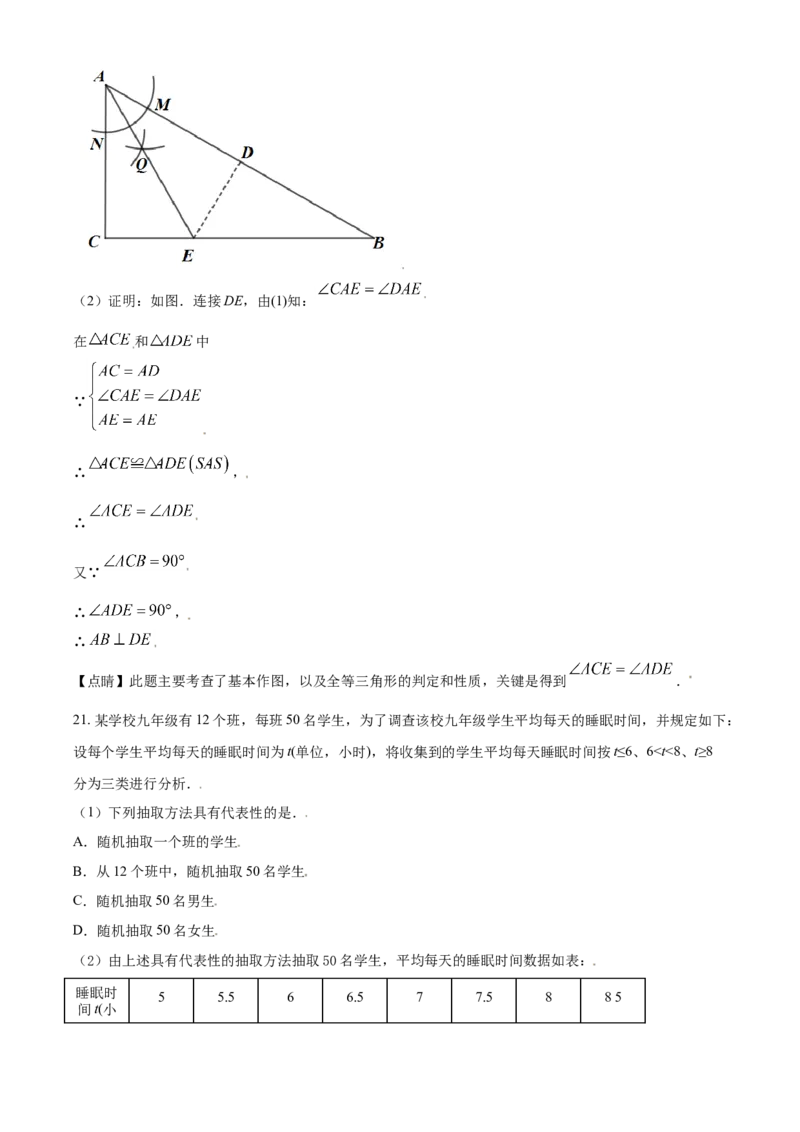
20. 如图,在Rt ABC中,∠ACB=90°,且AC=AD.
(1)作∠BAC△的平分线,交BC于点E;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接DE,证明 .
【答案】(1)见解析;(2)见解析
【解析】
【分析】(1)首先以A为圆心,小于AC长为半径画弧,交AC、AB于N、M,再分别以N、M为圆心,
大于 MN长为半径画弧,两弧交于点Q,再画射线AQ交CB于E;
(2)依据 证明 得到 ,进一步可得结论.
【详解】解:(1)如图, 为所作 的平分线;(2)证明:如图.连接DE,由(1)知:
在 和 中
∵
∴ ,
∴
又∵
∴ ,
∴
【点睛】此题主要考查了基本作图,以及全等三角形的判定和性质,关键是得到 .
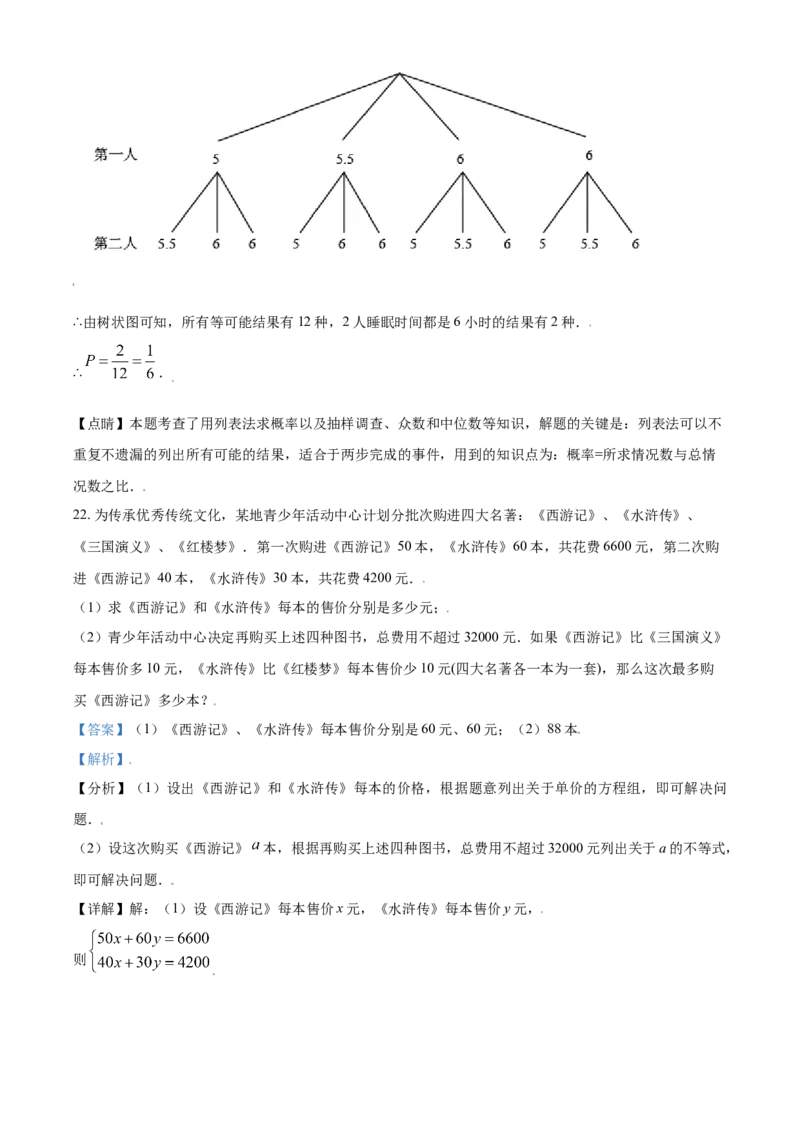
21. 某学校九年级有12个班,每班50名学生,为了调查该校九年级学生平均每天的睡眠时间,并规定如下:
设每个学生平均每天的睡眠时间为t(单位,小时),将收集到的学生平均每天睡眠时间按t≤6、6