数学（广东专用01，新题型结构）（参考答案）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷

2024年高考押题预测卷【广东专用01】
数学·参考答案
第一部分（选择题 共58分）
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要
求的。
1 2 3 4 5 6 7 8
C A B A A D C B
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部
选对的得6分，部分选对的得部分分，有选错的得0分．
9 10 11
BC ABD BC
第二部分（非选择题 共92分）
三、填空题：本题共3小题，每小题5分，共15分。
13． 14．1 15． ，
四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步棸。
15.
f xxaexb fxxa1ex
【详解】（1）解：由函数 ，可得 ，....................................1分
f x 1,1 f x
x0
因为函数 过点 ，且 是 的极值点，
f 11aeb1

可得 f01a0 ，解得a1,b1，......................................................................................3分
经检验符合题意；..........................................................................................................................................5分
f x f xx1ex1
所以函数 的解析式为 ..........................................................................................6分
fxxex
（2）解：由（1）知 ，
1
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司fx0 fx0
x0 x0
令 ，解 ；令 ，解 ，......................................................................................8分
f x (0,) (,0)
所以函数 在 上单调递增，在 上单调递减，.............................................................10分
f x f 00
x0
所以，当 时，函数 取得最小值，最小值为 ，无最大值........................................12分
f x (0,) (,0) 0
即函数 的增区间为 ，减区间为 ，最小值为 ，无最大值.....................................13分
16.
AB F FC,FE,EC
【详解】（1）如图所示，取 的中点 ，连接 ，...........................................................1分
AB AC EDC BED120,EDEBDC  AD AE  AD AE 2 EF  AB
由题意易知 ， ， ，
..........................................................................................................................................................................2分
不妨设AB2a，则AC 2a，
 2
CE2 ED2DC22EDDCcosEDC  2 3 12
由余弦定理可知 ，
CF2  AF2AC22AFACcosBAC
2a22a242
a24a24a2 8a2
8a2 ，..............................................................................................4分
由勾股定理知EF2 22a2，
CE2 CF2EF2 EF CF
所以 ，..........................................................................................................5分
又CFABF,CF、AB平面ABC，
所以EF平面ABC，
因为EF 平面ABE，
所以平面ABE 平面ABC；.......................................................................................................................7分
2
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司（2）
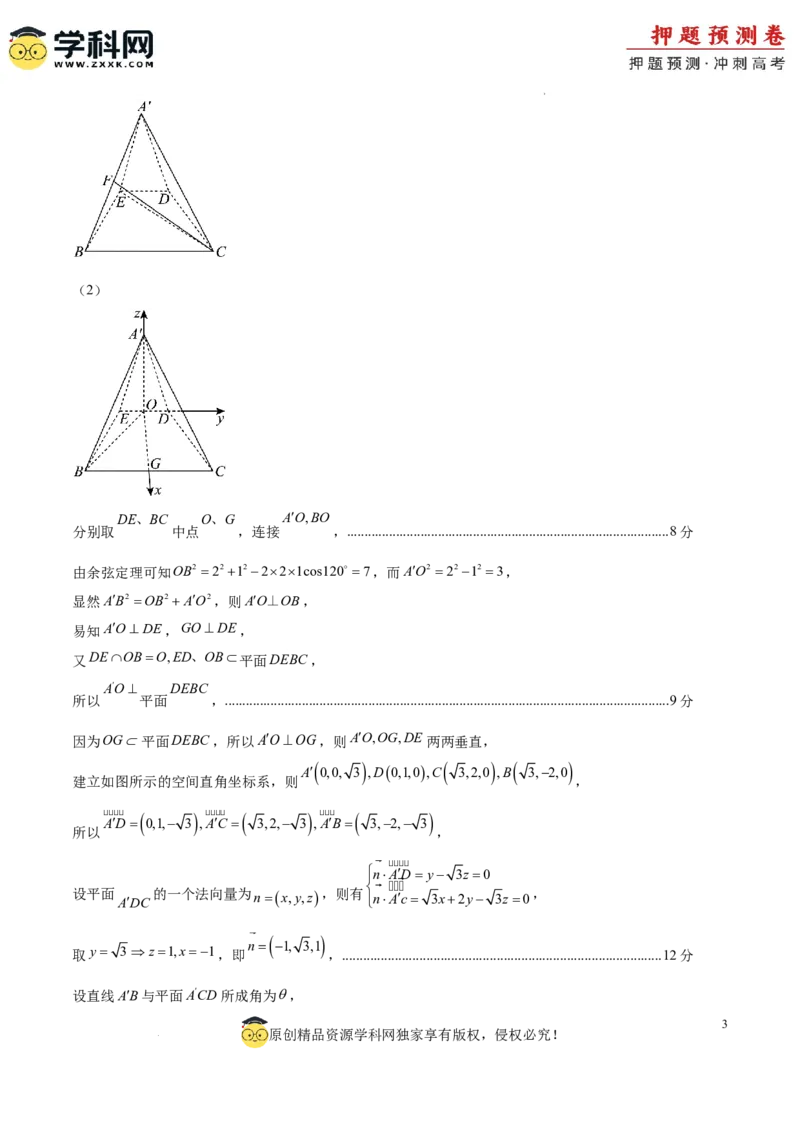
DE、BC O、G AO,BO
分别取 中点 ，连接 ，............................................................................................8分
由余弦定理可知OB2 2212221cos120 7，而AO2 2212 3，
显然AB2 OB2AO2，则AO⊥OB，
易知AODE，GODE，
又DEOBO,ED、OB平面DEBC，
AO DEBC
所以 平面 ，...............................................................................................................................9分
因为OG平面DEBC，所以AOOG，则AO,OG,DE两两垂直，
A  0,0, 3  ,D0,1,0,C  3,2,0  ,B  3,2,0 
建立如图所示的空间直角坐标系，则 ，
(cid:3) (cid:3) (cid:3)
     
AD 0,1, 3 ,AC  3,2, 3 ,AB 3,2, 3
所以 ，
(cid:3)
(cid:3)
 nAD y 3z0
设平面
ADC
的一个法向量为
n
(cid:3) x,y,z，则有 
n
(cid:3)


A
(cid:3)


c 3x2y 3z0
，
(cid:3)  
n 1, 3,1
取y 3 z1,x1，即 ，...........................................................................................12分
设直线AB与平面ACD所成角为，
3
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司(cid:3) (cid:3) n (cid:3)   A (cid:3)   B 2 6
则
sin cosn,AB 
(cid:3)
(cid:3) 
，...................................................................................................14分
n  AB 5
2 6
所以直线 与平面 所成角的正弦值为 ................................................................................15分
AB ACD 5
17.
【详解】（1）记电压“不超过200V”、“在200V~240V之间”、“超过240V”分别为事件A，B，C，
“该机器生产的零件为不合格品”为事件D．..........................................................................................1分
1PZ  10.68
因为U ~ N  220,202，所以PAPU 200  0.16，
2 2
PBP200U 240PZ 0.68
，
1PZ  10.68
PCPU 240  0.16．............................................................4分
2 2
PDPAPD|APBPD|BPCPD|C
所以
0.160.150.680.050.160.20.09，..............................................................................................6分
所以该机器生产的零件为不合格品的概率为0.09．..................................................................................7分
X ~ Bn,0.09
（2）从该机器生产的零件中随机抽取n件，设不合格品件数为X，则 ，...................9分
p PX 2C20.91n20.092
所以 n n ．...................................................................................................10分
p C2 0.91n10.092 n1 191
n1  n1  0.911 2n
由 p C20.91n20.092 n1 ，解得 9 ．...........................................................13分
n n
2n21 p  p
所以当 时， n n1；
n22 p  p p
当 时，
n n1
；所以
22
最大．
n22 p
因此当 时， n最大．.......................................................................................................................15分
18.
 x2   x2   x2 
Ax , 0  Bx, 1  Dx , 2 
【详解】（1）设  0 4  ，  1 4 ，  2 4 ，..........................................................................1分
4
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司 x2
x , 0 
由
AC//x
轴得，点C的坐标为 0 4 ，
1 x
由 x2 4y 得y  4 x2 ，y  2 ，
x
所以抛物线在点 处的切线斜率为k  0 ，.............................................................................................3分
A 1 2
x2 x2
2  1
又k  4 4  x 2 x 1 ，由 得x 2 x 1  x 0 ，所以 ，
BD x x 4 BD//l 4 2 x x 2x
2 1 2 1 0
x2 x2 x2 x2
2  0 1  0
因为k 4 4  x 2 x 0 ，k  4 4  x 1 x 0 ，..................................................................................5分
x x 4 x x 4
2 0 1 0
x x x x x x 2x
所以kk  2 0  1 0  2 1 0 0；........................................................................................7分
4 4 4
（2）因为tanBCA2，所以k 2，k2，
x2 x2
所以直线 的方程为y 0 2xx  ，即y2x2x  0 ，............................................................8分
CB 4 0 0 4
x2 4y

 x2
由

y2x2x
0

4
0 ，得
x28x8x x2 0
，
0 0
x x 8x x2 x x 8
所以 1 0 0 0，得 1 0 ，
x2 x2
又直线 的方程为y 0 2xx  ，即y2x2x  0 ，
CD 4 0 0 4
x2 4y

 x2
由

y2x2x
0

4
0 ，得
x28x8x x2 0
，
0 0
x x 8x x2 x x 8
所以 2 0 0 0，得 2 0 ，
x 82 x x x2
y 0  0xx 8 y 0 x16 0
所以直线BD的方程为 4 2 0 ，即 2 4 ，
5
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司 32 x2
Px  , 0 
所以  0 x 4 ，..................................................................................................................................11分
0
32
x x  x
由x x x ，即 0 0 x 0 ，解得：x >4，........................................................................12分
0 P 0 0 0
 32 32  32 32
PA  x x    PC  x  x 2x 
因为 0  0 x  x ，  0 x  0 0 x ，
0 0 0 0
1 32 x 82 x 82 1 32
S  2x   0  0  2x  8x 8  x216 
所以 1 2 0 x  4 4 2 0 x  0 0 ，
0 0
1 32 x2 x 82 64x 4
S    0  0  0
2 2 x 4 4 x ，
0 0
S 1 1
1   x24x   x 224
所以S 8 0 0 8 0  ，.................................................................................................15分
2
S S
1 4 1
又
x >4
，所以
S
，即
S
的取值范围为4,.............................................................................17分
0 2 2
19.
10
 a 0
【详解】（1）若q1，则S 10a 0，解得a 0，则 i ，与题设矛盾，舍去；............1分
10 1 1 i1
a
 1q10
S  1 0
若q1，则 10 1q ，得 q1 ，
10
1 1
 a 10 a 1 a  a 
而 i 1 ，解得 1 10或 1 10，.........................................................................................3分
i1
1 1
a  (1)n11n10 a  (1)n1n10
故 n 10 或 n 10 ...........................................................................4分
a,a ,a ,,a m1
（2）设等差数列 1 2 3 2m 的公差为d，
2ma a 
因为 ，则 1 2m 0，则 ，...............6分
a a a a 0 2 a a a a 0,a a
1 2 3 2m 1 2m m m1 m m1
6
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司a a d 0,a 0,a 0
m m1 m m1
由 ，得 ，
2m 1 1
而  a 1，故a a a a  ,a a a a  ，..........................................8分
i 1 2 3 m 2 m1 m2 m3 2m 2
i1
1
d 
两式相减得 ，即 ，
m2d 1 m2
mm1 1 2m1
又am d  ，得a  ，
1 2 2 1 2m2
所以a a n1d  2m1 n1   1   2n2m1  1n2m,mN* ...............................10分
n 1 2m2  m2  2m2
a 1 ,a 2 ,a 3 ,,a N A B
（3）记 中所有非负项之和为 ，负项之和为 ，
AB0,
1 1
因为数列 a n  为“N 阶可控摇摆数列”，则  AB1,得 A 2 ,B 2，.......................................11分
1 1 1
故

2
BS
n
 A
2
n1,2,3,,N
，所以
S
n

2 .
N 1
若存在 ，使得  a 2S ，即S  ，
1mN i m m 2
i1
a 0,a 0,,a 0,a 0,a 0,,a 0
1 2 m m1 m2 N
则 ，
1
且
a
m1
a
m2
a
N

2 .........................................................................................................................12分
假设数列
S
n

也为“ N 阶可控摇摆数列”，记数列
S
n

的前 n 项和为 T n，
1
则T S S S S  ,
m 1 2 3 m 2
1
因为S m  2 ，所以S S S S 0...........................................................................................13分
1 2 3 m1
1
所以
a
1
a
2
a
3
a
m1
0,a
m

2 ；
1
又
a
m1
a
m2
a
N

2 ，则S ,S ,,S 0...............................................................................15分
m1 m2 N
S  S  S  S S S S S
所以 1 2 3 N 1 2 3 N；
7
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司S S S S 0 S  S  S  S 1
即 1 2 3 N 与 1 2 3 N 不能同时成立.
S 
故数列 n 不为“ N 阶可控摇摆数列”...................................................................................................17分
8
原创精品资源学科网独家享有版权，侵权必究！
学科网（北京）股份有限公司