文档内容
方法精讲-资料 2
(笔记)
主讲教师:邓健
授课时间:2024.05.30
粉笔公考·官方微信方法精讲-资料 2(笔记)
资料分析 方法精讲2
学习任务:
1.课程内容:一般增长率、增长量
2.授课时长:3小时
3.对应讲义:第178~190页
4.重点内容:
(1)增长率相关术语的联系与区别
(2)一般增长率的题型识别及计算公式
(3)一般增长率的比较技巧
(4)增长量的计算与比较技巧
第三节 一般增长率
常考术语辨析
计算类
比较类
【注意】常考术语辨析:增长率涉及的术语较多,如降幅。
1.计算类。
2.比较类。
常考术语辨析:
①百分数与百分点
②增长率与倍数
③成数与翻番
④增幅、降幅与变化幅度
【注意】常考术语辨析:
1.百分数与百分点。
2.增长率与倍数。
13.成数与翻番。
4.增幅、降幅与变化幅度,较难。
基本术语:
增长率
增长率是用来表述基期量与现期量变化的相对量。增长率又称增速、增幅或
者增长幅度、增值率等,增长率为负时表示下降,下降率也可直接写成负的增长
率。
百分数与百分点
百分数:用来反映量之间的比例关系。
百分点:用来反映百分数的变化。
增长率与倍数
增长率指比基数多出的比率,倍数指两数的直接比值。
若A是B的n倍,则n=r+1(r指A相对于B的增长率)。
成数与翻番
成数:几成相当于十分之几。
翻番:翻一番为原来的2倍;翻两番为原来的4倍;依此类推,翻n番为原
来的2n倍。
增幅、降幅与变化幅度
增幅一般就是指增长率,有正有负。
降幅指下降的幅度,降幅比较大小时,只比较增长率的绝对值(前提必须为
下降)。
变化幅度指增长或下降的绝对比率,变化幅度比较大小时,用增长率的绝对
值。
【注意】基本术语:
1.百分数与百分点:
(1)百分数:表示两个量的比例关系,如增长率,比重,都是百分数的形
式。
(2)百分点:表示两个百分数的差,a比 b高一个百分点,就是 a-b=1%,
2百分数是相对量,表示百分数的差值用百分点表达比较精准,一个百分点就是
1%。
(3)例 1:2023 年老邓体重 300 斤,2022 年 200 斤,则 2023 年老邓体重
的同比增长率为?
答:r=增量/基期=(现期值- 基期值)/基期值,是百分数的形式,r=(300-200)
/200=50%。
(4)百分数和百分点的衔接,例 2:2023 年老邓体重的增速是 50%,比身
高的增速高30个百分点,则2023年老邓身高的增速为?
答:“高30个百分点”即差值是30%,百分数之间的比较用百分点表达可以
避免歧义,如果说高30%,可能表示两个增速之间的增长率,表述不规范。2023
年老邓身高的增速=50%-30%=20%。
2.增长率与倍数:增长率指比基数多出的比率,倍数指两数的直接比值。若
A是B的n倍,则n=r+1(r指A相对于B的增长率)。
(1)倍数=现期/基期。
例:2019年小张收入150 元,2018年 100元,问 2019 年收入是 2018年的
( )倍。
答:倍数直接除,150/100=1.5倍。
(2)增长率=(现期- 基期)/基期。
例:2019年小张收入150 元,2018年 100元,问 2019 年收入比 2018年增
长( )%。
答:增长率=(现期值- 基期值)/基期值=(150-100)/100=50%。
(3)50%即0.5,1.5和0.5之间差1,即增长率和倍数之间关系:增长率=
倍数-1。如,2020年收入增长率是37%,问2020年/2019年,即问2020年是2019
年的多少倍,反推公式为:倍数=增长率+1,则所求=1+37%=1.37倍。
3.成数与翻番:比如武侠小说中,你得到了我的三成功力,就是30%(3/10),
五成功力就是50%=5/10=1/2。
(1)成数:几成相当于十分之几,百分之几十。比如问,……同比增长三
成多,即比三成多,又没有到四成,表示增长率在30%~40%之间。
(2)翻番:翻一番为原来的2倍(21);翻两番为原来的4倍(22);3番就
3是原来的 8 倍(23),依此类推,翻 n番为原来的 2n倍。麻将中经常用到这个概
念,或是欢乐斗地主中的加倍、超级加倍。
4.增幅、降幅与变化幅度:幅就是幅度,比例的变化,和增长率挂钩。
(1)增幅就是指增长率,一般简称增速,也有叫增长速度的,都是别称,
比如邓老师,女儿叫他爸爸,妻子叫他老公,称呼不同,都是一个人。有正有负,
可升可降,比大小时带符号比。
(2)降幅前提是下降的,指下降的幅度,降幅比较大小时,只比较增长率
的绝对值(前提必须为下降),看下降的,比绝对值,比较特殊,需要记住。
(3)变化可能变好变坏,变高变矮,变化幅度指增长或下降的绝对比率,
变化幅度比较大小时,用增长率的绝对值,比如收入比去年高了20万和低了20
万都是变了20万,可升可降,只看数值本身,比绝对值(负数去掉负号)。
(4)例:A.比去年增长60%,B.比去年增长40%,C.比去年下降50%,D.比
去年下降30%,选出增幅(增长率)、降幅、变化幅度最大的。
答:A 项:增幅(增长率):60%;是增长的,降幅无;变化幅度:60%。B
项:增幅(增长率):40%;降幅无;变化幅度:40%。C项:增幅(增长率):-50%,
不要被幅度误导,增幅即增长率,增长率有正有负;降幅:50%;变化幅度(只
看数字):50%。D项:增幅(增长率):-30%;降幅(绝对值):30%;变化幅度:
30%。则增幅最大为A项,A、B项没有降幅,C项50%>D项30%,降幅最大为C
项,变化幅度最大为A项(60%)。如果增幅里面选最小的:要带着符号比较,负
数<正数,-50%是最小的,选C项。
(5)记住规则,切勿纠结。增长的就没有降幅,已经下降的降幅取绝对值,
如分数比去年下降5分,那么和其他人说下降的分数就是5分,不会说-5分。
一、计算
2022年,全国软件业利润总额 12648亿元,同比增长 5.7%,增速较上年同
期回落 1.9 个百分点。软件业务出口额 524.1 亿美元,同比增长 3.0%,增速较
上年同期回落5.8个百分点。其中,软件外包服务出口额同比增长9.2%。
【例1】(2024四川)2021年,全国软件业利润总额同比增速比软件业务出
口额同比增速:
4A.低1.2个百分点 B.低2.7个百分点
C.高1.2个百分点 D.高2.7个百分点
【解析】1.找到增长率,求同比增速的差值,问2021年,材料时间是2022
年,数据不能直接用,需要结合比上年变化计算。“同比增长5.7%,增速较上年
同期回落1.9个百分点”,回落即降低,则去年更高,2021年全国软件业利润总
额同比增速为 5.7%+1.9%=7.6%。同理,“同比增长 3.0%,增速较上年同期回落
5.8 个百分点”,比去年回落,则去年更高,软件业务出口额同比增速为
3%+5.8%=8.8%,7.6%<8.8%,降低,排除 C、D项,全国软件业利润总额同比增
速比软件业务出口额同比增速低8.8%-7.6%=1.2%,低1.2个百分点。对应A项。
【选A】
【注意】假如今年收入5.7个亿,比去年回落1.9亿,“回落”即比去年低,
则去年收入为5.7+1.9=7.6,换成增速也是一样的道理。
高频易错点:
2017年收入10万元,同比增长10%,增速比去年提高5个百分点。则2016
年的增长率为:
2017年收入10万元,同比增长10%,增速比去年降低5个百分点。则2016
年的增长率为:
“高减低加”:比去年高就用减法,比去年低就用加法。
【注意】高频易错点:
1.例:2017年收入 10 万元,同比增长 10%,增速比去年提高 5个百分点。
则2016年的增长率为:
答:增速比去年提高5个百分点,则去年低一些,10%-5%=5%。
2.2017年收入10万元,同比增长10%,增速比去年降低5个百分点。则2016
年的增长率为:
答:比去年降低5个百分点,“回落”的意思,则加上这5个百分点,10%+5%=15%。
3.“高减低加”:比去年高就用减法,比去年低就用加法。高就用减法,低
就用加法。比去年高5个百分点→-5%,比去年低5个百分点→+5%。
54.降幅的分析:降幅就是下降的幅度,下降取绝对值。
(1)例:2017年收入10万元,同比下降10%,降幅比去年扩大5个百分点。
则2016年的增长率为:
答:2017 年的降幅(10%),比去年扩大 5 个百分点,就是高的意思,2016
年的降幅(10%-5%=5%),降幅是5%,即下降5%,则增长率为负值,2016年的增
长率(-5%)。
(2)例:2017年收入10万元,同比下降10%,降幅比去年收窄5个百分点。
则2016年的增长率为:。
答:2017年的降幅(10%),比去年收窄5个百分点,窄就是低,高减低加,
2016 年的降幅(10%+5%=15%)。是下降的,增长率是负值,要补上负号,2016
年的增长率(-15%)。
5.材料会给出今年的情况,可能上升也可能下降,主要看后面的变化,如果
问增速变化,高减低加。若分析的是降幅,也是高减低加,下降的时候取绝对值,
最后求增长率记得添加负号。
2020年全年,汽车产销降幅收窄至2%以内。汽车产量为2522.5万辆,销量
为2531.1万辆,同比分别下降2.0%和1.9%,降幅分别比2020年上半年收窄14.8
和15.0个百分点。2020年全年,新能源汽车销量为136.7万辆,同比增长10.9%。
【例2】(2021联考)2020年上半年汽车销量降幅估计在:
A.10个百分点以内 B.10~12个百分点
C.12~14个百分点 D.15个百分点以上
【解析】2.材料有全年的销量,问降幅。“同比分别下降2.0%和1.9%”,前
面是产量后面是销量,2020年全年汽车销量下降1.9%,降幅就是1.9%,降幅比
2020年上半年收窄15.0个百分点。“收窄”就是低,故2020年上半年汽车销量
降幅为1.9%+15%=16.9%,即降幅在15个百分点以上。对应D项。【选D】
【注意】
1.如果题目问的是增长率,需要在结果上加一个符号(-16.9%)。
2.同比和增长率无必然关系,是时间上的关系,同比就是和去年同期相比,
6环比是和上个月/季度相比,本题同比下降是 2020年和 2019年的关系,题目问
的是2020年上半年汽车销量降幅,要根据幅度的变化分析。
3.注意问的是“销量”的数据,要看1.9%,不能错用产量的2%。
4.刚接触基础概念会比较纠结,实际做题中没有很复杂,基础概念都是辅助
的东西,计算公式才是“正菜”。
增长率的计算
识别:问增长率/增速,增长/下降+%(选项)
公式:r=增长量/基期量=增长量/(现期-增长量)=(现期- 基期)/基期。
速算:截位直除
【注意】增长率的计算:
1.识别:
(1)直接问增长率/增速是多少
(2)题干中增长/下降+选项带%就是增长率(选项带具体单位就是增长量)。
2.公式:r=增长量/基期量=增长量/(现期-增长量)=(现期- 基期)/基期。
r=增长量/基期量为定义式,考试中一般不会同时给出增长量和基期量,更多的
是给出现期量和增长量/现期值和基期值,要记住后两个公式。
3.例:24年老邓有10套别墅,同比增长4套,求r?
答:2024年的10套为现期量,增长+单位,4套为增长量,增长量是相对去
年的值,现期量-增长量=基期量=10-4=6,r=增长量/基期量=4/6。
4.例:24年老邓有存款10亿,22年8亿,求r?
答:虽然隔了一年,但不是间隔增长率。2024年的值为现期量,2022年的
值为基期量,已知现期和基期,r=(现期- 基期)/基期=(10-8)/8=2/8=25%。
5.归根到底就是要找到增长量/基期量的值。
6.速算:截位直除。差距大截两位,差距小截三位。
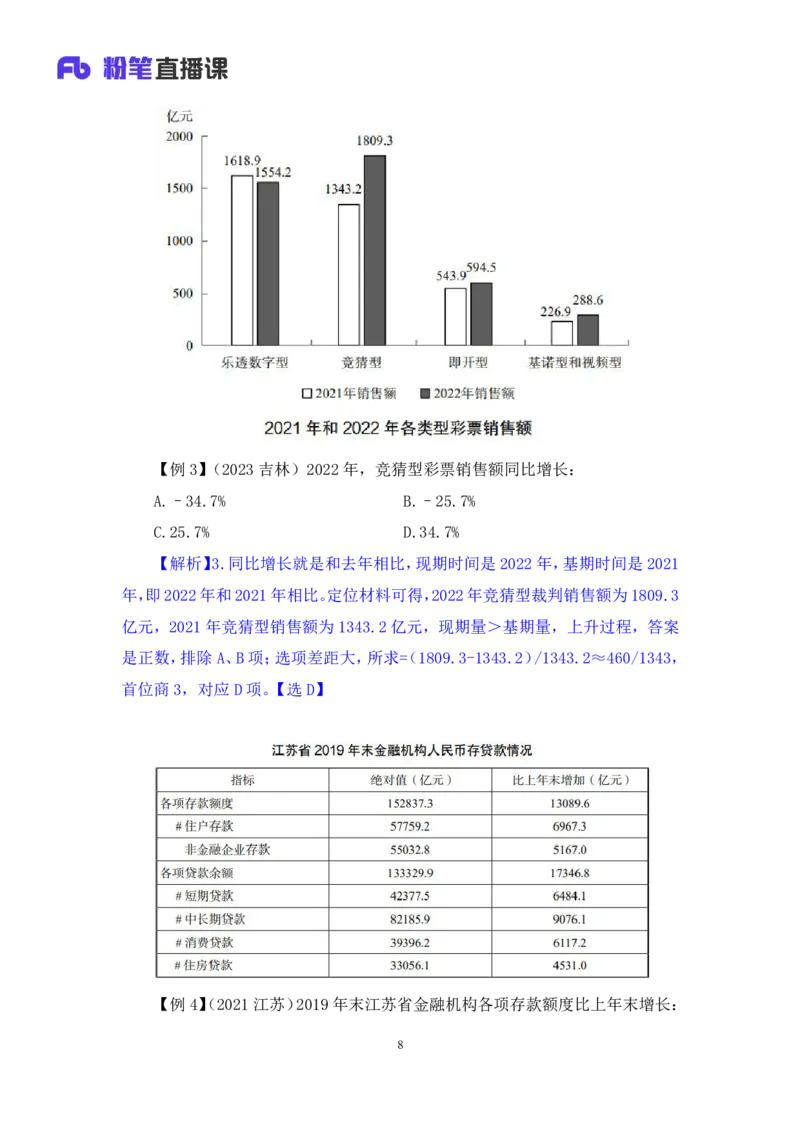
7【例3】(2023吉林)2022年,竞猜型彩票销售额同比增长:
A.–34.7% B.–25.7%
C.25.7% D.34.7%
【解析】3.同比增长就是和去年相比,现期时间是2022年,基期时间是2021
年,即2022年和2021年相比。定位材料可得,2022年竞猜型裁判销售额为1809.3
亿元,2021 年竞猜型销售额为1343.2亿元,现期量>基期量,上升过程,答案
是正数,排除A、B项;选项差距大,所求=(1809.3-1343.2)/1343.2≈460/1343,
首位商3,对应D项。【选D】
【例4】(2021江苏)2019年末江苏省金融机构各项存款额度比上年末增长:
8A.8.5% B.9.4%
C.10.2% D.10.8%
【解析】4.材料时间和问题时间都是2019年,现期是2019年。比上年末增
加(亿元)为增长量,绝对值(亿元)看作现期量,如果忽略分母是基期量,会
错列式:13089/152837,首位商8,导致错选A项。公式:r=增长量/基期量=增
长 量 / ( 现 期 - 增 长 量 ) =13089/ ( 153000-13089 ) ≈ 13089/140000 ,
140000*10%=14000>13089,则 13089/140000<10%,首位不能商 1,排除 C、D
项;剩余A、B项,13089/140000,首位商9,对应B项。【选B】
【注意】
1.增长率=增长量/基期量,题目可能给出现期量和增长量,分母是基期,不
要误用现期,与选项差距大还是小无关。
2.截位一般是两位和三位,89和153000相比差距很大,如果差距过大就不
会在意太小的差异,如月入15万就不会在乎89块钱。
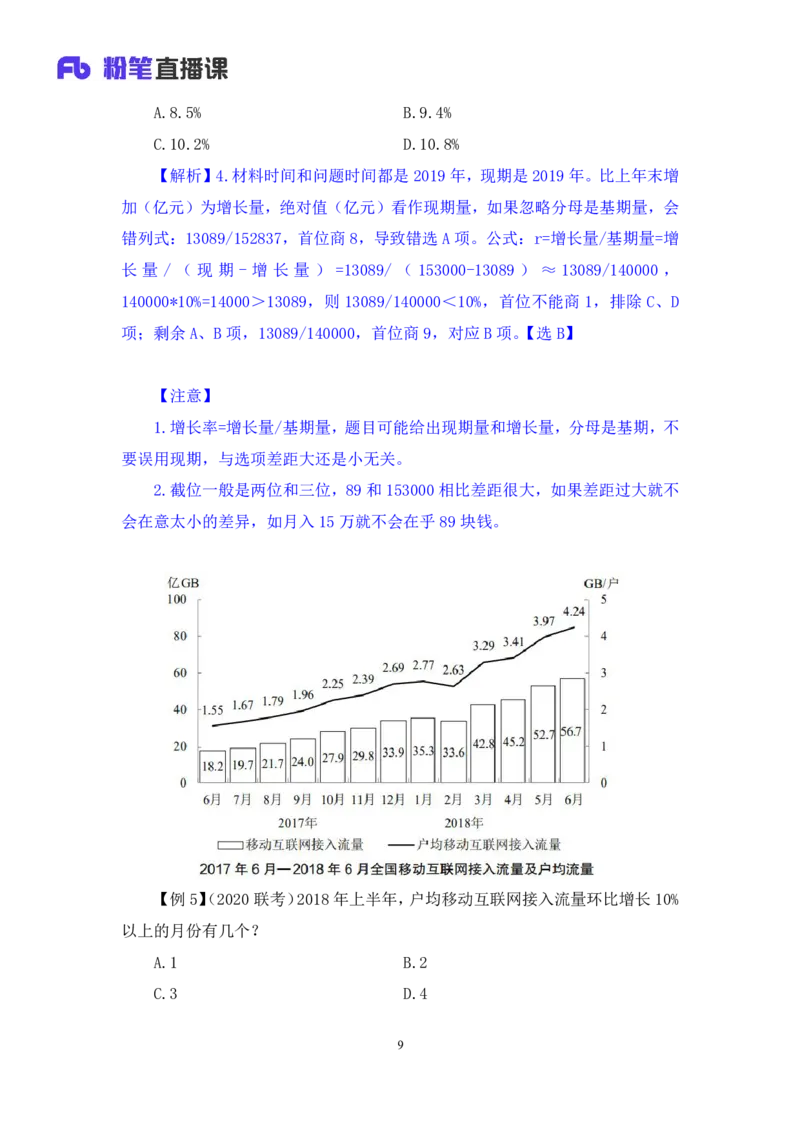
【例5】(2020联考)2018年上半年,户均移动互联网接入流量环比增长10%
以上的月份有几个?
A.1 B.2
C.3 D.4
9【解析】5.问题时间2018年上半年,上半年为1~6月,主体“户均移动互
联网接入流量”,问“环比增长10%以上”,看折线,如果用柱形图也做对了,是
因为总量和户均变化趋势大致相同,只算10%以上有可能一样。环比是与上个月
相比,即 1月与 12月相比、2月比 1月比、3月与 2月比、4月与 3月比、5月
与4月比、6月与5月比;
方法一:减法:满足增长量>基期*10%,1 月:2.77-2.69=0.08<
2.69*10%=0.269,不满足;2 月为下降(2.77→2.63),不满足;3 月:
3.29-2.63=0.66 > 2.63*10%=0.263 , 满 足 ; 4 月 : 3.41-3.29=0.12 <
3.29*10%=0.329,不满足;5 月:3.97-3.41=0.56>3.41*10%=0.341,满足;6
月:4.24-3.97=0.27<3.97*10%=0.397,不满足;只有 3 月和 5 月满足,共 2
个,对应B项。
方法二:加法:满足现期>1.1*基期,错位相加,1月:2.69+0.26=2.9+>
2.77,不满足;2月为下降(2.77→2.63),不满足;3月:2.63+0.26=2.89<3.29,
满足;4 月:3.29+0.32=3.61>3.41,不满足;5 月:3.41+0.34=3.7+<3.97,
满足;6月:3.97+0.39=4.3+>4.24,不满足。只有 3 月和5 月满足,共 2个,
对应B项。【选B】
【注意】
1.环比是和上个月相比。
2.本题就是增长率计算最难的形式,方法学清楚,结论式子记清楚,练多了
就会更快。
多个年份(月份)增长率>10%
r=(现期- 基期)/基期>10%
(现期- 基期)>10%基期
现期>(1+10%)基期(错位相加)
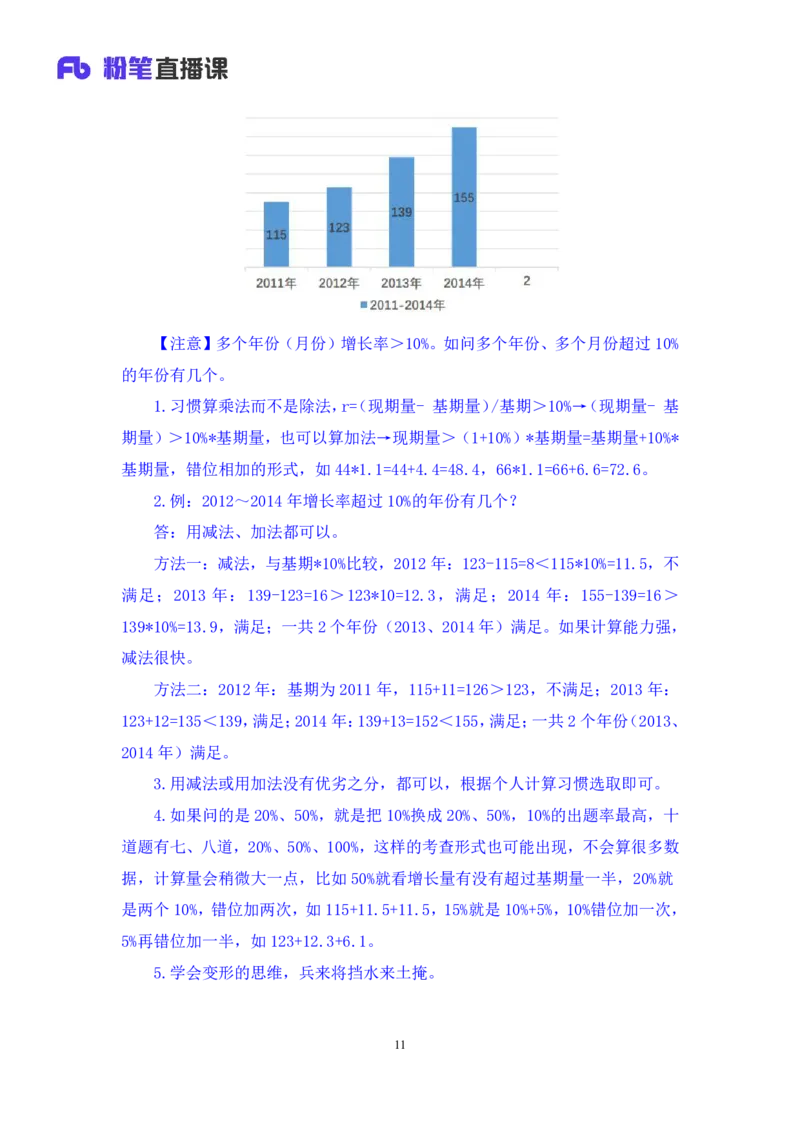
2012年~2014年增长率超过10%的年份有几个?
10【注意】多个年份(月份)增长率>10%。如问多个年份、多个月份超过10%
的年份有几个。
1.习惯算乘法而不是除法,r=(现期量- 基期量)/基期>10%→(现期量- 基
期量)>10%*基期量,也可以算加法→现期量>(1+10%)*基期量=基期量+10%*
基期量,错位相加的形式,如44*1.1=44+4.4=48.4,66*1.1=66+6.6=72.6。
2.例:2012~2014年增长率超过10%的年份有几个?
答:用减法、加法都可以。
方法一:减法,与基期*10%比较,2012年:123-115=8<115*10%=11.5,不
满足;2013 年:139-123=16>123*10=12.3,满足;2014 年:155-139=16>
139*10%=13.9,满足;一共2个年份(2013、2014年)满足。如果计算能力强,
减法很快。
方法二:2012年:基期为 2011年,115+11=126>123,不满足;2013年:
123+12=135<139,满足;2014年:139+13=152<155,满足;一共2个年份(2013、
2014年)满足。
3.用减法或用加法没有优劣之分,都可以,根据个人计算习惯选取即可。
4.如果问的是20%、50%,就是把10%换成20%、50%,10%的出题率最高,十
道题有七、八道,20%、50%、100%,这样的考查形式也可能出现,不会算很多数
据,计算量会稍微大一点,比如50%就看增长量有没有超过基期量一半,20%就
是两个10%,错位加两次,如115+11.5+11.5,15%就是10%+5%,10%错位加一次,
5%再错位加一半,如123+12.3+6.1。
5.学会变形的思维,兵来将挡水来土掩。
11二、比较
增长率的比较
识别:增长率(增速)最大;增长+快/慢
已知:现期、基期
比较:增长率→r=(现期- 基期)/基期=现期/基期- 基期/基期=现期/基期
-1。
方法:看现期和基期的倍数关系,倍数越大,增长率就越大
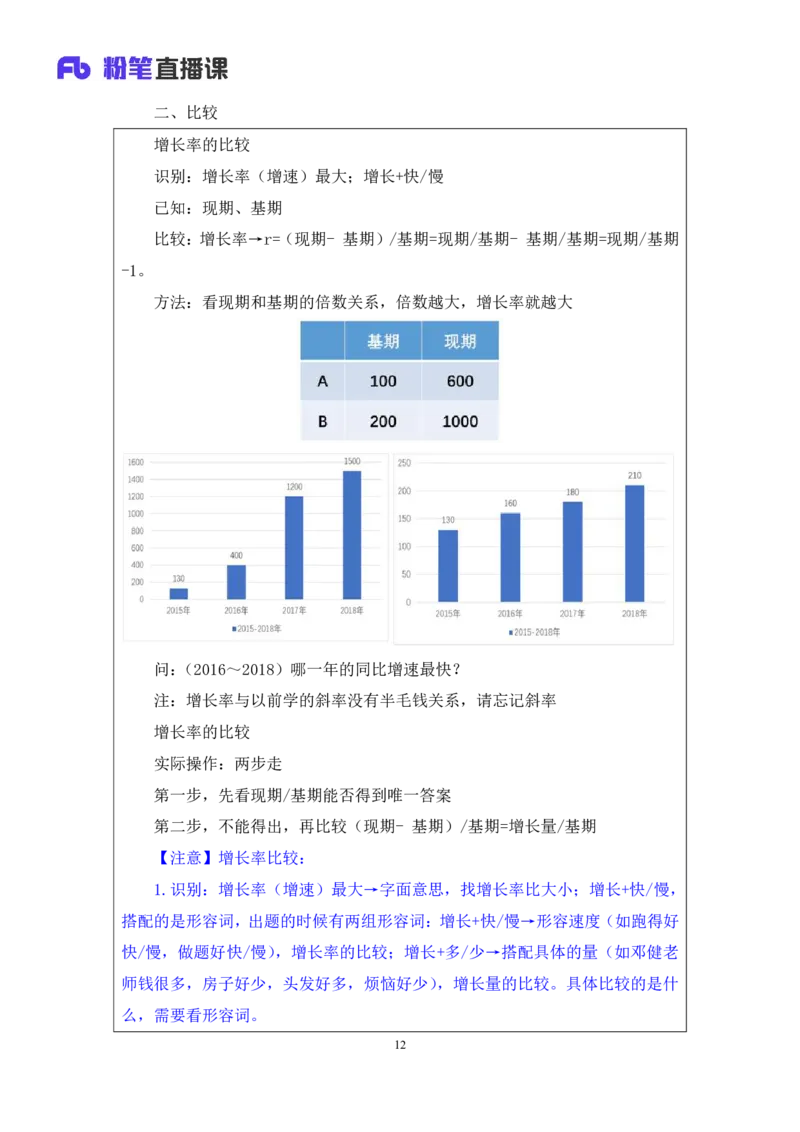
问:(2016~2018)哪一年的同比增速最快?
注:增长率与以前学的斜率没有半毛钱关系,请忘记斜率
增长率的比较
实际操作:两步走
第一步,先看现期/基期能否得到唯一答案
第二步,不能得出,再比较(现期- 基期)/基期=增长量/基期
【注意】增长率比较:
1.识别:增长率(增速)最大→字面意思,找增长率比大小;增长+快/慢,
搭配的是形容词,出题的时候有两组形容词:增长+快/慢→形容速度(如跑得好
快/慢,做题好快/慢),增长率的比较;增长+多/少→搭配具体的量(如邓健老
师钱很多,房子好少,头发好多,烦恼好少),增长量的比较。具体比较的是什
么,需要看形容词。
122.已知:现期量、基期量,比较增长率,公式推导:r=(现期- 基期)/基
期=现期/基期-(基期/基期)=现期/基期-1(也就是倍数-1)。
3.例:A和B谁增长得更快?
答:增长+快/慢,增长率的比较,不要去作差。可以看出“现期/基期”的
倍数,A:600/100=6,B:1000/20=5;增长率=现期/基期-1=倍数-1,A:
r=600/100-1=6-1=5,B:r=1000/200-1=5-1=4;原来“6>5”,“-1”后是“5
>4”,比大小的时候不需要“-1”,只需要看“现期/基期”的倍数关系。
4.方法:看现期和基期的倍数关系,倍数越大,增长率就越大。
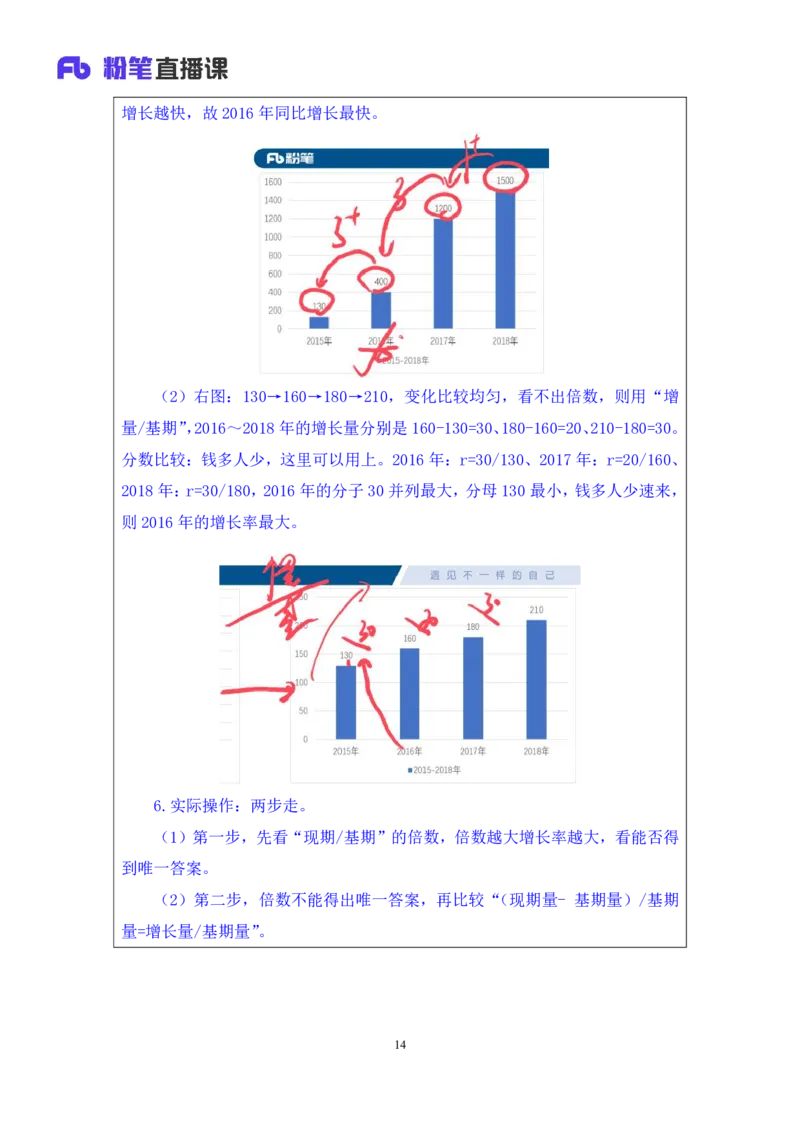
5.问:(2016~2018)哪一年的同比增速最快。
(1)左图:
①2017 年是错误的,正确答案是 2016 年。有 2017 年的误区:是因为思维
存在误区,中学时候学数学遇到这种图会连点,看函数图像中谁上升最快、斜率
最大,发现 2016 年→2017 年上升最快,斜率最大,认为 2017 年增速最快,这
样做是错误的。斜率k=△y/△x=任意两点纵坐标之差/任意两点横坐标之差(即
tan倾斜角=对边/邻边),r=增长量/基期量,分母不是同一个东西。增长率与以
前学的斜率没有半毛钱关系,请忘记斜率,不要混为一谈。
②增长率的快慢,不要看上升的快或慢,比较的时候直接看数字本身,数字
是不会骗人的,我们要研究的是倍数关系。“现期/基期”的倍数,2016 年:
400/130=3+倍、2017 年:1200/400=3 倍、2018 年:1500/1200=1+倍,倍数越大
13增长越快,故2016年同比增长最快。
(2)右图:130→160→180→210,变化比较均匀,看不出倍数,则用“增
量/基期”,2016~2018年的增长量分别是160-130=30、180-160=20、210-180=30。
分数比较:钱多人少,这里可以用上。2016年:r=30/130、2017年:r=20/160、
2018年:r=30/180,2016年的分子30并列最大,分母130最小,钱多人少速来,
则2016年的增长率最大。
6.实际操作:两步走。
(1)第一步,先看“现期/基期”的倍数,倍数越大增长率越大,看能否得
到唯一答案。
(2)第二步,倍数不能得出唯一答案,再比较“(现期量- 基期量)/基期
量=增长量/基期量”。
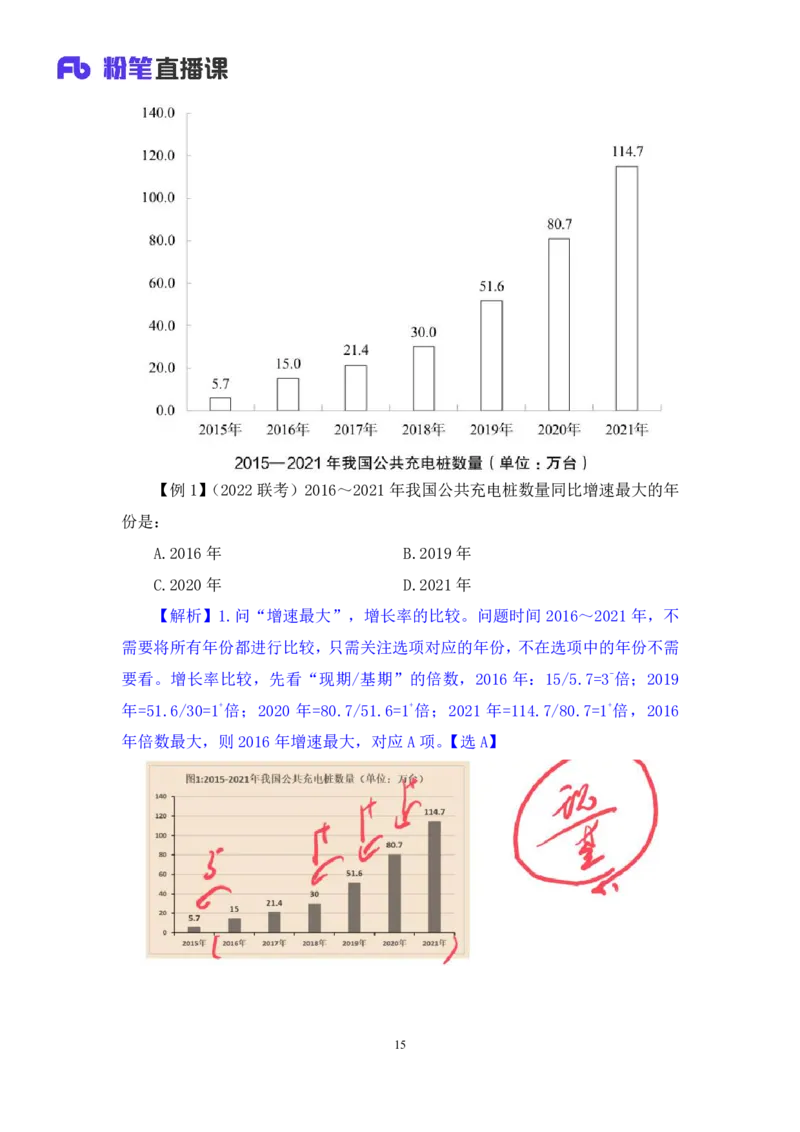
14【例1】(2022联考)2016~2021年我国公共充电桩数量同比增速最大的年
份是:
A.2016年 B.2019年
C.2020年 D.2021年
【解析】1.问“增速最大”,增长率的比较。问题时间 2016~2021年,不
需要将所有年份都进行比较,只需关注选项对应的年份,不在选项中的年份不需
要看。增长率比较,先看“现期/基期”的倍数,2016 年:15/5.7=3-倍;2019
年=51.6/30=1+倍;2020 年=80.7/51.6=1+倍;2021 年=114.7/80.7=1+倍,2016
年倍数最大,则2016年增速最大,对应A项。【选A】
15【例2】(2023联考)下列折线图中,能准确反映2022年第四季度竞猜型彩
票月销售额的环比增长率变化趋势的是:
A. B.
C. D.
【解析】2.问题时间2022年第四季度,第四季度对应10~12月,即表格中
16后三行;主体为“竞猜型彩票月销售额”,定位到材料对应位置。月环比是和上
个月相比,10月和9月比,11月和10月比,12月和11月比;问的是变化趋势,
折线图上的三个点分别对应四季度(10、11、12月)的环比增长率;如三个数
据是1、2、3,则画成折线图是1最低、2次之、3最高。
选项给折线图,需要看每个月增长率的大小,先不着急计算。观察数据,发
现有且只有10月相对上个月下降,故r <0,r 和r 一定>0,说明r 最
10月 11月 12月 10月
小,则第一个点最低,结合选项,排除B、D项。剩下A、C项,增长率的比较,
优先看“现期/基期”的倍数关系,11 月:31081.42/11341.84=3-倍,12 月:
42994.68/31081.42=1+倍,r >r ;综上,10月点最低,11 月点最高,其次
11月 12月
是12月,对应的折线趋势是最低→最高→下降到12月,只有C项符合。【选C】
【注意】思维点拨:选项为折线图时,可以先观察正负来判断点的高低。
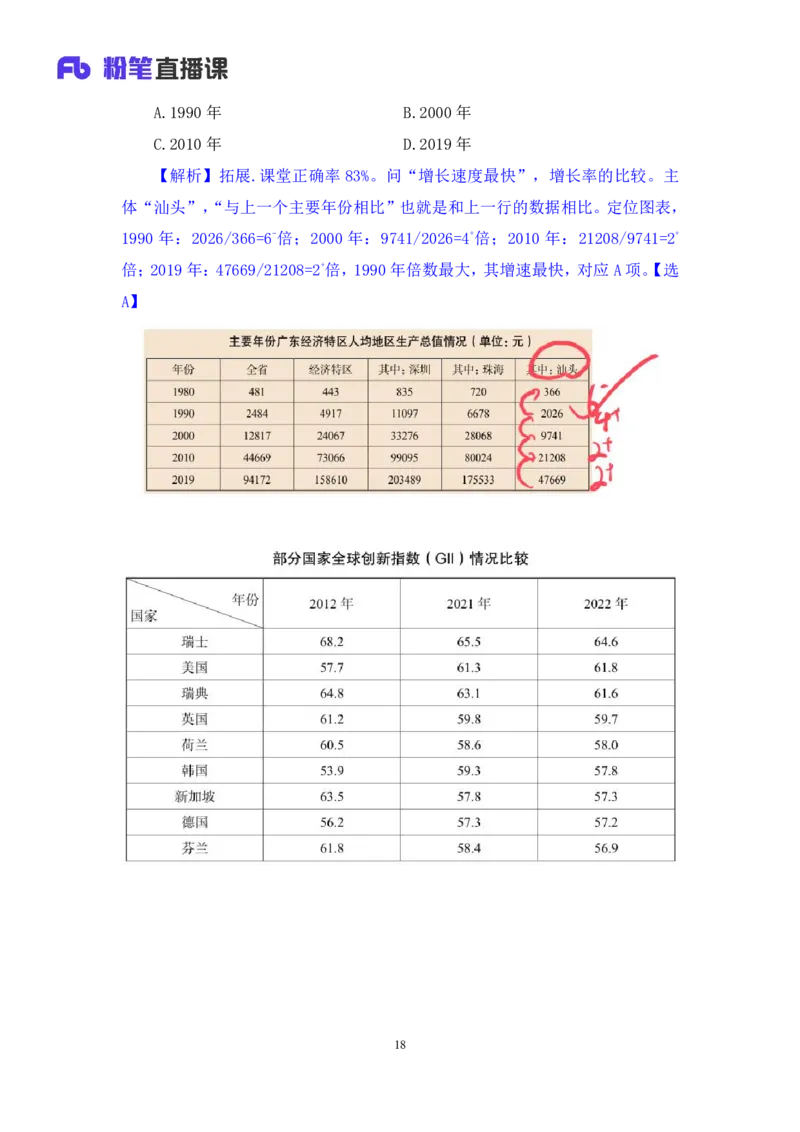
【拓展】(2021广东选调)下列年份中,与上一个主要年份相比,汕头人均
地区生产总值增长速度最快的是:
17A.1990年 B.2000年
C.2010年 D.2019年
【解析】拓展.课堂正确率 83%。问“增长速度最快”,增长率的比较。主
体“汕头”,“与上一个主要年份相比”也就是和上一行的数据相比。定位图表,
1990 年:2026/366=6-倍;2000 年:9741/2026=4+倍;2010 年:21208/9741=2+
倍;2019年:47669/21208=2+倍,1990年倍数最大,其增速最快,对应A项。【选
A】
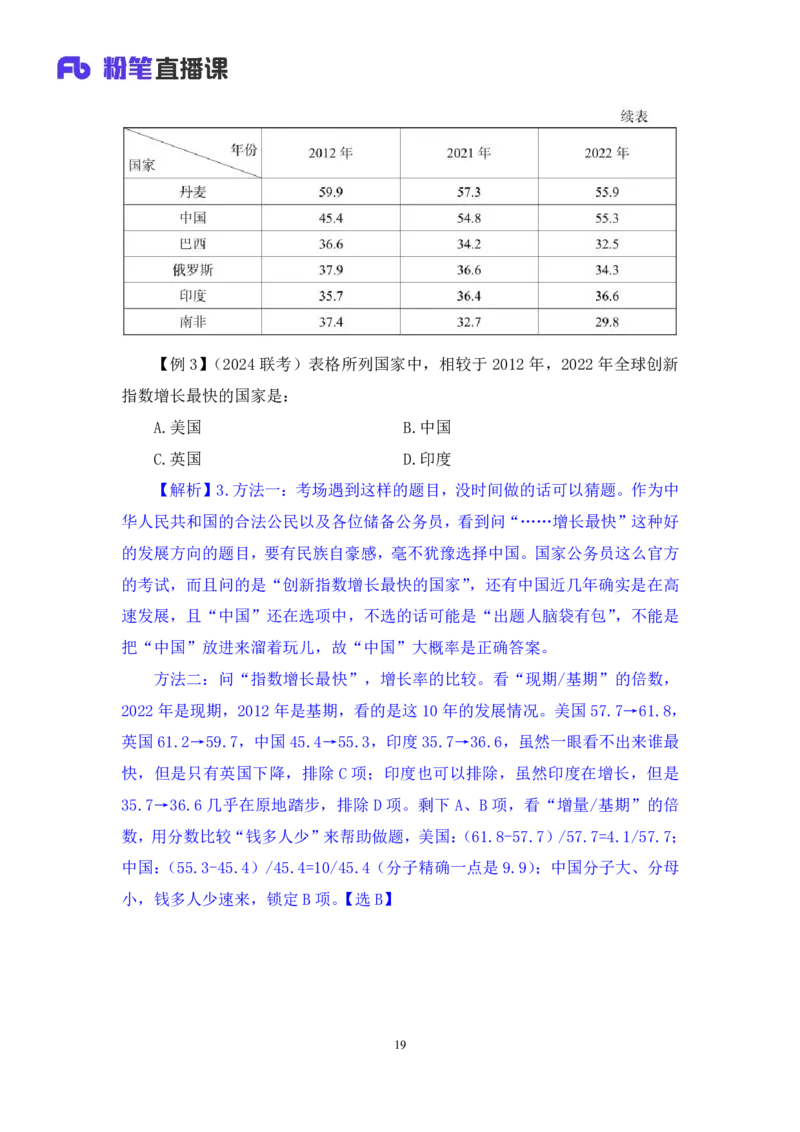
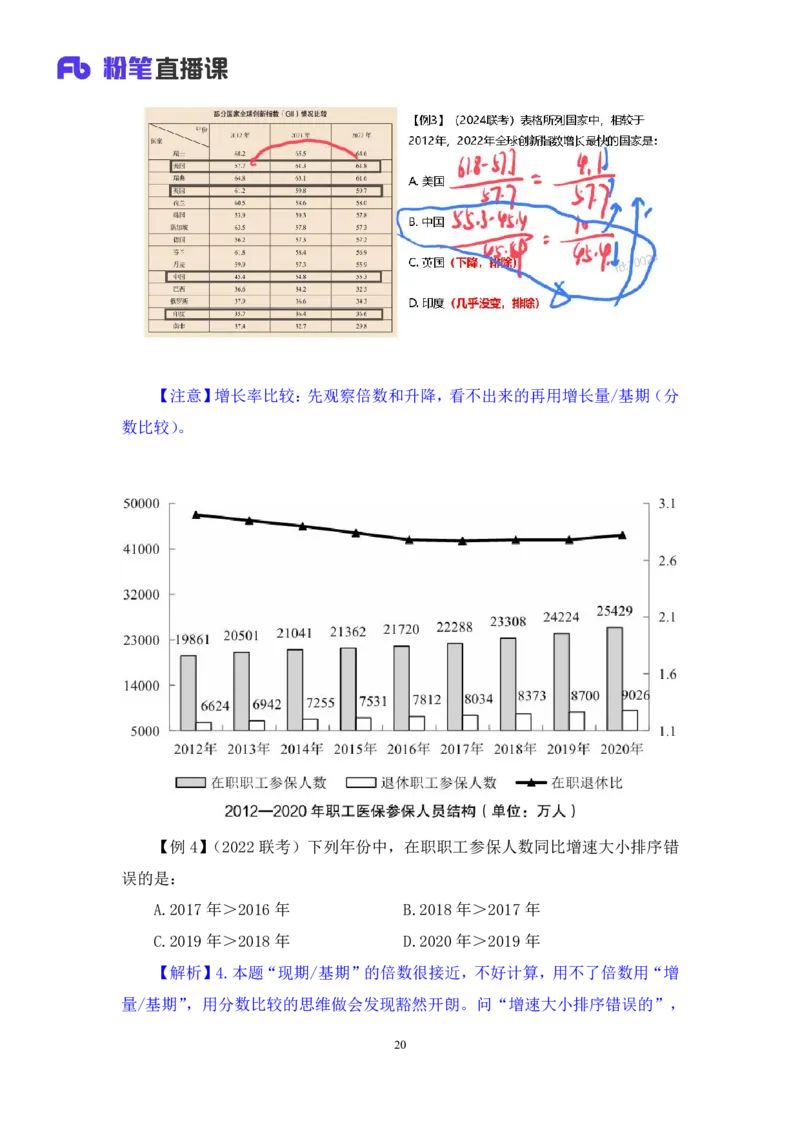
18【例 3】(2024 联考)表格所列国家中,相较于 2012 年,2022 年全球创新
指数增长最快的国家是:
A.美国 B.中国
C.英国 D.印度
【解析】3.方法一:考场遇到这样的题目,没时间做的话可以猜题。作为中
华人民共和国的合法公民以及各位储备公务员,看到问“……增长最快”这种好
的发展方向的题目,要有民族自豪感,毫不犹豫选择中国。国家公务员这么官方
的考试,而且问的是“创新指数增长最快的国家”,还有中国近几年确实是在高
速发展,且“中国”还在选项中,不选的话可能是“出题人脑袋有包”,不能是
把“中国”放进来溜着玩儿,故“中国”大概率是正确答案。
方法二:问“指数增长最快”,增长率的比较。看“现期/基期”的倍数,
2022年是现期,2012年是基期,看的是这10年的发展情况。美国57.7→61.8,
英国61.2→59.7,中国45.4→55.3,印度35.7→36.6,虽然一眼看不出来谁最
快,但是只有英国下降,排除 C 项;印度也可以排除,虽然印度在增长,但是
35.7→36.6 几乎在原地踏步,排除 D 项。剩下 A、B 项,看“增量/基期”的倍
数,用分数比较“钱多人少”来帮助做题,美国:(61.8-57.7)/57.7=4.1/57.7;
中国:(55.3-45.4)/45.4=10/45.4(分子精确一点是9.9);中国分子大、分母
小,钱多人少速来,锁定B项。【选B】
19【注意】增长率比较:先观察倍数和升降,看不出来的再用增长量/基期(分
数比较)。
【例4】(2022联考)下列年份中,在职职工参保人数同比增速大小排序错
误的是:
A.2017年>2016年 B.2018年>2017年
C.2019年>2018年 D.2020年>2019年
【解析】4.本题“现期/基期”的倍数很接近,不好计算,用不了倍数用“增
量/基期”,用分数比较的思维做会发现豁然开朗。问“增速大小排序错误的”,
20需要把每一年的增长率写出来,相邻的两年去比较。2016年:360/21362;2017
年:560/21720;2018年:1020/22288(不需要口算这么精确,1100/22288也可
以);2019年:900/23308;2020年:1200/24224。题目的排序是2016年<2017
年<2018年<2019年<2020年,在做题的时候可以先看有没有哪两个的顺序是
反着的。分数比较,先看钱多人少,2018年和2019年相比,2019年分子变小、
分母变大,钱少人多,分数值更小,故 2019 年<2018 年,而 C 项说的是 2019
年>2018年,故C项表述错误,选择C项。【选C】
【注意】
1.Tips:倍数不明显时,看“增长量/基期量”,因为基期量(分母)一直
在变大,因此一旦增长量(分子)变小,分数就会变小,可直接排除。
2.2016~2019年增量分别是:300+、500+、1100左右、900,出现分子变小
的情况,分数值一定变小,2019年分子变小,则2019年增长率<2018年增长率,
C项排序错误,选择C项。
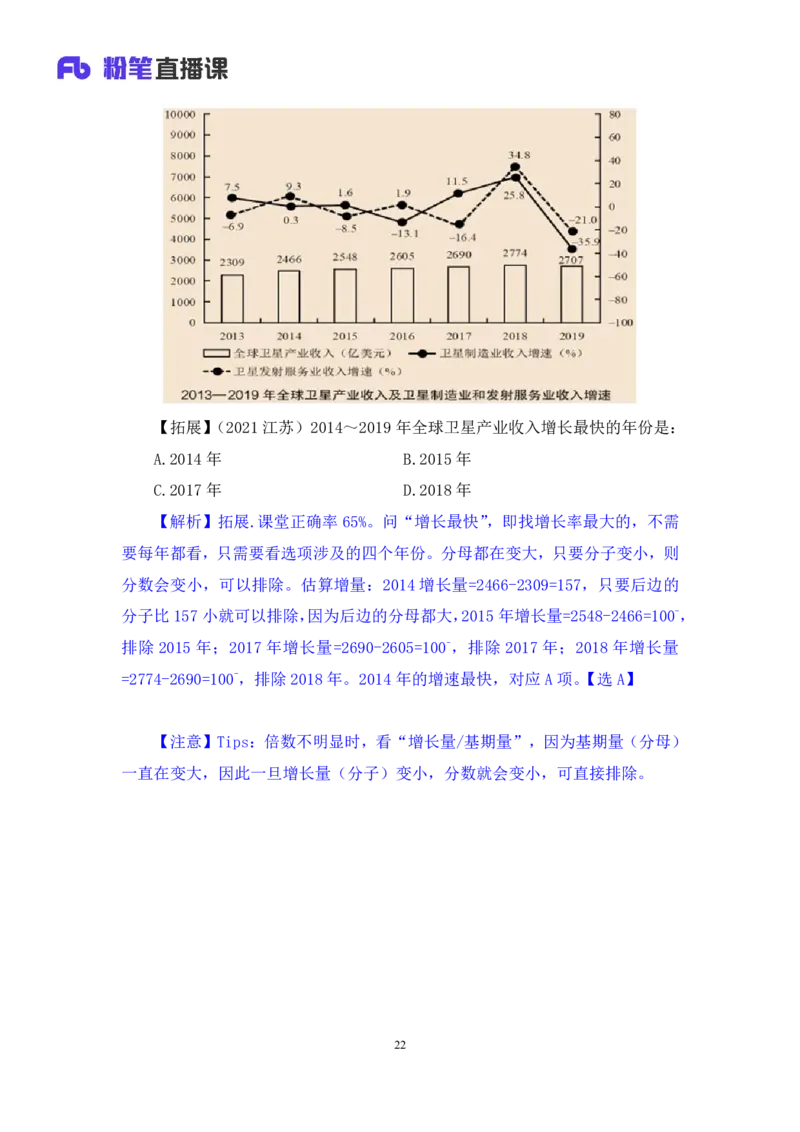
21【拓展】(2021江苏)2014~2019年全球卫星产业收入增长最快的年份是:
A.2014年 B.2015年
C.2017年 D.2018年
【解析】拓展.课堂正确率65%。问“增长最快”,即找增长率最大的,不需
要每年都看,只需要看选项涉及的四个年份。分母都在变大,只要分子变小,则
分数会变小,可以排除。估算增量:2014 增长量=2466-2309=157,只要后边的
分子比157小就可以排除,因为后边的分母都大,2015年增长量=2548-2466=100-,
排除 2015 年;2017 年增长量=2690-2605=100-,排除 2017 年;2018 年增长量
=2774-2690=100-,排除2018年。2014年的增速最快,对应A项。【选A】
【注意】Tips:倍数不明显时,看“增长量/基期量”,因为基期量(分母)
一直在变大,因此一旦增长量(分子)变小,分数就会变小,可直接排除。
22【注意】导图需要给一个明确的数字,“2”是人为定义的值,都是1+倍的时
候看不出来,当≥2 倍的时候分界比较明显,故用“2”为分界线,分界线的内
核也就是老师刚刚讲解的能看出来“现期/基期”倍数就看倍数,看不出来再看
“增量/基期”,不用过于纠结。
第四节 增长量
基本术语:
增长量是用来表述基期量与现期量变化的绝对量,增长率则是用来表述两者
变化的相对量。
年均增长量=(现期量- 基期量)/年份差。
一、计算
增长量计算
识别:增长+具体单位
公式:增长量=现期- 基期(简单)
【注意】增长量计算:
1.识别:增长+具体单位(如收入增长多少亿,房子增长多少套,车子增长
多少辆)。
2.公式:增长量=现期- 基期(简单)。
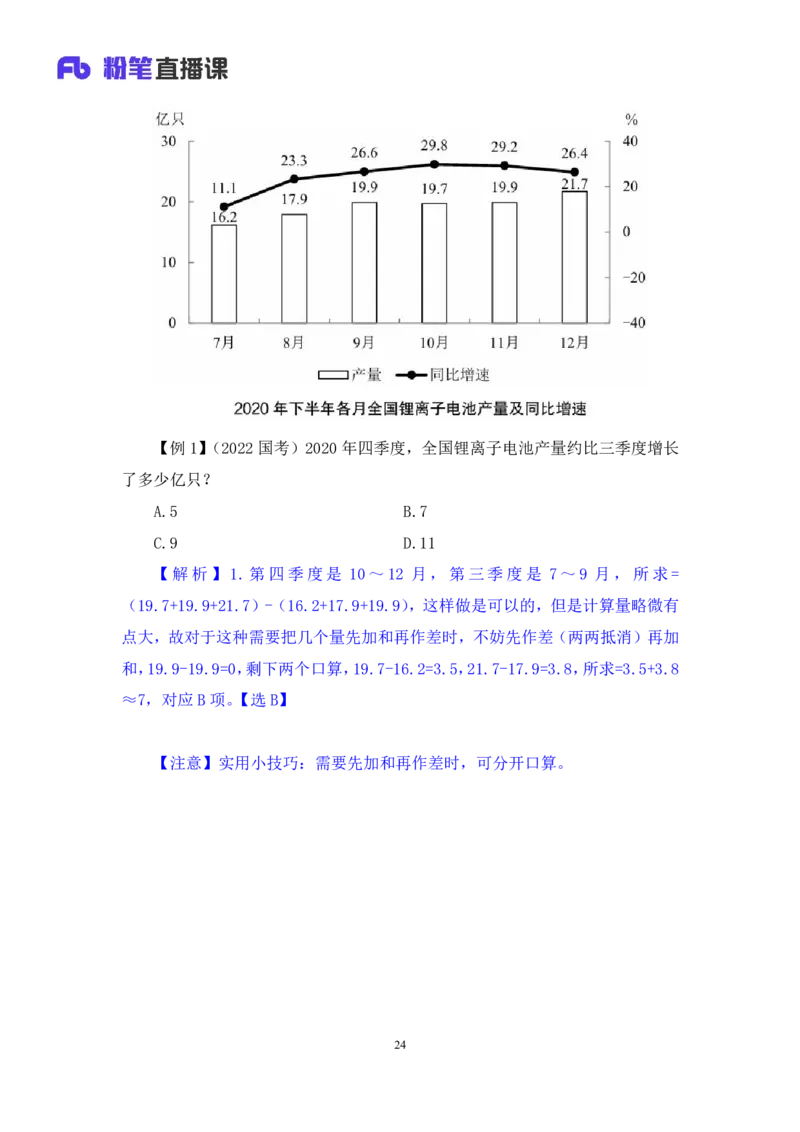
23【例1】(2022国考)2020年四季度,全国锂离子电池产量约比三季度增长
了多少亿只?
A.5 B.7
C.9 D.11
【解析】1.第四季度是 10~12 月,第三季度是 7~9 月,所求=
(19.7+19.9+21.7)-(16.2+17.9+19.9),这样做是可以的,但是计算量略微有
点大,故对于这种需要把几个量先加和再作差时,不妨先作差(两两抵消)再加
和,19.9-19.9=0,剩下两个口算,19.7-16.2=3.5,21.7-17.9=3.8,所求=3.5+3.8
≈7,对应B项。【选B】
【注意】实用小技巧:需要先加和再作差时,可分开口算。
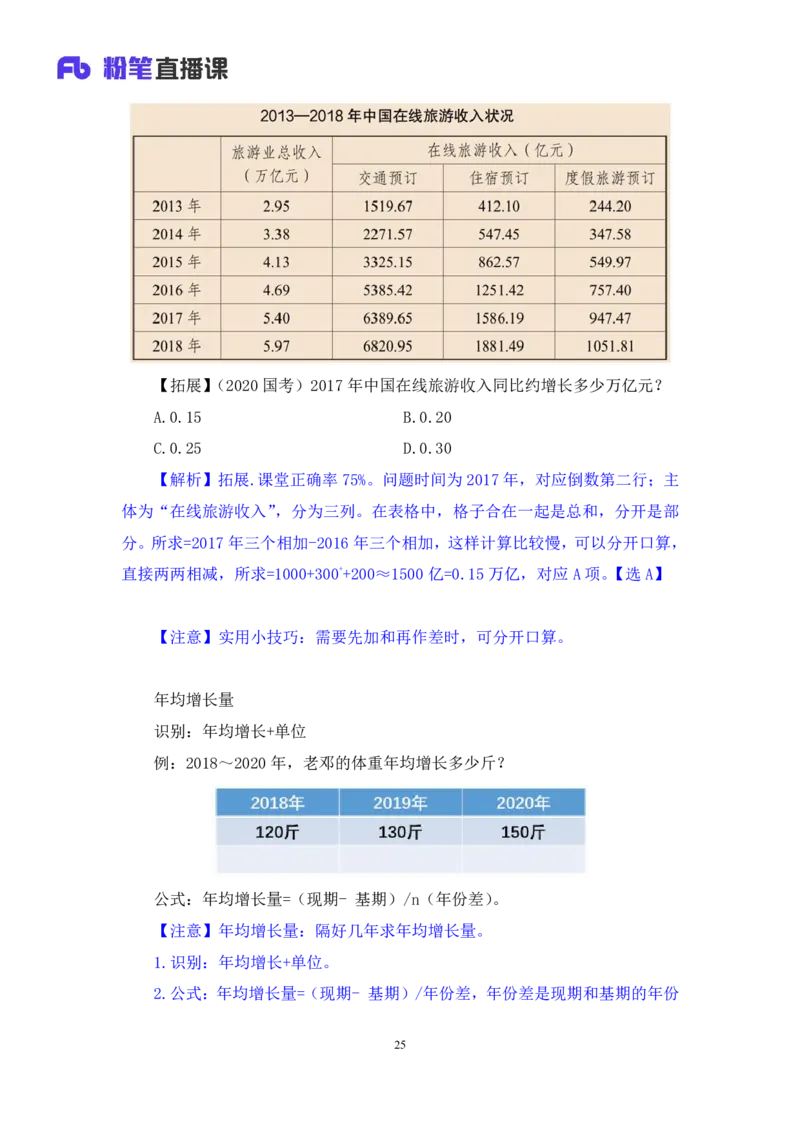
24【拓展】(2020国考)2017年中国在线旅游收入同比约增长多少万亿元?
A.0.15 B.0.20
C.0.25 D.0.30
【解析】拓展.课堂正确率75%。问题时间为2017年,对应倒数第二行;主
体为“在线旅游收入”,分为三列。在表格中,格子合在一起是总和,分开是部
分。所求=2017年三个相加-2016年三个相加,这样计算比较慢,可以分开口算,
直接两两相减,所求=1000+300++200≈1500亿=0.15万亿,对应A项。【选A】
【注意】实用小技巧:需要先加和再作差时,可分开口算。
年均增长量
识别:年均增长+单位
例:2018~2020年,老邓的体重年均增长多少斤?
公式:年均增长量=(现期- 基期)/n(年份差)。
【注意】年均增长量:隔好几年求年均增长量。
1.识别:年均增长+单位。
2.公式:年均增长量=(现期- 基期)/年份差,年份差是现期和基期的年份
25差。
3.例:2018~2020年,老邓的体重年均增长多少斤?
答:2018年120斤,2019年130斤,2020年150斤。注意算的是增长量,
总增长量=150-120=30,除以3得到10,除以2得到15。2019 年比2018年的增
长量=10,虽然有两年,但是增长量只有 1 个,故不能除以 2;故虽然此处有三
年,但是 2018 年→2019 年增长 1 次,2019 年→2020 年增长 1 次,总共增长 2
次,故所求=(150-120)/2=30/2=15。
(2022国考)在表中所列各类 LED应用市场中,2013~2019 年产值年均增
速(以2013年为基期)最快的应用市场,2019年产值约占LED行业总产值的( )。
(2023国考)将①甘肃、②广东、③上海和④浙江按2016~2021年集成电
路产量年均增速(以2016年为基期计算)从高到低排列,以下正确的是:
【注意】正常情况:
1.(2022 国考)在表中所列各类 LED应用市场中,2013~2019年产值年均
增速(以2013年为基期)最快的应用市场,2019年产值约占LED行业总产值的
( )。
答:2013年为基期,2019年为现期,年份差是6。
2.(2023国考)将①甘肃、②广东、③上海和④浙江按2016~2021年集成
电路产量年均增速(以2016年为基期计算)从高到低排列,以下正确的是。
答:2016年为基期,2021年为现期。
3.国考是最标准的考试,出题人在考试试卷上白纸黑字,明明白白给出,就
是以开头的年份为基期,没有可以争议的地方。
年均增长类问题基期的选择
➢一般情况(除江苏外):2012年~2018年:年份差为6,基期:2012年;
现期:2018年
26➢五年规划(全国统一):“十三五”期间:年份差为5(基期往前推一年),
基期:2015年;现期:2020年
五年计划,全称为中华人民共和国国民经济和社会发展五年计划纲要,是中
国国民经济长期计划的重要部分。
中国从 1953年开始制订第一个“五年计划”,“十一五”起,改称为“五年
规划”。
“十一五”2006~2010年
“十二五”2011~2015年
“十三五”2016~2020年
“十四五”2021~2025年
➢江苏省考(刷题遇到、了解即可):2012年~2018年:年份差为7(基期
往前推一年),基期:2011年;现期:2018年
【注意】年均增长类问题基期的选择:
1.一般情况(除江苏外):给哪两年用哪两年。2012年~2018年:基期:2012
年;现期:2018年;年份差为8-2=6。
2.五年规划(全国统一):
(1)五年计划,全称为中华人民共和国国民经济和社会发展五年计划纲要,
是中国国民经济长期计划的重要部分。中国从 1953年开始制订第一个“五年计
划”,“十一五”起,改称为“五年规划”。
①“十一五”2006~2010年。
②“十二五”2011~2015年。
③“十三五”2016~2020年。
④“十四五”2021~2025年。
⑤都是连续的五年,且都是6~10、1~5。有的同学认为年份多记不住,但
是只需要记一个可以都记住,记“十三五”,现在是2024年,正处于“十四五”
期间,也就是“十四五”的数据还没有,做题肯定是做已有数据,也就是考试一
般考“十三五”的情况,且都是连续的五年,记住“十三五”就可以都记住了。
(2)“十三五”期间(2016~2020 年):年份差为 5(基期往前推一年),
基期:2015年;现期:2020年。细化一下时间,“十三五”说的是2016年1月
271日到2020年12月31日的事情,这才是完整的“十三五”(五年)。要想算“十
三五”的情况,2016年1月1日的数据是之前留存的,也就是2016年1月1日
的数据来自于 2015 年 12 月 31 日,故十三五期间的年均增长情况=2020 年年末
-2015年年末(即2020年-2015年),则列式为(2020年的值-2015年的值)/5。
记忆“三五一十五”→十三五的基期是2015年。
3.江苏省考(刷题遇到、了解即可):只要考查年均增长问题,出题人默认
基期都需要前推,不管是不是“十几五”。因为江苏的出题人达成一致,认为2012
年~2018年:求年均增长的时候,第一年也需要计算,故基期:2011年;现期:
2018年;年份差为7(基期往前推一年)。
4.只有江苏特殊,其余所有省份都一致。
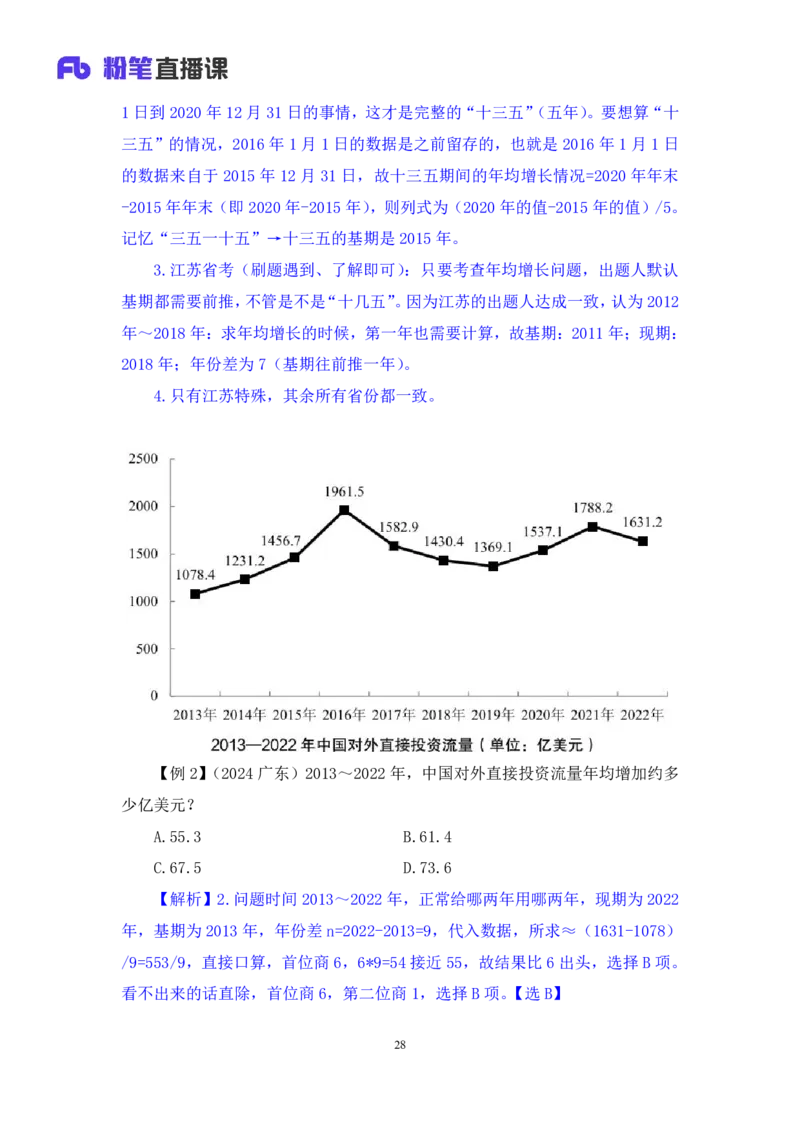
【例2】(2024广东)2013~2022年,中国对外直接投资流量年均增加约多
少亿美元?
A.55.3 B.61.4
C.67.5 D.73.6
【解析】2.问题时间2013~2022年,正常给哪两年用哪两年,现期为2022
年,基期为2013年,年份差n=2022-2013=9,代入数据,所求≈(1631-1078)
/9=553/9,直接口算,首位商6,6*9=54接近55,故结果比6出头,选择B项。
看不出来的话直除,首位商6,第二位商1,选择B项。【选B】
28【例3】(2022江苏)“十三五”时期,我国集成电路出口额的年均增量是:
A.79亿美元 B.95亿美元
C.111亿美元 D.139亿美元
【解析】3.问题时间为“十三五”时期,基期需要往前推一年,年份差为5;
“十三五”时期对应2016~2020 年,现期为2020 年、基期为 2015年;主体为
“出口额”,所求=(2020 年-2015 年)/5=(1166-691)/5=475/5=95,对应 B
项。【选B】
【注意】年均增长量:涉及五年规划,基期往前推一年,年份差为5;江苏
的题目,基期往前推一年。
已知现期、增长率,求增长量
例:2024年老邓零花钱是100元,同比增长33.3%。
29求:2024年老邓零花钱同比增长了多少元?
增长量=基期*r=现期/(1+r)*r
①增长率百化分,|r|=1/n(n是百化分的分母)
②增长量=现期/(n+1),(r>0);减少量=现期/(n-1),(r<0)
推导过程:增长量=现期/(1+r)*r=现期÷(1+1/n)*(1/n)=现期/(n+1)
【注意】已知现期、增长率,求增长量:
1.例:2024 年老邓零花钱是 100 元,同比增长 33.3%。求:2024 年老邓零
花钱同比增长了多少元?
答:给出现期值、r,求增长量;按照预习的方法,所求=现期- 基期=100-100/
(1+33.3%),或者所求=基期*r=100/(1+33.3%)*33.3%,比较麻烦。|r|=1/n
→33.3%≈1/3→n≈3,增长量=现期/(n+1)≈100/(3+1)=100/4=25。
2.公式推导(不重要):增长量=基期*r=现期/(1+r)*r,|r|=1/n→增长量
=现期÷(1+1/n)*(1/n)=现期÷[(1+1/n)*n]=现期/(n+1)。
3.方法:
(1)增长率百化分,|r|=1/n(n是百化分的分母)。
(2)r>0,增长量=现期/(n+1);r<0,减少量=现期/(n-1)。
4.拓展:2024 年老邓零花钱是 100 元,同比下降 33.3%。求:2024 年老邓
零花钱同比增长了多少元?
答:r为负,求减少量。|r|=1/n→33.3%≈1/3→n≈3,减少量=现期/(n-1)
≈100/(3-1)=50。
5.答疑:40%=40/100=1/2.5,则n=2.5。
【常见百化分记忆】
1/2=50%、1/4=25%、1/8=12.5%、1/16≈6.3%
1/3≈33.3%、1/6≈16.7%、1/12≈8.3%
1/5=20%、1/10=10%、1/20=5%
1/7≈14.3%、1/14≈7.1%
1/9≈11.1%、1/11≈9.1%
1/13≈7.7%、1/15≈6.7%
301/17≈5.9%、1/18≈5.6%、1/19≈5.3%
【注意】常见百化分记忆:如果了然于心,对于增长量计算、百分数乘除相
关的题目,则可以大大地减少计算量。
1.“一半”的关系:
(1)1/2=50%、1/4=25%、1/8=12.5%、1/16≈6.3%。
(2)1/3≈33.3%、1/6≈16.7%、1/12≈8.3%。
(3)1/5=20%、1/10=10%、1/20=5%。
2.一组数:
(1)7和14是一组数:1/7≈14.3%、1/14≈7.1%。
(2)9和11是一组数:1/9≈11.1%、1/11≈9.1%。
3.单独记忆(比较特殊):1/13≈7.7%、1/15≈6.7%。
4.5.0、3、6、9:1/17≈5.9%、1/18≈5.6%、1/19≈5.3%(重点)、1/20=5.0%。
增长率百化分之抢救法
如果遇到百分数实在想不起来
那么请记住:n=100/百分号前的数字(保留小数点后一位)
【注意】增长率百化分之抢救法:
1.如果遇到百分数实在想不起来,那么请记住:n=100/百分号前的数字(保
留小数点后一位),考场上尽量不做这一步除法。例:100/50=2→50%=1/2,
100/33.3≈3→33.3%≈1/3。
2.练习:比如37%,100/37≈2.7→37%≈1/2.7。
国家能源局发布2022年1~7月,全国全社会用电量累计49303亿千瓦时,
同比增长3.4%。分产业看,第一产业用电量634亿千瓦时,同比增长11.1%;第
二产业用电量32552亿千瓦时,同比增长1.1%;第三产业用电量8531亿千瓦时,
同比增长4.6%;城乡居民生活用电量7586亿千瓦时,同比增长12.5%。7月份,
全社会用电量8324亿千瓦时,同比增长6.3%。分产业看,第一产业用电量121
亿千瓦时,同比增长 14.3%;第二产业用电量 5132亿千瓦时,同比下降 0.1%;
第三产业用电量1591亿千瓦时,同比增长11.5%;城乡居民生活用电量1480亿
31千瓦时,同比增长26.8%。
【例4】(2023联考)2022年1~7月份,全国城乡居民生活用电量比2021
年1~7月份约多:
A.672亿千瓦时 B.843亿千瓦时
C.925亿千瓦时 D.1020亿千瓦时
【解析】4.多+具体单位,求增长量。主体为“全国城乡居民生活用电量”,
对应材料找数据,已知现期量和r,考虑百化分。|r|=1/n:r=12.5%=1/8→n=8;
增长量=现期量/(n+1)=7586/(8+1)=7586/9,首位商8,对应B项。【选B】
2016 年国产工业机器人销量继续增长,全年累计销售 29144 台,较上年增
长16.8%,增速较上年提升。
【拓展】(2020山东)2016年国产工业机器人累计销售量较上年约增加了多
少万台?
A.0.20 B.0.31
C.0.42 D.0.53
【解析】拓展.增加+单位,求增长量。|r|=1/n:r=16.8%≈1/6→n≈6;增
长量=现期量/(n+1)≈29144/(6+1)=29144/7,首位商4,对应C项。【选C】
2023 年前 5 个月,汽车出口带动天津口岸整体出口同比增加。汽车出口占
同期天津口岸出口商品总值的 2.2%,较上年同期提升 0.3个百分点。1~5月民
营企业出口活力明显,民营企业出口约 10.6 万辆,同比增长 64.3%,占同期天
津口岸汽车出口总量的 61.6%,占比较上年同期提升 13 个百分点。新能源汽车
出口成为新的增长点,出口约11万辆,同比增长50.2%。
【例 5】(2024 联考)2023 年 1~5 月,民营企业出口汽车同比约增加了多
少万辆?
A.3 B.4
C.5 D.6
【解析】5.增加+多少万辆,求增长量。主体是“民营企业出口汽车”,对
应材料找数据,给出现期量和 r,考虑百化分。|r|=1/n:r=64.3%≈32.2%*2≈
3233.3%*2≈1/3*2=2/3=1/1.5→n≈1.5;增长量=现期量/(n+1)≈10.6/(1.5+1)
=10.6/2.5,首位商4,对应B项。【选B】
【注意】100/64.3≈1.55,“64.3%”也可以看成1/1.6,不影响选择答案。
增长率百化分之倍数法
利用与背过的百分数的倍数关系,实现百化分
练习:
1.25%=
65%≈
【注意】增长率百化分之倍数法(适用于r很小或很大的情况):
1.利用与背过的百分数的倍数关系,实现百化分。
2.练习:
(1)1.25%=12.5%/10=1/8÷10=1/80。
(2)65%≈33%*2≈1/3*2=2/3=1/1.5(“1/n”的形式)。
增长率百化分之取中法
如果遇到百分数左右难取舍,取中即可
练习:
15.4%≈
18.5%≈
【注意】增长率百化分之取中法:
1.如果遇到百分数左右难取舍(主要集中在1X%),取中即可。
2.练习:
(1)15.4%:介于14.3%(1/7)和16.7%(1/6)之间,取中→15.4%≈1/6.5。
(2)18.5%:介于16.7%(1/6)和20%(1/5)之间,取中→18.5%≈1/5.5。
2023年4月份,我国社会消费品零售总额34910亿元,同比增长18.4%。其
中,除汽车以外的消费品零售额31290亿元,增长16.5%。
33【例6】(2023事业单位)2023年4月,我国社会消费品零售总额同比增加:
A.4678亿元 B.5425亿元
C.6414亿元 D.7212亿元
【解析】6.增加+单位,求增长量。主体为“社会消费品零售总额”,对应材
料找数据,给出现期量和 r,考虑百化分。|r|=1/n:18.4%介于 20%(1/5)和
16.7%(1/6)之间,取中为 1/5.5→n≈5.5;增长量=现期量/(n+1)≈34910/
(5.5+1)=34910/6.5,选项的首位各不相同,直接判断大概商几,首位商 5,
对应B项。【选B】
2022 年,我国废钢铁、废有色金属等十个品种再生资源回收总重量约为
37067.7万吨,同比下降2.62%;回收总金额约为13140.6亿元,同比下降4.05%。
2022 年废有色金属中废铅回收重量同比增长 5.56%。2022 年我国报废机动车回
收数量399.1万辆,同比增长32.9%,回收数量占我国机动车保有量的9.57‰。
【例 7】(2024 联考)相比 2021 年,2022 年我国十个品种再生资源回收总
金额同比下降了约:
A.511亿元 B.532亿元
C.555亿元 D.578亿元
【解析】7.下降+单位,求减少量,主体是“回收总金额”。|r|=1/n:
|r|=|-4.05%|,25%=1/4→4.05%≈1/25,则n≈25;减少量=现期/(n-1)≈13140/
(25-1)=13140/24,首位商 5、第二位商不到 5(很接近 5)→第二位商 4、第
三位商7,结果为547开头,最接近C项。【选C】
【注意】
1.如果利用“13140/(25+1)”计算,则会错选A项;如果利用“13140/25”
计算,则会错选B项。
2.求基期量,|r|<5%,可以利用化除为乘,求增长量不能利用该方法。
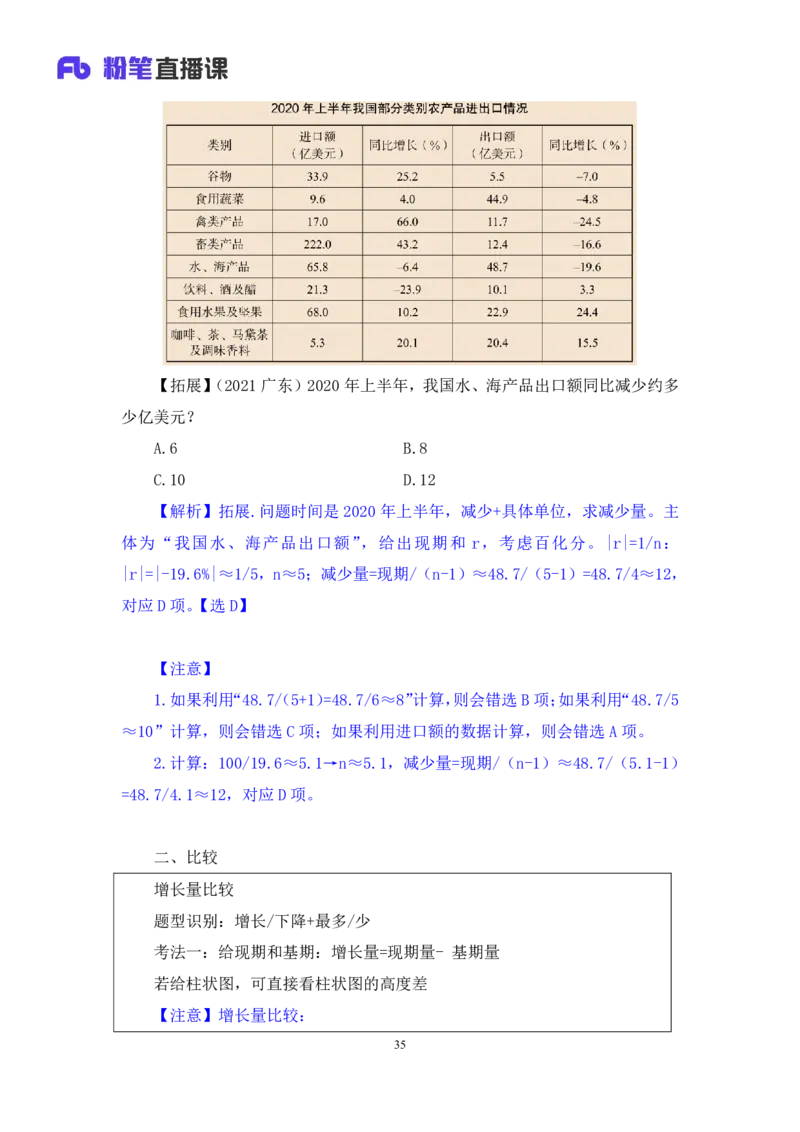
34【拓展】(2021广东)2020年上半年,我国水、海产品出口额同比减少约多
少亿美元?
A.6 B.8
C.10 D.12
【解析】拓展.问题时间是2020年上半年,减少+具体单位,求减少量。主
体为“我国水、海产品出口额”,给出现期和 r,考虑百化分。|r|=1/n:
|r|=|-19.6%|≈1/5,n≈5;减少量=现期/(n-1)≈48.7/(5-1)=48.7/4≈12,
对应D项。【选D】
【注意】
1.如果利用“48.7/(5+1)=48.7/6≈8”计算,则会错选B项;如果利用“48.7/5
≈10”计算,则会错选C项;如果利用进口额的数据计算,则会错选A项。
2.计算:100/19.6≈5.1→n≈5.1,减少量=现期/(n-1)≈48.7/(5.1-1)
=48.7/4.1≈12,对应D项。
二、比较
增长量比较
题型识别:增长/下降+最多/少
考法一:给现期和基期:增长量=现期量- 基期量
若给柱状图,可直接看柱状图的高度差
【注意】增长量比较:
351.题型识别:增长/下降+最多/少。
2.考法一(最简单):给现期和基期。
(1)增长量=现期量- 基期量。
(2)若给柱状图,可直接看柱状图的高度差,高度差即增长量,折线图
两个点的高度差也代表增长量。
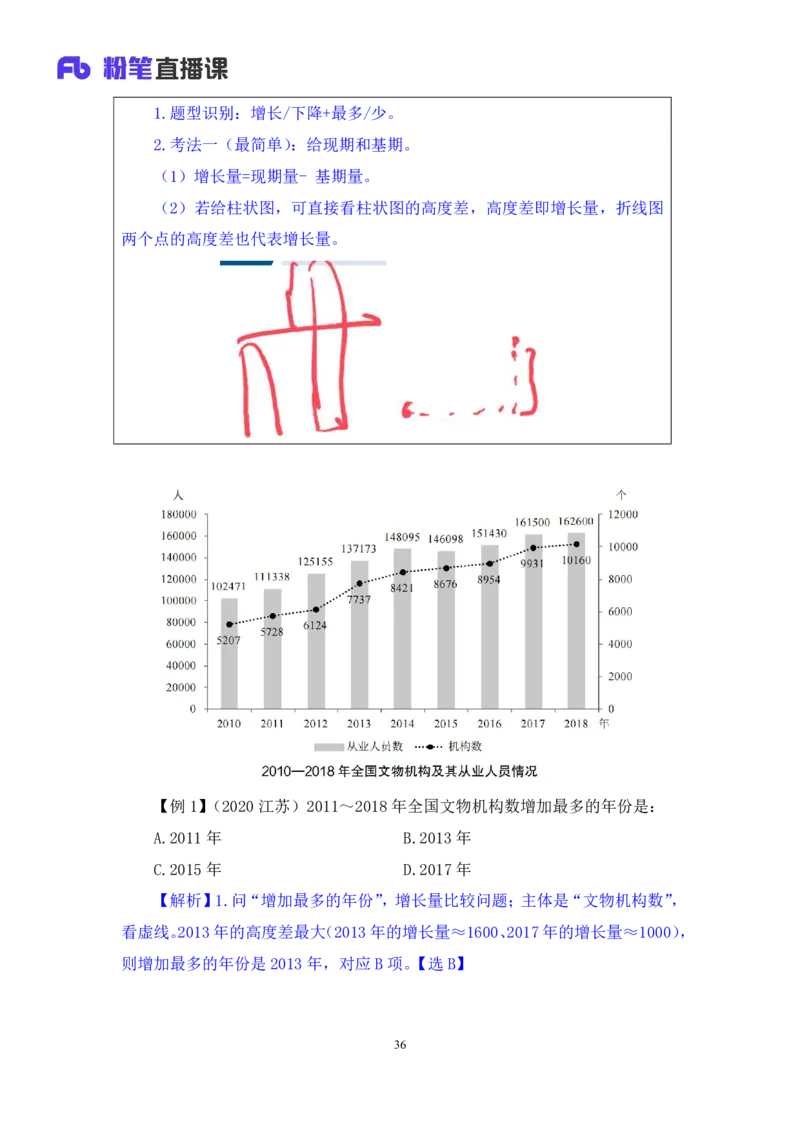
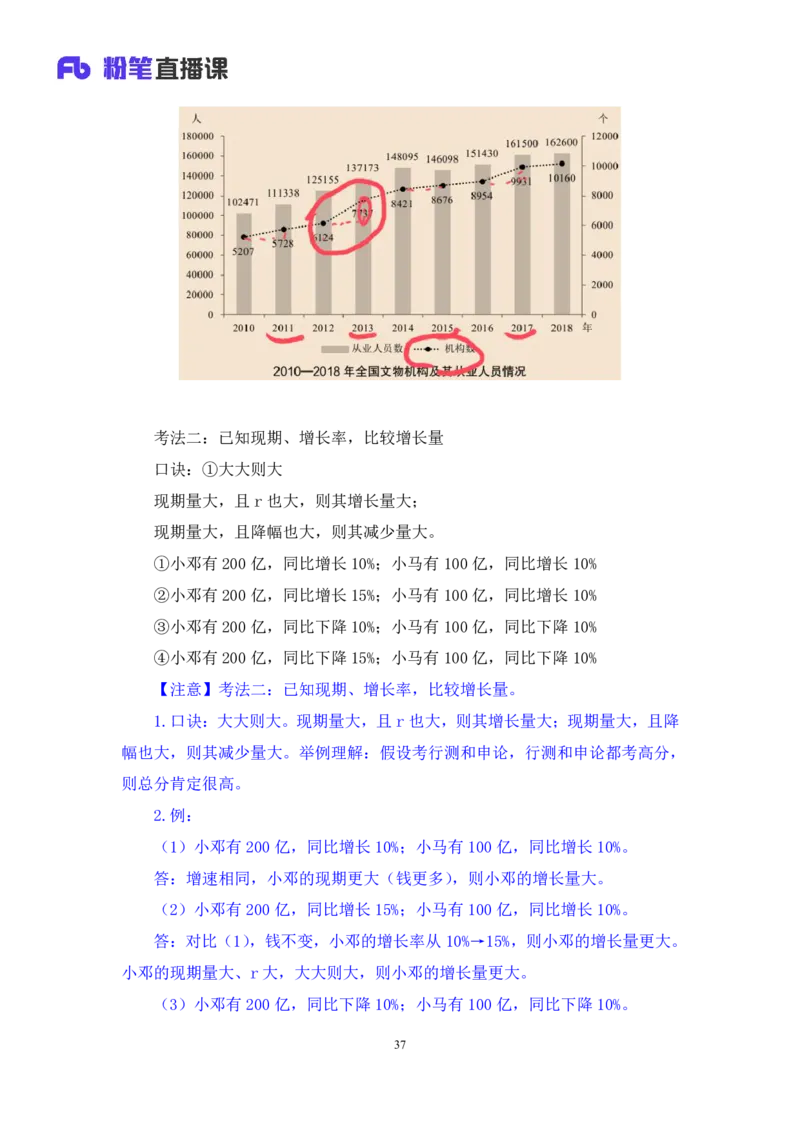
【例1】(2020江苏)2011~2018年全国文物机构数增加最多的年份是:
A.2011年 B.2013年
C.2015年 D.2017年
【解析】1.问“增加最多的年份”,增长量比较问题;主体是“文物机构数”,
看虚线。2013年的高度差最大(2013年的增长量≈1600、2017年的增长量≈1000),
则增加最多的年份是2013年,对应B项。【选B】
36考法二:已知现期、增长率,比较增长量
口诀:①大大则大
现期量大,且r也大,则其增长量大;
现期量大,且降幅也大,则其减少量大。
①小邓有200亿,同比增长10%;小马有100亿,同比增长10%
②小邓有200亿,同比增长15%;小马有100亿,同比增长10%
③小邓有200亿,同比下降10%;小马有100亿,同比下降10%
④小邓有200亿,同比下降15%;小马有100亿,同比下降10%
【注意】考法二:已知现期、增长率,比较增长量。
1.口诀:大大则大。现期量大,且r也大,则其增长量大;现期量大,且降
幅也大,则其减少量大。举例理解:假设考行测和申论,行测和申论都考高分,
则总分肯定很高。
2.例:
(1)小邓有200亿,同比增长10%;小马有100亿,同比增长10%。
答:增速相同,小邓的现期更大(钱更多),则小邓的增长量大。
(2)小邓有200亿,同比增长15%;小马有100亿,同比增长10%。
答:对比(1),钱不变,小邓的增长率从 10%→15%,则小邓的增长量更大。
小邓的现期量大、r大,大大则大,则小邓的增长量更大。
(3)小邓有200亿,同比下降10%;小马有100亿,同比下降10%。
37答:相同的降幅,钱越多→降得越多,则小邓的减少量更大。
(4)小邓有200亿,同比下降15%;小马有100亿,同比下降10%。
答:对比(3),钱不变,小邓的降幅从 10%→15%,小邓的降幅变大,说明
小邓的减少量更多。小邓的现期量大、降幅大,大大则大,则减少量更大。
2018年木家具进口金额9.24亿美元,同比增长3.6%,木框架坐具进口金额
3.32亿美元,增长13.8%。刨花板2016年进口增幅41%,2017年增幅21%,2018
年进口69.2万吨,为负增长(-2.7%)。2018年木制品出口金额仅增长2%。2018
年木家具出口数量增长5.68%,金额负增长1.6%;木地板出口26.6万吨、3.85
亿美元,分别下降24.8%和下降25.9%;胶合板出口1137.8万立方米、55.56亿
美元,数量增长 5%,金额增长 9%;纤维板出口 179 万吨、38.35 亿美元,数量
下降 14.9%,金额增长 6.2%。木制品出口企业普遍效益下降。2018 年进口针叶
原木4159.7万立方米,金额57.86亿美元,同比分别增长8.8%和12.6%。
【例2】(2021新疆兵团)2018年,下列三种产品出口金额增长值从大到小
的顺序排列正确的是:
A.木地板、胶合板、纤维板 B.胶合板、纤维板、木地板
C.木地板、纤维板、胶合板 D.胶合板、木地板、纤维板
【解析】2.问“增长值(增长量)从大到小的顺序”,增长量比较大小。根
据选项的主体定位材料找数据,比较“出口金额”的增长量。观察发现,只有木
地板是下降的→增长量为负,正的>负的,木地板最小,选择B项。【选B】
【注意】比较胶合板、纤维板:胶合板的现期量大(55.56>38.35)、r 大
(9%>6.2%),大大则大,则胶合板的增长量大。
已知现期、增长率,比较增长量
口诀:
(1)大大则大:现期量大,同时 r也大,则其增长量大;现期量大,同时
降幅也大,则其减少量大。
①小邓有200亿,同比增长10%;小马有100亿,同比增长10%
38②小邓有200亿,同比增长15%;小马有100亿,同比增长10%
③小邓有200亿,同比下降10%;小马有100亿,同比下降10%
④小邓有200亿,同比下降15%;小马有100亿,同比下降10%
(2)一大一小,百化分计算增量比大小
⑤小邓有250亿,同比增长11%;小马有120亿,同比增长20%
【注意】已知现期、增长率,比较增长量——口诀:
1.大大则大:现期量大,同时r也大,则其增长量大;现期量大,同时降幅
也大,则其减少量大。
2.一大一小,百化分计算增量比大小。
3.例:小邓有250亿,同比增长11%;小马有120亿,同比增长20%。
答:小邓的现期量大、r小,属于一大一小。
方法一:最通用的方法→百化分(永远不会出错)。小邓:11%≈1/9,增长
量≈250/(9+1)=25;小马:20%=1/5,增长量=120/(5+1)=20;综上,小邓的
增长量>小马的增长量。
方法二:看倍数,分别看现期量、增长率之间的倍数,倍数大的说了算。举
例理解:A 同学行测考90+、申论考 60+,B 同学行测考 60+、申论考 70+,属于一
大一小;A同学虽然申论低一点,但行测的优势更明显→起决定性作用,则A同
学的成绩更高。现期量:120→250 为 2+倍;增长率:11%→20%为 1+倍;现期量
的倍数大→现期量说了算,现期量大的增长量大,小邓的增长量>小马的增长量。
4.拓展:小邓有 250 亿,同比增长 11%;小马有 120亿,同比增长 40%。现
期量之间为2+倍、增长率之间为4-倍,增长率的倍数大→看增长率,增长率大的
增长量大,小马的增长量>小邓的增长量。
5.看倍数是估算的方法,略微有一点点风险。例:A 同学行测考 70+、申论
考60+,B同学行测考60+、申论考70+,差距很接近,则无法看出来谁的总分高;
小邓有 250亿,同比增长11%;小马有 150亿,同比增长 40%,现期量之间为 1+
倍、增长率之间为1+倍,则无法看倍数。这种极端情况下,不容易看倍数,且存
在误差,则会出错。
6.总结:给出现期量、r,比较增长量。
(1)大大则大。
39(2)一大一小:考场思维→看倍数。
①若差距明显(比如一个 2 倍、一个 4倍,或者一个 2 倍、一个 1 倍),直
接看。
②若差距不明显(比如都是 1+倍或 2+倍),则百化分是最稳妥的方法(托底
的方法)。
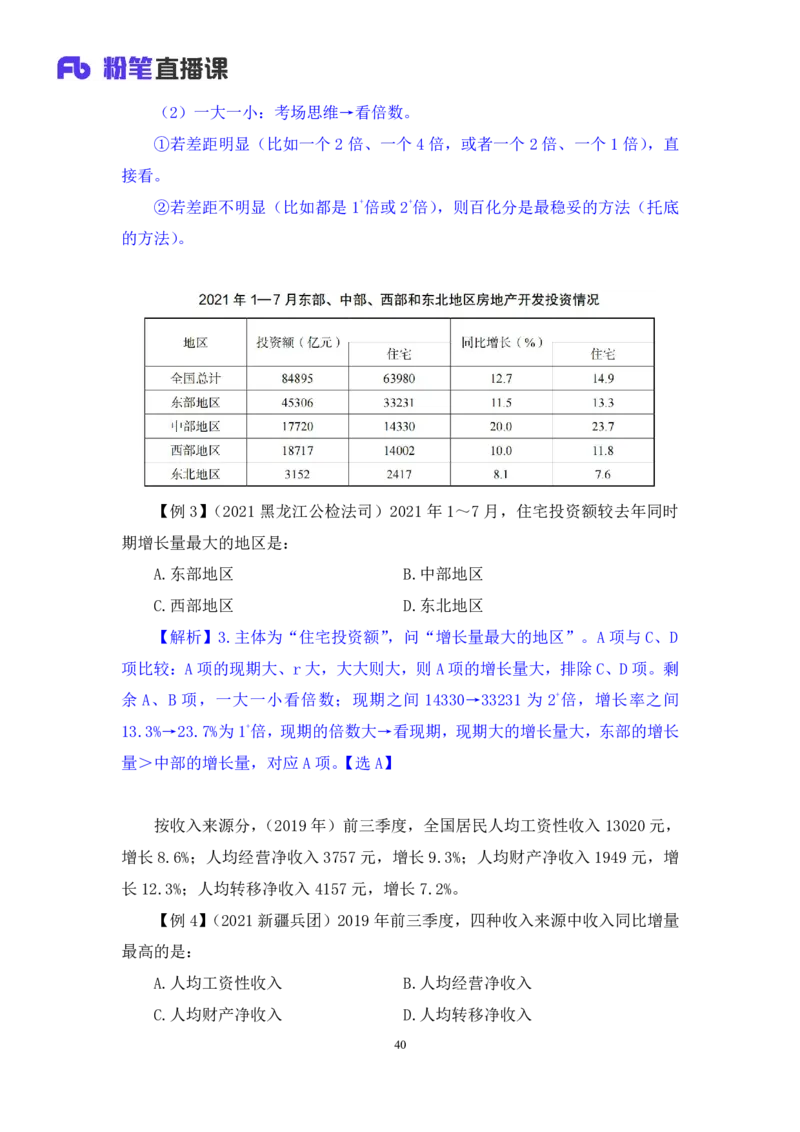
【例 3】(2021 黑龙江公检法司)2021 年 1~7 月,住宅投资额较去年同时
期增长量最大的地区是:
A.东部地区 B.中部地区
C.西部地区 D.东北地区
【解析】3.主体为“住宅投资额”,问“增长量最大的地区”。A项与C、D
项比较:A项的现期大、r大,大大则大,则A项的增长量大,排除C、D项。剩
余 A、B 项,一大一小看倍数;现期之间 14330→33231 为 2+倍,增长率之间
13.3%→23.7%为1+倍,现期的倍数大→看现期,现期大的增长量大,东部的增长
量>中部的增长量,对应A项。【选A】
按收入来源分,(2019年)前三季度,全国居民人均工资性收入13020元,
增长8.6%;人均经营净收入 3757 元,增长 9.3%;人均财产净收入 1949元,增
长12.3%;人均转移净收入4157元,增长7.2%。
【例4】(2021新疆兵团)2019年前三季度,四种收入来源中收入同比增量
最高的是:
A.人均工资性收入 B.人均经营净收入
C.人均财产净收入 D.人均转移净收入
40【解析】4.问“同比增量最高”,结合选项的主体定位材料找数据,先观察
有无大大则大。A、D项比较:A项的现期大、r大,排除D项。A、B项比较:现
期之间约为4倍,增长率之间为1+倍,现期的倍数大,现期大的增长量大,A项
的增长量>B项的增长量,排除 B项;A、C项比较:现期之间为6+倍,增长率之
间为1+倍,现期的倍数大,现期大的增长量大,A项的增长量>C项的增长量。
综上,A项的增长量最大,选择A项。【选A】
课后作业两件事
①复习:知识点填空,讲义题目独立过一遍,整理课堂笔记
41②预习:P202~213(比重和平均数),重难点
把题做一遍,有时间的同学可以自己尝试推导思维导图的公式
不求快,重要的是过程
明天晚上6:55提前5分钟开课,一起回顾本节课知识点
【注意】课后作业两件事:
1.复习:知识点填空,利用老师讲解的方法将讲义题目独立过一遍,整理课
堂笔记。
2.预习:P202~213(比重和平均数),重难点;把题做一遍,有时间的同学
可以自己尝试推导思维导图的公式;不求快,重要的是过程。
3.明天晚上6:55提前5分钟开课,一起回顾本节课知识点。
【答案汇总】
一般增长率计算1-5:ADDBB
一般增长率比较1-4:ACBC
增长量计算1-5:BBBBB;6-7:BC
增长量比较1-4:BBAA
42遇见不一样的自己
Be your better self
43