文档内容
方法精讲-资料 2
(讲义+笔记)
主讲教师:焦点
授课时间:2024.04.30
粉笔公考·官方微信方法精讲-资料 2(笔记)
今日内容(P177~190)
第三节 一般增长率
第四节 增长量
【注意】今日内容:非常高频。
1.一般增长率。
2.增长量。
增长率的相关统计术语
一、增长率与倍数
二、成数与番数
三、增幅、降幅、变化幅度
四、百分数与百分点
【注意】增长率的相关统计术语:昨天学习了基期和现期,是相对而言的,
基期时间靠前,现期时间靠后。
概念辨析 1:增长率与倍数增长率的定义:
增长率指的是现期量与基期量的差值(即增长量)与基期量之间的比率
例:现期为 120,基期为 100,增长率为?
注 1:增长率又称增速、增幅或者增长幅度、增值率等
注 2:增长率有正有负,增长率为负时表示下降
例:A国第三季度GDP同比下降 0.6%
【注意】概念辨析1:增长率与倍数增长率的定义。
1.增长率比如今年工资比去年工资增长 10%,10%就是增长率。增长率指的
是现期量与基期量的差值(即增长量)与基期量之间的比率,用 r来表示,r=增
长量/基期量,单位是%。
例:现期为 120,基期为 100,增长率为?
答:增长量=120-100=20,增长率 r=20/100=20%。
12.注 1:增长率又称增速、增幅或者增长幅度、增值率等。都是增长率的表
述,常用的是增长率和增速。
3.注 2:增长率有正有负,比如老师的体重可能比去年胖,也可能比去年瘦,
胖了即增长率为正数,瘦了即增长率为负数,计算中,增长率带符号计算,增长
率为负时表示下降。例:A国第三季度 GDP同比下降0.6%,即 r为-0.6%。
概念辨析 1:增长率与倍数
倍数的定义:倍数指两数的直接比值(第四节还会专门讲)
120 是100的___倍
120 比100增长___%
两者关系:
增长率=是几倍-1
是几倍=增长率+1
例:A比B增长了50%,则 A 是B的_____倍
例:A是B的1.7倍,则 A比 B增长_____%
【注意】概念辨析1:增长率与倍数。
1.倍数的定义:倍数指两数的直接比值(第四节还会专门讲)。
(1)120是100的几倍:120/100=1.2。
(2)120比100增长多少%:为(120-100)/100=120/100-1=1.2-1=0.2=20%。
2.两者关系:
(1)增长率=是几倍-1。
(2)是几倍=增长率+1。
3.例:A比B增长了50%,则 A是B的几倍。
答:增长率为 50%,倍数为 1+50%=1.5倍。
4.例:A是B的1.7倍,则 A比B增长多少%。
答:增长率为 1.7-1=0.7=70%。
概念辨析 2:成数与番数
成数:几成相当于十分之几
23成=_____
7成=_____
翻番:翻一番为原来的 2 倍;翻两番为原来的 4倍
遇番数化倍数(是几倍),依此类推,翻 n番为原来的2n倍
200 变为800,翻了_____番
300 变为2400,翻了_____番
【注意】概念辨析2:成数与番数。
1.成数:比如男生占全班人数的五成,五成即 50%,几成相当于十分之几。
(1)3成=3/10=30%。
(2)7成=7/10=70%。
2.翻番:比如今年一个月赚 10 元,好好努力,明年翻一番,常识理解,就
是“double”,明年一个月要赚 20 元,再翻一番为 40,再翻一番为 80,再翻一
番为160,翻一番为原来的2倍;翻两番为原来的 4倍。遇番数化倍数(是几倍),
依此类推,翻 n番为原来的2n倍。
(1)200变为800,800/200=4,2=2²,翻了2番。
(2)300变为2400,2400/300=8,8=2³,翻了3番。
小重点——概念辨析3:增幅、降幅、变化幅度(易错概念)
增幅(增长率)一般就是指增长率,有正有负。计算比较带符号。
例 1:以下增长率,哪一个增幅(增长率)最大?
A.30% B.20%
C.10% D.-40%
降幅指下降的幅度,计算比较看增长率的绝对值(前提:增长率必须为负)。
例 2:以下增长率,哪一个降幅最大?
A.-30% B.-20%
C.-10% D.40%
变化幅度指增长或下降的绝对比率,计算比较看增长率的绝对值。
例 3:以下增长率,哪一个变化幅度最大?
A.30% B.-20%
3C.10% D.-40%
【注意】小重点——概念辨析 3:增幅、降幅、变化幅度(易错概念),很重
要。
1.增幅(增长率):一般就是指增长率,有正有负,计算比较带符号,正数
>负数。
例 1:以下增长率,哪一个增幅(增长率)最大?
A.30% B.20%
C.10% D.-40%
答:正数大于负数,正数中最大的是 A项。
2.降幅指下降的幅度,计算比较看增长率的绝对值(前提:增长率必须为负,
不能说当增长率为 10%的时候降幅是-10%,然后负负得正,没有这样表述的)。
例 2:以下增长率,哪一个降幅最大?
A.-30% B.-20%
C.-10% D.40%
答:D 项是没有资格谈降幅的,降幅比较增长率的绝对值,A、B、C 项中,
绝对值最大的是 A项。
3.变化幅度指增长或下降的绝对比率,计算比较看增长率的绝对值。重点突
出变化,比如老师胖了10%,你瘦了 10%,你和老师都变了,都可以谈变化幅度,
正负都可以参与比较,变化的时候看绝对值。
例 3:以下增长率,哪一个变化幅度最大?
A.30% B.-20%
C.10% D.-40%
答:比较绝对值,最大的是 D项。
概念辨析 4:百分数与百分点(易错概念)
百分数表示两个量的比例关系,用除法计算
例:男生 100人,全班500 人,则男生占全班的100/500=20%
百分点表示百分数的变化,用加减法计算
例:男生占比 20%,女生占比 80%
4女生占比,比男生多 80%-20%=60%,即60个百分点
【注意】概念辨析4:百分数与百分点(易错概念),百分数和百分点在数值
上是相等的,比如 2%和2个百分点在计算的时候,代表一样的数值。
1.百分数表示两个量的比例关系,用除法计算,例男生100 人,全班500人,
则男生占全班的 100/500=20%,不能说男生占全班 20个百分点。
2.百分点表示百分数的变化,用加减法计算,例如男生占比 20%,女生占比
80%,女生占比比男生多 80%-20%=60%,即60个百分点,
第三节 一般增长率
一、计算类
二、比较类
【注意】一般增长率:
1.计算类。
2.比较类。
一、一般增长率的计算
识别:增长/下降+%、几成、几倍;增长速度、增长幅度
题型:1.给一个百分数和百分点:高减低加
【注意】一般增长率的计算:先识别,再列式,最后速算,选项为王。
1.识别:
(1)增长/下降+%、几成(几成就是百分之几十,也相当于%)、几倍,比如
我今年工资为 120,去年工资为 100,问我今年的工资比去年增长了几倍、我今
年的工资是去年的几倍,两个问题的答案是不同的,增长率=(120-100)/100=0.2,
今年是去年的 120/100=1.2倍。
(2)增长速度、增长幅度:也都是增长率的意思。
2.题型 1:给一个百分数和百分点——高减低加。
高频小知识点
➢2017 年收入10万元,同比增长 10%,增速比去年提高 5个百分点。则2016
5年的增长率为
➢2017 年收入10万元,同比增长 10%,增速比去年降低 5个百分点。则2016
年的增长率为
“高减低加”:比去年高就用减法,比去年低就用加法
【注意】高频小知识点:
1.2017 年收入10万元,同比增长 10%,增速比去年提高 5个百分点。则2016
年的增长率为?根据题意,2017 年增速10%-2016年增速=5%→2016年增速=10%-
5%,每一题都这样做很慢,说明“比去年提高”,高减,所求=10%-5%=5%。
2.2017 年收入10万元,同比增长 10%,增速比去年降低 5个百分点。则2016
年的增长率为?比去年低,去年高,2016 年增速-10%=5%→2016 年增速
=10%+5%=15%,这样做慢,“低加”,所求=10%+5%。
3.“高减低加”:比去年高就用减法,比去年低就用加法。
易错点——关于“降幅”的高减低加
例:2020年A企业营业收入同比下降 10%,降幅比去年扩大 4个百分点
问:2019年的降幅为_____→增长率为_____
例:2020年B企业营业收入同比下降 6%,降幅比去年收窄 2个百分点
问:2019年的降幅为_____→增长率为_____
“高减低加”:比去年高就用减法,比去年低就用加法
*若分析的是降幅,最后求增长率记得添加负号
【注意】易错点——关于“降幅”的高减低加:
1.例:2020 年 A 企业营业收入同比下降 10%,降幅比去年扩大 4 个百分点。
问:2019年的降幅为_____→增长率为_____。
答:问的是降幅,按照高减低加,求出的是降幅,2019年降幅=10%-4%=6%,
增长率为-6%。
2.例:2020年B企业营业收入同比下降 6%,降幅比去年收窄 2个百分点。
问:2019年的降幅为_____→增长率为_____。
答:收窄即低,高减低加,2019年的降幅为6%+2%=8%,增长率为-8%。
3.“高减低加”:比去年高就用减法,比去年低就用加法。
64.若分析的是降幅,最后求增长率记得添加负号。
练习
例 1:2022 年增长 25%,增速比上年同期降低 7 个百分点,则 2021 年增长
率为_____
例 2:2022 年下降 17%,增速比上年同期提高 5 个百分点,则 2021 年增长
率为_____
例 3:2022 年我增长 10%,增速比你低 6 个百分点,则 2022 年你的增长率
为_____
例 4:2022 年下降 17%,降幅比上年同期扩大 5 个百分点,则 2021 年增长
率为_____
例 5:2022 年下降 17%,降幅比上年同期收窄 5 个百分点,则 2021 年增长
率为_____
【注意】练习:用主语高减低加。
1.例 1:主语是增速,高减低加,2021年增速为25%+7%。
2.例 2:主语是增速,用增速高减低加,2021年增速为-17%-5%=-22%。
3.例 3:主语是增速,用增速高减低加,注意不是去年和今年的关系,是我
和你的关系,我的增速比你低,求你,是比字后的主语,低加,你的增速为 10%+6%。
4.例 4:出现扩大,高减,主语是降幅,2022年降幅为 17%,2021年降幅为
17%-5%,2021年增长率为-(17%-5%)=-12%。
5.例 5:主语是降幅,先用降幅高减低加,收窄即低,低加,2021年降幅为
17%+5%=22%,增长率为-22%。
2021 年H省商品、服务类电子商务交易额为 11526.13亿元,比上年同期增
长21.8%,高于全国增速2.3 个百分点。H省跨境电商进出口交易额为 2018.3亿
元,其中,……
【例 1】(2023国考)2021 年,全国商品、服务类电子商务交易额同比增长
了:
A.17.2% B.19.5%
7C.21.8% D.24.1%
【解析】1.增长+%,求增长率,根据材料,给出百分点,高减低加,所求=21.8%-
2.3%=19.5%,或者根据尾数法,选择尾数为 5的,对应B项。【选 B】
2020 年全年,汽车产销降幅收窄至 2%以内。汽车产量为 2522.5万辆,销量
为2531.1万辆,同比分别下降2.0%和1.9%,降幅分别比2020年上半年收窄14.8
和15.0个百分点。2020年全年,新能源汽车销量为136.7万辆,同比增长10.9%。
【例 2】(2021联考)2020 年上半年汽车销量降幅估计在:
A.10 个百分点以内 B.10~12个百分点
C.12~14个百分点 D.15个百分点以上
【解析】2.问降幅,问题时间是 2020 年上半年,材料时间是 2020 年全年,
主语是销量,根据材料高减低加,问降幅,用降幅高减低加,所求=1.9%+15%>
15%,对应 D项。【选D】
2.给具体量型,套公式
公式:r=增长量/基期=增长量/(现期-增长量)=(现期- 基期)/基期
速算:截位直除
【注意】给具体量型,套公式:
1.公式:r=增长量/基期(定义式),根据定义式可以衍生出多个公式,根据
材料给出的条件来选择公式,r=增长量/(现期-增长量)=(现期- 基期)/基期。
2.速算:截位直除。
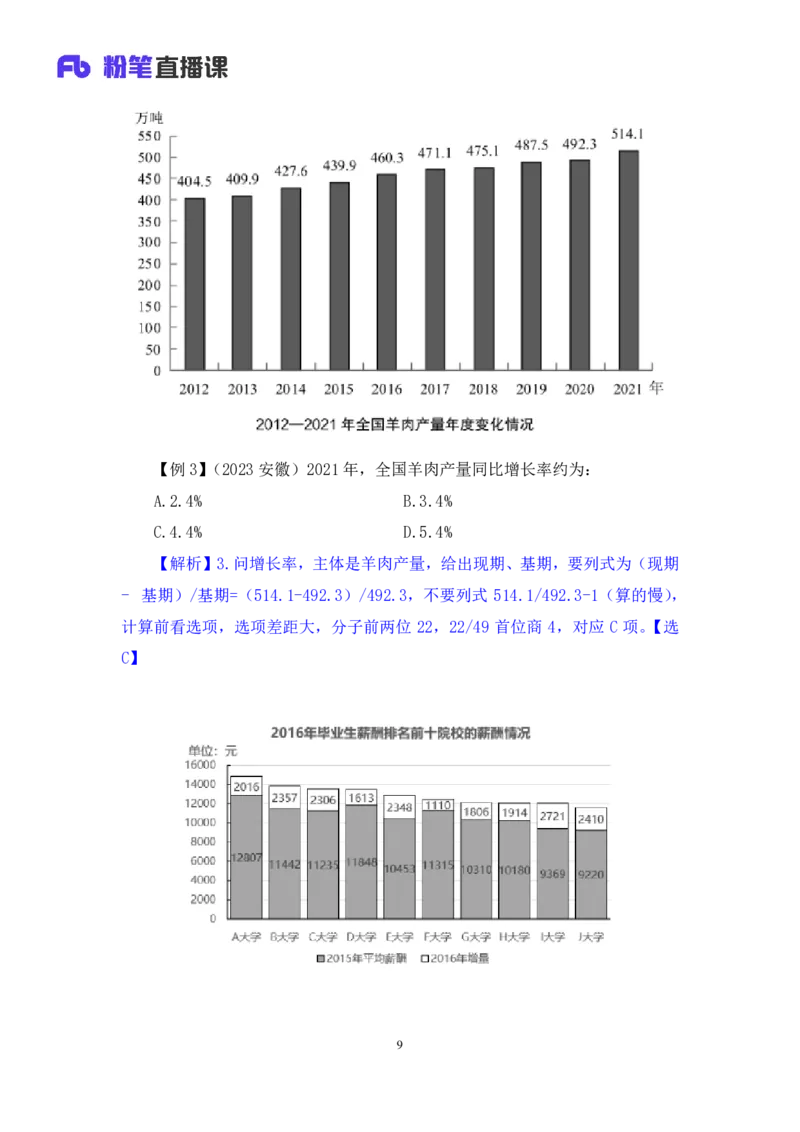
8【例 3】(2023安徽)2021 年,全国羊肉产量同比增长率约为:
A.2.4% B.3.4%
C.4.4% D.5.4%
【解析】3.问增长率,主体是羊肉产量,给出现期、基期,要列式为(现期
- 基期)/基期=(514.1-492.3)/492.3,不要列式 514.1/492.3-1(算的慢),
计算前看选项,选项差距大,分子前两位 22,22/49 首位商 4,对应 C 项。【选
C】
9【例 4】(2020四川)2016 年语言类大学平均薪酬排名第二的院校,其毕业
生平均薪酬同比增长约为:
A.18% B.20%
C.22% D.24%
【解析】4.增长+%,求增长率,但是没有给出具体的主体,是找 A求B类题
型,需要先找出 2016 年语言类大学平均薪酬排名第二的院校,定位材料,不要
直接认为 B大学是排名第二的,问的是语言类大学,只有 E大学和 G大学是语言
类,第二即找二者中小的,为 G大学,求G大学毕业生平均薪酬同比增长率,灰
色柱子相当于基期,白色柱子相当于增长量,给出增长量和基期量,r=增长量/
基期量=1806/10310,选项看似差距小,但是所求首位商不到 2,直接选择A项。
【选A】
【例5】(2021江苏)2019年末江苏省金融机构各项存款额度比上年末增长:
A.8.5% B.9.4%
10C.10.2% D.10.8%
【解析】5.增长+%,求增长率,主体是各项存款额度,表格中的绝对值是具
体量的意思,比上年末增长(亿元)是增长量,给出增长量和现期量,r=增长量
/(现期-增长量)≈13089/(152837-13089),列式可以如下图,方便计算,C、
D项选项差距小,截三位计算,应该是加减后剩下三位,不要直接每一项截三位,
原式转化为 13089/139,首位商不到 1,排除C、D项,A、B项差距大,直接计算
13089/14,首位商9,对应B 项。【选 B】
多个年份增长率>10%
(现期量- 基期量)/基期量>10%
现期量- 基期量>基期量*10%
现期量>(1+10%)*基期量
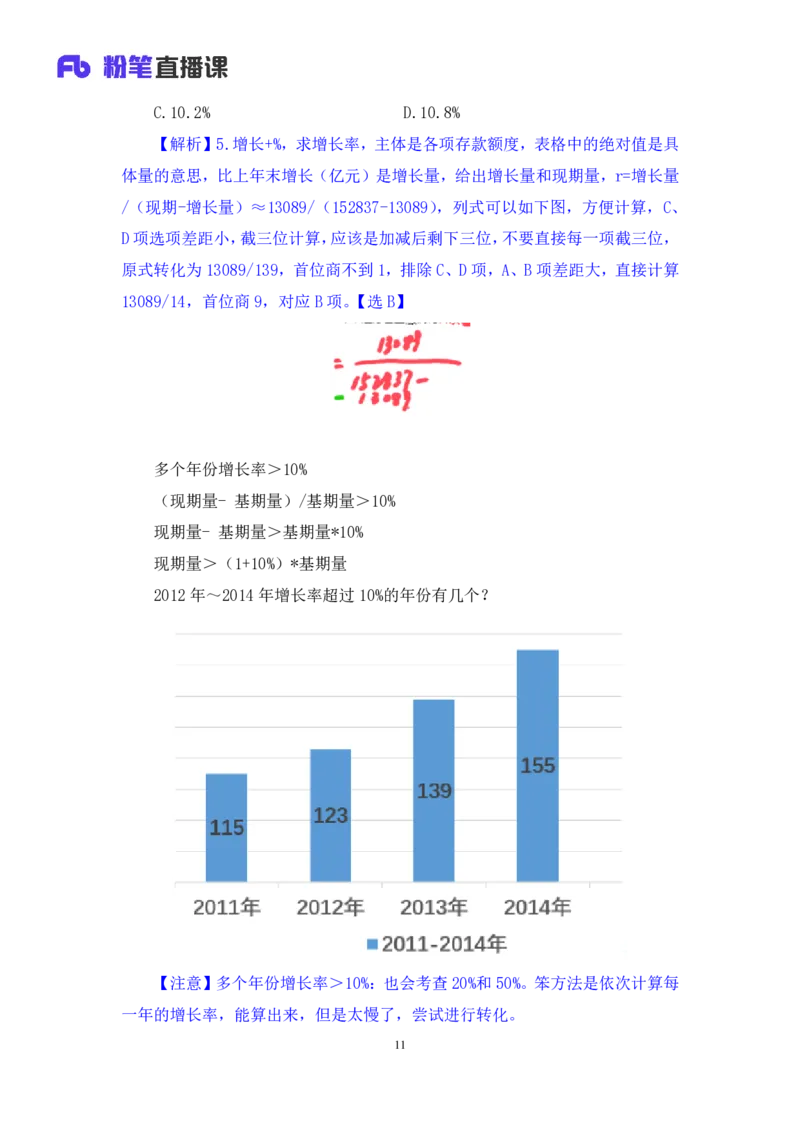
2012 年~2014年增长率超过 10%的年份有几个?
【注意】多个年份增长率>10%:也会考查20%和50%。笨方法是依次计算每
一年的增长率,能算出来,但是太慢了,尝试进行转化。
111.(现期量- 基期量)/基期量>10%→现期量- 基期量>基期量*10%→现期
量>基期量+0.1基期量,“基期量+0.1基期量”为错位相加,计算的时候不需要
抄数据,比如12345+12345*0.1,直接错位口算,估算到第三位即可,现期>基
期错位相加即增长率>10%,反之是增长率<10%。
2.如果是 20%,(现期量- 基期量)/基期量>20%→现期量- 基期量>基期
量*20%→现期量>基期量+0.2 基期量,道理是一样的,比如 12345+12345*0.2,
计 算 12345+1234.5*2=12345+2469 , 实 际 不 需 要 这 么 麻 烦 , 直 接 计 算
12345+2468=748 开头。
3.2012 年~2014年增长率超过 10%的年份有几个?
答:2012年的基期是2011 年,错位相加,115+11.5=126.5>123,增长率没
有超过 10%;2013年:123+12.3=135.3<139,满足;2014 年:139+13.9≈152<
155,满足。
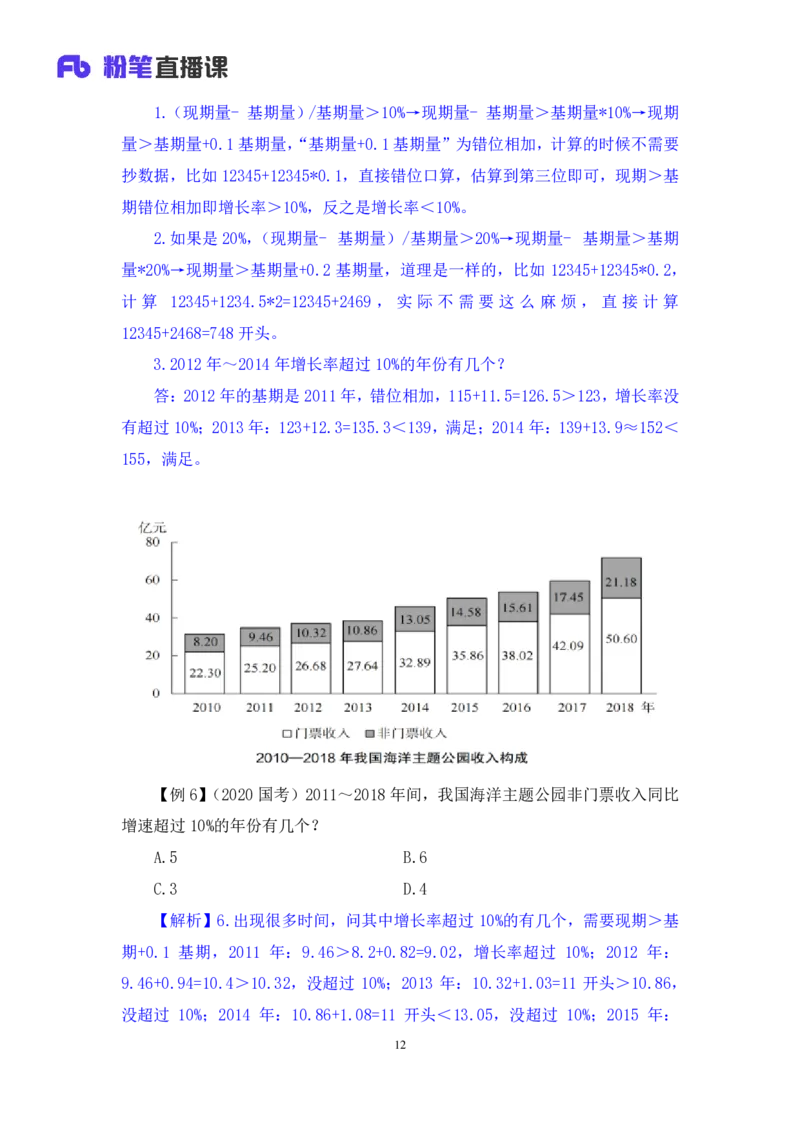
【例 6】(2020国考)2011~2018年间,我国海洋主题公园非门票收入同比
增速超过 10%的年份有几个?
A.5 B.6
C.3 D.4
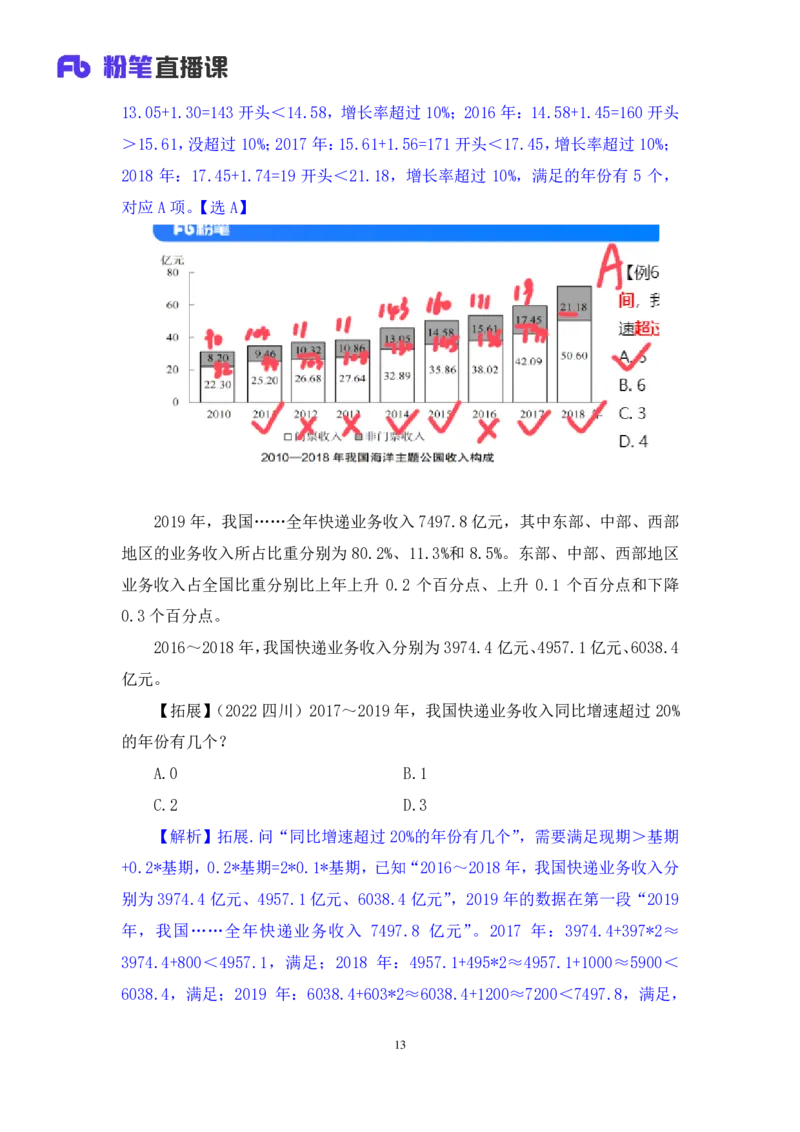
【解析】6.出现很多时间,问其中增长率超过 10%的有几个,需要现期>基
期+0.1 基期,2011 年:9.46>8.2+0.82=9.02,增长率超过 10%;2012 年:
9.46+0.94=10.4>10.32,没超过 10%;2013 年:10.32+1.03=11 开头>10.86,
没超过 10%;2014 年:10.86+1.08=11 开头<13.05,没超过 10%;2015 年:
1213.05+1.30=143 开头<14.58,增长率超过10%;2016年:14.58+1.45=160 开头
>15.61,没超过10%;2017年:15.61+1.56=171 开头<17.45,增长率超过10%;
2018 年:17.45+1.74=19 开头<21.18,增长率超过 10%,满足的年份有 5 个,
对应A项。【选 A】
2019 年,我国……全年快递业务收入 7497.8亿元,其中东部、中部、西部
地区的业务收入所占比重分别为 80.2%、11.3%和 8.5%。东部、中部、西部地区
业务收入占全国比重分别比上年上升 0.2 个百分点、上升 0.1 个百分点和下降
0.3个百分点。
2016~2018年,我国快递业务收入分别为 3974.4亿元、4957.1 亿元、6038.4
亿元。
【拓展】(2022四川)2017~2019年,我国快递业务收入同比增速超过 20%
的年份有几个?
A.0 B.1
C.2 D.3
【解析】拓展.问“同比增速超过 20%的年份有几个”,需要满足现期>基期
+0.2*基期,0.2*基期=2*0.1*基期,已知“2016~2018年,我国快递业务收入分
别为3974.4 亿元、4957.1亿元、6038.4亿元”,2019年的数据在第一段“2019
年,我国……全年快递业务收入 7497.8 亿元”。2017 年:3974.4+397*2≈
3974.4+800<4957.1,满足;2018 年:4957.1+495*2≈4957.1+1000≈5900<
6038.4,满足;2019 年:6038.4+603*2≈6038.4+1200≈7200<7497.8,满足,
133个年份满足,对应D项。【选 D】
【注意】如果考 15%,计算现期>基期+0.1*基期+0.1*基期/2。
二、一般增长率的比较
识别
增长最快/最慢;增速/增幅/增长率最高/最低
比较方法
r=增长量/基期量=(现期量- 基期量)/基期量=现期量/基期量-1
①当现期量/基期量≥2(倍数明显),比较现期量/基期量
②当现期量/基期量<2(倍数不明显),比较增长量/基期量
速算技巧:分数比较
【注意】一般增长率的比较:
1.识别:增长最快/最慢;增速/增幅/增长率最高/最低。
2.比较方法:r=增长量/基期量=(现期量- 基期量)/基期量=现期量/基期
量-1。比较“现期/基期”即可,“现期/基期”越大,则增长率越大。
(1)当现期量/基期量≥2(倍数明显),即能口算出来的时候,考虑比较现
期量/基期量。
(2)当现期量/基期量<2(倍数不明显),口算不出来大小关系,考虑比较
增长量/基期量。比如比较现期/基期,A项是1.1,B项是1.2,大小关系口算不
好算,转化为增长量/基期量,就是 10%和20%,就会很明显。
3.速算技巧:分数比较。
增长率的比较
实际操作:两步走
第一步,先看现期/基期能否得到唯一答案
第二步,不能得出,再比较(现期- 基期)/基期=增长量/基期
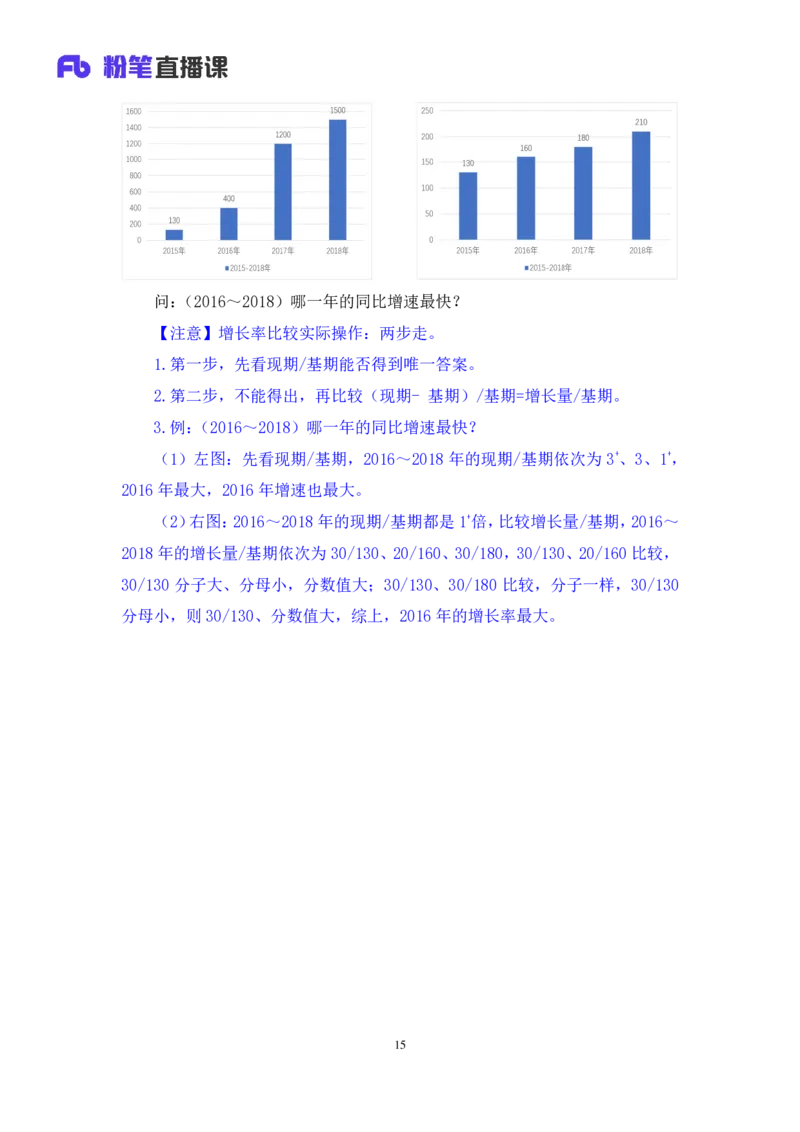
14问:(2016~2018)哪一年的同比增速最快?
【注意】增长率比较实际操作:两步走。
1.第一步,先看现期/基期能否得到唯一答案。
2.第二步,不能得出,再比较(现期- 基期)/基期=增长量/基期。
3.例:(2016~2018)哪一年的同比增速最快?
(1)左图:先看现期/基期,2016~2018 年的现期/基期依次为 3+、3、1+,
2016年最大,2016年增速也最大。
(2)右图:2016~2018年的现期/基期都是1+倍,比较增长量/基期,2016~
2018年的增长量/基期依次为 30/130、20/160、30/180,30/130、20/160比较,
30/130 分子大、分母小,分数值大;30/130、30/180 比较,分子一样,30/130
分母小,则 30/130、分数值大,综上,2016年的增长率最大。
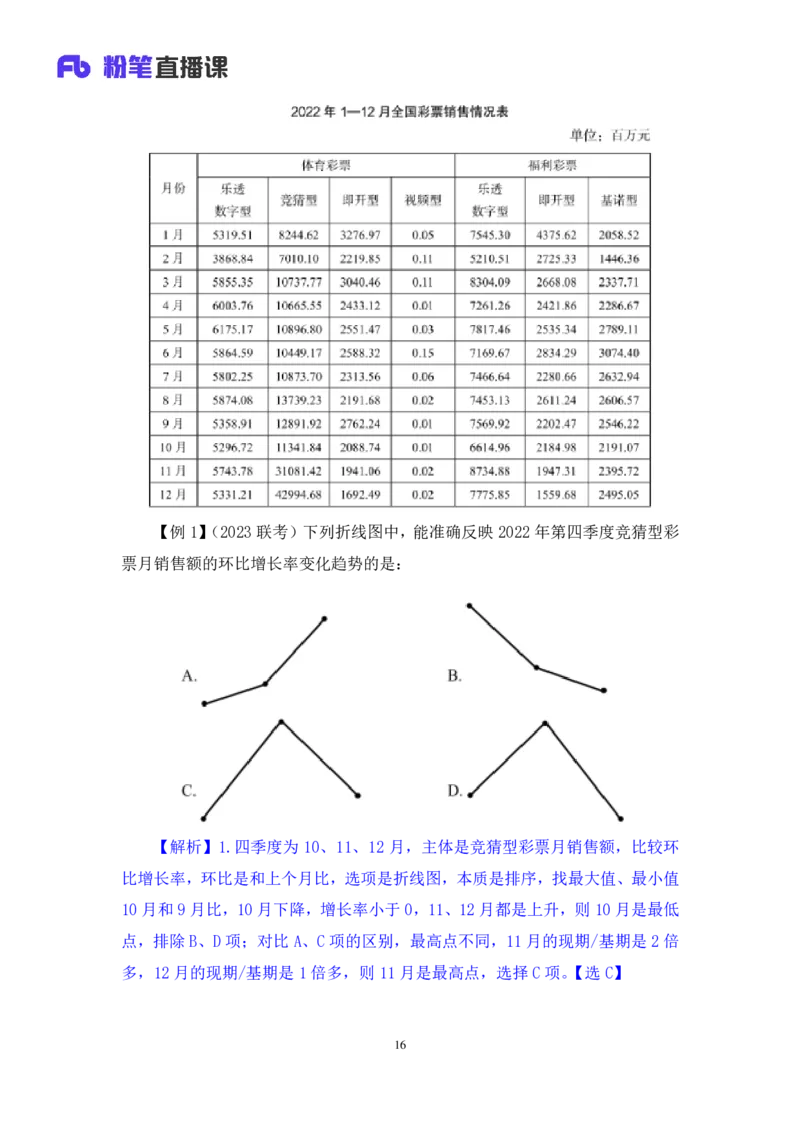
15【例 1】(2023联考)下列折线图中,能准确反映 2022年第四季度竞猜型彩
票月销售额的环比增长率变化趋势的是:
【解析】1.四季度为 10、11、12 月,主体是竞猜型彩票月销售额,比较环
比增长率,环比是和上个月比,选项是折线图,本质是排序,找最大值、最小值
10月和 9月比,10月下降,增长率小于 0,11、12月都是上升,则 10月是最低
点,排除B、D项;对比A、C 项的区别,最高点不同,11月的现期/基期是2倍
多,12 月的现期/基期是1倍多,则 11月是最高点,选择C 项。【选C】
16【注意】小贴士:折线图,本质是排序,可利用最低点或最高点排除错误选
项。
【例 2】(2022 广东)按不重复距离计算,以下年份中,国际航线里程同比
增速最快的是:
A.2017 年 B.2018年
C.2019 年 D.2020年
【解析】2.找数的时候存在坑点。要求“按不重复距离计算”,主体是国际
航线,定位最后一行数据,找增速最快的年份,D 项是下降,其他选项是上升,
先排除 D项,其他选项的现期/基期都是1+倍,考虑比较增长量/基期量,2017年
的增长量为 41+,2018年的增长量为 30+,2017年的增长量比 2018年大、基期量
比2018 年小,则2017年增长率>2018年增长率,排除2018 年;2019年的增长
量也是 41+,和2017年比较,增长量差不多,2017年基期量更小,则 2017年增
长率更大,对应 A项。【选A】
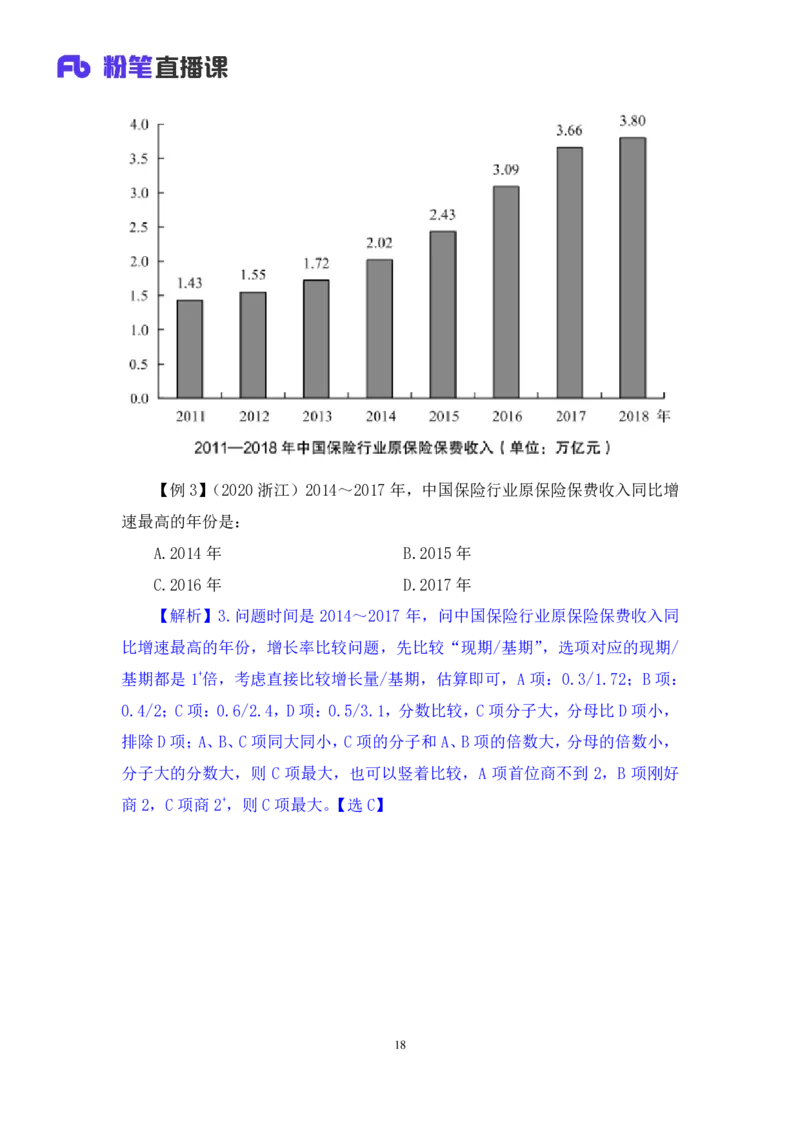
17【例 3】(2020浙江)2014~2017年,中国保险行业原保险保费收入同比增
速最高的年份是:
A.2014 年 B.2015年
C.2016 年 D.2017年
【解析】3.问题时间是 2014~2017 年,问中国保险行业原保险保费收入同
比增速最高的年份,增长率比较问题,先比较“现期/基期”,选项对应的现期/
基期都是 1+倍,考虑直接比较增长量/基期,估算即可,A 项:0.3/1.72;B 项:
0.4/2;C项:0.6/2.4,D项:0.5/3.1,分数比较,C项分子大,分母比 D项小,
排除D项;A、B、C项同大同小,C项的分子和A、B项的倍数大,分母的倍数小,
分子大的分数大,则 C 项最大,也可以竖着比较,A 项首位商不到 2,B 项刚好
商2,C 项商2+,则C项最大。【选 C】
18【练习】(2022 四川)将 2019 年 A 市①工伤保险、②生育保险和③失业保
险按参保人数同比增速从高到低的顺序排列,以下正确的是:
A.①②③ B.①③②
C.②③① D.②①③
【解析】练习.要求增速排序,均给出现期、基期,现期/基期都是1+倍,考
虑比较增长量/基期,估算即可,①、②、③的增长量依次为 80+、27、25,三者
的基期量差不多,则明显①增长率最大;②和③比,②增长量大、基期小,则②
>③,对应 A项。【选A】
【注意】一般增长率:比较的时候先看现期/基期,比较不出来的时候看增
长量/基期量,记住定义式是增长量/基期量,其他公式都根据定义式衍生而来。
19第四节 增长量
一、增长量计算
二、增长量比较
【注意】增长量:对应题型用对应方法。
1.增长量计算。
2.增长量比较。
考点 1:增长量计算的识别与公式一
识别:增长+单位(绝对量)
例:2023年,互联网企业收入同比约增长了_____亿元
公式一:给了现期和基期,增长量=现期- 基期
速算:精确用尾数,估算看范围
【注意】增长量计算的识别与公式一:
1识别:增长+单位(绝对量)。增长率是增长/下降+%。
2.例:2023年,互联网企业收入同比约增长了_____亿元?
答:增长+单位,求增长量。
3.公式一:
(1)给了现期和基期,增长量=现期- 基期。
(2)速算:精确用尾数(比如 1234-561,只有 1 个选项的尾数为 3,则可
以直接选择);如果不能看尾数,则估算看范围。
20【例 1】(2023国考)2021 年下半年,我国固定互联网宽带接入用户中,光
纤用户数增量超过 500万户的月份有几个?
A.2 B.3
C.4 D.5
【解析】1.下半年对应7~12月,主体为“光纤用户数增长量超过500万户
的月份”,问增长量。材料分别给出每个月的数据,与 500 比较,直接看百位。
7 月:84-79=5,但 16-68 不够减,故不到 500;8 月:89-84=5,21-16>0,为
500多;9月:96-89>5,为 500 多;10月:500-496=4,不到 500;11月:466-
077<400;12 月:551-466<100。满足的有 2 个,分别是 8 月和 9 月,对应 A
项。【选 A】
考点 2:年均增长量的识别与公式
识别:时间段+年均+增长+单位
公式:年均增长量=(现期- 基期)/年份差
例:2023年点点体重为 150斤,2020年为120斤。问2020~2023年,点点
体重年均增长多少斤?
【注意】年均增长量的识别与公式:
1.识别:时间段+年均+增长+单位。
2.公式:年均增长量=总增长量/年份差=(现期- 基期)/年份差。
3.例:2023年点点体重为 150斤,2020年为120斤。问 2020~2023年,点
21点体重年均增长多少斤?
答:总增长量=150-120=30,共增长了 3年(年份差),所求=30/3=10。
年均增长类问题基期的选择
一般情况(除江苏外)2012 年~2018年:年份差为6
基期:2012年;现期:2018 年
五年规划(全国统一)“十三五”期间:年份差为 5(基期往前推一年)
基期:2015年;现期:2020 年
江苏省考 2012年~2018 年:年份差为 7(基期往前推一年)
(刷题遇到、了解即可)基期:2011年;现期:2018年
【注意】年均增长类问题基期的选择:
1.一般情况(除江苏外):2012年~2018年,年份差为2018-2012=6。基期:
2012年;现期:2018年。
2.五年规划(全国统一):“十三五”期间,年份差为 5(基期往前推一年)。
基期:2015 年;现期:2020 年。
3.江苏省考(刷题遇到、了解即可):2012年~2018年,年份差为7(基期
往前推一年)。基期:2011年;现期:2018年。
五年规划
五年计划,全称为中华人民共和国国民经济和社会发展五年计划纲要,是中
国国民经济长期计划的重要部分。
中国从 1953 年开始制订第一个“五年计划”,“十一五”起,改称为“五年
规划”。
“十一五”2006~2010年
“十二五”2011~2015年
“十三五”2016~2020年
“十四五”2021~2025年
【注意】五年规划:
1.“五年计划”全称为中华人民共和国国民经济和社会发展五年计划纲要,
22是中国国民经济长期计划的重要部分。
2.中国从 1953 年开始制订第一个“五年计划”,“十一五”起,改称为“五
年规划”。
3.常见:
(1)“十一五”:2006~2010 年。
(2)“十二五”:2011~2015 年。
(3)“十三五”:2016~2020 年。
①第一种理解:与“十二五”的尾巴比较,故基期是 2015 年。
②第二种理解:“十三五”统计的是 2016 年初~2020 年尾,2016 年年初即
2016年 1月1日,相当于2015 年 12月31日,即2015年底的数据。
(4)“十四五”:2021~2025 年。
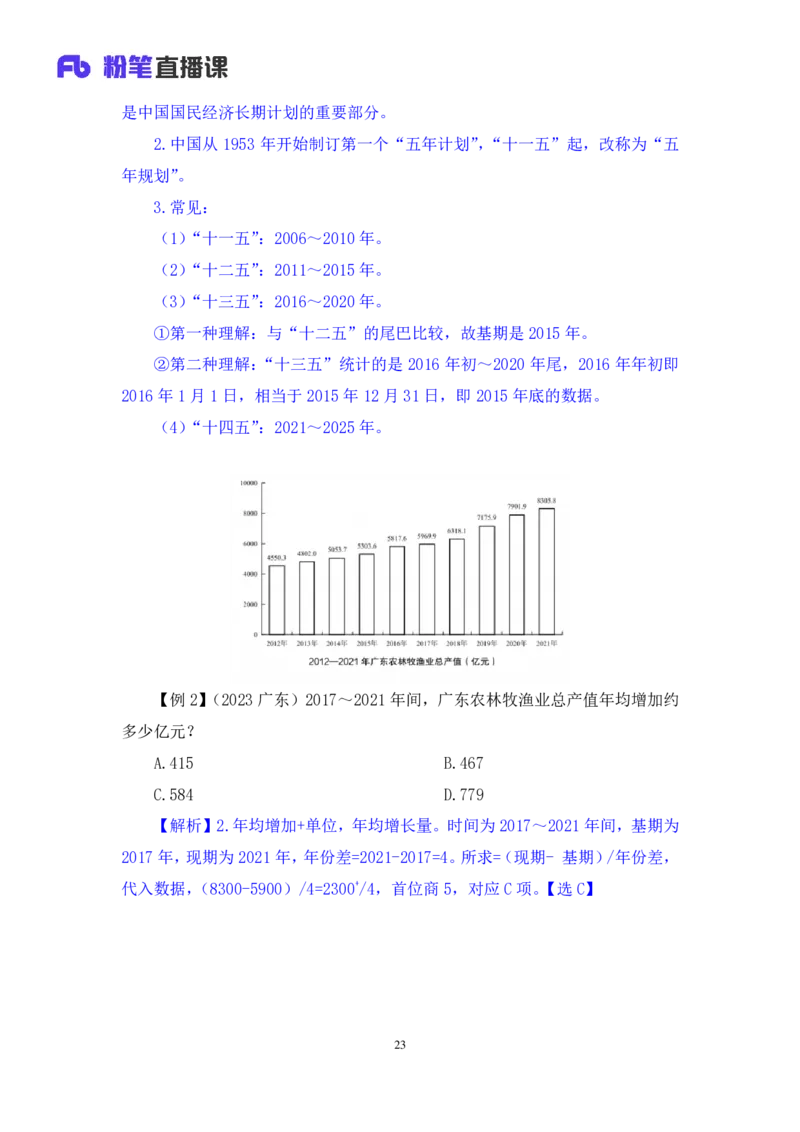
【例 2】(2023广东)2017~2021年间,广东农林牧渔业总产值年均增加约
多少亿元?
A.415 B.467
C.584 D.779
【解析】2.年均增加+单位,年均增长量。时间为 2017~2021年间,基期为
2017年,现期为2021年,年份差=2021-2017=4。所求=(现期- 基期)/年份差,
代入数据,(8300-5900)/4=2300+/4,首位商5,对应C项。【选 C】
23【例 3】(2022 江苏)“十三五”时期,我国集成电路出口额的年均增量是:
A.79 亿美元 B.95亿美元
C.111 亿美元 D.139亿美元
【解析】3.求年均增长量,“十三五”时期对应2016~2020 年,基期为2015
年,现期为 2020 年,年份差为 5。所求=(现期- 基期)/年份差,代入数据,
(1166-591)=466+/5,首位商 9,对应B项。【选B】
超级重点:增长量的高频考法之百化分
已知:现期、增长率,计算增长量
公式:增长量=现期/(1+r)*r
例:2023 年点点工资 100 元,同比增长 25%。问:2023 年点点工资增长了
多少元?
增长量=100/(1+25%)*25%=100/(1+1/4)*(1/4)=100/(4+1)
【注意】超级重点:增长量的高频考法之百化分。
1.已知:现期、增长率,计算增长量。
2 公式:r=增长量/基期,基期=现期/(1+r),则增长量=现期/(1+r)*r。
3.例:2023 年点点工资 100 元,同比增长 25%。问:2023 年点点工资增长
了多少元?
答:增长量=现期/(1+r)*r=100/(1+25%)*25%,25%=1/4,原式=100÷(1+1/4)
*(1/4)=100/(4+1)=20。
增长量——百化分
已知:现期、增长率,计算增长量
公式:增长量=现期/(1+r)*r
24结论:
第一步,|r|=1/N
第二步,增长量=现期/(N+1),减少量=现期/(N-1)
练习:
例:2020年某价格4000 元,同比增长33.3%,问:2020 年此价格同比增长
了约多少元?
例:2020年某价格3600 元,同比减少12.5%,问:2020 年此价格同比减少
了多少元?
【注意】增长量——百化分:
1..结论:
(1)第一步,|r|=1/N。
(2)第二步,增长量=现期/(N+1),减少量=现期/(N-1)。
2.练习:
(1)例:2020 年某价格 4000元,同比增长33.3%,问:2020年此价格同比
增长了约多少元?
答:r=33.3%≈1/3,n=3,则增长量=现期/(n+1)=4000/4=1000。
(2)例:2020 年某价格 3600元,同比减少12.5%,问:2020年此价格同比
减少了多少元?
答:|r|=12.5%=1/8,则减少量=现期/(n-1)=3600/7。
【百化分表】
【注意】背诵百化分表。
25分组记忆百化分
【注意】
1.不用背,我也会。
2.互为倒数:(6&16)、(17&14)、(8&12)、(9&11)。
3.等差数列:5.0-3-6-9(20-19-18-17)。
4.77 老师腿长1米3,66 老师腿长 1米5。
1、增长率百化分之放缩法
利用与背过的百分数的倍数关系,放大缩小若干倍,实现百化分练习:
2.5%=
67%=
2、增长率百化分之取中法
如果遇到百分数左右难取舍,取中即可
练习:18.5%=
15.4%=
3、增长率百化分之倒数法:20以内的整数%,即n%
如果你记住了 a%=1/n,则你同时也就记住了 n%=1/a
练习:1/18≈5.6%,则18%≈
8%=
13%=
26增长率百化分之公式法(急救法)如果遇到百分数实在想不起来
硬除:n=100/百分号前的数字(保留小数点后一位)
练习:25%=
43%=
【注意】
1.增长率百化分之放缩法:
(1)利用与背过的百分数的倍数关系,放大缩小若干倍,实现百化分
(2)练习:
①2.5%=25%*0.1=1/4*0.1=1/40。
②67%≈2/3=1/1.5。或者看 1/15=6.7%。
2.增长率百化分之取中法:
(1)如果遇到百分数左右难取舍,取中即可
(2)练习:
①18.5%:介于1/6~1/5 之间,取中为 1/5.5。
②15.4%:介于1/7~1/6 之间,取中为 1/6.5。
3.增长率百化分之倒数法:20以内的整数%,即n%。
(1)如果你记住了a%=1/n,则你同时也就记住了 n%=1/a。
(2)练习:1/18≈5.6%,则 18%≈1/5.6。
①8%=1/12.5。
②13%≈1/7.7。
4.增长率百化分之公式法(急救法):
(1)如果遇到百分数实在想不起来,可以硬除:n=100/百分号前的数字(保
留小数点后一位)
(2)练习:
①25%=25/100=1/4,因为 25*4=100*1,x%=1/n,则x*n=100。
②43%:100/43≈2.3,则 43%≈1/2.3。
国家能源局发布 2022年 1~7月,全社会用电量累计49303 亿千瓦时,同比
增长3.4%。分产业看,第一产业用电量 634亿千瓦时,同比增长 11.1%;第二产
27业用电量 32552亿千瓦时,同比增长 1.1%;第三产业用电量 8531亿千瓦时,同
比增长 4.6%;城乡居民生活用电量 7586亿千瓦时,同比增长 12.5%。7月份,……
【例 4】(2023 联考)2022 年 1~7 月份,全国城乡居民生活用电量比 2021
年1~7 月份约多:
A.672 亿千瓦时 B.843亿千瓦时
C.925 亿千瓦时 D.1020亿千瓦时
【解析】4.多+单位,求增长量。材料给出现期、r,考虑百化分。r=12.5%=1/8,
增长量=现期/(n+1)=7586/9,首位商 8,对应B项。【选B】
2020 年全国人口共141178 万人,比2010年增长了约5.38%。从地区分布上
看,……
【例 5】(2022 联考)2020 年全国人口比 2010 年全国人口增加的数量位于
以下哪个区间?
A.5000 万~6000万人 B.6000万~7000 万人
C.7000 万~8000万人 D.8000万~9000 万人
【解析】5.求增长量。材料给出现期、r,考虑百化分。r=5.38%≈1/19,增
长量=现期/(n+1)=141178/20=7000+,对应C项。【选C】
2023 年4月份,我国社会消费品零售总额 34910亿元,同比增长 18.4%。其
中,除汽车以外的消费品零售额 31290亿元,增长16.5%。
【例 6】(2023河北事业单位)2023年4月,我国社会消费品零售总额同比
增加:
A.4678 亿元 B.5425亿元
C.6414 亿元 D.7212亿元
【解析】6.增加+单位,求增长量。材料给出现期、r,考虑百化分。r=18.4%,
介于1/6~1/5之间,取中为1/5.5,或者18.4%≈2/11=1/5.5,或者1/18≈5.6%,
故18.4%≈1/5.5。增长量=现期/(n+1)=34910/6.5,首位商 5,对应 B项。【选
B】
282019 年6月,全国发行地方政府债券 8996亿元,同比增长 68.37%,环比增
长195.63%。其中,……
【例 7】(2020联考)2019 年6月,全国发行的地方政府债券比 2018年6月
多约:
A.6151 亿元 B.5953亿元
C.3653 亿元 D.3043亿元
【解析】7.多+单位,求增长量。材料给出现期、r,考虑百化分。2019年6
月比2018 年6月,用同比增长率(如果问比 2019年5月,才能用环比增长率),
r=68.37%≈2/3=1/1.5,增长量=现期/(n+1)=8996/2.5。
方法一:直除,首位商 3,比 3多很多,对应C项。
方法二:A/2.5,在不考虑小数点的情况下,相当于乘 4。9000/2.5=900*
(10/2.5)=900*4=3600,但选项没有小数点的差别,直接用 8996*4≈
9000*4=36000,对应C项。【选 C】
【例 8】(2021广东)2020 年上半年,我国水、海产品出口额同比减少约多
少亿美元?
A.6 B.8
C.10 D.12
【解析】8.减少+单位,求减少量。材料给出现期、r,考虑百化分。|r|=19.6%
≈20%=1/5,减少量=现期/(n-1)=48.7/4≈12,对应D项。【选 D】
健步如飞——百化分
已知:现期、增长率,计算增长量公式:增长量=现期/(1+r)*r
29结论:
第一步,|r|=1/N
第二步,增长量:现期/(N+1),减少量=现期/(N-1)
温馨提示:不要忘记+1或-1 哦
【注意】健步如飞——百化分:一定要背百化分表。
1.已知:现期、增长率,计算增长量公式:增长量=现期/(1+r)*r。
2.结论:
(1)第一步,|r|=1/N。
(2)第二步,增长量:现期/(N+1),减少量=现期/(N-1)。
3.温馨提示:不要忘记+1 或-1哦。
二、增长量比较
题型识别:增长最多/少,下降最多/少
(一)给现期量和基期量:增长量=现期量- 基期量
若给柱状图或折线图,可直接看图的高度差
【注意】增长量比较:
1.题型识别:增长最多/少,下降最多/少(如果问增长最快/最慢,指的是
速度,比较增长率)。
2.给现期量和基期量:增长量=现期量- 基期量。
3.若给柱状图或折线图,可直接看图的高度差。
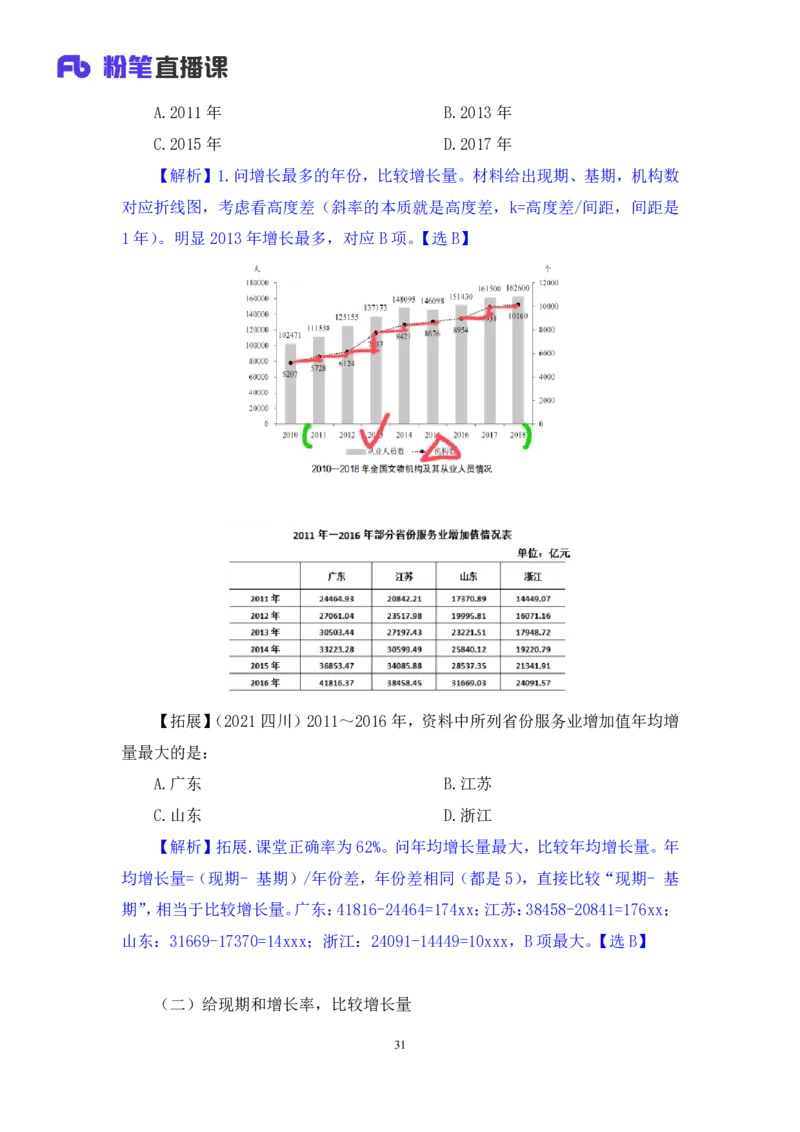
【例 1】(2020江苏)2011~2018年全国文物机构数增加最多的年份是:
30A.2011 年 B.2013年
C.2015 年 D.2017年
【解析】1.问增长最多的年份,比较增长量。材料给出现期、基期,机构数
对应折线图,考虑看高度差(斜率的本质就是高度差,k=高度差/间距,间距是
1年)。明显 2013年增长最多,对应 B项。【选B】
【拓展】(2021四川)2011~2016年,资料中所列省份服务业增加值年均增
量最大的是:
A.广东 B.江苏
C.山东 D.浙江
【解析】拓展.课堂正确率为 62%。问年均增长量最大,比较年均增长量。年
均增长量=(现期- 基期)/年份差,年份差相同(都是 5),直接比较“现期- 基
期”,相当于比较增长量。广东:41816-24464=174xx;江苏:38458-20841=176xx;
山东:31669-17370=14xxx;浙江:24091-14449=10xxx,B项最大。【选 B】
(二)给现期和增长率,比较增长量
31大大则大:①现期大、增长率大,则增量大
②现期大、降幅大,则减少量大
一大一小:百化分计算
推导(了解):
增长量=现期/(N+1)=现期/(1/r+1)
减少量=现期/(N-1)=现期/(1/r-1)
【注意】给现期和增长率,比较增长量:
1.大大则大:
(1)现期大、增长率大,则增量大(不用百化分,直接瞪)。
(2)现期大、降幅大,则减少量大。
(3)甲工资100、增长率为 10%,乙工资200、增长率为-10%,问二者谁的
增长量大。然后问谁的增长量大,正数>负数,甲>乙。
2.一大一小:百化分计算。
3.推导(了解):现期大、r 大,则1/r小,即分母小,分子大、分母小,分
数值大。
(1)增长量=现期/(N+1)=现期/(1/r+1)。
(2)减少量=现期/(N-1)=现期/(1/r-1)。
大大则大,一大一小百化分
2022 年,我老公的私房钱为 200 块,同比增长 20%;我的私房钱为 100 块,
同比增长 10%。
2022 年,我老公的私房钱为 200 块,同比下降 20%;我的私房钱为 100 块,
同比下降 10%。
2022 年,我老公的私房钱为 250 块,同比增长 20%;我的私房钱为 110 块,
同比增长 50%。
【注意】大大则大,一大一小百化分:
1.2022 年,我老公的私房钱为 200块,同比增长20%;我的私房钱为 100块,
同比增长 10%。
答:我老公的现期大、增长率大,大大则大,我老公的增长量大。
322.2022 年,我老公的私房钱为 200块,同比下降20%;我的私房钱为 100块,
同比下降 10%。
答:我老公的现期大、增长率(绝对值)大,大大则大,我老公的减少量大。
3.2022 年,我老公的私房钱为 250块,同比增长20%;我的私房钱为 110块,
同比增长 50%。
答:一大一小百化分,我老公:250/(5+1)=40+,我:100/(2+1)=40-,我
老公的增长量大。如果我改为 11、50%,我老公的现期有绝对优势,即使增长率
小一点也不影响,还是我老公的增长量大。
2018 年木家具进口金额 9.24 亿美元,增长3.6%,木框架坐具进口金额 3.32
亿美元,增长13.8%。刨花板……。2018年木制品……。2018 年木家具出口数量
增长5.68%,金额负增长1.6%,
木地板出口 26.6万吨,3.85 亿美元,分别下降24.8%和下降 25.9%。
胶合板出口 1137.8 万立方米,55.56 亿美元,数量增长 5%,金额增长 9%,
纤维板出口 179万吨,38.35 亿美元,数量下降14.9%,金额增长 6.2%。……
【例 2】(2021新疆兵团)2018年,下列三种产品出口金额增长值从大到小
的顺序排列正确的是:
A.木地板、胶合板、纤维板 B.胶合板、纤维板、木地板
C.木地板、纤维板、胶合板 D.胶合板、木地板、纤维板
【解析】2.增长值从大到小的顺序排列,比较增长量。材料分别给出现期、
r。有明显最小值,只有木地板是减少的,故一定是最低,木地板排在最后,只
有B项满足。【选 B】
【注意】小贴士:排序题,利用选项。
按收入来源分,(2019年)前三季度,全国居民
人均工资性收入 13020元,增长 8.6%;
人均经营净收入 3757元,增长 9.3%;
人均财产净收入 1949元,增长 12.3%;
33人均转移净收入 4157元,增长 7.2%。
【例 3】(2021新疆兵团)2019年前三季度,四种收入来源中收入同比增量
最高的是:
A.人均工资性收入 B.人均经营净收入
C.人均财产净收入 D.人均转移净收入
【解析】3.问“同比增量最高”,比较增长量。材料分别给出现期、r。增长
率差不多,但人均工资性收入的现期非常大,有压倒性的优势,故人均工资性收
入的增长量最大,对应 A项。【选 A】
2018年前三季度,S省物流相关行业实现总收入1912.8亿元,同比增长6.6%。
其中:
运输环节收入 1321.9亿元,同比增长 6.0%;
保管环节收入 226.2亿元,同比增长 6.4%;
邮政业收入 82.8亿元,同比增长 16.7%;
配送、加工、包装业收入 98.8 亿元,同比增长6.4%。
【例 4】(2020国考)将2018 年前三季度S省物流相关行业不同类型的收入
按照同比增量从高到低排列,以下正确的是:
A.运输收入>保管收入>邮政业收入>配送、加工、包装业收入
B.运输收入>配送、加工、包装业收入>邮政业收入>保管收入
C.运输收入>保管收入>配送、加工、包装业收入>邮政业收入
D.运输收入>邮政业收入>配送、加工、包装业收入>保管收入
【解析】4.问“同比增量从高到低排列”,比较增长量。材料分别给出现期、
r。选项最大的都是运输收入,如果看最低,结合选项,保管和配送的增长率相
同,保管的现期大,则保管>配送,比较邮政和配送,邮政和配送一大一小,且
很接近,考虑百化分,邮政为 82.8/(6+1)=10+,配送为 98.8/(16+1)=10-,
最小的是配送,对应 A项。【选 A】
34【注意】增长量:
1.计算:
(1)百化分(要背百化分表)。
(2)年均增长量=(现期- 基期)/年份差。
2.比较:问“最多/最少”。大大则大,一大一小百化分(如果有压倒性优势,
至少3倍以上,可以不百化分)。
【知识梳理】
1.增长率计算题型识别:增长/下降+____________;增长量计算题型识别:
增长/下降+____________。
2.已知今年增长率和去年增长率相比提高了 x 个百分点,求去年增长率用
________;已知今年增长率和去年增长率相比降低了 x个百分点,求去年增长率
用________。
3.已知现期量和基期量,增长率计算公式为____________________;已知现
期量和增长量,增长率计算公式为____________________。
4.增长率比较题型识别:问增长最________;增长量比较题型识别:问增长
最________。
5.增长率比较,先看________,看不出来再比较__________
6.已知现期量和基期量,增长量计算公式为____________________;已知现
期量和增长率,求增长量:先将________,则增长量=____________,下降量
=____________。
7.年均增长量计算公式为________________________;一般情况(非江苏),
35对于 2021~2024 年,现期为________,基期为________,年份差为________;
“十三五”期间,现期为________,基期为________,年份差为________。
8.增长量的比较,若________大________大,则增长量________;若________
大________大,则减少量________;若一大一小,则________。
【注意】知识梳理:
1.增长率计算题型识别:增长/下降+%/倍数/成数;增长量计算题型识别:
增长/下降+单位(元/斤/亩/平方米)。
2.已知今年增长率和去年增长率相比提高了 x个百分点,求去年增长率用减
法;已知今年增长率和去年增长率相比降低了 x 个百分点,求去年增长率用加
法。
3.已知现期量和基期量,增长率计算公式为(现期- 基期)/基期;已知现
期量和增长量,增长率计算公式为增长量/(现期-增长量)。
4.增长率比较题型识别:问增长最快/慢;增长量比较题型识别:问增长最
多/少。
5.增长率比较,先看“现期/基期”,看不出来再比较“(现期- 基期)/基期”。
6.已知现期量和基期量,增长量计算公式为现期- 基期;已知现期量和增长
率,求增长量:先将|r|=1/n,则增长量=现期/(n+1),下降量=现期/(n-1)。
7.年均增长量计算公式为(现期- 基期)/年份差;一般情况(非江苏),对
于2021~2024年,现期为2024 年,基期为2021年,年份差为 3;“十三五”期
间,现期为 2020年,基期为 2015 年,年份差为5。
8.增长量的比较,若现期大增长率大,则增长量大;若现期大降幅大,则减
少量大;若一大一小,则百化分。
2020 年末,全国公共图书馆实际使用房屋建筑面积 1785.77 万平方米,比
上年末增长 12.2%;全国图书总藏量 117929.99万册,增长6.1%;阅览室坐席数
126.47 万个,增长6.2%;计算机 226234台,增加419台;其中供读者使用的电
子阅览终端 143714台,减少 2022 台。
【课后练习 1】(2022四川)2020年,全国供读者使用的电子阅览终端数量
同比增速约为:
36A.3.4% B.2.7%
C.-1.4% D.-2.8%
【解析】练习1.课堂正确率为 91%。求同比增速,求增长率。主体为“电子
阅览终端数量”,材料给出现期、增长量,r=增长量/(现期-增长量)=-2022/
(143714+2022),结果为负数,排除 A、B项。C、D项差距大,分母截两位 2022/14,
首位商 1,对应C项。【选C】
2017 年全年,上海口岸货物进出口总额 79211.40亿元,比上年增长 15.1%。
【课后练习 2】(2021四川)2017 年,上海口岸货物进出口总额比上年增加:
A.1 万亿元以上 B.0.7~1万亿元之间
C.0.4~0.7万亿元之间 D.不到0.4万亿元
【解析】练习2.课堂正确率为 77%。增加+单位,求增长量。材料给出现期、
r,考虑百化分。r=15.1%≈1/6.7(1/15≈6.7%),增长量=现期/(n+1)
=79211.4/7.7=1+万,对应A项。【选 A】
【答案汇总】
增长率计算 1-5:BDCAB;6:A
增长率比较 1-3:CAC
增长量计算1-5:ACBBC;6-8:BCD
增长量比较1-4:BBAA
37遇见不一样的自己
Be your better self
38