文档内容
方法精讲-资料 4
(笔记)
主讲教师:邓健
授课时间:2024.06.01
粉笔公考·官方微信方法精讲-资料 4(笔记)
【注意】回顾上节课的课后作业:
1.比重:部分在总体中所占的比率;平均数:后除以前。
2.现期比重公式:A/B;现期平均数公式:A/B。
3.基期比重公式:A/B*[(1+b)/(1+a)];基期平均数公式:A/B*[(1+b)
/(1+a)]。若选项差距大,就上下截两位约分化简;若选项差距小,先算左边
A/B,再看右边(1+b)/(1+a)与1的大小关系,利用范围结合选项做题。
4.两期比重题型识别:有两个时间(有时会用“同比”表示),问题中有“占
比/比重”;两期平均题型识别:有两个时间,问题中有“平均每”。
5.两期比重判升降:a>b,比重上升;a<b,比重下降;a=b,比重不变。
6.两期平均数判升降:a>b,平均数上升;a<b,平均数下降;a=b,平均
数不变。
7.两期比重差值题型识别:比重+上升/下降+百分点;方法及公式:
(1)通过a、b,判升降。
(2)定大小:<|a-b|。
(3)公式:A/B*[(a-b)/(1+a)]。
8.平均数增长率题型识别:平均数增长/下降+%;公式:r=(a-b)/(1+b)。
倍数
关键字:倍
题型:一、现期倍数(多)
二、基期倍数(少)
【注意】倍数:整体难度不高,分为两类(现期倍数、基期倍数)。
现期倍数
➢题型识别:求现在,A是B的多少倍
➢计算公式:A/B
➢速算技巧:截位直除
1【注意】现期倍数:只要是一步除法,都用A/B的形式表示,求倍数就是做
除法,再根据选项差距计算。
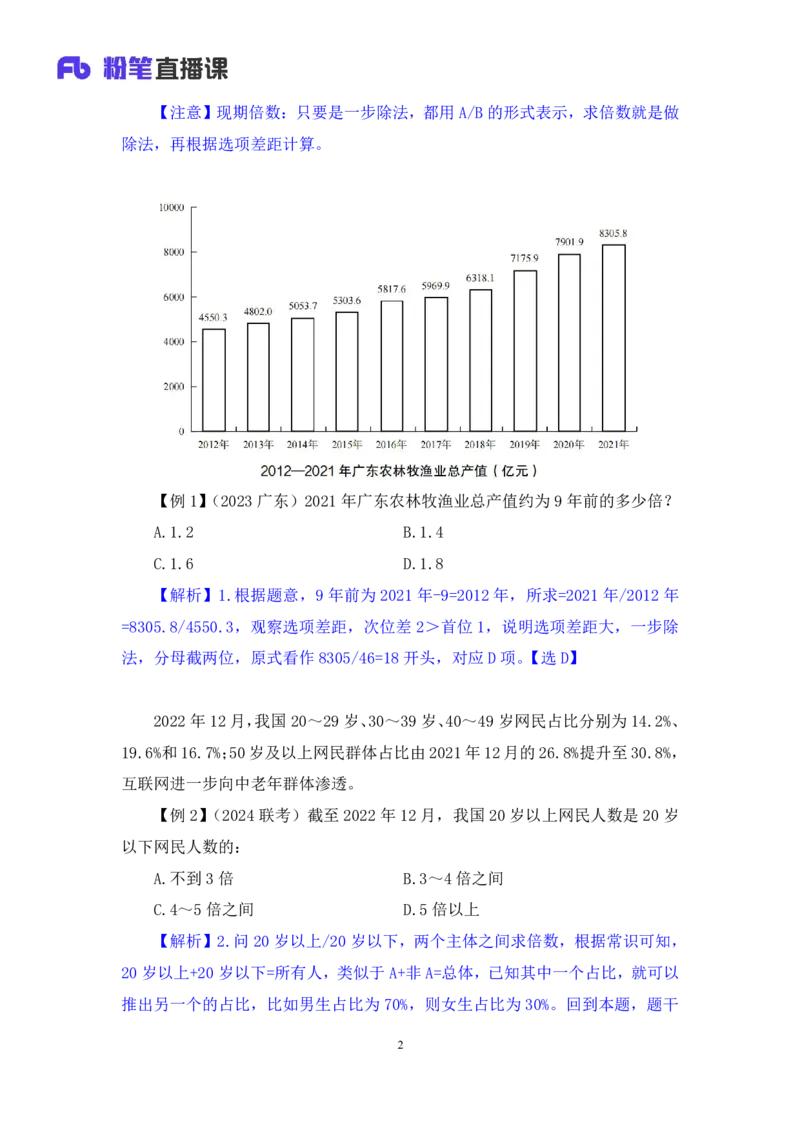
【例1】(2023广东)2021年广东农林牧渔业总产值约为9年前的多少倍?
A.1.2 B.1.4
C.1.6 D.1.8
【解析】1.根据题意,9 年前为 2021 年-9=2012年,所求=2021 年/2012 年
=8305.8/4550.3,观察选项差距,次位差 2>首位 1,说明选项差距大,一步除
法,分母截两位,原式看作8305/46=18开头,对应D项。【选D】
2022年12月,我国20~29岁、30~39岁、40~49岁网民占比分别为14.2%、
19.6%和16.7%;50岁及以上网民群体占比由2021年12月的26.8%提升至30.8%,
互联网进一步向中老年群体渗透。
【例2】(2024联考)截至 2022 年12月,我国 20岁以上网民人数是 20 岁
以下网民人数的:
A.不到3倍 B.3~4倍之间
C.4~5倍之间 D.5倍以上
【解析】2.问20岁以上/20岁以下,两个主体之间求倍数,根据常识可知,
20岁以上+20岁以下=所有人,类似于A+非A=总体,已知其中一个占比,就可以
推出另一个的占比,比如男生占比为 70%,则女生占比为 30%。回到本题,题干
2给出的各年龄段占比之和对应20岁以上的占比,即14.2%+19.6%+16.7%+30.8%,
凑整加和约为80%,则20岁以下的占比为1-80%=20%,所求倍数=80%/20%=4倍。
无法确定答案,说明需要更严谨的计算,整数部分14%+19%+16%+30%=79%,小数
部分 0.2%+0.6%+0.7%+0.8%=2+%,故20 岁以上的占比=79%+2+%=81+%,则 20 岁以
下占比为18+%,所求=81+%/18+%>4倍,对应C项。【选C】
【注意】总量相同,可以用占比代替具体数据算倍数。
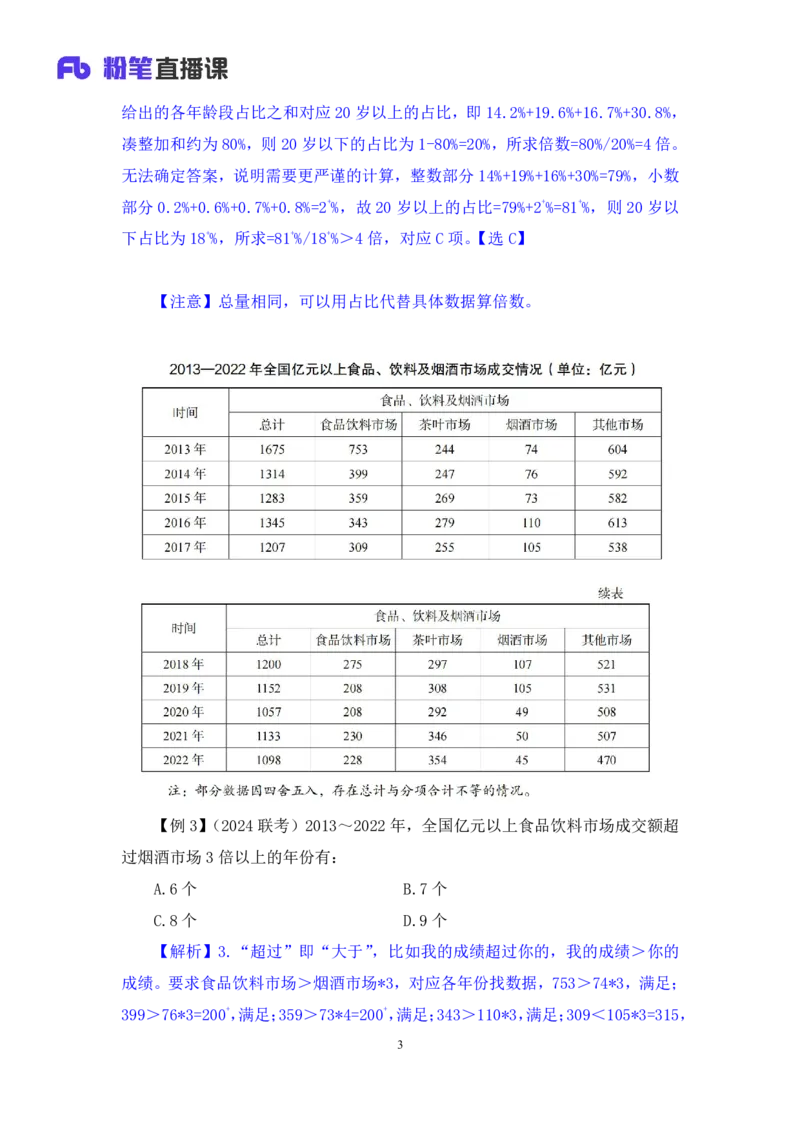
【例3】(2024联考)2013~2022年,全国亿元以上食品饮料市场成交额超
过烟酒市场3倍以上的年份有:
A.6个 B.7个
C.8个 D.9个
【解析】3.“超过”即“大于”,比如我的成绩超过你的,我的成绩>你的
成绩。要求食品饮料市场>烟酒市场*3,对应各年份找数据,753>74*3,满足;
399>76*3=200+,满足;359>73*4=200+,满足;343>110*3,满足;309<105*3=315,
3不满足;275<107*3=300+,不满足;208<105*3=300+,不满足;208>49*3=100+,
满足;230>50*3=150,满足;228>45*3=100+,满足。综上,满足的有 7 个,
对应B项。【选B】
概念辨析
①A是B的几倍:A/B
②A比B多(高)几倍:(A-B)/B=A/B-1
③A超过B的几倍:超过就是大于
【注意】概念辨析:
1.A是B的几倍:A/B。
2.A比B多(高)几倍:完整的表述应该是“A比B多的部分是B的几倍”,
A比B多的部分为A-B,减完之后再除以B,因此为(A-B)/B=A/B-1。
3.A 超过 B 的几倍:超过就是大于。“超过”就是字面意思,比如你跑步超
过某人,就是在他前面,比他跑得多。A 超过 B 的 3 倍,就是 A>B*3,可以是
3.1倍、3.5倍、6倍、10倍、100倍等。
4.举例:
(1)问法一:小邓的收入为100万,小马的收入为20万,问小邓的收入是
小马的多少倍?
答:所求=100/20=5倍。
(2)问法二:小邓的收入为100万,小马的收入为20万,问小邓比小马多
(高)几倍?
答:所求=(100-20)/20=4倍,或者100/20-1=4倍。
(3)问法三:小马的收入为40万,小邓的收入超过小马收入的4倍,问小
邓的收入?
答:超过就是大于,小邓>小马*4=40*4=160万,只能得到小邓的范围。有
的同学认为超过就要“+1倍”,这样是不对的,可以理解成:你的考试分数超过
60分,不能说明你的得分是70分,“超过”只能说明你的分数大于60分,可能
是65分、100分,并没有明确的倍数关系。
42023年一季度,全国社会消费品零售总额114922亿元,同比增长5.8%,上
年四季度为下降 2.7%。按经营单位所在地分,城镇消费品零售额 99664 亿元,
增长5.7%;乡村消费品零售额15258亿元,增长6.2%……
【例4】(2023事业单位)按经营单位所在地分,2023年一季度,城镇消费
品零售额约比乡村消费品零售额多多少倍?
A.4.5 B.5.5
C.6.5 D.7.5
【解析】4.问题时间2023 年一季度,找数据,城镇消费品零售额 99664 亿
元,乡村消费品零售额 15258亿元,注意问的是“多多少倍”(这是倍数问题的
经典陷阱),所求=99664/15258-1=6+-1=5+倍,对应B项。【选B】
【注意】
1.A比B多(高)几倍:(A-B)/B=A/B-1。
2.资料分析的计算逻辑:找数据列出式子先看选项,看出来答案就直接选;
看不出来再考虑截位操作,选项差距大→截两位,选项差距小→截三位。
从输入地看,2020年在东部地区就业的农民工15132万人,比上年减少568
万人,下降 3.6%,占农民工总量的 53%……在西部地区就业农民工 6279万人,
比上年增加106万人,增长1.7%,占农民工总量的22.0%。在东北地区就业农民
工853万人,比上年减少42万人,下降4.7%,占农民工总量的3.0%。
【拓展】(2021广东)2020年,在西部地区就业农民工约比在东北地区就业
农民工多多少倍?
A.9.3 B.8.3
C.7.4 D.6.4
【解析】拓展.问题时间2020年,问西部地区比东北地区多多少倍。
方法一:西部地区就业农民工 6279万人,东北地区就业农民工 853万人,
所求=6279/853-1=7+-1=6+倍,对应D项。
方法二:题干给了占比,且都是占农民工总量的比重,利用比重计算更友好,
西部地区就业农民工占农民工总量的22.0%,东北地区就业农民工占农民工总量
5的3.0%,所求=22%/3%-1=7+-1=6+倍,对应D项。【选D】
【注意】
1.总量相同,可以用占比代替具体数据算倍数。
2.一般没有“少几倍”的说法。
基期倍数
➢识别:求去年,A是B的几倍
➢公式:A/B*[(1+b)/(1+a)]
A:分子的现期量 B:分母的现期量
a:分子的增长率 b:分母的增长率
(多步除法)速算:
选项差距大:上下截两位,约分计算
选项差距小:先算A/B,再看(1+b)/(1+a)与1的关系,结合选项
例:2023年,老邓体重为A,增速为a;小邓体重为B,增速为b,问2022
年老邓体重是小邓的多少倍?
【注意】基期倍数:
1.识别:求去年,A是B的几倍。
2.公式:A/B*[(1+b)/(1+a)]。不管是基期比重、基期平均、基期倍数,
只要是基期比例都是用这个公式,A、B永远都是问题中分子、分母对应的数据。
A:分子的现期量 B:分母的现期量
a:分子的增长率 b:分母的增长率
3.例:2023年,老邓体重为A,增速为a;小邓体重为B,增速为b,问2022
年老邓体重是小邓的多少倍?
答:推导过程:老邓/小邓=[A/(1+a)]÷[B/(1+b)]=[A/(1+a)]*[(1+b)
/B]=A/B*[(1+b)/(1+a)]。
4.(多步除法)速算:
(1)选项差距大:上下截两位,约分计算。
(2)选项差距小:先算A/B,再看(1+b)/(1+a)与1的关系,结合选项。
62023年第14周,H市哨点医院共报告流感样病例总数为5187例,比上周增
加4.49%,比去年同期减少
56.16%,其中国家级哨点医院455例,比上周减少6.57%,比去年同期减少
55.04%。城区哨点医院1899例,比上周减少19.40%,比去年同期减少55.46%;
郊区、县(市)哨点医院3288例,比上周增加26.07%,比去年同期减少56.55%。
本周全市哨点医院 ILI%为5.98%,比上周低 0.07个百分点,其中国家级哨点医
院ILI%为2.12%,比上周高 0.23个百分点。城区哨点医院 ILI%为 4.45%,比上
周低 0.56 个百分点;郊区、县(市)哨点医院 ILI%为 7.46%,比上周高 0.01
个百分点。
【例5】(2024浙江)2023年第13周,H市郊区、县(市)哨点医院报告流
感样病例约是城区的多少倍?
A.1.7 B.1.5
C.1.3 D.1.1
【解析】5.材料时间2023年第 14 周,问题时间第 13周为基期时间,问倍
数,判定为基期倍数问题。通过括号快速定位,分子为郊区、县(市)哨点医院,
对应 A=3288例,a=26.07%,分母为城区,对应 B=1899例,b=-19.40%,将数据
代入公式,A/B*[(1+b)/(1+a)]=3288/1899*[(1-19.4%)/(1+26.07%)]。
式子比较复杂,观察选项差距,首位相同,次位差 2>首位1,说明选项差距比
较大,多步除法,上下均截两位,原式看作(33/19)*(80/13),能约分就约分,
不能约分就微调,将19看作20,(33/19)*(80/13)≈(33/20)*(80/13)=
(33*4)/13=132/13=1+开头(多一点点),对应D项。【选D】
【注意】3288/1899≈1.7算出来是现期倍数,会错选A项。
特殊增长率
➢间隔增长率(常考,简单套路)
➢年均增长率(常考比较,计算几乎不考)
➢混合增长率(必考重点,技巧性强)
7【注意】特殊增长率:分为三个考点,每个题型都有特殊的解法。
1.间隔增长率:常考,简单套路。
2.年均增长率:常考比较,属于送分题,计算几乎不考。
3.混合增长率:必考重点,属于重难点,技巧性强,学会之后很简单,大部
分不用算。
一、间隔增长率
识别:2020年比2018年增长+%(隔一年,求增长率)
已知:2020年收入同比增长率为r,2019年同比增长率为r,求:2020年
1 2
与2018年相比的增长率是多少?
现期=基期*(1+r)
2020年=2019年*(1+r)=2018年*(1+r)*(1+r)
1 1 2
r=(现期- 基期)/基期=(2020年-2018年)/2018年
r =r+r+r*r
间隔 1 2 1 2
r:今年的增长率
1
r:去年的增长率
2
【注意】间隔增长率
1.识别:2020年比2018年增长+%(隔一年,求增长率)。如果给出2020年
为100元,2018年为50元,则r=(现期- 基期)/基期=(100-50)/50=100%,
但材料一般不会给2018年的数据,只给出2020年,就需要利用增长率把这两个
时间点联系起来。
2.已知:2020年收入同比增长率为r,2019年同比增长率为r,求:2020
1 2
年与2018年相比的增长率是多少?
答:先通过 r 、r 把 2018 年和 2020 年衔接起来,基本公式:现期=基期*
1 2
(1+r),则 2020 年=2019 年*(1+r )=2018 年*(1+r )*(1+r );代回基本公
1 1 2
式,r=(现期- 基期)/基期=(2020 年-2018 年)/2018 年,则有:[2018 年*
8(1+r)*(1+r)-2018年]/2018年,约掉2018年,原式化简为1+r+r+r*r-1,
1 2 1 2 1 2
推导出r =r+r+r*r。
间隔 1 2 1 2
3.方便记忆:称作“笑脸公式”,上面r、r 是“眼睛”,2020年对于2019
1 2
年增长率为 r,2019 年对于 2018 年增长率为r ,则r =r+r+r*r,r:今年
1 2 间隔 1 2 1 2 1
的增长率,r:去年的增长率。
2
4.有同学会疑问间隔两年、三年呢?
答:隔很多年就不是间隔增长率,而是后面讲到的年均增长率。
➢速算技巧 r=r+r+r*r
1 2 1 2
1、先计算r+r,结合选项
1 2
【练习1】8.5%+36%+8.5%*36%≈( )
A.47.6% B.40.4%
C.34.5% D.27.6%
2、若r、r 的绝对值均小于10%(r*r<1%),结合选项乘积可忽略
1 2 1 2
【练习2】5.6%+6.3%+5.6%*6.3%≈( )
A.12.26% B.10.87%
C.13.21% D.9.69%
3、结合选项不能排除:百化分
【练习3】11.6%+25.4%+11.6%*25.4%≈( )
A.38.8% B.39.9%
C.37.7% D.36.6%
【注意】速算技巧:r=r+r+r*r,做题要学会利用选项。
1 2 1 2
1.先计算r+r,结合选项。
1 2
练习1.8.5%+36%+8.5%*36%≈( )
A.47.6% B.40.4%
9C.34.5% D.27.6%
答:先算 8.5%+36%=44.5%,加法是核心部分,后面是两个百分数相乘,越
乘越小,对结果的影响不大,算完加和先看选项能否锁定答案,大于44.5%的有
且只有A项。
2.若r、r 的绝对值均小于10%(r*r<1%),结合选项乘积可忽略。
1 2 1 2
练习2.5.6%+6.3%+5.6%*6.3%≈( )
A.12.26% B.10.87%
C.13.21% D.9.69%
答:先算 5.6%+6.3%=11.9%,排除 B、D 项;如果两个增长率都是 10%,
10%*10%=1%(比较小),若两个增长率都小于 10%,则乘积一定远小于 1%,此时
乘积可以忽略,选一个比11.9%大一点的即可,对应A项。
3.结合选项不能排除:百化分。
练习3.11.6%+25.4%+11.6%*25.4%≈( )
A.38.8% B.39.9%
C.37.7% D.36.6%
(1)答:先算11.6%+25.4%=37%,两个百分数都比10%大,乘积不能忽略,
可以利用百化分计算,把 25.4%近似看作 1/4,11.6%*25.4%≈11.6%*1/4≈3%,
则37%+3%=40%,对应B项。
(2)注意:并不是看到百化分就“+1”,百化分就是单纯的把百分数化成分
数,比如50%=1/2;如果题目求增长量,才需要“n+1”,增长量=现期/(n+1)。
(3)拓展练习:63%*14.3%≈63%*1/7=9%。
一、间隔增长率
➢识别:中间隔一年,求增长率
➢公式:r=r+r+r*r(和+积)
1 2 1 2
➢计算:①先算加法,结合选项排除
②再算乘法:若r、r 均小于10%,则乘积小于1%,一般可忽略
1 2
有超过10%,可百化分快速计算
【注意】间隔增长率:
101.识别:中间隔一年,求增长率。很多同学只是沉溺于记公式、技巧,忽略
了题型识别,学习要掌握窍门,什么样的题目应该对应什么样的考点,才能有后
续的解题。
2.公式:r=r+r+r*r (和+积),r 、r 分别为今年、去年的增长率,如果
1 2 1 2 1 2
把r、r 的顺序记反了也没关系,因为加法和乘法互换位置不影响结果。
1 2
3.计算:
(1)先算加法(加法是核心),结合选项排除。
(2)再算乘法:若 r、r 均小于 10%,则乘积小于 1%,一般可忽略;有超
1 2
过10%,可百化分快速计算。
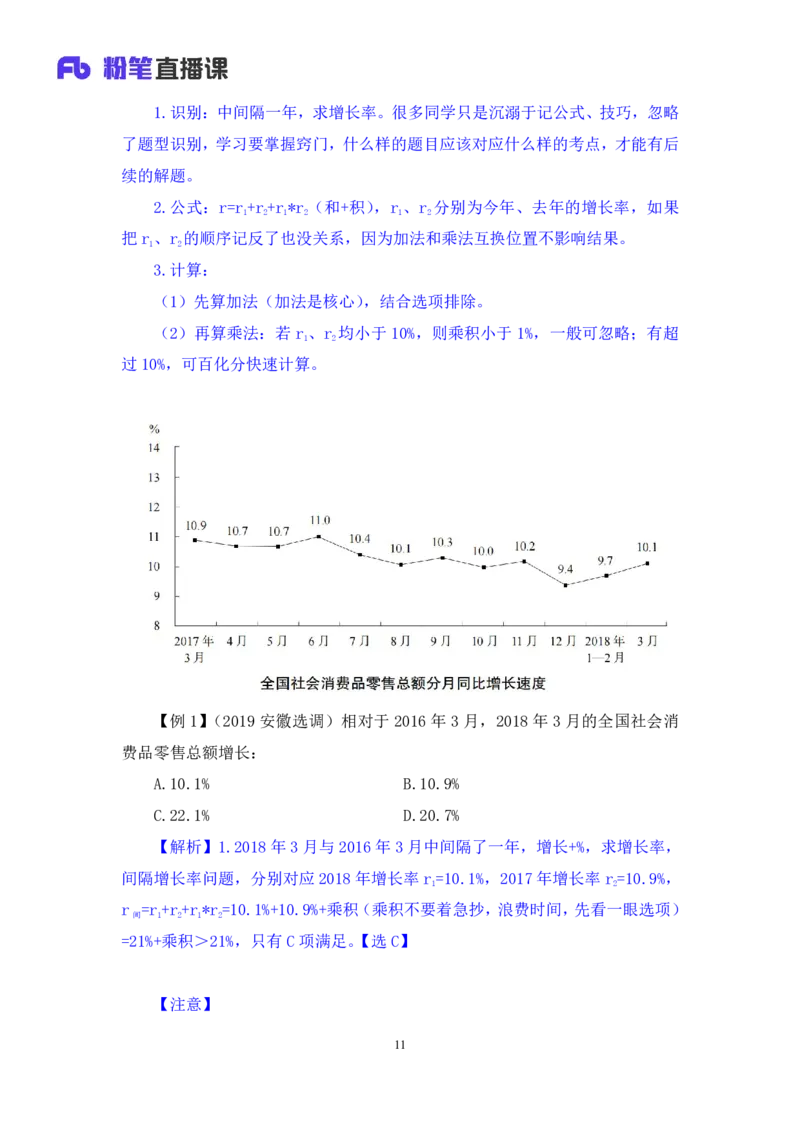
【例 1】(2019 安徽选调)相对于 2016 年 3 月,2018 年 3 月的全国社会消
费品零售总额增长:
A.10.1% B.10.9%
C.22.1% D.20.7%
【解析】1.2018年3月与2016年3月中间隔了一年,增长+%,求增长率,
间隔增长率问题,分别对应2018年增长率r=10.1%,2017年增长率r=10.9%,
1 2
r =r+r+r*r=10.1%+10.9%+乘积(乘积不要着急抄,浪费时间,先看一眼选项)
间 1 2 1 2
=21%+乘积>21%,只有C项满足。【选C】
【注意】
111.要想清楚时间的对应关系,老师给出的结论与2016年无关,r 对应2018
1
年,r 对应2017年。
2
2.有同学认为,求比2016年……,需要找2016年的增长率。
答:间隔增长率与 2016 年的增长率无关,如果题目给 2016 年、2018 年具
体的量,可以直接利用公式做;但本题给的是同比增长率,r=10.1%指的是2018
1
年比2017年的增长情况,r=10.9%指的是2017年比2016年的增长率,利用r、
2 1
r 做题就是找到2018年与2016年的关系。
2
2022 年,全国软件和信息技术服务业规模以上企业超 3.5 万家,累计完成
软件业务收入 108126 亿元,同比增长 11.2%,增速较上年同期回落 6.5 个百分
点。
【例2】(2024四川)2022年,全国软件和信息技术服务业规模以上企业累
计完成软件业务收入约比2020年增长了:
A.16% B.23%
C.29% D.31%
【解析】2.问 2022 年比 2020 年,中间隔一年求增长率,r 为 2022 年增长
1
率,r 为 2021 年增长率,找数据,“同比增长 11.2%”→r=11.2%,没有直接给
2 1
出r,“增速较上年同期回落6.5个百分点”,高减低加,r=11.2%+6.5%=17.7%。
2 2
r=r+r+r*r=11.2%+17.7%+乘积(先不要抄)=28.9%+乘积,有同学会错选 C项,
1 2 1 2
两个百分数均大于 10%,则 11.2%*17.7%>1%,28.9%+1+%>29.9%,锁定 D 项。
或者百化分,11.2%≈1/9,11.2%*17.7%≈1/9*18%=2%,28.9%+2%=30.9%≈31%,
对应D项。【选D】
2018年,我国全社会用电量 68449 亿千瓦时,同比增长 8.5%,增幅同比提
高 1.9 个百分点。具体来看,第一产业用电量 728 亿千瓦时,同比增长 9.8%;
第二产业用电量 47235 亿千瓦时,同比增长 7.2%;第三产业用电量 10801 亿千
瓦时,同比增长12.7%;城乡居民生活用电量9685亿千瓦时,同比增长10.4%。
【拓展】(2019广东)2018年,我国全社会用电量较2016年增加了约( )。
A.13.7% B.15.7%
12C.17.9% D.19.9%
【解析】拓展.2018年比2016年间隔一年,求增长率,间隔增长率问题。“同
比增长8.5%”,即2018年增速r=8.5%,“增幅同比提高1.9个百分点”,高减低
1
加,r=8.5%-1.9%=6.6%,r=r+r+r*r=8.5%+6.6%+乘积(r、r 均小于10%,乘
2 1 2 1 2 1 2
积可以忽略)≈15.1%,结果比 15.1%只大一点点,大的超不过 1%,对应 B 项。
【选B】
题型延伸①:间隔倍数
特征:隔一年,求倍数
2020年工资同比增长了25%,2019年同比增长了20%,则2020年工资是2018
年的多少倍?
两步走:
①先求出间隔增长率
②间隔倍数=间隔增长率+1
【注意】题型延伸——间隔倍数:
1.特征:隔一年,求倍数。
2.两步走:
(1)先求出间隔增长率。
(2)倍数=r+1(例如同比增长率为37%,则今年是去年的1.37倍)→间隔
倍数=间隔增长率+1。
3.例:2020 年工资同比增长了 25%,2019年同比增长了 20%,则 2020年工
资是2018年的多少倍?
答:r =25%+20%+25%*20%=45%+25%*(1/5)=50%,间隔倍数=50%+1=1.5倍。
间
题型延伸②:间隔基期量
特征:隔一年,求基期
2020年工资额是400元,同比增长了10%,2019年同比增长了20%,则2018
年的工资是多少元?
两步走:
13①先求出间隔增长率
②间隔基期=现期量/(1+间隔增长率)
【注意】题型延伸——间隔基期量:
1.特征:隔一年,求基期。例如已知现期2018年6月的值,问法1→求2017
年6月的值→求去年(同比关系)→现期/(1+r );问法 2→求 2018年5 月
同比
的值→求上个月(环比关系)→现期/(1+r );问法3→求2016年 6月的值
环比
→求前年(间隔)→现期/(1+r );注意时间的对应关系。
间隔
2.例:2020年工资额是400元,同比增长了10%,2019年同比增长了20%,
则2018年的工资是多少元?
答:给2020年、求2018年,求基期,间隔一年,求间隔基期量。若求2019
年→400/(1+10%),但本题求的是2018年,r =r+r+r*r=10%+20%+10%*20%=32%,
间 1 2 1 2
间隔基期=现期/(1+r )=400/(1+32%)=400/1.32≈300。
间
3.计算方法:两步走。
(1)先求出间隔增长率。
(2)间隔基期=现期量/(1+间隔增长率)。
2018年全年H市保费收入65.4亿元,同比增长0.7%。其中,寿险业务保费
收入39.5亿元,下降5.1%;健康和意外险业务保费收入9.1亿元,增长21.6%,
增速同比增加5个百分点;财产险业务保费收入3.4亿元,增长25.2%;车险业
务保费收入 13.3 亿元,增长 1.8%。全年支付各类赔款及给付 21.2 亿元,增长
5.3%。其中,寿险业务保费赔付11.0亿元,增长1.4%;健康和意外险业务保费
赔付3.0亿元,增长68.7%;财产险业务保费赔付0.9亿元,增长5.7%;车险业
务保费赔付6.4亿元,下降5.0%。
【例 3】(2021 新疆兵团)2016 年全年 H 市健康和意外险业务保费收入约
为多少亿元?
A.7.5 B.6.9
C.6.4 D.6.1
【解析】3.给2018年,求2016年的值,中间间隔一年,求间隔基期量;先
求出r ,间隔基期=现期/(1+r )。主体为“健康和意外险业务保费收入”,
间 间
14根据“健康和意外险业务保费收入9.1亿元,增长21.6%,增速同比增加5个百
分 点 ” 可 知 , r=21.6% , 高 减 低 加 → r=21.6%-5%=16.6% , r
1 2 间
=21.6%+16.6%+21.6%*16.6%≈21.6%+16.6%+21.6%*(1/6)=38.2%+3.6%=41.8%;
间隔基期=现期/(1+r )≈9.1/(1+41.8%),选项差距小,截三位,原式转化
间
为91/142。
方法一:正常计算。首位商6、次位商4,结果64开头,对应C项。
方法二:百化分。14.3%≈1/7,则142可以看成1/7,转化为9.1÷(1/7)
=9.1*7→有效数字637,四舍五入取前两位→64,对应C项。【选C】
【注意】
1.可以先“现期/(1+21.6%)”算出2017年的量,再“2017年的量/(1+16.6%)”
算出2016年的量,但计算两次除法比较麻烦。
2.以材料的时间2018年为现期。
3.所有乘法除法只要有特殊数字,都可以用百化分,甚至没有百分数也可以
用百化分,本质是数字之间的转化,只考虑有效数字,不用考虑小数点。
二、年均增长率
例:2015年存款100万,每年利率都是10%(复利),18年有多少钱?
年均增长率——比较大小
识别:年均增长最快、年均增速排序
公式:(1+r)n=现期量/基期量(n为现期和基期的年份差)
技巧:n相同,直接比较“现期/基期”
注:n的确定和年均增长量相同
【注意】年均增长率:
151.例:2015年存款100万,每年利率都是10%(复利),2018年有多少钱?
答:与“复利”相对的是“单利”→假设本金为100万、一年的利率为10%,
则每年的利息都是10万,2年总利息是 20万,5年总利息是50万;“复利”→
利滚利,2015 年为 100 万,2016 年=100*(1+10%),2017 年=100*(1+10%)*
(1+10%)=100*(1+10%)²,2018年=100*(1+10%)*(1+10%)*(1+10%)=100*
(1+10%)³;2018 年是现期、2015 年是基期,现期=基期*(1+r )³→现期/
年均
基期=(1+r )³→(1+r )n=现期量/基期量,n是现期和基期的年份之差。
年均 年均
2.年均增长率——比较大小(主要考查):
(1)识别:年均增长最快/最慢、年均增速排序。
(2)公式:(1+r)n=现期量/基期量(n为现期和基期的年份差)。
(3)技巧:n相同,直接比较“现期/基期”(送分题)。
(4)注:n(常规给哪两年就用哪两年;五年规划→基期前推一年,年份差
n一定为5)的确定和年均增长量相同。
(5)例:小邓在2016年有100万、2024年有800万,小马在2016年有1000
亿、2024年有3000亿。问:2016~2024年,小邓和小马谁年均增长得更快?
答:小邓→800万/100 万→8倍,小马:3000 亿/1000亿→3 倍;问题时间
都是2016~2024年,“现期/基期”倍数越大,年均增长更快,小邓整体增长更
快,则小邓平均每年增长更快。感兴趣的同学可以课后算一下,保持r 不变,
年均
哪一年小邓超过小马。
16【例 1】(2021 联考)2009~2019 年,城镇私营单位平均工资年均增长率
最高的是:
A.科学研究、技术服务和地质勘查业
B.信息传输、计算机服务和软件业
C.金融业
D.建筑业
【解析】1.问题时间为2009~2019 年;问“年均增长率最高”,年均增长
率比较问题。给的就是平均工资,不涉及平均数,主体为“城镇私营单位”。现
期为2019 年,基期为 2009 年,n相同,直接比较“现期/基期”,找“2019年
/2009年”最大的。科学研究、技术服务和地质勘查业:67642/26187=2+;信息
传输、计算机服务和软件业:85301/28166=3+;金融业:76107/30452=2+;建筑
17业:54167/19867=2+。综上,仅信息传输、计算机服务和软件业倍数超过3倍,
其年均增长率最大,对应B项。【选B】
【注意】利用常识选题:科研行业可能不了解,可能工资待遇不是特别高;
信息传输、计算机服务和软件业属于互联网相关(例如进大厂→阿里巴巴、字节
跳动、网易、华为,大厂程序员工资高),这10年是互联网的10年,增长是最
快的。若不了解这些行业、角度,可以慢慢养成这样的意识,遇到了解的行业可
能对做题有帮助。
【例2】(2022北京)将①金属耐磨材料、②陶瓷耐磨材料和③树脂耐磨材
料按2014~2020年消费量年均增速(以2014年为基础)从高到低排列,以下正
确的是:
A.①②③ B.③②①
C.②③① D.①③②
【解析】2.以2014年为基础→2014年是基期,2020年是现期。“年均增速
从高到低排列”→年均增长率比较,比较“现期/基期”。①金属耐磨材料:
416/359=1+;②陶瓷耐磨材料:24/30=0.8;③树脂耐磨材料:48/50=0.9+。综上,
从高到低排列为①③②,对应D项。【选D】
【注意】
1.一整篇材料有5道题,做题时从材料中筛选需要的数据。
2.很多同学认为:陶瓷耐磨材料、树脂耐磨材料是下降的→年均增长率为负,
从高到低排列为①②③,会错选 A项。“现期/基期”倍数越大→r 越大,无论
18是上升、还是下降,必然成立。例如基期为 100,现期为 80→“现期/基期”的
倍数为0.8、r为-20%,现期为90→“现期/基期”的倍数为0.9、r为-10%,发
现0.8倍<0.9倍、-20%<-10%。
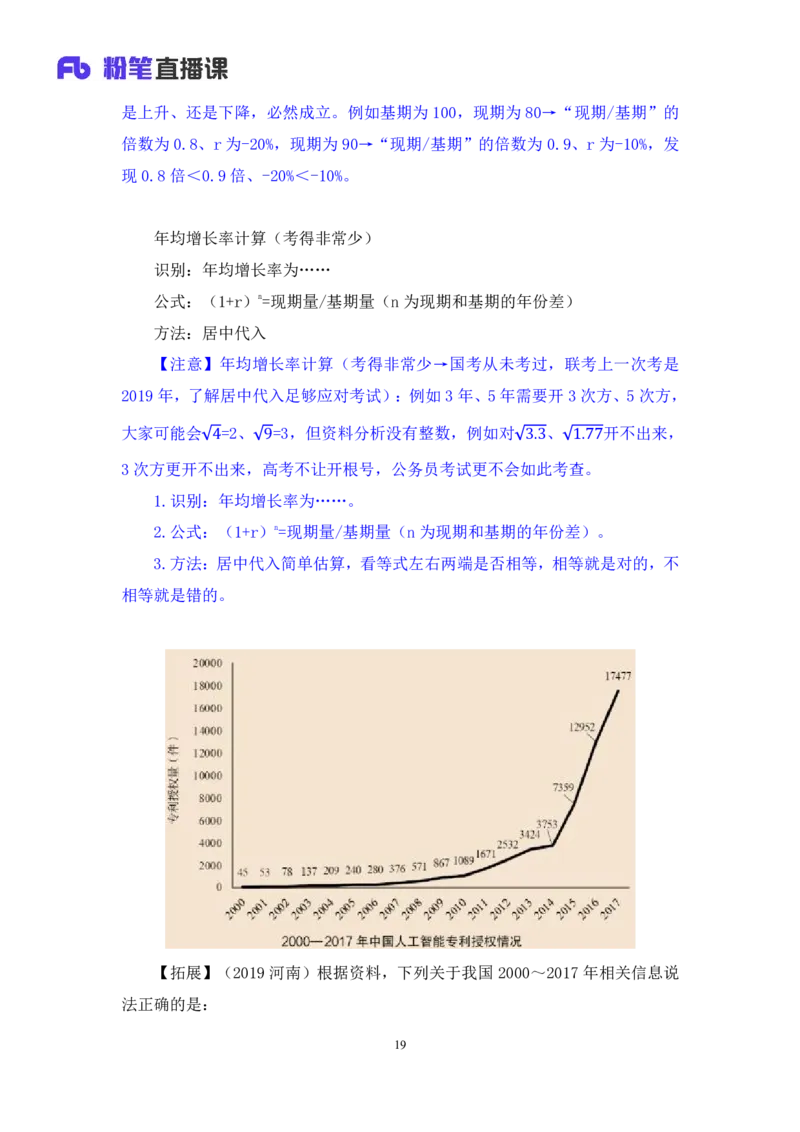
年均增长率计算(考得非常少)
识别:年均增长率为……
公式:(1+r)n=现期量/基期量(n为现期和基期的年份差)
方法:居中代入
【注意】年均增长率计算(考得非常少→国考从未考过,联考上一次考是
2019年,了解居中代入足够应对考试):例如3年、5年需要开3次方、5次方,
大家可能会 =2、 =3,但资料分析没有整数,例如对 、 开不出来,
3次方更开不4出来,高9 考不让开根号,公务员考试更不会如3.此3 考查1.。77
1.识别:年均增长率为……。
2.公式:(1+r)n=现期量/基期量(n为现期和基期的年份差)。
3.方法:居中代入简单估算,看等式左右两端是否相等,相等就是对的,不
相等就是错的。
【拓展】(2019河南)根据资料,下列关于我国2000~2017年相关信息说
法正确的是:
19B.2014年至2017年人工智能领域专利授权量年均增速为120%
【解析】拓展.B项:问题时间为2014年~2017年,年均增速计算问题,代
入公式:(1+r )n=现期/基期→(1+r )³=17477/3753=4+,代入r =120%=1.2,
年均 年均 年均
(1+1.2)³=2.2³>2³=8>4+,说明不成立,描述错误。【不选】
【例 3】(2024 广东)2019~2021 年,全国县域农业农村信息化建设县均
社会资本投入的年均增长率约为:
A.10% B.21%
C.32% D.43%
【解析】3.问题时间为2019~2021 年,主体为“全国县域农业农村信息化
建设县均社会资本投入”,代入公式:(1+r )n=现期/基期→(1+r)²≈3588/2054,
年均
选项差距大,截2位→3588/21→1.7,结合选项居中代入(代入介于选项正中间、
最好算、比较整的数),假设r =30%(B、C项的中间),1.3²=1.69,比1.7
年均
略小一点点,则真实r 比30%略大一点点,对应C项。【选C】
年均
【注意】
1.不建议两个增长率相加再除以2或总增长率/2,有时误差比较大,容易出
错,且没有居中代入好算。例如本题标准增长率是75%左右,75%/2≈37%,与答
案32%差很远,误差很大。
202.20以内常见平方数、10以内立方数可以不背,会背是好事,因为考频很
低,出现了现场算一下即可,但百化分一定要背。
3.居中代入→例如57%和43%→挑50%代入。
三、混合增长率
题型识别:
①求增长率,无法直接计算
②主体之间有和差关系
例:已知前三季度增长率,四季度增长率,求全年增长率。
例如:
①固定搭配:进口+出口=进出口、城镇+农村=全国、邮政+电信=邮电
②时间累计型:1至11月+12月=全年、一季度+二季度=上半年
③逻辑型:A+非A=全部(税收收入+其他收入=总收入)
判断口诀:
(1)混合后总体居中(最小r<总体r<最大r)
补例1:2019 年进口增长了 10%,出口增长了 20%,则进出口可能增长了多
少?
A.8% B.9%
C.14% D.21%
补例2:2019 年进出口增长了 10%,出口增长了 20%,则进口可能增长了多
少?
A.8% B.12%
C.14% D.21%
【注意】混合增长率(必考、考频高):重点、难点。
1.题型识别:
(1)求增长率,无法直接计算。
(2)主体之间有和差关系。
21(3)例如已知前三季度增长率,四季度增长率,求全年增长率,不知道全
年今年、去年的量、增长量,无法直接计算,不要想直接算的角度,考虑材料所
给数据有无和差关系→前三季度+四季度=全年,考查混合增长率。
2.常见和差关系:
(1)固定搭配:进口+出口=进出口、城镇+农村=全国、邮政+电信=邮电、
研究生=博士研究生+硕士研究生(2016年山东考查过)。甚至材料涉及进出口、
城乡、邮政、电信基本必考混合增长率。
(2)时间累计型(考查最多,所有材料都有可能把时间作为区分):1 至
11月+12月=全年、一季度+二季度=上半年、前三季度+四季度=全年。
(3)逻辑型:A+非A=全部(税收收入+其他收入=总收入)、20岁以上+20
岁以下=总体、限额以上+限额以下=总体、实物+非实物=总体、男生+女生=总体。
3.判断口诀:混合后总体居中(最小r<总体r<最大r)。
(1)例如男生行测平均分为 70 分,女生行测平均分为 80分,则全班整体
平均分在70~80分之间(是加权平均的过程,不是简单的加和→70+80)。再如
男生平均身高为1.9米,女生平均身高为1.7米,则全班所有人的平均身高介于
1.7~1.9米之间。
(2)补例:
①2019年进口增长了10%,出口增长了20%,则进出口可能增长了多少?
A.8% B.9%
C.14% D.21%
答:混合后总体居中,10%<r <20%,仅C项满足。
进出口
②2019年进出口增长了10%,出口增长了20%,则进口可能增长了多少?
A.8% B.12%
C.14% D.21%
答:混合后总体居中,r <r (10%)<20%,仅A项满足。
进口 进出口
2021年,中国跨境电商交易规模达14.2万亿元,占我国货物进出口总额的
比例为36.3%。其中出口跨境电商交易规模11万亿元,同比增速13.4%;进口跨
境电商交易规模3.2万亿元,同比增速14.3%。2017—2022年第一季度,中国跨
22境电商领域共发生262次投资,投资总金额654.91亿元。
【例1】(2023山东)2021年,我国跨境电商交易规模同比增长:
A.12.8% B.13.4%
C.13.6% D.14.3%
【解析】1.“2021年,中国跨境电商交易规模达14.2万亿元”,有现期值
14.2 万亿,没有基期量,也没有增长量,没有办法算同比增速,“其中出口跨
境电商交易规模 11 万亿元,同比增速 13.4%;进口跨境电商交易规模 3.2 万亿
元,同比增速14.3%”,出现“其中”,就是总分结构,后面分了两个部分,一
个部分是出口,一个部分是进口,跨境就是和中国之外的地方做交易,跨境其实
就是进出口的事情,求进出口总体的增速,混合后总体居中,在 13.4%~14.3%
之间,只有C项满足。【选C】
2020年江苏省……全省网上零售额10602亿元,增长10.0%。其中,实物商
品网上零售额增长13.9%,增速比上年快5.2个百分点,占社会消费品零售总额
37086亿元的比重为24.9%,提高2.7个百分点。
【例2】(2022江苏)能够从上述资料中推出的是:
A.略
B.2020年江苏非实物商品网上零售额增速高于13.9%
C.略
D.略
【解析】2.综合分析,只看B项即可。
B项:出现“非”,一定是矛盾关系,求增速,一定考查混合增长率。想到
总体居中,找数据,出现非实物,就有实物,不是拿数比大小然后去排列,永远
把总体摆在中间,全省增长率 10%一定在中间,实物增长率13.9%在右边,非实
物增长率在左边,非实物增长率<10%<13.9%,说法错误,不选。【不选】
2022年1月末,我国人民币存款余额236.07万亿元,同比增长9.2%,增速
分别比上月末和上年同期低0.1个和1.2个百分点,1月份人民币存款增加3.83
万亿元,同比多增2627亿元,其中,住户存款增加5.41万亿元,非金融企业存
23款减少1.4万亿元,财政性存款增加5849亿元。1月末,外币存款余额1.02万
亿美元,同比增长9%。1月份外币存款增加272亿美元,同比少增228亿美元。
【拓展】(2022联考)2022年1月末,我国本外币存款余额同比增速在以下
哪个范围内?
A.低于5% B.5%~10%之间
C.10%~19%之间 D.高于19%
【解析】拓展.本题有些另类,没有任何计算量,用了一个比较新颖的词,
本外币,本外币=本币+外币,求本外币的同比增速。本币是人民币,“2022年1
月末,我国人民币存款余额 236.07 万亿元,同比增长9.2%”,增长率是 9.2%;
外币是所有的外汇储备,“1月末,外币存款余额1.02万亿美元,同比增长9%”,
增长率是9%。本外币存款余额同比增速9%~9.2%之间,选择B项。【选B】
②偏向基数较大的(材料无基期,做题时用现期近似代替基期)
例:100gA溶液浓度5%,100gB溶液浓度10%,混合之后浓度?
A.6% B.7.5%
C.9%
例:100gA溶液浓度5%,400gB溶液浓度10%,混合之后浓度?
A.6% B.7.5%
C.9%
例:出口400万同比增速5%,进口100万同比增速10%,混合之后增速约?
A.6% B.7.5%
C.9%
【注意】偏向基数较大的(材料无基期,做题时用现期近似代替基期)。比
如男生平均分80分,女生平均分70分,总平均分在70~80分之间,更靠近70
还是80看人数。如果男生人数和女生人数一样多,则平均分是75分。如果男生
人数多,想象一个天平,天平会向男生倾斜,会更靠近80分,在75~80分之间。
如果女生人数多,天平会向女生倾斜,则在 70~75分之间。资料分析的材料一
般都不给基期量,给现期量,混合增长率一般是用来比一下大小,所以一般用现
期近似代替基期即可。
241.例1:100gA溶液浓度5%,100gB溶液浓度10%,混合之后浓度?
A.6% B.7.5%
C.9%
答:等量混合,取中点,选择B项。
2.例2:100gA溶液浓度5%,400gB溶液浓度10%,混合之后浓度?
A.6% B.7.5%
C.9%
答:B 溶液的量更多,混合后会从 7.5%更靠近 B溶液的 10%,在 7.5%~10%
之间,选择C项。
3.例:出口400万同比增速5%,进口100万同比增速10%,混合之后增速约?
A.6% B.7.5%
C.9%
答:混合后中点是7.5%,偏向量大的,靠近400万的5%,在5%~7.5%之间,
选择A项。
2018年H市完成邮电业务总量108.2亿元。其中,邮政业务总量40.8亿元,
同比增长26.5%;电信业务总量67.4亿元,同比增长56.7%。年末移动电话用户
达到 341 万户,其中,3G 移动电话用户达到 25.7 万户,4G 移动电话用户达到
241.4万户。全市互联网接入用户89.9万户,其中,新增互联网用户23.8万户。
【例3】(2021新疆兵团)2018年H市邮电业务总量同比增速在下列哪一个
范围内?
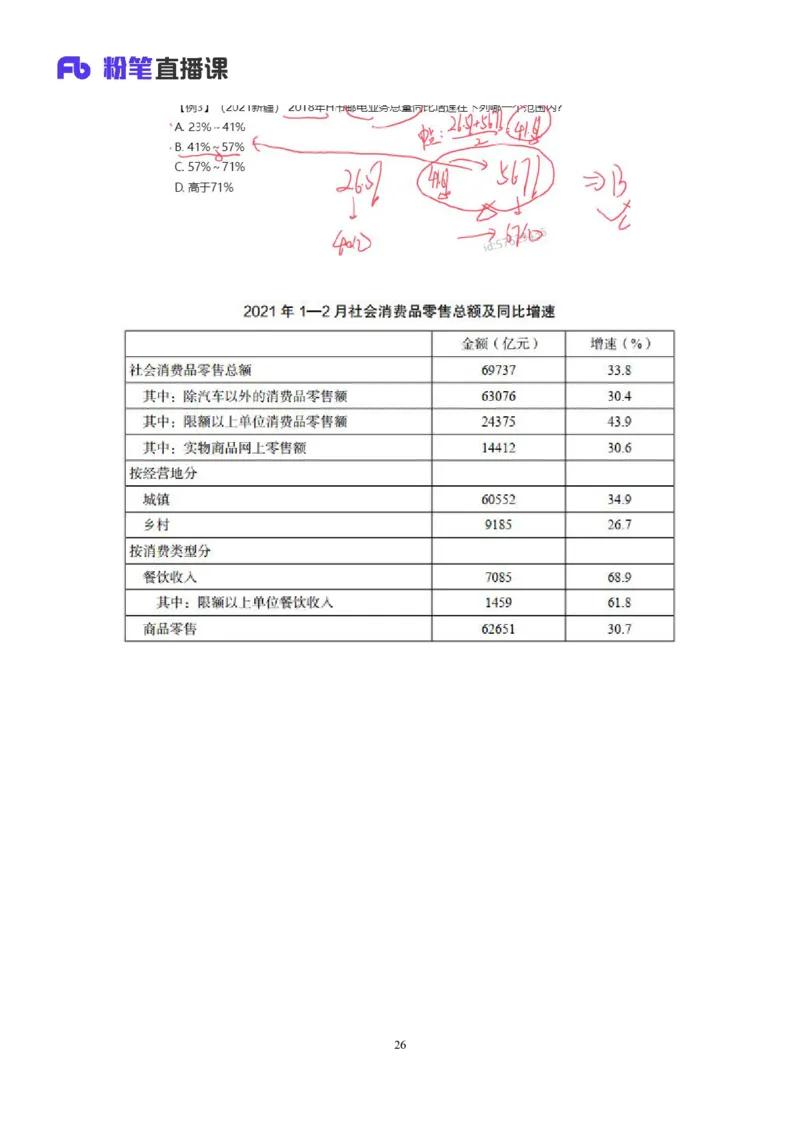
A.23%~41% B.41%~57%
C.57%~71% D.高于71%
【解析】3.问题时间与材料时间一致,是现期。“2018 年 H 市完成邮电业
务总量108.2亿元”,后面出现“其中”,有总分结构,邮电业务总量分为邮政
业务和电信业务,而且 40.8+67.4=108.2,是混合增长率,故总体增长率在
26.5%~56.7%之间,但是 A、B 项都和这个区间都有一段交叉,26.5%对应40亿
元,56.7%对应67亿元,靠近大的67亿元这边,中点是(26.5%+56.7%)/2=41.6%,
偏向右边,在41.6%~56.7%之间,在B项内,选择B项。【选B】
2526【例 4】(2024 四川)2021 年 1~2 月,限额以下单位餐饮收入同比约增长
了:
A.67% B.71%
C.76% D.83%
【解析】4.餐饮收入有前缀,是限额以下,限额以下单位餐饮收入+限额以
上单位餐饮收入=总的单位餐饮收入,总的单位餐饮收入增长率 68.9%在中间,
限额以上单位餐饮收入增长率61.8%在左边,剩下的限额以下单位餐饮收入增长
率在右边,比 68.9%大,B、C、D 项都满足比 68.9%大。看偏向,限额以上单位
餐饮收入是1459亿,餐饮收入是7085亿,有和差关系,则限额以下单位餐饮收
入是5000+,靠近右边限额以下单位餐饮收入,离右边更近,用左边衡量,左边
距离是 68.9%-61.8%=7.1%,右边距离<7.1%,限额以下单位餐饮收入增长率会
小于68.9%+7.1%=76%,选择B项。【选B】
27【注意】还可以代入,已经排除了A项,代入D项83%,左边距离是7.1%,
右边距离是14.1%,左边还更近,右边量大,应该右边更近,所以D项不对,排
除。代入 C 项,左边和右边距离都是 7.1%,说明左右两边一样重,右边量大,
应该右边更近,所以C项是不对的,排除,选择B项。
2020年,东部地区互联网业务收入11227亿元,同比增长14.8%,增速较上
年同期回落9个百分点。中部地区互联网业务收入448.1亿元,同比增长3.4%,
增速较上年同期回落 53.1个百分点。西部地区互联网业务收入 497.2 亿元,同
比增长6.9%,增速较上年同期回落15.2个百分点。东北地区互联网业务收入47.1
亿元,同比增长9.1%。
2020 年,互联网业务累计收入居前 5 名的广东(增长 5.2%)、北京(增长
21.5%)、上海(增长 20.9%)、浙江(增长 24.4%)和江苏(增长 8.0%)共完成
互联网业务收入10706亿元,同比增长15.1%,增速超过全国平均水平2.6个百
分点,占全国(扣除跨地区企业)比重达87.6%,占比较上年同期提高0.8个百
分点。
【例5】(2021联考)2020年,东部地区除广东、北京、上海、浙江和江苏
之外的省市互联网业务收入约比2019年:
A.增长9% B.增长19%
28C.减少9% D.减少19%
【解析】5.除什么之外也是矛盾关系,5 省市+除它们之外的=东部,“2020
年,东部地区互联网业务收入11227亿元,同比增长14.8%……2020年,互联网
业务累计收入居前 5 名的广东(增长 5.2%)、北京(增长 21.5%)、上海(增长
20.9%)、浙江(增长24.4%)和江苏(增长8.0%)共完成互联网业务收入10706
亿元,同比增长 15.1%”,混合增长率,总体居中,除它们之外的增长率<14.8%
<15.1%,做题还有一个常识角度,正常国家经济是稳中有升的,除了某些夕阳
产业可能下降,其他大部分都是增长的,所以 90%概率是增长的,A项大概率正
确。C、D 项为什么不对,可以通过精准计算明确排除。线段法,画一条线段,
14.8%写中间,前 5 名 15.1%写右边,剩下的写左边,量写下面,右边是 10706
亿,左边是东部-前 5 名≈11200-10700≈500,量之比是 500:10700≈1:20,
距离之比是 20:1,右边是 15.1%-14.8%=0.3%,20 份是 20*0.3%=6%,故?
=14.8%-6%=8.8%,最接近A项。【选A】
知识点强化——线段法(用于混合增长率的精确计算)
解题逻辑:
混合增长率的题目先用口诀“混合之后总体居中,偏向量大的”来解决(90%
以上);
如果无法锁定唯一答案才需要用线段法计算
【注意】知识点强化——线段法(用于混合增长率的精确计算)。解题逻辑:
混合增长率的题目先用口诀“混合之后总体居中,偏向量大的”来解决(90%以
上)。如果无法锁定唯一答案才需要用线段法计算。
29线段法的运用口诀:
1.部分在两边,总体在中间;
2.距离和量成反比。
例:溶液 A克,浓度 a%;溶液 B 克,浓度 b%。混合后的溶液浓度为 x%(a
<x<b)
3分钟证明原理,感兴趣就听,不感兴趣就记操作
练习 1.A 溶液 100 克,浓度 10%;B 溶液 100 克,浓度 30%。混合后的溶液
浓度为多少?
练习 2.A 溶液 100 克,浓度 10%;B 溶液 200 克,浓度 40%。混合后的溶液
浓度为多少?
练习 3:全年消费 4000 元,同比增长 5%,上半年消费 1000 元,同比增长
2%,下半年消费3000元,问下半年消费同比增长率为多少?
【注意】线段法的运用口诀:
1.部分在两边,总体在中间;
2.距离和量成反比。
(1)例:溶液 A 克,浓度 a%;溶液 B 克,浓度 b%。混合后的溶液浓度为
x%(a<x<b)。
(2)原理(3分钟证明原理,感兴趣就听,不感兴趣就记操作):(A*a%+B*b%)
/(A+B)=x%,A*a%+B*b%=A*x%+B*x%,合并同类项,B*b%-B*x%=A*x%-A*a%,去
掉百分号,B(b-x)=A*(x-a),(b-x)/(x-a)=A/B。如下图,画一条线段,
左边两个点的距离是x-a,右边两个点的距离是b-x,下面是A:B,距离和量成
反比。
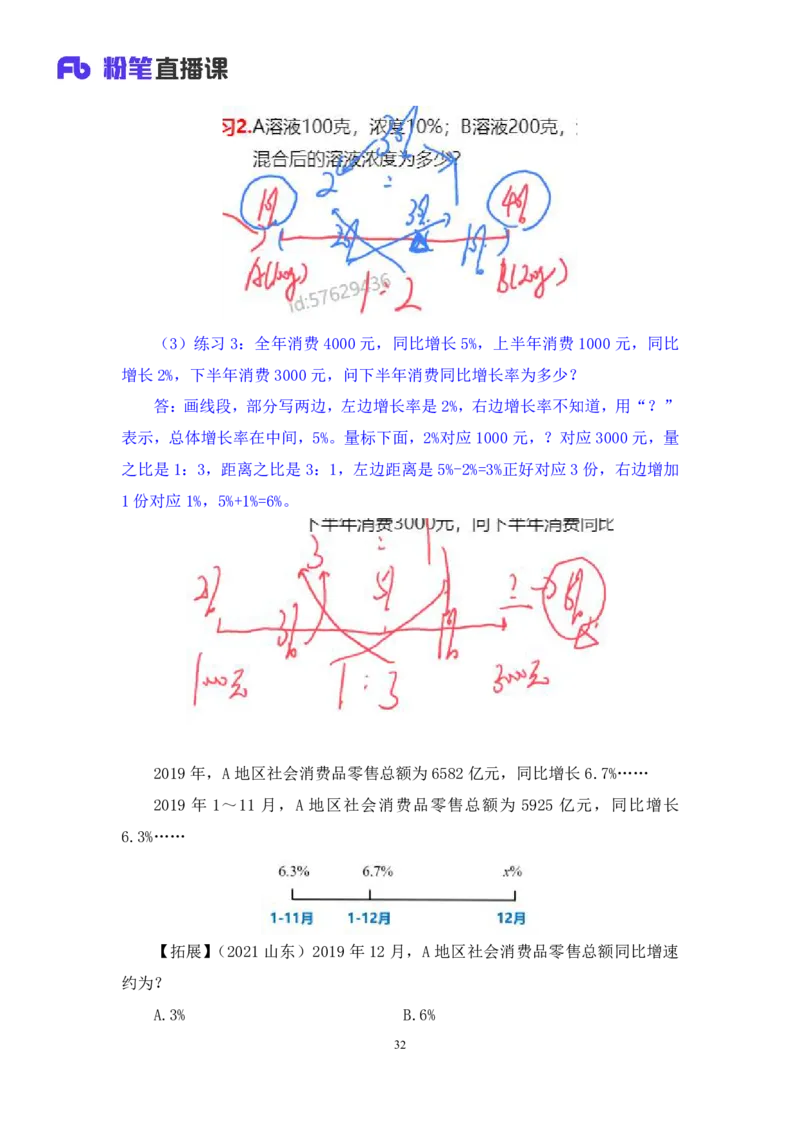
303.练习:
(1)练习1.A溶液100克,浓度10%;B溶液100克,浓度30%。混合后的
溶液浓度为多少?
答:等量混合,混合后是20%,(10%+30%)/2=20%。画线段,把部分写两边,
小的在左边,大的在右边。左边是A溶液100g,浓度是10%;右边是B溶液100g,
浓度是30%。量之比是1:1,距离和量成反比,距离之比也是1:1,混完后中
点距离左边右边都是1份,混合后相当于在正中点,即20%。
(2)练习2.A溶液100克,浓度10%;B溶液200克,浓度40%。混合后的
溶液浓度为多少?
答:画线段,把部分写两边,小的在左边,大的在右边。左边是A溶液100g,
浓度是 10%;右边是B 溶液 200g,浓度 40%。量之比 A:B=1:2,距离之比写上
面是2:1,说明左边长度:右边长度=2:1,10%到40%的总长度是30%,左边是
20%长度,右边是10%长度,混合后是30%。
31(3)练习 3:全年消费 4000元,同比增长 5%,上半年消费 1000 元,同比
增长2%,下半年消费3000元,问下半年消费同比增长率为多少?
答:画线段,部分写两边,左边增长率是2%,右边增长率不知道,用“?”
表示,总体增长率在中间,5%。量标下面,2%对应1000元,?对应3000元,量
之比是1:3,距离之比是3:1,左边距离是5%-2%=3%正好对应3份,右边增加
1份对应1%,5%+1%=6%。
2019年,A地区社会消费品零售总额为6582亿元,同比增长6.7%……
2019 年 1~11 月,A 地区社会消费品零售总额为 5925 亿元,同比增长
6.3%……
【拓展】(2021 山东)2019 年 12 月,A 地区社会消费品零售总额同比增速
约为?
A.3% B.6%
32C.10% D.15%
【解析】拓展.给了 2019 年、2019 年 1~11 月,求 2019 年 12 月,混合增
长率,1~11月+12月=全年,混合后增长率即1~12月增长率6.7%居中,排除A、
B项,C、D项都大于6.7%,距离和量成反比,1~11月的零售总额约为5900亿,
12月的零售总额约为6582-5925=600+亿,5900:600+≈10:1,距离和量成反比,
距离之比是1:10,左边1份对应0.4%,则右边10份对应4%,所求为6.7%+4%=10.7%,
最接近C项。【选C】
【注意】线段法的运用口诀:
1.部分在两边,总体在中间;
2.距离和量成反比。
33【注意】截位直除时不要把截几位记错。
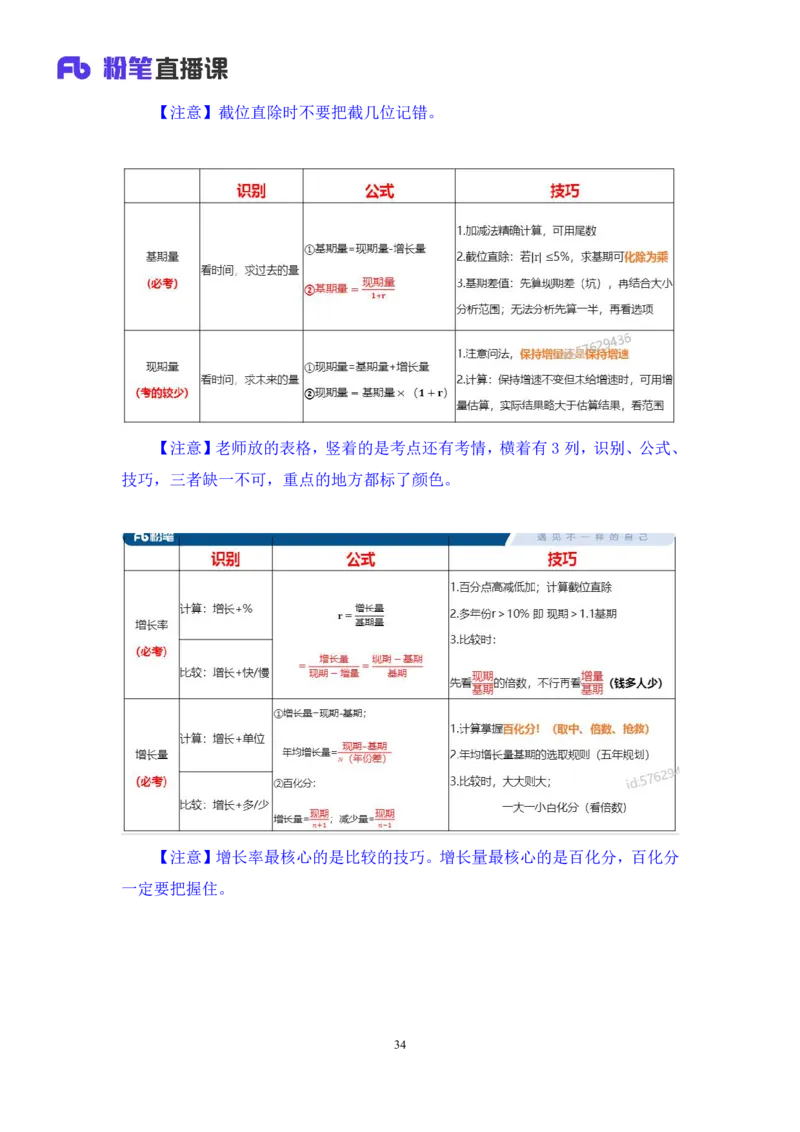
【注意】老师放的表格,竖着的是考点还有考情,横着有3列,识别、公式、
技巧,三者缺一不可,重点的地方都标了颜色。
【注意】增长率最核心的是比较的技巧。增长量最核心的是百化分,百化分
一定要把握住。
34【注意】平均数的增长量没有讲,联考 2020年考过一次,考频非常低,所
以课堂上没有讲,但是不难,A/B-A/B*[(1+b)/(1+a)],化简后和两期比重
差的公式一样,但是不能用两期比重差的结论,因为平均数的增长量是具体值,
不是百分数,不会小于增速之差。
【注意】
1.年均增长率的计算考查非常少,上次考到是四五年前。
2.复习建议(最后再唠叨几句)。
(1)课程至少再看一遍,重点看不懂的地方,查缺补漏,不留死角。看到
能条理清晰的默写题型识别、公式、技巧为止。
(2)把每天上课的知识点、思维导图,手写整理成笔记。要求:根据我给
35的模板内容调整成自己的内容。
(3)找数与速算的练习:微信小程序搜“粉笔快练”,小程序是免费的,
没有广告和链接,纯福利。有4个模块,下面两部分是帮助做言语理解,上面两
部分提供给资料分析的,速算点进去是右边的界面,里面有很多内容,只练首位
计算和百化分与分数即可。
(4)基础扎实后,每天做 3~4 篇资料分析。不建议一天“50 篇”,细水
长流即可,反复巩固。4 篇 25 分钟就是普通人的水平,如果数学很强,可以定
到20分钟以内。注意:前期以正确率为主,准确率达到80%左右后掐时间。
(5)上课人数一直减少,很多人坚持不住。请你坚持,资料分析一定会提
高。
【答案汇总】
倍数1-5:DCBBD
特殊增长率:间隔增长率1-3:CDC;年均增长率1-3:BDC;混合增长率1-5:
C不选BAA
36遇见不一样的自己
Be your better self
37