文档内容
方法精讲-资料 4
(笔记)
主讲教师:戚七
授课时间:2024.03.16
粉笔公考·官方微信方法精讲-资料 4(笔记)
资料分析 方法精讲4
学习任务:
1.课程内容:倍数与比值、特殊增长率
2.授课时长:3小时
3.对应讲义:第 193~201页
4.重点内容:
(1)倍数与增长率的相互转化
(2)间隔增长率的对应公式
(3)年均增长率的比较技巧
(4)混合增长率的两个结论
07 倍数与比值
08 特殊增长率
【注意】
1.本节课是资料精讲阶段最后一节课,包含两部分内容:倍数与比值(给比
例问题做收尾)、特殊增长率(对增长类知识的补充)。
2.最后会对资料分析进行一个整体梳理。
第七节 倍数与比值
基本术语:
倍数与比值用来表示两个量的相对关系。
A是 B的n倍:n=A/B。
A比 B增长(多)r倍:r=A/B-1。
A比 B的比值:A/B。
倍数:
1.倍数用来表示两者的相对关系。
12.问法区分:
(1)现期倍数。
(2)基期倍数。
【注意】倍数与比值:本质也是比例,是 A/B的形式,分子 A、分母B的增
长率对应a和b。
1.倍数用来表示两者的相对关系。
2.倍数考法简单,只考现期和基期,不考两期;可能在问法上设陷阱,审题
一定要注意看好问法。
倍数的问法区分
①A 是B的几倍:A/B
②A 比B增长(多、高)几倍:(A-B)/B=A/B-1
倍数=增长率+1
增长倍数=增长率
③A 超过B的 N倍→A>B*N
【注意】倍数的问法区分:
1.A 是B的几倍:A/B。
2.A 比B增长(多、高)几倍:(A-B)/B=A/B-1。本质上可理解为增长率,
注意列式形式上有“-1”;倍数=增长率+1、增长倍数=增长率。例:r=70%→是
1.7倍→增长0.7 倍。
3.A 超过B的 N倍→A>B*N:“超过”即“>”,不存在任何加减关系,“A
超过B的 N倍”即 A/B>N或A>B*N。
倍数
1.现期倍数
2.基期倍数
一、现期倍数
现期倍数
2识别:问题时间与材料时间一致+A 是B的多少倍
题型:倍数=A/B
速算:截位直除
【注意】现期倍数:
1.识别:问题时间与材料时间一致(现期时间)+A是B的多少倍。
2.题型:倍数=A/B。
3.速算:截位直除。
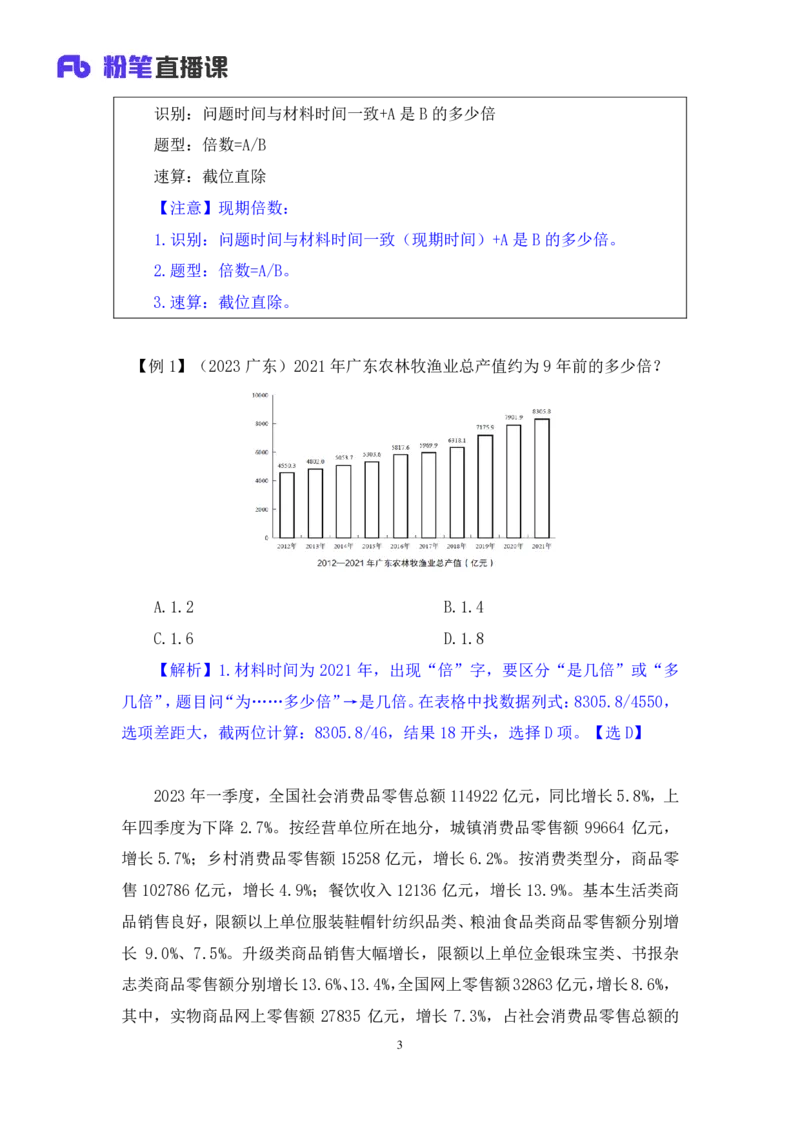
【例1】(2023 广东)2021年广东农林牧渔业总产值约为9 年前的多少倍?
A.1.2 B.1.4
C.1.6 D.1.8
【解析】1.材料时间为 2021 年,出现“倍”字,要区分“是几倍”或“多
几倍”,题目问“为……多少倍”→是几倍。在表格中找数据列式:8305.8/4550,
选项差距大,截两位计算:8305.8/46,结果 18开头,选择D 项。【选D】
2023 年一季度,全国社会消费品零售总额 114922亿元,同比增长 5.8%,上
年四季度为下降 2.7%。按经营单位所在地分,城镇消费品零售额 99664 亿元,
增长 5.7%;乡村消费品零售额 15258 亿元,增长 6.2%。按消费类型分,商品零
售 102786 亿元,增长 4.9%;餐饮收入 12136 亿元,增长 13.9%。基本生活类商
品销售良好,限额以上单位服装鞋帽针纺织品类、粮油食品类商品零售额分别增
长 9.0%、7.5%。升级类商品销售大幅增长,限额以上单位金银珠宝类、书报杂
志类商品零售额分别增长13.6%、13.4%,全国网上零售额32863亿元,增长8.6%,
其中,实物商品网上零售额 27835 亿元,增长 7.3%,占社会消费品零售总额的
3比重为24.2%。
【例 2】(2023 重庆事业单位)按经营单位所在地分,2023 年一季度,城
镇消费品零售额约比乡村消费品零售额多多少倍?
A.4.5 B.5.5
C.6.5 D.7.5。
【解析】2.问题时间与材料时间一致,问“比……多多少倍”→A/B-1,找
数据,由“城镇消费品零售额 99664亿元;乡村消费品零售额 15258亿元”可列
式:A/B-1=99664/15258-1=6+-1=5+,选择 B项。【选B】
二、基期倍数
基期倍数
1.识别:问题时间在材料之前+A是 B的多少倍。
2.题型:
(1)没有给增长率:按照定义计算,基期 A/基期B。
(2)给增长率:A/B*[(1+b)/(1+a)](同基期比重、基期平均数公式)。
3.速算(同基期比重、基期平均数速算):
(1)选项差距大:所有数字截两位直除。
(2)选项差距小:
①计算 A/B(截位直除)。
②分析(1+b)/(1+a)与1的大小关系,结合选项确定答案。
【注意】基期倍数:
1.识别:问题时间在材料之前(过去的时间)+A是B的多少倍(倍数问法)。
2.题型:
(1)没有给增长率:按照定义计算→基期 A/基期B。
(2)给增长率:A/(1+a)÷[B/(1+b)]=A/B*[(1+b)/(1+a)](同基
期比重、基期平均数公式)。
3.速算(同基期比重、基期平均数速算):
(1)选项差距大:所有数字截两位直除。
(2)选项差距小:
4①计算 A/B(截位直除)。
②分析(1+b)/(1+a)与1的大小关系,结合选项确定答案。
2017 年,国内旅游市场高速增长,入出境市场平稳发展,供给侧结构性改
革成效明显。国内旅游人数50.01亿人次,比上年同期增长 12.8%;入出境旅游
总人数2.7亿人次,增长 3.7%;全年实现旅游总收入5.40万亿元,增长 15.1%;
全年全国旅游业对 GDP的综合贡献为9.13 万亿元,占 GDP总量的 11.04%;旅游
直接就业 2825 万人,旅游直接和间接就业 7990 万人,占全国就业总人口的
10.28%。
【例 3】(2021 浙江)2016 年,全国国内旅游人数约为入出境旅游总人数
的多少倍?
A.17 B.19
C.21 D.23
【解析】3.问题时间在材料时间之前→基期时间,问“为……多少倍”,题
型为基期倍数问题。找数据:“国内旅游人数 50.01 亿人次,比上年同期增长
12.8%;入出境旅游总人数 2.7亿人次,增长 3.7%”,列式:50.01/2.7*(1+3.7%)
/(1+12.8%),选项差距小,截三位,50.01/2.7=19-,(1+3.7%)/(1+12.8%)
<1,故所求=19-*1-<19,只有A项满足,选择 A项。【选A】
2020 年全国人口共141178万人,比 2010年增长了约5.38%。从地区分布上
看,2020 年东部地区人口占 39.93%,中部地区占 25.83%,西部地区占 27.12%,
东北地区占6.98%。与2010年相比,东部地区人口所占比重上升2.15个百分点,
中部地区下降0.79 个百分点,西部地区上升 0.22个百分点,东北地区下降 1.20
个百分点。
【例 4】(2022 青海)2010年,东部地区人口是东北地区人口的:
A.约 4.6倍 B.约5.7倍
C.约 6.5倍 D.约7.3倍
【解析】4.材料给 2020年,问题问 2010年,时间不一致,问过去,基期时
间;选项出现“倍”字,问的是“……是……的”,问是几倍→A/B,A 是东部
5地区人口、B 是东北地区人口。结合材料找数,“2020 年东部地区人口占
39.93%,……,东北地区占 6.98%。与 2010 年相比,东部地区人口所占比重上
升2.15 个百分点,……,东北地区下降 1.20个百分点”,给的是占比,没有给
具体量,占比都是针对于全国人口,总体相同,部分量之比=比重之比;求基期,
高减低加,所求=2010 年 A 的占比/2010 年 B 的占比=(39.93%-2.15%)/
(6.98%+1.2%)=37.78/8.18=4+,对应 A项。【选A】
【注意】
1.相同整体中,部分量之比=部分比重之比。
2.材料没有直接给 a和b,可以回归本质:基期 A/基期B。
【注意】倍数总结:题型识别上,关键是“倍”字。
1.A 是B+倍→A/B。
2.看到“倍”问法,往前看:
(1)是→直除。
(2)比……多→-1。
(3)超过→>。
3.现在时间→现期倍数→直接除。
4.过去时间→基期倍数→A/B*[(1+b)/(1+a)],套不了公式,直接“基
期A/基期 B”。
65.选项差距小速算:
(1)根据选项差距,截位直除 A/B。
(2)根据(1+b)/(1+a)与1的大小关系,结合选项选择。
6.相同整体中,部分量之间的倍数=部分所占比重之间的倍数。
【注意】上节课讲了比重、平均数共同的公式,倍数的公式也是通用的,A/B
是现期比例,A/B*[(1+b)/(1+a)]是基期比例。倍数不讨论两期,不会出现
两期倍数的题型。
第八节 特殊增长率
特殊增长率
1.间隔增长率
2.年均增长率
3.混合增长率
【注意】特殊增长率:无论是一般增长率还是特殊增长率,都属于增长率。
1.题型识别:增长+%,判定为增长率问题;增长+快/慢,为增长率比较问题。
2.常规能算的叫一般增长率,特殊增长率是材料给的数据不支持用常规方法
算,由于时间特殊或数据关系特殊,会有特殊技巧。
3.常见的考法有三类:
(1)间隔增长率(☆☆):难度不高,考频还可以,知道公式算法即可。
(2)年均增长率(☆):考频低,了解为主。
7(3)混合增长率(☆☆☆):考频高,技巧性强。
一、间隔增长率
1.识别:常见中间隔一年,求增长率。
2.引例:2020 年比 2019 年收入增长率为 r,2019 年比 2018 年收入增长率
1
为r,问 2020年比 2018年收入增长率是多少?
2
【注意】间隔增长率:
1.识别:常见中间隔一年,求增长率。
2.引例:2020 年比 2019 年收入增长率为 r,2019 年比 2018 年收入增长率
1
为r,问 2020年比 2018年收入增长率是多少?
2
3.推导:假设 2018年的量为M,现期=基期*(1+r),则 2019 年=M*(1+r),
2
2020 年=M*(1+r )*(1+r),求 2020 年比 2018 年的增长率,则 2020 年为现
2 1
期、2018年为基期,已知现期、基期,r=现期/基期-1=M*(1+r )*(1+r )/M-1=
2 1
(1+r)*(1+r)-1=1+r+r+r*r-1=r +r+r*r。
2 1 1 2 1 2 1 2 1 2
4.公式记忆:两个增长率之和(r+r )+两个增长率之积(r*r)。
1 2 1 2
5.间隔增长率一般都是三个时间、中间隔一个,不会出现隔好几个的问法;
即考试中只会隔一个时间,只要知道隔一个时间的算法即可。
间隔增长率 r=r+r+r*r 速算思路:
1 2 1 2
1.优先计算 r+r,结合选项排除。
1 2
【练习 1】(2017联考)8.5%+36%+8.5%*36%≈( )
A.47.6% B.40.4%
C.34.5% D.27.6%
2.若 r、r 的绝对值均小于 10%(|r *r|<1%),结合选项 r*r 可以忽略。
1 2 1 2 1 2
【练习 2】(2019广东)8.5%+6.6%+8.5%*6.6%≈( )
8A.13.7% B.15.7%
C.17.9% D.19.9%
3.排除无法确定答案——计算:一个不变,另一个百化分。
【练习 3】(2015北京)14.8%+10.1%+14.8%*10.1%≈( )
A.低于 20% B.20%~30%之间
C.30%~40%之间 D.高于40%
【注意】间隔增长率 r=r+r+r*r 速算思路:加法简单,重点放在加法上。
1 2 1 2
1.优先计算 r+r,结合选项排除。
1 2
练习 1:8.5%+36%=44.5%,后面还需要加乘积(正数),结果比 44.5%大,
选项中仅A项满足。
2.若 r、r 的绝对值均小于 10%(0.1-*0.1-=0.01-=1-%→|r *r|<1%),结
1 2 1 2
合选项r*r 可以忽略。
1 2
练习 2:8.5%+6.6%=15.1%,乘积是正数,结果>15.1%,排除 A项;8.5%、
6.6%都比 10%小,乘积=1-%,结果比15.1%大一点点(不到1%),对应 B项。
3.排除无法确定答案——计算:一个不变,另一个百化分。
(1)练习 3:14.8%+10.1%=24.9%,14.8%、10.1%均比 10%大,乘积不能忽
略,14.8%*10.1%≈14.8%*(1/10)=1.48%,所求≈24.9%+1.48%<30%,选择 B
项。
(2)只需要对其中一个百化分,另一个保留百分号形式即可,如果将 14.8%
看成1/7、10.1%看成1/10,1/7*(1/10)=1/70,还要转化成百分数,反而浪费
时间。
间隔增长率:
1.识别:常见中间隔一年,求增长率。
2.公式:r=r +r+r*r。
1 2 1 2
3.速算:
(1)先计算 r+r,结合选项排除。
1 2
(2)r、r 的绝对值均小于 10%时,|r*r|<1%(结合选项可忽略)。
1 2 1 2
(3)计算:百化分——把其中一个增长率转化为 1/n。
9【注意】间隔增长率:
1.识别:常见中间隔一年,求增长率。
2.公式:r=r +r+r*r。
1 2 1 2
3.速算:
(1)先计算 r+r,结合选项排除。
1 2
(2)r、r 的绝对值均小于 10%时,|r*r|<1%(结合选项可忽略)。
1 2 1 2
(3)计算:百化分——把其中一个增长率转化为 1/n。
4.间隔增长率不一定是隔一年,比如 2013 年、2015 年、2020 年,可以求
2020年对2013年的增长率。总结:只要是 3 个时间点可以从前往后写出来,给
了前与中、中与后时间的增长率,就可以用间隔增长率公式。看起来像“笑脸”,
称为“笑脸公式”,只要 3个时间点之间能连成一个笑脸,就可以利用间隔增长
率分析。
5.不需要刻意区分 r 和r,因为在列式中的计算过程是完全一样的。
1 2
6.r 、r 对应的是谁:比如 2018年、2019年、2020年,给了 2018 年、2019
1 2
年、2020 年的增长率,此时应该用 2019 年、2020年的增长率,所要的增长率是
中比前、后比中的两个增长率。
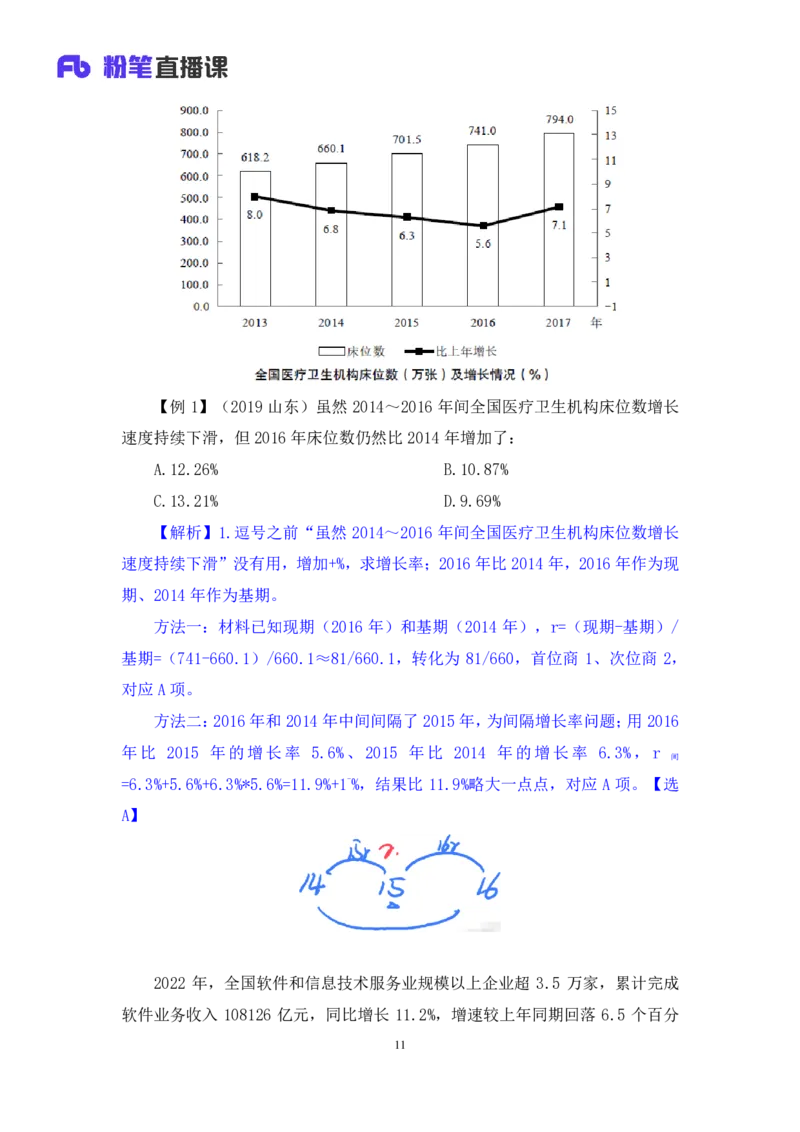
10【例 1】(2019 山东)虽然 2014~2016 年间全国医疗卫生机构床位数增长
速度持续下滑,但 2016年床位数仍然比 2014年增加了:
A.12.26% B.10.87%
C.13.21% D.9.69%
【解析】1.逗号之前“虽然 2014~2016 年间全国医疗卫生机构床位数增长
速度持续下滑”没有用,增加+%,求增长率;2016年比2014年,2016年作为现
期、2014 年作为基期。
方法一:材料已知现期(2016 年)和基期(2014 年),r=(现期-基期)/
基期=(741-660.1)/660.1≈81/660.1,转化为 81/660,首位商 1、次位商 2,
对应A项。
方法二:2016 年和2014年中间间隔了 2015年,为间隔增长率问题;用 2016
年比 2015 年的增长率 5.6%、2015 年比 2014 年的增长率 6.3%,r
间
=6.3%+5.6%+6.3%*5.6%=11.9%+1-%,结果比 11.9%略大一点点,对应 A 项。【选
A】
2022 年,全国软件和信息技术服务业规模以上企业超 3.5 万家,累计完成
软件业务收入 108126 亿元,同比增长 11.2%,增速较上年同期回落 6.5 个百分
11点。
【例 2】(2024 四川)2022 年,全国软件和信息技术服务业规模以上企业
累计完成软件业务收入约比2020年增长了:
A.16% B.23%
C.29% D.31%
【解析】2.问 2022年比2020年+增长+%,题型为间隔增长率问题。先找 2022
年、2021年的同比增长率,2022 年r=11.2%,2021年r=11.2%+6.5%=17.7%,间
隔 r=11.2%+17.7%+11.2%*17.7%=28.9%+11.2%*17.7%>28.9%,排除 A、B 项,
11.2%*17.7%≈1/9*17.7%≈2%,所求=28.9%+2%=31.9%,与 D项最接近。【选 D】
题型延伸 1:间隔倍数
识别:间隔一年,求倍数
2020年工资同比增长了10%,2019年同比增长了20%。则2020年工资是2018
年的多少倍?
两步走:
①先求出间隔增长率
②间隔倍数=间隔增长率+1
倍数=增长率 r+1
增长倍数=增长率 r
【注意】题型延伸 1:间隔倍数。
1.识别:间隔一年,求倍数。
2.例:时间上还是 2020 年比 2018 年,问“是几倍”,间隔时间+倍数,间
隔倍数问题,倍数=r+1→间隔倍数=间隔 r+1,先求出间隔增长率,间隔
r=10%+20%+10%*20%=30%+2%=32%,间隔倍数=32%+1=1.32倍。
3.倍数=增长率 r+1;增长倍数=增长率 r。
4.两步走:
(1)先求出间隔增长率。
(2)间隔倍数=间隔增长率+1。
12题型延伸 2:间隔基期量
识别:间隔一年,求基期。
2020 年工资额是 4000元,2020年工资同比增长了 10%,2019 年同比增长了
20%。则 2018年工资是多少元?
两步走:
①先求出间隔增长率。
②间隔基期=现期量/(1+间隔增长率)
基期量=现期量/(1+增长率r)
【注意】题型延伸 2:间隔基期量。
1.识别:间隔一年,求基期。
2.例:给2020 年,问2018 年,是之前的时间,2020年和 2018年中间间隔
2019 年,间隔时间,问量是多少,求间隔基期量。r =10%+20%+10%*20%=32%,
间
基期量=现期量/(1+增长率 r)→间隔基期=现期/(1+间隔 r)=4000/(1+32%)
≈3000。
3.两步走:
(1)先求出间隔增长率。
(2)间隔基期=现期量/(1+间隔增长率)。
2018年全年全市保费收入 65.4亿元,增长 0.7%。其中,寿险业务保费收入
39.5 亿元,下降 5.1%;健康和意外险业务保费收入 9.1 亿元,增长 21.6%,增
速同比增加5个百分点;财产险业务保费收入 3.4亿元,增长 25.2%;车险业务
保费收入13.3亿元,增长1.8%。全年支付各类赔款及给付21.2亿元,增长5.3%。
其中,寿险业务保费赔付 11.0亿元,增长 1.4%;健康和意外险业务保费赔付 3.0
亿元,增长68.7%;财产险业务保费赔付 0.9亿元,增长5.7%;车险业务保费赔
付6.4亿元,下降 5.0%。
【例 3】(2021 新疆兵团)2016 年全年全市健康和意外险业务保费收入约
为多少亿元?
A.7.5 B.6.9
13C.6.4 D.6.1
【解析】3.问 2016年,材料给2018 年,问过去,为间隔的基期时间;问“……
亿元”,求间隔基期量。结合材料找“全市健康和意外险业务保费收入”,已知
r=21.6%,“增加”用减法,r=21.6%-5%=16.6%,间隔r=21.6%+16.6%+21.6%*16.6%
1 2
≈38.2%+21.6%*(1/6)=38.2%+3.6%=41.8%。间隔基期=现期/(1+间隔r)=9.1/
(1+41.8%),选项差距小,截三位,原式转化为 91/142,首位商 6、次位商4,
对应C项。【选 C】
【注意】间隔类题型:
1.间隔增长率(☆):有三个时间点,增长率可以用“笑脸”形式连起来,
求出增长率,间隔 r=r+r+r*r。
1 2 1 2
2.间隔倍数:间隔增长率+1。
3.间隔基期:现期/(1+间隔r)。
4.间隔增长量:r =1/n,现期/(n+1)。
间
5.间隔平均数增长率:算出间隔 a、间隔 b,代入公式(a-b)/(1+b)。
二、年均增长率
1.识别:年均增长最快、年均增速排序;年均增长率为……。
2.例:2020 年收入 A 元,2017 年收入为 B 元。2017 年到 2020 年每年的同
比增长率均为r。
143.公式:(1+r)N=现期量/基期量,N为现期和基期的年份差。
4.技巧:比较:N相同,直接比较“现期量/基期量”(考查较多)。
5.年均增长率与年均增长量的年份差 N完全相同。
【回顾】年均增长问题——年份差 N的确定:年份差N=现期时间-基期时间
(没有差异)。
注:五年规划和江苏省考,基期均需往前推一年
【注意】年均增长率:考频不高,技巧性较强,了解思路很重要。年均增长
量是每年增长量相同,年均增长率是每年增长率相同。
1.识别:年均增长最快、年均增速排序;年均增长率为……。
2.例:2020 年收入 A 元,2017 年收入为 B 元。2017 年到 2020 年每年的同
比增长率均为r。2018年=B*(1+r)、2019 年=B*(1+r)*(1+r)=B*(1+r)²、
2020 年=B*(1+r)³=A→A/B=(1+r)³,A 是时间靠后的数据→现期,B 是时间
靠前的数据→基期,r为年均增长率,3=增长次数=年份差。
3.公式:(1+r)N=现期量/基期量,N 为现期和基期的年份差。年均增长率
与年均增长量的年份差 N完全相同(一般情况直接减、五年规划年份差为 5)。
154.技巧:比较(考查较多)→N 相同,直接比较“现期量/基期量”。年均
增长率问题本身考查不多,一般考查比较题型,比如给 2015~2018 年,问谁的
年均增长率大,时间段一样,现期、基期一致,说明年份差 N相同,r的大小只
受到“现期/基期”倍数的影响,故年均增长率大小比较问题,只需要比较“现
期/基期”的倍数大小。
【例 1】(2022 联考)关于中国部分钓具进出口贸易状况,能从上述资料中
推出的是:
A.2017~2020 年,进口额年均同比增速钓鱼竿快于钓线轮
B.略
C.略
D.略
【解析】1.A 项:问进口额年均同比增速。定位材料找钓鱼竿和钓线轮的进
口额数据,时间为 2017~2020 年,现期为 2020 年,基期为 2017 年,年份差相
同,比较“现期/基期”,钓鱼竿:5081/2184=2+,钓线轮:7623/1903=4+,即钓
鱼竿年均增速<钓线轮年均增速,说法错误。【不选】
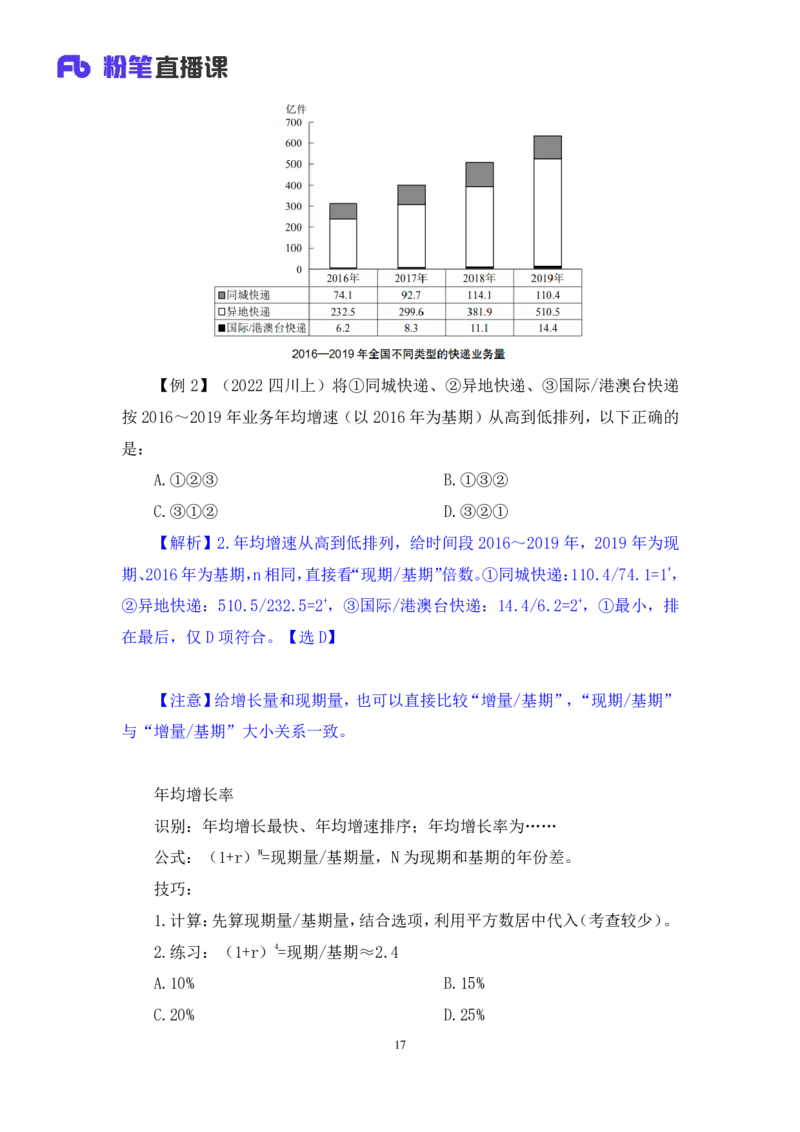
16【例 2】(2022 四川上)将①同城快递、②异地快递、③国际/港澳台快递
按2016~2019年业务年均增速(以2016 年为基期)从高到低排列,以下正确的
是:
A.①②③ B.①③②
C.③①② D.③②①
【解析】2.年均增速从高到低排列,给时间段 2016~2019 年,2019年为现
期、2016年为基期,n相同,直接看“现期/基期”倍数。①同城快递:110.4/74.1=1+,
②异地快递:510.5/232.5=2+,③国际/港澳台快递:14.4/6.2=2+,①最小,排
在最后,仅D项符合。【选 D】
【注意】给增长量和现期量,也可以直接比较“增量/基期”,“现期/基期”
与“增量/基期”大小关系一致。
年均增长率
识别:年均增长最快、年均增速排序;年均增长率为……
公式:(1+r)N=现期量/基期量,N 为现期和基期的年份差。
技巧:
1.计算:先算现期量/基期量,结合选项,利用平方数居中代入(考查较少)。
2.练习:(1+r)4=现期/基期≈2.4
A.10% B.15%
C.20% D.25%
173.必背平方数:11²=121;12²=144;13²=169;14²=196;15²=225;16²=256;
17²=289;18²=324;19²=361;21²=441。
【注意】年均增长率:
1.公式:(1+r)N=现期量/基期量,N 为现期和基期的年份差。不需要硬开
N次方,有技巧。
2.技巧:计算(考查较少)→先算“现期量/基期量”,结合选项,利用平
方数居中代入。
3.练习:(1+r)4=现期/基期≈2.4。
A.10% B.15%
C.20% D.25%
(1)答:(1+r)4=现期/基期≈2.4,居中代入(找中间比较整的数代入),
观察选项,15%和 20%比较居中,但是 20%比较整,因此比较好算,先代入 C 项:
(1+20%)4=1.24=1.44²<1.5²=2.25<2.4,说明(1+20%)4<(1+r)4,即 20%
<r,20%代小了,要选比 20%大的D项。
(2)居中代入,至少可以排除两个选项,如果只排除一个,就再代一次;
比如代入20%太大,排除 C、D项,再代入 10%,合适就选,小了就选 B项,最多
代两次可以出答案。
4.必背平方数(10²~21²):11²=121;12²=144;13²=169;14²=196;15²
=225;16²=256;17²=289;18²=324;19²=361;21²=441。
(1)11²=121:一个数*11,错位相加。
(2)12²=144、21²=441,成对记忆。
(3)13²=169、14²=196,放在一起记,3²的尾数对应9,4²的尾数对应 6。
(4)15²=225、25²=625、35²=1225、45²=2025:尾数均为“25”;2=1*2、
6=2*3、12=3*4、20=4*5→十位数字*(十位数字+1),则 95²=9025→9*10=90,
后两位为25。
(5)16²=256=28=44,联想手机内存,尾数为 6(64、128、256、1024 中只
有256尾数为 6)。
(6)17²=289(尾数为 9,7*4=28);18²=324(尾数为 4,8*4=32);19²
=361(尾数为 1,9*4=36)。
18(7)19²=361,联想到361°的品牌。
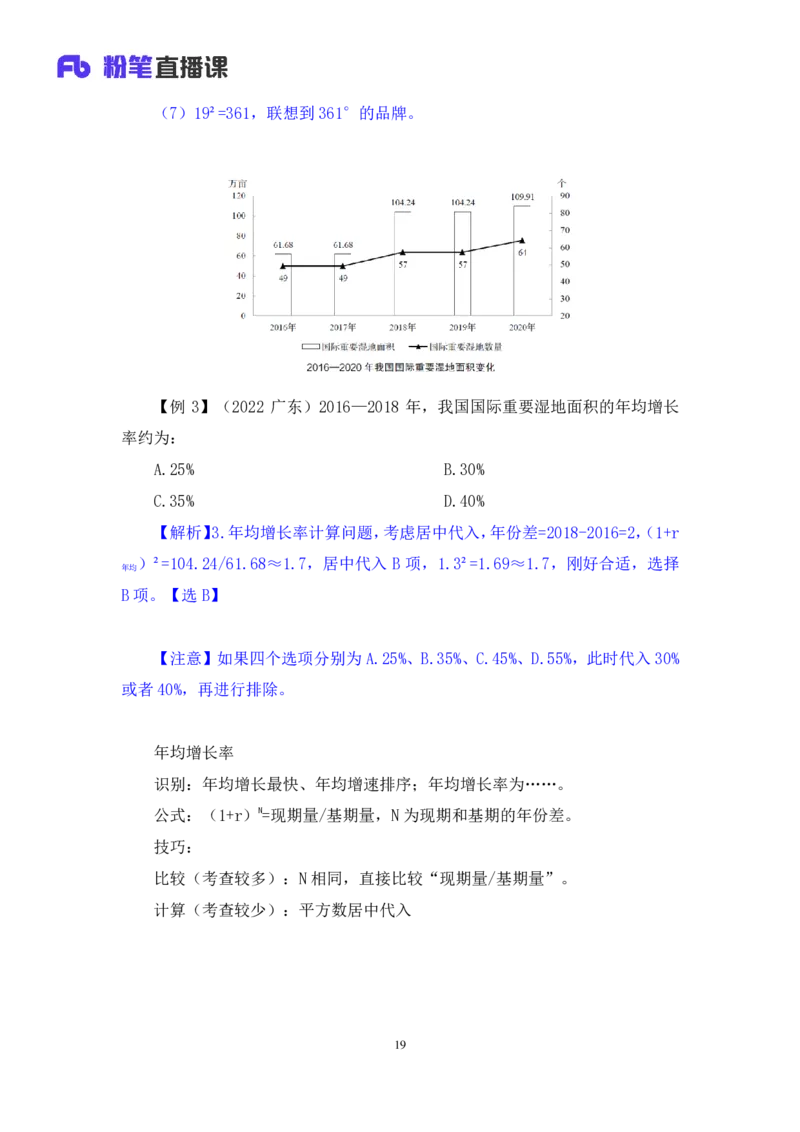
【例 3】(2022 广东)2016—2018 年,我国国际重要湿地面积的年均增长
率约为:
A.25% B.30%
C.35% D.40%
【解析】3.年均增长率计算问题,考虑居中代入,年份差=2018-2016=2,(1+r
)²=104.24/61.68≈1.7,居中代入 B 项,1.3²=1.69≈1.7,刚好合适,选择
年均
B项。【选B】
【注意】如果四个选项分别为 A.25%、B.35%、C.45%、D.55%,此时代入30%
或者40%,再进行排除。
年均增长率
识别:年均增长最快、年均增速排序;年均增长率为……。
公式:(1+r)N=现期量/基期量,N 为现期和基期的年份差。
技巧:
比较(考查较多):N相同,直接比较“现期量/基期量”。
计算(考查较少):平方数居中代入
19【注意】年均增长率:
1.识别:年均增长最快、年均增速排序;年均增长率为……。
2.公式:(1+r)N=现期量/基期量,N为现期和基期的年份差。
3.技巧:
(1)比较(考查较多):N相同,直接比较“现期量/基期量”。
(2)计算(考查较少):利用平方数居中代入;如果选项特别小,都在 10%
以内,随便蒙一个。
三、混合增长率
题型识别:部分 +部分 =整体,增长率关系
1 2
识别口诀:量之间是相加关系,率之间是混合关系
【常见】
①固定搭配:进口+出口=进出口、房产+地产=房地产、邮政+电信=邮电、城
镇+农村=全国
②时间累计:如:一季度+二季度=上半年
③逻辑型:A+非A=整体。如:税收收入+其他收入=总收入,规模以上+规模
以下=整体量
混合口诀:
(1)整体增速居中但不正中
(2)偏向基期量较大的
(3)计算:增速差与基期量成反比
混合口诀:整体增速居中但不正中(最小 r<整体r<最大 r)
【补例 1】2019 年进口增长了 10%,出口增长了 20%,则进出口可能增长了
20多少?
A.8% B.9%
C.14% D.21%
【补例 2】2019 年进出口增长了 10%,出口增长了 20%,则进口可能增长了
多少?
A.8% B.12%
C.14% D.21%
【注意】混合增长率:考频高、技巧性强,重点是识别。
1.题型识别:部分 +部分 =整体(部分相加得到整体),增长率关系。
1 2
2.识别口诀:量之间是相加关系(部分和整体之间有加法关系),率之间是
混合关系。
3.常见:
(1)固定搭配:进口+出口=进出口、房产+地产=房地产、邮政+电信=邮电、
城镇+农村=全国。
(2)时间累计:一季度+二季度=上半年。
(3)逻辑型:A+非 A=整体。如:税收收入+其他收入=总收入、规模以上+
规模以下=整体量。
(4)男生人数+女生人数=全班人数,则男生增长率和女生增长率混合得到
全班增长率。
4.混合口诀:
(1)整体增速居中但不正中。
(2)偏向基期量较大的。
(3)计算:增速差与基期量成反比。
5.混合口诀 1:整体增速居中但不正中(最小 r<整体 r<最大 r)。理解:
课间喝水,有100 度的开水和0度的冰水,想要得到能喝的温水,需要两杯水混
合,结果一定是 0度~100度之间。
(1)例:2019 年进口增长了 10%,出口增长了 20%,则进出口可能增长了
多少?
A.8% B.9%
21C.14% D.21%
答:进口和出口满足量之间的加法关系,此时增长率之间满足混合关系,结
果介于10%~20%之间,排除A、B、D项,直接选 C项。
(2)例:2019 年进出口增长了 10%,出口增长了 20%,则进口可能增长了
多少?
A.8% B.12%
C.14% D.21%
答:已知出口和进出口的增长率,出口20%和进口r混合,混合后整体是10%。
因为混合后居中,说明进口和出口一个大于 10%、一个小于 10%,即进口 r<进
出口(10%)<出口(20%),只有A项满足。
2021 年,中国跨境电商交易规模达 14.2万亿元,占我国货物进出口总额的
比例为36.3%。其中出口跨境电商交易规模 11万亿元,同比增速 13.4%;进口跨
境电商交易规模 3.2万亿元,同比增速 14.3%。2017—2022年第一季度,中国跨
境电商领域共发生 262次投资,投资总金额 654.91亿元。
【例 1】(2023 山东)2021年,我国跨境电商交易规模同比增长:
A.12.8% B.13.4%
C.13.6% D.14.3%
【解析】1.问题时间与材料时间一致,求增长率。中国跨境电商(14.2)=
出口跨境电商(11)+进口跨境电商(3.2),即混合关系。混合后居中→介于
13.4%~14.3%,只有 C项满足。【选C】
22【例 2】(2022四川下)2019年1~2月,我国包裏寄递量比去年同期:
A.下降了不到 10% B.下降了10%以上
C.上升了不到 10% D.上升了10%以上
【解析】2.问题时间 2019年1~2月,材料已知一季度(1~3月)和3月,
1~2 月=1~3 月-3 月,因为量相加时率才混合,减法转化成加法,转化为 1~2
月+3月=1~3月。主体是包裏寄递量,已知 3月为-10.8%,一季度为-12.3%,根
据混合后居中,因为-10.8%>-12.3%,则 r <-12.3%,对应 B项。【选B】
1~2月
2022 年,全国居民人均可支配收入 36883 元,比上年增长(以下如无特别
说明,均为同比名义增长)5.0%。分城乡看,城镇居民人均可支配收入 49283
元,增长3.9%;农村居民人均可支配收入 20133元,增长 6.3%。2022年,全国
居民人均消费支出 24538 元,比上年增长 1.8%。分城乡看,城镇居民人均消费
支出30391 元,增长 0.3%;农村居民人均消费支出 16632元,增长 4.5%。
23【例 3】(2023 广东)2022 年,全国居民人均收支盈余比上一年:(注:
收支盈余=收入-消费支出)
A.增加了约 5% B.减少了约5%
C.增加了约 12% D.减少了约12%
【解析】3.收支盈余=收入-消费支出→收入=收支盈余+消费支出,量相加、
率混合,收入的增速 5%,消费支出的增速 1.8%,混合后居中,故收支盈余的增
速大于 5%,肯定是正的,排除 B、D项;选择比 5%大的,只有C 项满足。【选 C】
混合口诀:
(2)偏向基期量较大的(哪个部分的基期量大,整体的增速就离谁近)
注:做题时一般用现期量近似代替基期量进行判断
【补例 3】2019 年出口额1500亿元,增长了 20%进口额1000 亿元,增长了
25%。则进出口总额增长了约多少?
A.19% B.22%
C.24% D.26%
【注意】混合口诀 2:混合后居中但不正中,偏向基期量较大的(哪个部分
的基期量大,整体的增速就离谁近)。
1.例:一杯 100 度的开水和一桶 0 度的冰水混合,混合后温度非常接近 0
度。如果是一杯 100度的开水和一滴 0度的冰水混合,0度的冰水对整体影响不
大,混合后温度非常接近 100度。
2.补例 3:利用混合后居中,20%和 25%混合,结果介于 20%~25%之间,排
除 A、D 项。偏向于(基期)量大的一方,即 1500/(1+20%)和 1000/(1+25%)
比较,因为题目中很少给基期,多数给现期,如果每道题都用“现期/(1+r)”
计算基期比较慢,从真题经验出发,多数题目一般用现期代替基期量分析即可。
现期比较,1500亿>1000亿,混合后偏向于 1500亿(出口),正中间=(20%+25%)
24/2=22.5%,结果介于 20%~22.5%之间,对应 B项。
3.注:做题时一般用现期量近似代替基期量进行判断。先计算平均值,然后
向一侧偏,最后选答案。
2018年H市完成邮电业务总量108.2亿元。其中,邮政业务总量40.8亿元,
同比增长26.5%;电信业务总量 67.4亿元,同比增长 56.7%。年末移动电话用户
达到 341 万户,其中,3G 移动电话用户达到 25.7 万户,4G 移动电话用户达到
241.4万户。全市互联网接入用户 89.9万户,其中,新增互联网用户 23.8万户。
【例 4】(2021 新疆兵团)2018 年 H 市邮电业务总量同比增速在下列哪一
个范围内?
A.23%~41% B.41%~57%
C.57%~71% D.高于71%
【解析】4.问题时间 2018 年,问同比增速,主体 H 市邮电业务总量,只给
了现期量,无法直接求。材料中给出邮政和电信,邮政+电信=邮电,考虑混合。
根据混合后居中,结果介于 26.5%~56.7%之间,排除C、D项。观察量,邮政 40.8
<电信 67.4,混合后偏向电信(56.7%),中间值=(26.5%+56.7%)/2≈41%,
所以结果介于41%~56.7%之间,对应B 项。【选B】
【拓展】(2024 国考)2023 年3月,我国机器人设备出口金额 0.7亿美元,
较上年增长 110.3%,进口金额 2.4 亿美元,较上年增长 68.5%。2023 年 1~3 月
我国机器人设备累计出口金额 1.9亿美元,较上年增长 62.1%,累计进口金额 6.9
亿美元,较上年增长 55.1%。
2023 年一季度,我国机器人设备进出口贸易逆差比上年同期:
25A.下降了不到 30% B.下降了30%以上
C.上升了不到 30% D.上升了30%以上
【解析】拓展.上升/下降+%,求增长率。材料没有给出逆差的数据,给出口
和进口,逆差=进口-出口→进口=出口+逆差,结合材料找数据,r =62.1%,r
出口
=55.1%,混合后居中,则62.1%>55.1%>r ,选项均符合;再根据偏向量大
进口 逆差
的,逆差=6.9-1.9=5 亿,偏向 5 亿,即右边离得近,左边离得远,左边距离为
62%-55%=7%,右边离得近→右边离不到 7 个点,r =55%-7-%=48+%,对应 D 项。
逆差
【选D】
混合增长率方法拓展——线段法(分析过程理解即可)
1.引例 1:浓度为 13%的溶液 A 克与浓度为 23%的溶液 B 克,混合后的浓度
为17%。求 A:B。
2.线段法口诀:混合之前写两边,混合之后写中间。距离和量成反比,根据
份数具体算。
3.距离指混合前和混合后的距离(也就是比例间作差)。
4.引例 2:浓度为 X%的溶液 200 克与浓度为 23%的溶液 50 克进行混合,混
合后的浓度是15%。求X。
5.引例 3:浓度为 13%的溶液 200 克与浓度为 23%的溶液 300 克进行混合。
求混合后的浓度。
【注意】混合增长率方法拓展——线段法(分析过程理解即可):学霸养成
课会有专项课程,非常详细地讲解了原理和和应用条件。
1.线段法口诀:混合之前写两边,混合之后写中间。距离和量成反比,根据
份数具体算。
262.距离指混合前和混合后的距离(也就是比例间作差)。
3.引例 1(混合前推混合后的比例):混合之前写两边(13%、A写左边,23%、
B写右边),混合之后(17%)写中间。距离与量成反比:距离就是比例的差值,
17%-13%=4%,23%-17%=6%,距离之比是 4%/6%=4/6=2/3;量对应比例的分母,所
以量(溶液)之比是 3/2=A/B。拓展——根据份数具体算:假设混合后是 100g,
按照3:2分,一共 5份,其中 1份对应 20g,所以3份就是60g,2份就是40g。
4.引例 2(混合后推混合前):混合之前写两边(x%、200 和 23%、50),
混合之后(15%)写中间。距离与量成反比:右侧距离是 8%,左侧距离未知;量
之比已知,200/50=4/1,所以距离之比为 1/4,4份对应8%,则 1份对应2%,说
明x%和 15%相差 2%,利用混合后居中,说明 15%>x%,则x%=13%。
5.引例 3(混合前推混合后的结果):混合之前写两边(13%、200 和 23%、
300),混合之后(r)写中间。距离与量成反比:距离未知,已知量之比,200/300=2/3,
则距离之比为 3/2,不能确定 3 份和 2 份具体对应多少,整体看:一共有 5 份,
即 13%到 23%有 5 份,总距离=23%-13%=10%,10%对应 5 份,所以 1 份对应 2%,
则2份对应 4%,3份对应6%。所求=13%+6%=19%,或者所求=23%-4%=19%。
27混合口诀:
(3)计算:增速差与基期量成反比(线段法)
增速差(距离):部分增速与整体增速的差值
注:做题时一般用现期量近似代替基期量进行计算
补例 4:2019 年进口额10亿元,增长了 20%;出口额40亿元,增长了 10%。
则进出口总额增长了约多少?
A.17.2% B.15.3%
C.13.5% D.11.9%
【注意】混合口诀:
1.补例 4:混合前写两边(20%、10,10%、40),混合后居中,偏向量大的
一边,中间值是 15%,结果介于10%~15%之间,排除A、B项。距离与量成反比:
增速差就是距离,严谨的“量”是比例的分母,r=增长量/基期量,所以是与基
期量成反比,但多数题目可以用现期量代替,量之比为 10/40=1/4,反比就是 4/1,
整体观察,一共是 1+4=5份,对应 20%-10%=10%,1份对应2%,所求=10%+2%=12%,
与D项最接近,当选。
2.误差来源:用现期量代替基期量会产生误差,根据真题数据分析,误差不
会很大,从经验来讲,选接近的结果即可。
混合增长率
题型识别:部分 +部分 =整体,增长率关系
1 2
识别口诀:量之间是相加关系,率之间是混合关系
速算口诀
(1)整体增速居中但不正中
(2)偏向基期量较大的
28(3)计算:增速差与基期量成反比。
注:
(1)做题时一般用现期量近似代替基期量。
(2)增速差:部分增速与整体增速的差值。
【注意】混合增长率:
1.题型识别:部分 +部分 =整体,增长率关系。
1 2
2.识别口诀:量之间是相加关系,率之间是混合关系。
3.速算口诀:能分析优先分析,利用前两条,能排除优先排除,能不动笔尽
量不动笔,不能排除再计算。
(1)整体增速居中但不正中。
(2)偏向基期量较大的。
(3)计算:增速差与基期量成反比。
4.注:
(1)做题时一般用现期量近似代替基期量。
(2)增速差:部分增速与整体增速的差值。
【注意】增长率问法小结:增长率考法很多,很丰富。
1.识别:增长/下降+%;增长/下降+快慢。
2.公式:r=增长量/基期量。
3.有三个时间,可以出现笑脸,考查间隔增长率,公式:r=r+r+r*r。
1 2 1 2
4.好多个年份,每年增长率都是 r,考查年均增长率(或者直接问年均增长
29率),公式:(1+r)N=现期/基期。
5.量之间满足①+②=③,此时率考虑混合,方法:混合后居中,偏向量大的
一方,增速差与基期量成反比(能分析先分析,最后再计算)。
6.出现平均/每/单位+增长/下降+%,考查平均数的增长率,公式:r=(a-b)
/(1+b)。
【练 1】(2019 广东)2018 年,我国全社会用电量 68449 亿千瓦时,同比
增长 8.5%,增幅同比提高 1.9 个百分点。具体来看,第一产业用电量 728 亿千
瓦时,同比增长 9.8%;第二产业用电量 47235 亿千瓦时,同比增长 7.2%;第三
产业用电量 10801 亿千瓦时,同比增长 12.7%;城乡居民生活用电量 9685 亿千
瓦时,同比增长 10.4%。
2018 年,我国全社会用电量较 2016 年增加了约:
A.13.7% B.15.7%
C.17.9% D.19.9%
【解析】练 1.2018 年和 2016 年中间间隔一年,问增加+%,求间隔增长率。
已知“2018 年,我国全社会用电量 68449 亿千瓦时,同比增长 8.5%,增幅同比
提高1.9 个百分点”,r =8.5%,r =8.5%-1.9%=6.6%,r =8.5%+6.6%+8.5%*6.6%。
1 2 间
两个数都不到 10%,乘积(不到 1%)可以忽略不计,r ≈15.1%+1-%,结果略大
间
于15.1%,对应B 项。【选B】
30【练 2】(2017 山东)合并计算 2016 年 1 季度营业收入最高的两个产业,
其营业收入总体增速最接近以下哪个数字?
A.4.4 B.5.1
C.5.7 D.6.4
【解析】练 2.“合并计算”就是相加,问“总体增速”。最高的两个产业
是工艺美术品和文化用品,量相加,率混合,考虑混合问题。混合后居中,结果
介于4.4%~6.3%之间,排除 A、D 项。看偏向,文化用品 6422>工艺美术品 3272,
中间值=(4.4%+6.3%)/2=5.35%,偏向文化用品(6.3%),结果介于 5.35%~6.3%
之间,对应C项。【选 C】
【注意】
1.资料公式总结:很多人公式不熟,不知道什么时候用哪个公式(不会审题),
所以从审题开始梳理。
(1)审题:先看时间+问题,判断基础题型,比如是现期还是基期,增长量
还是增长率。
(2)再看主题词,有两类情况:①一个词:对应一个量,比如产量、面积;
②两个词:有连接,比如占、均、倍,考查比例问题。
31(3)现期量:
①量的两种表达形式:基期+增长量,基期*(1+r)。
②比例:A/B。
(4)基期量:
①量的两种表达形式:现期-增长量,现期/(1+r)。
②比例:A/B*(1+b)/(1+a)。
(5)增长量:
①量的两种表达形式:现期-基期;如果已知现期量和增长率,百化分,
|r|=1/n,现期/(n±1)。
②比例:A/B*(a-b)/(1+a)。
(6)r:
①量:增长量/基期量。
②比例——平均数增长率:(a-b)/(1+b)。
2.复习建议(最后再唠叨几句):
(1)课程至少再看一遍(听一遍肯定不够),重点看不懂的地方,查缺补
漏,不留死角。
(2)把每天上课的知识点、思维导图,手写整理成笔记,截图不属于自己,
一定要手写强化记忆。建议格式:①题型特征;②公式/方法;③速算技巧。
(3)整理笔记后,每天做题。要求:前 30 天每天 10~15 道单题:按照单
个知识点刷题,速度不是问题,以做对为目标,目标正确率90%以上;30天后每
天 2~3 篇资料:限定时间,目标平均 7 分钟一篇,开始比较慢,逐渐提速,考
试中建议三篇资料 18~25分钟,正确率 80%以上。
(4)请你坚持到考前,资料分析一定会有质的提高。
3.寄语:曾经的“基期”都随它而去,未来的“现期”有无限可能。心态稳、
肯坚持,每天保持“持续增长”,多刷题,多总结,成绩提高才能“大大则大”。
不随波逐流做“平均数”,“混合平均”才会偏向你。最后,祝每位同学在公考
路上都能成为“比重”的分子!
4.作业:
(1)梳理公式、整理笔记,及时回顾。
32(2)今年的岸上,你们一个都不许少。
【答案汇总】
第七节:倍数与比值 1-4:DBAA
第八节:特殊增长率:间隔增长率 1-3:ADC;年均增长率 1-3:不选/DB;
混合增长率1-4:CBCB
33遇见不一样的自己
Be your better self
34