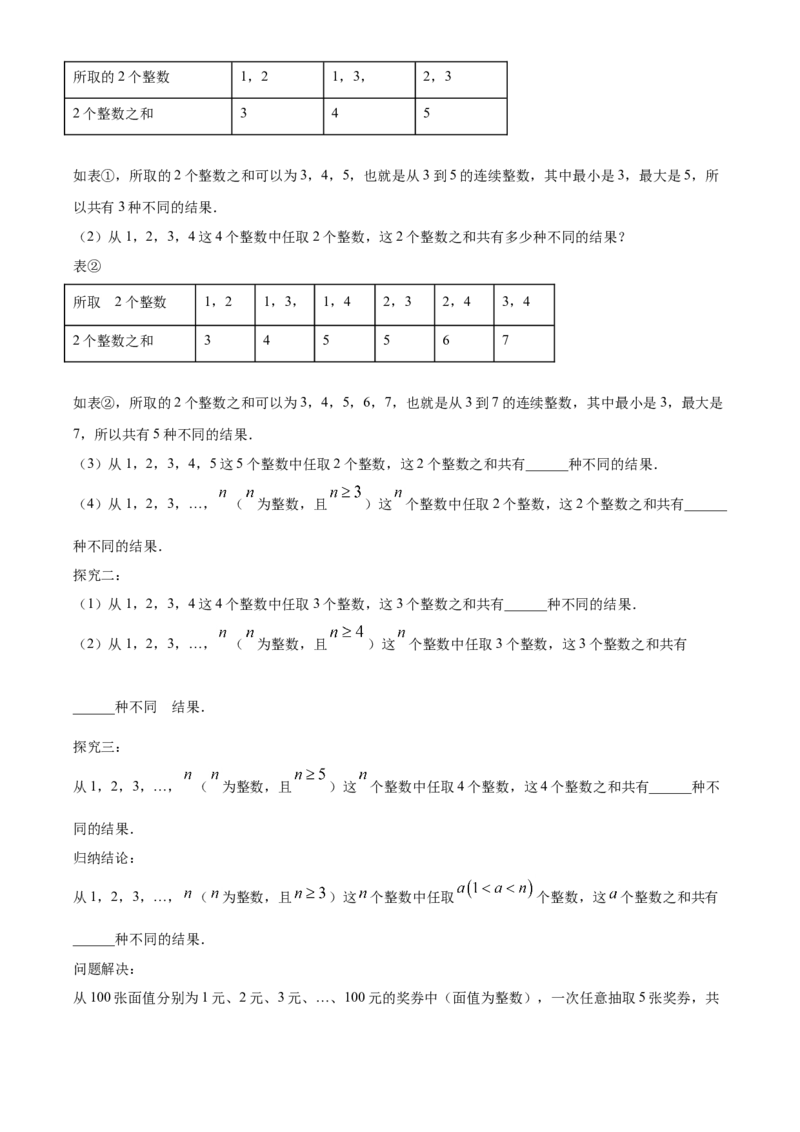文档内容
山东省青岛市 2020 年中考数学真题
(考试时间:120分钟;满分:120分)
说明:
1.本试题分第I卷和第II卷两部分,共24题,第I卷为选择题,共8小题,24分;
第II卷为填空题、作图题、解答题,共16小题,96分.
2.所有题目均在答题卡上作答,在试题上作答无效.
第I卷(共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.-4的绝对值是( )
A. 4 B. C. -4 D.
2.下列四个图形中,中心对称图形是( )
A. B. C. D.
3.2020年6月23日,中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号
的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用,22纳米=0.000000022米,将
0.000000022用科学记数法表示为( )
A. 22×108 B. 2.2×10-8 C. 0.22×10-7 D. 22×10-9
4.如图所示的几何体,其俯视图是( )
.
A B. C. D.
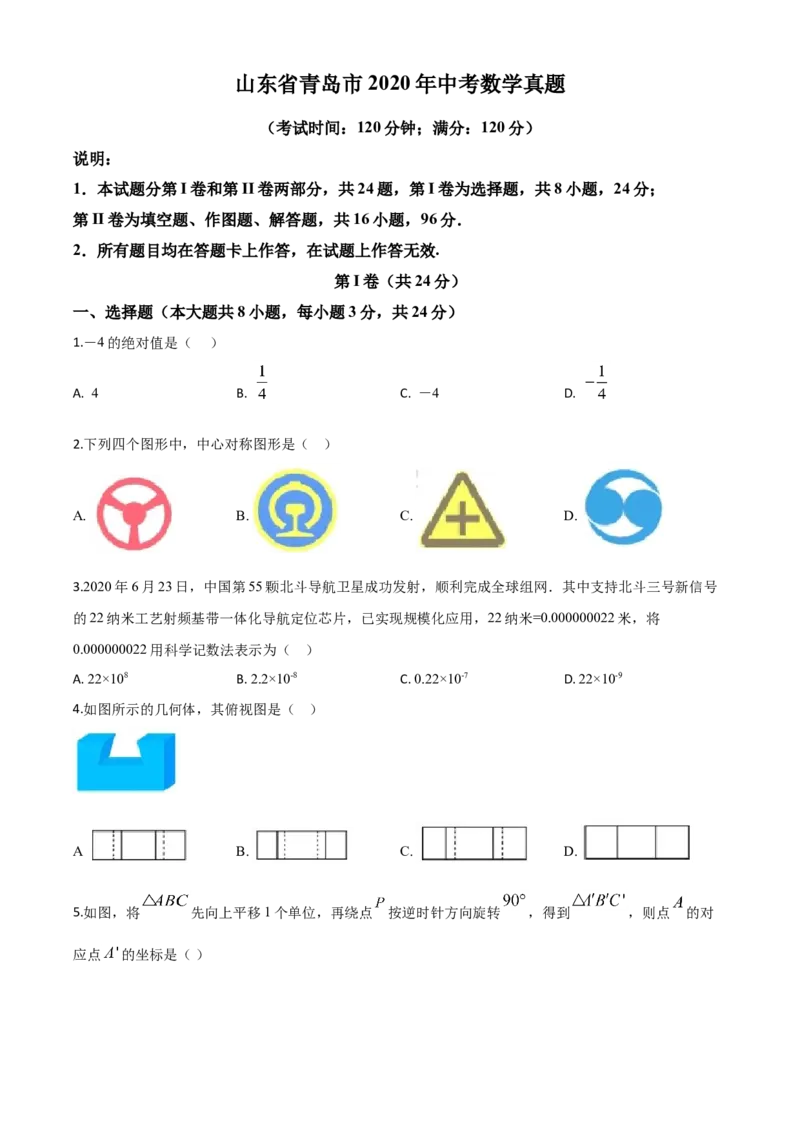
5.如图,将 先向上平移1个单位,再绕点 按逆时针方向旋转 ,得到 ,则点 的对
应点 的坐标是( )A. (0,4) B. (2,-2) C. (3,-2) D. (-1,4)
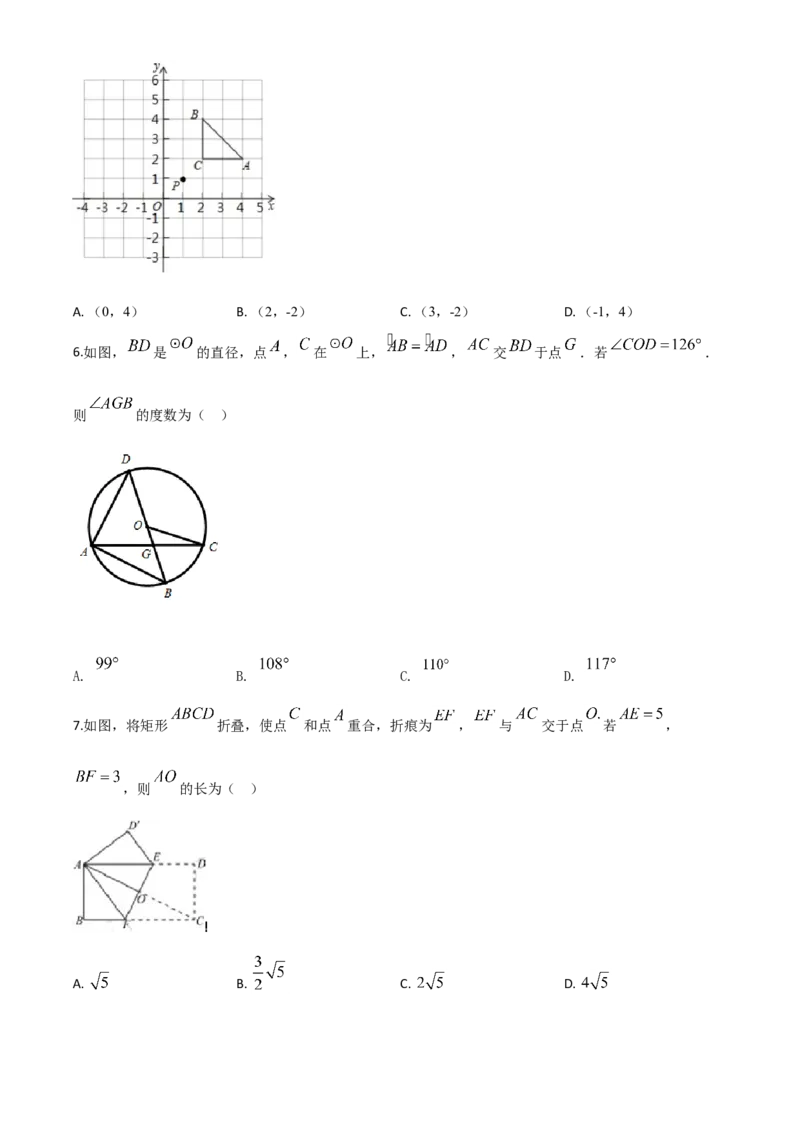
6.如图, 是 的直径,点 , 在 上, , 交 于点 .若 .
则 的度数为( )
A. B. C. D.
7.如图,将矩形 折叠,使点 和点 重合,折痕为 , 与 交于点 若 ,
,则 的长为( )
A. B. C. D.8.已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示,则一次函数
的图象可能是( )
A. B. C. D.
第Ⅱ卷(共96分)
二、填空题(本大题共6小题,每小题3分,共18分)
9.计算 的结果是___.
10.某公司要招聘一名职员,根据实际需要,从学历、经验和工作态度三个方面对甲、乙两名应聘者进行
了测试.测试成绩如下表所示.如果将学历、经验和工作态度三项得分按2:1:3的比例确定两人的最终得
分,并以此为依据确定录用者,那么__________将被录用(填甲或乙)
应聘者
甲 乙
项目
学历 9 8
经验 7 6
工作态度 5 7
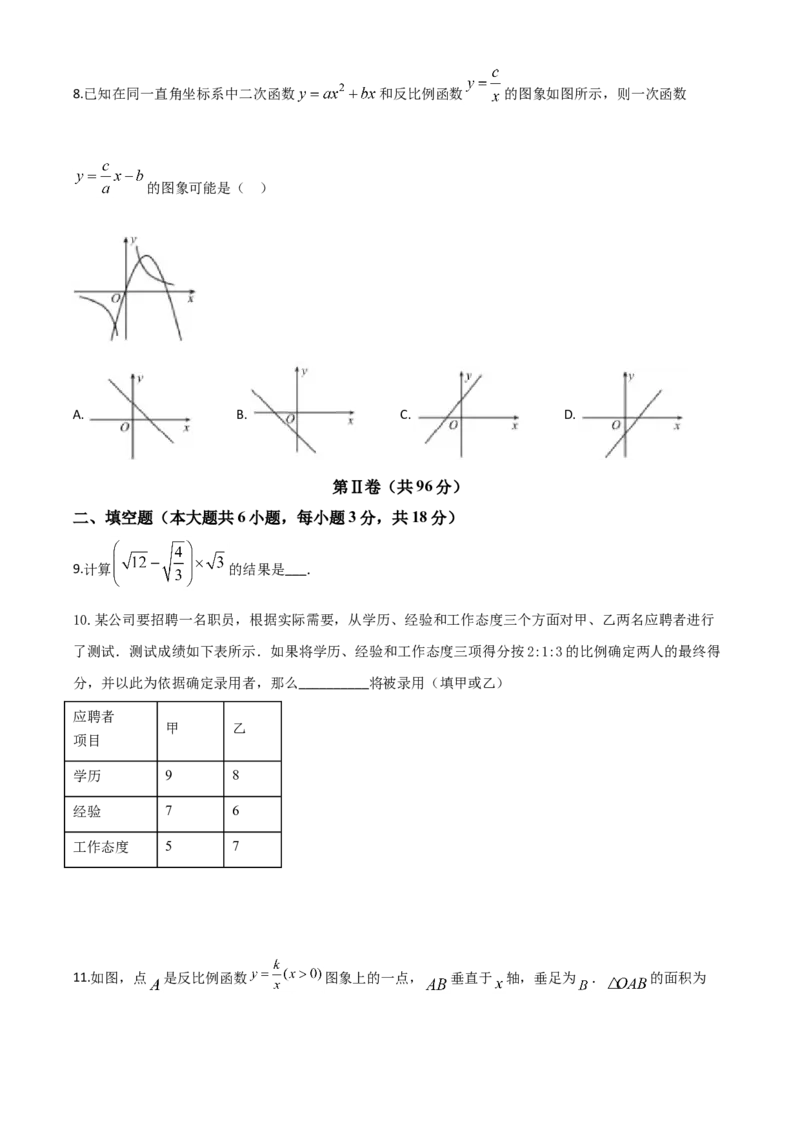
11.如图,点 是反比例函数 图象上的一点, 垂直于 轴,垂足为 . 的面积为6.若点 也在此函数的图象上,则 __________.
12.抛物线 ( 为常数)与 轴交点的个数是__________.
13.如图,在正方形 中,对角线 与 交于点 ,点 在 的延长线上,连接 ,点 是
的中点,连接 交 于点 .若 , ,则点 到 的距离为__________.
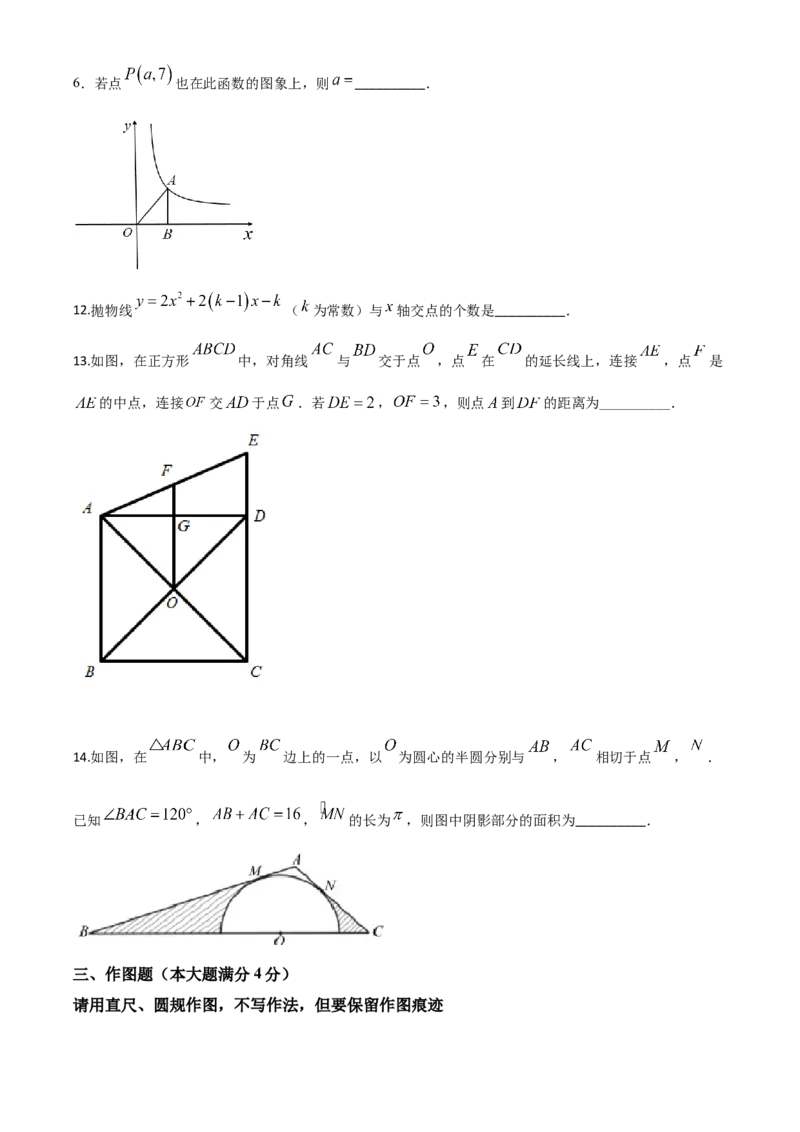
14.如图,在 中, 为 边上的一点,以 为圆心的半圆分别与 , 相切于点 , .
已知 , , 的长为 ,则图中阴影部分的面积为__________.
三、作图题(本大题满分4分)
请用直尺、圆规作图,不写作法,但要保留作图痕迹15.已知: ..
求作: ,使它经过点 和点 ,并且圆心 在 的平分线上,
四、解答题(本大题共9小题,共74分)
16.(1)计算: (2)解不等式组:
17.小颖和小亮都想去观看“垃圾分类”宣传演出,但只有一张入场券,于是他们设计了一个“配紫色”游
戏: , 是两个可以自由转动的转盘,每个转盘都被分成面积相等的几个扇形、同时转动两个转盘,如
果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色.若配成紫色,则小颖去观看,
否则小亮去观看.这个游戏对双方公平吗?请说明理由.
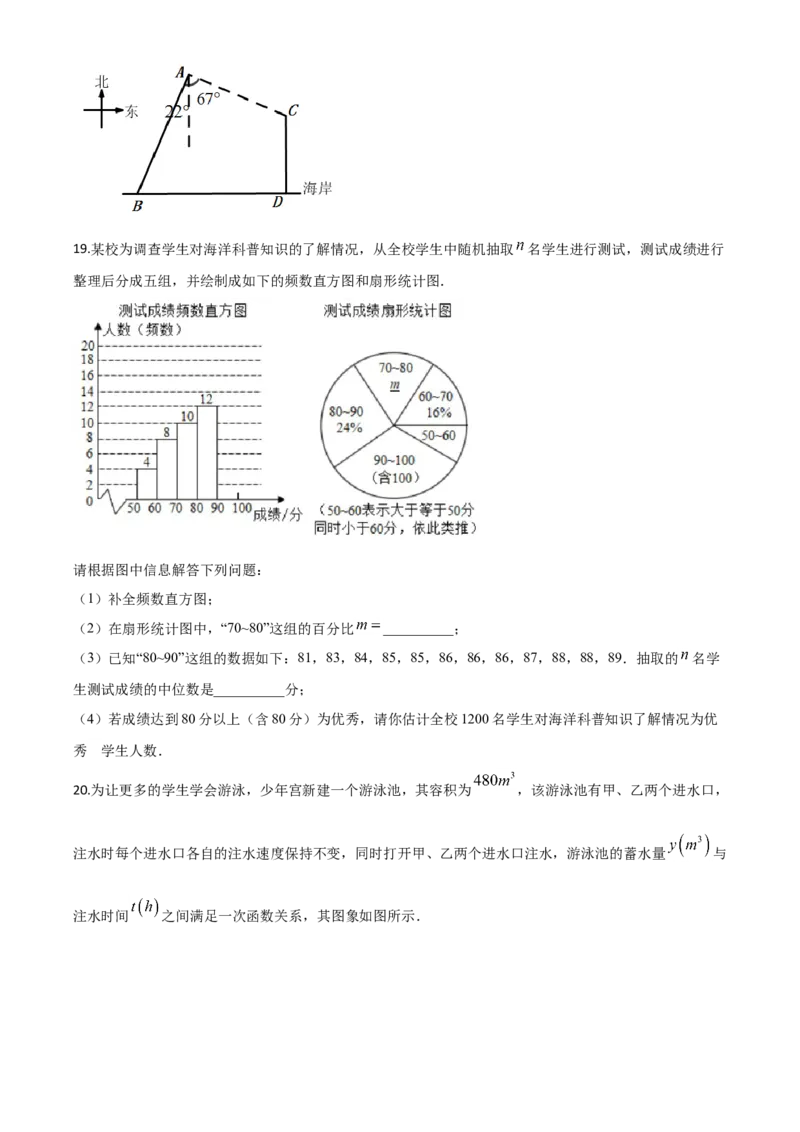
18.如图,在东西方向的海岸上有两个相距6海里的码头 , .某海岛上的观测塔 距离海岸5海里,
在 处测得 位于南偏西 方向.一艘渔船从 出发,沿正北方向航行至 处,此时在 处测得 位
于南偏东 方向,求此时观测塔 与渔船 之间的距离(结果精确到0.1海里).
(参考数据: , , , , , )19.某校为调查学生对海洋科普知识的了解情况,从全校学生中随机抽取 名学生进行测试,测试成绩进行
整理后分成五组,并绘制成如下的频数直方图和扇形统计图.
请根据图中信息解答下列问题:
(1)补全频数直方图;
(2)在扇形统计图中,“70~80”这组的百分比 __________;
(3)已知“80~90”这组的数据如下:81,83,84,85,85,86,86,86,87,88,88,89.抽取的 名学
生测试成绩的中位数是__________分;
(4)若成绩达到80分以上(含80分)为优秀,请你估计全校1200名学生对海洋科普知识了解情况为优
秀 的学生人数.
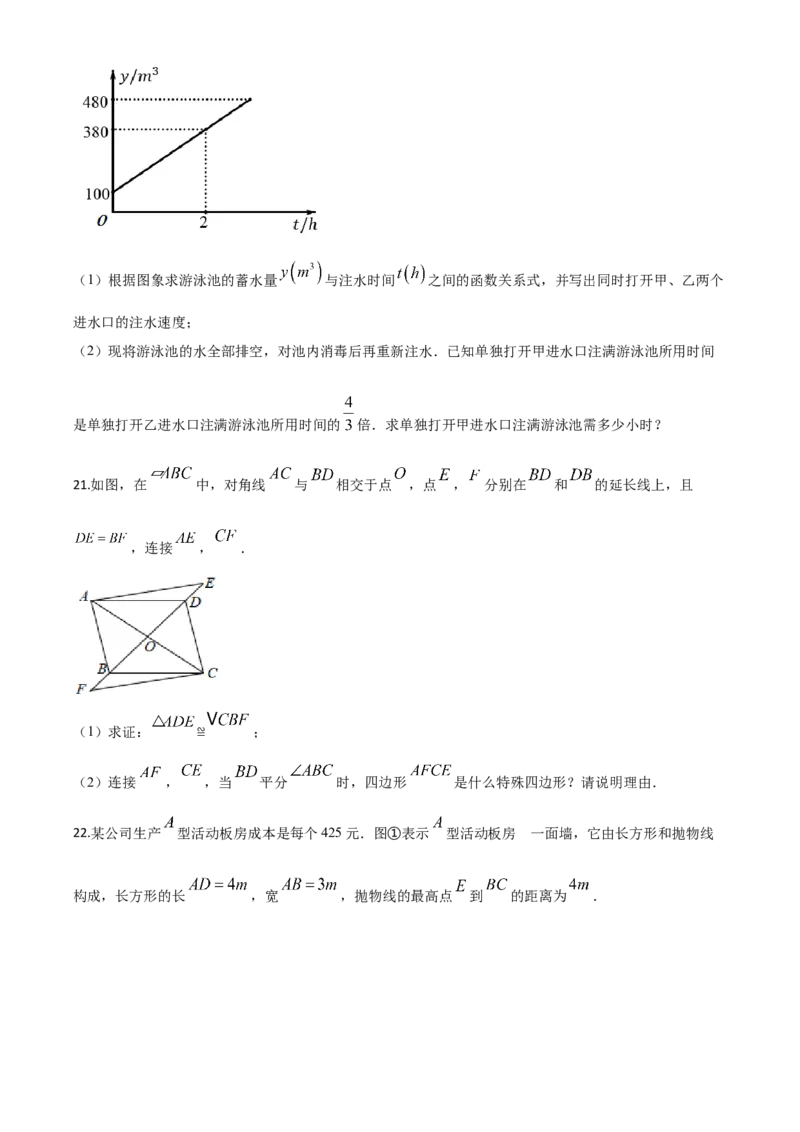
20.为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为 ,该游泳池有甲、乙两个进水口,
注水时每个进水口各自的注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量 与
注水时间 之间满足一次函数关系,其图象如图所示.(1)根据图象求游泳池的蓄水量 与注水时间 之间的函数关系式,并写出同时打开甲、乙两个
进水口的注水速度;
(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间
是单独打开乙进水口注满游泳池所用时间的 倍.求单独打开甲进水口注满游泳池需多少小时?
21.如图,在 中,对角线 与 相交于点 ,点 , 分别在 和 的延长线上,且
,连接 , .
(1)求证: ≌ ;
(2)连接 , ,当 平分 时,四边形 是什么特殊四边形?请说明理由.
的
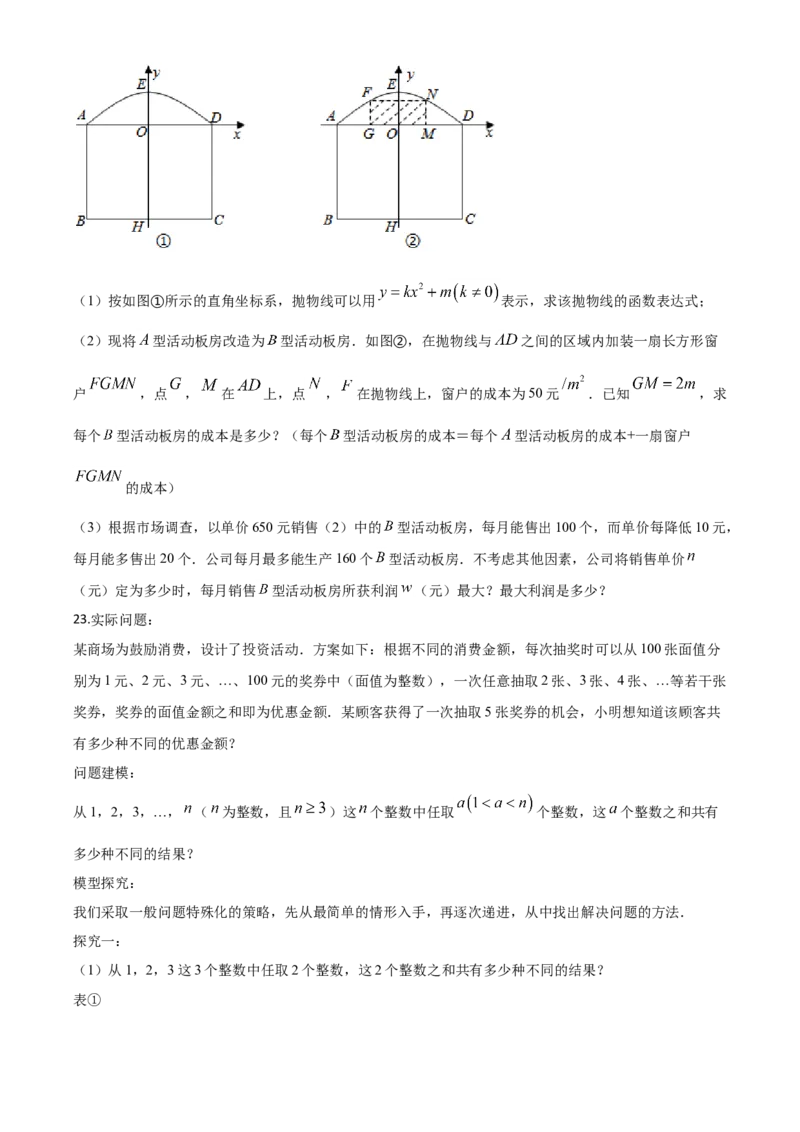
22.某公司生产 型活动板房成本是每个425元.图①表示 型活动板房 一面墙,它由长方形和抛物线
构成,长方形的长 ,宽 ,抛物线的最高点 到 的距离为 .(1)按如图①所示的直角坐标系,抛物线可以用 表示,求该抛物线的函数表达式;
(2)现将 型活动板房改造为 型活动板房.如图②,在抛物线与 之间的区域内加装一扇长方形窗
户 ,点 , 在 上,点 , 在抛物线上,窗户的成本为50元 .已知 ,求
每个 型活动板房的成本是多少?(每个 型活动板房的成本=每个 型活动板房的成本+一扇窗户
的成本)
(3)根据市场调查,以单价650元销售(2)中的 型活动板房,每月能售出100个,而单价每降低10元,
每月能多售出20个.公司每月最多能生产160个 型活动板房.不考虑其他因素,公司将销售单价
(元)定为多少时,每月销售 型活动板房所获利润 (元)最大?最大利润是多少?
23.实际问题:
某商场为鼓励消费,设计了投资活动.方案如下:根据不同的消费金额,每次抽奖时可以从100张面值分
别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取2张、3张、4张、…等若干张
奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取5张奖券的机会,小明想知道该顾客共
有多少种不同的优惠金额?
问题建模:
从1,2,3,…, ( 为整数,且 )这 个整数中任取 个整数,这 个整数之和共有
多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
探究一:
(1)从1,2,3这3个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表①所取的2个整数 1,2 1,3, 2,3
2个整数之和 3 4 5
如表①,所取的2个整数之和可以为3,4,5,也就是从3到5的连续整数,其中最小是3,最大是5,所
以共有3种不同的结果.
(2)从1,2,3,4这4个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表②
所取 的2个整数 1,2 1,3, 1,4 2,3 2,4 3,4
2个整数之和 3 4 5 5 6 7
如表②,所取的2个整数之和可以为3,4,5,6,7,也就是从3到7的连续整数,其中最小是3,最大是
7,所以共有5种不同的结果.
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和共有______种不同的结果.
(4)从1,2,3,…, ( 为整数,且 )这 个整数中任取2个整数,这2个整数之和共有______
种不同的结果.
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和共有______种不同的结果.
(2)从1,2,3,…, ( 为整数,且 )这 个整数中任取3个整数,这3个整数之和共有
的
______种不同 结果.
探究三:
从1,2,3,…, ( 为整数,且 )这 个整数中任取4个整数,这4个整数之和共有______种不
同的结果.
归纳结论:
从1,2,3,…, ( 为整数,且 )这 个整数中任取 个整数,这 个整数之和共有
______种不同的结果.
问题解决:
从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取5张奖券,共有______种不同的优惠金额.
拓展延伸:
(1)从1,2,3,…,36这36个整数中任取多少个整数,使得取出的这些整数之和共有204种不同的结
果?(写出解答过程)
(2)从3,4,5,…, ( 为整数,且 )这 个整数中任取 个整数,这
个整数之和共有______种不同的结果.
24.已知:如图,在四边形 和 中, , ,点 在 上,
, , ,延长 交 于点 ,点 从点 出
发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为
,过点 作 于点 ,交 于点 .设运动时间为 .
解答下列问题:
(1)当 为何值时,点 在线段 的垂直平分线上?
(2)连接 ,作 于点 ,当四边形 为矩形时,求 的值;
(3)连接 , ,设四边形 的面积为 ,求 与 的函数关系式;
(4)点 在运动过程中,是否存在某一时刻 ,使点 在 的平分线上?若存在,求出 的值;若不
存在,请说明理由.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635