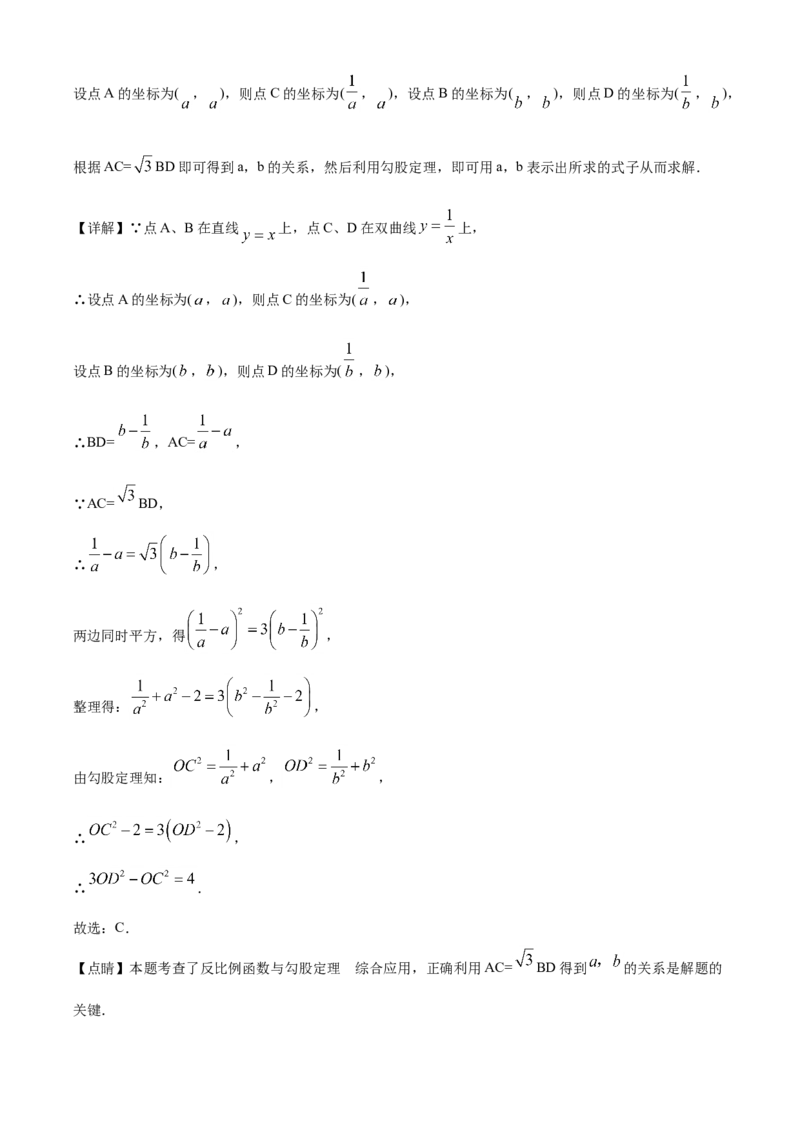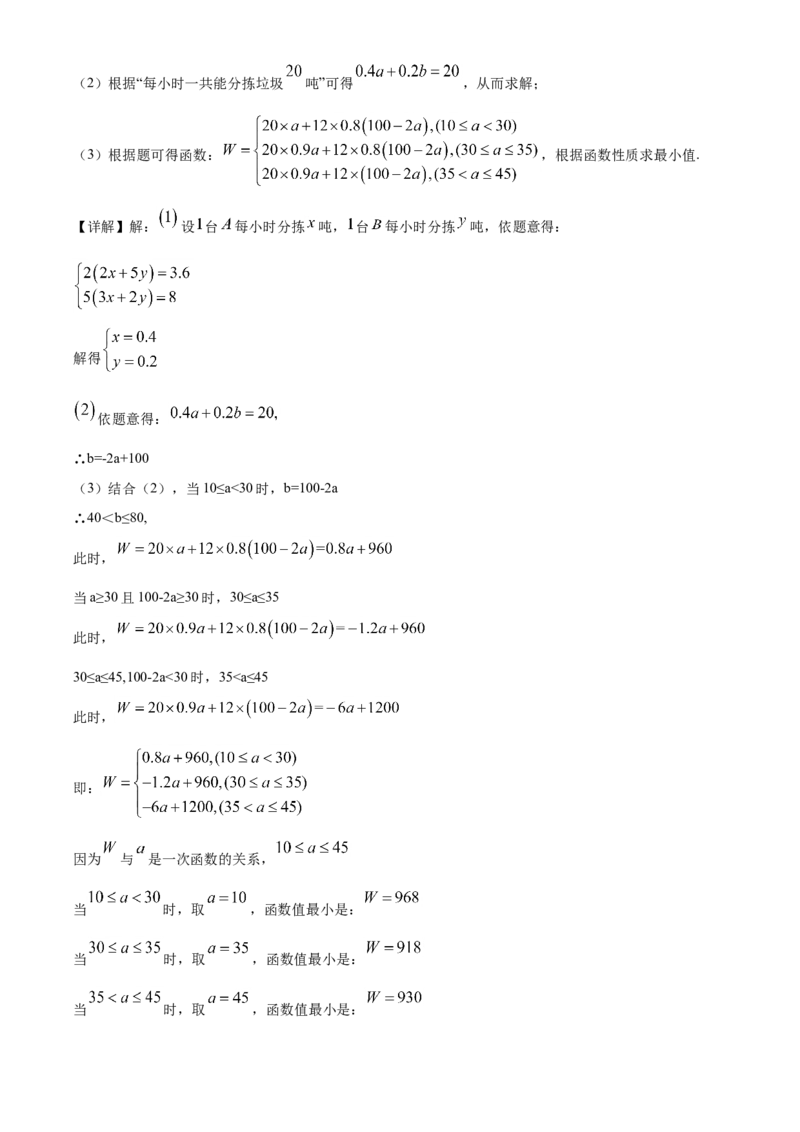文档内容
2020 年广西北部湾经济区初中学业水平考试
数学
(考试时间:120分钟 满分:120分)
注意事项:
1.本试卷分试题卷和答题卡两部分.答案一律填写在答题卡上,在试题卷上作答无效.
2.答题前,请认真阅读答题卡上的注意事项.
3.不能使用计算器.考试结束时,将本试题卷和答题卡一并交回.
第I卷
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.下列实数是无理数的是( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据无理数的三种形式求解即可.
【详解】解:1,0,-5是有理数, 是无理数.
故选:A.
【点睛】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无
限不循环小数,③含有π的数.
2.下列图形是中心对称图形的是( )
A. B.
C. D.
【答案】D
【解析】【分析】
由中心对称图形的定义逐一判断即可.
【详解】解:A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项正确,
故选:D.
【点睛】本题主要考查了中心对称图形的概念,关键是要寻找对称中心,图形旋转180°后与原图重合.
3.2020年2月至5月,由广西教育厅主办,南宁市教育局承办的广西中小学“空中课堂”是同期全国服务
中小学学科最齐、学段最全、上线最早的线上学习课程,深受广大师生欢迎.其中某节数学课的点击观看
次数约 次,则数据 用科学记数法表示为( )
A. B. C. D.
【答案】C
【解析】
【分析】
科学记数法的表示形式为a×10n的形式.其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,
小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的
绝对值<1时,n是负数.
【详解】 这个数据用科学记数法表示为 .
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为
整数,表示时关键要正确确定a的值以及n的值.
的
4.下列运算正确 是( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据合并同类项法则,幂的乘方与积的乘方,同底数幂的乘法以及单项式除以单项式分别求出每个式子的
值,再判断即可.【详解】A. ,故本选项不符合题意;
B. ,故本选项不符合题意;
C. ,故本选项不符合题意;
D. ,正确.
故选:D.
【点睛】本题考查了合并同类项法则,幂的乘方与积的乘方,同底数幂的乘法以及单项式除以单项式等知
识点,能正确求出每个式子的值是解答此题的关键.
5.以下调查中,最适合采用全面调查的是( )
A. 检测长征运载火箭的零部件质量情况 B. 了解全国中小学生课外阅读情况
C. 调查某批次汽车的抗撞击能力 D. 检测某城市的空气质量
【答案】A
【解析】
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似
解答即可.
【详解】A.检测长征运载火箭的零部件质量情况,必须全面调查才能得到准确数据;
B.了解全国中小学生课外阅读情况,量比较大,用抽样调查;
C.调查某批次汽车的抗撞击能力,具有破坏性,用抽样调查;
D.检测某城市的空气质量,不可能全面调查,用抽样调查.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征
灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,
对于精确度要求高的调查,事关重大的调查往往选用普查.
6.一元二次方程 的根的情况是( )
A. 有两个不等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
【答案】B
【解析】
【分析】
求出其根的判别式,然后根据根的判别式的正负情况即可作出判断.【详解】∵ , , ,
∴ ,
∴方程有两个相等的实数根.
故选:B.
【点睛】本题考查了一元二次方程 ( )的根的判别式 :当 >0,方
程有两个不相等的实数根;当 =0,方程有两个相等的实数根;当 <0,方程没有实数根.
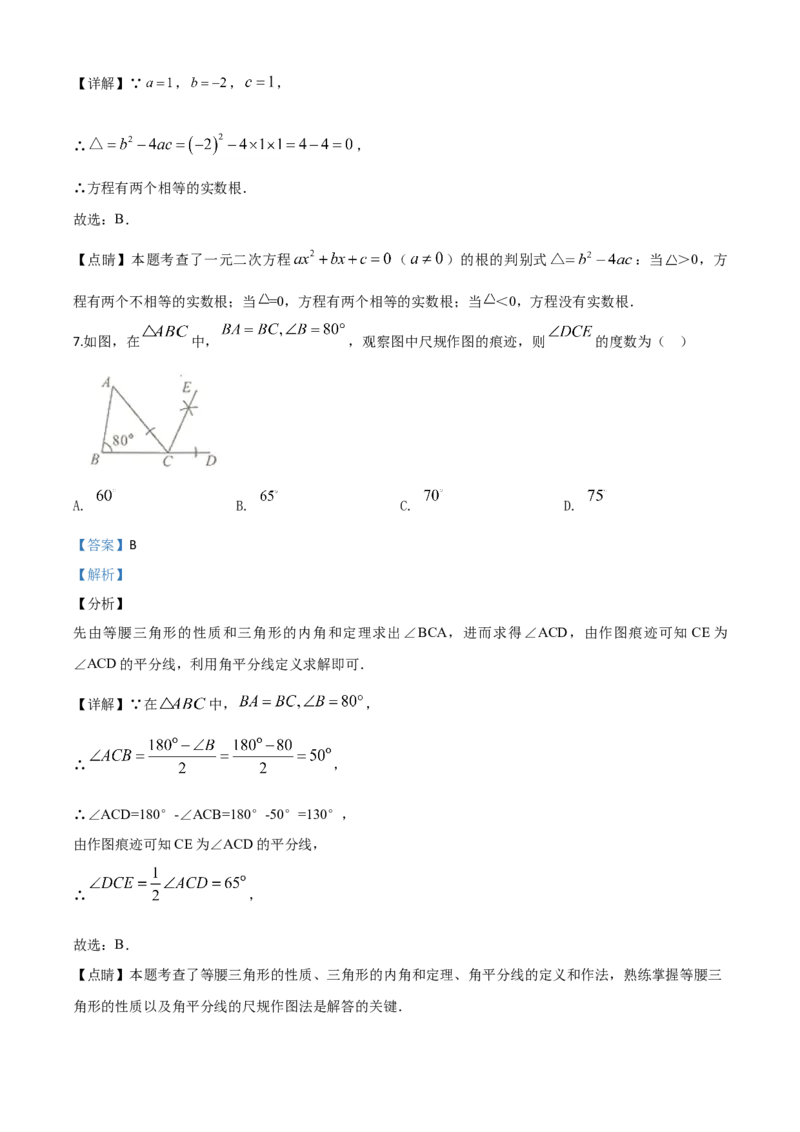
7.如图,在 中, ,观察图中尺规作图的痕迹,则 的度数为( )
A. B. C. D.
【答案】B
【解析】
【分析】
先由等腰三角形的性质和三角形的内角和定理求出∠BCA,进而求得∠ACD,由作图痕迹可知CE为
∠ACD的平分线,利用角平分线定义求解即可.
【详解】∵在 中, ,
∴ ,
∴∠ACD=180°-∠ACB=180°-50°=130°,
由作图痕迹可知CE为∠ACD的平分线,
∴ ,
故选:B.
【点睛】本题考查了等腰三角形的性质、三角形的内角和定理、角平分线的定义和作法,熟练掌握等腰三
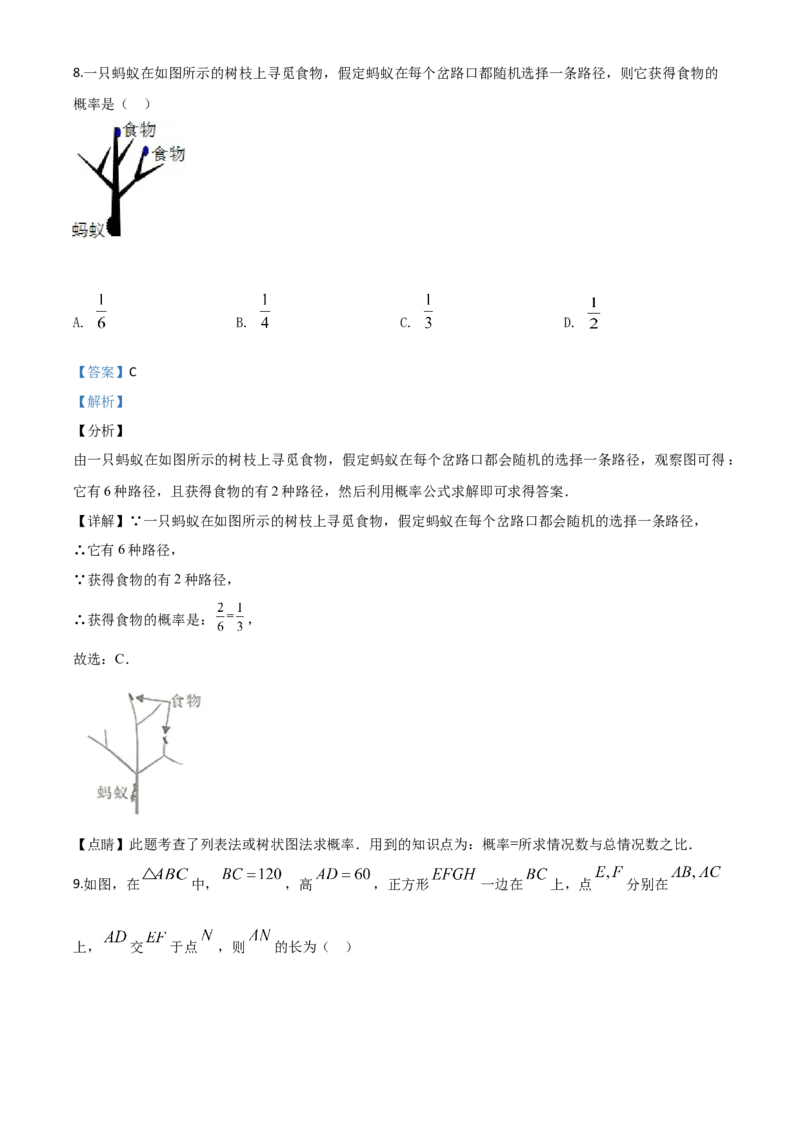
角形的性质以及角平分线的尺规作图法是解答的关键.8.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都随机选择一条路径,则它获得食物的
概率是( )
A. B. C. D.
【答案】C
【解析】
【分析】
由一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,观察图可得:
它有6种路径,且获得食物的有2种路径,然后利用概率公式求解即可求得答案.
【详解】∵一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机的选择一条路径,
∴它有6种路径,
∵获得食物的有2种路径,
∴获得食物的概率是: ,
故选:C.
【点睛】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
9.如图,在 中, ,高 ,正方形 一边在 上,点 分别在
上, 交 于点 ,则 的长为( )A. B. C. D.
【答案】B
【解析】
【分析】
证明△AEF∽△ABC,根据相似三角形对应边上的高线的比等于相似比即可求得.
【详解】解:∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴ .
设AN=x,则EF=FG=DN=60-x,
∴
解得:x=20
所以,AN=20.
故选:B.
【点睛】本题考查了正方形以及相似三角形的应用,注意数形结合的运用是解题关键.
10.甲、乙两地相距 ,提速前动车的速度为 ,提速后动车的速度是提速前的 倍,提速后
行车时间比提速前减少 ,则可列方程为( )
A. B.
C. D.
【答案】A【解析】
【分析】
行驶路程都是600千米;提速前后行驶时间分别是: ;因为提速后行车时间比提速前减少
,所以,提速前的时间-提速后的时间= .
【详解】根据提速前的时间-提速后的时间= ,可得
即
故选:A
【点睛】应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.本题
考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
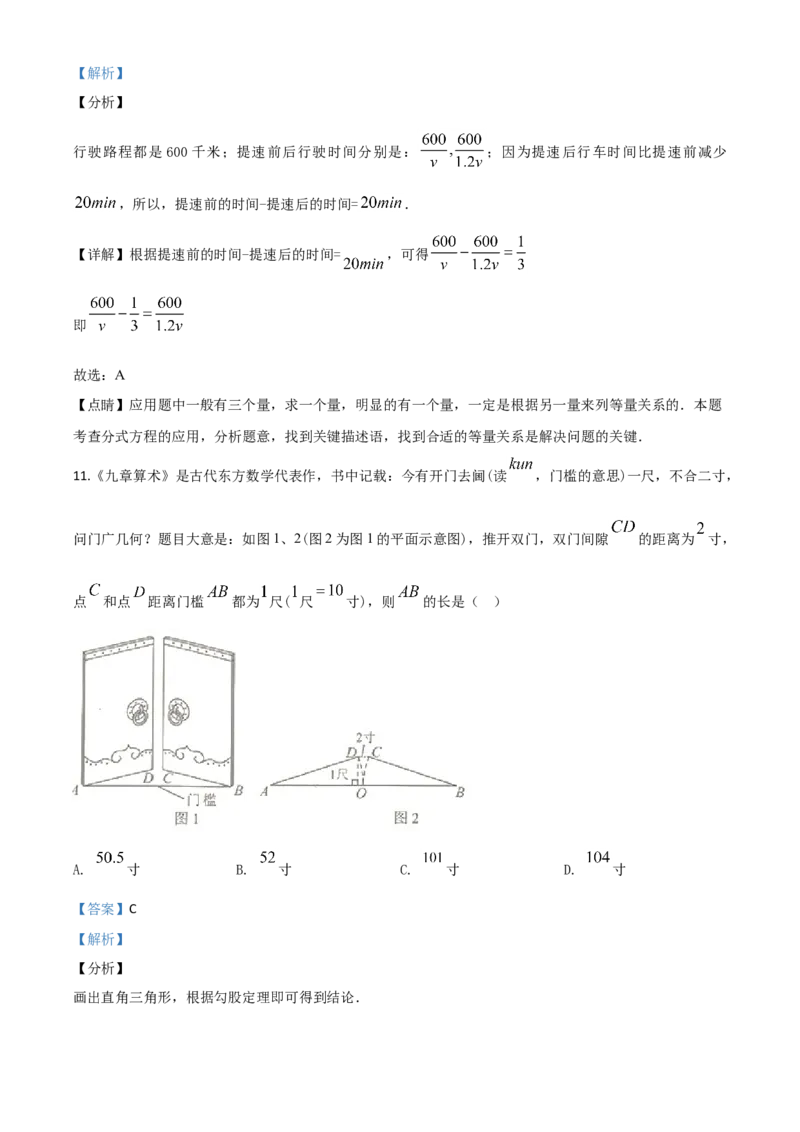
11.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 ,门槛的意思)一尺,不合二寸,
问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙 的距离为 寸,
点 和点 距离门槛 都为 尺( 尺 寸),则 的长是( )
A. 寸 B. 寸 C. 寸 D. 寸
【答案】C
【解析】
【分析】
画出直角三角形,根据勾股定理即可得到结论.【详解】设OA=OB=AD=BC= ,过D作DE⊥AB于E,
则DE=10,OE= CD=1,AE= .
在Rt△ADE中,
,即 ,
解得 .
故门的宽度(两扇门的和)AB为101寸.
故选:C.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
12.如图,点 是直线 上的两点,过 两点分别作 轴的平行线交双曲线 于点
.若 ,则 的值为( )
A. B. C. D.
【答案】C
【解析】
【分析】设点A的坐标为( , ),则点C的坐标为( , ),设点B的坐标为( , ),则点D的坐标为( , ),
根据AC= BD即可得到a,b的关系,然后利用勾股定理,即可用a,b表示出所求的式子从而求解.
【详解】∵点A、B在直线 上,点C、D在双曲线 上,
∴设点A的坐标为( , ),则点C的坐标为( , ),
设点B的坐标为( , ),则点D的坐标为( , ),
∴BD= ,AC= ,
∵AC= BD,
∴ ,
两边同时平方,得 ,
整理得: ,
由勾股定理知: , ,
∴ ,
∴ .
故选:C.
的
【点睛】本题考查了反比例函数与勾股定理 综合应用,正确利用AC= BD得到 的关系是解题的
关键.第II卷
二、填空题(每题3分,满分18分,将答案填在答题纸上)
13.如图,数轴上所表示的x的取值范围为_____.
【答案】﹣1<x≤3
【解析】
【分析】
根据数轴上表示的不等式的解集即可得结论.
【详解】解:观察数轴可知:
x>﹣1,且x≤3,
所以x的取值范围为﹣1<x≤3.
故答案为﹣1<x≤3.
【点睛】本题考查的是不等式的解集在数轴上的表示,注意数轴上的点是空心点还是实心点.
14.计算: .
【答案】
【解析】
15.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
“射中 环以上”的次数
“射中 环以上”的频率(结
果保留小数点后两位)
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是_______(结果保留小数点后一
位).
【答案】0.8
【解析】
【分析】
根据大量的实验结果稳定在0.8左右即可得出结论.【详解】∵从频率的波动情况可以发现频率稳定在0.8附近,
∴这名运动员射击一次时“射中9环以上”的概率大约是0.8.
故答案为:0.8.
【点睛】本题考查了利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并
且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似
值就是这个事件的概率.
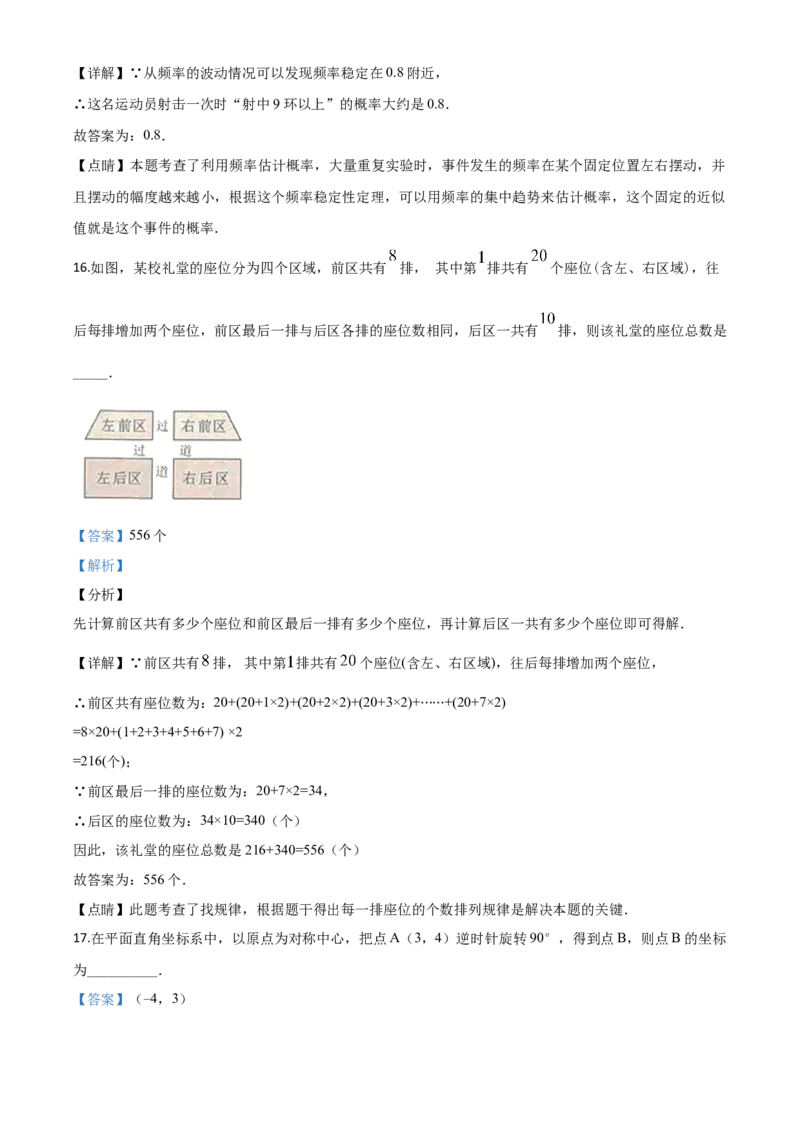
16.如图,某校礼堂的座位分为四个区域,前区共有 排, 其中第 排共有 个座位(含左、右区域),往
后每排增加两个座位,前区最后一排与后区各排的座位数相同,后区一共有 排,则该礼堂的座位总数是
_____.
【答案】556个
【解析】
【分析】
先计算前区共有多少个座位和前区最后一排有多少个座位,再计算后区一共有多少个座位即可得解.
【详解】∵前区共有 排, 其中第 排共有 个座位(含左、右区域),往后每排增加两个座位,
∴前区共有座位数为:20+(20+1×2)+(20+2×2)+(20+3×2)+ +(20+7×2)
=8×20+(1+2+3+4+5+6+7) ×2 ⋯⋯
=216(个);
∵前区最后一排的座位数为:20+7×2=34,
∴后区的座位数为:34×10=340(个)
因此,该礼堂的座位总数是216+340=556(个)
故答案为:556个.
【点睛】此题考查了找规律,根据题干得出每一排座位的个数排列规律是解决本题的关键.
17.在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标
为__________.
【答案】(-4,3)【解析】
【分析】
建立平面直角坐标系,作出图形,然后根据图形写出点B的坐标即可.
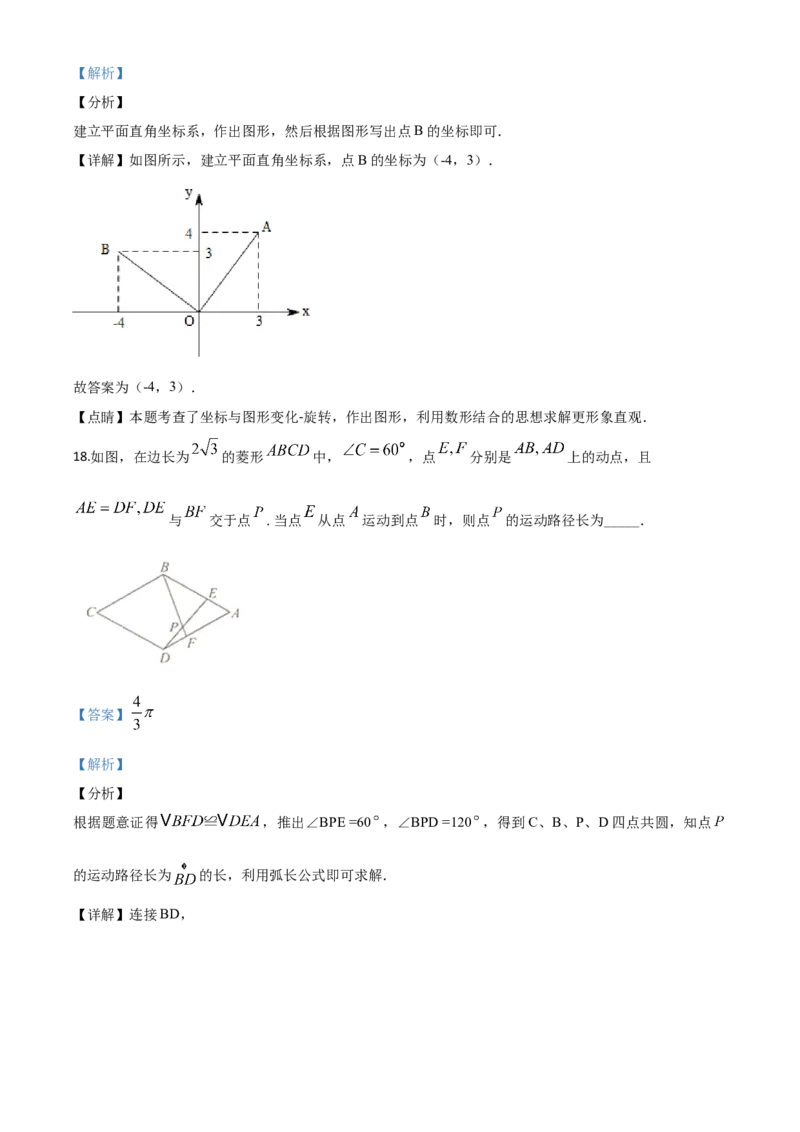
【详解】如图所示,建立平面直角坐标系,点B的坐标为(-4,3).
故答案为(-4,3).
【点睛】本题考查了坐标与图形变化-旋转,作出图形,利用数形结合的思想求解更形象直观.
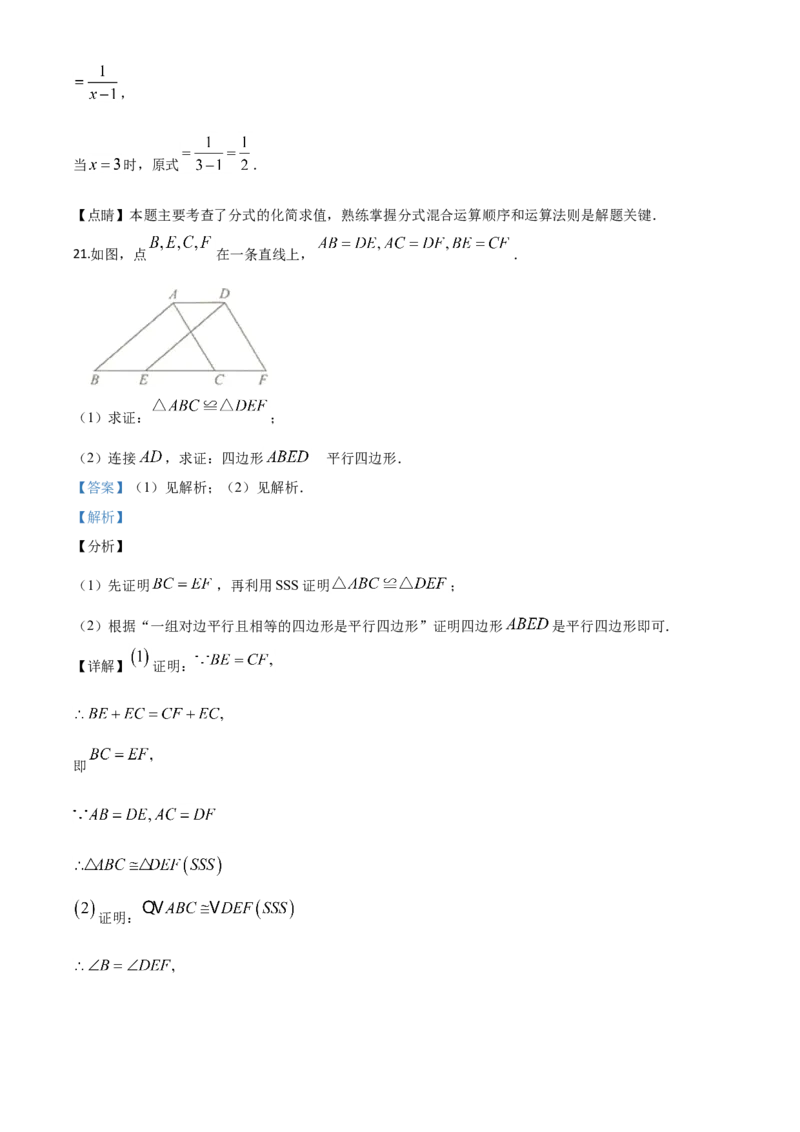
18.如图,在边长为 的菱形 中, ,点 分别是 上的动点,且
与 交于点 .当点 从点 运动到点 时,则点 的运动路径长为_____.
【答案】
【解析】
【分析】
根据题意证得 ,推出∠BPE =60 ,∠BPD =120 ,得到C、B、P、D四点共圆,知点
的运动路径长为 的长,利用弧长公式即可求解.
【详解】连接BD,∵菱形 中, ,
∴∠C=∠A=60 ,AB=BC=CD=AD,
∴ ABD和 CBD都为等边三角形,
∴△BD=AD,△∠BDF=∠DAE=60 ,
∵DF=AE,
∴ ,
∴∠DBF=∠ADE,
∵∠BPE=∠BDP+∠DBF =∠BDP+∠ADE=∠BDF =60 ,
∴∠BPD=180 -∠BPE=120 ,
∵∠C=60 ,
∴∠C+∠BPD =180 ,
∴C、B、P、D四点共圆,即⊙O是 的外接圆,
∴当点 从点 运动到点 时,则点 的运动路径长为 的长,
∴∠BOD =2∠BCD =120 ,
作OG⊥BD于G,
根据垂径定理得:BG=GD= BD= ,∠BOG = ∠BOD =60 ,
∵ ,即 ,
∴ ,
从而 点的路径长为 .
【点睛】本题考查了菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,圆内接四边形的性质,弧长公式等知识,解题的关键是学会准确寻找点的运动轨迹.
三、解答题(本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
19.计算: .
【答案】-5
【解析】
【分析】
根据有理数的运算法则计算即可得到答案.
【详解】
.
【点睛】本题考查了有理数的混合运算,掌握运算法则是解决本题的关键.
20.先化简,再求值: ,其中 .
【答案】 ;
【解析】
【分析】
先用异分母加法法则计算括号内的,再把除法运算转化为乘法运算,化简化把x的值代入求值.
【详解】,
当 时,原式 .
【点睛】本题主要考查了分式的化简求值,熟练掌握分式混合运算顺序和运算法则是解题关键.
21.如图,点 在一条直线上, .
(1)求证: ;
(2)连接 ,求证:四边形 是平行四边形.
【答案】(1)见解析;(2)见解析.
【解析】
【分析】
(1)先证明 ,再利用SSS证明 ;
(2)根据“一组对边平行且相等的四边形是平行四边形”证明四边形 是平行四边形即可.
【详解】 证明:
即
证明:四边形 是平行四边形.
【点睛】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形
的判定方法,证明三角形全等是解决问题的关键.
22.小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发
放问卷进行测评,从中随机抽取 份答卷,并统计成绩(成绩得分用 表示,单位:分),收集数据如下:
整理数据:
分析数据:
平均分 中位数 众数
根据以上信息,解答下列问题:
(1)直接写出上述表格中 的值;
(2)该校有 名家长参加了此次问卷测评活动,请估计成绩不低于 分的人数是多少?
(3)请从中位数和众数中选择一个量, 结合本题解释它的意义.
【答案】(1)5;91;100 (2)1040人 (3)中位数:在统计的问卷的成绩中,最中间的两个分数的
平均数是91分;众数:在统计的问卷的成绩中,得 分的人数最多
【解析】
【分析】(1)用总人数减去已知人数即可得到a的值;将这20个数据按大小顺序排列,第10和11个数据的平均
数即为中位数,出现次数最多的数据即为人数;
(2)先求出样本中不低于90分的人数所占样本的百分比,再乘以1600即可得到结果;
(3)根据中位数和众数的意义进行回答即可.
【详解】(1)a=20-3-4-8=5;
将这组数据按大小顺序排列为:
81,82,83,86,87,88,89,90,90,90,92,93,96,96,98,99,100,100,100,100,
其中第10个和第11个数据分别是90,92,
所以,这组数据的中位数b= ;
100出现了4次,出现的次数最多,所以,众数c是100;
(2) ,
(人)
(3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;
众数:在统计的问卷的成绩中,得 分的人数最多.
【点睛】本题主要考查了平均数、众数、中位数在实际问题中的正确应用,熟练掌握定义和计算公式是解
题的关键.
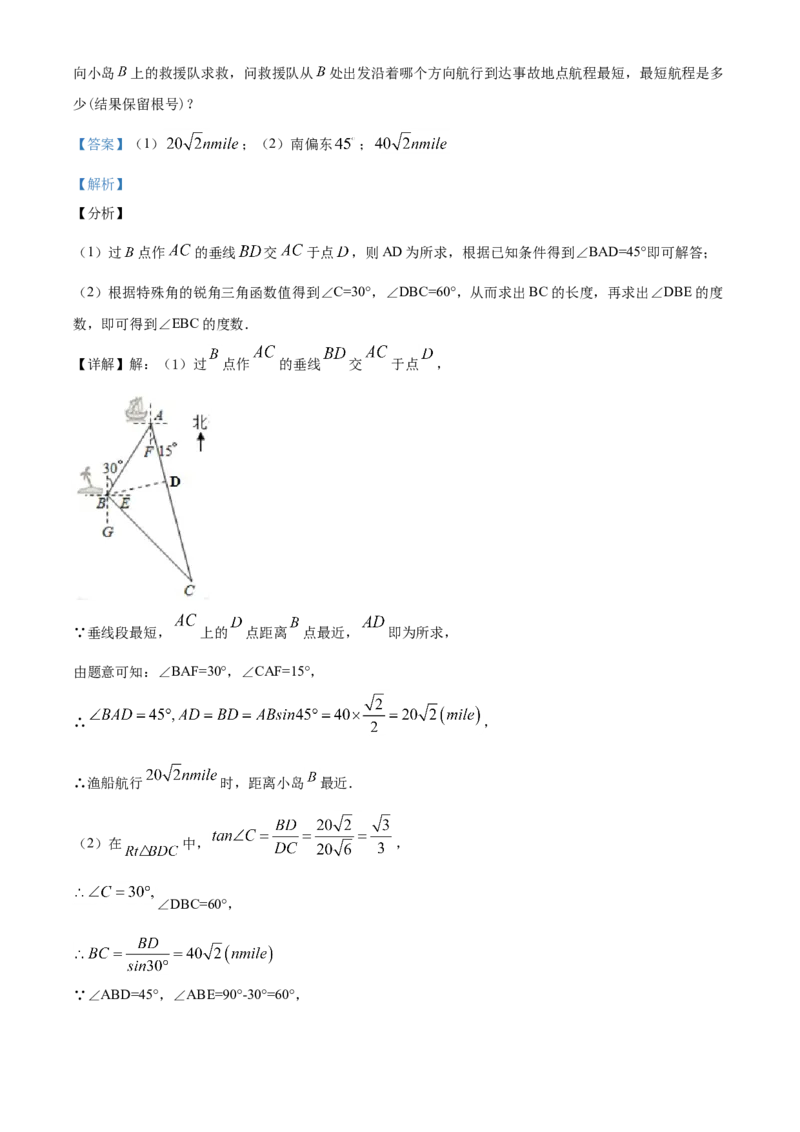
23.如图,一艘渔船位于小岛 的北偏东 方向,距离小岛 的点 处,它沿着点 的南偏东
的方向航行.
(1)渔船航行多远距离小岛 最近(结果保留根号)?
(2)渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多
少(结果保留根号)?
【答案】(1) ;(2)南偏东 ;
【解析】
【分析】
(1)过 点作 的垂线 交 于点 ,则AD为所求,根据已知条件得到∠BAD=45°即可解答;
(2)根据特殊角的锐角三角函数值得到∠C=30°,∠DBC=60°,从而求出BC的长度,再求出∠DBE的度
数,即可得到∠EBC的度数.
【详解】解:(1)过 点作 的垂线 交 于点 ,
∵垂线段最短, 上的 点距离 点最近, 即为所求,
由题意可知:∠BAF=30°,∠CAF=15°,
∴ ,
∴渔船航行 时,距离小岛 最近.
(2)在 中, ,
∠DBC=60°,
∵∠ABD=45°,∠ABE=90°-30°=60°,∴ ,
.
答:从 处沿南偏东 出发,最短行程 .
【点睛】本题考查了解直角三角形的应用中的方向角问题,结合航海中的实际问题,将解直角三角形的相
关知识有机结合,体现了数学应用于实际生活的思想.
24.倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出 型和 型
两款垃圾分拣机器人,已知 台 型机器人和 台 型机器人同时工作 共分拣垃圾 吨, 台 型机
器人和 台 型机器人同时工作 共分拣垃圾 吨.
(1)1台 型机器人和 台 型机器人每小时各分拣垃圾多少吨?
(2)某垃圾处理厂计划向机器人公司购进一批 型和 型垃圾分拣机器人,这批机器人每小时一共能分
拣垃圾 吨.设购买 型机器人 台 , 型机器人 台,请用含 的代数式表示 ;
(3)机器人公司的报价如下表:
型号 原价 购买数量少于 台 购买数量不少于 台
型 万元/台 原价购买 打九折
型 万元/台 原价购买 打八折
在 的条件下,设购买总费用为 万元,问如何购买使得总费用 最少?请说明理由.
【答案】(1)0.4吨;0.2吨;(2) ;(3)购买A型35台,B型30台费用最少,理由见
解析
【解析】
【分析】
(1)设 台 每小时分拣 吨, 台 每小时分拣 吨,依题意得: ,解方程组可得;(2)根据“每小时一共能分拣垃圾 吨”可得 ,从而求解;
(3)根据题可得函数: ,根据函数性质求最小值.
【详解】解: 设 台 每小时分拣 吨, 台 每小时分拣 吨,依题意得:
解得
依题意得:
∴b=-2a+100
(3)结合(2),当10≤a<30时,b=100-2a
∴40<b≤80,
此时,
当a≥30且100-2a≥30时,30≤a≤35
此时,
30≤a≤45,100-2a<30时,35