文档内容
一、选择题:本大题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.复数的Z =-1-2ii为虚数单位在复平面内对应的点位于模为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设点Px,y,则“ x=2且y =-1” 是“ 点P在直线l:x+ y-1=0上” 的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.若集合A=1,2,3,B=1,3,4,则AÇB的子集个数为(
)
A.2 B.3 C.4 D.16
4.双曲线x2 - y2 =1的顶点到其渐近线的距离等于( )
1 2
A. B. C.1 D. 2
2 2
5.函数 f x=ln x2 +1 的图像大致是( )
ìx+ y£2
ï
6.若变量x,y满足约束条件íx³1, 则z =2x+ y的最大值和最小值分别为( )
ï
y³0,
î
A.4和3 B.4和2 C.3和2 D.2和0
7.若2x +2y =1,则x+ y的取值范围是( )
第1页 | 共6页A.0,2 B.-2,0 C.-2,+¥ D.-¥,-2
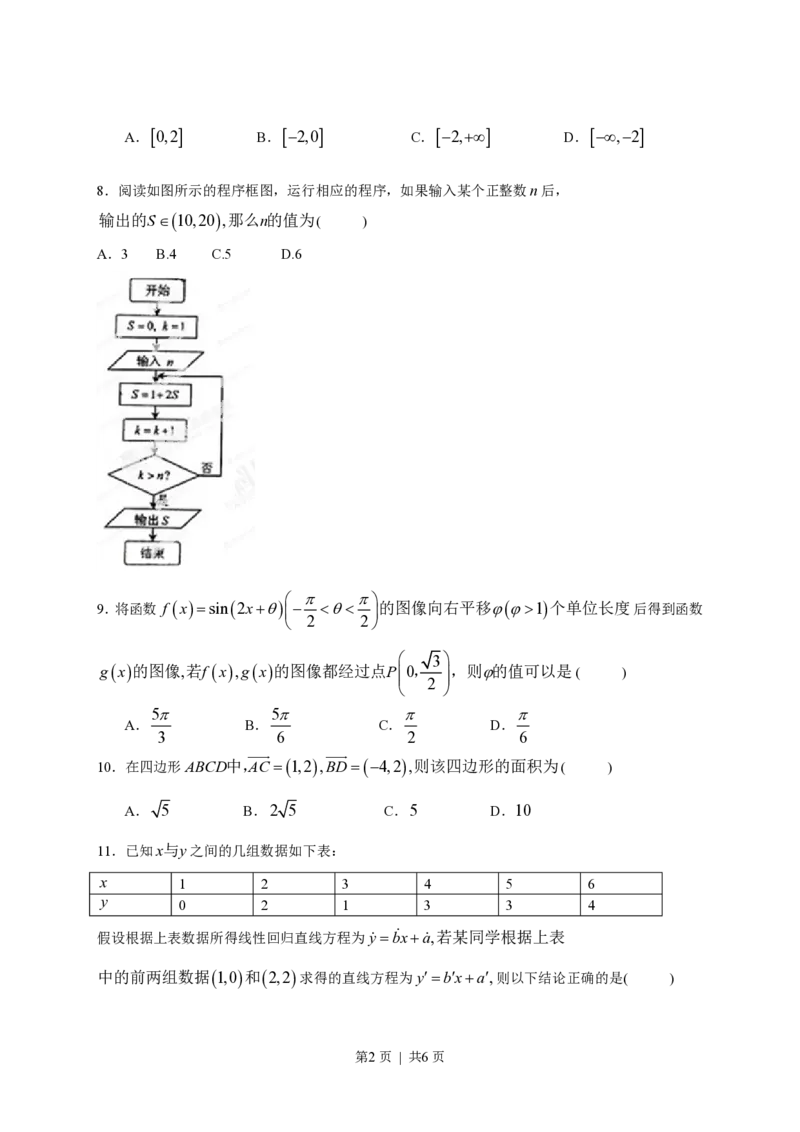
8.阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,
输出的SÎ10,20,那么n的值为(
)
A.3 B.4 C.5 D.6
æ p pö
9.将函数 f x=sin2x+q ç - 1个单位长度后得到函数
è 2 2ø
æ 3ö
gx的图像,若f x,gx的图像都经过点Pç0, ÷,则j的值可以是( )
ç ÷
2
è ø
5p 5p p p
A. B. C. D.
3 6 2 6
uuur uuur
10.在四边形ABCD中,AC =1,2,BD=-4,2,则该四边形的面积为( )
A. 5 B.2 5 C.5 D.10
11.已知x与y之间的几组数据如下表:
x 1 2 3 4 5 6
y
0 2 1 3 3 4
假设根据上表数据所得线性回归直线方程为y
&
=b&x+a
&
,若某同学根据上表
中的前两组数据1,0和2,2求得的直线方程为y¢=b¢x+a¢,则以下结论正确的是(
)
第2页 | 共6页A.b&>b¢,a
&
>a¢ B.b&>b¢,a
&
a¢ D.b&b>0)的左、右焦点分别为F、F,焦距为2c. 若直线
a2 b2 1 2
y = 3x+c与椭圆r的一个交点M满足ÐMFF =2ÐMF F,则该椭圆的离心率等
1 2 2 1
于 .
16.设S,T是R的两个非空子集,如果存在一个从S到T的函数y = f(x)满足:
(i)T =f(x) xÎS ;(ii)对任意x ,x ÎS,当x < x时,恒有f(x )< f(x ),
1 2 1 2 1 2
那么称这两个集合“保序同构”,现给出以下3对集合:
①A= N,B= N*;
②A= x -1£ x£3,B= x -8£ x£10;
③A= x 0£ x£1,B= R.
其中,“保序同构”的集合对的序号是_______.(写出“保序同构”的集合对的序号).
三、解答题:本大题共 6小题,共 74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知等差数列 a 的公差d =1,前n项和为S .
n n
(I)若1,a ,a 成等比数列,求 a ;
1 3 1
第3页 | 共6页(II)若S >aa,求a的取值范围。
5 1 9 1
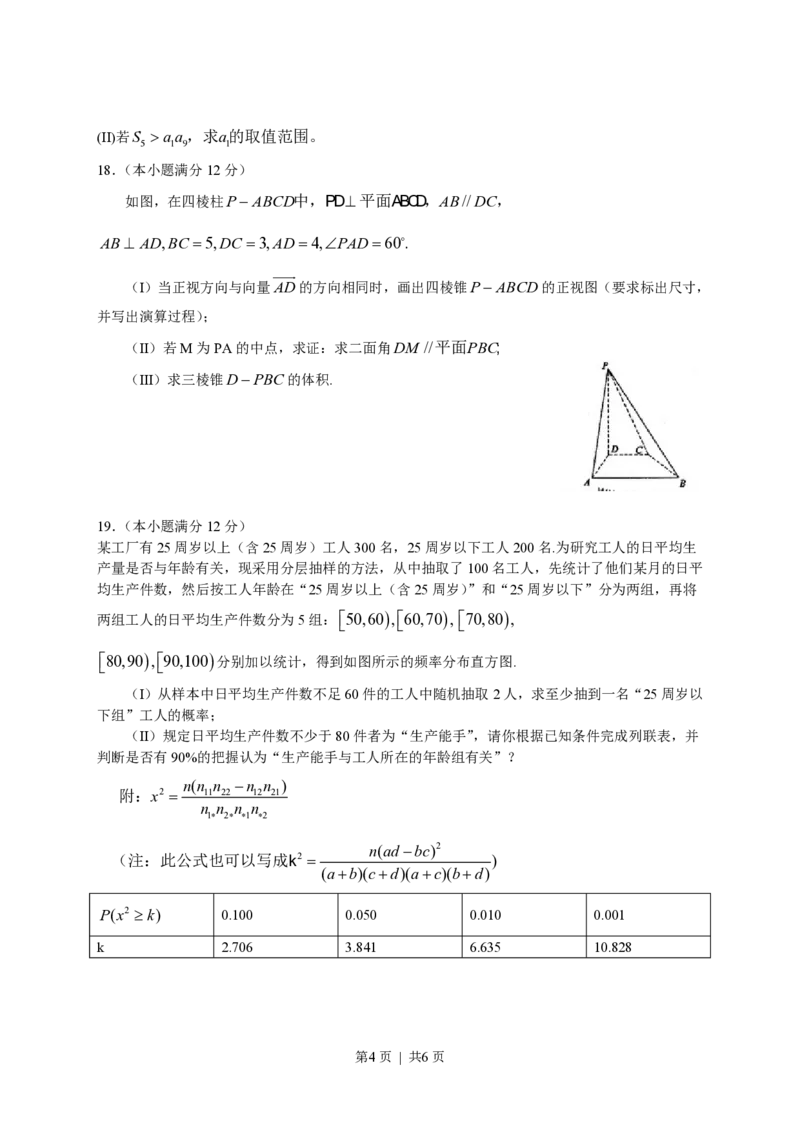
18.(本小题满分12分)
如图,在四棱柱P-ABCD中,PD^平面ABCD,AB//DC,
AB^ AD,BC =5,DC =3,AD=4,ÐPAD=60o.
uuur
(I)当正视方向与向量AD的方向相同时,画出四棱锥P-ABCD的正视图(要求标出尺寸,
并写出演算过程);
(II)若M为PA的中点,求证:求二面角DM //平面PBC;
(III)求三棱锥D-PBC的体积.
19.(本小题满分12分)
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生
产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平
均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将
两组工人的日平均生产件数分为5组:é
ë
50,60,é
ë
60,70, é
ë
70,80,
é
ë
80,90,é
ë
90,100分别加以统计,得到如图所示的频率分布直方图.
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以
下组”工人的概率;
(II)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并
判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
n(n n -n n )
附:x2 = 11 22 12 21
n n n n
1* 2* *1 *2
n(ad -bc)2
(注:此公式也可以写成k2 = )
(a+b)(c+d)(a+c)(b+d)
P(x2 ³k) 0.100 0.050 0.010 0.001
k 2.706 3.841 6.635 10.828
第4页 | 共6页25周岁以上组 25周岁以下组
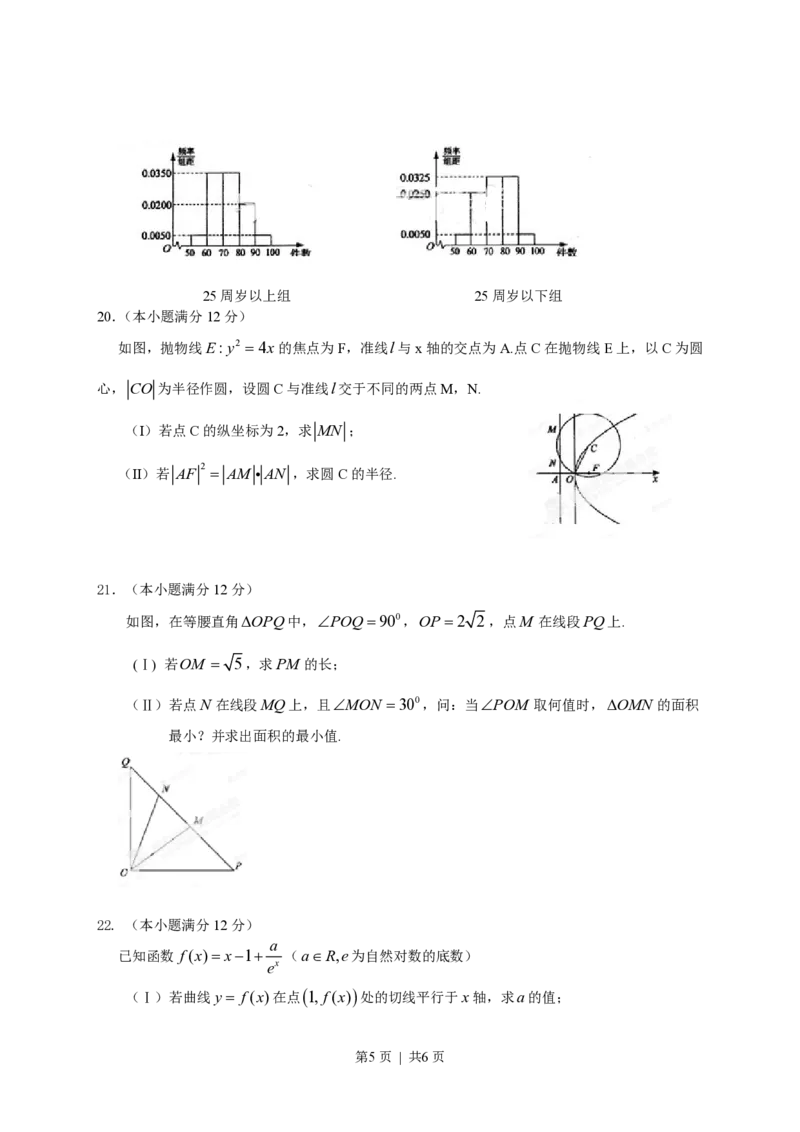
20.(本小题满分12分)
如图,抛物线E: y2 =4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆
心, CO 为半径作圆,设圆C与准线l交于不同的两点M,N.
(I)若点C的纵坐标为2,求 MN ;
2
(II)若 AF = AM AN ,求圆C的半径.
g
21.(本小题满分12分)
如图,在等腰直角DOPQ中,ÐPOQ=900,OP=2 2,点M 在线段PQ上.
(Ⅰ) 若OM = 5,求PM 的长;
(Ⅱ)若点N 在线段MQ上,且ÐMON =300,问:当ÐPOM 取何值时,DOMN 的面积
最小?并求出面积的最小值.
22. (本小题满分12分)
a
已知函数 f(x)= x-1+ (aÎR,e为自然对数的底数)
ex
(Ⅰ)若曲线y = f(x)在点1, f(x)处的切线平行于x轴,求a的值;
第5页 | 共6页(Ⅱ)求函数 f(x)的极值;
(Ⅲ)当a=1时,若直线l: y =kx-1与曲线y = f(x)没有公共点,求k的最大值.
第6页 | 共6页