文档内容
一.选择题:本大题共 10 小题,每小题 5 分,共 50 分.在每小题给出的四个
备选项中,只有一个选项是符合题目要求的.
zhangwlx
(1)已知集合U ={1,2,3,4},集合A={1,2},B={2,3},则ð (A B)=
U U
(A){1,3,4} (B){3,4} (C){3} (D){4}
(2)命题“对任意xÎR,都有x2 ³0”的否定为
(A)对任意xÎR,使得x2 <0 (B)不存在xÎR,使得x2 <0
(C)存在x ÎR,都有x2 ³0 (D)存在x ÎR,都有x2 <0
0 0 0 0
1
(3)函数y = 的定义域为
log (x-2)
2
(A)(-¥,2) (B)(2,+¥)
(C)(2,3) (3,+¥) (D)(2,4) (4,+¥)
U U
(4)设P是圆(x-3)2 +(y+1)2 =4上的动点,Q是直线x=-3上的动点,则 PQ 的最小
值为zhangwlx
(A)6 (B)4 (C)3 (D)2
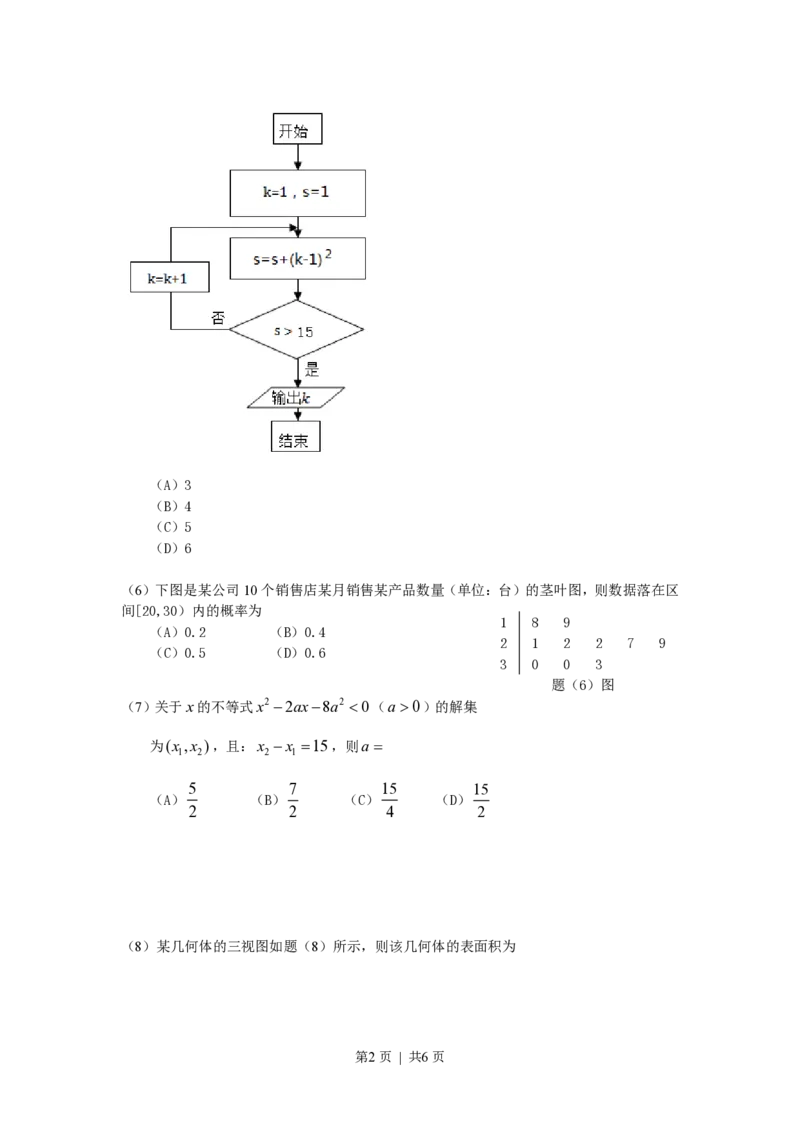
(5)执行如题(5)图所示的程序框图,则输出的k的值是
第1页 | 共6页(A)3
(B)4
(C)5
(D)6
(6)下图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区
间[20,30)内的概率为
1 8 9
(A)0.2 (B)0.4
2 1 2 2 7 9
(C)0.5 (D)0.6
3 0 0 3
题(6)图
(7)关于x的不等式x2 -2ax-8a2 <0(a>0)的解集
为(x ,x ),且:x -x =15,则a=
1 2 2 1
5 7 15 15
(A) (B) (C) (D)
2 2 4 2
zhangwlx
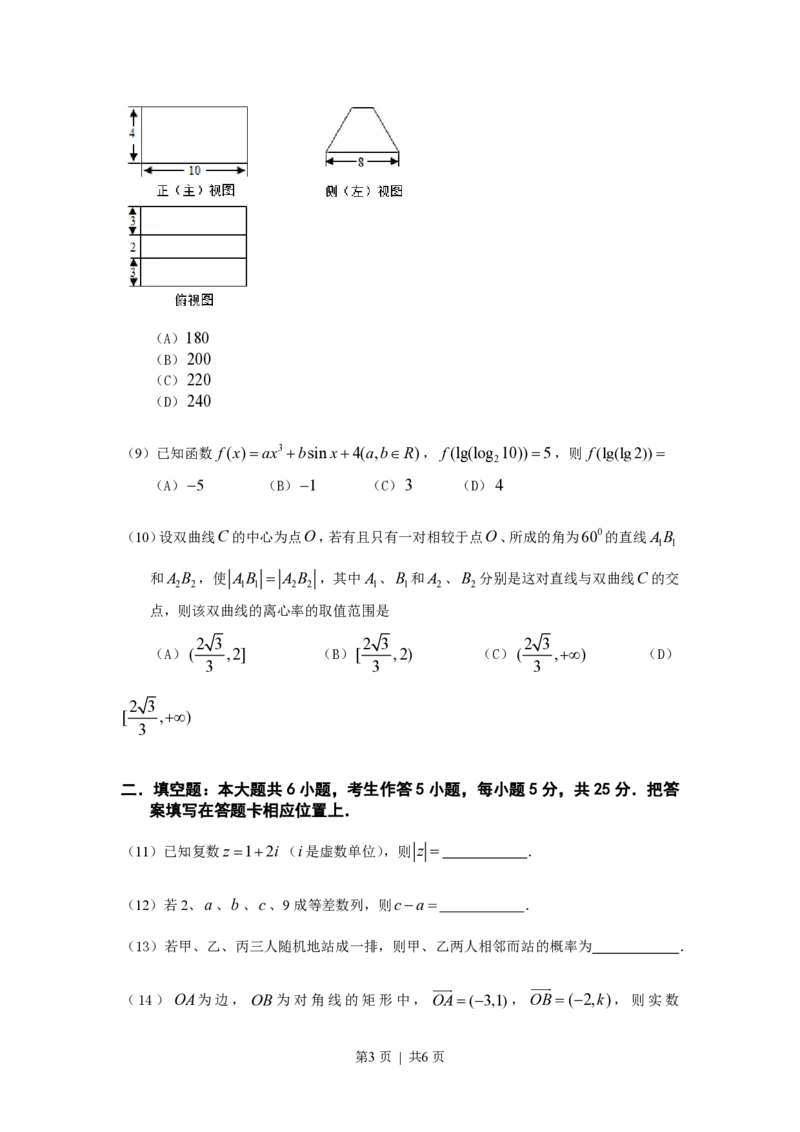
(8)某几何体的三视图如题(8)所示,则该几何体的表面积为
第2页 | 共6页(A)180
(B)200
(C)220
(D)240
(9)已知函数 f(x)=ax3+bsinx+4(a,bÎR), f(lg(log 10))=5,则 f(lg(lg2))=
2
(A)-5 (B)-1 (C)3 (D)4
(10)设双曲线C的中心为点O,若有且只有一对相较于点O、所成的角为600的直线AB
1 1
和A B ,使 AB = A B ,其中A、B 和A 、B 分别是这对直线与双曲线C的交
2 2 1 1 2 2 1 1 2 2
点,则该双曲线的离心率的取值范围是zhangwlx
2 3 2 3 2 3
(A)( ,2] (B)[ ,2) (C)( ,+¥) (D)
3 3 3
2 3
[ ,+¥)
3
二.填空题:本大题共 6 小题,考生作答 5 小题,每小题 5 分,共 25 分.把答
案填写在答题卡相应位置上.
(11)已知复数z =1+2i(i是虚数单位),则 z = .
hangwlx zhangwlx
(12)若2、a、b、c、9成等差数列,则c-a = .
zhangwlx
(13)若甲、乙、丙三人随机地站成一排,则甲、乙两人相邻而站的概率为 .
uuur uuur
(14) OA为边, OB为对角线的矩形中, OA=(-3,1), OB =(-2,k),则实数
第3页 | 共6页k = .
.
(15)设0£a£p,不等式8x2 -(8sina)x+cos2a³0对xÎR恒成立,则a的取值范
围为 .
三.解答题:本大题共 6 小题,共 75 分.解答应写出文字说明、证明过程或演
算步骤.
(16)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
设数列a 满足:a =1,a =3a ,nÎN .
n 1 n+1 n +
(Ⅰ)求a 的通项公式及前n项和S ;zhangwlx
n n
(Ⅱ)已知b 是等差数列,T 为前n项和,且b =a ,b =a +a +a ,求T .
n n 1 2 3 1 2 3 20
(17)(本小题满分13分,(Ⅰ)小问9分,(Ⅱ)、(Ⅲ)小问各2分)
从某居民区随机抽取10个家庭,获得第i个家庭的月收入x (单位:千元)与月储蓄y
i i
10 10 10
(单位:千元)的数据资料,算得 åx =80, åy =20, åx y =184,
i i i i
i=1 i=1 i=1
10
åx2 =720.
i
i=1
(Ⅰ)求家庭的月储蓄 y对月收入x的线性回归方程y =bx+a;
(Ⅱ)判断变量x与 y之间是正相关还是负相关;zhangwlx
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
n
åx y -nxy
i i
附:线性回归方程y =bx+a中,b= i=1 ,a= y-bx,
n
åx2 -nx 2
i
i=1
其中x, y为样本平均值,线性回归方程也可写为y =bx+a .zhangwlx
(18)(本小题满分13分,(Ⅰ)小问4分,(Ⅱ)小问9分)
在△ABC中,内角A、B、C的对边分别是a、b、c,且a2 =b2 +c2 + 3ab.
(Ⅰ)求A;
(Ⅱ)设a= 3,S 为△ABC的面积,求S +3cosBcosC的最大值,并指出此时B
第4页 | 共6页的值.
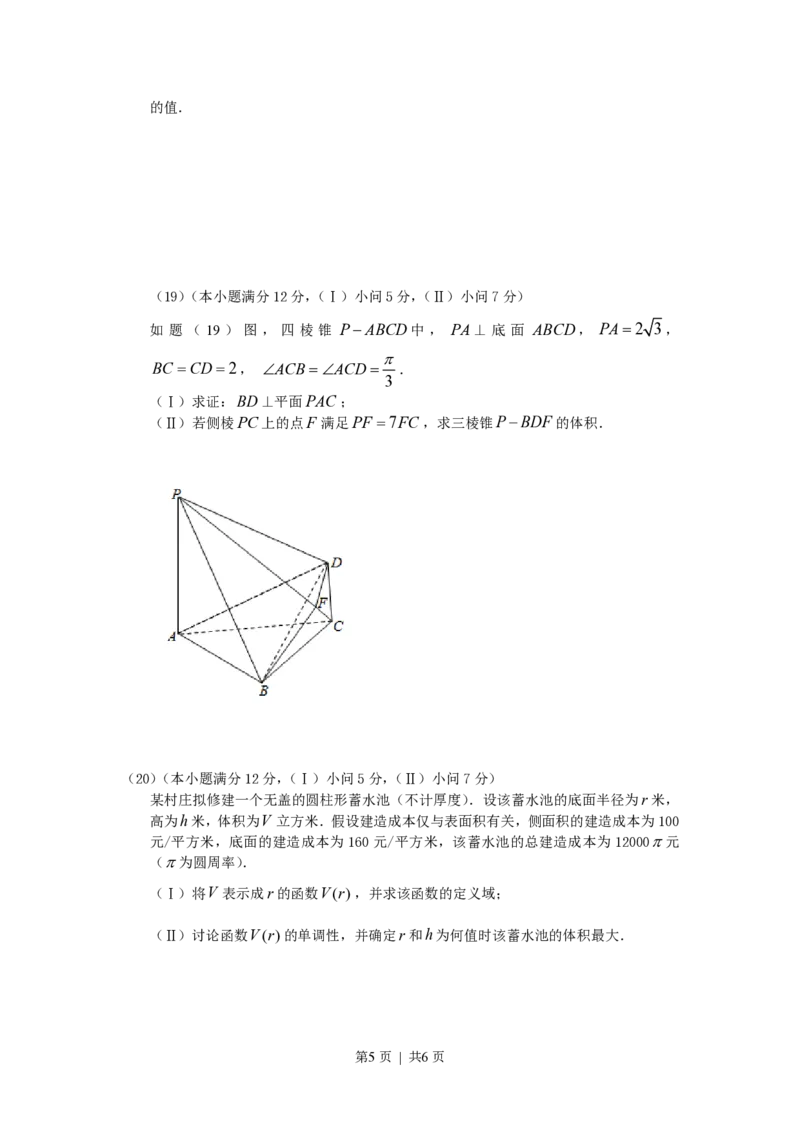
(19)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
如 题 ( 19 ) 图 , 四 棱 锥 P-ABCD中 , PA⊥ 底 面 ABCD, PA=2 3,
p
BC =CD=2, ÐACB=ÐACD= .zhangwlx
3
(Ⅰ)求证:BD⊥平面PAC ;
(Ⅱ)若侧棱PC上的点F 满足PF =7FC,求三棱锥P-BDF的体积.
(20)(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,
高为h米,体积为V 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100
元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000p元
(p为圆周率).
(Ⅰ)将V 表示成r的函数V(r),并求该函数的定义域;zhangwlx
(Ⅱ)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.zhangwlx
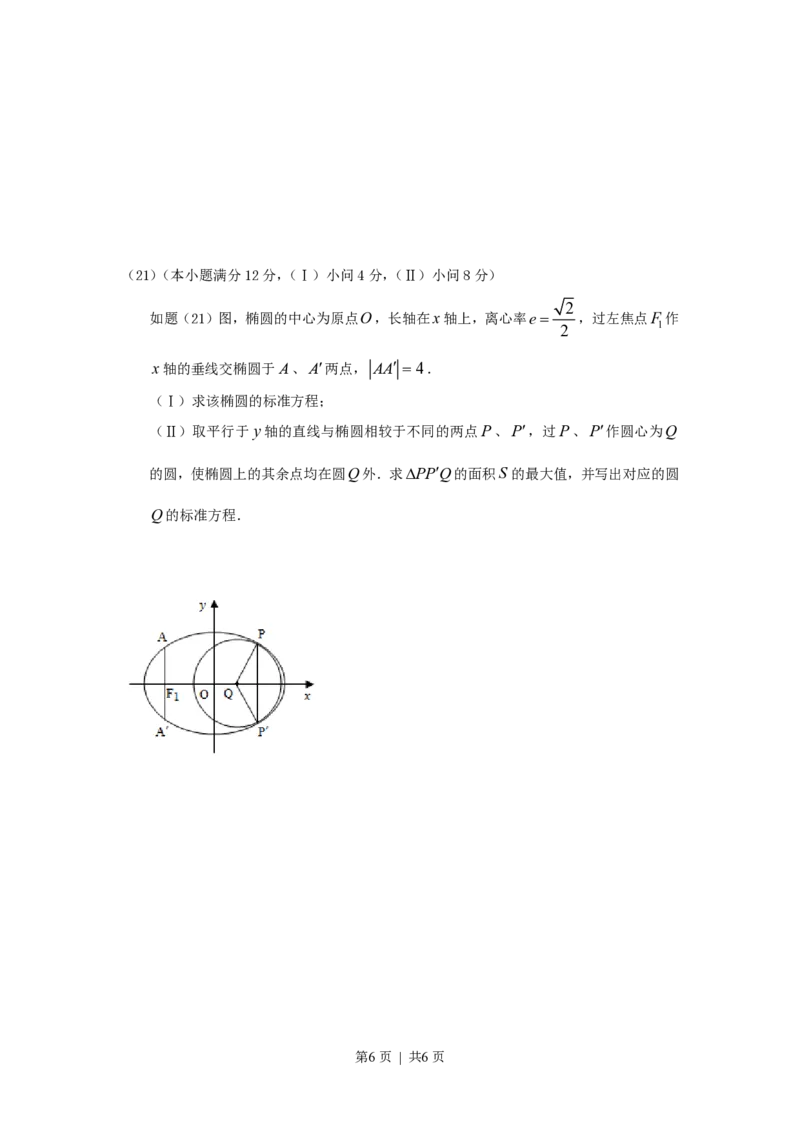
第5页 | 共6页(21)(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
2
如题(21)图,椭圆的中心为原点O,长轴在x轴上,离心率e= ,过左焦点F 作
2 1
x轴的垂线交椭圆于A、A¢两点, AA¢ =4.
(Ⅰ)求该椭圆的标准方程;zhangwlx
(Ⅱ)取平行于y轴的直线与椭圆相较于不同的两点P、P¢,过P、P¢作圆心为Q
的圆,使椭圆上的其余点均在圆Q外.求DPP¢Q的面积S 的最大值,并写出对应的圆
Q的标准方程.
第6页 | 共6页