文档内容
绝密★启用前
2024 年普通高等学校招生全国统一考试
全国甲卷文科数学
使用范围:陕西、宁夏、青海、内蒙古、四川
注意事项:
1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮
擦擦干净后,再选涂其它答案标号.
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
4.所有题目必须在答题卡上作答,在试题卷上答题无效.
5.考试结束后,只将答题卡交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 设 ,则 ( )
A. B. C. D. 2
【答案】D
【解析】
【分析】先根据共轭复数的定义写出 ,然后根据复数的乘法计算.
【详解】依题意得, ,故 .
故选:D
2. 若集合 , ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】根据集合 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合 中的元素 ,满足 ,
则 可能的取值为 ,即 ,
于是 .
故选:C
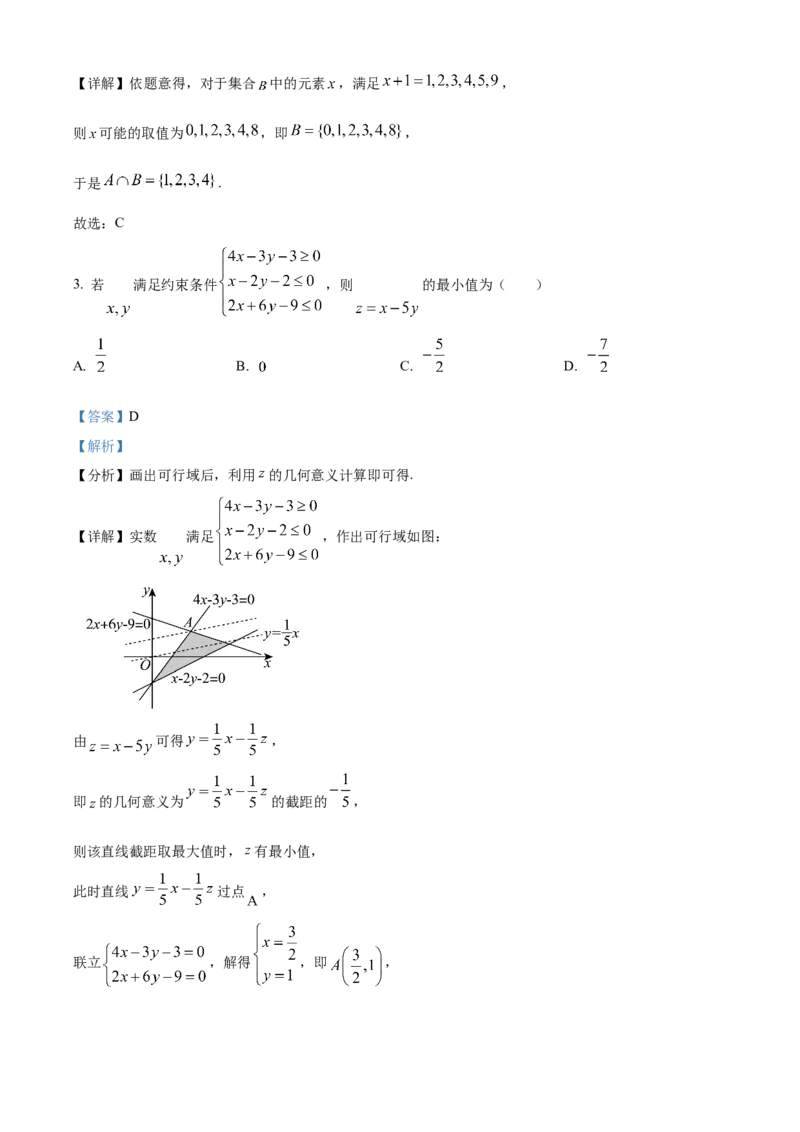
3. 若 满足约束条件 ,则 的最小值为( )
A. B. C. D.
【答案】D
【解析】
【分析】画出可行域后,利用 的几何意义计算即可得.
【详解】实数 满足 ,作出可行域如图:
由 可得 ,
即 的几何意义为 的截距的 ,
则该直线截距取最大值时, 有最小值,
此时直线 过点 ,
联立 ,解得 ,即 ,则 .
故选:D.
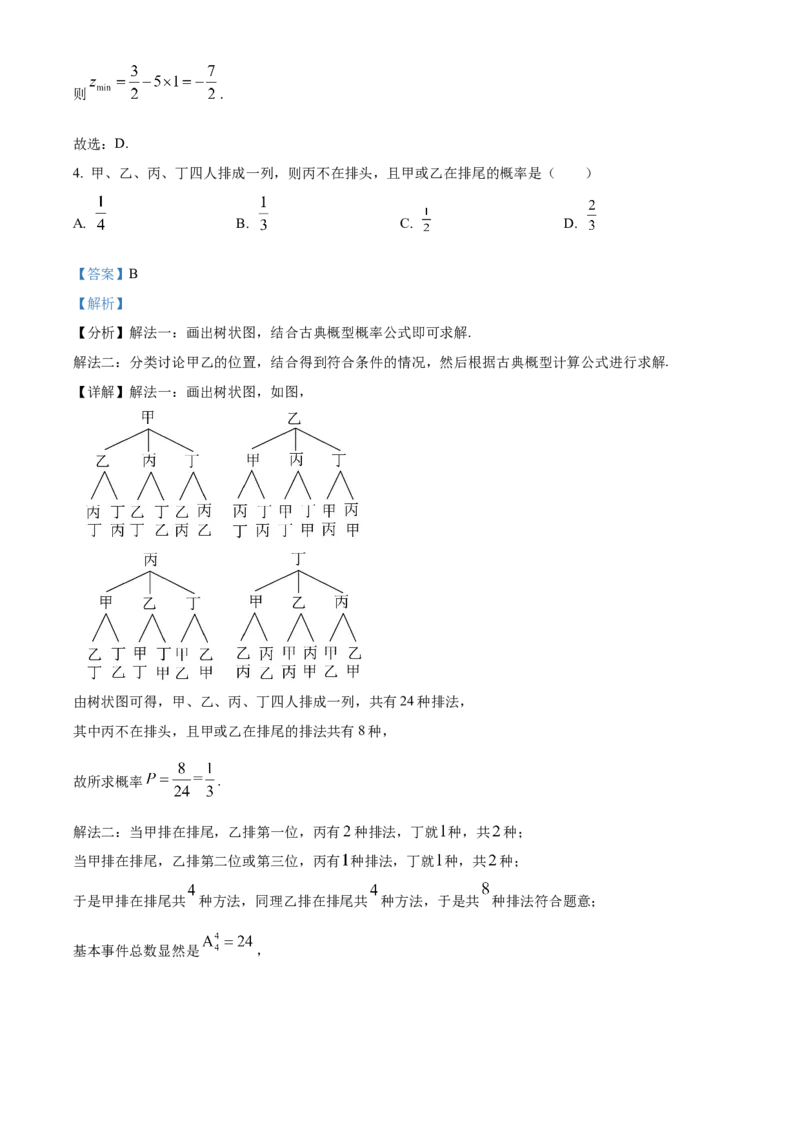
4. 甲、乙、丙、丁四人排成一列,则丙不在排头,且甲或乙在排尾的概率是( )
A. B. C. D.
【答案】B
【解析】
【分析】解法一:画出树状图,结合古典概型概率公式即可求解.
解法二:分类讨论甲乙的位置,结合得到符合条件的情况,然后根据古典概型计算公式进行求解.
【详解】解法一:画出树状图,如图,
由树状图可得,甲、乙、丙、丁四人排成一列,共有24种排法,
其中丙不在排头,且甲或乙在排尾的排法共有8种,
故所求概率 .
解法二:当甲排在排尾,乙排第一位,丙有 种排法,丁就 种,共 种;
当甲排在排尾,乙排第二位或第三位,丙有 种排法,丁就 种,共 种;
于是甲排在排尾共 种方法,同理乙排在排尾共 种方法,于是共 种排法符合题意;
基本事件总数显然是 ,根据古典概型的计算公式,丙不在排头,甲或乙在排尾的概率为 .
故选:B
5. 已知等差数列 的前 项和为 ,若 ,则 ( )
A. B. C. 1 D.
【答案】D
【解析】
【分析】可以根据等差数列的基本量,即将题目条件全转化成 和 来处理,亦可用等差数列的性质进行
处理,或者特殊值法处理.
【详解】方法一:利用等差数列的基本量
由 ,根据等差数列的求和公式, ,
又 .
故选:D
方法二:利用等差数列的性质
根据等差数列的性质, ,由 ,根据等差数列的求和公式,
,故 .
故选:D
方法三:特殊值法
不妨取等差数列公差 ,则 ,则 .
故选:D
6. 已知双曲线的两个焦点分别为 ,点 在该双曲线上,则该双曲线的离心率为(
)A. 4 B. 3 C. 2 D.
【答案】C
【解析】
【分析】由焦点坐标可得焦距 ,结合双曲线定义计算可得 ,即可得离心率.
【详解】由题意,设 、 、 ,
则 , , ,
则 ,则 .
故选:C.
7. 设函数 ,则曲线 在点 处的切线与两坐标轴所围成的三角形的面积为
( )
A. B. C. D.
【答案】A
【解析】
【分析】借助导数的几何意义计算可得其在点 处的切线方程,即可得其与坐标轴的交点坐标,即可
得其面积.
【详解】 ,
则 ,
为
即该切线方程 ,即 ,
令 ,则 ,令 ,则 ,故该切线与两坐标轴所围成的三角形面积 .
故选:A.
8. 函数 在区间 的图象大致为( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用函数的奇偶性可排除A、C,代入 可得 ,可排除D.
【详解】 ,
又函数定义域为 ,故该函数为偶函数,可排除A、C,
又 ,
故可排除D.
故选:B.
9. 已知 ,则 ( )
A. B. C. D.
【答案】B
【解析】【分析】先将 弦化切求得 ,再根据两角和的正切公式即可求解.
【详解】因为 ,
所以 , ,
所以 ,
故选:B.
10. 已知直线 与圆 交于 两点,则 的最小值为(
)
A. 2 B. 3 C. 4 D. 6
【答案】C
【解析】
【分析】根据题意,由条件可得直线过定点 ,从而可得当 时, 的最小,结合勾股
定理代入计算,即可求解.
【详解】因为直线 ,即 ,令 ,
则 ,所以直线过定点 ,设 ,
将圆 化为标准式为 ,
所以圆心 ,半径 ,
当 时, 的最小,
此时 .
故选:C
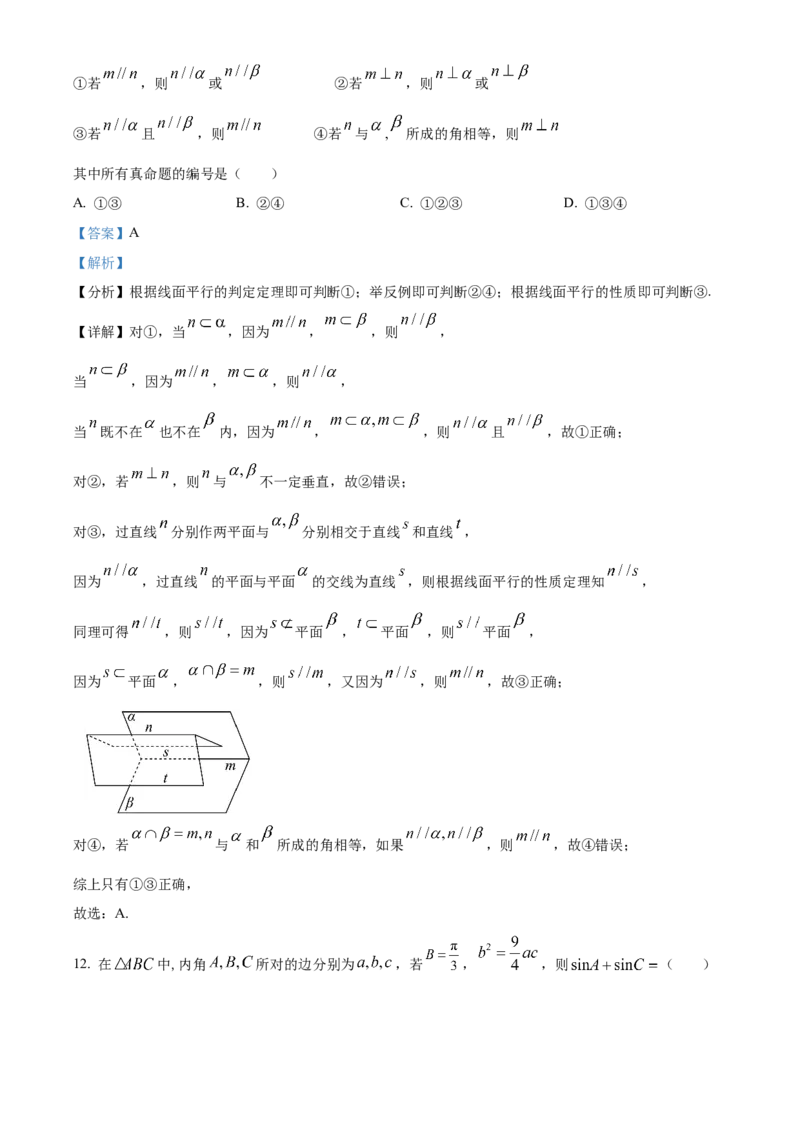
11. 设 为两个平面, 为两条直线,且 .下述四个命题:①若 ,则 或 ②若 ,则 或
③若 且 ,则 ④若 与 , 所成的角相等,则
其中所有真命题的编号是( )
A. ①③ B. ②④ C. ①②③ D. ①③④
【答案】A
【解析】
【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③.
【详解】对①,当 ,因为 , ,则 ,
当 ,因为 , ,则 ,
当 既不在 也不在 内,因为 , ,则 且 ,故①正确;
对②,若 ,则 与 不一定垂直,故②错误;
对③,过直线 分别作两平面与 分别相交于直线 和直线 ,
因为 ,过直线 的平面与平面 的交线为直线 ,则根据线面平行的性质定理知 ,
同理可得 ,则 ,因为 平面 , 平面 ,则 平面 ,
因为 平面 , ,则 ,又因为 ,则 ,故③正确;
对④,若 与 和 所成的角相等,如果 ,则 ,故④错误;
综上只有①③正确,
故选:A.
12. 在 中,内角 所对的边分别为 ,若 , ,则 ( )A. B. C. D.
【答案】C
【解析】
【分析】利用正弦定理得 ,再利用余弦定理有 ,由正弦定理得到
的值,最后代入计算即可.
【详解】因为 ,则由正弦定理得 .
由余弦定理可得: ,
即: ,根据正弦定理得 ,
所以 ,
因为 为三角形内角,则 ,则 .
故选:C.
二、填空题:本题共4小题,每小题5分,共20分.
13. 函数 在 上的最大值是______.
【答案】2
【解析】
【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.
【详解】 ,当 时, ,
当 时,即 时, .故答案为:2
14. 已知圆台甲、乙的上底面半径均为 ,下底面半径均为 ,圆台的母线长分别为 , ,
则圆台甲与乙的体积之比为______.
【答案】
【解析】
【分析】先根据已知条件和圆台结构特征分别求出两圆台的高,再根据圆台的体积公式直接代入计算即可
得解.
【详解】由题可得两个圆台的高分别为 ,
,
所以 .
故答案为: .
15. 已知 且 ,则 ______.
【答案】64
【解析】
【分析】将 利用换底公式转化成 来表示即可求解.
【详解】由题 ,整理得 ,
或 ,又 ,
所以 ,故
故答案为:64.
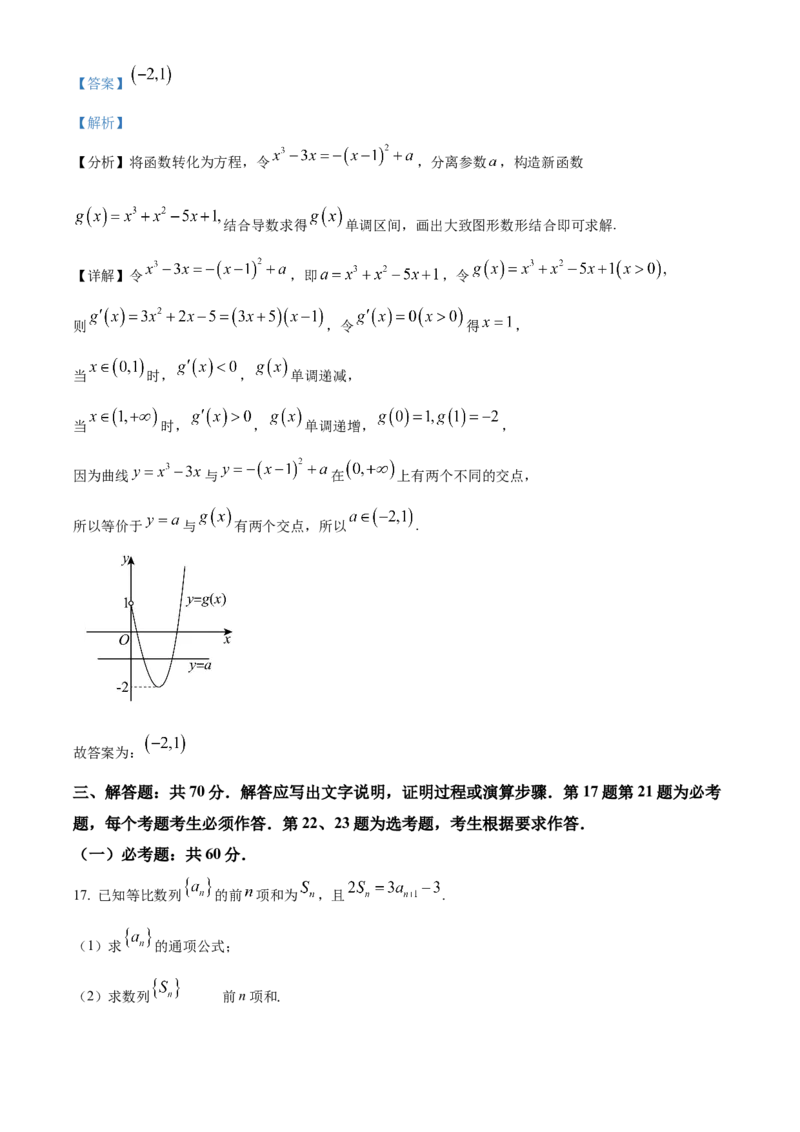
16. 曲线 与 在 上有两个不同 的交点,则 的取值范围为______.【答案】
【解析】
【分析】将函数转化为方程,令 ,分离参数 ,构造新函数
结合导数求得 单调区间,画出大致图形数形结合即可求解.
【详解】令 ,即 ,令
则 ,令 得 ,
当 时, , 单调递减,
当 时, , 单调递增, ,
因为曲线 与 在 上有两个不同的交点,
所以等价于 与 有两个交点,所以 .
故答案为:
三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17题第21题为必考
题,每个考题考生必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17. 已知等比数列 的前 项和为 ,且 .
(1)求 的通项公式;
(2)求数列 的前n项和.【答案】(1)
(2)
【解析】
【分析】(1)利用退位法可求公比,再求出首项后可求通项;
(2)利用分组求和法即可求 .
【小问1详解】
因为 ,故 ,
所以 即 故等比数列 的公比为 ,
故 ,故 ,故 .
【小问2详解】
由等比数列求和公式得 ,
所以数列 的前n项和
.
18. 某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取 150件
进行检验,数据如下:
优级 合格 不合格 总
品 品 品 计甲车
26 24 0 50
间
乙车
70 28 2 100
间
总计 96 52 2 150
(1)填写如下列联表:
优级 非优级
品 品
甲车
间
乙车
间
能否有 的把握认为甲、乙两车间产品的优级品率存在差异?能否有 的把握认为甲,乙两车间产
品的优级品率存在差异?
(2)已知升级改造前该工厂产品的优级品率 ,设 为升级改造后抽取的n件产品的优级品率.如果
,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认
为生产线智能化升级改造后,该工厂产品的优级品率提高了?( )
附:
0.050 0.010 0.001
k 3.841 6.635 10.828
【答案】(1)答案见详解
(2)答案见详解
【解析】
【分析】(1)根据题中数据完善列联表,计算 ,并与临界值对比分析;(2)用频率估计概率可得 ,根据题意计算 ,结合题意分析判断.
【小问1详解】
根据题意可得列联表:
优级品 非优级品
甲车间 26 24
乙车间 70 30
可得 ,
因为 ,
所以有 的把握认为甲、乙两车间产品的优级品率存在差异,没有 的把握认为甲,乙两车间产品
的优级品率存在差异.
【小问2详解】
由题意可知:生产线智能化升级改造后,该工厂产品的优级品的频率为 ,
用频率估计概率可得 ,
又因为升级改造前该工厂产品的优级品率 ,
则 ,
可知 ,
所以可以认为生产线智能化升级改造后,该工厂产品的优级品率提高了.
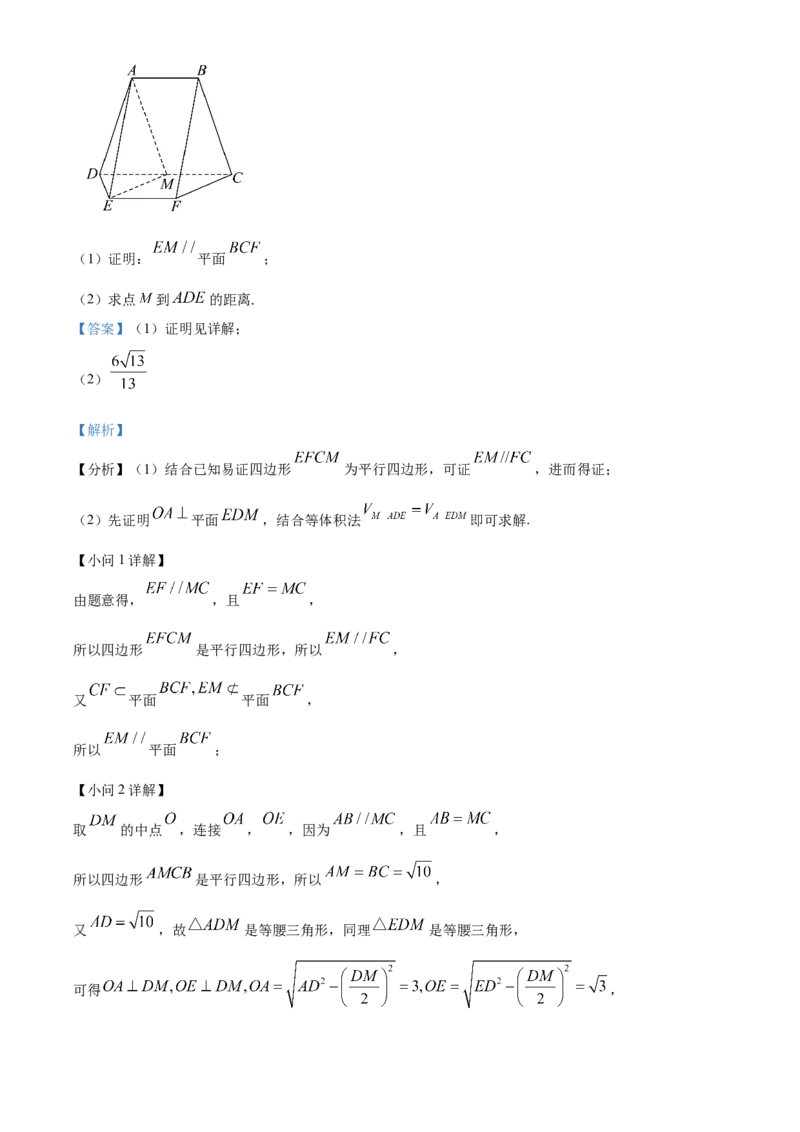
19. 如图, , , , ,
为 的中点.(1)证明: 平面 ;
(2)求点 到 的距离.
【答案】(1)证明见详解;
(2)
【解析】
【分析】(1)结合已知易证四边形 为平行四边形,可证 ,进而得证;
(2)先证明 平面 ,结合等体积法 即可求解.
【小问1详解】
由题意得, ,且 ,
所以四边形 是平行四边形,所以 ,
又 平面 平面 ,
所以 平面 ;
【小问2详解】
取 的中点 ,连接 , ,因为 ,且 ,
所以四边形 是平行四边形,所以 ,
又 ,故 是等腰三角形,同理 是等腰三角形,
可得 ,又 ,所以 ,故 .
又 平面 ,所以 平面 ,
易知 .
在 中, ,
所以 .
设点 到平面 的距离为 ,由 ,
得 ,得 ,
故点 到平面 的距离为 .
20. 已知函数 .
(1)求 的单调区间;
(2)当 时,证明:当 时, 恒成立.
【答案】(1)见解析 (2)见解析
【解析】
【分析】(1)求导,含参分类讨论得出导函数的符号,从而得出原函数的单调性;
(2)先根据题设条件将问题可转化成证明当 时, 即可.【小问1详解】
定义域为 ,
当 时, ,故 在 上单调递减;
当 时, 时, , 单调递增,
当 时, , 单调递减.
综上所述,当 时, 的单调递减区间为 ;
时, 的单调递增区间为 ,单调递减区间为 .
【小问2详解】
,且 时, ,
令 ,下证 即可.
,再令 ,则 ,
显然 在 上递增,则 ,
即 在 上递增,
故 ,即 在 上单调递增,
故 ,问题得证
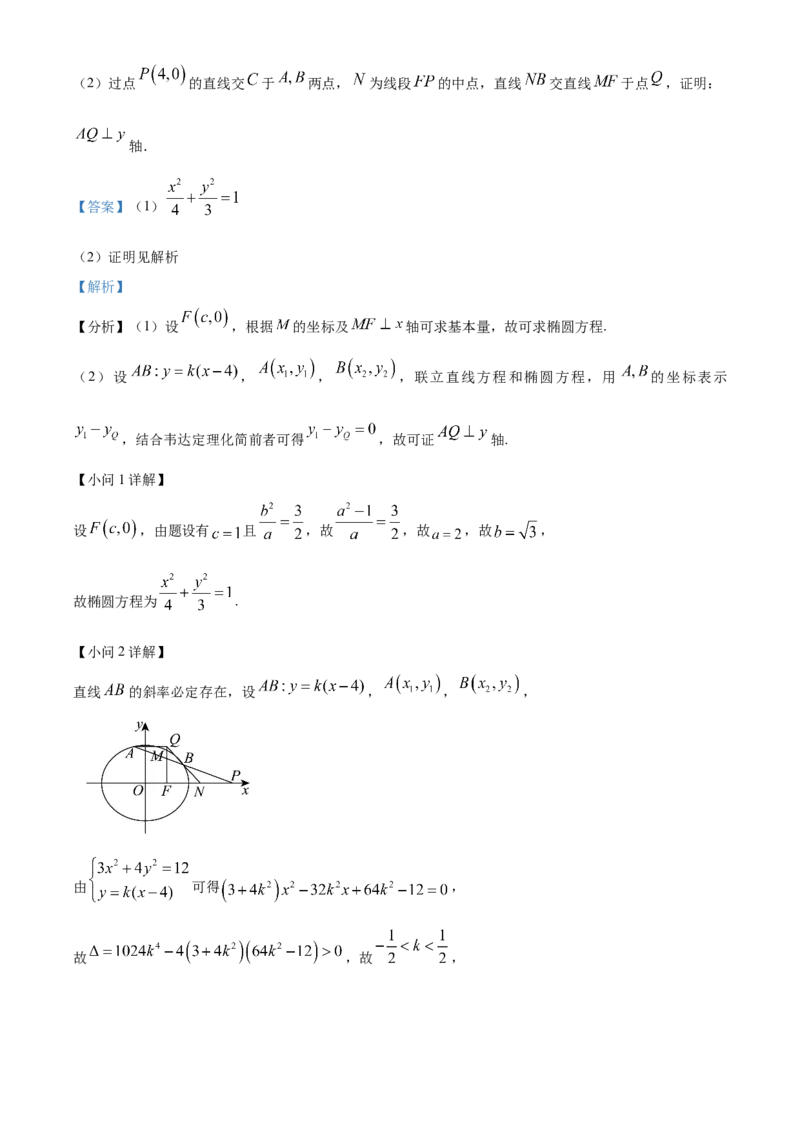
21. 已知椭圆 的右焦点为 ,点 在 上,且 轴.
(1)求 的方程;(2)过点 的直线交 于 两点, 为线段 的中点,直线 交直线 于点 ,证明:
轴.
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)设 ,根据 的坐标及 轴可求基本量,故可求椭圆方程.
(2)设 , , ,联立直线方程和椭圆方程,用 的坐标表示
,结合韦达定理化简前者可得 ,故可证 轴.
【小问1详解】
设 ,由题设有 且 ,故 ,故 ,故 ,
故椭圆方程为 .
【小问2详解】
直线 的斜率必定存在,设 , , ,
由 可得 ,
故 ,故 ,又 ,
而 ,故直线 ,故 ,
所以
,
故 ,即 轴.
【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:
(1)设直线方程,设交点坐标为 ;
(2)联立直线与圆锥曲线的方程,得到关于 (或 )的一元二次方程,注意 的判断;
(3)列出韦达定理;
(4)将所求问题或题中的关系转化为 、 (或 、 )的形式;
(5)代入韦达定理求解.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,并用2B铅笔将所选题号涂
黑,多涂、错涂、漏涂均不给分,如果多做,则按所做的第一题计分.
22. 在直角坐标系 中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
.(1)写出 的直角坐标方程;
(2)设直线l: ( 为参数),若 与l相交于 两点,若 ,求 .
【答案】(1)
(2)
【解析】
【分析】(1)根据 可得 的直角方程.
(2)将直线的新的参数方程代入 的直角方程,
法1:结合参数 的几何意义可得关于 的方程,从而可求参数 的值;
法2:将直线的直角方程与曲线的直角方程联立,结合弦长公式可求 的值.
【小问1详解】
由 ,将 代入 ,
故可得 ,两边平方后可得曲线的直角坐标方程为 .
【小问2详解】
对于直线 的参数方程消去参数 ,得直线的普通方程为 .
法1:直线 的斜率为 ,故倾斜角为 ,
故直线的参数方程可设为 , .
将其代入 中得
设 两点对应的参数分别为 ,则 ,且 ,故 ,
,解得 .
法2:联立 ,得 ,
,解得 ,
设 , ,
则 ,
解得
23. 已知实数 满足 .
(1)证明: ;
(2)证明: .
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】(1)直接利用 即可证明.
(2)根据绝对值不等式并结合(1)中结论即可证明.
【小问1详解】
因为 ,
当 时等号成立,则 ,
因为 ,所以 ;
【小问2详解】