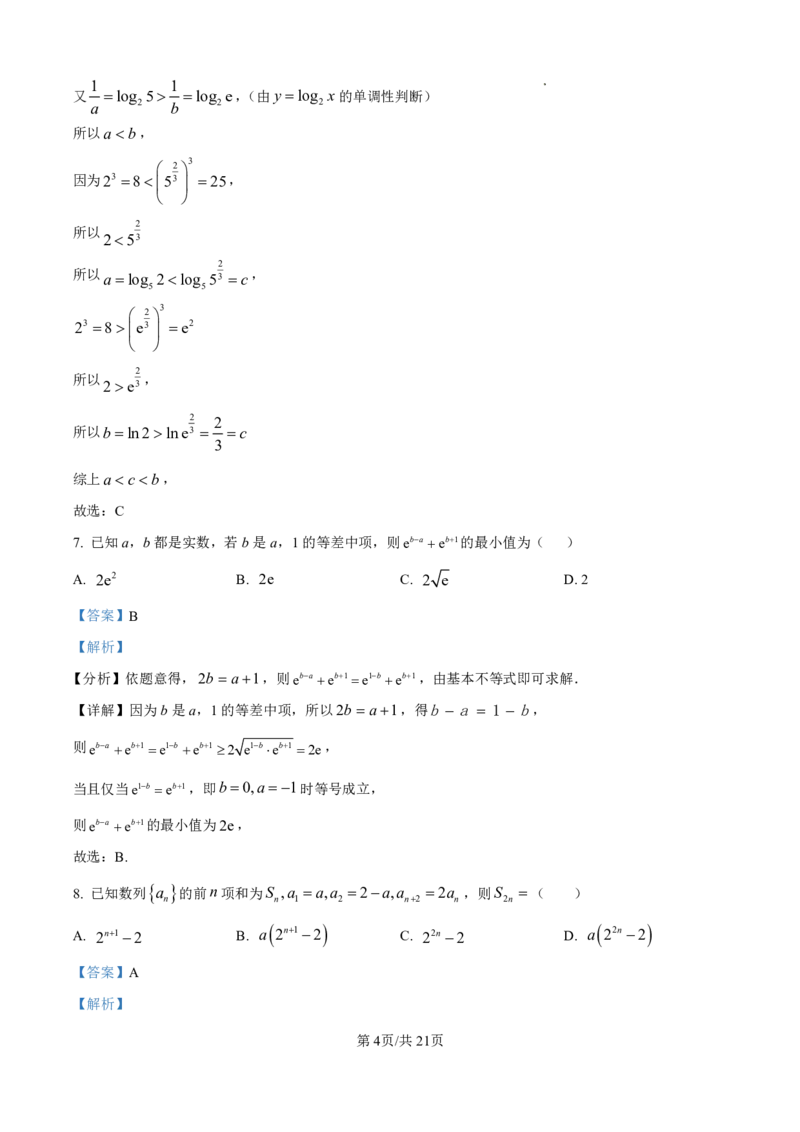南开中学（高三上学期）第二次月考（数学）2025-2026学年试卷解析(1)_2026年1月_260103天津市南开中学2025-2026学年高三上学期第二次月考

2026 届高三年级第二次质量检测
数学试卷
2025-12
一 、选择题（共 9小题，每题 5分，共 45分）
A 0,1,2,3,4 ，B x∣x2  A ð B  
1. 已知集合 ，则 R （ ）
       
A. 0,1,2,3 B. 0,1,2 C. 2,3,4 D. 3,4
【答案】D
【解析】
【分析】利用交集和补集的概念计算即可.
【详解】因为A 0，1，2，3，4 ，ð B{x∣x2}，所以Að B  3，4  ．
R R
故选：D
2. 设S 为数列  a  的前n项和，“  a  是递增数列”是“  S  是递增数列”的（ ）．
n n n n
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
【答案】D
【解析】
【分析】利用充分条件和必要条件的定义判断.
【详解】数列-3，-2，-1，0，1，2，3，…是递增数列，
n  n1  1 7
但S 3n  n2 n 不是递增数列，故不充分；
n 2 2 2
数列1，1，1，1，…的前n项和为S n是递增数列，
n
数列不是递增数列，故不必要；
故选：D
3. 函数 f (x)的部分图象如图所示，则 f (x)的解析式可能是（ ）
第1页/共21页
学科网（北京）股份有限公司2x3 2x 2x3 2  x2 1 
A. f(x) B. f(x) C. f(x) D. f(x)
1 x x2 1 x2 1 x2 1
【答案】C
【解析】
【分析】结合函数图象，利用性质和特值排除可得答案.
【详解】对于A中的函数 f (x)，当x 1时， f(x)0，与图象不符，故排除；
对于B中的函数 f (x)的定义域为R，故排除；
对于D中的函数 f (x)为偶函数，故排除．
 
对于C中的函数 f (x)，定义域为 x x  1 ，且满足 f(x)f(x)，其图象关于原点对称，
当0 x1时， f(x)0，当x 1时， f(x)0，与图象一致.
故选：C
4. 已知一组样本数据 x,y ， x,y  ，  x ,y  ，，  x ,y  ，画出相应散点图，发现变量x，y有
1 1 2 2 3 3 12 12
较强的线性关系，利用最小二乘法得其回归方程为 yˆ 2x6 ．若 y  y  y  y  24 ，则
1 2 3 12
x x x x （ ）
1 2 3 12
A. 24 B. 4 C. 15 D. 48
【答案】D
【解析】
【分析】由回归方程性质可得解.
【详解】由线性回归方程的性质，知回归直线 yˆ 2x6恒过点  x,y  ，
因为 y  y  y  y  24，所以 y 2，
1 2 3 12
所以22x6，解得x 4，
第2页/共21页
学科网（北京）股份有限公司所以x x x x 12x 48，
1 2 3 12
故选：D．
5. 已知平面，，直线a,b，则下列结论正确的是（ ）
A. 若a，b//a，则b// B. 若//,a,b，则a//b
 
C. 若a//，b，则ab D. 若//,a//，则a//
【答案】C
【解析】
【分析】根据线面平行的判定定理、面面平行的性质、平行性的性质、面面平行的性质逐一判断即可.
【详解】A：当b时，也可以满足a，b//a，因此本选项结论不正确；
B：当//,a,b时，直线a,b可以是异面直线，因此本选项结论不正确；
C：设过直线a的平面  与平面相交于直线c，
根据直线与平面平行的性质定理可知a//c，因为b，且c，
 
所以bc，而a//c，所以ab，因此本选项结论正确；
D：当//,a//时，a可以成立，所以本选项结论不正确，
故选：C
2 lg 2
6. 设alog 4log 2,bln ln3,c10 3，则a,b,c的大小关系为（ ）
5 5 3
A. a bc B. ca b C. a cb D. bac
【答案】C
【解析】
3
2 1 1  2 
【分析】由指数的运算性质得到alog 2,bln2,c ，通过  判断a b，再通过23 53  ，
5 3 a b
 
3
 2 
23 e3  判断a,c和b,c的大小即可.
 
【详解】alog 4log 2log 20，
5 5 5
2 lg 2 2
bln ln3ln20,c10 3  ，
3 3
第3页/共21页
学科网（北京）股份有限公司1 1
又 log 5 log e，（由 y log x的单调性判断）
a 2 b 2 2
所以a b，
3
 2 
因为23 853  25，
 
2
所以
253
2
所以 ，
a log 2log 53 c
5 5
3
 2
23 8e3 e2
 
2
所以 ，
2e3
2 2
所以bln2lne3  c
3
综上a cb，
故选：C
7. 已知a，b都是实数，若b是a，1的等差中项，则eba eb1的最小值为（ ）
A. 2e2 B. 2e C. 2 e D.2
【答案】B
【解析】
【分析】依题意得，2b  a1，则eba eb1e1b eb1，由基本不等式即可求解．
【详解】因为b是a，1的等差中项，所以2b  a1，得b a  1  b，
则 eba eb1 e1b eb12 e1beb1 2e ，
当且仅当e1b eb1，即b0,a 1时等号成立，
则eba eb1的最小值为2e，
故选：B.
8. 已知数列  a  的前n项和为S ,a a,a 2a,a 2a ，则S （ ）
n n 1 2 n2 n 2n
A. 2n12 B. a  2n12  C. 22n 2 D. a  22n 2 
【答案】A
【解析】
第4页/共21页
学科网（北京）股份有限公司【分析】由题意可得a a 2、a a 2  a a  ，再借助等比数列求和公式计算即可得.
1 2 n3 n2 n1 n
【详解】由a a,a 2a ，则a a a2a  2，
1 2 1 2
由a 2a ，则a 2a ，故a a 2  a a  ，
n2 n n3 n1 n3 n2 n1 n
则a a 2  a a 22、a a 23、、a a 2n，
4 3 2 1 6 5 2n 2n1
 
2 12n
则S a a a a 222 232n  2n12.
2n 1 2 2n1 2n 12
故选：A.
 π  
9. 已 知 函 数 f  x 2sin x  0  在 区 间  ,  上 有 且 仅 有 一 个 零 点 ， 且
 3  2 
 2025 i
f  3 2f  ，则  f   （ ）
 2   2 
i1
A.2 B. 2 3 C.  3 D.1
【答案】B
【解析】
 π 3 2 π 2
【 分 析 】 由 题 意 得 sin 2    2sin   ， 令  ， 可 得
 3 2  2 3 2
 π 3  π
sin2   2sin   ，求得 cos1 或 tan 3 ，求得所以 4kπ,kN* 或
 3 2  3
 2kπ 4π ,kN，再由 f  x  在    ,  上有且仅有一个零点，求得2 4π，进而得到 10π
3  2  3
i 5π π
时，化简得到 f   2sin i ，结合三角函数的周期性，即可求解.
 2   3 3
 π
【详解】由函数 f  x 2sin x  0  ，
 3
  π 2 π
因为 f  3 2f  ，可得2sin 2    3 4sin  ，
 2   3  2 3
 π 3 2 π
即sin 2    2sin  ，
 3 2  2 3
第5页/共21页
学科网（北京）股份有限公司2  π 3  π
令 ，可得sin2

 2sin 

，
2  3 2  3
整理得(sin 3cos)cossin 3cos，解得cos1或tan 3 ，
2π
则2kπ,kN*或kπ ,kN，
3
4π
所以 4kπ,kN*或 2kπ ,kN，
3
  π 2 π π
当x  , ，可得x   ,2  ，
 2  3  2 3 3
  2
由函数 f  x  在 , 上有且仅有一个零点，可得 2π，即2 4π，
 2  2
π 7π 13π
若 4kπ,kN*，当k 1时， 4π ，可得x   , ，
3  3 3 
π π
此时x 3π或x  4π，使得 f  x 0，不符合题意；
3 3
4π 4π 10π
若 2kπ ,kN，当k 0时， ；当k 1时， ，
3 3 3
当 4π 时，可得x π   π, 5π ，函数 f  x  在    ,  上无零点；
3 3  3   2 
当 10π 时，可得x π   2π, 11π ，当且仅当x π 3π时， f  x 0，符合题意，
3 3  3  3
10π i i2 π  5π π
所以 ，则 f   2sin  2sin i  ，
3  2   2 3  3 3
(6i5) 5π π
可得 f( )2sin[ (6i5) ]0，
2 3 3
(6i4) 5π π (6i3) 5π π
f( )2sin[ (6i4) ] 3， f( )2sin[ (6i3) ] 3
2 3 3 2 3 3
(6i2) 5π π
f( )2sin[ (6i2) ]0
2 3 3
 6i1  5π π
f  2sin   6i1    3，
 2   3 3
第6页/共21页
学科网（北京）股份有限公司6i 5π π
f   2sin  6i   3 ，
 2   3 3

又由202533763，
2025 i
所以f   337(0 3 30 3 3)0 3 3 2 3 .
 2 
i1
故选：B.
二、填空题：（共 6小题，每题 5分，共 30分）
10
10. 已知复数z  （i为虚数单位），则 z  _____．
(3i)2
【答案】1
【解析】
【分析】先将复数z运算化简，再根据求模的方法直接求解即可.
10 10 5 5  43i  4 3
【详解】z       i,
(3i)2 86i 43i  43i  43i  5 5
骣 2 骣 2
4 3
\ z = 琪 琪 +琪 琪 - =1.
桫5 桫5
故答案为：1.
【点睛】本题考查复数的除法运算及模的求法，属于基础题.
2
11. 在(x )5的展开式中，x1的系数是________．（用数字作答）
x2
【答案】40
【解析】
【分析】根据二项式展开式的通项公式，得到x1的系数.
5 r
 2   2 
【详解】 x

的展开式的通项公式为：T Crx5r



Cr(2)rx53r，令53r 1，解得：
 x2  r1 5  x2  5
r 2，x1的系数是C2(2)2 40．
5
故答案为：40
第7页/共21页
学科网（北京）股份有限公司12. 已知函数 f  x 
ex 1
,g  x  f  x1 1， a  g


1
 g


2
 g


2n1

 nN
，则数
ex 1 n n n  n 
 
列 a 的通项公式为____________．
n
【答案】a 2n1
n
【解析】
【分析】由 f x f  x  得 f  x  为奇函数，进而得 g  x  f  x1 1 关于  1,1  对称，即
g  x g  2x 2，最后利用倒序相加法即可求解.
【详解】由题意有：f x
ex 1

1ex
f x，所以 f  x  为奇函数，所以g  x  f  x1 1关
ex 1 1ex
于  1,1  对称，所以g  x g  2x 2，
1 2 2n1
所以 a  g  g  g ①，
n n n  n 
2n1 2n2 1
又 a  g  g  g ②，
n  n   n  n
由①②有：
 1 2n1  2 2n2  2n1 1
2a  g  g   g  g   g  g  2  2n1  ，
n  n  n   n  n    n  n
所以a 2n1，
n
故答案为：a 2n1.
n
π
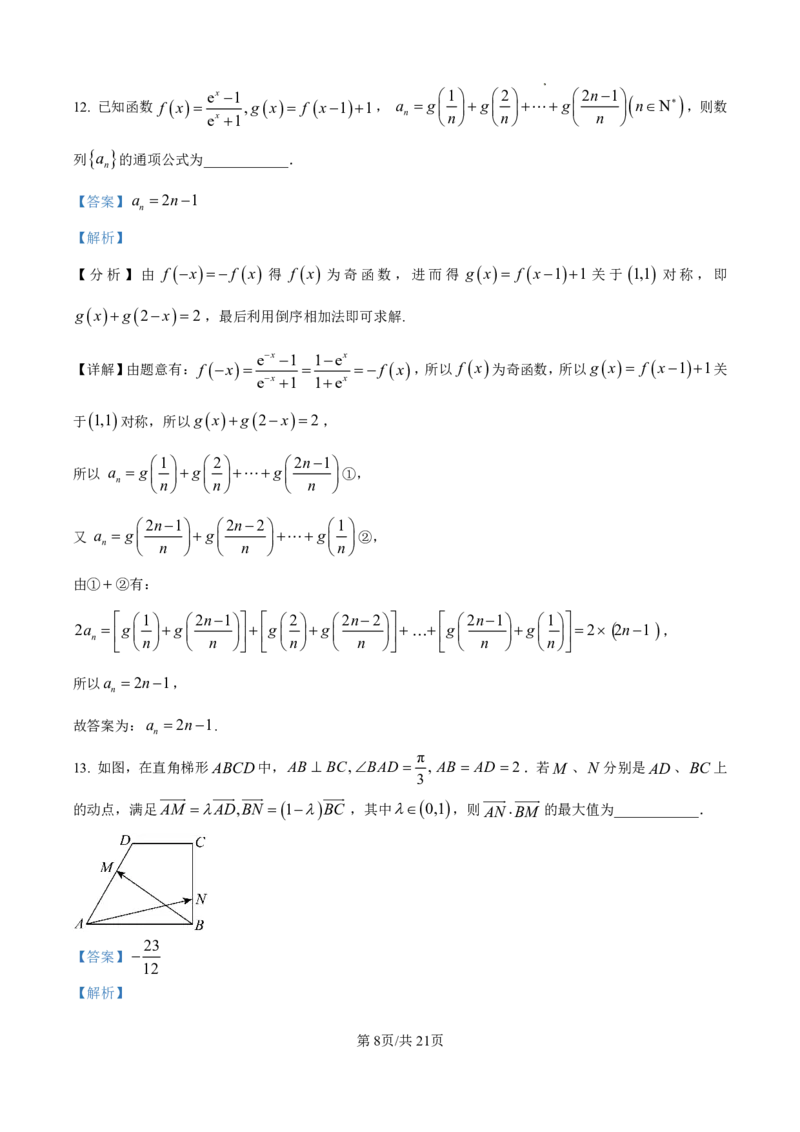
13. 如图，在直角梯形ABCD中，AB  BC,BAD  , AB  AD  2．若M 、N 分别是AD、BC上
3
     
的动点，满足AM AD,BN   1 BC ，其中 0,1  ，则ANBM 的最大值为____________．
23
【答案】
12
【解析】
第8页/共21页
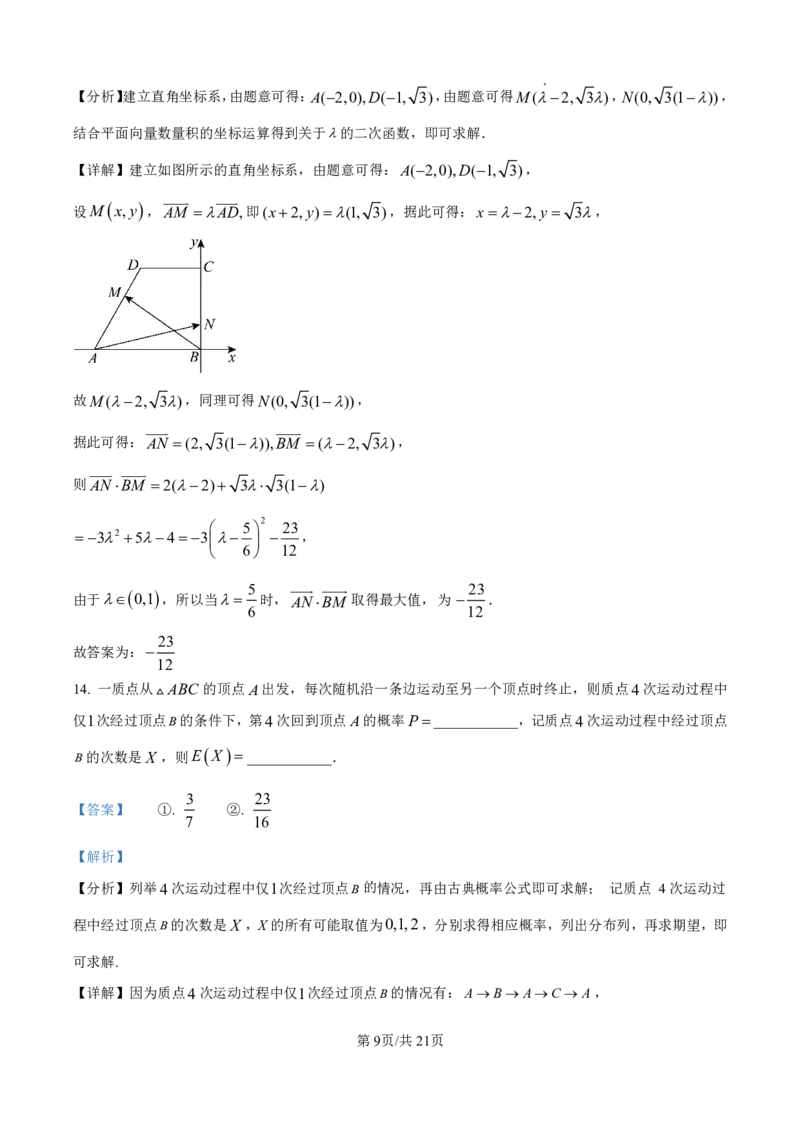
学科网（北京）股份有限公司【分析】建立直角坐标系，由题意可得：A(2,0),D(1, 3)，由题意可得M(2, 3)，N(0, 3(1))，
结合平面向量数量积的坐标运算得到关于的二次函数，即可求解．
【详解】建立如图所示的直角坐标系，由题意可得：A(2,0),D(1, 3)，
 
 
设M x,y ，AM AD,即(x2,y)(1, 3)，据此可得：x2,y  3，
故M(2, 3)，同理可得N(0, 3(1))，
 
据此可得：AN (2, 3(1)),BM (2, 3)，
 
则ANBM 2(2) 3 3(1)
2
 5 23
32 543 

 ，
 6 12
5   23
由于 0,1  ，所以当 时，ANBM 取得最大值，为  ．
6 12
23
故答案为：
12
14. 一质点从ABC 的顶点A出发，每次随机沿一条边运动至另一个顶点时终止，则质点4次运动过程中
仅1次经过顶点B的条件下，第4次回到顶点A的概率P ____________，记质点4次运动过程中经过顶点
B的次数是X ，则E

X
____________．
3 23
【答案】 ①. ②.
7 16
【解析】
【分析】列举4次运动过程中仅1次经过顶点B 的情况，再由古典概率公式即可求解； 记质点 4次运动过
程中经过顶点B的次数是X ，X的所有可能取值为0,1,2，分别求得相应概率，列出分布列，再求期望，即
可求解.
【详解】因为质点4次运动过程中仅1次经过顶点B的情况有：AB AC A，
第9页/共21页
学科网（北京）股份有限公司ABC AC ，AC  AB A,AC  ABC ，
AC B AC,AC BC  A ，AC ACB，共7种，
第四次回到顶点A有3种，所以质点4次运动过程中仅1次经过顶点B的条件下，第4次回到顶点A的概率
3
P  .
7
记质点 4次运动过程中经过顶点B的次数是X ，X的所有可能取值为0,1,2，
质点4次运动，共有222216种情况，
1
当X=0时，AC AC A，共有1种情况，则PX 0 ，
16
当X=1时，AB AC A， ABC AC ，
AC AB A， AC ABC ，
ACB AC ，ACBC A，AC ACB，共有7种情况，
7 1 7 1
所以PX 1 ，又PX 21   ，
16 16 16 2
所以X的分布列为：
X 0 1 2
1 7
p 1
16 16 2
1 7 1 23
EX0 1 2  ，
16 16 2 16
3 23
故答案为： ， .
7 16
15. 已知方程 4x2 2ax1ax2 x0有且仅有两个不相等的正实数根，则实数a的取值范围是
__________.
 15 
【答案】 ,
 
 2 
【解析】
【分析】根据a的正负以及4x2 2ax1的正负分类讨论，结合图象确定a的取值范围.
【详解】（1）当a 0时，方程 4x2 2ax1ax2 x0化为：4x2 x10，此时无解，舍去；
（2）当a 0时，考虑方程正实数根情况，只需研究当x 0时方程 4x2 2ax1ax2 x0解的情况，
第10页/共21页
学科网（北京）股份有限公司即此时方程化为4x2 2ax1ax2 x 0,(4a)x2 (2a1)x10 ，
 15
 Δ  2a1 24  4a 0 
a2 
4
 
 2a1 1  1
若此时方程有两个不相等的正实数根，则需 0, 0, a  a
4a 4a 2
 
 a0  a0



a a2
（3）当0a2时，因为4x2 2ax14(x )2 1 0 ，
4 4
所以方程 4x2 2ax1ax2 x0化为(4a)x2 (2a1)x10，
 15
a2 
Δ (2a1)24(4a)0
2


 2a1 1  1 15
若此时方程有两个不相等的正实数根，则需 0, 0,  a   a2
4a 4a 2 2
 
 0a2  0a2



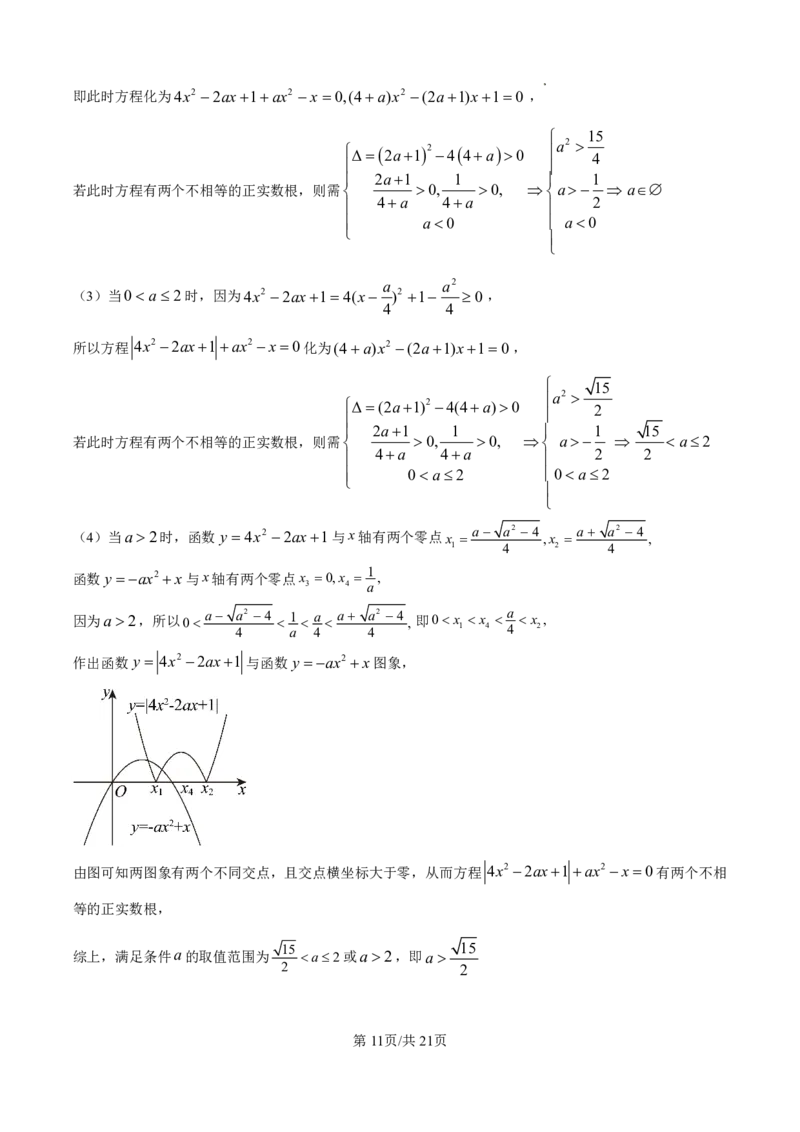
（4）当a2时，函数 y  4x2 2ax1与x轴有两个零点 x  a a2 4 ,x  a a2 4 ,
1 4 2 4
1
函数 y ax2x与x轴有两个零点x 0,x  ,
3 4 a
因为a2，所以 0 a a2 4  1  a  a a2 4 , 即0 x  x  a  x ,
4 a 4 4 1 4 4 2
作出函数 y  4x2 2ax1 与函数 y ax2x图象，
由图可知两图象有两个不同交点，且交点横坐标大于零，从而方程 4x2 2ax1ax2 x0有两个不相
等的正实数根，
15 15
综上，满足条件a的取值范围为 a2或a2，即a 
2 2
第11页/共21页
学科网（北京）股份有限公司 15 
故答案为： ,
 
2
 
三、解答题（共 5小题，共 75分．解答应写出文字说明，证明过程或演算步骤）
1
16. 在ABC 中，角A,B,C 所对的边分别为a,b,c．已知a 2 3，b3c，cosA ．
3
（1）求c的值；
（2）求sinC的值；
（3）求sin  2AC  的值．
【答案】（1）c1
6
（2）sinC 
9
6
（3）
3
【解析】
【分析】（1）根据条件，利用余弦定理即可求出结果；
2 2
（2）根据条件，利用同角三角函数间的关系，得到sin A ，再利用正弦定理即可求出结果；
3
（3）法一，利用二倍角公式，求出sin2A,cos2A，利用同角三角函数间的关系求出cosC，即可求出结果；
法二，利用ABCπ，得到sin  2AC sin  BA ，再计算出sinB,cosB即可求出结果.
【小问1详解】
1
因为a 2 3，b3c，cosA ，
3
b2 c2 a2 9c2 c2 12 1
由余弦定理可得cosA   ，整理得c2 10，
2bc 6c2 3
解得c1.
【小问2详解】
1 1 2 2
因为cosA ，A 0,π  ，所以sinA 1cos2 A  1  ，
3 9 3
2 3 1
a c 
由正弦定理  ，可得 2 2 sinC ，
sinA sinC
3
第12页/共21页
学科网（北京）股份有限公司6
解得sinC  .
9
【小问3详解】
2 2  1 4 2
（法一）由（2）得，sin2A2sin AcosA2 



 ，
3  3 9
2
 1 7
cos2A2cos2 A12



1 ，
 3 9
2
 6  5 3
cosC  1sin2C  1   ，
 
 9  9
4 2 5 3 7 6 6
所以sin  2AC sin2AcosCcos2AsinC      ，
9 9 9 9 3
6
所以sin  2AC  ．
3
 2
a2 c2 b2 2 3 12 32 3
（法二）由余弦定理可得 ，
cosB  
2ac 22 31 3
6
∴sinB  1cos2B  ，
3
∴sin  2AC sin

 AC  A

sin  πB A  sin

π  BA 

 sin  BA 
6  1 3 2 2 6
sinBcosAcosBsin A        .
3  3 3 3 3
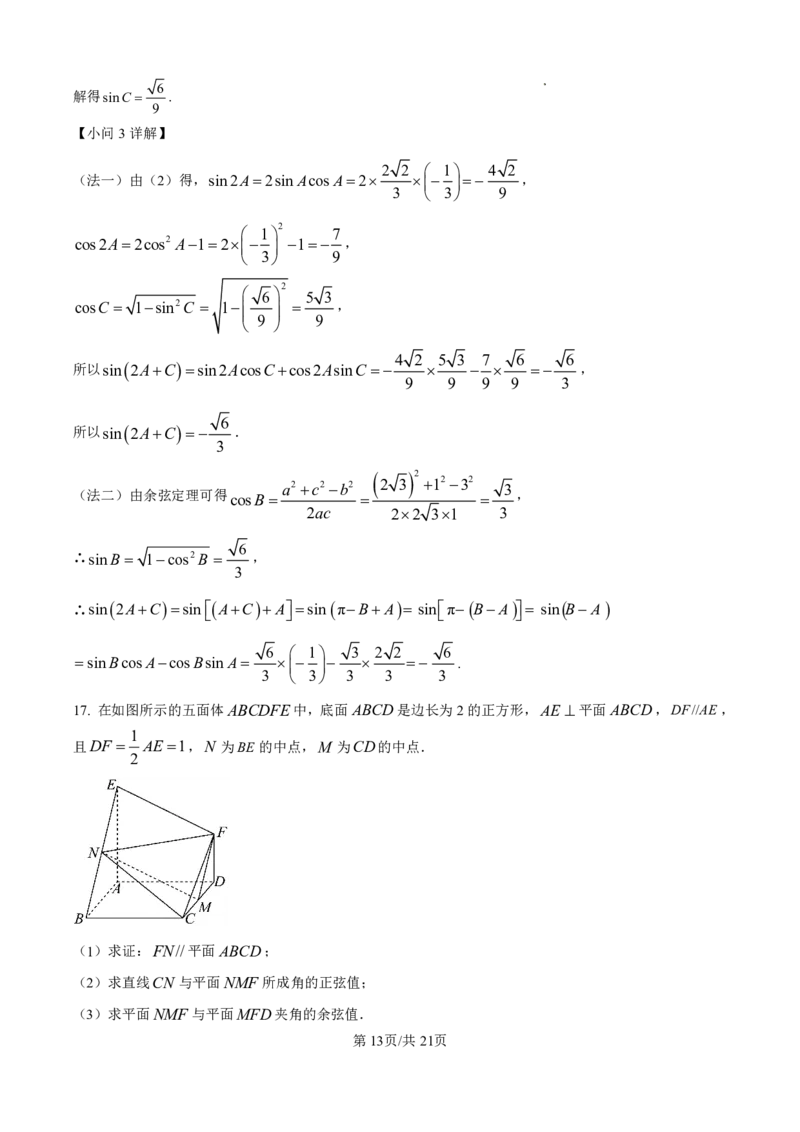
17. 在如图所示的五面体ABCDFE中，底面ABCD是边长为2的正方形，AE 平面ABCD，DF//AE，
1
且DF  AE 1，N 为BE 的中点，M 为CD的中点．
2
（1）求证：FN//平面ABCD；
（2）求直线CN 与平面NMF 所成角的正弦值；
（3）求平面NMF 与平面MFD夹角的余弦值．
第13页/共21页
学科网（北京）股份有限公司【答案】（1）证明见解析
6
（2）
9
1
（3）
3
【解析】
【分析】（1）建系，求得直线方向向量，和平面法向量，通过向量位置关系即可判断；
（2）求得直线方向向量，和平面法向量，代入夹角公式即可求解；
（3）求得平面法向量，代入夹角公式即可求解.
【小问1详解】
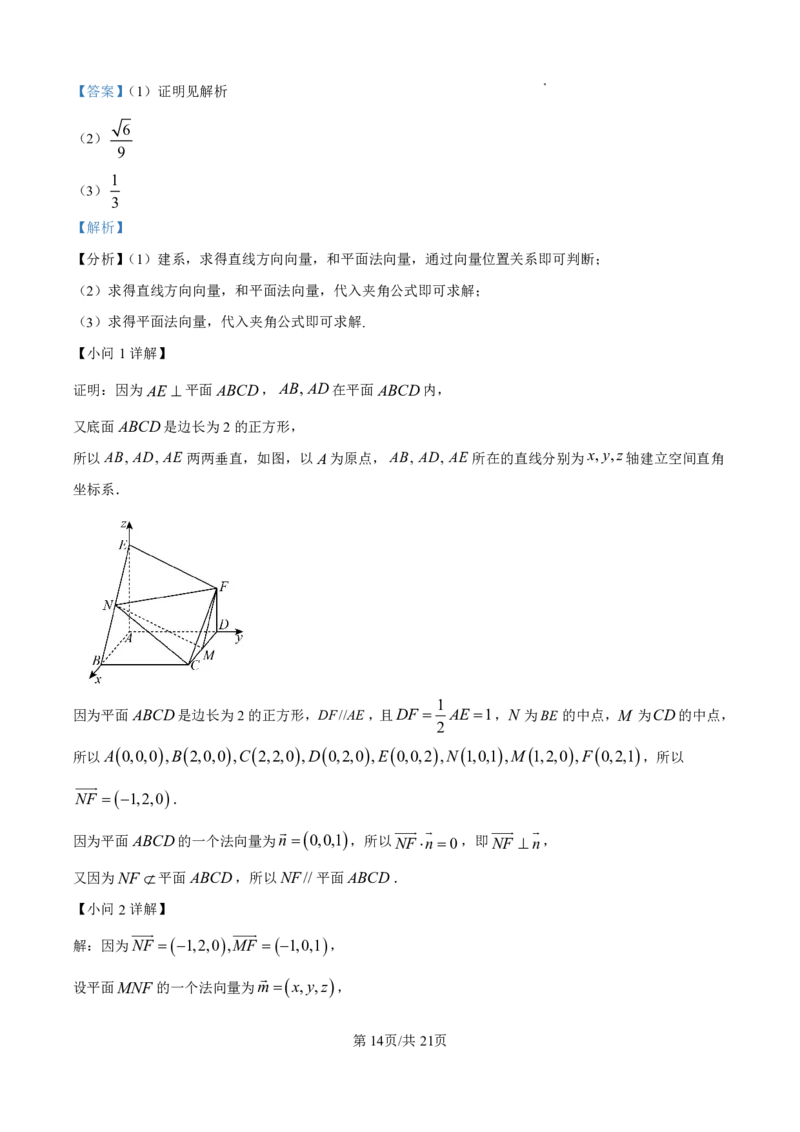
证明：因为AE 平面ABCD，AB, AD在平面ABCD内，
又底面ABCD是边长为2的正方形，
所以AB, AD, AE 两两垂直，如图，以A为原点，AB, AD, AE 所在的直线分别为x,y,z轴建立空间直角
坐标系．
1
因为平面ABCD是边长为2的正方形，DF//AE，且DF  AE 1，N 为BE 的中点，M 为CD的中点，
2
               
所以A 0,0,0 ,B 2,0,0 ,C 2,2,0 ,D 0,2,0 ,E 0,0,2 ,N 1,0,1 ,M 1,2,0 ,F 0,2,1 ，所以

NF
1,2,0 ．
    
因为平面ABCD的一个法向量为n

0,0,1

，所以NFn0，即NF n，
又因为NF 平面ABCD，所以NF//平面ABCD．
【小问2详解】
 
解：因为NF 1,2,0  ,MF  1,0,1 ，

设平面MNF
的一个法向量为m
x,y,z

，
第14页/共21页
学科网（北京）股份有限公司

 mNF x2y 0
则  ，

mMF xz  0

令 y 1，则x z 2，所以m 2,1,2  ．

CN 1,2,1 ，设直线CN 与平面NMF 所成角为，


CNm 222 6
则sin    ．

CN m 114 414 9
【小问3详解】
因为AE 平面ABCD，DF//AE，所以DF 平面ABCD，
因为AD 平面ABCD，所以DFAD．
又因为AD  DC, DC DF  D, DC, DF  平面MFD，

所以AD 平面MFD，所以平面MFD的一个法向量为AD  0,2,0 ．


  mAD 1
设平面NMF 与平面MFD的夹角为，则cos cosmAD    ．

m AD 3
18. 已知数列  a  的前n项和为S ，a 1,na  S n  n1  nN ．
n n 1 n n
 
（1）求数列 a 的通项公式；
n
  2a   2 a n 1
 
n
（2）求数列 的前n项和为T ；
a a n
 n n1 
 
 
（3）求数列 a 16 的前n项和W ．
n n
【答案】（1）a 2n1
n
2n1
（2）T 2
n 2n1
n2 16n,n8
（3）W 
n n2 16n128,n9
【解析】
【分析】（1）根据a 与S 的关系，结合等差数列定义求解；
n n
（2）利用裂项相消法求解；
（3）根据b 的符号，分段求解.
n
第15页/共21页
学科网（北京）股份有限公司【小问1详解】
na S n  n1  ①
n n
 n1  a S  n1  n2  n2  ②
n1 n1
①②得na  n1  a a 2  n1  ∴  n1  a  n1  a 2  n1  n2 
n n1 n n n1
∴a a 2  n2 
n n1
故数列  a  是首项a 1，公差为2的等差数列．∴a 1 n1 22n1．
n 1 n
【小问2详解】
令
 2a
n
  2 a n 1

 32n 2n

2n

2n1
，
a a  2n1  2n1  2n1 2n1
n n1
2 22 22 23 2n 2n1 2n1
所以T        2 ，
n 1 3 3 5 2n1 2n1 2n1
【小问3详解】
令b a 162n17，当n8时，b 0；当n9时，b 0
n n n n
设数列  b  的前n项和为M ，
n n
n  b b  n 152n17  n  2n32 
则M  1 n   n  n16 ，
n 2 2 2
当n8时，则W  b  b  b b b b M n2 16n，
n 1 2 n 1 2 n n
当n9时，则W  b  b  b  b  b  b b b b b
n 1 2 8 9 n 1 2 8 9 n
M  M M M 2M n2 16n128
8 n 8 n 8
n2 16n,n8
综上：W  ．
n n2 16n128,n9
 
19. 在 数 列 a 中 ， 按 照 下 面 方 式 构 成 “ 次 生 数
n
列 ”  b  :b a ,b min  a ,a  ,b min  a ,a ,a  ,,b min  a ,a ,,a  n2  ， 其 中
n 1 1 2 1 2 3 1 2 3 n 1 2 n
min  a ,a ,,a  2in  表示数列a ,a ,,a ，中最小的项．
1 2 i 1 2 i
（1）若数列  a  中各项均不相等且只有4项，a 1,a  2,3,4  n1,3,4  ，请写出  a  的所有“次生
n 2 n n
第16页/共21页
学科网（北京）股份有限公司 
数列” b ；
n
a 
（2）若  a  满足a 2,a 64，且 n为等比数列，  a  的“次生数列”为  b  ．
n 1 4  n  n n
（i）求b b 的值；
3 10
 10  9S 20
（ii）设  b  的前n项和S ，若对任意的nN，不等式 27 18n  2n 恒成立，求实数
n n  n  a
n
的取值范围．
【答案】（1）2，1，1，1或3，1，1，1或4，1，1，1．
（2）（i）b b  4632；（ii）,4 ．
3 10
【解析】
【分析】（1）根据次生数列的定义得到b a 1,b b b 1，从而得到  b  有3个，分别为2,1,1,1或
1 1 2 3 4 n
3,1,1,1或4,1,1,1.
a 
（2）（i）根据 n为等比数列，求出公比，求出a n(2)n，从而根据次生数列的定义得到b b  a  2，
 n  n 1 2 1
b b 4608，得到b b 的值；
9 10 3 10
20 56n 20 56n
（ ii ） 由 错 位 相 减 法 求 和 ， 求 出 S   2 2n2   4n1 ． 由
2n 9 9 9 9
 10  9S 20 9S 20  56n 2n2 2 n2
 27 18n  2n  2n  
 n  a  10  18n227n 10 3n 2 ， 令
n 27 18n  a
 n  n
n2
c  ，求出数列

c
的单调性求解．
n 3n2 n
【小问1详解】
因为a  2,3,4  n1, 3,4  ,a 1，  a  中各项均不相等，
n 2 n
所以b a 1,b b b 1，
1 1 2 3 4
若b a 2，此时“次生数列”  b  为2，1，1，1，
1 1 n
若b a 3，此时“次生数列”  b  为3，1，1，1，
1 1 n
第17页/共21页
学科网（北京）股份有限公司若b a 4，此时“次生数列”  b  为4，1，1，1，
1 1 n
   
所以“次生数列” b 的定义可知 b 有3个，
n n
分别为2，1，1，1或3，1，1，1或4，1，1，1．
【小问2详解】
a 
（i）设数列 n的公比为q，
 n 
a  a a
因为 n为等比数列，且a 2,a 64，所以 4  1q3，即16 2q3，解得q 2，
 n  1 4 4 1
a
所以 n 22 n1 ，则a n2 n．
n n
由“次生数列”  b  的定义，可知b b a 2,b b 24,,
n 1 2 1 3 4
b b 9512 4608，故b b  4632．
9 10 3 10
（ii）由（i）
b b a 12  ,b b a 32 3 ,,b b a  2n1 2 2n1 ，
1 2 1 3 4 3 2n1 2n 2n1
S 2  12 32 3 2n1 2 2n1 ，①
2n  
4S 2  12 332 5  2n1 2 2n1 ，②
2n  
由①②得3S 2  12 22 322 2n1 2n1 2 2n1
2n  
 2 32 2n1
20 56n
22 2 2  2n1 2 2n1   2 2n2
 14  3 3
 
20 56n 20 56n
所以S   2 2n2   4n1．
2n 9 9 9 9
∵27
10
18n0
 nN
n
 10  9S 20 9S 20  56n 2n2 2 n2
 27 18n  2n  2n  
∴  n  a  10  18n227n 10 3n 2
n 27 18n  a
 n  n
n2 2n3 2n2  3n5 2n2
令c  ，则c c   
n 3n2 n1 n 3n1 3n2  3n1  3n2 
当n1时，c c ；当n2时，c c ，即c c c c ．
n1 n n1 n 1 2 3 4
第18页/共21页
学科网（北京）股份有限公司24
∴c  4，故的取值范围为
,4 
．
2 322
20. 已知函数 f xx1lnxax1．
 
（1）当a 0时，求 f x 在x1处的切线方程；
（2）证明：当x0时，  x1  ex cosx；
（3）当a0时，令g  x  f  x 2  a1  xa2，记g  x  的唯一零点为x ，若x a sinx ，证
0 1 1
明：ex 1  x ．
0
【答案】（1） y 2  x1 
（2）证明见解析 （3）证明见解析
【解析】
1
【分析】（1）当a 0时，求得 f x lnx1 ，得到 f 1 2, f  1 0，结合导数的几何意义，即
x
可求解；
（2）根据题意，先证得sinx x，令T  x ex x1 cosx，则T x 0，得到T  x  在 ,0  上
单调递增，得出T

x
T 
0

，即可得证；
1
（3）求得g x lnx a1，令u  x  g x  ，求得g x  的单调性，得到g  x  单调递增，得出存
x
 x 1  lnx 2
在x   ea2,1  ，使得g  x 0，化简得a  0 0  2，由x a sinx 和t lnx ，得到
0 0 x 1 1 0
0
 
 et 1 t2 x2
2sinx x ，再设G  x x 2，利用导数求得G  x  在 ,0  上单调递减，
et 1 1 ex
x2
再设H  x  2sinx，结合（2）得到H  x  在 ,0  上单调递减，得到G  x  F  x  ，即可
ex
得证.
【小问1详解】
1
解：当a 0时， f  x  x1  lnx，则 f x lnx1 ，
x
可得 f 1 2, f  1 0，则切线方程为y02  x1  ，即 y2  x1  ．
【小问2详解】
证明：先证：x0时，sinx x
第19页/共21页
学科网（北京）股份有限公司设F

x
sinxx，则F
x
cosx10，所以F 
x

在R上单调递减，
因为F

0
0，所以当且仅当x0时，F 
x
F 
0
0，即sinx
x；
令T  x ex x1 cosx，则T x xex sinx xxex 0，
所以T  x  在 ,0  上单调递增，所以T  x T  0 0，所以  x1  ex cosx.
【小问3详解】
证明：由函数g  x  f  x 2  a1  xa2 x1  lnx a2  x2
1
可得g x lnx a1，
x
1 1 1 x1
令u  x  g x lnx a1，则u x    ，
x x x2 x2
当x
0,1
 时，u
x
0，g
x

在（0，1）上单调递减；
当x 1, 时，u
x
0，g
x

在
 1,
上单调递增，
所以g x  g 1 a0，所以g  x  在  0, 上单调递增，且g  1 a，
当a 0时，g  x  存在唯一零点x 1；
0
当a0时，g  1 a0，可知ea2 0,1  ，
则g  ea2    ea2 1  a2  a2  ea2 24ea2 a0
所以由零点存在性定理可知，存在x   ea2,1  ，使得g  x 0，
0 0
 
综上可得，函数g x 存在唯一零点x ，
0
则g  x  x 1  lnx  a2  x 20，且0 x 1，
0 0 0 0 0
 x 1  lnx 2
所以a  0 0  2，
x
0
 x 1  lnx 2
因为x a sinx ，所以a sinx  x ，则 0 0 2sinx x ，
1 1 1 1 x 1 1
0
因为a0，所以x 0，
1
 
 et 1 t2
令t lnx ，则x et,t 0，所以 2sinx x ，
0 0 et 1 1
第20页/共21页
学科网（北京）股份有限公司下面证明t  x ，
1
 
设 G  x   ex 1 x2 2x x2 2,x 0 ，则G x ex x1 1，
ex ex
令P  x G x ex x1 1，则P x xex 0，
所以G
x

在
,0  上单调递增，G
x
G
0
0，所以G 
x

在
,0 
上单调递减，
x2
再设H  x G  x F  x  2sinx,x0，
ex
由（2）知H x ex x1 cosx0，所以H  x  在 ,0  上单调递减，
所以H  x H  0 0，所以G  x  F  x  ，当x0时取等号．
因为 G  x  在 ,0  上单调递减，由（2）知F  x  在 ,0  上单调递减且G  x  F  x  ，
则G

0

F

0
0,G 
t

F

x
G 
x

，
1 1
所以t  x ，即x lnx 0，所以ex 1  x ．
1 1 0 0
第21页/共21页
学科网（北京）股份有限公司