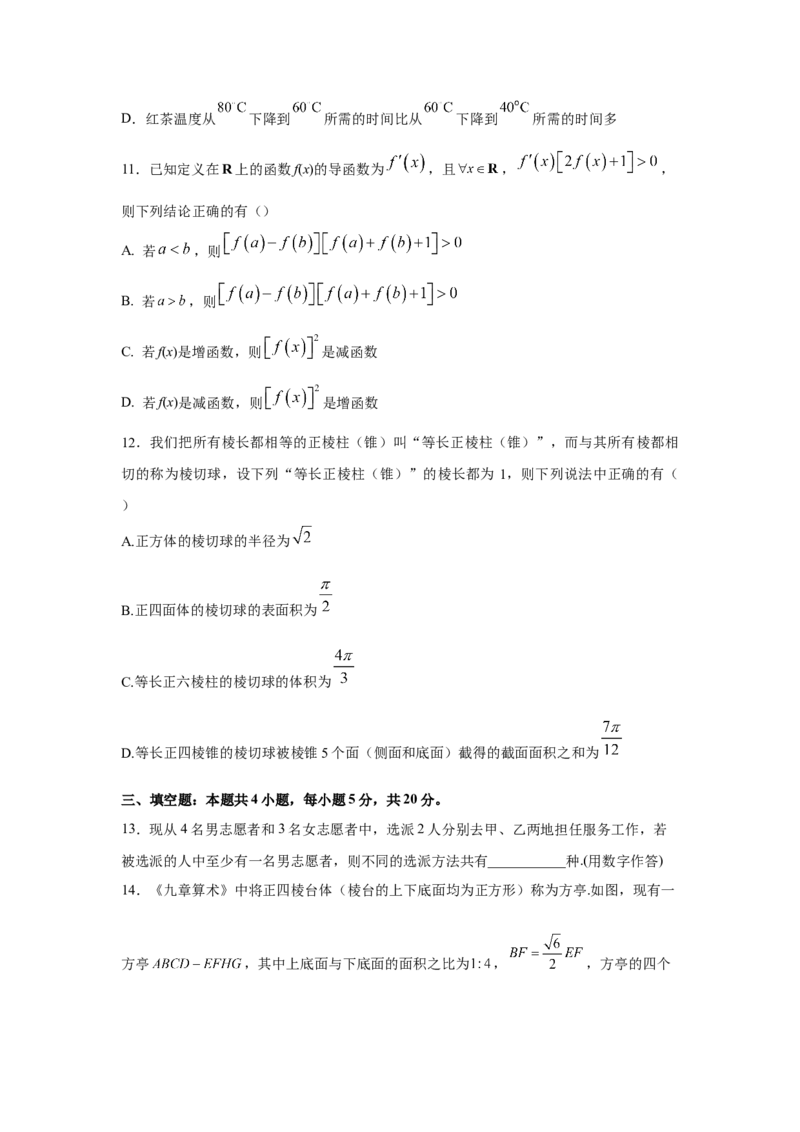文档内容
2024 届新高三开学摸底考试卷(新高考专用)01
数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答
卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1.设集合 ,B= ,则 ( )
A. {-2,-1,1} B. {-2, 0, 1}
C. {-2,-1} D. {-1, 1}
2.已知复数 , 为z的共轭复数,则 ( )
A. B. 2 C. D.
3.已知向量 ,且 ,则 ( )
A. B. C. 2 D. -2
4.已知函数f(x)=log (6-ax)(a>0,且a≠1)在(0,2)上单调递减,则实数a的取值范围是(
a
)
A.(1,3] B.(1,3)
C.(0,1) D.(1,+∞)
5.椭圆 的焦点在y轴上,长轴长是短轴长的2倍,则m的值为( )A. 2 B. 4 C. D.
6.已知直线 是圆C: 的对称轴,过点A
作圆C的一条切线,切点为B,则|AB|=( )
A. 1 B. 2 C. 4 D. 87.等比数列{a}的公比为q,前n项和为S,设甲: ,乙:{S}是递增数列,则(
n n n
)
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
8.已知sin +cos α=,则sin 等于( )
A. B. C.- D.-
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合
题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.维生素C又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的
必需营养素,现从猕猴桃、柚子两种食物中测得每100克维生素 的含量(单位:mg),
得到数据如下.则下列说法不正确的是()
猕猴桃
柚子
A. 每100克柚子维生素C含量的众数为121
B. 每100克柚子维生素C含量的75%分位数为121
C. 每100克猕猴桃维生素C含量的平均数高于每100克柚子维生素C含量的平均数
D. 每100克猕猴桃维生素C含量的方差高于每100克柚子维生素C含量的方差
10.牛顿曾提出了物体在常温环境下温度变化的冷却模型:若物体初始温度是 (单位:
),环境温度是 (单位: ),其中 则经过 分钟后物体的温度 将满足
且 ).现有一杯 的热红茶置于 的房间里,根
据这一模型研究红茶冷却情况,下列结论正确的是( )(参考数值A.若 ,则
B.若 ,则红茶下降到 所需时间大约为7分钟
C.若 ,则其实际意义是在第3分钟附近,红茶温度大约以每分钟 的速率下
降D.红茶温度从 下降到 所需的时间比从 下降到 所需的时间多
11.已知定义在R上的函数f(x)的导函数为 ,且 , ,
则下列结论正确的有()
A. 若 ,则
B. 若 ,则
C. 若f(x)是增函数,则 是减函数
D. 若f(x)是减函数,则 是增函数
12.我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相
切的称为棱切球,设下列“等长正棱柱(锥)”的棱长都为 1,则下列说法中正确的有(
)
A.正方体的棱切球的半径为
B.正四面体的棱切球的表面积为
C.等长正六棱柱的棱切球的体积为
D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为
三、填空题:本题共4小题,每小题5分,共20分。
13.现从4名男志愿者和3名女志愿者中,选派2人分别去甲、乙两地担任服务工作,若
被选派的人中至少有一名男志愿者,则不同的选派方法共有___________种.(用数字作答)
14.《九章算术》中将正四棱台体(棱台的上下底面均为正方形)称为方亭.如图,现有一
方亭 ,其中上底面与下底面的面积之比为 , ,方亭的四个侧面均为全等的等腰梯形,已知方亭四个侧面的面积之和为 ,则方亭的体积为______.
15.设函数f(x)=sin 在区间(0,π)上恰有三个极值点、两个零点,则ω的取值范
围是x2 y2
C: − =1(a>0,b>0)
a2 b2
16.已知F为双曲线 的右焦点,A、B是双曲线C的一条渐近
线上关于原点对称的两点,
⃗AF⋅ ⃗BF=0
且线段AF的中点在双曲线C上,则双曲线C的
离心率e= .
四、解答题:共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
c sinA2sinBcosA
17.记△ABC的内角A、B、C的对边分别为a、b、c,且a 2sin A .
(1)求B的大小;
b2 2 2 3
(2)若 ,△ABC的面积为 ,求△ABC的周长.
18.如图,在四棱锥 中,底面 为直角梯形, , ,平面
底 面 , 为 的 中 点 , 是 棱 ( 不 与 端 点 重 合 ) 上 的 点 ,
, .
(1)求证:平面 平面 ;
(2)当 的长为何值时,平面 与平面 所成的角的大小为 ?
19.已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,令g(x)=.证明:当x>0时,g(x)>1.
20.已知数列 是以d为公差的等差数列, 为 的前n项和.
(1)若 ,求数列 的通项公式;
(2)若 中的部分项组成的数列 是以 为首项,4为公比的等比数列,且 ,
求数列 的前n项和 .21.甲、乙两选手进行一场体育竞技比赛,采用 局 胜制的比赛规则,即先赢下 局比赛者最终获胜. 已知每局比赛甲获胜的概率为 ,乙获胜的概
率为 ,比赛结束时,甲最终获胜的概率为 .
(1)若 ,结束比赛时,比赛的局数为 ,求 的分布列与数学期望;
(2)若采用5局3胜制比采用3局2胜制对甲更有利,即 .
(i)求 的取值范围;
(ii)证明数列 单调递增,并根据你的理解说明该结论的实际含义.
22.已知圆 ,定点 是圆 上的一动点,线段 的垂直平分
线交半径 于点 .
(1)求 的轨迹 的方程;
(2)若过 的直线 分别交轨迹 与 和 ,且直线 的斜率之积为 ,求四
边形 面积的取值范围.公众号:高中试卷君