24届高三文科数学热身考试试卷_2024年6月(1)_01按日期_01号_2024届四川省成都七中高三下学期热身考试_四川省成都市第七中学2024届高三下学期热身考试数学（文）试卷

数学(文) 本试卷分第I卷(选择题)和第II卷(非选择题)两部分，共150分，考试时间120分钟. 第 I 卷 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有 一项是符合题目要求的) 1. 设全集U ={xN|x7}，M ={3,7}， N ={0,1,2,3,6}，则 U 1 M N = （ ） A．  B．{7} C．{3,4,5,7} D． U y2 2.双曲线x2 − =1的离心率为（ ） 2 A． 3 B． 3 C．5 D． 5 1 3.函数y=3x与y=− 的图象（ ） 3x A．关于 x 轴对称 B．关于 y 轴对称 C．关于原点对称 D．关于 y = x 对称  4.若函数 f(x)=sin(x)(0)在 ( 0 , 4 ) 上单调递增，则的取值范围为（ ） 1 A．(0, ) B．(0,2) C． 2 ( 0 , 1 2 ] D． (0,2] 5.设向量 a ， b 满足(a−b)⊥(a+2b)，且2|a|=3|b|0，则cosa,b=（ ） 1 3 A．− B．− C． 6 8 1 6 D． 3 8 6.设x， y 1− y0,  满足约束条件x− y0, 则  x+ y−1, z = x + 5 y 的最小值为（ ） A． 3 B． 6 C． − 3 D． − 6 7.一个多面体的三视图如右，图中所示外轮廓都是边长为1的正方形， 则该多面体的体积为（ ） 1 2 A． B． 3 3 1 5 C． D． 6 6 8.设点A(2,3)，动点 P 在抛物线C:y2 =4x上，记 P 到直线x=−2的距离为 d ，则|AP|+d 的 最小值为（ ） A． 1 B．3 C． 10−1 D． 10+1 9.圆O :x2 + y2 +2x+8y−8=0与圆O :x2 + y2 −4x−4y−2=0的位置关系为（ ） 1 2 A．外切 B．相交 C．内切 D．相离 {#{QQABbQiAggAIQJBAAQgCEwEiCAIQkACACQgGhBAMsAABAAFABAA=}#}{#{QQABbQiAggAIQJBAAQgCEwEiCAIQkACACQgGhBAMsAABAAFABAA=}#}18. (12分)记数列 3 { a n } 的前 n 项和为 S n ，已知 2 S n = n 2 + a n + a 1 − 1 . (1)若a 1，证明： 1 { a n − n } 是等比数列； 1 (2)若a 是a 和a 的等差中项，设b = ，求数列{b }的前 2 1 3 n a a n n n+2 n 项和为T . 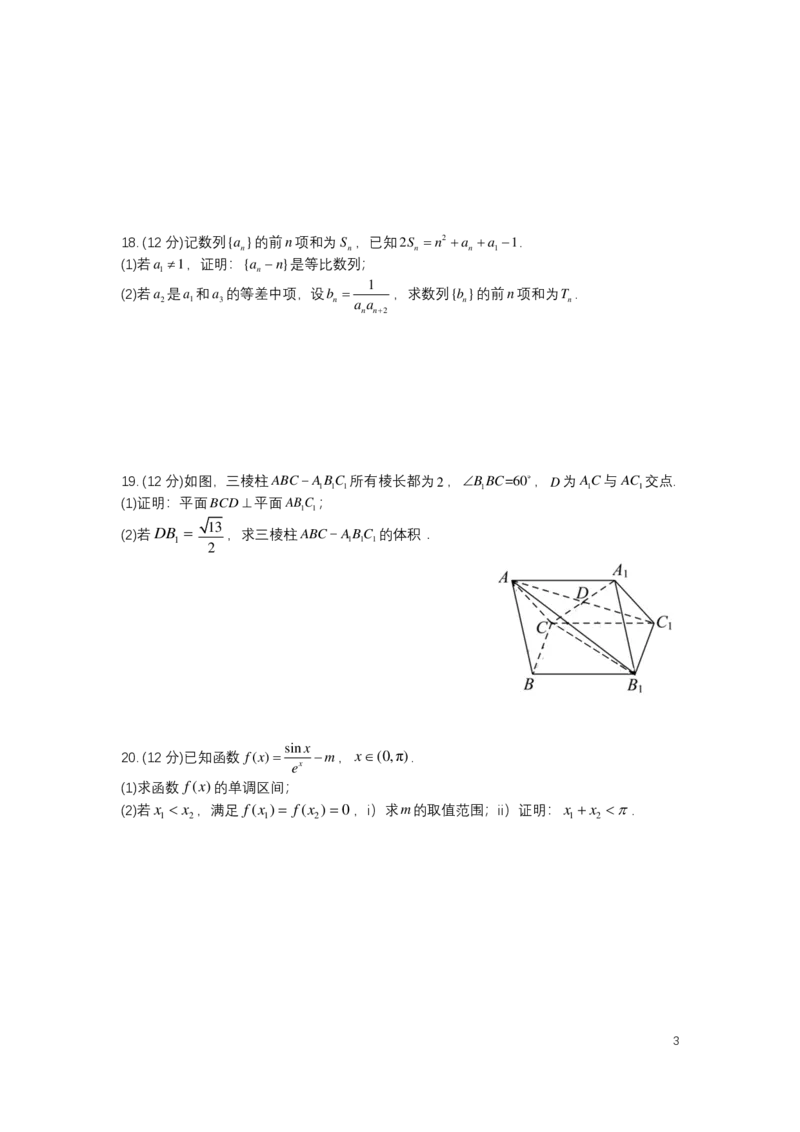n 19. (12分)如图，三棱柱 A B C A 1 B C1 1 所有棱长都为 2 ，  B 1 B C = 6 0 ， D 为 A C1 与 A C 1 交点. (1)证明：平面 B C D ⊥ 平面ABC ； 1 1 13 (2)若DB = ，求三棱柱ABC ABC 的体积． 1 1 1 1 2 sinx 20. (12分)已知函数 f(x)= −m， ex x  ( 0 , π ) . (1)求函数 f(x)的单调区间； (2)若x  x ，满足 f(x )= f(x )=0，i）求m的取值范围；ii）证明： 1 2 1 2 +   x 1 x 2 . {#{QQABbQiAggAIQJBAAQgCEwEiCAIQkACACQgGhBAMsAABAAFABAA=}#}21. (12分)已知椭圆 4 C 1 x2 ： + y2 =1与抛物线 2 C 2 ： y = a x 2 − 2 有四个公共点 A 、B、 C 、 D ， 分别位于第一、二、三、四象限内. (1)求实数 a 的取值范围； (2)直线 A C 、AD与 y 轴分别交于 M 、 N 两点，求 | M N | 的取值集合. 请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分. 22.(10分)选修4-4：坐标系与参数方程 在直角坐标系xOy 中，以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线 C 的极坐  3 1 标方程为= 2cos(− )(0 )，已知M(1, )，动直线 4 4 2 l x=1+tcos,  的参数方程为 1 y= +tsin   2  （t为参数，0 ）. 2 (1)写出C在直角坐标系下的普通方程； (2)若直线 l 与曲线 C 有两个公共点 A 和 B ，线段AB上一点 K 满足|KM |2=|AM ||BM |，以 为参数写出K 轨迹的参数方程. 23.(10分)选修4—5：不等式选讲 已知a,b,c0，且a+b+c=abc2. (1)求abc2的最小值 m ； (2)证明：mabc+(a+b)c2 m2. {#{QQABbQiAggAIQJBAAQgCEwEiCAIQkACACQgGhBAMsAABAAFABAA=}#}