文档内容
2024 年高三 10 月联考卷
数学
本试卷满分 150 分,考试时间 120 分钟
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴
在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,写
在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和
答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(选择题)
一、单选题(本题共 8小题,每小题 5分,共 40分)
1.已知集合 ln ,集合 ,则 ( )
2
A. 𝐴𝐴 = {𝑥𝑥|B.(𝑥𝑥−1) ≥ 0} C𝐵𝐵 . = {𝑥𝑥|𝑥𝑥 −3𝑥𝑥 < 0D}. 𝐴𝐴∪𝐵𝐵 =
2.已(0知,2] i为虚数单位,复[2数,3)满足 (0,+ i ∞) ,则 的[值2,为+(∞) )
𝑧𝑧 |𝑧𝑧+1| = |𝑧𝑧+ | = √5 |𝑧𝑧|
A.1 B. C. 或 D.1或
√2 √2 2√2 √2
3.已知向量 , ,若向量 在向量 上的投影向量 ,则 ( )
√3 1
𝑎𝑎⃗ = (2,0) 𝑏𝑏�⃗ = �𝜆𝜆, 2� 𝑏𝑏�⃗ 𝑎𝑎⃗ 𝑐𝑐⃗ = �2,0� �𝑏𝑏�⃗� =
A. B. C. D.1
√10
4.已√3知函数 满足 √7 ,且在4区间 上单调递减.设 ,
,
𝑓𝑓(𝑥𝑥) 𝑓𝑓
,
(𝑥𝑥
则
)
(
= 𝑓𝑓 (
)
2 −𝑥𝑥) [1,+∞) 𝑎𝑎 = 𝑓𝑓(−ln1.1) 𝑏𝑏 =
0.4
A𝑓𝑓(. 2 ) 𝑐𝑐 = 𝑓𝑓 (log25) B.
C.
𝑎𝑎 > 𝑏𝑏 > 𝑐𝑐
D.
𝑏𝑏 > 𝑐𝑐 > 𝑎𝑎
5.已
𝑐𝑐 >
知
𝑏𝑏
圆
>
锥
𝑎𝑎
的母线长为定值R,当圆锥的体
𝑏𝑏
积
>
最
𝑎𝑎
大
>
时
𝑐𝑐
,圆锥的底面半径为( )
学科网(北京)股份有限公司A. B. C. D.
√3 √6 1 1
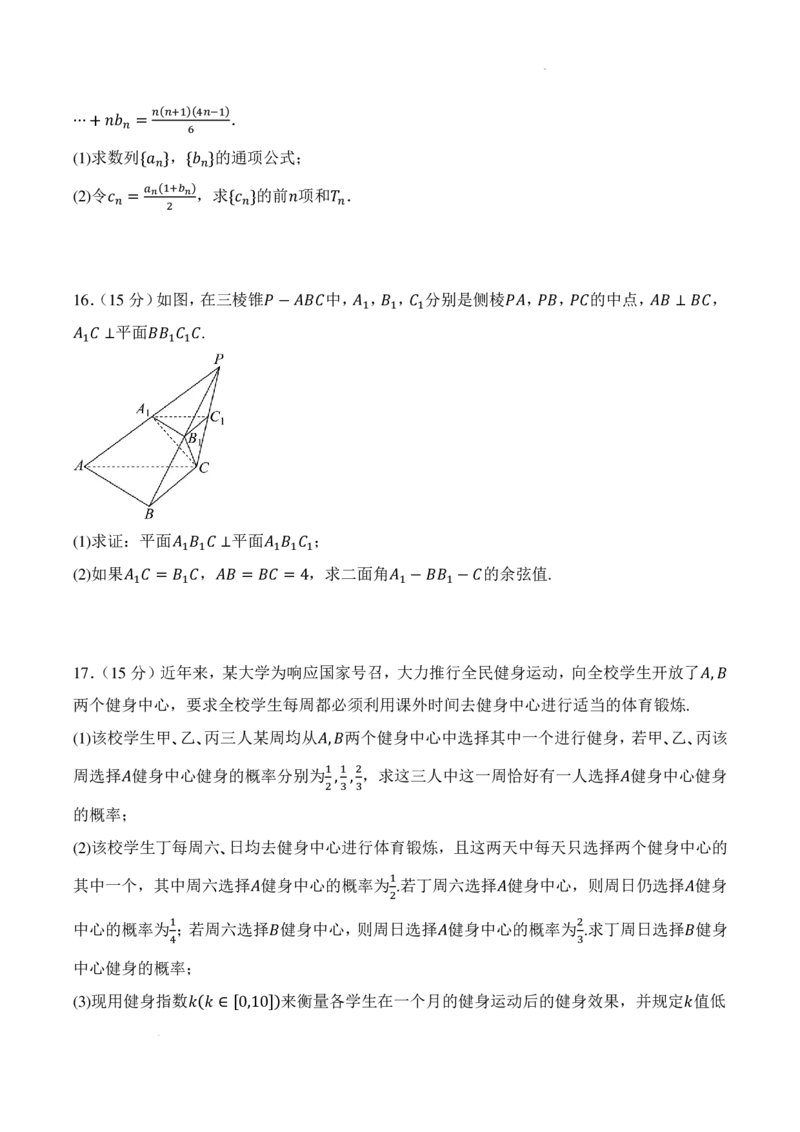
6.已3知𝑅𝑅函数 的图象如3 𝑅𝑅图所示,则不等式2𝑅𝑅 的3解𝑅𝑅集为( )
′
𝑓𝑓(𝑥𝑥) (𝑥𝑥+1)𝑓𝑓 (𝑥𝑥) < 0
A. B.
1
(−∞,−1)∪�2,2� (−∞,−1)∪(2,+∞)
C. D.
1
7.若(−正1,项1)等∪比(3数,+列∞) 满足 �−∞,*−,2�则∪数(2列,+∞)的前 4 项的和 的值是( )
2𝑛𝑛
A. { B 𝑎𝑎. 𝑛𝑛} 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 = 2 C.�𝑛𝑛 ∈ 𝐍𝐍 � D {𝑎𝑎. 𝑛𝑛} 𝑆𝑆4
15√2
8.已 15 知√小 2 明射箭命中靶心4的概率为 ,且每次 8√射 2 击互不影响,则 6 小√明 2+ 在 6 射击4次后,恰好命中
3
两次的概率是( ) 5
A. B. C. D.
36 9 144 216
二、6选25择题(本题共 3小25题,每小题 6分,6共2518分在每小题给出625的选项中,至少有两项是符
合题目要求,若全部选对得 6分,部分选对得部分分,选错或不选得 0分)
二、多选题(本题共 4小题,每小题 5分,共 20分)
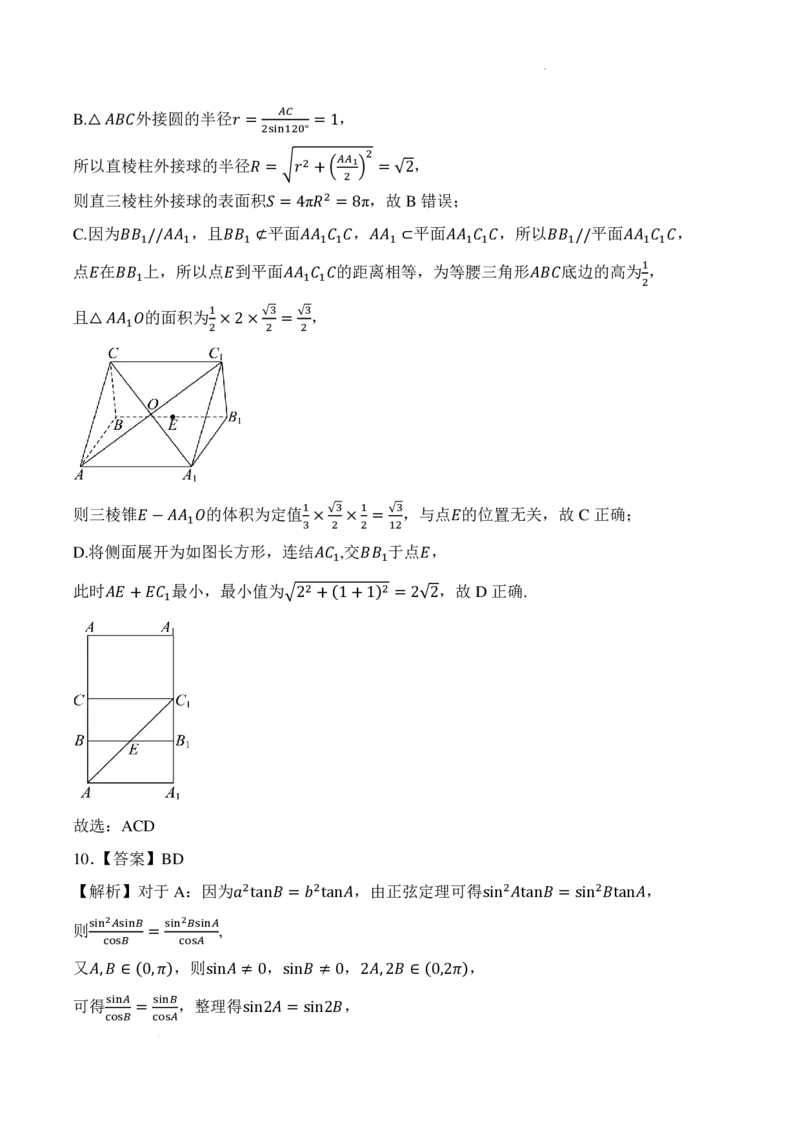
9.如图,在直三棱柱 中, , , ,侧面
°
的对角线交点 ,点 𝐴𝐴 是 𝐵𝐵 侧 𝐴𝐴 棱 −𝐴𝐴1𝐵𝐵1上 𝐴𝐴1的一个 𝐴𝐴𝐴𝐴 动1点 = , 2 下 𝐴𝐴 列 𝐵𝐵 结 = 论 𝐵𝐵 正 𝐴𝐴 = 确 1 的是 ∠ ( 𝐴𝐴𝐵𝐵 𝐴𝐴 = ) 12 0 𝐴𝐴𝐴𝐴1𝐴𝐴1𝐴𝐴
𝑂𝑂 𝐸𝐸 𝐵𝐵𝐵𝐵1
A.直三棱柱的侧面积是
B.直三棱柱的外接球表面4+积2是√3π
C.三棱锥 的体积与点
4
的位置无关
D. 𝐸𝐸 −的𝐴𝐴最𝐴𝐴1 小𝑂𝑂值为 𝐸𝐸
𝐴𝐴𝐸𝐸 +𝐸𝐸𝐴𝐴1 2√2
学科网(北京)股份有限公司10.已知 的内角A,B,C的对边分别为a,b,c,则下列说法正确的有( )
A.若
△𝐴𝐴𝐵𝐵𝐴𝐴
,则
2 2
B.若𝑎𝑎 tan𝐵𝐵 = 𝑏𝑏,ta则n𝐴𝐴此三角𝑎𝑎形=为𝑏𝑏 直角三角形
2𝐴𝐴 𝑏𝑏+𝑐𝑐
cos 2 = 2𝑐𝑐
C.若 ,则解此三角形必有两解
𝜋𝜋
𝑎𝑎 = 3,𝑏𝑏 = 4,𝐵𝐵 = 6
D.若 是锐角三角形,则 >
△𝐴𝐴𝐵𝐵𝐴𝐴 sin𝐴𝐴+sin𝐵𝐵 cos𝐴𝐴+cos𝐵𝐵
11.已知数列 的首项为 ,且 ,数列 、数列 、数
1 𝑛𝑛
{𝑎𝑎𝑛𝑛} 𝑎𝑎1 = 1 9𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 = 𝑎𝑎𝑛𝑛 −4𝑎𝑎𝑛𝑛+1 �𝑎𝑎𝑛𝑛� {4 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1}
列 的前 项和分别为 、 、 ,则( )
𝑛𝑛𝑎𝑎𝑛𝑛
�1+3𝑎𝑎𝑛𝑛� 𝑛𝑛 𝑆𝑆𝑛𝑛 𝑅𝑅𝑛𝑛 𝑇𝑇𝑛𝑛
A. B. C. D.
𝑛𝑛+1
𝑎𝑎𝑛𝑛+1 1 4 1 4 𝑛𝑛+1
三、填𝑎𝑎𝑛𝑛空<题5(本大题共 3𝑆𝑆𝑛𝑛 个<小题3 ,−每4小题 5𝑅𝑅分 𝑛𝑛 ,<共3 15分) 𝑇𝑇𝑛𝑛 < 9−4 𝑛𝑛+1
第Ⅱ卷(非选择题)
三、填空题(本题共 4小题,每小题 5分,共 20分)
12.已知 , ,且 ,则 的最小值是 .
2 1
13.已知𝑥𝑥函>数1 𝑦𝑦 > s 0 in π 𝑥𝑥+𝑦𝑦 = 2 在𝑥𝑥区−1间+𝑦𝑦 上有且仅有5个零点,则 的取值范围
是 . 𝑓𝑓(𝑥𝑥) = (2 𝜔𝜔𝑥𝑥)(𝜔𝜔 > 0) [0,18] 𝜔𝜔
14.设函数 给出下列四个结论:
|𝑥𝑥 +𝑚𝑚|,𝑥𝑥 < 0,
𝑓𝑓(𝑥𝑥) = �
√2𝑚𝑚
①当 时,函数− 2在√𝑥𝑥,𝑥𝑥 ≥ 0. 上单调递减;
②若函
𝑚𝑚
数
= 0
有且仅
𝑓𝑓
有(𝑥𝑥 两) 个(零
−∞
点
,
,
+∞
则) ;
③当 𝑓𝑓(时 𝑥𝑥),若存在实数 ,使得
𝑚𝑚 > 0
,则 的取值范围为 ;
④已 𝑚𝑚 知点 < 0 ,函数 𝑎𝑎,𝑏𝑏 的图象上 𝑓𝑓(存 𝑎𝑎)在 = 两 𝑓𝑓 点(𝑏𝑏) |𝑎𝑎−𝑏𝑏| (2,+∞), 关
于坐标原点𝑃𝑃(−的𝑚𝑚,对0)称点也在𝑓𝑓(函𝑥𝑥)数 的图象上.若𝑄𝑄1(𝑥𝑥1,𝑦𝑦1),𝑄𝑄2(𝑥𝑥2,𝑦𝑦2)(,𝑥𝑥1 则< 𝑥𝑥2 < 0.) 𝑄𝑄1,𝑄𝑄2
3√2
其中所有正𝑂𝑂确结论的序号是 𝑓𝑓 .(𝑥𝑥 ) |𝑃𝑃𝑄𝑄1|+|𝑃𝑃𝑄𝑄2| = 2 𝑚𝑚 = 1
四、解答题(本大题共 5个小题,共 77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知等比数列 的前 项和为 , , ,数列 满足
{𝑎𝑎𝑛𝑛} 𝑛𝑛 𝑆𝑆𝑛𝑛 𝑆𝑆5 = 62 𝑆𝑆10 = 2046 {𝑏𝑏𝑛𝑛} 𝑏𝑏1 +2𝑏𝑏2 +
学科网(北京)股份有限公司.
𝑛𝑛(𝑛𝑛+1)(4𝑛𝑛−1)
⋯(1)+求𝑛𝑛数𝑏𝑏𝑛𝑛 列= ,6 的通项公式;
(2)令 {𝑎𝑎𝑛𝑛} {𝑏𝑏, 𝑛𝑛}求 的前 项和 .
𝑎𝑎𝑛𝑛(1+𝑏𝑏𝑛𝑛)
𝑐𝑐𝑛𝑛 = 2 {𝑐𝑐𝑛𝑛} 𝑛𝑛 𝑇𝑇𝑛𝑛
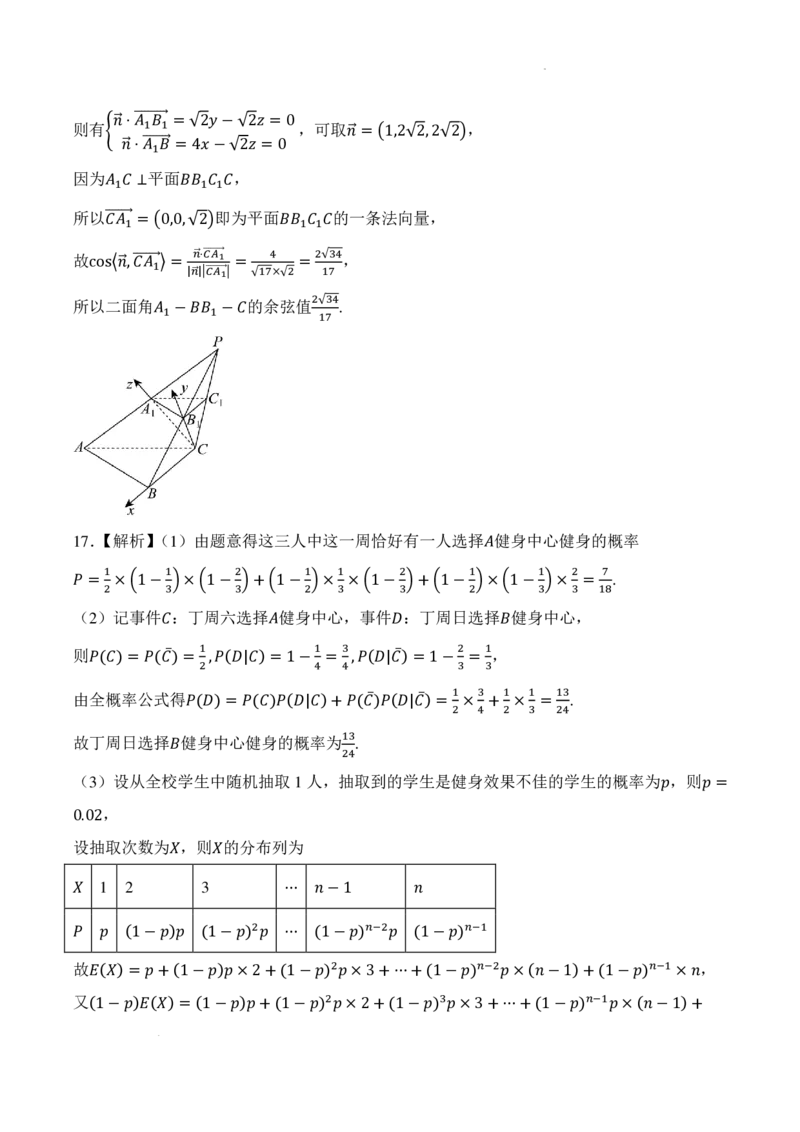
16.(15分)如图,在三棱锥 中, , , 分别是侧棱 , , 的中点, ,
平面 . 𝑃𝑃−𝐴𝐴𝐵𝐵𝐴𝐴 𝐴𝐴1 𝐵𝐵1 𝐴𝐴1 𝑃𝑃𝐴𝐴 𝑃𝑃𝐵𝐵 𝑃𝑃𝐴𝐴 𝐴𝐴𝐵𝐵 ⊥ 𝐵𝐵𝐴𝐴
𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵𝐵𝐵1𝐴𝐴1𝐴𝐴
(1)求证:平面 平面 ;
(2)如果 𝐴𝐴1𝐵𝐵1,
𝐴𝐴 ⊥
𝐴𝐴1𝐵𝐵1𝐴𝐴1,求二面角 的余弦值.
𝐴𝐴1𝐴𝐴 = 𝐵𝐵1𝐴𝐴 𝐴𝐴𝐵𝐵 = 𝐵𝐵𝐴𝐴 = 4 𝐴𝐴1 −𝐵𝐵𝐵𝐵1 −𝐴𝐴
17.(15分)近年来,某大学为响应国家号召,大力推行全民健身运动,向全校学生开放了
两个健身中心,要求全校学生每周都必须利用课外时间去健身中心进行适当的体育锻炼.
𝐴𝐴,𝐵𝐵
(1)该校学生甲、乙、丙三人某周均从 两个健身中心中选择其中一个进行健身,若甲、乙、丙该
周选择 健身中心健身的概率分别为𝐴𝐴,𝐵𝐵 ,求这三人中这一周恰好有一人选择 健身中心健身
1 1 2
的概率𝐴𝐴; 2,3,3 𝐴𝐴
(2)该校学生丁每周六、日均去健身中心进行体育锻炼,且这两天中每天只选择两个健身中心的
其中一个,其中周六选择 健身中心的概率为 .若丁周六选择 健身中心,则周日仍选择 健身
1
𝐴𝐴 2 𝐴𝐴 𝐴𝐴
中心的概率为 ;若周六选择 健身中心,则周日选择 健身中心的概率为 .求丁周日选择 健身
1 2
中心健身的概4率; 𝐵𝐵 𝐴𝐴 3 𝐵𝐵
(3)现用健身指数 来衡量各学生在一个月的健身运动后的健身效果,并规定 值低
𝑘𝑘(𝑘𝑘 ∈ [0,10]) 𝑘𝑘
学科网(北京)股份有限公司于1分的学生为健身效果不佳的学生,经统计发现从全校学生中随机抽取一人,其 值低于1
分的概率为0.02.现从全校学生中随机抽取一人,如果抽取到的学生不是健身效果不
𝑘𝑘
佳的学生,
则继续抽取下一个,直至抽取到一位健身效果不佳的学生为止,但抽取的总次数不超过 .若抽
取次数的期望值不超过23,求 的最大值.
𝑛𝑛
参考数据: 9 557 9 𝑛𝑛 545 9 535.
29 30 31
0. 8 ≈ 0. ,0. 8 ≈ 0. ,0. 8 ≈ 0.
18.(17分)已知椭圆 的离心率为 ,过点 的直线 交椭圆
2 2
𝑥𝑥 𝑦𝑦 √3
2 2
𝐴𝐴:𝑎𝑎 +𝑏𝑏 = 1(𝑎𝑎 > 1 > 𝑏𝑏 > 0) 2 𝑀𝑀(1,0) 𝑙𝑙
于点 ,且当 轴时, .
(𝐴𝐴1)求椭𝐴𝐴圆,𝐵𝐵 的方程𝑙𝑙;⊥ 𝑥𝑥 |𝐴𝐴𝐵𝐵| = √3
(2)记椭圆
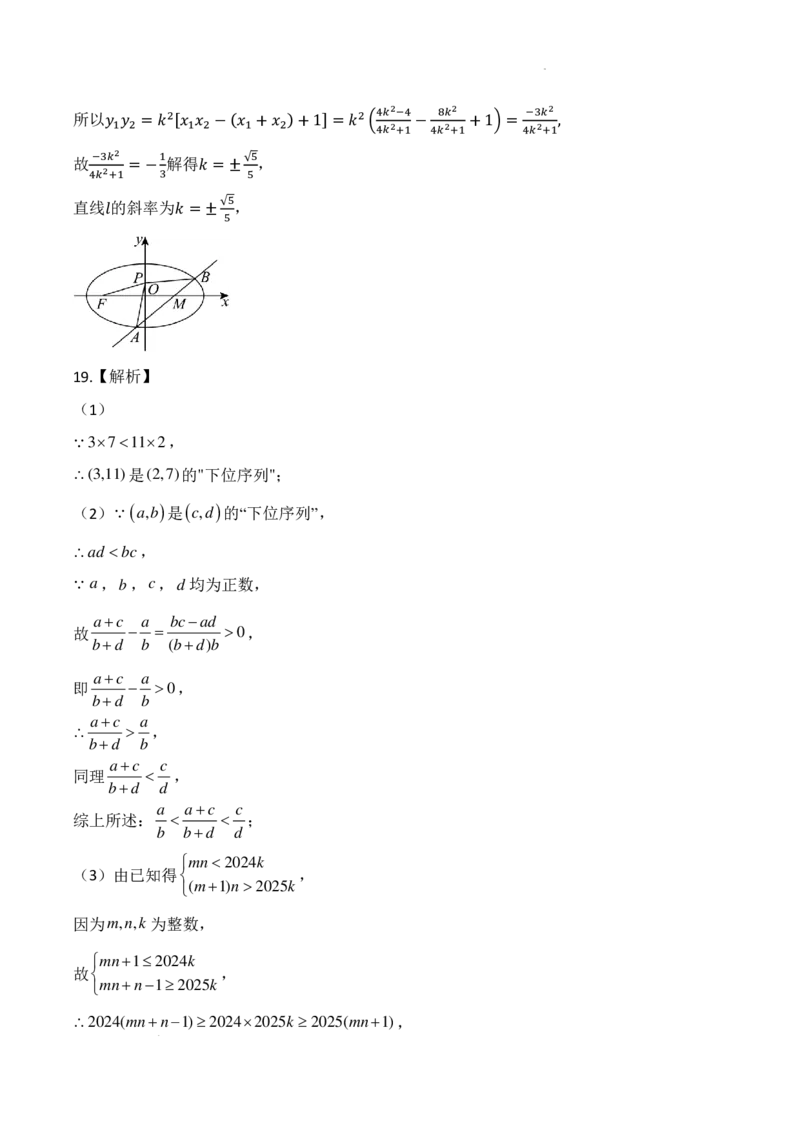
𝐴𝐴
的左焦点为 ,若过 三点的圆的圆心恰好在 轴上,求直线 的斜率.
𝐴𝐴 𝐹𝐹 𝐹𝐹,𝐴𝐴,𝐵𝐵 𝑦𝑦 𝑙𝑙
19.
对于四个正数m、n、p、q,若满足mq 𝑓𝑓(2+ln1.1) > 𝑓𝑓(log25) 𝑏𝑏 > 𝑎𝑎 > 𝑐𝑐
5.【答案】B
【解析】设圆锥的底面半径为 ,高为 ,则 ,
2 2 2
可得 ,
𝑟𝑟 ℎ 𝑟𝑟 +ℎ = 𝑅𝑅
2 2 2
则圆锥𝑟𝑟 的=体𝑅𝑅积−ℎ ,ℎ ∈ (π0,𝑅𝑅) π π ,则 π ,
1 2 1 2 2 1 2 3 ′ 1 2 2
𝑉𝑉(ℎ) = 3 𝑟𝑟 ℎ = 3 (𝑅𝑅 −ℎ )ℎ = 3 (𝑅𝑅 ℎ−ℎ ) 𝑉𝑉 = 3 (𝑅𝑅 −3ℎ )
当 时, ;当 时, ;
√3 ′ √3 ′
0 < ℎ < 3 𝑅𝑅 𝑉𝑉 (ℎ) > 0 3 𝑅𝑅 < ℎ < 𝑅𝑅 𝑉𝑉 (ℎ) < 0
则 在 上单调递增,在 内单调递减,
√3 √3
𝑉𝑉(ℎ) �0, 3 𝑅𝑅� �3 𝑅𝑅,𝑅𝑅�
可知当 ,即 时,圆锥的体积取到最大值.
√3 √6
故选:ℎB.= 3 𝑅𝑅 𝑟𝑟 = 3 𝑅𝑅
学科网(北京)股份有限公司6.【答案】A
【解析】由函数 的图象可得:
当 时,𝑓𝑓(函𝑥𝑥)数单调递增,则 ,
1 ′
𝑥𝑥 ∈ (−∞,2) 𝑓𝑓 (𝑥𝑥) > 0
当 时,函数单调递减,则 .
1 ′
当𝑥𝑥 ∈ (2,2) 时,函数单调递增,𝑓𝑓则(𝑥𝑥) < 0 ,
′
由𝑥𝑥 ∈ (2,+∞) ①或𝑓𝑓 (𝑥𝑥) > 0 ②
′ ′
′
𝑓𝑓 (𝑥𝑥) > 0 𝑓𝑓 (𝑥𝑥) < 0
(𝑥𝑥+1)𝑓𝑓 (𝑥𝑥) < 0 ⇔ � �
解①得, ,解②得
𝑥𝑥+
,
1 < 0
,
𝑥𝑥 +1 > 0
1
𝑥𝑥 < −1 2 < 𝑥𝑥 < 2
综上,不等式 的解集为 .
′ 1
故选:A. (𝑥𝑥+1)𝑓𝑓 (𝑥𝑥) < 0 (−∞,−1)∪�2,2�
7.【答案】A
【解析】设正项等比数列 的公比为 ,
因为 N {𝑎𝑎, 𝑛𝑛}所以 𝑞𝑞 > 0 ,
2(𝑛𝑛+1)
2𝑛𝑛 ∗ 𝑎𝑎𝑛𝑛+1𝑎𝑎𝑛𝑛+2 2 2
解得𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+ , 1 =所2以 (𝑛𝑛 ∈ ) 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1,= 2 2𝑛𝑛 = 4 = 𝑞𝑞
2 2𝑛𝑛
所以𝑞𝑞 = 2 ,𝑎𝑎所 𝑛𝑛 以×2 = 2 (𝑎𝑎𝑛𝑛 >,0)
2𝑛𝑛−1 2−1
2 2
𝑎𝑎𝑛𝑛 = 2 𝑎𝑎1 = 2 = √2
所以 ,
4
√2(1−2 )
𝑆𝑆4 = 1−2 = 15√2
所以数列 的前4项的和 的值为 .
故选:A. {𝑎𝑎𝑛𝑛} 𝑆𝑆4 15√2
8.【答案】D
【解析】由已知命中的概率为 ,不命中的概率为 ,射击4次,命中两次,
3 2
5 5
故概率 C .
2 2
2 3 2 216
故选:𝑃𝑃D.= 4�5� ×�5� = 625
9.【答案】ACD
【解析】A. 中, ,
1
2 2
所以直棱柱
△
的侧
𝐴𝐴𝐵𝐵
面
𝐴𝐴
积为
𝐴𝐴𝐴𝐴 = �1 +1 −2×1×1×
,
�
故
−2
A
�
正
=
确
√3
;
�1+1+√3�×2 = 4+2√3
学科网(北京)股份有限公司B. 外接圆的半径 ,
𝐴𝐴𝐴𝐴
∘
△𝐴𝐴𝐵𝐵𝐴𝐴 𝑟𝑟 = 2sin120 = 1
所以直棱柱外接球的半径 ,
𝐴𝐴𝐴𝐴1 2
2
则直三棱柱外接球的表面𝑅𝑅积= �𝑟𝑟π+� 2 �π,=故√2B 错误;
2
C.因为 ,且
𝑆𝑆
平
=
面
4 𝑅𝑅 = 8
, 平面 ,所以 平面 ,
点 在 𝐵𝐵𝐵𝐵1 上//,𝐴𝐴𝐴𝐴所 1 以点𝐵𝐵𝐵𝐵到 1 平⊄面 𝐴𝐴𝐴𝐴1𝐴𝐴1 的𝐴𝐴距离𝐴𝐴𝐴𝐴相 1 等⊂,为𝐴𝐴等𝐴𝐴腰 1𝐴𝐴1 三𝐴𝐴角形 𝐵𝐵𝐵𝐵底 1/边/的高𝐴𝐴为𝐴𝐴1 ,𝐴𝐴1 𝐴𝐴
1
𝐸𝐸 𝐵𝐵𝐵𝐵1 𝐸𝐸 𝐴𝐴𝐴𝐴1𝐴𝐴1𝐴𝐴 𝐴𝐴𝐵𝐵𝐴𝐴 2
且 的面积为 ,
1 √3 √3
△𝐴𝐴𝐴𝐴1𝑂𝑂 2×2× 2 = 2
则三棱锥 的体积为定值 ,与点 的位置无关,故C 正确;
1 √3 1 √3
D.将侧面展𝐸𝐸 −开𝐴𝐴为𝐴𝐴如1𝑂𝑂图长方形,连结3× 2,交×2 = 于12点 , 𝐸𝐸
此时 最小,最小值为 𝐴𝐴𝐴𝐴1 𝐵𝐵𝐵𝐵1 𝐸𝐸 ,故D正确.
2 2
𝐴𝐴𝐸𝐸 +𝐸𝐸𝐴𝐴1 �2 +(1+1) = 2√2
故选:ACD
10.【答案】BD
【解析】对于A:因为 ,由正弦定理可得 ,
2 2 2 2
则 , 𝑎𝑎 tan𝐵𝐵 = 𝑏𝑏 tan𝐴𝐴 sin 𝐴𝐴tan𝐵𝐵 = sin 𝐵𝐵tan𝐴𝐴
2 2
sin 𝐴𝐴sin𝐵𝐵 sin 𝐵𝐵sin𝐴𝐴
又 cos𝐵𝐵 = ,co则s𝐴𝐴 , , ,
可𝐴𝐴得,𝐵𝐵 ∈ (0,𝜋𝜋) ,整s理in𝐴𝐴得≠ 0 sin𝐵𝐵 ≠ 0, 2𝐴𝐴,2𝐵𝐵 ∈ (0,2𝜋𝜋)
sin𝐴𝐴 sin𝐵𝐵
cos𝐵𝐵 = cos𝐴𝐴 sin2𝐴𝐴 = sin2𝐵𝐵
学科网(北京)股份有限公司又因为 ,
可得 𝐴𝐴+𝐵𝐵 或∈ (0,𝜋𝜋) ,即 或 ,
𝜋𝜋
所以2𝐴𝐴 =或2𝐵𝐵 2𝐴𝐴+2𝐵𝐵 =,𝜋𝜋故A错𝐴𝐴 误=;𝐵𝐵 𝐴𝐴+𝐵𝐵 = 2
2 2 2
对于𝑎𝑎B=:𝑏𝑏因为𝑎𝑎 +𝑏𝑏 = 𝑐𝑐 ,则 ,
1+cos𝐴𝐴 𝑏𝑏+𝑐𝑐 sin𝐵𝐵+sin𝐴𝐴
所以 2 = 2𝑐𝑐 = 2sin𝐴𝐴 2sin𝐴𝐴 +2cos𝐴𝐴sin𝐴𝐴 = 2sin𝐵𝐵 +2sin𝐴𝐴 ,
所以 cos𝐴𝐴sin𝐴𝐴 = si , n𝐵𝐵 = sin[𝜋𝜋−(𝐴𝐴+𝐴𝐴)] = sin(𝐴𝐴+𝐴𝐴) = sin𝐴𝐴cos𝐴𝐴 +cos𝐴𝐴sin𝐴𝐴
在三s角in形𝐴𝐴c中os,𝐴𝐴 = 0> ,所以 ,所以 ,
𝜋𝜋
则此三角形为直sin角𝐴𝐴三0角形,故co B s𝐴𝐴正=确0; 𝐴𝐴 = 2
对于C:因为 ,所以 ,所以 < < ,
𝜋𝜋 3
则解此三角形𝑎𝑎只=有3一,𝑏𝑏解=,4故,𝐵𝐵C=错6误; 𝑎𝑎sin𝐵𝐵 = 2 𝑎𝑎sin𝐵𝐵 𝑎𝑎 𝑏𝑏
对于D:因为 是锐角三角形,
所以 < < ,△所𝐴𝐴𝐵𝐵以𝐴𝐴 < < ,
𝜋𝜋 𝜋𝜋
0 𝐴𝐴 2 2 𝐴𝐴+𝐵𝐵 𝜋𝜋
所以 < < < ,所以 < ,即 < ,
𝜋𝜋 𝜋𝜋 𝜋𝜋
0 2 −𝐵𝐵 𝐴𝐴 2 sin�2 −𝐵𝐵� sin𝐴𝐴 cos𝐵𝐵 sin𝐴𝐴
同理 < ,
cos𝐴𝐴 sin𝐵𝐵
则 > ,故D正确.
故选sin:𝐴𝐴B+Ds.i n𝐵𝐵 cos𝐴𝐴+cos𝐵𝐵
11.【答案】BCD
【解析】若数列 中存在某项 ,由 可推得 ,
进而 所有项均{𝑎𝑎 为𝑛𝑛} 0,与 𝑎𝑎𝑘𝑘矛 = 盾 0 ,故数 9𝑎𝑎 列𝑛𝑛𝑎𝑎𝑛𝑛+1均 = 为 𝑎𝑎𝑛𝑛非 − 零 4 项 𝑎𝑎𝑛𝑛.+1 𝑎𝑎𝑘𝑘−1 = 𝑎𝑎𝑘𝑘+1 = 0
由 {𝑎𝑎𝑛𝑛} 两𝑎𝑎边1同=时1 除以 ,{可𝑎𝑎𝑛𝑛得} ,
1 4
9𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 = 𝑎𝑎𝑛𝑛 −4𝑎𝑎𝑛𝑛+1 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 9 = 𝑎𝑎𝑛𝑛+1 −𝑎𝑎𝑛𝑛
所以 ,
1 1 1
𝑎𝑎𝑛𝑛+1 +3 = 4�𝑎𝑎𝑛𝑛+3�,𝑎𝑎1 +3 = 4 ≠ 0
故数列 是以4为首项,公比为4的等比数列,所以 ,即 ,
1 1 𝑛𝑛 1
�𝑎𝑎𝑛𝑛 +3� 𝑎𝑎𝑛𝑛+3 = 4 𝑎𝑎𝑛𝑛 = 4 𝑛𝑛 −3
对于A,因为 ,可得 ,矛盾,所以A错误;
1 1 1 𝑎𝑎3 13 1
𝑎𝑎𝑛𝑛 = 4 𝑛𝑛 −3 𝑎𝑎2 = 13,𝑎𝑎3 = 61,𝑎𝑎2 = 61 > 5
对于B,由
𝑛𝑛+1
1 2 𝑛𝑛 4 𝑛𝑛 4 4
𝑆𝑆𝑛𝑛 = (4 −3)+(4 −3)+⋯+(4 −3) = 3(4 −1)−3𝑛𝑛 = 3 −3−3𝑛𝑛 <
学科网(北京)股份有限公司,
𝑛𝑛+1 𝑛𝑛+1
4 4
3 −1−3 = 3 −4
所以 成立,所以B 正确;
𝑛𝑛+1
4
对于 𝑆𝑆 C 𝑛𝑛 , < 由3 −4 ,
𝑛𝑛
𝑛𝑛 4 1 1 1
4 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 = (4 𝑛𝑛 −3)(4 𝑛𝑛+1 −3) = 3�4 𝑛𝑛 −3−4 𝑛𝑛+1 −3�
所以 ,所以C 正
1 1 1 1 1 1 1 1 1
确; 𝑅𝑅𝑛𝑛 = 3��1−4 2 −3�+�4 2 −3−4 3 −3�+⋯+�4 𝑛𝑛 −3−4 𝑛𝑛+1 −3�� = 3�1−4 𝑛𝑛+1 −3� < 3
对于D,因为 ,则 ,
𝑛𝑛𝑎𝑎𝑛𝑛 𝑛𝑛 1 2 3 𝑛𝑛 1 1 2 3 𝑛𝑛
1+3𝑎𝑎𝑛𝑛 = 4 𝑛𝑛 ,𝑇𝑇𝑛𝑛 = 4+4 2 +4 3 +⋯+4 𝑛𝑛 4𝑇𝑇𝑛𝑛 = 4 2 +4 3 +4 4 +⋯+4 𝑛𝑛+1
错位相减得 1 1 𝑛𝑛 ,
3 1 1 1 1 1 𝑛𝑛
4�1−�4� �
𝑛𝑛 1 1 𝑛𝑛
4𝑇𝑇𝑛𝑛 = 4+4 2 +4 3 +4 4 ⋯+4 𝑛𝑛 −4 𝑛𝑛+1 = 1− 1 4 −4 𝑛𝑛+1 = 3−3×4 𝑛𝑛 −4 𝑛𝑛+1
则 成立,所以D正确.
4 4 1 𝑛𝑛 4 4 1 𝑛𝑛 4 𝑛𝑛+1
故𝑇𝑇选 𝑛𝑛 :=B9C−D3 ×�3×4 𝑛𝑛 +4 𝑛𝑛+1 � < 9−4×�4×4 𝑛𝑛 +4 𝑛𝑛+1 � = 9−4 𝑛𝑛+1
12.【答案】 / .
【解析】由
3+2√2
,
2√得 2+3
,
2 2
因为 ,𝑥𝑥+𝑦𝑦 =,2 𝑥𝑥−1+𝑦𝑦 = 1
所以
𝑥𝑥 > 1 𝑦𝑦 > 0
,
所以𝑥𝑥−1 > 0,𝑦𝑦 > 0
1 2 1 2 2
𝑥𝑥−1+𝑦𝑦 = �𝑥𝑥 −1+𝑦𝑦��𝑥𝑥−1+𝑦𝑦� = 3+(𝑥𝑥−1)𝑦𝑦+(𝑥𝑥−1)𝑦𝑦 ≥ 3+2�(𝑥𝑥−1)𝑦𝑦⋅(𝑥𝑥−1)𝑦𝑦 = 3+
,
2 当√且 2 仅当 ,即 , 时,等号成立,
2
(𝑥𝑥−1)𝑦𝑦 = (𝑥𝑥−1)𝑦𝑦 𝑥𝑥 = √2 𝑦𝑦 = 2+√2
所以 的最小值是 .
1
𝑥𝑥−1+𝑦𝑦 3+2√2
故答案为: .
3+2√2
13.【答案】
1 5
【解析】因为 9 ≤ 𝜔𝜔 < 3 si 6 n π ,所以函数 的最小正周期 π .
π
2 1
因为 在区间𝑓𝑓(𝑥𝑥) = 上(有2 5𝜔𝜔个𝑥𝑥)零点, 𝑓𝑓(𝑥𝑥) 𝑇𝑇 = 2 𝜔𝜔 = 𝜔𝜔(𝜔𝜔 > 0)
所以𝑓𝑓(𝑥𝑥) [0,,18即] ,
5 2 5
2𝑇𝑇 ≤ 18 < 2𝑇𝑇 𝜔𝜔 ≤ 18 < 2𝜔𝜔
学科网(北京)股份有限公司可得 ;
1 5
9 ≤ 𝜔𝜔 < 36
故答案为: .
1 5
14.【答案】9②≤③𝜔𝜔④< 36
【解析】当 时, 时, ,故在 上不是单调递减,①错误;
对于②,当 𝑚𝑚 = 0 显然 𝑥𝑥 不 ≥ 成 0 立,故 𝑓𝑓(𝑥𝑥) = 0 , (−∞,+∞)
当 时,𝑚𝑚令= 0 ,即 𝑚𝑚 ≠ 0 ,得 , ,要使
√2𝑚𝑚
有且𝑥𝑥 ≥仅0有两个零𝑓𝑓(点𝑥𝑥),=则0 − ,2 故√𝑥𝑥 = 0 ,②𝑥𝑥正=确0,𝑥𝑥 < 0,|𝑥𝑥+𝑚𝑚| = 0 ⇒ 𝑥𝑥 = −𝑚𝑚 𝑓𝑓(𝑥𝑥)
−𝑚𝑚 < 0 𝑚𝑚 > 0
对于③, 当 时, ,此时 在 单调递减,在 )单调递
−𝑥𝑥−𝑚𝑚,𝑥𝑥 < 0,
𝑚𝑚 < 0 𝑓𝑓(𝑥𝑥) = �
√2𝑚𝑚
𝑓𝑓(𝑥𝑥) (−∞,0) [0,+∞
增,如图: − 2 √𝑥𝑥,𝑥𝑥 ≥ 0.
若 ,由 ,故 ,所以 的取值范围为 ;
√2𝑚𝑚
③𝑓𝑓正(𝑎𝑎确) = 𝑓𝑓(𝑏𝑏) −𝑚𝑚 = − 2 √𝑥𝑥 ⇒ 𝑥𝑥 = 2 |𝑎𝑎−𝑏𝑏| > 2 |𝑎𝑎−𝑏𝑏| (2,+∞)
对于④,由①③可知: 时,显然不成立,故 ,
要使
𝑚𝑚 ≤ 0
, 关
𝑚𝑚
于
>
坐
0
标原点 的对称点也在函数 的图象上,
则只𝑄𝑄需 1 要(𝑥𝑥1,𝑦𝑦1),𝑄𝑄2(𝑥𝑥2,𝑦𝑦2)(𝑥𝑥1 <的𝑥𝑥图 2 象<与0) 𝑄𝑄1,𝑄𝑄2 𝑂𝑂有两个不同的交点,𝑓𝑓(如𝑥𝑥)图:
√2𝑚𝑚
𝑥𝑥 > 0,𝑦𝑦 = −|𝑥𝑥−𝑚𝑚| 𝑥𝑥 ≥ 0,𝑓𝑓(𝑥𝑥) = − 2 √𝑥𝑥
故 ,
𝑥𝑥1 < −𝑚𝑚 < 𝑥𝑥2 < 0
3√2
|𝑃𝑃𝑄𝑄1|+|𝑃𝑃𝑄𝑄2| = √2|−𝑚𝑚−𝑥𝑥1|+√2|𝑥𝑥2 +𝑚𝑚| = −√2(𝑚𝑚+𝑥𝑥1)+√2(𝑥𝑥2 +𝑚𝑚) = 2 ⇒ 𝑥𝑥2 −𝑥𝑥1 =
学科网(北京)股份有限公司,
3
2
由对称可得 ,
√2𝑚𝑚
𝑓𝑓(−𝑥𝑥1) = − 2 √−𝑥𝑥1 = −|−𝑥𝑥1−𝑚𝑚| = 𝑥𝑥1 +𝑚𝑚
化简可得 ,故
√2𝑚𝑚 1 2
,
√2𝑚𝑚 2 √2𝑚𝑚 2 ±�2𝑚𝑚 +4𝑚𝑚
𝑥𝑥1 +𝑚𝑚+ 2 √−𝑥𝑥1 = 0 (√−𝑥𝑥1) −,2化√简−得𝑥𝑥1 −𝑚𝑚 = 0 ⇒ √−𝑥𝑥1 = 2
√2𝑚𝑚 2 √2𝑚𝑚
𝑓𝑓(−𝑥𝑥2) = − 2 √−𝑥𝑥2 = −|−𝑥𝑥2 −𝑚𝑚| = −𝑥𝑥2 −𝑚𝑚 (√−𝑥𝑥2) + 2 √−𝑥𝑥2 −𝑚𝑚 = 0
所以
√2𝑚𝑚 1 2
− 2 ±�2𝑚𝑚 +4𝑚𝑚
由于√−𝑥𝑥2 =
均大于
2
0,所以
√2𝑚𝑚 1 2
,
√2𝑚𝑚 1 2
,
2 +�2𝑚𝑚 +4𝑚𝑚 − 2 +�2𝑚𝑚 +4𝑚𝑚
−𝑥𝑥1,−𝑥𝑥2 √−𝑥𝑥1 = 2 √−𝑥𝑥2 = 2
因此
√2𝑚𝑚 1 2
2
√2𝑚𝑚 1 2
2
2 +�2𝑚𝑚 +4𝑚𝑚 − 2 +�2𝑚𝑚 +4𝑚𝑚
2 2
𝑥𝑥2 −𝑥𝑥1 = (√−𝑥𝑥1) −(√−𝑥𝑥2) = � 2 � −� 2 �
√2𝑚𝑚 1 2 √2 1 4 3
= � 𝑚𝑚 +4𝑚𝑚 = � 𝑚𝑚 +4𝑚𝑚
由于2 2, 2 2 为 单调递增函数,且 ,
1 4 3 9
𝑚𝑚 > 0 𝑓𝑓(𝑚𝑚) = 2𝑚𝑚 +4𝑚𝑚 (0,+∞) 𝑓𝑓(1) = 2
此时 ,因此 ,④正确,
√2 1
4 3
3
故答𝑥𝑥案2为−:𝑥𝑥1②=③2④� 2𝑚𝑚 +4𝑚𝑚 = 2 𝑚𝑚 = 1
15.【解析】(1)由题意知, ,即 𝑎𝑎1(1−𝑞𝑞 5 ) ,
𝑆𝑆5 = 62 1−𝑞𝑞 = 62
10
� �𝑎𝑎1(1−𝑞𝑞 )
𝑆𝑆10 = 2046
1−𝑞𝑞 = 2046
解得 ,所以 ;
𝑎𝑎1 = 2 𝑛𝑛−1 𝑛𝑛
� 𝑎𝑎𝑛𝑛 = 𝑎𝑎1𝑞𝑞 = 2
由 𝑞𝑞 = 2 ,
𝑛𝑛(𝑛𝑛+1)(4𝑛𝑛−1)
𝑏𝑏1 +2𝑏𝑏2 +⋯+(𝑛𝑛−1)𝑏𝑏𝑛𝑛−1 +𝑛𝑛𝑏𝑏𝑛𝑛 = 6
得 ,
(𝑛𝑛−1)𝑛𝑛(4𝑛𝑛−5)
𝑏𝑏1 +2𝑏𝑏2 +⋯+(𝑛𝑛−1)𝑏𝑏𝑛𝑛−1 = 6 (𝑛𝑛 ≥ 2)
两式相减,得 ,
𝑛𝑛(𝑛𝑛+1)(4𝑛𝑛−1) (𝑛𝑛−1)𝑛𝑛(4𝑛𝑛−5)
所以 𝑛𝑛𝑏𝑏𝑛𝑛 ,= 6 − 6 = 𝑛𝑛(2𝑛𝑛−1)
当 𝑏𝑏𝑛𝑛 = 时 2 , 𝑛𝑛−1 满足上式,
故 𝑛𝑛 = 1 𝑏𝑏1. = 1
(𝑏𝑏 2) 𝑛𝑛 =由2(𝑛𝑛 1 −)1知, , ,所以 ,
𝑛𝑛
𝑛𝑛 𝑎𝑎𝑛𝑛(1+𝑏𝑏𝑛𝑛) 2 ⋅(2𝑛𝑛) 𝑛𝑛
𝑎𝑎𝑛𝑛 = 2 𝑏𝑏𝑛𝑛 = 2𝑛𝑛−1 𝑐𝑐𝑛𝑛 = 2 = 2 = 𝑛𝑛⋅2
学科网(北京)股份有限公司,
1 2 3 𝑛𝑛−1 𝑛𝑛
𝑇𝑇𝑛𝑛 = 1⋅2 +2⋅2 +3⋅2 +⋯+(𝑛𝑛−1)⋅2 +𝑛𝑛⋅2 ,
2 3 4 𝑛𝑛 𝑛𝑛+1
2
两
𝑇𝑇
式𝑛𝑛
=
加
1
减
⋅
,
2 +2⋅2 +3⋅2 +⋯+(𝑛𝑛−1)⋅2 +𝑛𝑛⋅2
得 ,
𝑛𝑛
1 2 3 𝑛𝑛 𝑛𝑛+1 2(1−2 ) 𝑛𝑛+1 𝑛𝑛+1
所−以𝑇𝑇𝑛𝑛 = 2 +2 +2 +⋯+. 2 −𝑛𝑛⋅2 = 1−2 −𝑛𝑛⋅2 = (1−𝑛𝑛)⋅2 −2
𝑛𝑛+1
16.【𝑇𝑇𝑛𝑛 答=案(】𝑛𝑛
(
−
1)
1证)⋅明2见解+析2;(2)
2√34
【解析】(1)因为 , , 分别17是侧棱 , , 的中点,
所以 // 𝐴𝐴/1/ 𝐵𝐵 ,1 𝐴𝐴1 𝑃𝑃𝐴𝐴 𝑃𝑃𝐵𝐵 𝑃𝑃𝐴𝐴
因为 𝐴𝐴1𝐵𝐵1 𝐴𝐴𝐵𝐵 , ,𝐵𝐵 所1𝐴𝐴 以1 𝐵𝐵𝐴𝐴 ,
因为 𝐴𝐴𝐵𝐵 ⊥ 𝐵𝐵 平 𝐴𝐴 面 𝐴𝐴1𝐵𝐵 ,1 ⊥ 𝐵𝐵1𝐴𝐴1平面 ,
所以 𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵 , 𝐵𝐵1 𝐴𝐴1𝐴𝐴 𝐵𝐵1𝐴𝐴1 ⊂ 𝐵𝐵𝐵𝐵1𝐴𝐴1𝐴𝐴
又 𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵1𝐴𝐴1 平面 ,
所 𝐴𝐴 以1𝐴𝐴 ∩𝐴𝐴1𝐵𝐵 平1面 = 𝐴𝐴1,𝐴𝐴1, 𝐴𝐴, 𝐴𝐴1𝐵𝐵1 ⊂ 𝐴𝐴1𝐵𝐵1𝐴𝐴
又因
𝐵𝐵
为1𝐴𝐴1
⊥
平
𝐴𝐴
面1𝐵𝐵1𝐴𝐴 ,
所以平 𝐵𝐵 面1𝐴𝐴1 ⊂ 平 𝐴𝐴1面 𝐵𝐵1𝐴𝐴1 ;
(2)因为 𝐴𝐴1𝐵𝐵1𝐴𝐴 ⊥ 平面 𝐴𝐴1𝐵𝐵1𝐴𝐴1, 平面 ,
所以 𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵𝐵𝐵1𝐴𝐴 ,1𝐴𝐴 𝐵𝐵𝐴𝐴,𝐵𝐵1𝐴𝐴 ⊂ 𝐵𝐵𝐵𝐵1𝐴𝐴1𝐴𝐴
因为 𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵1𝐴𝐴,𝐴𝐴1, 𝐴𝐴 所 ⊥ 以 𝐵𝐵𝐴𝐴 ,
所以𝐴𝐴𝐵𝐵 = 𝐵𝐵𝐴𝐴 = 4 , 𝐴𝐴1𝐵𝐵1 = 𝐵𝐵1𝐴𝐴1 = 2
因为𝐴𝐴1𝐴𝐴 =平𝐵𝐵1面𝐴𝐴 = √2 , // ,
所以 𝐵𝐵1𝐴𝐴1 平 ⊥ 面 𝐴𝐴1𝐵𝐵1, 𝐴𝐴 𝐵𝐵1𝐴𝐴1 𝐵𝐵𝐴𝐴
又 𝐵𝐵𝐴𝐴 ⊥ 平面 𝐴𝐴1𝐵𝐵1𝐴𝐴 ,所以 ,
所 𝐵𝐵 以1𝐴𝐴 ⊂ 𝐴𝐴1𝐵𝐵1两 𝐴𝐴 两垂直, 𝐵𝐵𝐴𝐴 ⊥ 𝐵𝐵1𝐴𝐴
如图,
𝐴𝐴𝐴𝐴
以1, 点
𝐴𝐴𝐵𝐵,
为
𝐴𝐴𝐵𝐵
原1 点,建立空间直角坐标系,
则 𝐴𝐴 ,
𝐵𝐵(4,0,0),𝐴𝐴(0,0,0),𝐴𝐴1�0,0,√2�,𝐵𝐵1�0,√2,0�
故 ,
设𝐴𝐴�平���1��面𝐵𝐵���1⃗ = �0,√的2法,−向√2量�,为𝐴𝐴����1��𝐵𝐵�⃗ = �4,0,−,√2 �
𝐴𝐴1𝐵𝐵𝐵𝐵1 𝑛𝑛�⃗ = (𝑥𝑥,𝑦𝑦,𝑧𝑧)
学科网(北京)股份有限公司则有 ,可取 ,
𝑛𝑛�⃗⋅𝐴𝐴����1��𝐵𝐵���1⃗ = √2𝑦𝑦−√2𝑧𝑧 = 0
� 𝑛𝑛�⃗ = �1,2√2,2√2�
因为 𝑛𝑛�⃗⋅𝐴𝐴��平��1��𝐵𝐵�面⃗ = 4𝑥𝑥 −√,2𝑧𝑧 = 0
所以𝐴𝐴1𝐴𝐴 ⊥ 𝐵𝐵𝐵𝐵1𝐴𝐴即 1𝐴𝐴为平面 的一条法向量,
𝐴𝐴����𝐴𝐴���1⃗ = �0,0,√2� 𝐵𝐵𝐵𝐵1𝐴𝐴1𝐴𝐴
故 ,
𝑛𝑛�⃗⋅�𝐴𝐴���𝐴𝐴����1⃗ 4 2√34
cos�𝑛𝑛�⃗,𝐴𝐴����𝐴𝐴���1⃗� = |𝑛𝑛�⃗|��𝐴𝐴���𝐴𝐴����1⃗� = √17×√2 = 17
所以二面角 的余弦值 .
2√34
𝐴𝐴1 −𝐵𝐵𝐵𝐵1−𝐴𝐴
17
17.【解析】(1)由题意得这三人中这一周恰好有一人选择 健身中心健身的概率
𝐴𝐴 .
1 1 2 1 1 2 1 1 2 7
𝑃𝑃(=2)2记×事�1件−3:�×丁�周1−六3选�择+�1健−身2中�×心3,×事�1件−3:�+丁�周1日−选2�择×�1健−身3中�×心3,= 18
则 𝐴𝐴 𝐴𝐴 𝐷𝐷 ,𝐵𝐵
1 1 3 2 1
𝑃𝑃(𝐴𝐴) = 𝑃𝑃(𝐴𝐴̅) = 2,𝑃𝑃(𝐷𝐷|𝐴𝐴) = 1−4 = 4,𝑃𝑃(𝐷𝐷|𝐴𝐴̅) = 1−3 = 3
由全概率公式得 .
1 3 1 1 13
𝑃𝑃(𝐷𝐷) = 𝑃𝑃(𝐴𝐴)𝑃𝑃(𝐷𝐷|𝐴𝐴)+𝑃𝑃(𝐴𝐴̅)𝑃𝑃(𝐷𝐷|𝐴𝐴̅) = 2×4+2×3 = 24
故丁周日选择 健身中心健身的概率为 .
13
(3)设从全校𝐵𝐵学生中随机抽取1人,抽24取到的学生是健身效果不佳的学生的概率为 ,则
,
𝑝𝑝 𝑝𝑝 =
0
设
.0
抽
2
取次数为 ,则 的分布列为
𝑋𝑋 𝑋𝑋
1 2 3
𝑋𝑋 ⋯ 𝑛𝑛−1 𝑛𝑛
2 𝑛𝑛−2 𝑛𝑛−1
𝑃𝑃故 𝑝𝑝 (1−𝑝𝑝)𝑝𝑝 (1−𝑝𝑝) 𝑝𝑝 ⋯ (1−𝑝𝑝) 𝑝𝑝 (1−𝑝𝑝) ,
2 𝑛𝑛−2 𝑛𝑛−1
又 𝐸𝐸(𝑋𝑋) = 𝑝𝑝+(1−𝑝𝑝)𝑝𝑝×2+(1−𝑝𝑝) 𝑝𝑝×3+⋯+(1−𝑝𝑝) 𝑝𝑝×(𝑛𝑛−1)+(1−𝑝𝑝) ×𝑛𝑛
2 3 𝑛𝑛−1
(1−𝑝𝑝)𝐸𝐸(𝑋𝑋) = (1−𝑝𝑝)𝑝𝑝+(1−𝑝𝑝) 𝑝𝑝×2+(1−𝑝𝑝) 𝑝𝑝×3+⋯+(1−𝑝𝑝) 𝑝𝑝×(𝑛𝑛−1)+
学科网(北京)股份有限公司,
𝑛𝑛
(
两
1
式
−
相
𝑝𝑝)
减
×
得
𝑛𝑛
,
2 𝑛𝑛−2 𝑛𝑛−1
所以
𝑝𝑝𝐸𝐸(𝑋𝑋) = 𝑝𝑝+(1−𝑝𝑝)𝑝𝑝+(1−𝑝𝑝) 𝑝𝑝+⋯+(1−𝑝𝑝) 𝑝𝑝+ (1−𝑝𝑝) 𝑝𝑝
2 𝑛𝑛−2 𝑛𝑛−1
𝐸𝐸(𝑋𝑋) = 1+(1−𝑝𝑝)+(918−,𝑝𝑝 ) +⋯+(1−𝑝𝑝) +(1−𝑝𝑝)
𝑛𝑛 𝑛𝑛 0 𝑛𝑛
1−(1−𝑝𝑝) 1−(1−𝑝𝑝) 1−0.
=
所以
1−(1−𝑝𝑝) = 9𝑝𝑝8
在
=
N
0. 2
时单调递增,
0 𝑛𝑛
1−0. ∗
𝐸𝐸(𝑋𝑋) = 0. 2 𝑛𝑛 ∈
可知当 时, ;
29
1−0.98 1−0.557
当
𝑛𝑛 =
时
2
,
9 𝐸𝐸(𝑋𝑋) = 0.02 ≈5450.02 = 2
;
2. 15
30
1−0.98 1−0.
当
𝑛𝑛 = 30
时,
𝐸𝐸(𝑋𝑋) = 0.02 ≈ 0.05235 = 22.75
.
31
1−0.98 1−0.
若𝑛𝑛抽=取3次1数的𝐸𝐸期(望𝑋𝑋)值=不超0.0过2 2≈3,则0.02的=最2大3.值25为30.
18.【解析】(1)椭圆 的方程为 𝑛𝑛 ,
2 2
𝑥𝑥 𝑦𝑦
2 2
𝐴𝐴 𝑎𝑎 +𝑏𝑏 = 1
当 轴时, ,所以点 在椭圆上,
√3
𝑙𝑙 ⊥ 𝑥𝑥 |𝐴𝐴𝐵𝐵| = √3 �1,± 2�
依题意 𝑐𝑐 √3 ,解得 , , ,
⎧ 𝑒𝑒 = 𝑎𝑎 = 2
1 3
2 2 𝑏𝑏 = 1 𝑎𝑎 = 2 𝑐𝑐 = √3
𝑎𝑎 +4𝑏𝑏 = 1
⎨
2 2 2
椭圆 ⎩的
𝑐𝑐
方
+
程
𝑏𝑏
为
= 𝑎𝑎
;
2
𝑥𝑥 2
∴ 𝐴𝐴 4 +𝑦𝑦 = 1
(2)设圆心 , , , , , ,
显然直线 的斜𝑃𝑃(率0,存𝑚𝑚)在𝐴𝐴,(𝑥𝑥设1 𝑦𝑦1)𝐵𝐵(𝑥𝑥2 𝑦𝑦2) 𝐹𝐹�,−√ 3,0�
由
𝑙𝑙
,
𝑙𝑙
则
:𝑦𝑦 = 𝑘𝑘(𝑥𝑥−1)
,
2 2 2 2 2 2
又 |𝑃𝑃𝐴𝐴| = |𝑃𝑃𝐵𝐵| = , | 代 𝑃𝑃𝐹𝐹 入 | 得到: 𝑥𝑥1 +(𝑦𝑦1 −𝑚𝑚) = 𝑚𝑚 + , 3
2 2 2
同理 𝑥𝑥1可 = 得 4(1−𝑦𝑦1) , 3 𝑦𝑦1 +2𝑚𝑚𝑦𝑦1 −1 = 0
2
则 分 3 别 𝑦𝑦2是 +2𝑚𝑚𝑦𝑦2 −1 = 0 的两根,
2
由𝑦𝑦韦 1,达𝑦𝑦2 定理可得3𝑦𝑦 +2𝑚𝑚𝑦𝑦−,1 = 0
1
𝑦𝑦1𝑦𝑦2 = −3
又联立 与 ,
2
𝑥𝑥 2
得 𝑙𝑙:𝑦𝑦 = 𝑘𝑘(𝑥𝑥−1) 4 +𝑦𝑦 = 1 ,
2 2 2 2
(4𝑘𝑘 +1)𝑥𝑥 −8𝑘𝑘 𝑥𝑥+4𝑘𝑘 −,4 = 0
2 2
8𝑘𝑘 4𝑘𝑘 −4
∴ 𝑥𝑥1 +𝑥𝑥2 = 4𝑘𝑘 2 +1,𝑥𝑥1𝑥𝑥2 = 4𝑘𝑘 2 +1
学科网(北京)股份有限公司所以
2 2 2
2 2 4𝑘𝑘 −4 8𝑘𝑘 −3𝑘𝑘
𝑦𝑦1𝑦𝑦2 = 𝑘𝑘 [𝑥𝑥1𝑥𝑥2 −(𝑥𝑥1 +𝑥𝑥2)+1] = 𝑘𝑘 �4𝑘𝑘 2 +1−4𝑘𝑘 2 +1+1� = 4𝑘𝑘 2 +1,
故 解得 ,
2
−3𝑘𝑘 1 √5
2
4𝑘𝑘 +1 = −3 𝑘𝑘 = ± 5
直线 的斜率为 ,
√5
𝑙𝑙 𝑘𝑘 = ± 5
19.【解析】
(1)
3×7<11×2,
∴(3,11)是(2,7)的"下位序列";
(2)( a,b )是( c,d )的“下位序列”,
∴ad 0,
b+d b (b+d)b
a+c a
即 − >0,
b+d b
a+c a
∴ > ,
b+d b
a+c c
同理 < ,
b+d d
a a+c c
综上所述: < < ;
b b+d d
mn<2024k
(3)由已知得 ,
(m+1)n>2025k
因为m,n,k 为整数,
mn+1≤2024k
故 ,
mn+n−1≥2025k
∴2024(mn+n−1)≥2024×2025k ≥2025(mn+1),
学科网(北京)股份有限公司4049
∴n≥ ,
2024−m
{ }
该式对集合 m 0