文档内容
2025~2026 学年度第一学期期末学业质量水平诊断 高三数学
注意事项:
1. 本试题满分 150 分, 考试时间为 120 分钟。
2. 答卷前,务必将姓名和准考证号填涂在答题纸上。
3. 使用答题纸时,必须使用 0.5 毫米的黑色签字笔书写,要字迹工整,笔迹清
晰,超出答题区书写的答案无效,在草稿纸、试题卷上答题无效。
一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分。在每小题
给出的四个选项中, 只有一项 符合题目要求。
1. 设全集 U={1,2,3,4,5},A={2,3,4},B={4,5} ,则 (∁ A)∩(∁ B)=
U U
A. {1,2,3,5} B. {1,2,3} C. {1,5} D. {1}
1 2
2. 已知 a> ,则 a+ 的最小值为
2 2a−1
1 3 5
A. B. C. D. 3
2 2 2
2
3. 已知 a>0 且 a≠1 ,则 “ log <1 ” 是 “ a>1 ” 的
a3
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不
必要条件
4. 已知直线 l:mx+ y−2m+1=0 ,圆 C:(x−1) 2+ y2=4 ,当直线 l 被圆 C 截得的弦
长最短时,实数 m 的值为
A. -1 B. 1 C. -2 D. 2
π
5. 已知菱形 ABCD 的边长为 1,E,F 分别是 BC,CD 的中点, ∠ABC= ,
3
则 AE⋅BF=
5 3 3 5
A. − B. − C. D.
8 8 8 8
7√2
6. 若正三棱台 ABC−A B C 的体积为 ,且 AB=2 , A B =4 ,则侧棱
1 1 1 3 1 1
A A 的长度为
1A. √2 B. 2 C. √3 D. 3
(ωx π) ωx √3 (π 3π)
7. 若函数 f (x)=cos − cos − (ω>0) 在区间 , 内无零点,则 ω
2 6 2 4 4 4
的取值范围为
( 4] [4 ) ( 8] [8 )
A. 0, B. ,2 C. 0, D. ,2
9 9 9 9
8. 已知定义在 R 上的函数 f (x) 的导函数为 f′(x),f (x+2)=f (−x),(x−1)f′(x)≥0 ,
且对任意的 x∈R ,有 f (3−cos2x)≤f (msin2x) ,则实数 m 的取值范围为
A. (−∞,−1] B. [−1,1] C. [1,3] D. [3,+∞)
二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分。在每小题
给出的选项中, 有多项符合题 目要求。全部选对的得 6 分, 部
分选对的得部分分, 有选错的得 0 分。
1
9. 已知函数 f (x)=2x3−3x2+ ,f′(x) 为 f (x) 的导函数,则
2
A.
f′(1)
=−
3
B. 函数 f (x) 在
(1
,+∞
)
上单调递增
2 2 2
1 ( 1)
C. 函数 f (x) 的极大值为 D. 函数 y=f x+ 为奇函数
2 2
10. 已知抛物线 C:y2=mx 经过点 M(1,1) ,其焦点为 F,P 为 C 上一动点,点
( 1) 5
N 0, ,则 A. |M F|=
2 4
B. 直线 M N 与抛物线 C 有两个公共点
C. 满足 |PM|=√2|PN| 的点 P 有两个
√5
D. 点 P 到 y 轴的距离与其到点 N 的距离之和的最小值为
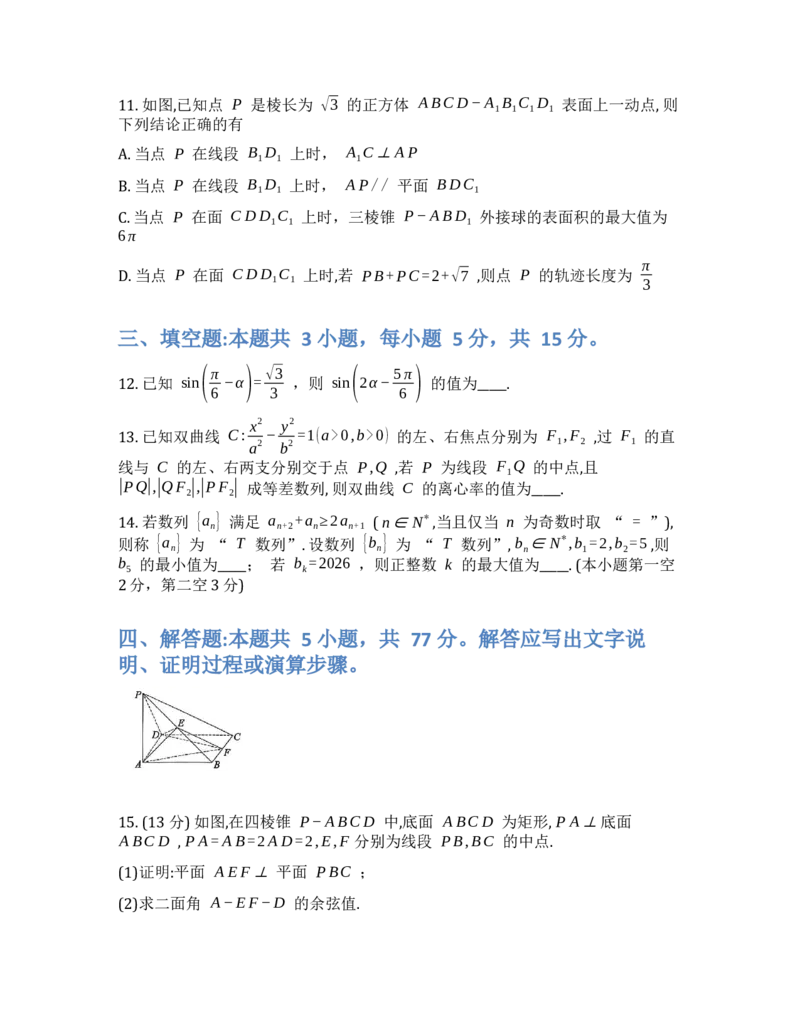
211. 如图,已知点 P 是棱长为 √3 的正方体 ABCD−A B C D 表面上一动点, 则
1 1 1 1
下列结论正确的有
A. 当点 P 在线段 B D 上时, A C⊥AP
1 1 1
B. 当点 P 在线段 B D 上时, AP// 平面 BDC
1 1 1
C. 当点 P 在面 CDD C 上时,三棱锥 P−ABD 外接球的表面积的最大值为
1 1 1
6π
π
D. 当点 P 在面 CDD C 上时,若 PB+PC=2+√7 ,则点 P 的轨迹长度为
1 1 3
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
(π ) √3 ( 5π)
12. 已知 sin −α = ,则 sin 2α− 的值为_____.
6 3 6
x2 y2
13. 已知双曲线 C: − =1(a>0,b>0) 的左、右焦点分别为 F ,F ,过 F 的直
a2 b2 1 2 1
线与 C 的左、右两支分别交于点 P,Q ,若 P 为线段 F Q 的中点,且
1
|PQ|,|QF |,|PF | 成等差数列, 则双曲线 C 的离心率的值为_____.
2 2
14. 若数列 {a } 满足 a +a ≥2a ( n∈N* ,当且仅当 n 为奇数时取 “ = ”),
n n+2 n n+1
则称 {a } 为 “ T 数列”. 设数列 {b } 为 “ T 数列”, b ∈N*,b =2,b =5 ,则
n n n 1 2
b 的最小值为_____; 若 b =2026 ,则正整数 k 的最大值为_____. (本小题第一空
5 k
2分,第二空3分)
四、解答题:本题共 5 小题,共 77 分。解答应写出文字说
明、证明过程或演算步骤。
15. (13 分) 如图,在四棱锥 P−ABCD 中,底面 ABCD 为矩形, PA⊥ 底面
ABCD , PA=AB=2AD=2,E,F 分别为线段 PB,BC 的中点.
(1)证明:平面 AEF⊥ 平面 PBC ;
(2)求二面角 A−EF−D 的余弦值.π
16.(15分)已知 △ABC 的内角 A,B,C 的对边分别为 a,b,c , B= ,点 D
3
满足 ⃗BC=4⃗BD .
(1)若 AD=1 ,求 △ABC 面积的最大值;
π
(2)若 ∠C AD= ,求 C .
3
17. (15 分) 已知点 P (x ,y ),P (x ,y ),⋯,P (x ,y ),⋯ 均在抛物线 x2=4 y 上,
1 1 1 2 2 2 n n n
x =1 , 0b>0) 的离心率为 ,其左、右焦点分别为
a2 b2 2
F ,F , 上顶点为 M ,且 △M F F 的面积为 1 .
1 2 1 2
(1)求 Γ 的方程;
(2)设过点 F 的直线 l 与过点 F 的直线 l 相交于点 P,l ,l 的斜率分别为
1 1 2 2 1 2
1 2
k ,k ,且 − =1
1 2 k k
1 2
(i) 若 Q 为 Γ 上的动点,求 |PQ| 的最小值;
(ii) 设 O 为坐标原点,若 l 与 Γ 相交于点 A,B,l 与 Γ 相交于点 C,D ,且直线
1 2
OA,OB,OC,OD 的斜率之和为 0,求点 P 的坐标.
axex
19.(17 分)已知函数 f (x)= (a∈R) .
ex−1
(1)当 x>0 时, f (x)>1 ,求 a 的取值范围;
1
(2)设 a=1,ex n+1=f (x ),n∈N* ,且 x = .
n 1 2
(i)证明:数列 {x } 是递减数列;
n
1
(ii) 证明: |ex n−1|< .
2n−12025~2026 学年度第一学期期末学业质量水平诊断 高三数学
参考答案
一、选择题:
1. D 2. C 3. B 4. A 5. B 6. A 7. C 8. A
二、选择题
9. ACD 10. AC 11. ABD
三、填空题
1
12. − 13.√1314.16,86
3
四、解答题
15. 解: (1) 证明: 因为 PA⊥ 平面 ABCD,BC⊂ 平面 ABCD ,所以
PA⊥BC.⋯⋯1 1 分因为底面 ABCD 为矩形,所以 BC⊥AB .
又 PA⊂ 平面 PAB,AB⊂ 平面 PAB,PA∩AB=A ,
所以 BC⊥ 面 PAB , 3 分
因为 AE⊂ 面 PAB ,所以 BC⊥AE , 4 分
在 △APB 中,因为 AP=AB,E 为 PB 中点,所以 AE⊥PB ,
因为 PB⊂ 平面 PBC,BC⊂ 平面 PBC,PB∩BC=B ,
所以 AE⊥ 平面 PBC . 5 分
又 AE⊂ 平面 AEF ,所以平面 AEF⊥ 平面 PBC . 6 分
(2)以 D 为原点, ⃗DA,⃗DC 的方向分别作为 x , y 轴的正方向,建立如图所
示空间直角坐标系, D−x yz ,则
(1 )
A(1,0,0),B(1,2,0),P(1,0,2),E(1,1,1),F ,2,0 , 7 分因为
2
⃗AE=(0,1,1),⃗AF= ( − 1 ,2,0 ) ,
2设 m=(x ,y ,z ) 为平面 AEF 的一个法向量,
1 1 1
{ y +z =0
1 1
则有 1 ,
− x +2y =0
2 1 1
令 x =4 ,得 y =1,z =−1 ,此时 m=(4,1,−1) . 9 分
1 1 1
(1 )
又 ⃗DE=(1,1,1),⃗DF= ,2,0 ,设 n=(x ,y ,z ) 为平面 DEF 的一个法向量,
2 2 2 2
{x + y +z =0
2 2 2
则有 1 ,令 x =4 ,得 y =−1,z =−3 ,所以 n=(4,−1,−3) . 11 分设二
x +2y =0 2 2 2
2 2 2
面角 A−EF−D 的平面角的大小为 θ ,则 cosθ=|cos| , 12 分又
|m⋅n| |16−1+3| 3√13
|cos|= = = .
|m||n| √18×√26 13
3√13
所以,二面角 A−EF−D 的余弦值为 . 13 分
13
16. 解: (1) 在 △ABD 中,由余弦定理得, AD2=AB2+BD2−2AB⋅BDcosB,⋯ 1 分
所以 1=c2+
(a) 2
−2c×
a
×
1
≥
ac
−
ac
=
ac
. 3 分
4 4 2 2 4 4
a
所以 ac≤4 ,当且仅当 “ =c ” 时取 “ = ”, 4 分
4
1 1 π
所以 S = acsinB≤ ×4×sin =√3 ,即 △ABC 面积的最大值为 √3 . 6 分
△ABC 2 2 3
3a
3asinC
4 AD AD=
(2)在 △ACD 中,由正弦定理得, = ,即 π , 8 分
π sinC 4sin
sin 3
3
a
π
4 AD asin
在 △ABD 中,由正弦定理得, = ,即 3 , 10 分
sin∠BAD π AD=
sin 4sin∠BAD
3
π π π
因为 ∠BAD+ + +C=π ,所以 ∠BAD= −C ,
3 3 3π
asin
3asinC 3 (π )
于是 = ,整理得 4sinCsin −C =1 , 11 分
π 4sin∠BAD 3
4sin
3
(π ) (√3 1 )
又 4sinCsin −C =4sinC cosC− sinC =√3sin2C+cos2C−1=1 ,
3 2 2
( π)
即 sin 2C+ =1 , 13 分
6
π π (π 5π) π π
因为 00 ,
n n n n 4 n
因为圆 P (x ,y ) 和圆 P (x ,y ) 外切且圆 P 均与 x 轴相切,
n n n n+1 n+1 n+1 n
所以 |P P |=r +r = y + y , 2 分
n n+1 n n+1 n n+1
所以 √(x −x ) 2+(y −y ) 2= y + y ,
n n+1 n n+1 n n+1
x2x2
整理得 (x −x ) 2=4 y y = n n+1 , 3 分
n n+1 n n+1 4
x x
因为 00 时, f (x)>1 ,即 axex−ex+1>0 ,
令 g(x)=axex−ex+1 ,则 g′(x)=ex(ax+a−1) , 1 分
当 a≤0 时,因为 x>0 ,所以 ax+a−1<0 ,即 g′(x)<0 在 (0,+∞) 上恒成立,所以
g(x)
在 (0,+∞) 上单调递减,所以 g(x)0 ,所以当 x∈ 0, 时,
a a
g′(x)<0,g(x)
(1−a ) (1−a)
单调递减,当 x∈ ,+∞ 时, g′(x)>0,g(x) 单调递增,则 g 0 在 (0,+∞) 上恒成立,所以
a
g(x)
在 (0,+∞) 上单调递增,所以 g(x)>g(0)=0 恒成立,符合题意. 4 分
综上, a 的取值范围为 [1,+∞) . 5 分
(2)因为 a=1 ,由(1)知,当 x>0 时, f (x)>1 .
1
( i ) 证明: 因为 x = >0 ,所以 ex 2=f (x )>1 ,所以 x >0 .
1 2 1 2
因为 x >0 ,所以 ex 3=f (x )>1 ,所以 x >0 . 以此类推, x >0(n∈N*) 6 分因为
2 2 3 n
x ex n x
x −x =lnex n+1−x =ln n −lnex n=ln n , 8 分令 g(x)=x−(ex−1) ,则
n+1 n n ex n−1 ex n−1g′(x)=1−ex ,当 x>0 时, g′(x)<0 ,所以 g(x) 在 (0,+∞) 单减,即 g(x)0) ,
x
所以 00 ,只需证 n −1< (ex n−1) ,即证
2 n ex n−1 2
(ex n) 2 −2x ex n−1>0 . 14 分令 h(x)=(ex) 2 −2xex−1(x>0) ,
n
则 h′(x)=2(ex) 2 −2(ex+xex)=2ex(ex−x−1) ,
由 (i) 知,当 x>0 时, ex−x−1>0 ,所以 h′(x)>0 ,所以 h(x) 在 (0,+∞) 上单调递增,
又 h(0)=0 ,故对任意的 x>0,h(x)>0 . 16 分所以 h(x )>0 ,即
n
1
|ex n+1−1|< |ex n−1|,n∈N* ,原题得证. 17 分
2